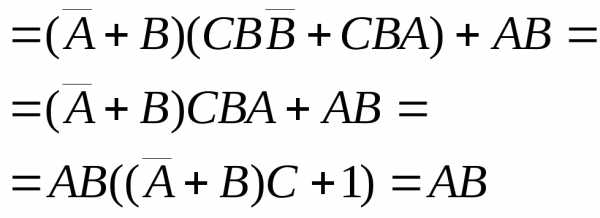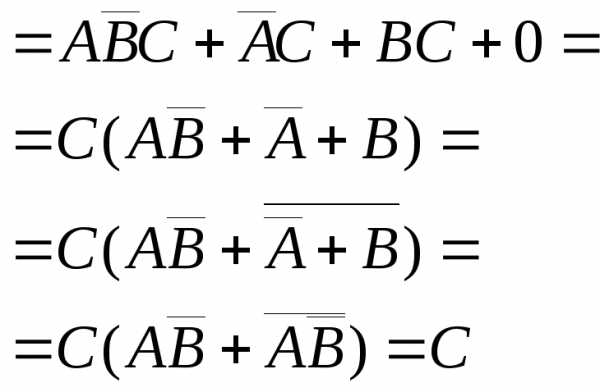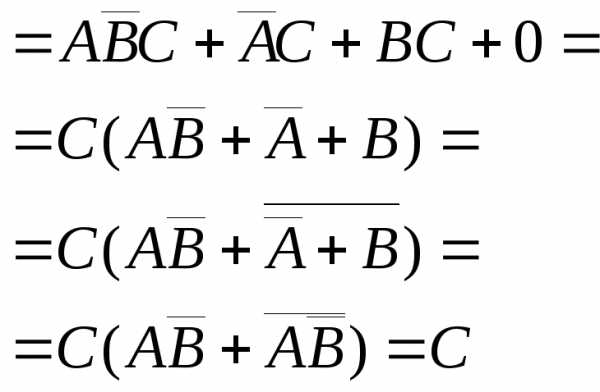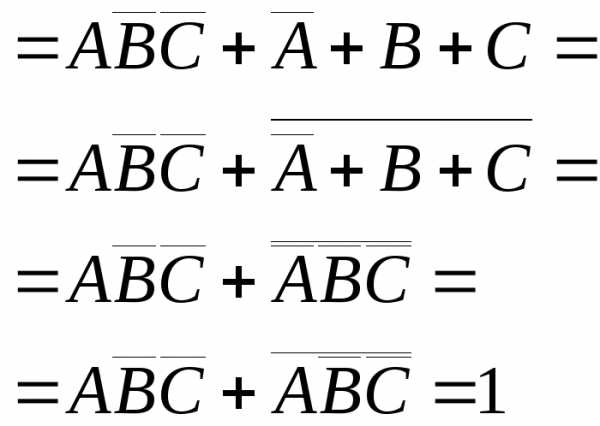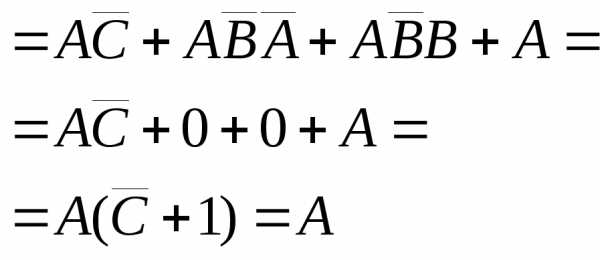Дискретная математика онлайн упростить выражение – Математическая логика · oнлайн с подробным объяснением

Дискретная математика1 | Решение задач по математике и другим предмет

Контрольная работа № 1

1. Даны множества A И B. Изобразить и записать с указанием характеристического свойства результат каждой операции:

А) AÈB ; б) AÇB; в) A \ B; г) B \ A; д) ; е) ; ж) A´ B; з) B´ A.

A = {X| xÎR, X > 2}, B = {X| xÎR,-5 £ X £ 8}

Решение:

Изобразим на числовой прямой множества А и В:

Тогда

А) AÈB= ;

Б) AÇB= ;

В) A \ B= ;

Г) B \ A= ;

Д) = ;

Е) = ;

Ж) A´ B= ;

З) B´

A= .

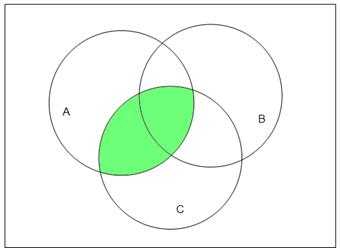
2. На диаграммах Эйлера-Венна изобразить результат операций, предварительно указав порядок действий в формуле.

Решение:

Порядок действий:

1.

2.

3.

4.

Изобразим на диаграмме Эйлера–Венна:

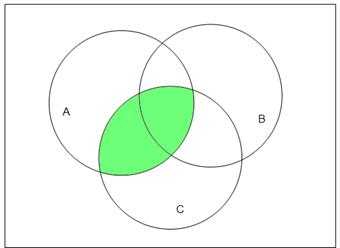
1.

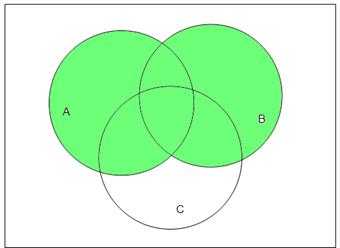
2.

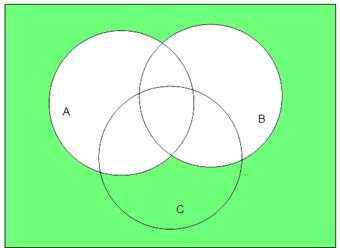
3.

4.

3. Упростить выражения, используя законы алгебры множеств

Решение:

.

4. На множестве M Бинарное отношение

RÍ M´M Задано характеристическим свойством. Представить отношение R Другими возможными способами. Выяснить какими свойствами оно обладает.

Решение:

Составим таблицу произведений элементов множества М, выделив те пары, которые удовлетворяют характеристическому свойству:

	-3	-2	0	1	2	3
-3	9	6	0	-3	-6	-9
-2	6	4	0	-2	-4	-6
0	0	0	0	0	0	0
1	-3	-2	0	1	2	3
2	-6	-4	0	2	4	6
3	-9	-6	0	3	6	9

Тогда выпишем в явном виде отношение:

Изобразим графически отношение:

Свойства отношения:

1)  Рефлексивность: так как , то данное отношение рефлексивно.

2)  Так как , то отношение будет симметричным.

3)  Тогда отношение не будет антирефлексивным и антисимметричным.

4)  Транзитивность выполняется: при положительном значении хотя бы одной переменной и две другие также будут положительны; при отрицательном значении одной переменной остальные также будут отрицательны. Тогда произведение любой их пары будет положительно.

5. Докажите тождество:

Доказательство:

6. Определите свойства отношений:

.

Решение:

1)  Рефлексивность: так как , то данное отношение рефлексивно.

2)  Так как из неравенства не следует неравенство , то отношение не будет симметричным.

3)  Так как неравенства и могут одновременно выполняться лишь при условии , то отношение антисимметричное.

4)  Транзитивность выполняется: .

7. Для отношения, заданного матрицей, определить является ли оно отношением эквивалентности

R	A	B	C	D	E	F
A	1	0	0	0	1	0
B	0	1	1	0	0	0
C	0	1	1	0	0	0
D	0	0	0	1	0	1
E	1	0	0	0	1	0
F	0	0	0	1	0	1

Решение:

Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Так как в матрице отношения по главной диагонали стоят все 1, то рефлексивность выполняется.

Так как матрица является симметричной, то отношение также является симметричным.

Исследуем на транзитивность:

Тогда транзитивность выполняется.

Следовательно, данное отношение является отношением эквивалентности.

< Предыдущая		Следующая >

matica.org.ua

шпоры — дискретная математика

1. Представить в СДНФ булеву функцию c вектором (0,0,0,0,0,0,1,1) СДНФ (0,0,0,0,0,0,1,1) № x1 x2 x3 f 0 0 0 0 0 1 0 0 1 0 2 0 1 0 0 3 0 1 1 0 4 1 0 0 0 5 1 0 1 0 6 1 1 0 1 7 1 1 1 1 выбираем строки где f = 1	2. Представить в СДНФ булеву функцию с вектором (0,0,0,1,0,0,1,0) СДНФ (0,0,0,1,0,0,1,0) № x1 x2 x3 f 0 0 0 0 0 1 0 0 1 0 2 0 1 0 0 3 0 1 1 1 4 1 0 0 0 5 1 0 1 0 6 1 1 0 1 7 1 1 1 0 выбираем строки где f = 1
3. Представить в СДНФ булеву функцию с вектором (0,1,0,0,0,1,0,0) СДНФ (0,1,0,0,0,1,0,0) № x1 x2 x3 f 0 0 0 0 0 1 0 0 1 1 2 0 1 0 0 3 0 1 1 0 4 1 0 0 0 5 1 0 1 1 6 1 1 0 0 7 1 1 1 0 выбираем строки где f = 1	4. Представить в СДНФ булеву функцию с вектором (1,0,0,0,0,0,1,0) СДНФ (1,0,0,0,0,0,1,0) № x1 x2 x3 f 0 0 0 0 1 1 0 0 1 0 2 0 1 0 0 3 0 1 1 0 4 1 0 0 0 5 1 0 1 0 6 1 1 0 1 7 1 1 1 0 выбираем строки где f = 1
5. Представить в СДНФ булеву функцию с вектором (0,0,0,0,0,1,0,1) СДНФ (0,0,0,0,0,1,0,1) № x1 x2 x3 f 0 0 0 0 0 1 0 0 1 0 2 0 1 0 0 3 0 1 1 0 4 1 0 0 0 5 1 0 1 1 6 1 1 0 0 7 1 1 1 1 выбираем строки где f = 1	6. Представить в СКНФ булеву функцию с вектором (1,1,0,1,1,1,1,1) СКНФ (1,1,0,1,1,1,1,1) № x1 x2 x3 f 0 0 0 0 1 1 0 0 1 1 2 0 1 0 0 3 0 1 1 1 4 1 0 0 1 5 1 0 1 1 6 1 1 0 1 7 1 1 1 1 выбираем строки где f = 0
7. Представить в СКНФ булеву функцию с вектором (1,1,1,1,0,1,1,1) СКНФ (1,1,1,1,0,1,1,1) № x1 x2 x3 f 0 0 0 0 1 1 0 0 1 1 2 0 1 0 1 3 0 1 1 1 4 1 0 0 0 5 1 0 1 1 6 1 1 0 1 7 1 1 1 1 выбираем строки где f = 0	8. Представить в СКНФ булеву функцию с вектором (1,1,1,1,1,0,1,1) СКНФ (1,1,1,1,0,1,1,1) № x1 x2 x3 f 0 0 0 0 1 1 0 0 1 1 2 0 1 0 1 3 0 1 1 1 4 1 0 0 1 5 1 0 1 0 6 1 1 0 1 7 1 1 1 1 выбираем строки где f = 0
9. Представить в СКНФ булеву функцию с вектором (1,0,1,1,1,1,1,1) СКНФ (1,0,1,1,1,1,1,1) № x1 x2 x3 f 0 0 0 0 1 1 0 0 1 0 2 0 1 0 1 3 0 1 1 1 4 1 0 0 1 5 1 0 1 1 6 1 1 0 1 7 1 1 1 1 выбираем строки где f = 0	10. Представить в СКНФ булеву функцию с вектором (1,1,1,0,1,1,1,1) СКНФ (1,1,1,0,1,1,1,1) № x1 x2 x3 f 0 0 0 0 1 1 0 0 1 1 2 0 1 0 1 3 0 1 1 0 4 1 0 0 1 5 1 0 1 1 6 1 1 0 1 7 1 1 1 1 выбираем строки где f = 0
11. Представить в виде полинома Жегалкина булеву функцию, заданную вектором (0,1,1,0) Общий вид полинома: f(0,0) = a0 =0 f(0,1) = a­2a0 = a2 0 = 1 => a2 = 1 f(1,0) = a­1a0 = a1 0 = 1 => a1 = 1 f(1,1) = a­12a1a2a0 = a­12110 = a­120 = 0 => a12 = 0 f = X1X2	12. Представить в виде полинома Жегалкина булеву функцию, заданную вектором (0,1,0,1) Общий вид полинома: f(0,0) = a0 = 0 f(0,1) = a­2a0 = a2 0 = 1 => a2 = 1 f(1,0) = a­1a0 = a1 0 = 0 => a1 = 0 f(1,1) = a­12a1a2a0 = a­12100 = a­121=1 => a12 = 0 f = X2
13. Представить в виде полинома Жегалкина булеву функцию, заданную вектором (1,0,1,0) Общий вид полинома: f(0,0) = a0 = 1 f(0,1) = a­2a0 = a2 1 = 0 => a2 = 1 f(1,0) = a­1a0 = a1 1 = 1 => a1 = 0 f(1,1) = a­12a1a2a0 = a­12101 = a­120 = 0 => a12 = 0 f = X21	14. Представить в виде полинома Жегалкина булеву функцию, заданную вектором (1,1,1,0) Общий вид полинома: f(0,0) = a0=1 f(0,1) = a­2a0 = a2 1 = 1 => a2 = 0 f(1,0) = a­1a0 = a1 1 = 1 => a1 = 0 f(1,1) = a­12a1a2a0 = a­12001 = a­121 = 0 => a12 = 1 f = X1X21
15. Представить в виде полинома Жегалкина булеву функцию, заданную вектором (1,0,0,1) Общий вид полинома: f(0,0) = a0 = 1 f(0,1) = a­2a0 = a2 1 = 0 => a2 = 1 f(1,0) = a­1a0 = a1 1 = 0 => a1 = 1 f(1,1) = a­12a1a2a0 = a­12111 = a­121 = 1 => a12 = 0 f = X1X21	16. Упростить выражение
17. Упростить выражение
18. Упростить выражение	19. Упростить выражение
20. Упростить выражение	21. Упростить выражение
22. Упростить выражение	23. Упростить выражение
24. Упростить выражение	25. Упростить выражение
26. Упростить выражение	27. Упростить выражение
28. Упростить выражение	29. Упростить выражение
30. Упростить выражение	31. Какие из следующих отношений являются отношениями эквивалентности «<» на множестве действительных чисел «быть подобными геометрическими фигурами» «≠» на множествеи целых чисел Ответ: 2, потому что явл-ся рефлексивным, симметричн. и транзитивн.
32. Какие из следующих отношений являются отношениями частичного порядка 1) “≤” на множестве всех множеств; 2) “быть подобными геометрическими фигурами”; 3) “” на множестве целых чисел; Ответ:1, потому что явл-ся рефлексивным, антисимметричн. и транзитивн.	33. Какие из следующих отношений являются отношениями линейного порядка 1) “” на множестве действительных чисел; 2) “быть подобными геометрическими фигурами”; 3) “” на множестве всех множеств Ответ:1
34. Какие из следующих отношений не являются отношениями эквивалентности 1) “=” на множестве действительных чисел; 2) “быть подобными геометрическими фигурами”; 3) “иметь непустое пересечение” на множестве непустых множеств Ответ:3	35. Какие системы функций являются функционально полными 1) 2) 3) Ответ:1,2 т.к через них можно выразить все функции стандартного базиса 1) 2)

studfiles.net

Алгебра логики

Алгебра логики

В алгебре логики используются переменные, которые могут иметь только два значения: истина и ложь.

Логические операции

В алгебре логики используются следующие логические операции:

1. Операция «И», логическое умножение, называетсяконъюнкция,обозначается следующим образом:

   1. A*B(где А и В — переменные) или АВ (знак умножения можно опускать)

   2. АВ

   3. А ANDВ (в программах)

Данная операция истинна, если все аргументы, участвующие в ней истинны, во всех остальных случаях она – ложна.

2. Операция «ИЛИ», логическое сложение, называетсядизъюнкция, обозначается следующим образом:

   1. А+В (где А и В — переменные)

   2. А В

   3. А ORВ (в программах)

Данная операция ложна, если все аргументы, участвующие в ней ложны, во всех остальных случаях она – истинна.

3. Операция «НЕ», логическое отрицание, обозначается следующим образом:

__

1. А

2. ¬А

3. NOTA(в программах).

Если А – истинно, то ¬А – ложно, а если А – ложно, то ¬А – истинно.

4. Операция «импликация», обозначается следующим образом:

   1. АВ

   2. А IMPВ (в программах).

Данная операция ложна, если первый аргумент (А) – истинный, а второй аргумент (В) – ложный. В остальных случаях данная операция – истинна.

5. Операция «эквиваленция», обозначается следующим образом:

   1. А В

   2. АВ

   3. А=В

   4. А↔В

   5. А EQVВ (в программах).

Данная операция истинна, если оба аргумента А и В – одинаковые (оба истинные или оба ложные). В остальных случаях данная операция ложна.

6. Операция «исключающее ИЛИ», обозначается следующим образом:

   1. А В

   2. А XOR В (в программах).

Данная операция ложна, если все аргументы, участвующие в ней ложны, либо все аргументы, участвующие в ней истинны, во всех остальных случаях она – истинна.

Приоритеты логических операций

Если в одном логическом выражении имеется несколько логических операций, то они выполняются в следующей последовательности:

1. Операции в скобках

2. Операция «НЕ»

3. Операция «И»

4. Операция «ИЛИ», операция «исключающее ИЛИ» — имеют одинаковый приоритет

5. Операция «импликация»

6. Операция «эквиваленция»

Таблицы истинности

Таблицы истинности применяются для вычисления логических выражений при всевозможных сочетаниях значений входящих в выражение аргументов. Значениями логических выражений и входящих в них переменных могут быть истина (1) или ложь (0). Количество всевозможных сочетаний значений входящих в выражение аргументов (переменных) определяется по формуле 2^к, где к – количество переменных, входящих в выражение. Сами сочетания можно определить следующим образом: общее количество сочетаний делится пополам, в первой половине для всех переменных устанавливаются значения 0 (ложь), а во второй половине для всех переменных устанавливаются значения 1 (истина). Затем каждая из этих половинок опять делится пополам и опять, в первой половине для всех переменных устанавливаются значения 0, а во второй половине для всех переменных устанавливаются значения 1. Затем опять каждая из полученных половинок делится пополам и опять, в первой половине для всех переменных устанавливаются значения 0, а во второй половине для всех переменных устанавливаются значения 1, т.д. Это производится до тех пор, пока в половинках не окажется по одной переменной, для первой из них устанавливаем значение 0, а для второй – 1.

Если при всех сочетаниях значений переменных, входящих в логическое выражение, значение этого выражения всегда 1, то такое выражение называется тождественно-истинным.

Если при всех сочетаниях значений переменных, входящих в логическое выражение значение этого выражения всегда 0, то такое выражение называется тождественно-ложным.

Если при всех сочетаниях значений переменных, входящих в логическое выражение значение этого выражения может быть равно 0 или 1, то такое выражение называется нейтральным или выполнимым.

Пример 1

Дано логическое выражение: F=((C+B) B)*(A*B)B. Построить для него таблицу истинности и определить тип логического выражения. Выражение может быть тождественно-истинным, тождественно-ложным или нейтральным.

Решение

В данном выражении 3 переменных (A,B,C), поэтому количество сочетаний значений этих переменных равно 2³=8.

Проставляем приоритеты (последовательность выполнения) логических операций:

1. C+B

2. (C+B)B

3. A*B

4. ((C+B)B))*(A*B)

5. F = ((C+B)B)*(A*B)B

Заполняем таблицу истинности в соответствии с указанными приоритетами и определениями логических операций:

A	B	C	C+B	(C+B)B	A*B	((C+B)B))*(A*B)	F
0	0	0	0	1	0	0	1
0	0	1	1	0	0	0	1
0	1	0	1	1	0	0	1
0	1	1	1	1	0	0	1
1	0	0	0	1	0	0	1
1	0	1	1	0	0	0	1
1	1	0	1	1	1	1	1
1	1	1	1	1	1	1	1

Так как при всех возможных сочетаниях значений переменных, входящих в данное логическое выражение, значение логического выражения равно 1,то это означает, что данное логическое выражение является тождественно-истинным.

Пример 2

Дано логическое выражение: F=A+B*CAB+C. Построить для него таблицу истинности и определить тип логического выражения.

Решение

В данном выражении 3 переменных (A,B,C), поэтому количество сочетаний значений этих переменных равно 2³=8.

Проставляем приоритеты (последовательность выполнения) логических операций:

1. B*C

2. A+B*C

3. B+C

4. A+B*CA

5. F = A+B*CAB+C

Заполняем таблицу истинности в соответствии с указанными приоритетами и определениями логических операций:

A	B	C	B*C	A+B*C	B+C	A+B*CA	F
0	0	0	0	0	0	1	0
0	0	1	0	0	1	1	1
0	1	0	0	0	1	1	1
0	1	1	1	1	1	0	0
1	0	0	0	1	0	1	0
1	0	1	0	1	1	1	1
1	1	0	0	1	1	1	1
1	1	1	1	1	1	1	1

Так как при всех возможных сочетаниях значений переменных, входящих в данное логическое выражение, значение логического выражения равно 1 или 0, то это означает, что данное логическое выражение является нейтральным.

Упрощение логических выражений

Для упрощения логических выражений нам понадобятся следующие соотношения алгебры логики:



1. X=X

2. XY=YX– переместительный закон умножения

3. X+Y=Y+X- переместительный закон сложения

4. X(YZ)=(XY)Z– сочетательный закон умножения

5. X+(Y+Z)=(X+Y)+Z- сочетательный закон сложения

6. X(Y+Z)=XY+XZ– первый распределительный закон

7. X+(YZ)=(X+Y)(X+Z) — второй распределительный закон

  

8. (X+Y)=XY– отрицание суммы равно произведению отрицаний слагаемых (для любого числа слагаемых)

  

9. (XY)=X+Y– отрицание произведения равно сумме отрицаний сомножителей (для любого числа сомножителей)

10. X+X=X



11. X+X=И – здесь И означает «истина»

12. XX=X



13. X*X=Л – здесь Л означает «ложь»

14. X*И=X

15. X+Л=X



16. XY=X+Y

 

17. XY=XY+XY

18. X+XY=X



19. X+XY=X+Y

 

20. X+XY=X+Y

 

21. XY=AB+AB

Все данные соотношения можно доказать с помощью таблицы истинности, используя определения логических операций.

Упрощение логического выражения заключается в приведении его к виду, содержащему минимальное количество логических операций. В упрощенном выражении должны, как правило, содержатся только простые логические операции: И, ИЛИ, НЕ. Если в результате упрощения логическое выражение становится равным «Л» (ложь), то такое логическое выражение является тождественно-ложным. Если в результате упрощения логическое выражение становится равным «И» (истина), то такое логическое выражение является тождественно-истинным. А если полученное в результате упрощения логическое выражение может быть равным «Л» или «И» в зависимости от значений входящих в него переменных, то такое выражение называется нейтральным.

Пример 1

 

Дано логическое выражение: (AB)(A(B+C). Упростить данное логическое выражение и определить тип полученного в результате упрощения выражения (тождественно-истинное, тождественно-ложное, нейтральное).

Решение

Упрощаем данное выражение по частям в соответствии с приоритетами логических операций:



1. (AB)=A+B (использовалось соотношение 16)

   

2. (A(B+C)=A+(B+C)=A+B+C

 

       

3. (AB)(A(B+C)=(A+B)(A+B+C)=(A+B)(A+B+C)+(A+B)(A+B+C)=

      

=(A+B)(A+B+C) +ABABC= (A+B)(A+B+C) (использовались соотношения 17,8,13,15)

Рассмотрим полученное логическое выражение:

 

(A+B)(A+B+C)

При A=1,B=0 и любом значении С, значением полученного выражения будет 0 (ложь), а при A=0,C=1 и любом значении В, значением полученного выражения будет 1 (истина).

Следовательно, полученное логическое выражение является нейтральным.

Пример 2

Дано логическое выражение:

Необходимо его упростить, упрощенный вид должен содержать не более трех логических операций.

Решение:

Упрощаем данное выражение по частям в соответствии с приоритетами логических операций:

1. (использовалось соотношение 16)

2. (использовалось соотношение 16)

3. (использовались соотношения 16,8,1)

4. (использовалось соотношение 20)

5. (использовалось соотношение 17)

(использовалось соотношение 8)

(использовались соотношения 12,10,1)

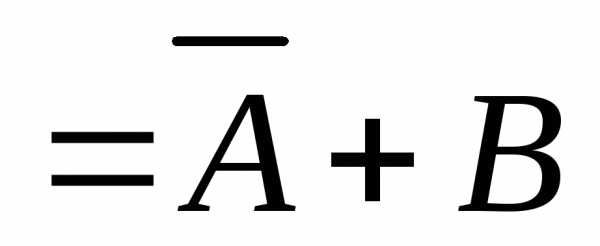(использовались соотношения 13,15,18)

Ответ: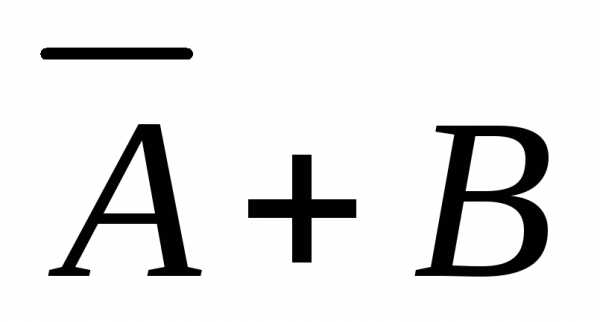

studfiles.net

Ответы@Mail.Ru: Упростить выражение, дискретная математика

Т. к. у нас только пересечения, объединения и дополнения, то можно один в один переписать выражение в терминах булевой алгебры: d(x) = x in D (x принадлежит D) и т. д.. ~ — отрицание = дополнение множества | — логическое сложение = объединение множеств & — логическое умножение = пересечение множеств Получаем для любого x: d(x) & c(x) & ~a(x) | ~d(x) & c(x) & ~a(x) | ~d(x) & ~c(x) & ~a(x) | ~(b(x) | a(x)) d & с & ~a | ~d & с & ~a | ~d & ~c & ~a | ~(b | a) вносим отрицание в последнюю скобку d & с & ~a | ~d & с & ~a | ~d & ~c & ~a | ~b & ~a выносим ~a за скобки ~a & (d & с | ~d & с | ~d & ~с | ~b) перегруппировываем ~a & ((d & с | ~d & с) | (~d & с | ~d & ~с) | ~b) выносим с и ~d за скобки ~a & (с & (d | ~d) | ~d & (с | ~с) | ~b) убираем тавтологии ~a & (с | ~d | ~b) В получившемся выражении просто меняем буквы на заглавные и значки логических операций на действия с множествами.

<img src=»//otvet.imgsmail.ru/download/u_839dacc8d70dca0bef2227cbb9454b68_120x120.jpg» data-hsrc=»https://otvet.imgsmail.ru/download/u_839dacc8d70dca0bef2227cbb9454b68_800.jpg» ><img src=»//otvet.imgsmail.ru/download/22904341_d6c3f2e32d8b88e55fe5eea40263f20e_120x120.jpg» data-hsrc=»//otvet.imgsmail.ru/download/22904341_d6c3f2e32d8b88e55fe5eea40263f20e_800.jpg» >

touch.otvet.mail.ru