Как найти объем зная длину и диаметр, формула расчета объема воды
Объем цилиндра
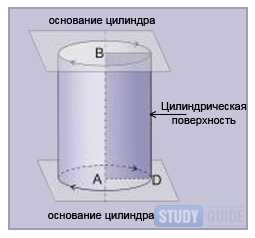
Цилиндр — геометрическое тело, которое образуется при помощи цилиндрической поверхности.
Причем данная цилиндрическая поверхность ограничена двумя плоскостями, параллельными друг к другу. Прямой цилиндр получают, вращая прямоугольник вокруг его стороны.
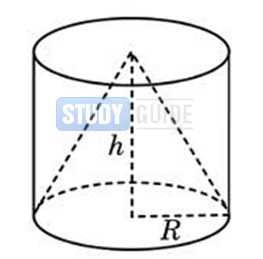
Для того чтобы точно вычислить объем цилиндра, можно выполнить достаточно простые приемы.
Для этого нам понадобятся:
- рулетка или линейка;
- маркер или карандаш;
- любой предмет с прямыми углами (можно использовать обычный лист картона или бумаги).
Например, мы имеем некоторую емкость для жидкости, она имеет цилиндрическую форму. Перед нами стоит задача заполнить данную емкость определенной жидкостью, но мы не знаем какое количество жидкости, заполнит емкость. Для этого нам нужно вычислить ее объем.
Еще в школьные годы на уроках геометрии мы изучали формулу для нахождения объема цилиндра:
V = SH
А это означает, для того чтобы найти объем цилиндра, нужно вычислить произведение площади основания цилиндра S на высоту цилиндра H.
Высоту цилиндра H достаточно легко измерить при помощи линейки или рулетки.
Определяем площадь основания цилиндра. Для этого нам нужно знать площадь круга. С данной формулой мы тоже знакомились на уроках геометрии в школе. Выглядит она так:
S = πR2
Число π в математике обозначает соотношение диаметра и длин окружности, оно равно 3.14159265… Радиус окружности — R.
Для того чтобы вычислить площадь окружности при помощи обычной измерительной линейки, используем школьный прием – впишем в окружность прямоугольный треугольник. В данном случае, гипотенуза вписанного в окружность треугольника будет равна диаметру нашей искомой окружности.
Используем лист картона или бумаги, либо другой предмет с прямыми углами. Накладываем его так на наш цилиндр, чтобы его прямой угол α упирался своей вершиной А в край нашего цилиндра.
Как провести расчет различных параметров труб: базовые формулы и примеры вычислений
Те стороны треугольника, что пересекаются с окружностью, нужно наметить при помощи маркера или карандаша, а также соединить их прямой линией. Выходит, что мы попадаем на вершины треугольника В и С. А это значит: полученный отрезок является диаметром нашей окружности. Так как половина диаметра окружности составляет ее радиус, то отрезок ВС нужно разделить на две части. Получаем центр окружности – точку О.
Выходит, что радиусом основания данного цилиндра являются отрезки ОС и ОВ. Можем смело подставить их полученные значения в формулу:
Вернуться к просмотру справок по дисциплине «Геометрия»
система комментирования CACKLE
Так как на улице уже практически лето, мы хотим вспомнить неделю, посвященную воде и специальным спортивным напиткам — изотоникам, и дополнить ее постом о питьевом режиме во время тренировок.
Начнем, пожалуй, с расчета необходимого количества воды. В среднем, взрослый человек должен выпивать в день 2 2,5 литра воды, в дни активных занятий спортом — 3 3,5 литра. Однако ваши личные потребности могут не совпадать с этим среднестатистическим, так как у каждого организма свой питьевой режим.
Рассчитать необходимое количество можно по двум простым формулам (для мужчин и для женщин):
- Мужчины: Вес тела х 35
- Женщины: Вес тела х 31
К примеру, я вешу 48 кг, значит, моя дневная норма воды составляет около 1,5 литров. Конечно же, в тренировочные дни эта норма будет выше. Мало воды это плохо, но и чрезмерное употребление воды так же может привести к неприятным последствиям, вплоть до летальных (известны случаи смерти во время марафонов от гипонатриемии). Поэтому, в первую очередь, вы должны прислушиваться к своему организму и смотреть на состояние своего тела.
Во время тренировок из нашего тела выводиться большее количество влаги (через пот и интенсивное дыхание), поэтому для восстановления водного баланса нужно пить больше воды.
Международная марафонская медицинская ассоциация директоров (IMMDA) выделила основные принципы употребления воды спортсменами во время марафонов — марафонцы должны употреблять 380-780 мл каждый час. Чем медленнее будет ваш темп, тем меньше воды нужно будет пить.
Согласно их же исследованиям, если ваша тренировка длится более 30 минут, простую воду лучше заменить изотониками.
Водные запасы можно пополнить перед тренировкой — 500 мл за несколько часов до пробежки или соревнования, и 150 мл прямо перед стартом.
Расчет тренировочного водного запаса
Для того чтобы понять, сколько воды нужно пить во время пробежки лично вам, нужно выполнить следующий алгоритм:
- Взвеситься без одежды прямо перед тестом.
- Бежать или идти в течение 1 часа со своим стандартным беговым темпом.
- Не пить во время тренировки.
- После пробежки снова проверить свой вес (без одежды). Разница в весе (в унциях) — это ваша почасовая интенсивность потоотделения. То есть, вы должны пить не менее и не более этого количества жидкости каждый час.
Так как у нас метрическая система, вес можно перевести в граммы и потом, на основании этого, посчитать необходимое количество воды в мл. К примеру, разница в весе после тестовой тренировки составила 350 г, это означает, что ваша почасовая норма употребления жидкости составляет 350 мл.
Объем цилиндра, формула.
Так как рекомендуется пить каждые 15-20 минут, делим это количество на 3 или 4 и получаем объем воды, который мы должны вливать в себя через эти промежутки (116 мл или 88 мл соответственно).
Затем следует провести еще один часовой забег, но при этом уже пить необходимое количество воды, которое вы получили во время расчетов. Снова взвешиваетесь без одежды до забега, затем после, и сравниваете результаты. Если разница незначительная, значит это и будет ваше идеальное количество воды для тренировки именно с таким темпом. Если же разница все равно будет ощутимой, то нужно немного откорректировать количество жидкости в большую сторону.
Также рекомендуется учитывать погодные условия (температуру, влажность воздуха), так как в жаркую погоду потеря жидкости будет больше, чем при средней температуре. То же самое касается и ветреных теплых дней, так как влага в этом случае будет испаряться с кожи значительно быстрее из-за ветра, а это означает, что объем воды, необходимый для поддержания баланса, снова возрастет.
Продуктивных вам тренировок, и не забывайте о воде!
Объем цилиндра
Цилиндр — геометрическое тело, которое образуется при помощи цилиндрической поверхности.
Причем данная цилиндрическая поверхность ограничена двумя плоскостями, параллельными друг к другу.
Расчет объема труб
Прямой цилиндр получают, вращая прямоугольник вокруг его стороны.

Для того чтобы точно вычислить объем цилиндра, можно выполнить достаточно простые приемы.
Для этого нам понадобятся:
- рулетка или линейка;
- маркер или карандаш;
- любой предмет с прямыми углами (можно использовать обычный лист картона или бумаги).
Например, мы имеем некоторую емкость для жидкости, она имеет цилиндрическую форму. Перед нами стоит задача заполнить данную емкость определенной жидкостью, но мы не знаем какое количество жидкости, заполнит емкость. Для этого нам нужно вычислить ее объем.
Еще в школьные годы на уроках геометрии мы изучали формулу для нахождения объема цилиндра:
V = SH
А это означает, для того чтобы найти объем цилиндра, нужно вычислить произведение площади основания цилиндра S на высоту цилиндра H.
Высоту цилиндра H достаточно легко измерить при помощи линейки или рулетки.
Определяем площадь основания цилиндра. Для этого нам нужно знать площадь круга. С данной формулой мы тоже знакомились на уроках геометрии в школе. Выглядит она так:

S = πR2
Число π в математике обозначает соотношение диаметра и длин окружности, оно равно 3.14159265… Радиус окружности — R.
Для того чтобы вычислить площадь окружности при помощи обычной измерительной линейки, используем школьный прием – впишем в окружность прямоугольный треугольник. В данном случае, гипотенуза вписанного в окружность треугольника будет равна диаметру нашей искомой окружности.
Используем лист картона или бумаги, либо другой предмет с прямыми углами. Накладываем его так на наш цилиндр, чтобы его прямой угол α упирался своей вершиной А в край нашего цилиндра.
Те стороны треугольника, что пересекаются с окружностью, нужно наметить при помощи маркера или карандаша, а также соединить их прямой линией. Выходит, что мы попадаем на вершины треугольника В и С. А это значит: полученный отрезок является диаметром нашей окружности. Так как половина диаметра окружности составляет ее радиус, то отрезок ВС нужно разделить на две части. Получаем центр окружности – точку О.
Выходит, что радиусом основания данного цилиндра являются отрезки ОС и ОВ. Можем смело подставить их полученные значения в формулу: V = πR2H.
Вернуться к просмотру справок по дисциплине «Геометрия»
система комментирования CACKLE
pasmr21.ru
Масса полой детали | Математика для ювелиров
1.06.2013 // Владимир ТруновНикогда не устану повторять, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Однако, в случае полой или пустотелой детали мы будем иметь дело не с объемом ее тела, а с объемом ее стенок. Объем стенок полой детали проще всего представить как разность объемов двух сплошных тел: с внешними размерами и с внутренними (из полного объема тела вычитается объем внутренней пустоты).
Формулы для объема сплошных тел можно найти в статье «Масса сплошной детали».
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно
1. Масса трубки (полого цилиндра)
Объем стенок трубки: , где — внешний диаметр трубки, — длина трубки, — толщина стенки.
После упрощения получаем формулу для объема:
Тогда масса трубки:
2. Масса полого (пустотелого) шара
Объем стенок шара: , где — внешний диаметр шара, — толщина стенки.
Тогда масса:
3. Масса полого сегмента шара
Объем стенок сегмента шара: , где — внешний диаметр основания сегмента, — высота сегмента, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:
4. Масса полого усеченного конуса
Объем стенок круглого усеченного конуса: , где — внешний диаметр большего основания, — внешний диаметр меньшего основания, — высота конуса, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:
5. Масса полой усеченной пирамиды
Для простоты рассмотрим усеченную пирамиду с квадратным основанием. Объем ее стенок: , где — внешний размер большего основания, — внешний размер меньшего основания, — высота пирамиды, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:
* в данном случае — это не вполне толщина стенки. Строго говоря, мы имеем тут дело с двумя величинами: та , что стоит в формулах за скобкой, это точно толщина стенки, а та , которую мы отнимаем от внешнего размера тела, чтобы получить его внутренний размер, — это толщина стенки, деленная на косинус угла наклона образующей. Но в большинстве случаев толщина стенки не превышает нескольких процентов от размеров тела, и ошибкой можно пренебречь. Однако, для толстостенных деталей это обстоятельство нужно учитывать.
tvlad.ru
Объем жидкости в цилиндрической таре
Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку.
И это не праздности ради, а дела для.
Цитирую запрос пользователя объем сегмента цилиндра (2):
Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?
Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем 🙂 Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения.
Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.
Знаков после запятой: 2
Объем жидкости
Процентов от общего объема
Общий объем цилиндра
Сохранить share extension
Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.
Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.
А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.
Площадь сектора находится как
, где альфа — это угол дуги в радианах.
Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,
соответственно
и ответ нам Javascript даст как раз в радианах, то что нам нужно.
Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его.
А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен
Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона — Расчет площади треугольника по формуле Герона.
где
Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.
planetcalc.ru
Масса сплошной детали | Математика для ювелиров
9.05.2013 // Владимир ТруновЭто странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:
4. Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:
5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
tvlad.ru
