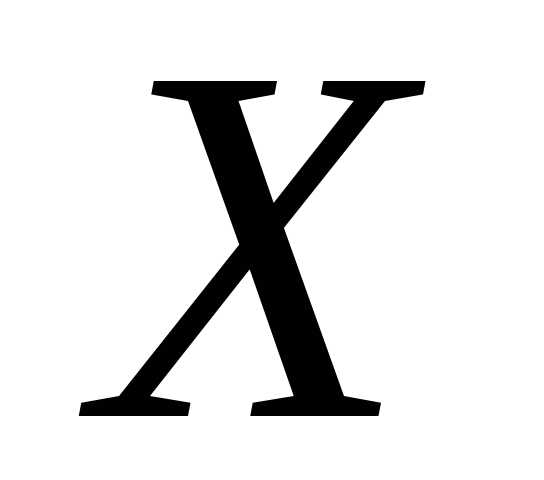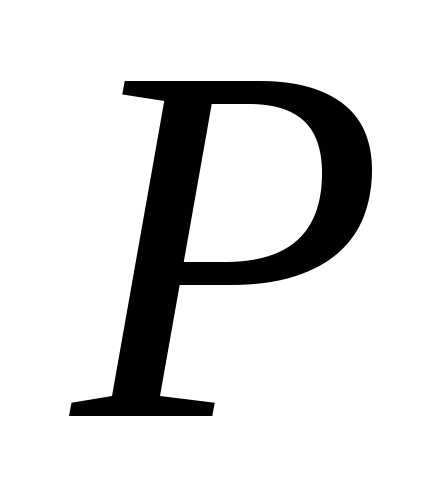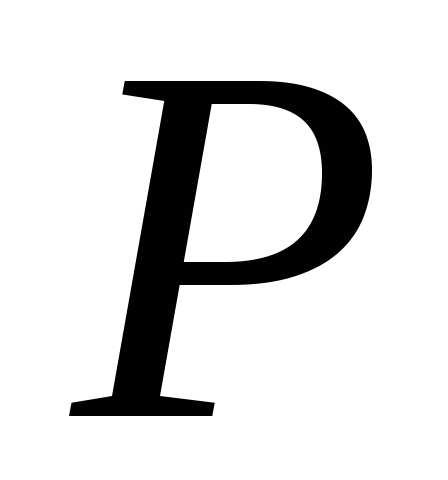2. Дисперсия и ее свойства
Важное значение для характеристики случайных величин имеет дисперсия.
Определение. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
.
Слово «дисперсия» означает «рассеяние», т.е. дисперсия характеризует рассеяние (разбросанность) значений случайной величины около ее математического ожидания.
Из определения следует, что дисперсия – это постоянная величина, т.е. числовая характеристика случайной величины, которая имеет размерность квадрата случайной величины.
С вероятной точки зрения, дисперсия является мерой рассеяния значений случайной величины около ее математического ожидания.
Действительно, рассмотрим дискретную случайную величину, которая имеет конечное множество значений. Тогда, согласно определению, дисперсия вычисляется по формуле
. (2)
Если
дисперсия 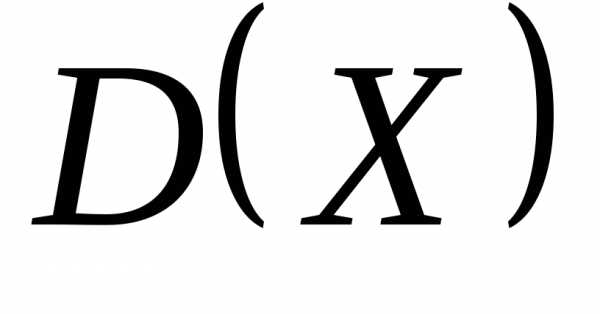 мала, то из формулы (2) следует, что малы
слагаемые.
Поэтому, если не рассматривать значения,
которым соответствует малая вероятность
(такие значения практически невозможны),
то все остальные значения
мала, то из формулы (2) следует, что малы
слагаемые.
Поэтому, если не рассматривать значения,
которым соответствует малая вероятность
(такие значения практически невозможны),
то все остальные значения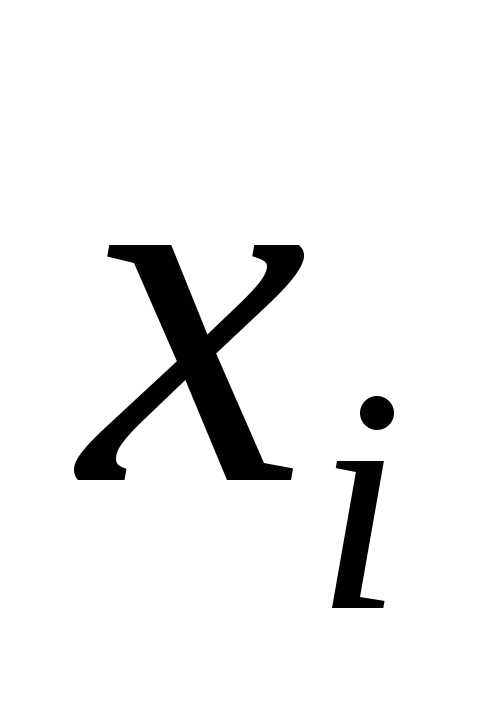 мало отклоняются от математического
ожидания
мало отклоняются от математического
ожидания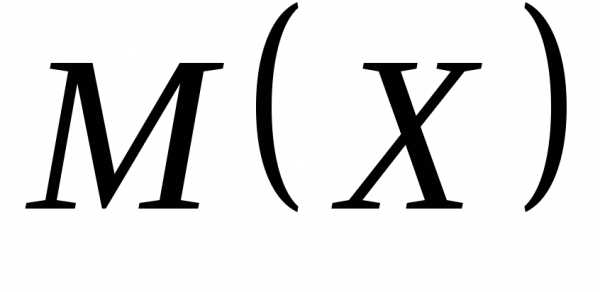 .
Следовательно,при
малой дисперсии возможные значения
случайной величины концентрируются
около ее математического ожидания (за
исключением, может быть, сравнительно
малого числа отдельных значений). Если
дисперсия
.
Следовательно,при
малой дисперсии возможные значения
случайной величины концентрируются
около ее математического ожидания (за
исключением, может быть, сравнительно
малого числа отдельных значений). Если
дисперсия 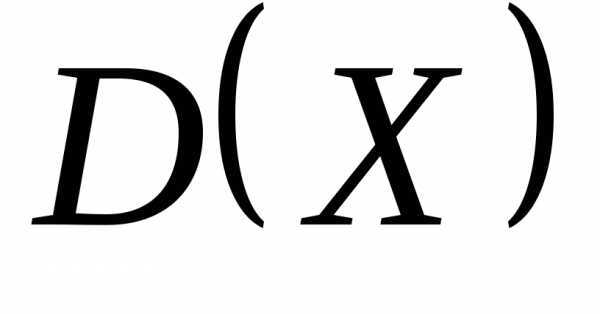 велика, то это означает большой разброс
значений случайной величины, концентрация
значений случайной величины около
какого-нибудь центра исключается.
велика, то это означает большой разброс
значений случайной величины, концентрация
значений случайной величины около
какого-нибудь центра исключается.
Пример. Пусть
случайные величины 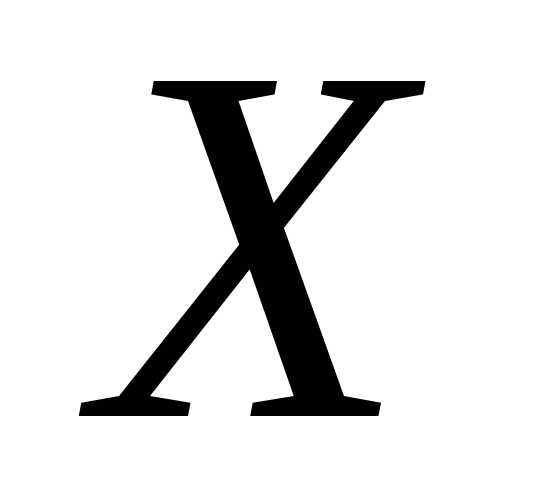 и
и имеют следующее законы распределения
имеют следующее законы распределения
Таблица 9. Таблица 10.
| 0 | 0,1 | 0,4 |
| -10 | 0,5 | 10 | ||
| 0,3 | 0,15 | 0,3 | 0,25 |
| 0,4 | 0,2 | 0,4 |
Найти математические ожидания и дисперсии этих случайных величин.
Решение. Воспользовавшись формулой для вычисления математических ожиданий, находим
.
.
С помощью формулы (2) вычислим дисперсии заданных случайных величин
.
Из
полученных результатов делаем вывод:
математические ожидания случайных
величин 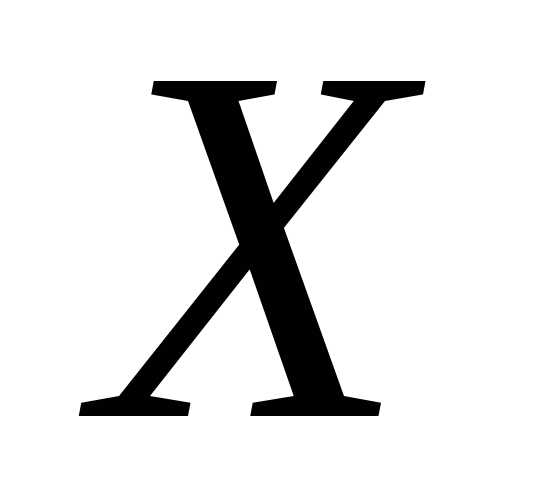 и
и одинаковы, однако дисперсии различны.
Дисперсия случайной величины
одинаковы, однако дисперсии различны.
Дисперсия случайной величины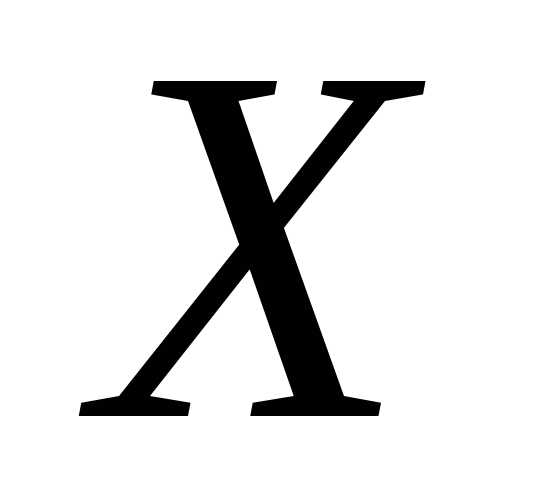 мала и мы видим, что ее значение
сконцентрированы около ее математического
ожидания.
Напротив, значения случайной величины
мала и мы видим, что ее значение
сконцентрированы около ее математического
ожидания.
Напротив, значения случайной величины
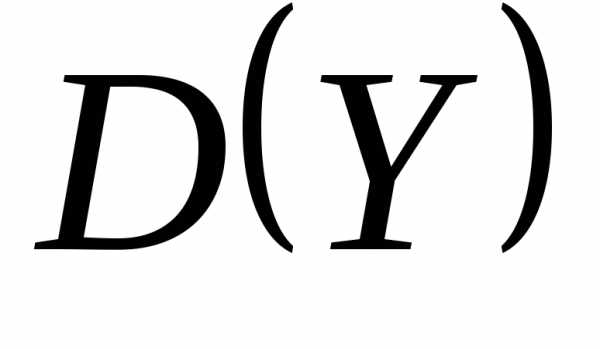 имеет большое значение. ●
имеет большое значение. ●Свойства дисперсии
Свойство 1. Дисперсия постоянной величины равна нулю
.
Доказательство.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
.
Доказательство.
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий
.
Доказательство. Воспользуемся определением дисперсии и свойствами 3, 2 математического ожидания, имеем
(3) Определение. Математическое
ожидание произведения отклонений
случайных величин 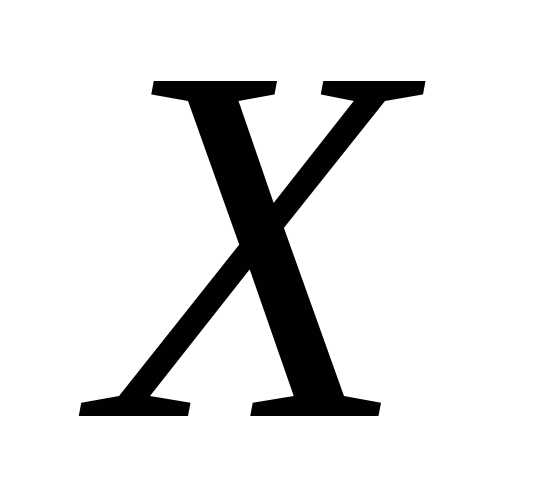 и
и  от их математических ожиданий называется корреляционным
моментом этих
величин
от их математических ожиданий называется корреляционным
моментом этих
величин
.
Если
случайные величины, величины 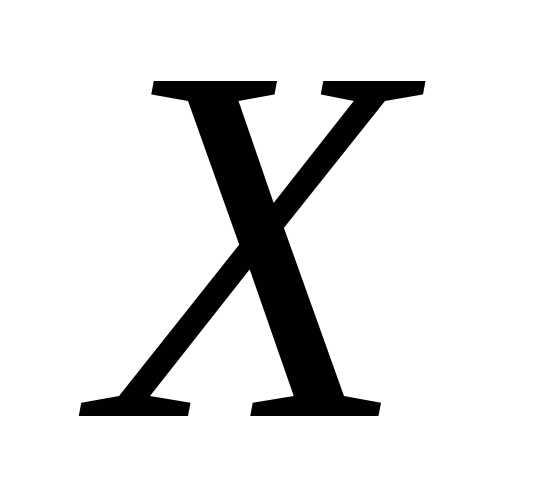 и
и независимы, то, воспользовавшись
свойствами 6 и 7 математических ожиданий,
находим
независимы, то, воспользовавшись
свойствами 6 и 7 математических ожиданий,
находим
.
Поэтому из формулы 3 имеем
,
откуда окончательно следует
. ●
С помощью метода математической индукции это свойство может быть распространено на случай любого конечного числа независимых случайных величин.
Свойство 4. Дисперсия суммы независимых случайных величин равна сумме их дисперсий
. ●
Свойство 5. Дисперсия разности двух случайных независимых величин равна сумме дисперсий этих величин
.
Доказательство.
Свойство 6. Дисперсия случайной величины равна математическому ожиданию
квадрата этой величины минус квадрат ее математического ожидания
.
(Эта формула применяется для вычисления дисперсии)
Доказательство.
studfiles.netДисперсией случайной величины называется число
то есть дисперсия есть математическое ожидание квадрата отклонения случайной величины от своего математического ожидания. Число называется среднеквадратичным отклонением, поэтому дисперсия часто обозначается σ2.
Свойства дисперсии следуют из ее определения и свойств математического ожидания.
10. D[С]=0, если С — неслучайная величина.
20. М[С X] = С2 . М[Х], если С — неслучайная величина.
30. D[X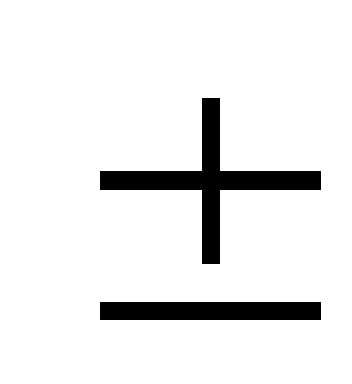
40. D[X] = M[X2] – (M[X])2 = M[X2] – m2
Приведем формулы вычисления дисперсии для дискретных случайных величин:
где m=М|Х] — математическое ожидание, рассчитываемое предварительно по формулам
Функция распределения. Плотность распределения и числовые характеристики непрерывной случайной величины М(Х), Д(Х),.
Функцией распределения случайной величины Х называется функция F(х), равная вероятности того, что Х примет значение меньше, чем число х, то есть F(х)=F(Х<х). Иногда ее называют интегральной функцией распределения.
Рассмотрим свойства функции распределения.
10. 0≤F(x)≤1.
20. F(х) — неубывающая функция, т. е. из х2>х1 следует F(х2)≥ F(х1).
30 . Р(х1≤Х<x2) =F(х2)-F(х1), если х2>x1.
40. Р(х) непрерывна слева, то есть для любой точки x0
60. Если F(х) непрерывна в точке x0 , то Р(Х=x0) = 0.
Если
функцию распределения F(х) непрерывной случайной величины можно
представить в виде 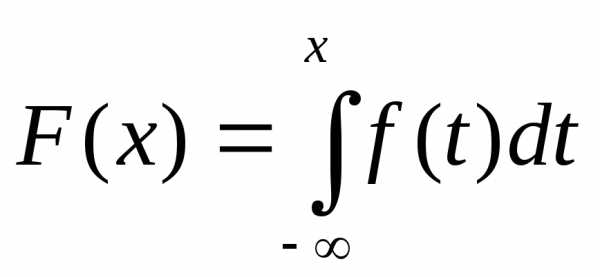 то функция f(x)
называется плотностью распределения
вероятности.
то функция f(x)
называется плотностью распределения
вероятности.
Свойства плотности распределения.
10. f(x)≥0 .
20. .
ПРИМЕР . Равномерное распределение. Говорят, что случайная величинаХравномерно распределена на отрезке[a,b], если она имеет следующую плотность:
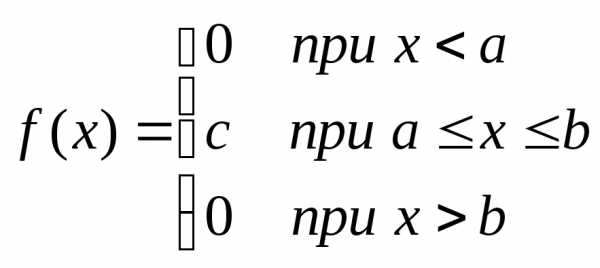
Значение постоянной с определяем из условия нормировки
,
откуда 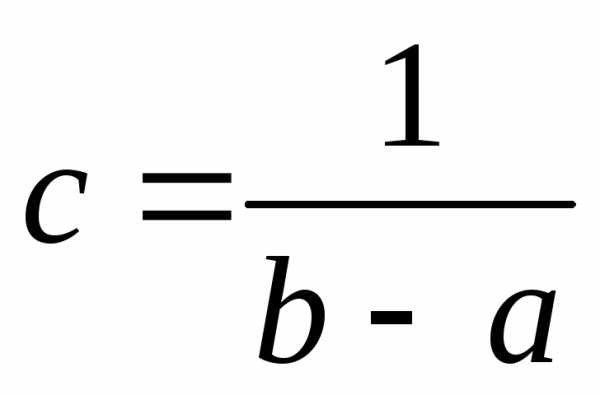 .
.
Г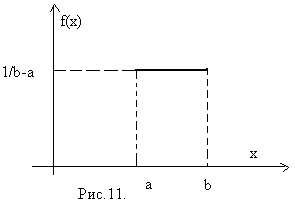 рафик
плотности распределения приведен на
рисунке. Если какой-либо отрезок [α,β]целиком содержится в [а,b],то вероятность попадания в него случайной
величины Х равна
рафик
плотности распределения приведен на
рисунке. Если какой-либо отрезок [α,β]целиком содержится в [а,b],то вероятность попадания в него случайной
величины Х равна
.
Поэтому можно сказать, что вероятность попадания равномерно распределенной случайной величины на какой-либо отрезок пропорциональна длине этого отрезка и не зависит от его положения внутри области возможных значений.
Построим теперь функцию распределения. При х<афункция распределения равна нулю, так какf(х)=0. При а≤x≤bполучаем
.
Для x>b получаем
 .
.
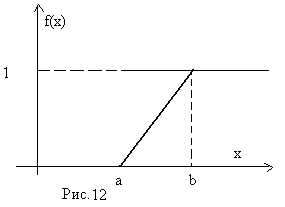
Таким образом,
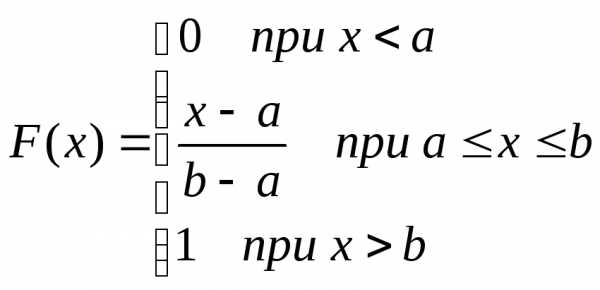
График функции распределения приведен на рис.12.
С равномерно распределенными случайными величинами мы сталкиваемся тогда, когда по условиям опыта случайная величина принимает значения на некотором конечном промежутке, причем все возможные значения из этого промежутка равновозможны. Например, Х — время ожидания на остановке автобуса — равномерно распределенная на отрезке [0,Т]случайная величина, где Т — интервал движения автобусов по расписанию.
ПРИМЕР. Нормальное распределение Гаусса. 1/σ√2π
,
гдеm – любое действительное число, а σ — любое положительное действительное число. Эти числа называются параметрами распределения. Нормальный закон распределения зависит, таким образом, от двух параметров. График плотности распределения имеет вид, приведенный на рис.13.
Если m=0 и σ =1, то нормальный закон распределения называется стандартным и имеет плотность
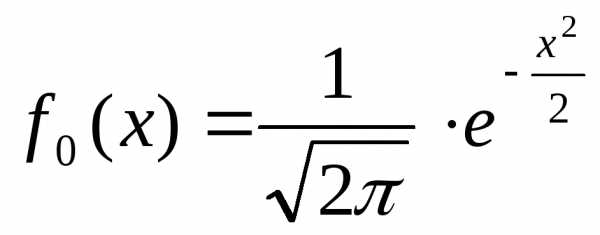
Однако далеко не во всякой задаче нам необходимо знать закон распределения случайной величины полностью. В ряде случаев можно обойтись несколькими числами, отражающими наиболее важные особенности закона распределения интересующей нас случайной величины. Например, числом, характеризующим среднее значение случайной величины, и числом, характеризующим средний размах отклонения случайной величины от своего среднего значения и т.п. Такого рода числа называются числовыми характеристиками случайных величин.
При переходе к непрерывным случайным величинам суммирование заменяется интегрированием. Поясним подробней. Разобьем множество возможных значений непрерывной случайной величины точками х1,х2,…,хn на небольшие отрезки длин ∆xk = xk– xk-1 (k=2,3,…n).
Тогда по свойству 2 плотности распределения и теореме о среднем для определенного интеграла получаем
,
где f(х) — плотность распределения случайной величины, а точка Мы заменяем приближенно нашу непрерывную случайную величину дискретной с законом распределения Р(Х=ξk)=рk. Поэтому
это интегральная сумма. Осталось перейти к пределу при и получить соответствующий интеграл.
Математическим ожиданием или средним значением непрерывной случайной величины, заданной своей плотностью распределения f(х), называется число
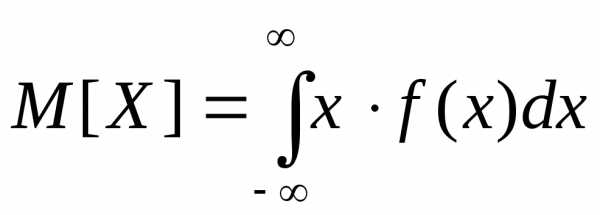
ПРИМЕР 3. Для равномерного на отрезке [а,b] распределения имеем
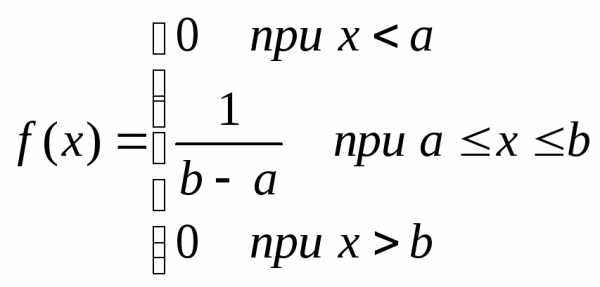
;
;
и т.д.
Приведем формулы вычисления дисперсии для непрерывных случайных величин:
,
где m=М|Х] — математическое ожидание, рассчитываемое предварительно по формулам
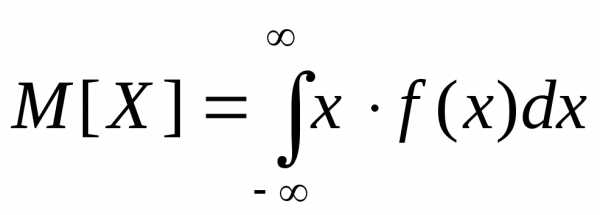
Нормальный закон распределения. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Функция Лапласа.
По определению плотность нормально распределенной случайной величины равна
Возможные значения такой величины Х могут принимать любые действительные значения -∞<Х<∞, а распределение зависит от двух параметров . -∞<m<∞ и -∞<σ<∞.
Таким образом, график функции f(х) будет таким:
При измененииm кривая f(x) скользит вдоль оси абсцисс, не меняя своей формы. При изменении σ кривая меняет свою форму: если σ увеличивается, то кривая становится ниже и шире и наоборот.
Если m=0 и σ=1, то закон нормального распределения называется стандартным. В этом случае
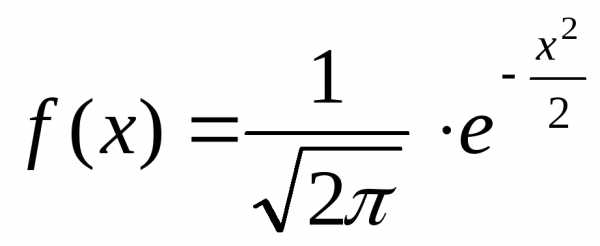
Если случайная величина Х распределена по нормальному закону с параметрами m и σ , то этот факт записывают так:.
Вычислим математическое ожидание случайной величины
Таким образом, параметр m — это математическое ожидание случайной величины X.
Вычислим теперь дисперсию
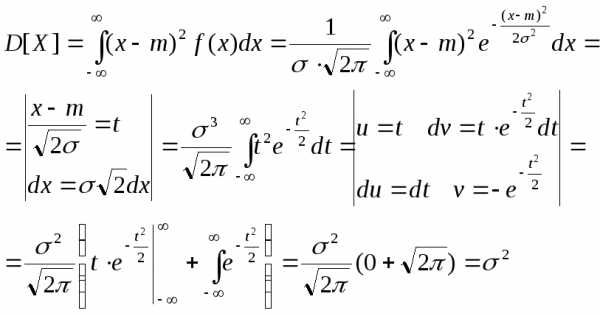
где мы использовали то, что по правилу Лопиталя
Таким образом, параметр σ — это среднеквадратическое отклонение, поскольку σ2— это дисперсия.
Мода и медиана нормального распределения совпадает с математическим ожиданием, т.к. максимум f(x) достигается при x=m и
где
функция распределения
закона 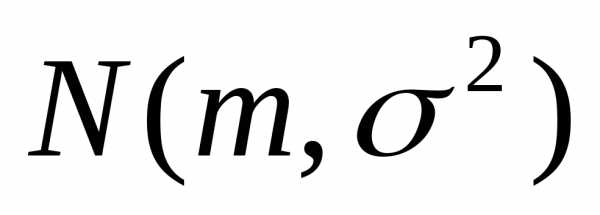 которая имеет график, представленный
на рисунке.
которая имеет график, представленный
на рисунке.
Пусть Вычислим Р(а<Х<b) — вероятность попадания нормально распределенной случайной величины в заданный интервал. По свойству плотности распределения имеем
где
мы использовали формулу Ньютона-Лейбница
для определенных интегралов, а 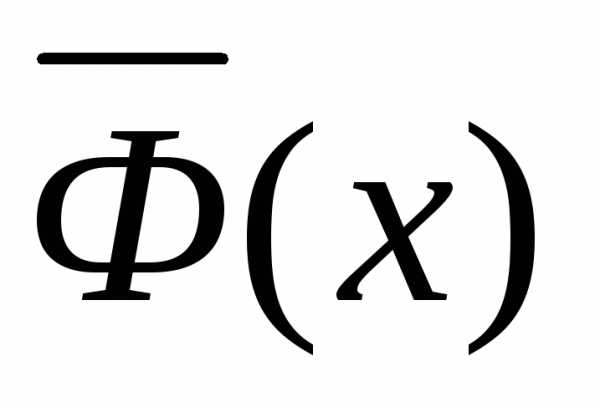 — любая первообразная для подынтегральной
функции
— любая первообразная для подынтегральной
функции
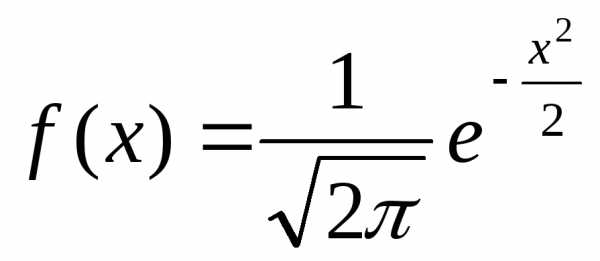
Любая первообразная может быть рассчитана по формуле
где С— произвольная постоянная. Это можно легко проверить дифференцированием .
При С=0 мы получаем функцию Лапласа
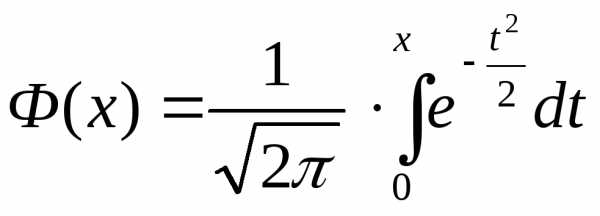
а при С=∞ — функцию распределения стандартного нормального закона
Нетрудно получить связь между Ф*(х) и Ф(х).
Окончательно получаем
В зависимости от имеющихся у нас под руками таблиц мы воспользуемся той или иной формулой. Отметим, что пользоваться таблицами функции Лапласа удобней, так как она нечетна и мы легко — находим ее значения при отрицательном аргументе (обычно, таблицы заданы только для положительных значений аргумента). Пользоваться таблицами функции Ф*(х) в этом случае несколько неудобнее, если она задана только для положительных значений аргумента.
ПРИМЕР 1. Пусть Найдем вероятность того, что Х примет значение из интервала ]0;3[.
По таблице функции Лапласа получаем
По таблице функции распределения стандартного нормального закона получаем, используя ее связь с функцией Лапласа:
Вэтом примере мы вывели полезную формулу
Ф*(-х)=1-Ф*(х),
которую легко пояснить следующим рисунком.
Найдем вероятность попадания нормальной случайной величины в интервал ]m—l,m+l[, симметричный относительно математического ожидания:
При различных l получаем
Как мы видим, хотя теоретически возможные значения Х могут быть любые, но практически все значения попадают в интервал ]m-3σ,m+3σ[. Этот факт обычно называют правилом «трех сигм». При нормальном распределении из 10000 измерений только 27 имеют «законное» право выйти из этого интервала ( событие маловероятное и им обычно пренебрегают). Поэтому можно считать, что все возможные значения нормальной случайной величины находятся в этом интервале.
Распределение монотонной функции случайной величины. Исследование системы двух случайных величин. Функциональная и вероятностная зависимость. Условная плотность.
Часто приходится рассматривать сразу несколько случайных величин одновременно. Например, при стрельбе по мишени точка попадания имеет две координаты, которые являются случайными величинами; при медицинском осмотре основными параметрами состояния здоровья считаются частота пульса, уровень кровяного давления, температура тела и т.д., которые при случайном выборе человека являются случайными величинами.
Пусть Х и Y — дискретные случайные величины. Двумерная случайная величина {X, Y} называется системой дискретного типа и задается следующей таблицей, называемой двумерным рядом распределения
Y X | У1 | У2 | Уз | … | Уj | … |
x1 | Р11 | P12 | P13 | … | P1j | … |
x2 | P21 | P22 | P23 | … | P2j | … |
… | … | … | … | … | … | … |
xi | Pi1 | Pi2 | Pi3 | … | Pij | … |
… | … | … | … | … |
|
|
где Pij=(X=xi;Y=yj).
studfiles.net
Дисперсией случайной величины называется число
то есть дисперсия есть математическое ожидание квадрата отклонения случайной величины от своего математического ожидания. Число называется среднеквадратичным отклонением, поэтому дисперсия часто обозначается σ2.
Свойства дисперсии следуют из ее определения и свойств математического ожидания.
10. D[С]=0, если С — неслучайная величина.
20. М[С X] = С2 . М[Х], если С — неслучайная величина.
30. D[XY] = D[X]+D[Y]. если случайные величины Х и Y независимы
40. D[X] = M[X2] – (M[X])2 = M[X2] – m2
Приведем формулы вычисления дисперсии для дискретных случайных величин:
где m=М|Х] — математическое ожидание, рассчитываемое предварительно по формулам
Функция распределения. Плотность распределения и числовые характеристики непрерывной случайной величины М(Х), Д(Х),.
Функцией распределения случайной величины Х называется функция F(х), равная вероятности того, что Х примет значение меньше, чем число х, то есть F(х)=F(Х<х). Иногда ее называют интегральной функцией распределения.
Рассмотрим свойства функции распределения.
10. 0≤F(x)≤1.
20. F(х) — неубывающая функция, т. е. из х2>х1 следует F(х2)≥ F(х1).
30 . Р(х1≤Х<x2) =F(х2)-F(х1), если х2>x1.
40. Р(х) непрерывна слева, то есть для любой точки x0
50. .
60. Если F(х) непрерывна в точке x0 , то Р(Х=x0) = 0.
Если функцию распределения F(х) непрерывной случайной величины можно представить в виде то функция f(x) называется плотностью распределения вероятности.
Свойства плотности распределения.
10. f(x)≥0 .
20. .
ПРИМЕР . Равномерное распределение. Говорят, что случайная величинаХравномерно распределена на отрезке[a,b], если она имеет следующую плотность:
Значение постоянной с определяем из условия нормировки
,
откуда .
График плотности распределения приведен на рисунке. Если какой-либо отрезок [α,β]целиком содержится в [а,b],то вероятность попадания в него случайной величины Х равна
.
Поэтому можно сказать, что вероятность попадания равномерно распределенной случайной величины на какой-либо отрезок пропорциональна длине этого отрезка и не зависит от его положения внутри области возможных значений.
Построим теперь функцию распределения. При х<афункция распределения равна нулю, так какf(х)=0. При а≤x≤bполучаем
.
Для x>b получаем
.
Таким образом,
График функции распределения приведен на рис.12.
С равномерно распределенными случайными величинами мы сталкиваемся тогда, когда по условиям опыта случайная величина принимает значения на некотором конечном промежутке, причем все возможные значения из этого промежутка равновозможны. Например, Х — время ожидания на остановке автобуса — равномерно распределенная на отрезке [0,Т]случайная величина, где Т — интервал движения автобусов по расписанию.
ПРИМЕР. Нормальное распределение Гаусса. 1/σ√2π
,
гдеm – любое действительное число, а σ — любое положительное действительное число. Эти числа называются параметрами распределения. Нормальный закон распределения зависит, таким образом, от двух параметров. График плотности распределения имеет вид, приведенный на рис.13.
Если m=0 и σ =1, то нормальный закон распределения называется стандартным и имеет плотность
Однако далеко не во всякой задаче нам необходимо знать закон распределения случайной величины полностью. В ряде случаев можно обойтись несколькими числами, отражающими наиболее важные особенности закона распределения интересующей нас случайной величины. Например, числом, характеризующим среднее значение случайной величины, и числом, характеризующим средний размах отклонения случайной величины от своего среднего значения и т.п. Такого рода числа называются числовыми характеристиками случайных величин.
При переходе к непрерывным случайным величинам суммирование заменяется интегрированием. Поясним подробней. Разобьем множество возможных значений непрерывной случайной величины точками х1,х2,…,хn на небольшие отрезки длин ∆xk = xk– xk-1 (k=2,3,…n).
Тогда по свойству 2 плотности распределения и теореме о среднем для определенного интеграла получаем
,
где f(х) — плотность распределения случайной величины, а точка Мы заменяем приближенно нашу непрерывную случайную величину дискретной с законом распределения Р(Х=ξk)=рk. Поэтому
это интегральная сумма. Осталось перейти к пределу при и получить соответствующий интеграл.
Математическим ожиданием или средним значением непрерывной случайной величины, заданной своей плотностью распределения f(х), называется число
ПРИМЕР 3. Для равномерного на отрезке [а,b] распределения имеем
;
;
и т.д.
Приведем формулы вычисления дисперсии для непрерывных случайных величин:
,
где m=М|Х] — математическое ожидание, рассчитываемое предварительно по формулам
Нормальный закон распределения. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Функция Лапласа.
По определению плотность нормально распределенной случайной величины равна
Возможные значения такой величины Х могут принимать любые действительные значения -∞<Х<∞, а распределение зависит от двух параметров . -∞<m<∞ и -∞<σ<∞.
Таким образом, график функции f(х) будет таким:
При измененииm кривая f(x) скользит вдоль оси абсцисс, не меняя своей формы. При изменении σ кривая меняет свою форму: если σ увеличивается, то кривая становится ниже и шире и наоборот.
Если m=0 и σ=1, то закон нормального распределения называется стандартным. В этом случае
Если случайная величина Х распределена по нормальному закону с параметрами m и σ , то этот факт записывают так:.
Вычислим математическое ожидание случайной величины
Таким образом, параметр m — это математическое ожидание случайной величины X.
Вычислим теперь дисперсию
где мы использовали то, что по правилу Лопиталя
Таким образом, параметр σ — это среднеквадратическое отклонение, поскольку σ2— это дисперсия.
Мода и медиана нормального распределения совпадает с математическим ожиданием, т.к. максимум f(x) достигается при x=m и
где
функция распределения закона которая имеет график, представленный на рисунке.
Пусть Вычислим Р(а<Х<b) — вероятность попадания нормально распределенной случайной величины в заданный интервал. По свойству плотности распределения имеем
где мы использовали формулу Ньютона-Лейбница для определенных интегралов, а — любая первообразная для подынтегральной функции
Любая первообразная может быть рассчитана по формуле
где С— произвольная постоянная. Это можно легко проверить дифференцированием .
При С=0 мы получаем функцию Лапласа
а при С=∞ — функцию распределения стандартного нормального закона
Нетрудно получить связь между Ф*(х) и Ф(х).
Окончательно получаем
В зависимости от имеющихся у нас под руками таблиц мы воспользуемся той или иной формулой. Отметим, что пользоваться таблицами функции Лапласа удобней, так как она нечетна и мы легко — находим ее значения при отрицательном аргументе (обычно, таблицы заданы только для положительных значений аргумента). Пользоваться таблицами функции Ф*(х) в этом случае несколько неудобнее, если она задана только для положительных значений аргумента.
ПРИМЕР 1. Пусть Найдем вероятность того, что Х примет значение из интервала ]0;3[.
По таблице функции Лапласа получаем
По таблице функции распределения стандартного нормального закона получаем, используя ее связь с функцией Лапласа:
Вэтом примере мы вывели полезную формулу
Ф*(-х)=1-Ф*(х),
которую легко пояснить следующим рисунком.
Найдем вероятность попадания нормальной случайной величины в интервал ]m—l,m+l[, симметричный относительно математического ожидания:
При различных l получаем
Как мы видим, хотя теоретически возможные значения Х могут быть любые, но практически все значения попадают в интервал ]m-3σ,m+3σ[. Этот факт обычно называют правилом «трех сигм». При нормальном распределении из 10000 измерений только 27 имеют «законное» право выйти из этого интервала ( событие маловероятное и им обычно пренебрегают). Поэтому можно считать, что все возможные значения нормальной случайной величины находятся в этом интервале.
Распределение монотонной функции случайной величины. Исследование системы двух случайных величин. Функциональная и вероятностная зависимость. Условная плотность.
Часто приходится рассматривать сразу несколько случайных величин одновременно. Например, при стрельбе по мишени точка попадания имеет две координаты, которые являются случайными величинами; при медицинском осмотре основными параметрами состояния здоровья считаются частота пульса, уровень кровяного давления, температура тела и т.д., которые при случайном выборе человека являются случайными величинами.
Пусть Х и Y — дискретные случайные величины. Двумерная случайная величина {X, Y} называется системой дискретного типа и задается следующей таблицей, называемой двумерным рядом распределения
Y X | У1 | У2 | Уз | … | Уj | … |
x1 | Р11 | P12 | P13 | … | P1j | … |
x2 | P21 | P22 | P23 | … | P2j | … |
… | … | … | … | … | … | … |
xi | Pi1 | Pi2 | Pi3 | … | Pij | … |
… | … | … | … | … |
|
|
где Pij=(X=xi;Y=yj).
studfiles.net
Дисперсия случайной величины.
Дисперсия DX случайной величиныXопределяется формулой
DX = E(X – EX)2
Дисперсия случайной величины — это математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
Рассмотрим случайную величину Xс законом распределения
Вычислим её математическое ожидание.
EX = 1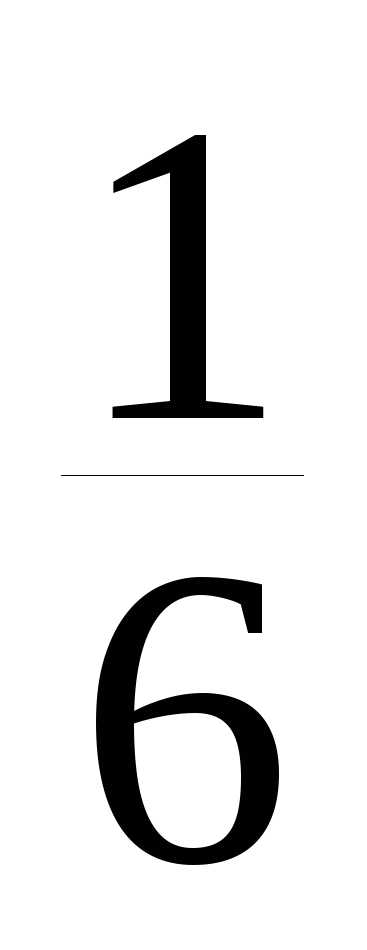 + 2
+ 2 + 3
+ 3 =
= 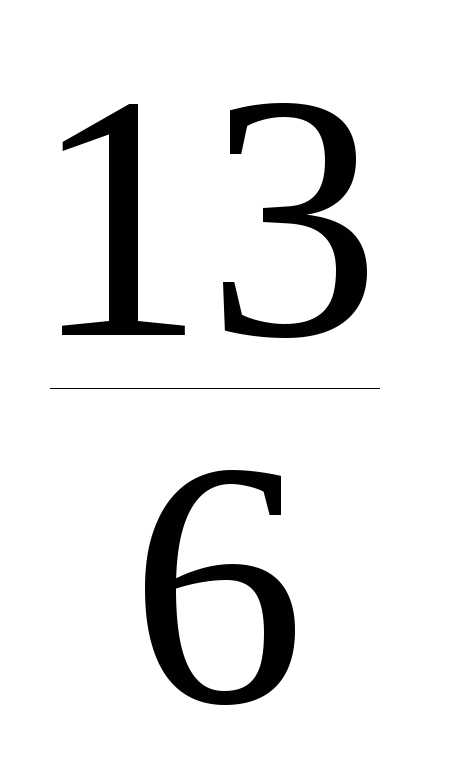
Составим закон распределения случайной величины X – EX
а затем закон распределения случайной величины (X-EX)2
Теперь можно рассчитать величину DX :
DX = 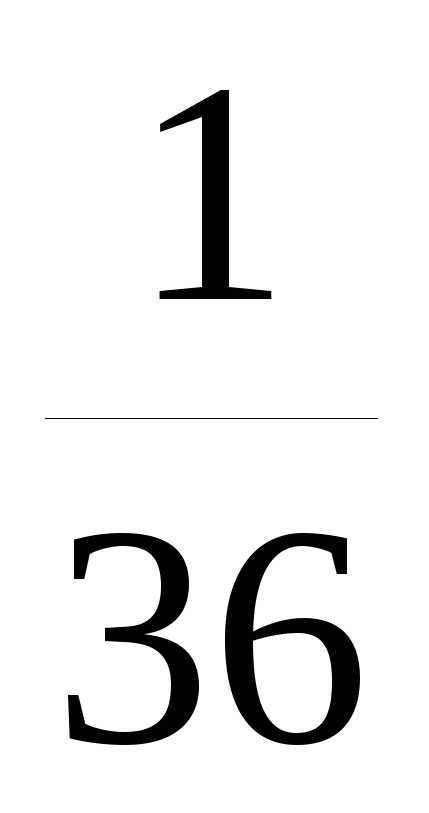
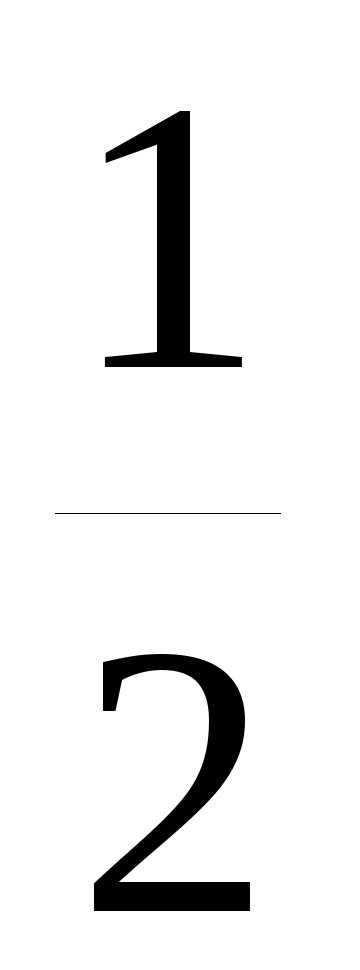 +
+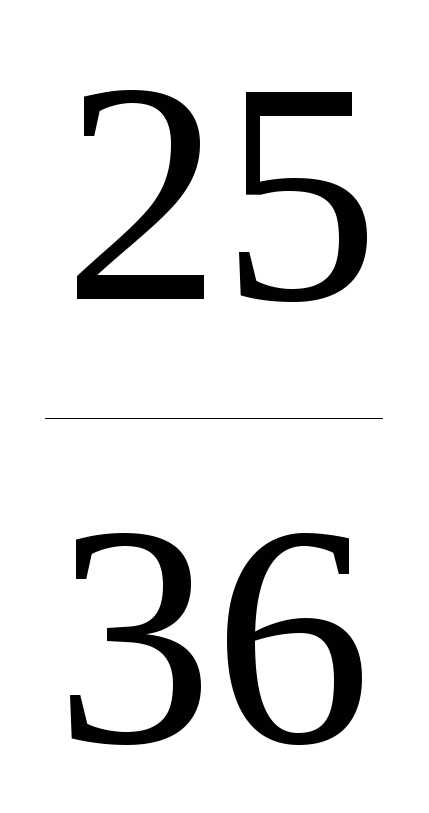
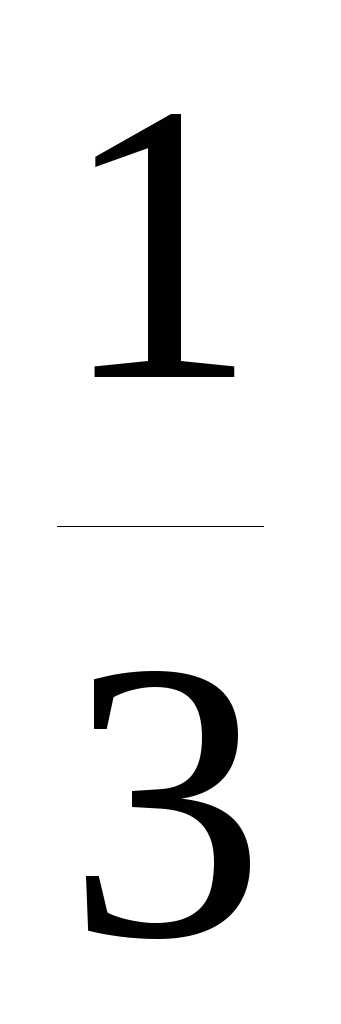 +
+
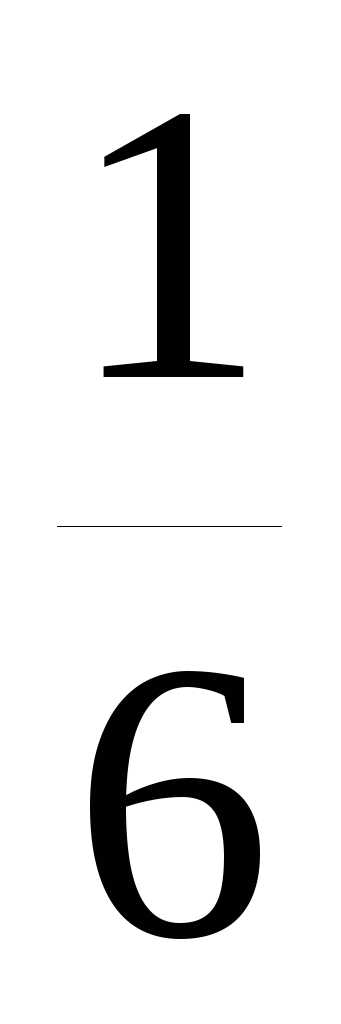 =
=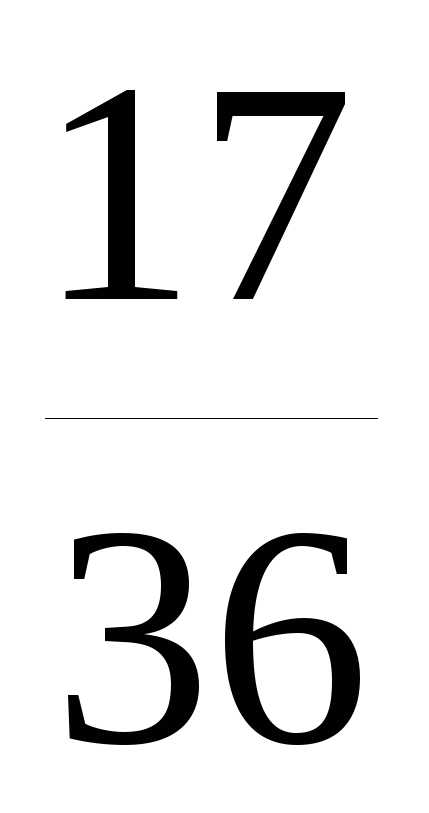
Замечание. Более удобной для вычисления может оказаться следующая формула, которую можно рассматривать как одно из свойств дисперсии:
DX = EX2 – (EX)2
Таким образом, дисперсия случайной величины равна разности математического ожидания квадрата случайной величины и квадрата её математического ожидания. Для использования этой формулы нужно составить таблицу:
и провести вычисления EX2 и (EX)2 по описанной схеме.
Пример.
Найти дисперсию случайной величины, заданной законом распределения
Выше было показано, что EX=р. Легко видеть, чтоEX2=р. Таким образом, получается, чтоDX=р–р2=pq.
Дисперсия характеризует степень рассеяния значений случайной величины относительно её математического ожидания. Если все значения случайной величины тесно сконцентрированы около её математического ожидания и большие отклонения от математического ожидания маловероятны, то такая случайная величина имеет малую дисперсию. Если значения случайной величины рассеяны и велика вероятность больших отклонений от математического ожидания, то такая случайная величина имеет большую дисперсию.
Пример
Найти дисперсию случайной величины Х, равномерно распределенной на [a,b]
Свойства дисперсии.
Если k – число, то D(kX) =k2 DX.
Для попарно независимых случайных величин X1,X2,,Xnсправедливо равенство
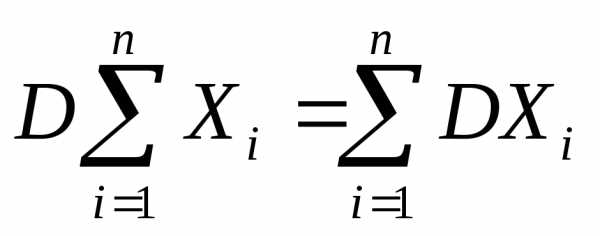
Если Х и Y независимы, D(X+Y) =DX+DY.
Предлагаем в качестве упражнения рассмотреть, чему равняется D(X– Y) в тех же условиях
Неравенства Маркова и Чебышева
Неравенства Маркова дают оценку для значений случайной величины в тех случаях, когда наши знания о случайной величине ограничиваются ее математическим ожиданием и дисперсией, и, хотя эти оценки достаточно грубы, они требуют минимальной информации о рассматриваемой случайной величине.
Если возможные значения дискретной случайной величины Х неотрицательны и существует ее математическое ожидание ЕХ = а , то для любого числа с > 0 справедливо неравенство
Р (Х <с ) >1 – а / с
Соответственно, выполняется и неравенство
Р (Х ≥ с ) ≤ а / с
Эти неравенства называются (первым и вторым) неравенствами Маркова
Пример 9.4. Пусть X — время опоздания студента на
лекцию, причем известно, что ЕХ = 1 мин. Воспользовавшись
первым неравенством Чебышева, оценим вероятность Р{Х >5}
того, что студент опоздает не менее, чем на 5 мин.
Имеем P(X≥5) ≤EX/5
Таким образом, искомая вероятность не более 0,2, т.е. в среднем,
из каждых пяти студентов опаздывает по крайней мере на 5 мин не более чем один студент.
Если Х – случайная величина, математическое ожидание которой ЕХ = а , дисперсия DХ конечна, то для любого числа с > 0 выполняются неравенства
P ( | X – a | ≥ c ) ≤DX / c2
P ( | X – a | < c ) >1 – DX / c2
Данные неравенства называются (первым и вторым) неравенствами Чебышева
Замечание. Иногда и неравенства Маркова и неравенства Чебышева называются первым и вторым неравенствами Чебышева.
Пример. Пусть в условиях предыдущего примера известно дополнительно, что а = y/DX = 1. Оценим минимальное значение хо, при котором вероятность опоздания студента на время не менее хо не превышает заданного значения Р3 = 0,1.
Для решения поставленной задачи воспользуемся неравенством Чебышева. Тогда
Р3 ≤ Р{Х ≥х0}
= Р{Х — ЕX ≥ хо — ЕX} ≤ Р{|Х – EХ|
>х0—
EX}≤ 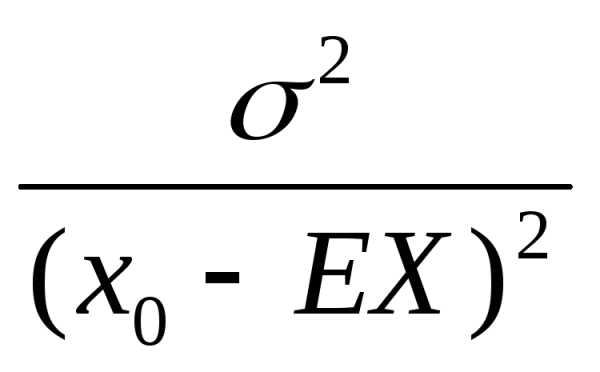
Значит,
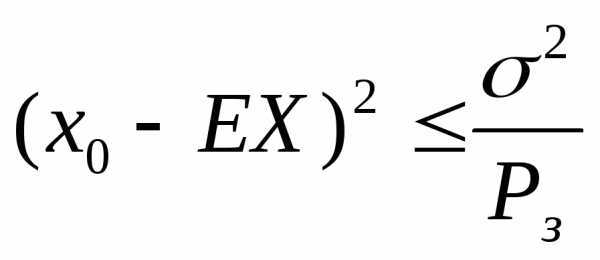 и
и 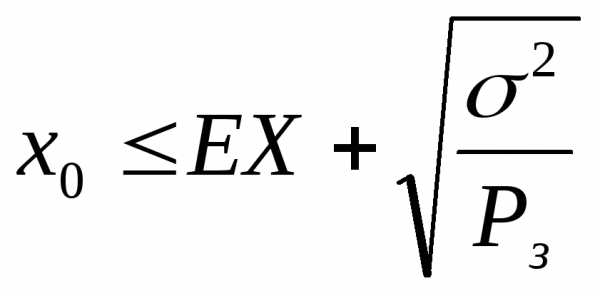
И,
подставляя конкретные значения, имеем 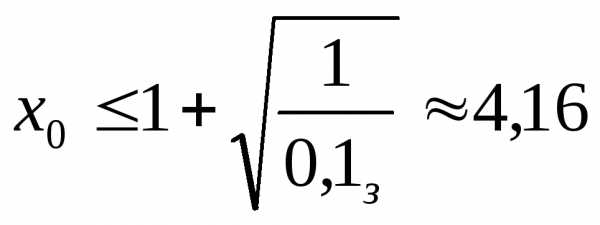
Таким образом, вероятность опоздания студента на время более 4,16 мин не более 0,1.
Сравнивая полученный результат с результатом предыдущего примера можно заметить, что дополнительная информация о дисперсии времени опоздания позволяет дать более точную оценку искомой вероятности.
Замечание. Элементарным следствием из неравенства Чебышева является Закон больших чисел (в форме Чебышева):
Определение. (Начальным)Моментом порядка k случайной величины Х называется число mk = Е(Хk )
Определение. (Центральным) моментом порядка k случайной величины Х называется число μk = Е(Х–ЕХ)k
Замечание. Нетрудно видеть, что математическое ожидание – начальный момент первого порядка, а дисперсия – центральный момент второго порядка.
Замечание.Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = EX , то все ее центральные моменты нечетного порядка равны нулю.
В тех случаях, когда какие-нибудь причины благоприятствуют более частому
появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения.
Определение. Асимметрией А случайной величины Х называют отношение третьего центрального момента к кубу среднеквадратичного отклонения. А=μ3 / σ3
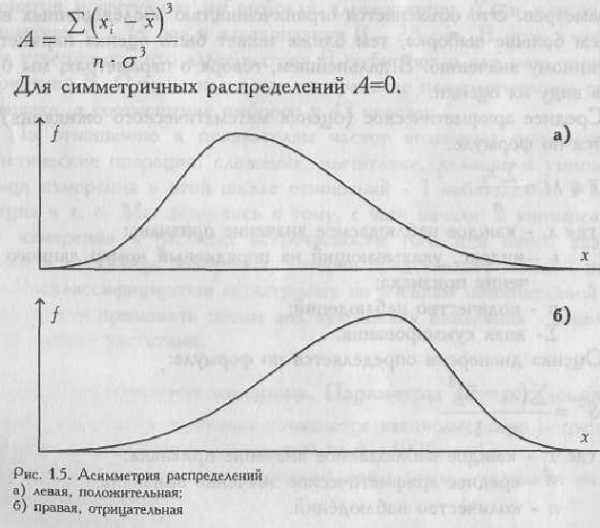
(по Е.В.Сидоренко)
Асимметрия — величина, характеризующая степень асимметрии распределения относительно математического ожидания.: Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находятся левее математического ожидания, и наоборот, если больше нуля , то правее.
В тех случаях, когда какие-нибудь причины благоприятствуют более частому
появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения. При левосторонней, или положительной, асимметрии в распределении чаще встречаются более низкие значения признака, а при правосторонней,
или отрицательной — более высокие
Очевидно, что для случайной величины, распределенной симметрично относительно математического ожидания, асимметрия равна нулю.
В тех случаях, когда какие-либо причины способствуют преимущественному
появлению средних или близких к средним значений, образуется распределение с положительным эксцессом. Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двувершинное (см следующий рисунок эксцесса).
Определение. Эксцессом γ случайной величины Х называют отношение
= (μ4 / σ4 ) –3
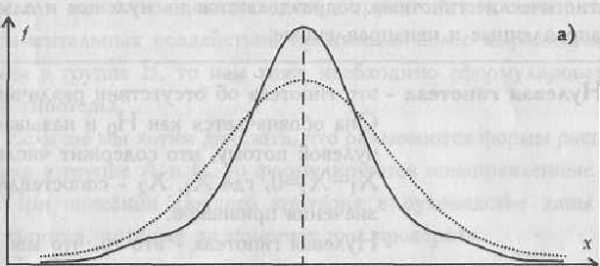
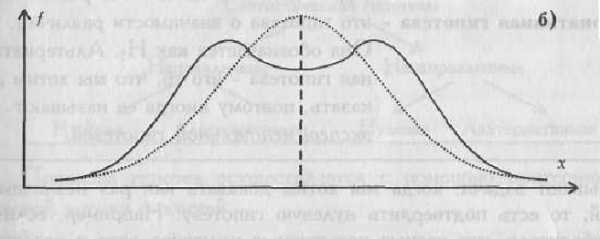
Эксцесс: а) положительный; 6) отрицательный. В распределениях с нормальной выпуклостьюγ =0.
Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины Х от нормального распределения, как раз и является эксцесс. Для нормального распределения γ=0, если γ >0 , то это значит, что график плотности «заострен» сильнее, чем у нормального, а если γ<0, то, соответственно, меньше.
Определение. Квантилью уровня α или α-квантилью (0<α<1) называют число Qα, удовлетворяющее неравенствам Р{X < Qα }≤α и P{X> Qα } ≤ 1 – α
½ -квантиль называют также Медианой М случайной величины Х.
Для непрерывной случайной величины Х α-квантиль Qα – это такое число, меньше которого Х принимает значение с вероятностью α.
Если известна плотность распределения ρ(х) случайной величины Х, то, учитывая связь между функцией распределения и плотностью, уравнение для определения квантили можно записать как
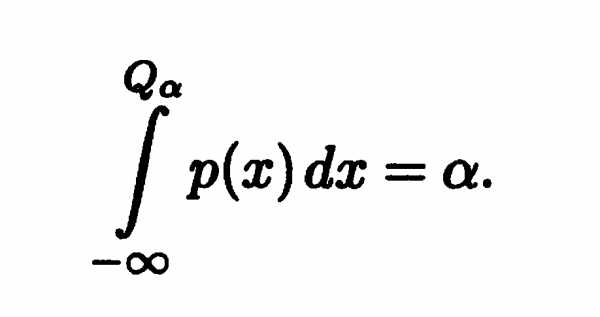
Иначе говоря, квантиль Qα – решение уравнения F(Qα )=α ,
Пример.
Найдем α-квантиль и медиану экспоненциального распределения
(Непрерывная случайная величина Х имеет показательное распределение с параметром > 0, если она принимает только неотрицательные значения, а ее плотность распределения имеет вид: (х) = е—х , x≥0 и 0, если х <0
,
поэтому 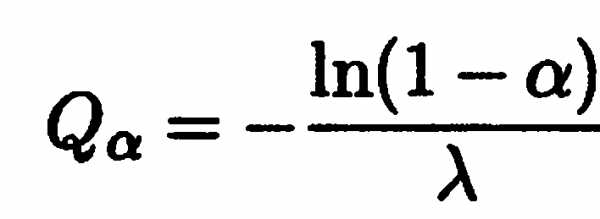 ,
а медиана равна
,
а медиана равна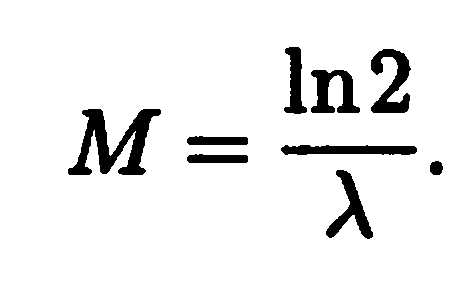
Определение. Модой непрерывной случайной величины называют точку максимума (локального) плотности распределения р(х). Различают унимодальные (имеющие одну моду), бимодальные (имеющие две моды) и мулътимодальные (имеющие несколько мод) распределения.
Для определения моды дискретной случайной величины предположим сначала, что ее значения x1, … xn расположены в порядке возрастания.
Модой дискретной случайной величины называют такое значение хi, при котором для вероятностей выполняются неравенства
pi-1 < pi и pi+1 < рi
В случае дискретных случайных величин распределения также могут быть унимодальными, бимодальными и мультимодальными.
Наивероятнейшим значением называют моду, при которой достигается глобальный максимум вероятности (дискретной случайной величины) или плотности распределения (непрерывной случайной величины).
Если распределение унимодальное, то мода также будет наивероятнейшим значением.
studfiles.net
Числовые характеристики дискретных случайных величин
Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться числами, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайной величины. К ним относятся: математическое ожидание, дисперсия.
Математическое ожидание дискретной случайной величины
Математическим ожиданием дсв называют сумму произведений всех её возможных значений на их вероятности и обозначается .
Если дсв задана законом распределения
, то
Пусть произведено испытаний, в которых случайная величинапринялараз значение,раз значение, …,раз значение, причём++…+=. Тогда сумма всех значений, принятых, равна. Найдём среднее арифметическоевсех значений. Итак, . Вероятностный смысл полученного результата таков: математическое ожидание приближённо равно среднему арифметическому наблюдаемых значений случайной величины.
Математическое ожидание обладает следующими свойствами:
Математическое ожидание постоянной величины равно самой постоянной, т.е.
В самом деле, постоянную можно рассмотреть как дискретную случайную величину, которая имеет одно возможное значение и принимает его с вероятностью.
Постоянный множитель можно выносить за знак математического ожидания, т.е. .
.
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е.
Если , то
Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых, т.е. .
Если , то
+
, т.к. .
Математическое ожидание числа появлений события А в независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытаний, т.е.
Дисперсия дискретной случайной величины
Математическое ожидание, или среднее значение, случайной величины в ряде вопросов является достаточной характеристикой изучаемой случайной величины. Но бывает так, что одно среднее значение не даёт практически исчерпывающей характеристики случайной величины, а требуется ещё знать, сколь велики отклонения отдельных значений случайной величины от её математического ожидания.
Например, по данным статистического наблюдения изучается: средний рост или вес человека в определённой группе. Результаты опыта или наблюдения может считаться удачным, если возможные значения случайной величины незначительно отличаются от математического ожидания. Поэтому возникает необходимость введения ещё понятия отклонения случайной величины от её математического ожидания.
Отклонением называют разность между случайной величиной и её математическим ожиданием: .
Это отклонение характеризует рассеяние случайной величины. На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение, т.е. математическое ожидание отклонения.
Покажем, что математическое ожидание отклонения равно нулю. В самом деле . Это объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. В случае замены абсолютными значениями приходится оперировать с абсолютными величинами, что приводит иногда к серьёзным затруднениям. Поэтому чаще всего идут по другому пути, вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания и обозначают . Таким образом:
При решении практических задач часто пользуются немного видоизменённой формулой дисперсии, а именно: . При преобразовании было учтено, что математическое ожидание есть постоянная величина, а значит,есть также постоянные величины. Итак,
Дисперсия обладает следующими свойствами:
Дисперсия постоянной величины равна нулю, т.е. .
В самом деле .
.
Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е. .
В самом деле .
.
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин, т.е.
Дисперсия разности двух независимых случайных величин равна сумме их дисперсии, т.е.
Дисперсия числа появления события А в независимых испытаниях, в каждом из которых вероятностьпоявления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании, т.е..
.
Среднее квадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг её среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии и обозначается σ(:
.
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность σ(совпадает с размерностью случайной величины. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию.
Функция распределения вероятностей случайной величины
Дискретная случайная величина может быть задана перечнем всех её возможных значений и их вероятностей. Такой способ задания не является общим: он не применим, например, для непрерывных случайных величин, так как в этом случае не предоставляется возможным перечислить все возможные значения. Поэтому вводят понятие функции распределения вероятностей случайной величины.
Пусть – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее, т.е. вероятность события, обозначим через.
Функцией распределения называется функция , определяющая вероятность того, что случайная величинв результате испытания примет значение, меньшее, т.е.
.
Функция распределения обладает следующими свойствами:
.
Если , то.
В самом деле, пусть . Событие, состоящее в том, чтопримет значение, меньшее, можно подразделить на два несовместных события:примет значение, меньшееипримет значение, удовлетворяющее неравенствут.е.). По теореме сложения имеем:), откуда
) или . Т.к. любая вероятность есть число неотрицательное, тоили.
Если и, то. Таким образом, вероятность того, что случайная величина примет значение, заключённое в интервале, равна приращению функции распределения на этом интервале:
Если возможные значения случайной величины принадлежат интервалу , то
а) , б). График функции распределения непрерывной случайной величины имеет вид:
studfiles.net
2.6. Дисперсия случайной величины
Математическое ожидание не всегда является достаточной характеристикой сл. величины, оно является наиболее типичным значением сл. величины в серии испытаний, а в каждом отдельном испытании значения сл. величины отклоняются от ее математического ожидания в ту или иную сторону. Поэтому наряду со средним значением сл. величины хорошо бы иметь величину, характеризующую отклонение сл. величины от своего среднего. Ведь одна ситуация, если отклонение сл. величины от своего среднего в ту или иную сторону (еще говорят: разброс вокруг среднего значения) составляет 1 единицу, но совсем другая – если, например, 10 единиц.
Такой характеристикой обычно служит дисперсия сл. величины.
Определение. Дисперсией случайной величины называют число
.(2.18)
Величина
()
≡=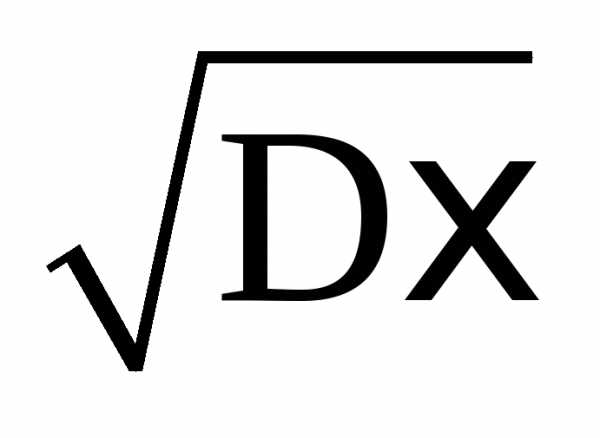 (2.19)
(2.19)
называется средним квадратическим отклонением случайной величины ξ.
Размерность среднеквадратичного отклонения такая же, как и у сл. величины ξ, размерность же дисперсии равна квадрату размерности сл. величины ξ; такое различие размерностей не очень удобно, потому и вводится среднее квадратичное отклонение.
Вычисляют дисперсию по формуле
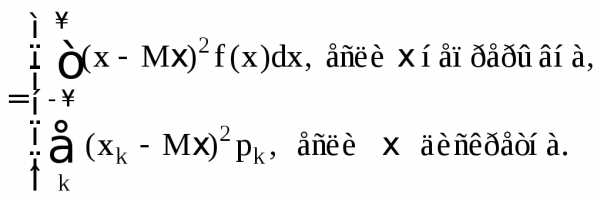 (2.20)
(2.20)
Пример 18. Вычислим дисперсию для сл. величины из примера 14.
Решение. D = .
Пример 19. Вычислим дисперсию сл. величины из примера 15.
Решение.
Из примера 19 видим, что вторым параметром в нормальном распределении является среднее квадратическое отклонение.
Свойства дисперсии.
D1. 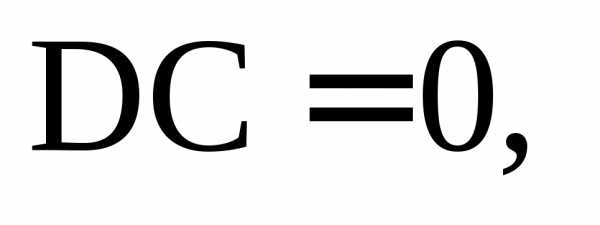 если.
если.
.
D2.
.
D3. ,
если величины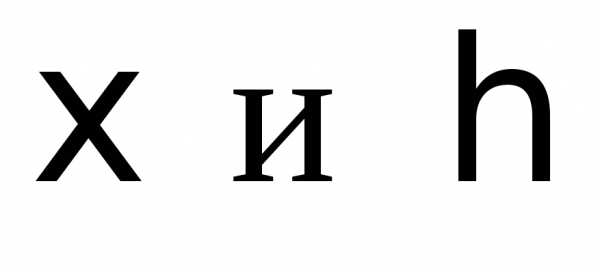 независимы.
независимы.
Рассмотрим выражение
По свойству математического ожидания,
если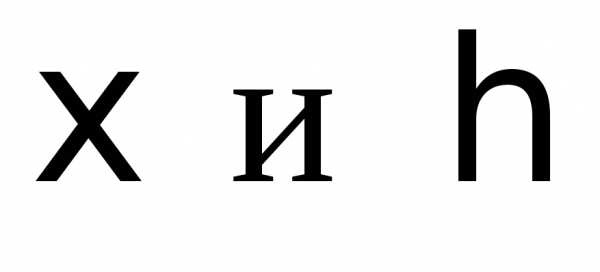 независимы – это с одной стороны; с
другой стороны
независимы – это с одной стороны; с
другой стороны
Следствия.
1) ;
2) ;
3) .
D4. Действительно, рассмотрим равенства
Пример 20. Вычислить дисперсию сл. величины из примера 16.
Решение. Для
вычисления дисперсии сл. величины,
имеющей -распределение,
воспользуемся свойством D4. 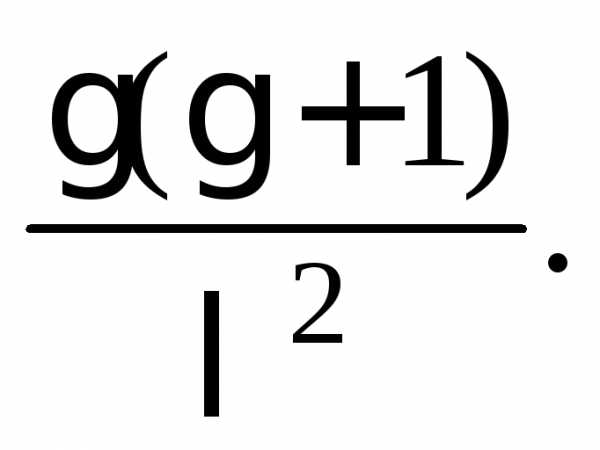 Из примера 16 возьмем величину
Из примера 16 возьмем величину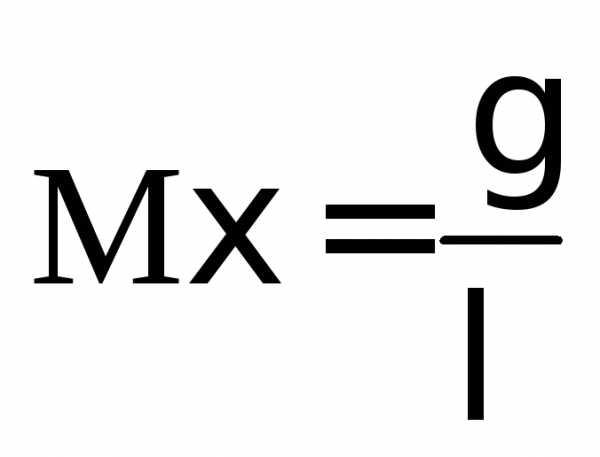
Замечание. Если сл. величина имеет математическое ожидание, то дисперсия всегда определена, но может принимать значение, равное ∞.
Пример 21. Пусть функция плотности распределения сл. величины ξ задана формулой
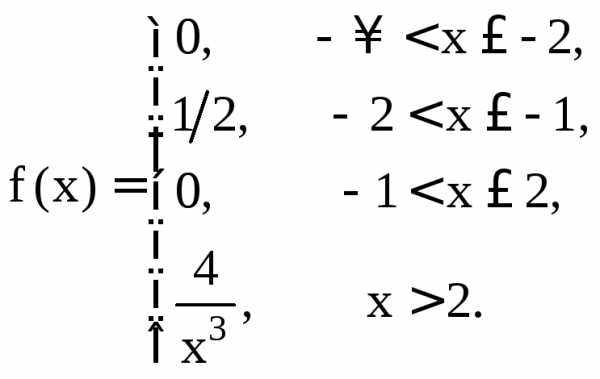
В точках –2, –1 и
2 функция f(x) имеет разрывы. Всем свойствам
плотности вероятностей функция 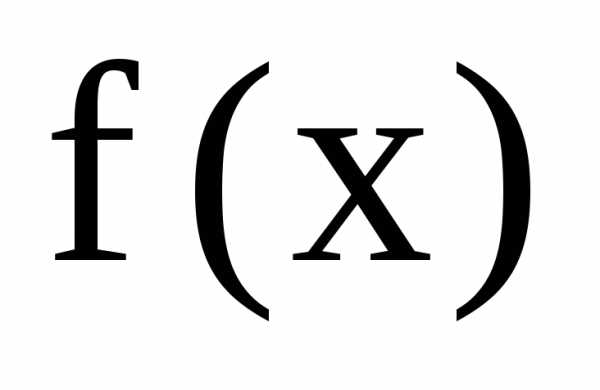 удовлетворяет, в частности,
удовлетворяет, в частности,
–конечной дисперсии нет.
Упражнение. Получить выражения для математических ожиданий и для дисперсий всех случайных величин, описанных выше в этом разделе, исключая распределение Вейбулла и гамма-распределение.
2.7. Моменты случайных величин. Другие числовые характеристики случайных величин
Математическое ожидание и дисперсия сл. величины являются представителями целого класса характеристик, которые называются моментами сл. величин.
Начальным моментом порядка 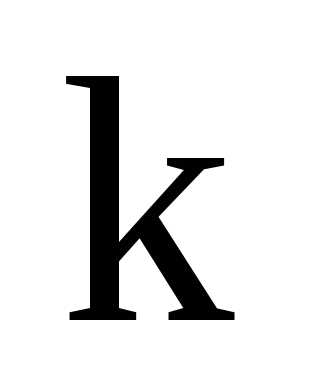 cл.
величины
cл.
величины  называется
число
называется
число
. (2.21)
При математическое ожидание – начальный момент 1-го порядка.
Центральным
моментом порядка 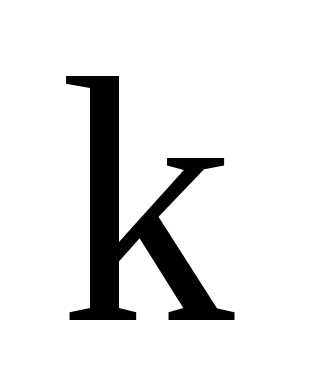 cл.
величины
cл.
величины  называется число
называется число
. (2.22)
При
дисперсия сл. величины – это центральный
момент второго порядка. Интересно
отметить, что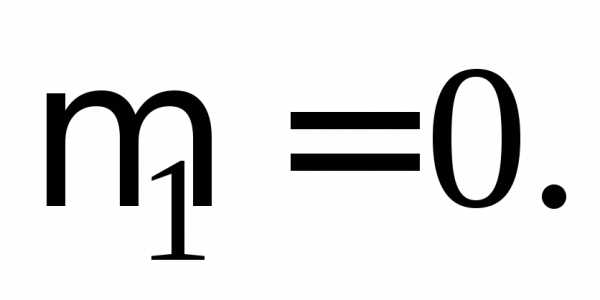
Абсолютным
моментом порядка 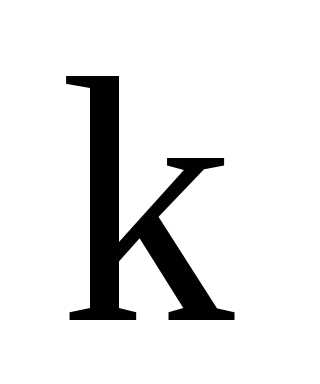 сл. величины ξ называются число
сл. величины ξ называются число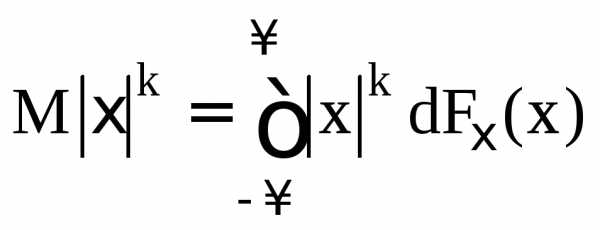 .
.
Между начальными и центральными моментами существуют связывающие их соотношения, для последующих вычислений нам будут интересны только два:
(2.23)
Моменты служат в дополнение к математическому ожиданию и дисперсии для более детального изучения особенностей распределения сл. величины. Особенно важны моменты 3-го и 4-го порядков, так как через них выражаются некоторые числа (такие, как асимметрия и эксцесс), характеризующие распределение сл. величин.
Таким образом, две характеристики положения, наиболее часто используемые для описания сл. величин, являются представителями широкого класса характеристик сл. величин – моментов сл. величин.
Из других
характеристик положения наиболее часто
используют медиану и моду случайной
величины, обозначают их символами 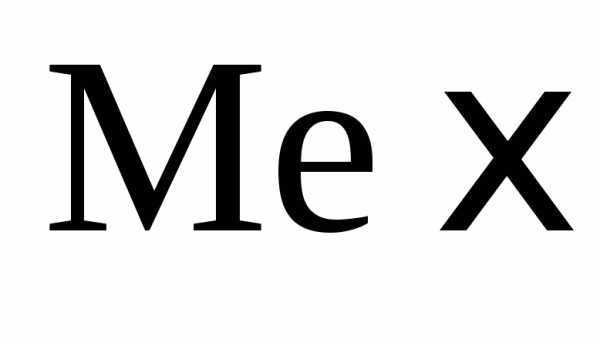 и Мо ξ соответственно.
и Мо ξ соответственно.
Медиана случайной величины ξ – число 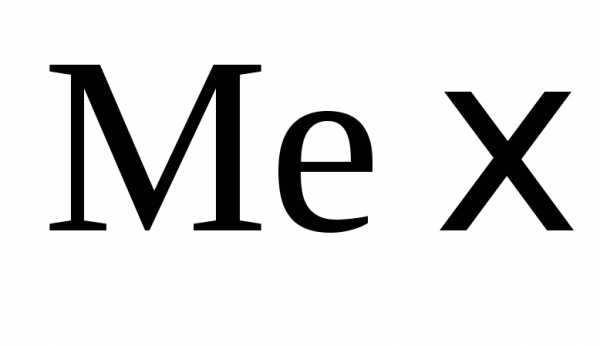 –
определяется из соотношения.
Из определения следует, что медиана сл.
величины – это любое решение уравнения
–
определяется из соотношения.
Из определения следует, что медиана сл.
величины – это любое решение уравнения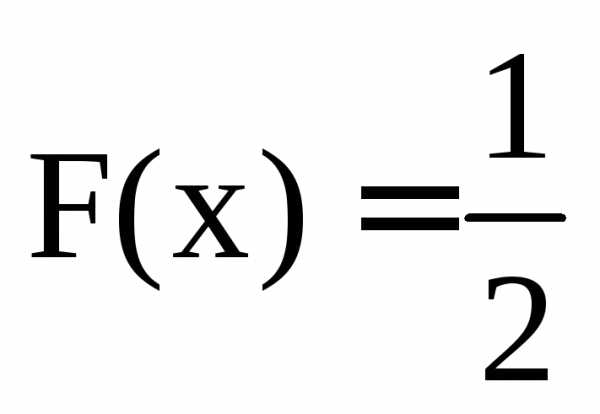 .
Поскольку решение этого уравнения не
единственно, то медиана сл. величины
определяется неоднозначно.
.
Поскольку решение этого уравнения не
единственно, то медиана сл. величины
определяется неоднозначно.
Модой непрерывной сл. величины ξ называют точку локального максимума ее плотности распределения f(x). По числу мод распределения бывают унимодальные (одна мода), бимодальные (две моды) и мультимодальные (более двух мод). Нормальное распределение, например, относится к числу унимодальных, причем Me = Мо ξ = m – математическому ожиданию.
Модой дискретной
сл. величины называют такое ее значение 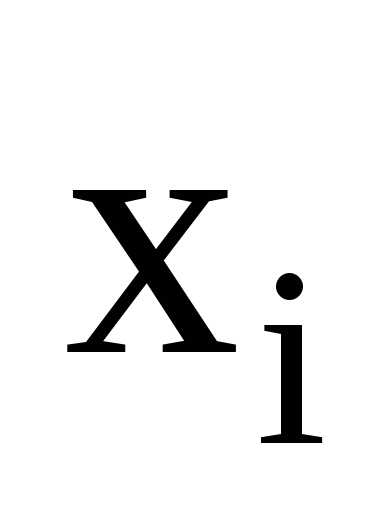 ,
для которого
,
для которого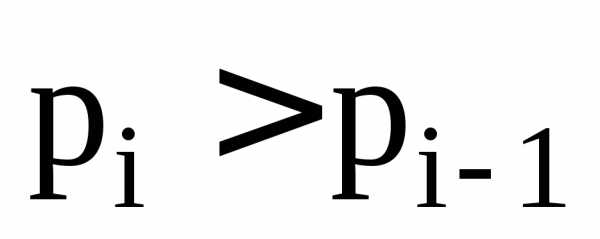 и
и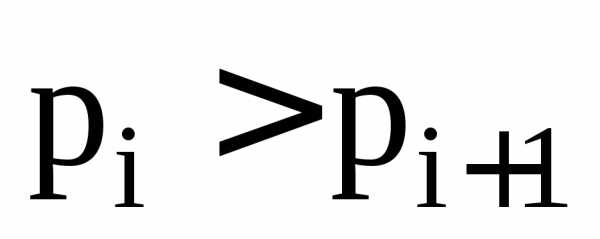 ,
при этом все ее значения должны быть
расположены в порядке возрастания.
,
при этом все ее значения должны быть
расположены в порядке возрастания.
Пример 22. Рассмотрим
сл. величину, имеющую распределение
Коши
Известно, что эта сл. величина не имеетматематического
ожидания (см. пример 17). Однако функция
f(х) имеет глобальный максимум в точке
х = 0, f(0) = 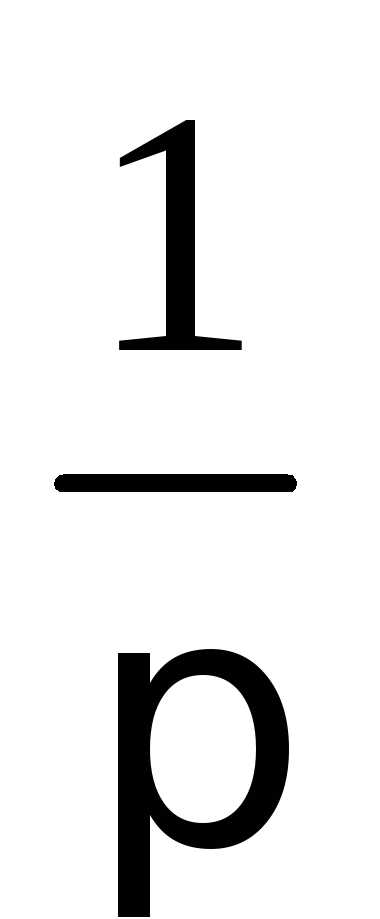 .
Следовательно, Мо ξ = 0.
.
Следовательно, Мо ξ = 0.
Широкое применение в математической статистике при построении доверительных интервалов и при проверке статистических гипотез находят α-квантили.
—квантилью (симметричной
—квантилью)
сл. величины называется
число, удовлетворяющее
уравнениям:
().
Отметим, что 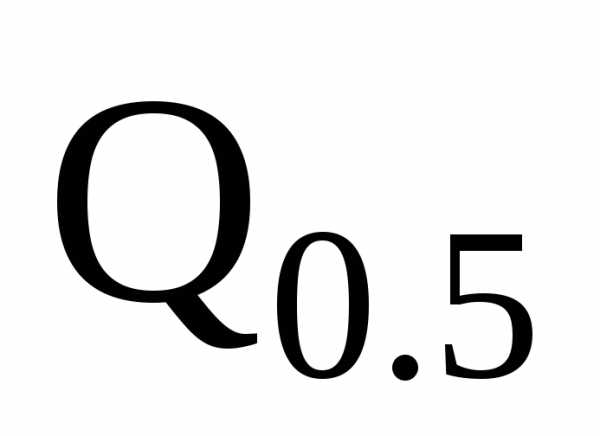 – это медиана случайной величиныMe :
– это медиана случайной величиныMe :
Пример 23. Найти —квантили и медиану экспоненциального распределения.
Решение. 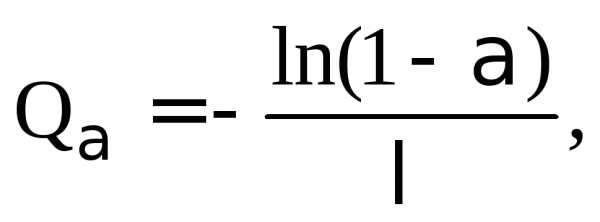
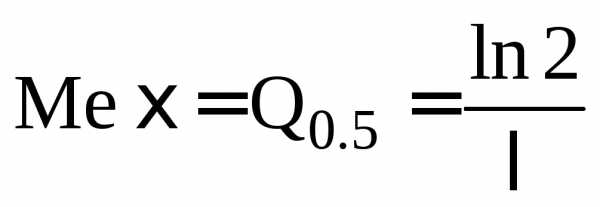 .
.
Для первой проверки сл. величины на нормальность в математической статистике используют асимметрию и эксцесс.
Асимметрией  сл. величины
называется число
сл. величины
называется число 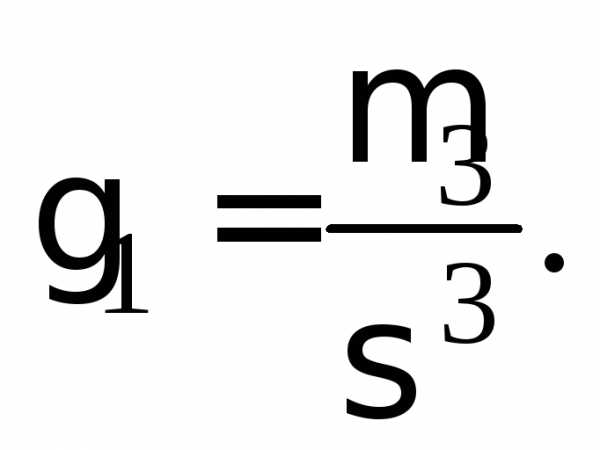 Еслидля
любого х, то
Еслидля
любого х, то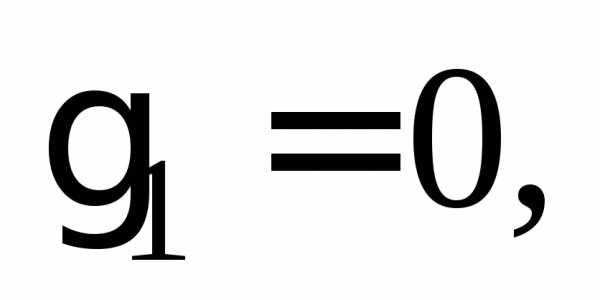 так как в этом случае все центральные
моменты нечетных порядков равны нулю.
Равенство вероятностей означает, что
сл. величина распределена симметрично
относительно своего математического
ожидания.
так как в этом случае все центральные
моменты нечетных порядков равны нулю.
Равенство вероятностей означает, что
сл. величина распределена симметрично
относительно своего математического
ожидания.
Таким образом,
коэффициент асимметрии
служит для характеристики степени
несимметричности функции плотности
распределения сл. величины. Если >
0, то функция плотности распределения
по отношению к ее математическому
ожиданию имеет сдвиг вправо; для
>
0, то функция плотности распределения
по отношению к ее математическому
ожиданию имеет сдвиг вправо; для < 0 – влево.
< 0 – влево.
Пример 24. Вычислить
асимметрию  для случайной величины, имеющей нормальный
закон распределения.
для случайной величины, имеющей нормальный
закон распределения.
Решение. Поскольку 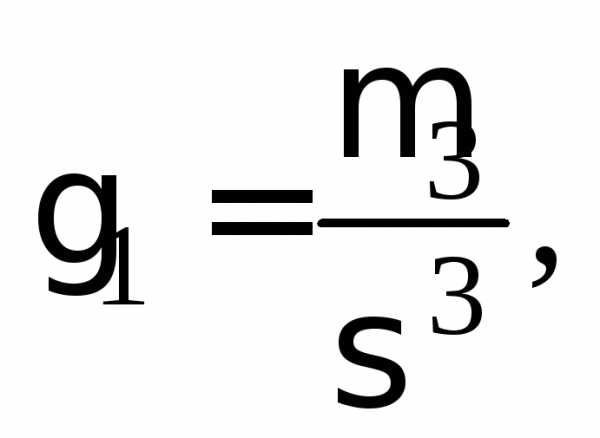 вычислим составляющие этойформулы:
– интеграл от нечетной подынтегральной
функции по симметричному промежутку.
Тогда
вычислим составляющие этойформулы:
– интеграл от нечетной подынтегральной
функции по симметричному промежутку.
Тогда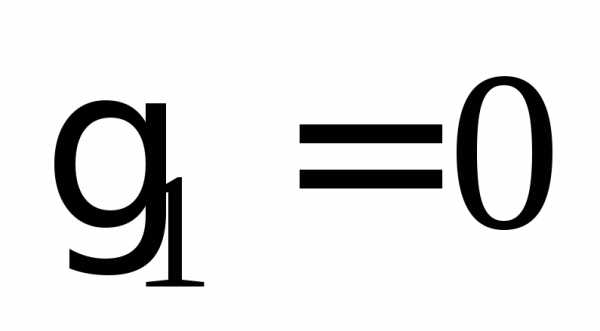 .
.
Из примера следует, что нормальное распределение является своего рода эталоном, с которым сравниваются другие распределения.
Замечание. При сравнении сл. величин их нужно
центрировать и нормировать, то есть от
сл. величины 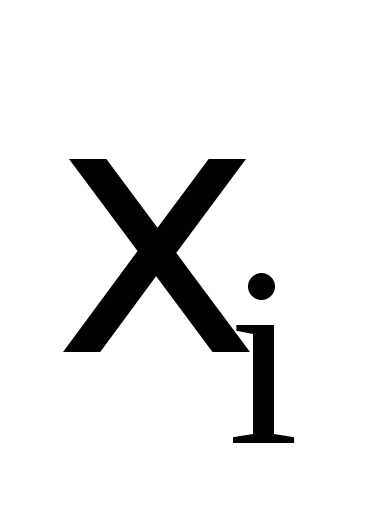 переходить к сл. величине
переходить к сл. величине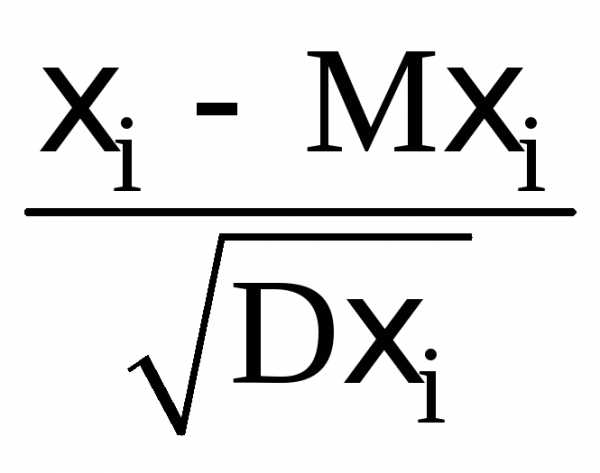 .
Вновь полученные сл. величины имеют те
же значения
.
Вновь полученные сл. величины имеют те
же значения ,
что и исходные.
,
что и исходные.
Эксцессом  сл. величины
называется число
сл. величины
называется число 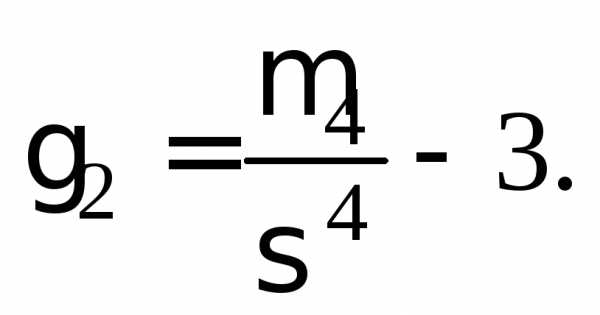 Эксцесс, как правило, используется для
характеристики симметричности
унимодальных распределений.
Эксцесс, как правило, используется для
характеристики симметричности
унимодальных распределений.
Пример 25. Для
нормального распределения  = 0, так как
= 0, так как
Если для некоторой
сл. величины  > 0, то кривая плотности распределения
более островершинна, чем при нормальном
распределении; если
> 0, то кривая плотности распределения
более островершинна, чем при нормальном
распределении; если < 0, то кривая плотности распределения
более плоская, чем при нормальном
распределении. При этом справедливо
замечание относительно преобразования
сравниваемых сл. величин, сделанное
выше. Более подробно эти вопросы можно
изучить по специальной литературе по
теории вероятностей и математической
статистике.
< 0, то кривая плотности распределения
более плоская, чем при нормальном
распределении. При этом справедливо
замечание относительно преобразования
сравниваемых сл. величин, сделанное
выше. Более подробно эти вопросы можно
изучить по специальной литературе по
теории вероятностей и математической
статистике.
studfiles.net
Дисперсия случайной величины — это… Что такое Дисперсия случайной величины?
У этого термина существуют и другие значения, см. Дисперсия.Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается в русской литературе и (англ. variance) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.
Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.
Определение
Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда
где символ обозначает математическое ожидание[1][2].
Замечания
Свойства
Пример
Пусть случайная величина имеет стандартное непрерывное равномерное распределение на то есть её плотность вероятности задана равенством
Тогда математическое ожидание квадрата случайной величины
и математическое ожидание случайной величины
Тогда дисперсия случайной величины
См. также
Примечания
- ↑ Колмогоров А. Н. Глава IV. Математические ожидания; §3. Неравенство Чебышева // Основные понятия теории вероятностей. — 2-е изд. — М.: Наука, 1974. — С. 63—65. — 120 с.
- ↑ Боровков А. А. Глава 4. Числовые характеристики случайных величин; §5. Дисперсия // Теория вероятностей. — 5-е изд. — М.: Либроком, 2009. — С. 93-94. — 656 с.
Литература
dic.academic.ru