Общая дисперсия
Характеризует вариацию признака, который зависит от всех условий в данной совокупности.
, где — общая средняя для всей изучаемой совокупности.
Межгрупповая дисперсия
Отражает вариацию изучаемого признака, который возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних около общей средней
, где — средняя по отдельным группам;- средняя общая; fi – численность отдельных групп.
Средняя из внутригрупповых дисперсий
Характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием других, не учитываемых факторов, и не зависит от условия (признака-фактора), положенного в основу группировки. Определяется:
1. Рассчитаем общую дисперсию.
Пример.
Расчет общей дисперсии, складывающейся под влиянием всех факторов (объема выручки предприятия и форма собственности)
Объем выручки продукции в среднем на 1 предприятие, млрд.р. (х) | Число предприятий по форме собственности | Расчет общей дисперсии | ||||||
Государ-ственные fr | Приватизи-рованные fn | Всего F0 | x/ | x/f0 | x/— | (x/-)2 | (x/-)2f0 | |
1,0-1,2 | 3 | 3 | 1,1 | 3,3 | -0,714 | 0,5098 | 1,5294 | |
1,2-1,4 | 4 | 4 | 1,3 | 5,2 | -0,514 | 0,2642 | 1,0568 | |
1,4-1,6 | 17 | 17 | 1,5 | 25,5 | -0,314 | 0,0986 | 1,6762 | |
1,6-1,8 | 11 | 15 | 26 | 1,7 | 44,2 | -0,114 | 0,0129 | 0,3354 |
1,8-2,0 | 13 | 6 | 19 | 1,9 | 36,1 | +0,086 | 0,0074 | 0,1406 |
2,0-2,2 | 18 | 5 | 23 | 2,1 | 48,3 | +0,286 | 0,0818 | 1,8814 |
2,2-2,4 | 6 | 6 | 2,3 | 13,8 | +0,486 | 0,2362 | 1,4172 | |
2,4-2,6 | 2 | 2 | 2,5 | 5,0 | +0,686 | 0,4706 | 0,9412 | |
Итого: | 50 | 50 | 100 | 181,4 | 8,9782 | |||
Находим выработку в среднем на одно предприятие
Определяем общую дисперсию
Т.е. колеблемость объема выручки по исследуемым предприятиям составила 0,089782 млрд.р, что обусловлено и мощностью предприятия и формой собственности.
2. Рассчитаем среднюю из внутригрупповых дисперсий
Теперь рассмотрим, как складываются показатели выручки и ее вариации по группам в зависимости от форм собственности.
Расчет средней дисперсии по государственным предприятиям
fГ | fГ | — | (-)2 | (-)2 fГ | |
1,7 | 11 | 18,7 | -0,3 | 0,09 | 0,99 |
1,9 | 13 | 24,7 | -0,1 | 0,01 | 0,13 |
2,1 | 18 | 37,8 | 0,1 | 0,01 | 0,18 |
2,3 | 6 | 13,8 | 0,3 | 0,09 | 0,54 |
2,5 | 2 | 5,0 | 0,5 | 0,25 | 0,5 |
Итого: | 50 | 100 | 2,34 |
В среднем на одно государственное предприятие выручка составила
, колеблемость его в совокупности гос.предприятий равна
или 46,8 млн.р.
Таким образом, 46,8 млн.р характеризуют вариацию признака внутри группы гос.предпр.
Производим расчет показателей по приватизированным предприятиям
FП | fП | — | (-)2 | (-)2 fП | |
1,1 | 3 | 3,3 | -0,528 | 0,7288 | 0,8363 |
1,3 | 4 | 5,2 | -0,328 | 0,1076 | 0,4303 |
1,5 | 17 | 25,5 | -0,128 | 0,0164 | 0,2785 |
1,7 | 15 | 25,5 | 0,0052 | 0,778 | |
1,9 | 6 | 11,4 | 0,72 | 0,0739 | 0,4439 |
2,1 | 5 | 10,5 | 0,272 | 0,2228 | 1,1139 |
Итого: | 50 | 81,4 | 0,472 | 3,1807 |
, что ниже выручки предприятий, находящихся в государственной собственности. Вариация равна
0,06361млрд.р. или 63,61 млн.р., что выше чем в группе гос.предприятий.
Средняя из групповых дисперсий дает обобщающую характеристику случайной вариации, возникающую под влиянием неучтенных факторов
3. Рассчитаем межгрупповую дисперсию
Мерой колеблемости частных средних вокруг общей средней является межгрупповая дисперсия (дисперсия групповых средних)
Расчет межгрупповой дисперсии
Группы предприятий по форме собственности | Средний объем выручки одного предприятия, | Число предприятий, | ()2 | ()2fi | |
Государственные | 2,0 | 50 | 0,186 | 0,0346 | 1,7298 |
Приватизированные | 1,628 | 50 | -0,186 | 0,0346 | 1,7298 |
Итого: | 100 | 3,4596 |
= 1,814 млрд.р.
studfiles.net
23) Дисперсия признака.
Дисперсия в статистике находится как среднее квадратическое отклонениеиндивидуальных значений признака в квадрате отсредней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n — частота (повторяемость фактора Х)
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя; ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
24) Закон сложения (разложения) вариации и дисперсии
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.
25) Понятие рядов распределения, их виды.
Часто встречаются группировки, где известна численность единиц в группах или удельный вес каждой группы в общем итоге. Такая группировка называется рядом распределения. Ряд распределения характеризуется двумя элементами:
1. Обозначение группы
2. Численность единиц в группах
Численность каждой группы называется частотами ряда распределения. Сумма всех частот определяет численность всей совокупности. Численность групп, выраженная в долях от общей численности единиц называется частостями и выражается в процентах.
Ряды распределения могут быть образованы по атрибутивному или количественному признакам. При группировке по атрибутивному признаку ряд распределения составляют отдельные группы, указываемые их наименованием и численность или удельный вес каждой группы в процентах к итогу.
При группировке данных по количественному признаку получаются ряды, называемые вариационными. В статистике различают вариационные ряды прерывные (дискретные) и непрерывные. Вариационный ряд будет дискретным, если его группы составлены по признаку изменяющемуся прерывно. Вариационный ряд называется непрерывным если группировочный признак, составляющий основание группировки может принимать в определенном интервале любые значения.
Статистический ряд распределения — это упорядоченое распределение единиц совокупности на группы по определенному варьирующему признаку.
В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам. Ряд распределения принято оформлять в виде таблиц. Ниже приведем атрибутивный ряд распределения юридической помощи адвокатов гражданам. Представленный в табл. 3.11 ряд показывает, как общее число случаев юридической помощи адвокатов распределялось по видам и формам правовой помощи в 1994 г.
Элементами этого ряда распределения являются значения атрибутивного признака, представленного названиями видов правовой помощи, оказанной адвокатами, и числа случаев, относящихся к каждому виду и форме помощи. Наибольший удельный вес (почти 79%) приходится на оказание юридической помощи и виде устных советов.
Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые на несколько периодов, эти данные позволят исследовать изменение структуры.
Вариационными называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду, т е. конкретное значение варьирующего признака. Частоты — это численности отдельных вариантов или каждой группы вариационного ряда, т. е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.
Как известно, вариация количественных признаков может быть дискретной (прерывной) или непрерывной.
В случае дискретной вариации величина количественного признака принимает только целые значения. Следовательно, дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку.
studfiles.net
Тема 2. Показатели описательной статистики. Среднее, дисперсия, стандартное отклонение, эксцесс, асимметрия, интервалы. Компьютерные технологии получения дескриптивной статистики.
Показатели описательной статистики
Для того чтобы обнаружить общие свойства совокупности, выявить закономерности и в результате получить правильные выводы, необходимы обобщающие, количественные показатели. Они позволят определить тенденцию развития процесса или явления, нивелировать случайные, индивидуальные отклонения, подсчитать риск того или иного решения и, кроме того, сравнить различные вариационнные ряды (различные наборы данных). Эти количественные показатели называются показателями описательной статистики. Средний курс валют на бирже, прожиточный минимум, дифференциация доходов населения, количество денег, которое потратят потребители — все это относится к показателям описательной статистики.
Показатели описательной статистики можно условно разделить на четыре группы:
1. Показатели уровня — описывают положение данных на числовой оси. К такого рода показателям относятся минимальный и максимальный элементы выборки, верхний и нижний квартили, перцентиль, а также различные средние и другие характеристики.
2. Показатели рассеяния — описывают степень разброса данных относительно своего центра. Примерами таких показателей являются, прежде всего, дисперсия, стандартное отклонение, размах выборки, межквартильный размах и т.д.
3. Показатели асимметрии — характеризуют симметрию распределения данных около своего центра. К этой группе показателей относятся коэффициент асимметрии, эксцесс, положение медианы относительно среднего и т.д.
4. Показатели, которые описывают закон распределения данных. К ним относятся таблицы частот, кумуляты, гистограммы.
Показатели описательной статистики. Показатели уровня.
К количественным характеристикам набора данных, которые относятся к показателям уровня относятся минимальный и максимальный элементы выборки, верхний и нижний квартили, перцентиль, а также различные средние и т.д.
Виды средних величин и методы их расчета.
Среди показателей описательной статистики большое значение имеют средние, поскольку они позволяют обобщить полученные данные и охарактеризовать их с помощью типичного значения.
Средней величиной называется показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Средняя величина заменяет большое число индивидуальных значений признака, обнаруживая общие свойства, присущие всем единицам совокупности. Это, в свою очередь, позволяет избежать случайных причин и выявить общие закономерности, обусловленные общими причинами. Используются две категории средних величин.
1. Степенные средние
2. Структурные средние
Первая категория — степенные средние — включает среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую. Вторая категория — это мода и медиана.
Средние величины, кроме того, бывают простые и взвешенные. Взвешенными средними называются величины, которые учитывают, что некоторые варианты значений признака могут иметь различную частоту, в связи с чем каждый вариант приходится умножать на эту частоту. Иными словами,»весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весом, или весом средней.
Средняя арифметическая — самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая — это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности. Формула средней арифметической (простой) имеет вид:
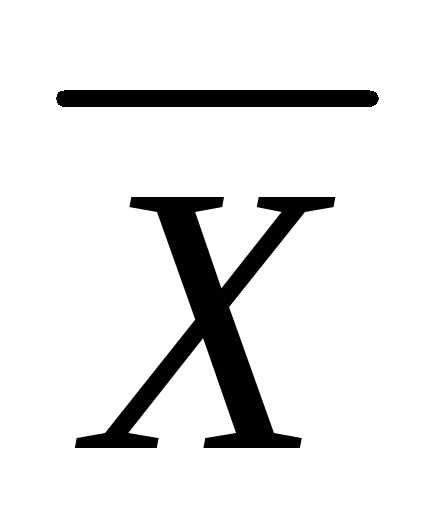 =
=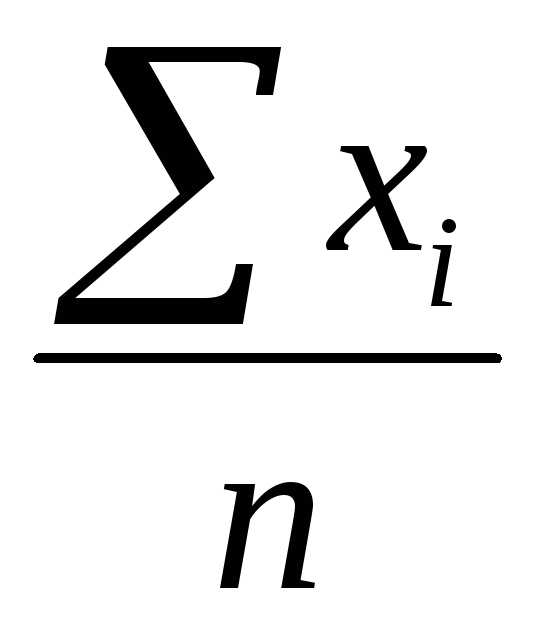
где n — численность совокупности.
Если данные сгруппированы в вариационные ряды, то расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании взвешенной средней арифметической, которая имеет вид:
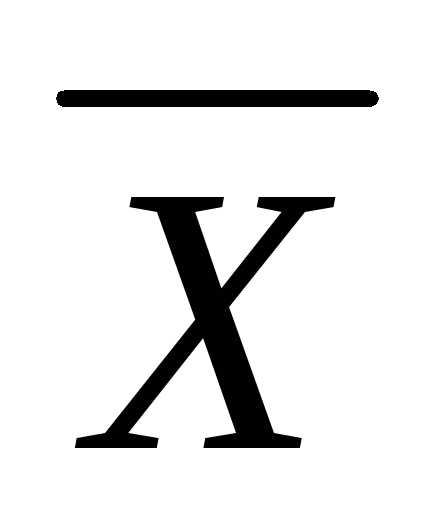 =
=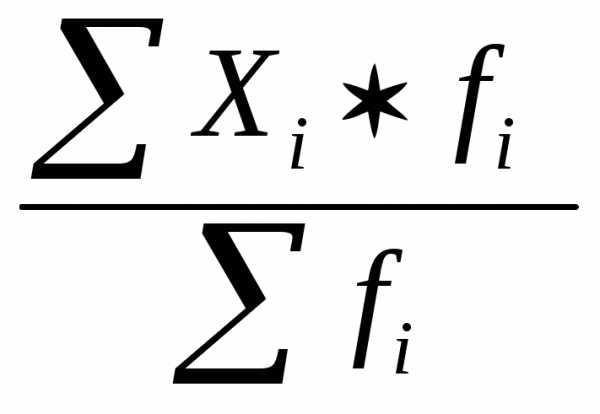
Среднюю гармоническую называют обратной средней геометрической. Просто средняя гармоническая используется тогда, когда весовые коэффициенты значений признака одинаковы. Её формула выглядит следующим образом.
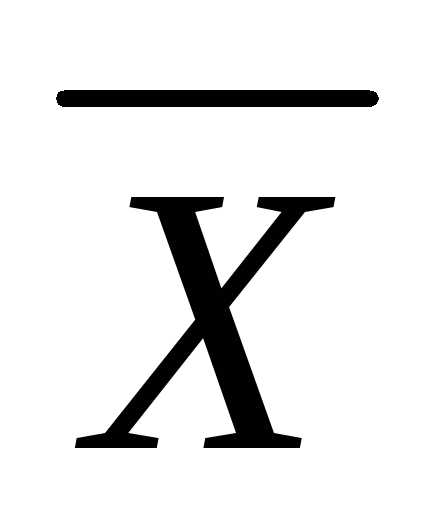 =
=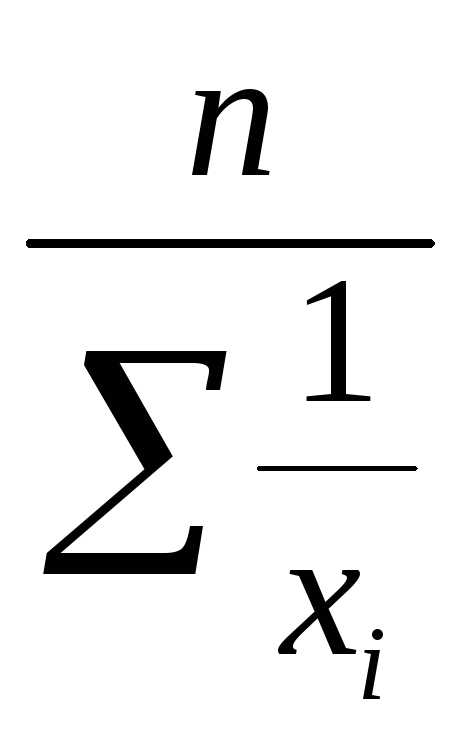
Однако в статистической практике чаще используется гармоническая взвешенная формула которой имеет вид:
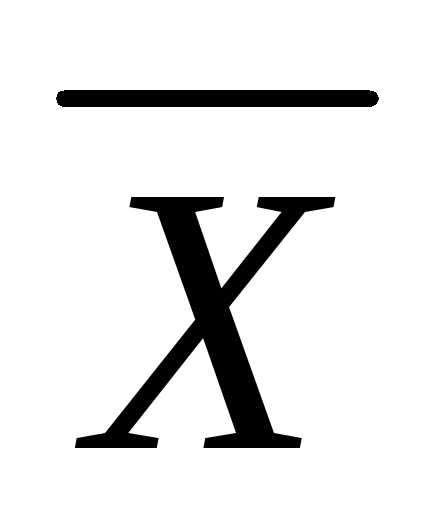 =
=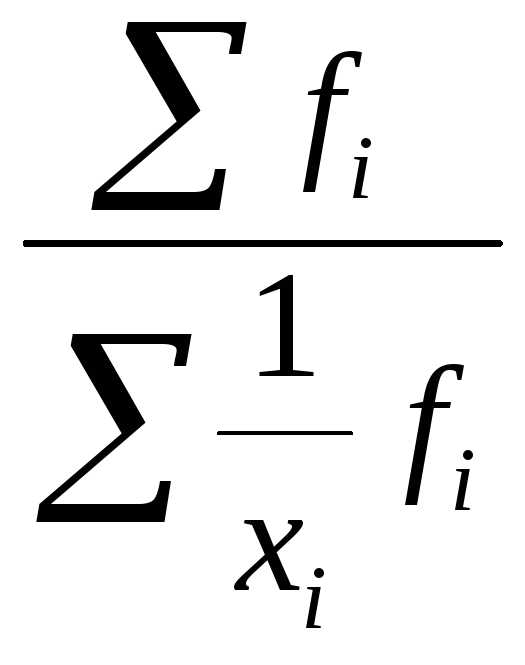
Средняя геометрическая чаще всего находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 100000). Формула для простой средней геометрической имеет следующий вид:
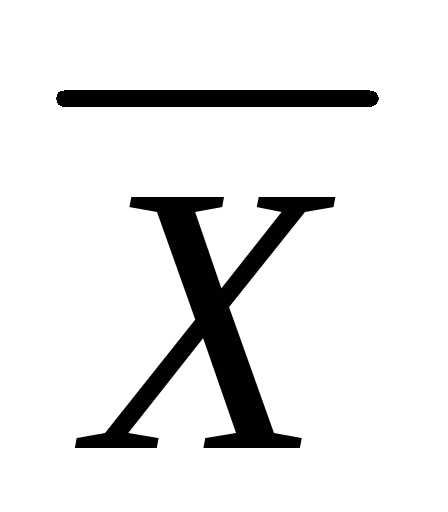 =
=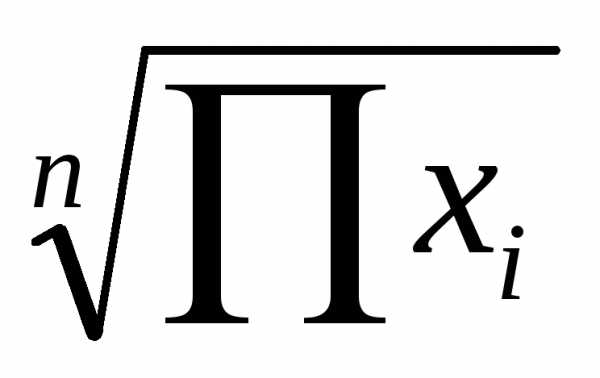
Медиана и мода.
Для определения структуры представленных данных используются особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном вариационном ряду.
Медиана (Me)— это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.
Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 8, 8, 10) медианой будет величина, которая, соответственно, расположена в центре ряда, т.е. пятая величина.
Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежным величин. Для нашего случая медиана равна (7 + 10)/2 = 8,5.
Иными словами, для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле:

где n — число единиц в совокупности.
Численное значение медианы определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений.
Ранг, перцентиль и квартиль
При анализе взаимного расположения значений признака в наборе данных, наряду с такими понятиями, как медиана и мода, используются также понятия ранга, перцентиля и квартиля. Под рангом (R) понимают номер (порядковое место) значения случайной величины в наборе данных. Правила присвоения рангов состоят в следующем.
1. Если в наборе данных все числа разные, то каждому числу х, присваивается уникальный ранг R.
2. Если в наборе данных встречается группа из k одинаковых чисел хi = хi+1 = хi+2 =… хi+k, то ранг у них одинаковый и равен рангу первого числа из этой группы Ri,. Число, следующее за этой группой, получает ранг, равный Ri+k.
3. Если данные упорядочены в порядке убывания, то
а) максимальное значение в наборе данных имеет ранг, равный 1;
б) минимальное значение в наборе данных имеет наибольшее значение ранга, равное n—kmin+1 где n — количество данных в наборе, kmin — количество повторяющихся минимальных значений в наборе данных.
4. Если данные упорядочены в порядке возрастания, то
а) минимальное значение в наборе данных имеет ранг, равный 1;
б) максимальное значение в наборе данных имеет наибольшее значение ранга, равное n-kmax+1, где n — количество данных в наборе, kmax — количество повторяющихся максимальных значений в наборе данных.
Перцентиль обобщает информацию о рангах, характеризуя значение, достигаемое заданным процентом общего количества данных, после того, как данные упорядочиваются (ранжируются) по возрастанию. Перцентили — это характеристики набора данных, которые выражают ранги элементов в виде процентов от 0 до 100%, а не в виде чисел от 1 до n, таким образом, что наименьшему значению соответствует нулевой перцентиль, наибольшему — 100-й, медиане — 50-й и т.д. Перцентили можно рассматривать как показатели, разбивающие наборы количественных и порядковых данных на определенные части. Например, 70-й перцентиль эффективности продаж может быть равен 60 тыс. тенге. (измерен не в процентах, а в тенге, как и элементы набора данных). Если этот 70-й перцентиль, равный 60 тыс. тенге., характеризует деятельность определенного агента по продажам , то это означает, что приблизительно 70% других агентов имеют результаты ниже, чем у этого агента, а 30% имеют более высокие результаты.
Перцентили используются для двух целей.
1. Чтобы показать значение элемента при заданном перцентильном ранге (например,
«20-й перцентиль равен 40 тыс. тенге.»).
2. Чтобы показать перцентильный ранг значения данного элемента в наборе данных (например, «эффективность продаж агента по сбыту А составляет 25 тыс. тенге., что соответствует 60-му перцентилю.
Дополняют набор базовых характеристик квартили, определяемые как 25-й и 75-й Перцентили. Ранги квартилей вычисляются по следующим формулам:
Ранг нижнего квартиля = (1 + int/{(1 + n)/2})/2
Ранг верхнего квартиля = n + 1 — pанг нижнего квартиля,
где int означает функцию взятия целого, которая отбрасывает дробную часть числа.
Такие характеристики, как наименьшее значение, нижний квартиль, медиана, верхний квартиль и наибольшее значение, дают достаточно ясное представление об особенностях набора данных. Два экстремума (наибольшее и наименьшее значение данных) характеризуют размах (диапазон) данных, медиана показывает центр, два квартиля определяют границы, которые расположены в центре каждой половины данных, а положение медианы относительно квартилей дает грубое представление о наличии или отсутствии асимметрии.
Показатели рассеяния
Степень разброса данных относительно своего центра описывают показатели рассеяния. К таким показателям относятся размах выборки, дисперсия, стандартное отклонение, межквартильный размах и т.д.
Размах выборки (Rs) — самый доступный (по простоте расчета) абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной выборки:
Rs = X max -X min
Размах выборки (размах колебаний) — важный показатель колебания признака, но позволяет увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колебаний используются другие показатели.
Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Все отклонения берутся по модулю.
Формула среднего линейного отклонения (простая)
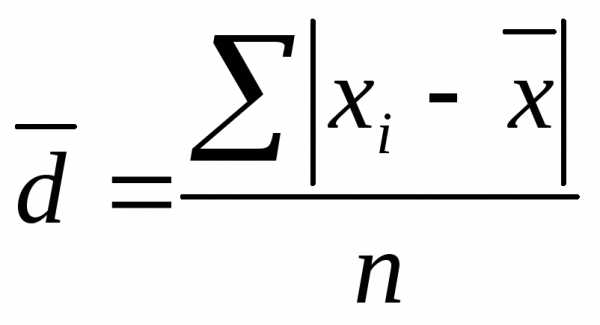
Формула среднего линейного отклонения (взвешенная)
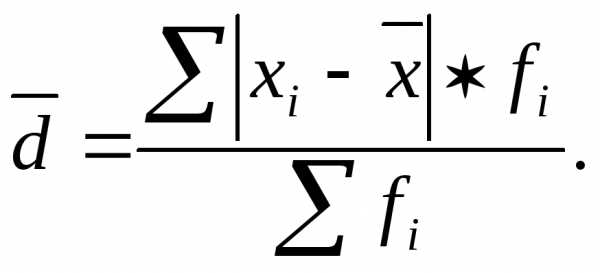
Оценки вариации
При использовании
показателей среднего линейного отклонения
возникают определенные неудобства,
связанные с тем, что приходится иметь
дело не только положительными, но и с
отрицательными величинами. Это привело
к поиску других способов оценки вариации,
чтобы иметь дело только с положительными
величинами. Таким способом стало
возведение всех отклонений во вторую
степень. Обобщающие показатели, найденные
с использованием вторых степеней
отклонений, получили широкое
распространение. К таким показателям
относятся среднее квадратическое
отклонение  и среднее квадратическое отклонение в
квадрате
и среднее квадратическое отклонение в
квадрате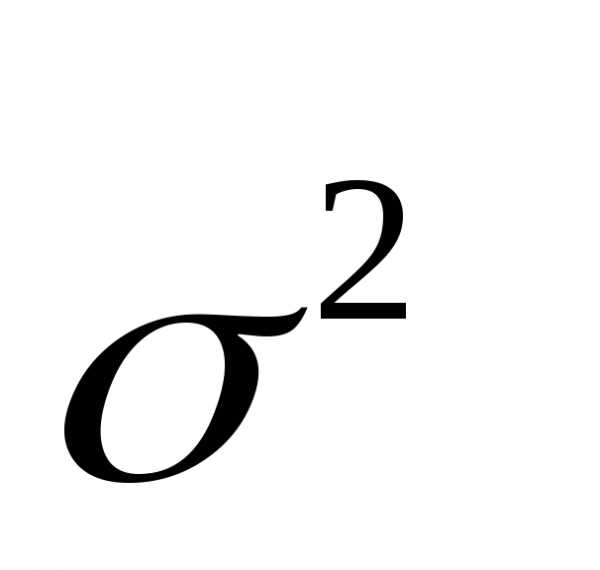 , которое называют дисперсией.
, которое называют дисперсией.
Среднее квадратическое отклонение позволяет оценить степень разброса случайных значений относительно средней величины. Для расчета среднего квадратического отклонения используется средняя квадратическая величина.
Формула простой средней квадратической
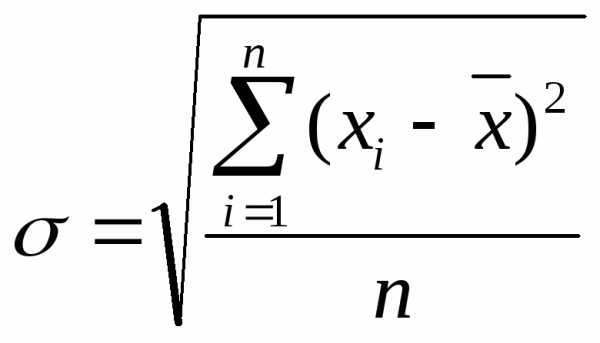
Формула для расчета взвешенной средней квадратической
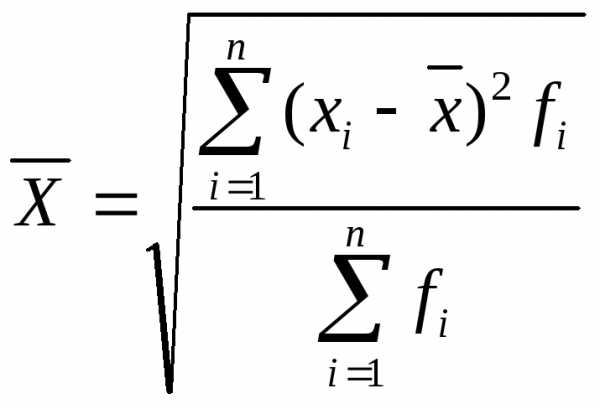
Дисперсия (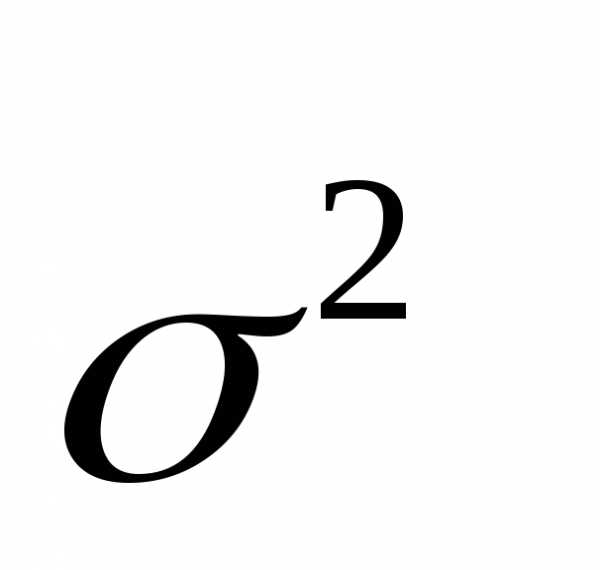 )
— это средний квадрат отклонений
индивидуальных значений признака от
его средней величины.
)
— это средний квадрат отклонений
индивидуальных значений признака от
его средней величины.
Формула дисперсии :
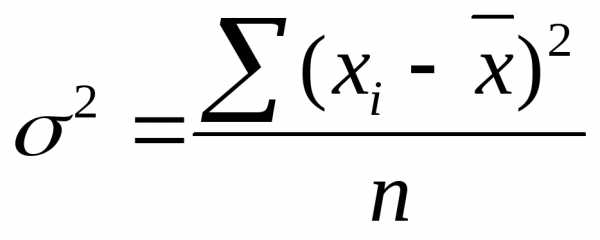 .
.
Формула несмещенной дисперсии:
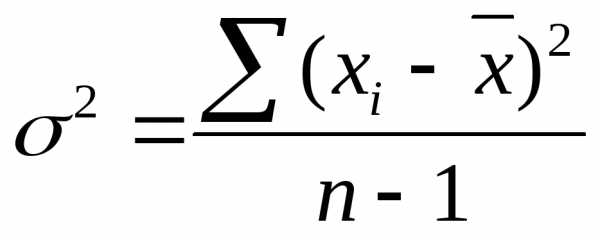 .
.
Формула дисперсии (взвешенной):
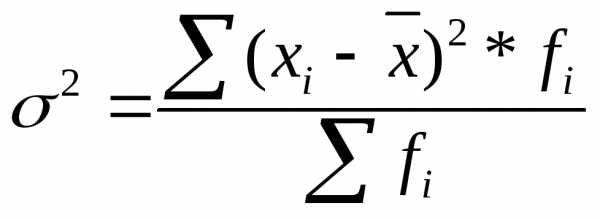 .
.
Средняя ошибка
(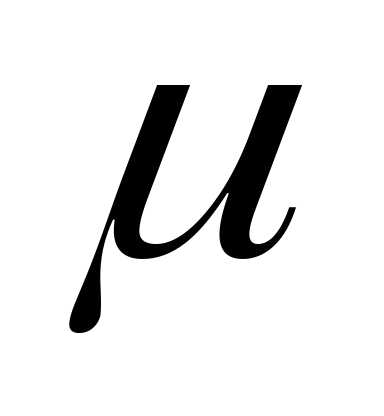 )
характеризует стандартное отклонение
выборочного среднего, рассчитанное по
выборке размераn из генеральной совокупности, и зависит
от дисперсии генеральной совокупности
и объема выборки n:
)
характеризует стандартное отклонение
выборочного среднего, рассчитанное по
выборке размераn из генеральной совокупности, и зависит
от дисперсии генеральной совокупности
и объема выборки n:
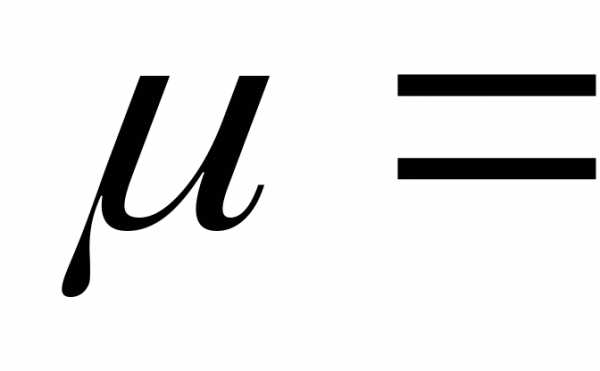
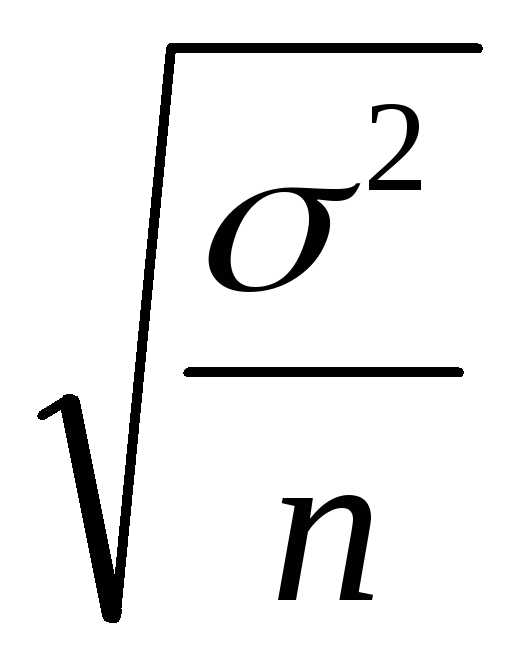
Средняя ошибка
выборки 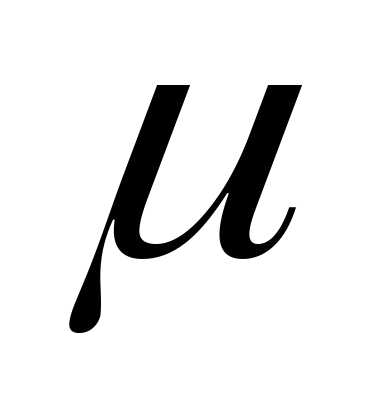 используется для расчета предельной
ошибки выборки
используется для расчета предельной
ошибки выборки
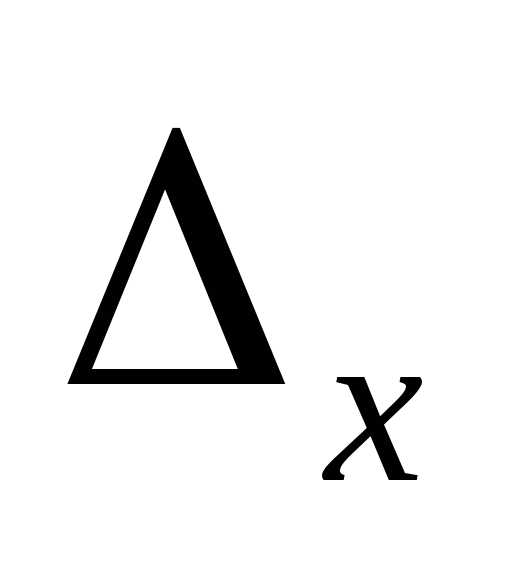 ,
которая позволяет выяснить, в каких
пределах находится величина средней
по генеральной совокупности.
,
которая позволяет выяснить, в каких
пределах находится величина средней
по генеральной совокупности.
Установлено, что
предельная ошибка выборки 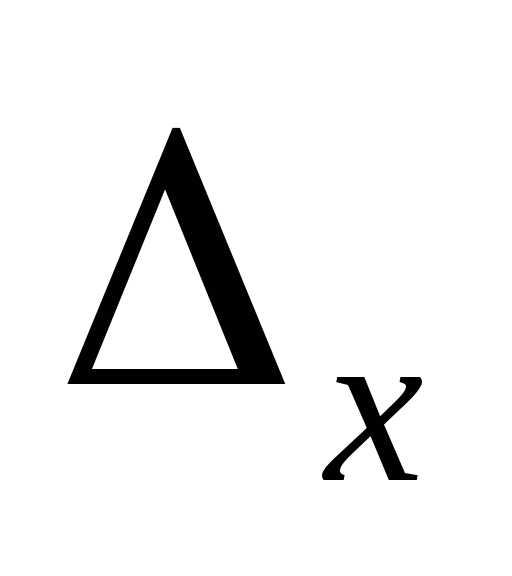 связана со средней ошибкой выборки
связана со средней ошибкой выборки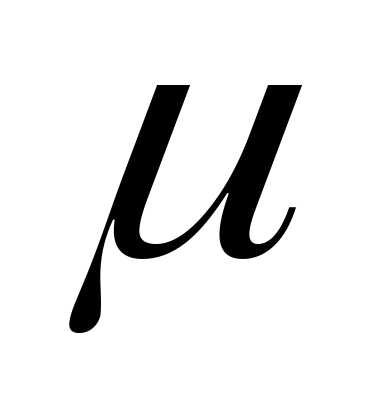 соотношением:
соотношением:
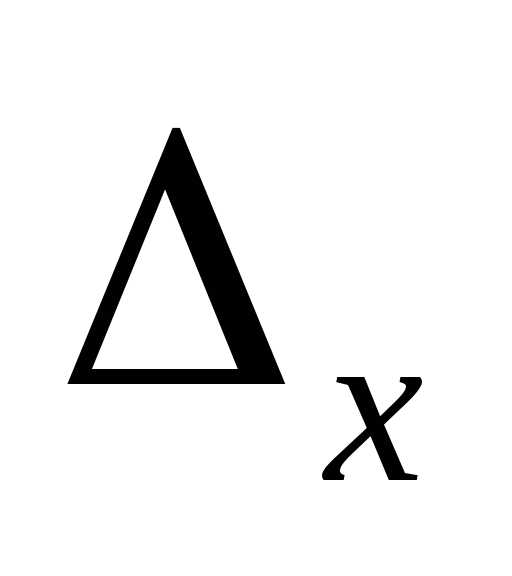 =t*
=t*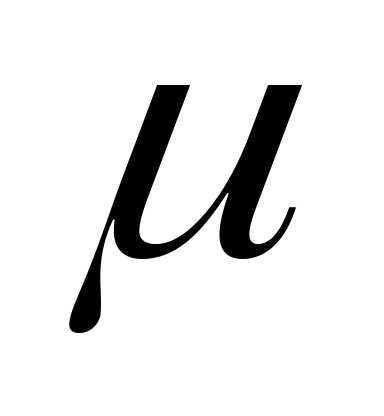
где t — коэффициент доверия (определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования).
Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах. Они используются для сравнения колебаний различных признаков одной и той же совокупности или для сравнения колебаний признака в нескольких совокупностях.
Данные показатели
рассчитываются как отношение размаха
вариации к средней величине признака
( ,
коэффициент осцилляции), отношение
среднего линейного отклонения к
средней величине признака (
,
коэффициент осцилляции), отношение
среднего линейного отклонения к
средней величине признака (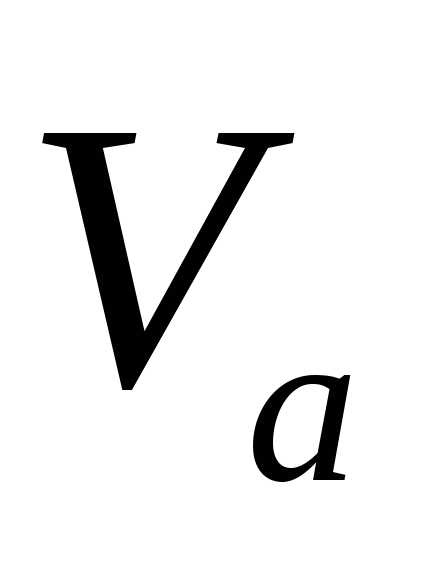 ,
линейный коэффициент вариации), отношение
среднего квадратического отклонения
к средней величине признака (
,
линейный коэффициент вариации), отношение
среднего квадратического отклонения
к средней величине признака (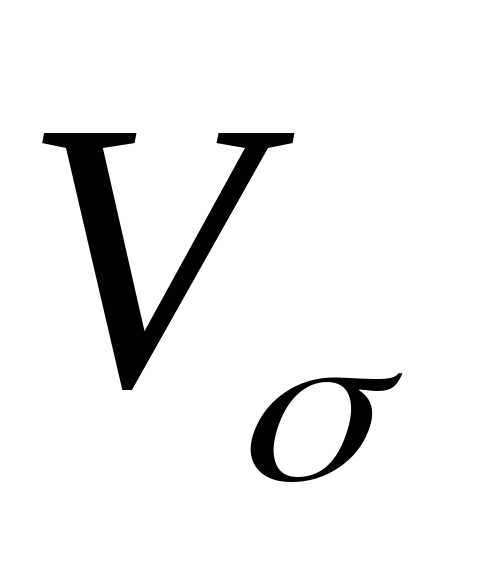 ,
коэффициент вариации) и, как правило,
выражаются в процентах.
,
коэффициент вариации) и, как правило,
выражаются в процентах.
Формулы расчета относительных показателей вариации:
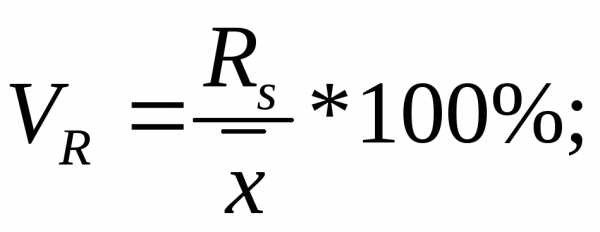
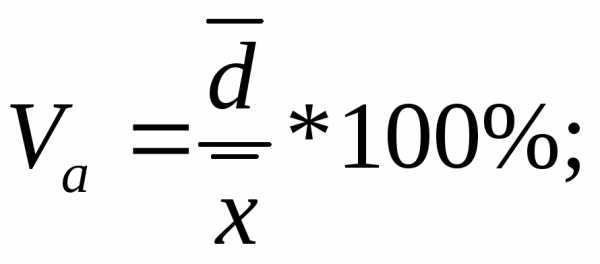
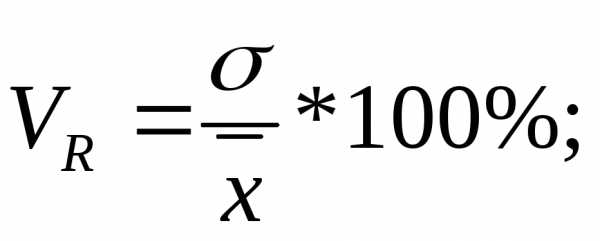
Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значения признака.
На практике наиболее часто используется коэффициент вариации. Он применяется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному распределению).
Показатели асимметричности
При использовании показателей асимметричности можно определить форму кривой распределения и выяснить общий характер распределения, что предполагает оценку степени его однородности, а также вычисления показателей эксцесса и асимметрии.
Эксцесс (Ek) характеризует
«крутизну», т.е островершинность или
плосковершинность распределения. Он
может быть рассчитан для любых
распределений. Если эксцесс больше
0 (Ek >0), то распределение островершинное,
если меньше 0 (Ek <0) — то плосковершинное.
характеризует
«крутизну», т.е островершинность или
плосковершинность распределения. Он
может быть рассчитан для любых
распределений. Если эксцесс больше
0 (Ek >0), то распределение островершинное,
если меньше 0 (Ek <0) — то плосковершинное.
Асимметричность имеет такой показатель, как коэффициент асимметрии (As). Асимметрия, или коэффициент асимметрии, является мерой несимметричности распределения. Если этот коэффициент отчетливо отличается от 0, распределение является асимметричным. Если разбить такое распределение пополам в точке среднего (или медианы), то распределения значений с двух сторон от этой центральной точки будут неодинаковыми (те несимметричными). Такое распределение можно назвать еще «скошенным». Если As > 0, то асимметрия будет правосторонней, если As < 0 — левосторонней Если этот коэффициент близок к 0, распределение является симметричным.
Как было показано, чтобы всесторонне охарактеризовать совокупность данных, необходимо рассчитать достаточно большое количество показателей. Это можно сделать различными способами, например с помощью соответствующих функций MS Excel. Однако расчет показателей с помощью функций — сравнительно длительный процесс, MS Excel располагает инструментом Descriptive Statictics, который может быть использован для получения статистического отчета одновременно по основным показателям уровня, разброса и асимметрии выборочной совокупности.
Литература:1осн. [164-203], 5 осн. [30-37], 6 осн. [14-16], 3доп. [114-159], 4доп. [64-77], 6доп. [172-180].
Контрольные вопросы
1. Какие задачи решаются на основе анализа показателей описательной статистики?
2. На какие группы делятся описательная статистика ?
3. Каковы виды средних и методы их расчета?
4. Каковы показатели, определяющие структуру статданных?
5. Каковы показатели, определяющие взаимное расположение статданных?
Тема 3. Закономерности распределения статданных, их применение в статистическом исследовании. Нормальное распределение их, его применение в статистическом исследовании. Компьютерные технологии анализа распределения статданных.
Закономерности распределения статданных.
При исследование статданных можно заметить определенную зависимость между изменением значений варьирующего признака и частот. Частоты с увеличением значения варьирующего признака первоначально увеличиваются, а затем после достижения какой-то максимальной величины в середине ряда уменьшаются. Это свидетельствует о том, что частоты в вариационных рядах изменяются закономерно в связи с изменением варьирующего признака. Такие закономерности изменения частот в вариационных рядах называются закономерностями.
Одна из важных целей статистического изучения вариационных рядов состоит в том, чтобы выявить закономерность распределения и определить ее характер. Основной путь в выявлении закономерностей распределения состоит в построении вариационных рядов для достаточно больших по численности статистических совокупностей. Кроме того, большое значение для нахождения закономерностей распределения имеет правильное построение самого вариационного ряда. Речь идет прежде всего о таком определении оптимального числа групп и размера интервала, при котором закономерность распределения видна более отчетливо. Закономерности распределения выражают свойства явлений, общие условия, влияющие на формирование вариации признака. Когда мы говорим о характере, типе закономерностей распределения, то имеем в виду отражение в них общих условий, определяющих распределение. При этом следует учитывать, что речь идет о распределениях, отражающих однородные явления. Многие явления, рассматриваемые каждое в отдельности, изолированно друг от друга, кажутся случайными. Однако если анализировать эти явления в совокупности с другими, аналогичными по своей сущности, то часто удается обнаружить закономерность, связанную с их возникновением. Если на практике часто встречается один и тот же тип распределения частот, целесообразно описать его с помощью математической формулы, которая может служить для сравнения и обобщения различных совокупностей аналогичных данных. В статистике широко используются различные виды теоретических распределений — нормальное распределение, биномиальное распределение, распределение Пуассона и др. Каждое из теоретических распределений имеет специфику и свою область применения в различных отраслях знания.
Нормальный закон распределения
Большинство экспериментальных исследований в биологии, медицине, технике и других областях связаны с измерениями, результаты которых могут принимать практически любые значения в заданном интервале и описываются моделью непрерывных случайных величин. Одним из важнейших непрерывных распределений является нормальное, или гауссово распределение.
Нормальное распределение получило широкое распространение для приближенного описания многих случайных явлений, в которых на результат воздействует большое количество независимых случайных факторов, среди которых нет сильно выделяющихся. Кроме того, многие распределения, связанные со случайной выборкой, при увеличении ее объема переходят в нормальное. Однако следует отметить, что в природе встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.
Плотность вероятностей нормально распределенной случайной величины задается формулой:
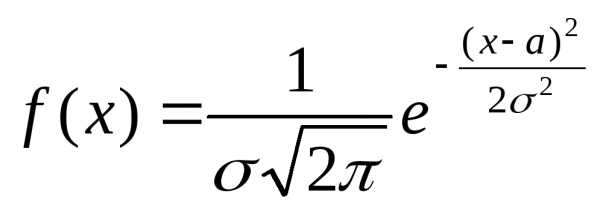 -∞<x<+∞.
(*)
-∞<x<+∞.
(*)
Таким образом, нормальное распределение определяется двумя параметрами: а и σ.
Здесь а и σ — параметры распределения. Иногда используют краткое обозначени N(a, σ2). Математическое ожидание и дисперсия случайной величины, распределенной как N(a, σ2), равны соответственно a и σ2.
Можно сказать, что нормальное распределение это совокупность объектов, в которой крайние значения некоторого признака — наименьшее и наибольшее — появляются редко; чем ближе значение признака к математическому ожиданию, тем чаще оно встречается. Например, распределение студентов по их весу приближается к нормальному распределению.
f(x)
x
Кривая плотности нормального распределения.
Диаграмма нормального распределения симметрична относительно точки а, то есть положительные и отрицательные равновеликие отклонения от центра распределения (математического ожидания) встречаются одинаково часто. Поэтому медиана нормального распределения равна а.
Параметр σ характеризует степень сжатия или растяжения (плотности) диаграммы. Чем больше σ, тем «шире» кривая, а ее максимальная высота ниже. Кривая как бы растягивается в стороны.
В область от а — σ до а + σ нормально распределенная случайная величина попадает с вероятностью 0,683. В пределы от -2σ до +2σ случайная величина попадает с вероятностью 0,955, а в пределы от -3σ до +3σ — с вероятностью 0,997. Последняя закономерность трактуется как правило трех сигм.
Формула (*) описывает целое семейство нормальных кривых, зависящих, как было сказано ранее, от двух параметров — а и σ, которые могут принимать любые значения, поэтому существует бесконечно много нормально распределенных совокупностей.
Особую роль играет нормальное распределение с параметрами а = 0 и σ =1,то есть распределение N(0,1), которое часто называют стандартным или нормированным нормальным распределением. Плотность стандартного нормального распределения вычисляют по формуле:
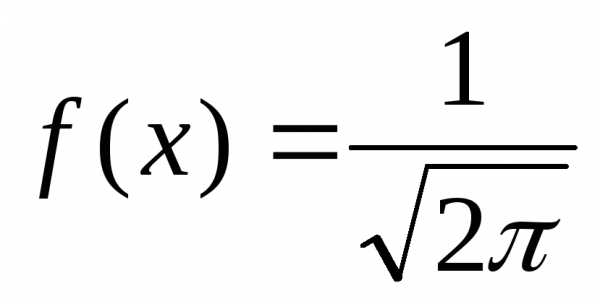

Проверка соответствия теоретическому распределению. Важной задачей, возникающей при анализе, статданных является оценка меры соответствия (расхождения) полученных эмпирических данных и каких-либо теоретических распределений. Это связано с тем, что в большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны. В то же время применяемые статистические методы в качестве предпосылок часто требуют определенного закона распределения.
Наиболее часто проверяется предположение о нормальном распределении генеральной совокупности, поскольку большинство статистических процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности.
Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют графический метод, выборочные параметры формы распределения и критерии согласия. Графический метод позволяет давать ориентировочную оценку расхождения или совпадений распределений .
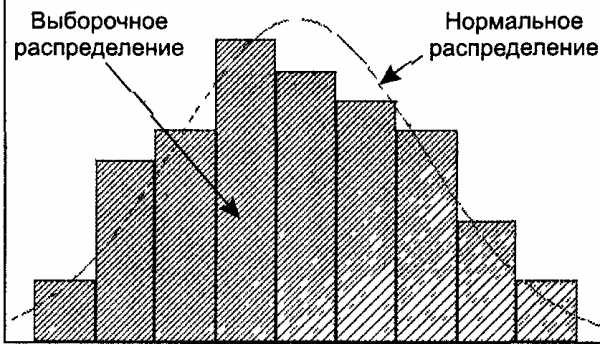
Сопоставление выборочного распределения и кривой нормального распределенния
При большом числе наблюдений (п > 100) неплохие результаты дает вычисление выборочных параметров формы распределения: эксцесса и асимметрии . Принято говорить, что предположение о нормальности распределения не противоречит имеющимся данным, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс — от 2 до 4. Наиболее убедительные результаты дает использование критериев согласия. Критериями согласия называют статистические критерии, предназначенные для проверки согласия опытных данных и теоретической модели. Здесь нулевая гипотеза Н0 представляет собой утверждение о том, что распределение генеральной совокупности, из которой получена выборка, не отличается от нормального. Среди критериев согласия большое распространение получил непараметрический критерий X2 (хи-квадрат). Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитанными па формулам нормального распределения.
Отметим, что сколько-нибудь уверенно о нормальности закона распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях меньшего числа данных можно говорить только о том, что данные не противоречат нормальному закону, и в этом случае обычно используют графические методы оценки соответствия. При большем числе наблюдений целесообразно совместное использование графических и статистических (например, тест хи-квадрат или аналогичные) методов оценки, естественно дополняющих друг друга.
Использование критерия согласия хи-квадрат. Для применения критерия желательно, чтобы объем выборки п > 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находилось не менее 5 наблюдений (частот).
Отметим, что сравниваться должны именно абсолютные частоты, а не относительные (частости). При этом, как и любой другой статистический критерий, критерий хи-квадрат не доказывает справедливость нулевой гипотезы (соответствие эмпирического распределения нормальному), а лишь может позволить ее отвергнуть с определенной вероятностью (уровнем значимости).
Как было отмечено, используются и другие распределения, например, Бернулли, Пуассона, дискретное, F-распределение, t-распределение, биномиальное. C помощью статистических функций, которыми располагает Microsoft Excel, можно рассчитать вероятность случайной величины, распределенной по одному из указанных выше законов распределения. Например, есть возможность генерировать последовательность случайных чисел, распределенных по одному из перечисленных выше законов распределения, также производить оценку выборку на принадлежность к тому или иному распределению.
Литература:
1осн. [197-211], 5осн. [30-37], 3доп. [182-190], 4 доп. [78-94], 6доп. [185-188].
Контрольные вопросы
1. Для чего необходимо знать вид распределения статданных при их анализе?
2. Почему нормальное распределение широко используется в статанализе?
3. Какие теоретические распеределения, кроме нормального, используются при анализе статданных?
4. Какие параметры влияют на форму нормально распределенных статданных?
5. Каков смысл правила «трех сигм»?
studfiles.net
Среднее квадратическое отклонение, Линейное отклонение
Среднее квадратическое отклонение
Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:
1. Для первичного ряда:
2. Для вариационного ряда:
Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:
Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.
Примеры нахождения cреднего квадратического отклонения: Пример 1, Пример 2
Для альтернативных признаков формула среднего квадратичного отклонения выглядит так:
где р — доля единиц в совокупности, обладающих определенным признаком;
q — доля единиц, не обладающих этим признаком.
Понятие среднего линейного отклонения
Среднее линейное отклонение определяется как средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средних арифметических.
1. Для первичного ряда:
2. Для вариационного ряда:
где сумма n — сумма частот вариационного ряда.
Пример нахождения cреднего линейного отклонения: Пример 1
Преимущество среднего абсолютного отклонения как меры рассеивания перед размахом вариации, очевидно, так как эта мера основана на учете всех возможных отклонений. Но этот показатель имеет существенные недостатки. Произвольные отбрасывания алгебраических знаков отклонений могут привести к тому, что математические свойства этого показателя являются далеко не элементарными. Это сильно затрудняет использование среднего абсолютного отклонения при решении задач, связанных с вероятностными расчетами.
Поэтому среднее линейное отклонение как мера вариации признака применяется в статистической практике редко, а именно тогда, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется оборот внешней торговли, состав работающих, ритмичность производства и т. д.
Среднее квадратическое
Среднее квадратическое применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.
Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.
Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
Средняя квадратичная взвешенная вычисляется по формуле:
где f — признак веса.
Средняя кубическая
Средняя кубическая применяется, например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:
Средняя кубическая взвешенная:
При расчете средних величин и дисперсии в интервальных рядах распределения истинные значения признака заменяются центральными значениями интервалов, которые отличны от средней арифметической значений, включенных в интервал. Это приводит к возникновению систематической погрешности при расчете дисперсии. В.Ф. Шеппард определил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала как в сторону повышения, так и в сторону понижения величины дисперсии.
Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по значительному количеству исходных данных (n > 500). Однако исходя из того, что в ряде случаев обе погрешности, действуя в разных направлениях компенсируют друг друга, можно иногда отказаться от введения поправок.
Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина.
В практике статистики часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для таких сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.
Для осуществления таких сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с разными средним арифметическим используется относительный показатель вариации — коэффициент вариации.
Структурные средние
Для характеристики центральной тенденции в статистических распределениях не редко рационально вместе со средней арифметической использовать некоторое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.
Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.
Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
univer-nn.ru
Виды дисперсии, правило сложения дисперсий
Изучение вариации (колеблемости, рассеивания) (см. Показатели вариации) признака по всей совокупности в целом, предусматривает изучение вариации для каждой из составляющих ее групп, а также между этими группами. В простейшем случае, когда совокупность разбита на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой.
Общая дисперсия D(x) измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака (хi) от общей средней величины и может быть вычислена как: 1. простая дисперсия 2. взвешенная дисперсия
Межгрупповая дисперсия (факторная) характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних от общей средней:
Внутригрупповая дисперсия (частная, остаточная, случайная) отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы (хi) от средней арифметической этой группы (xср) (групповой средней) и может быть исчислена как:
1. простая дисперсия 2. взвешенная дисперсия
На основании внутригрупповой дисперсии по каждой группе можно определить общую среднюю из внутригрупповых дисперсий:
Дисперсия и среднее значение доли альтернативного признака
Среди варьирующих признаков, которые изучает статистика, встречаются признаки, которые проявляются в том, что у одних единиц совокупности эти признаки наблюдаются, у других нет. Иными словами: альтернативный признак — это такой единственный признак, который может принимать единица совокупности из всех возможных вариантов. Если рассматривать продукцию по категориям (сортам), то она может быть либо только I категории (сорта), либо только II категории (сорта) — в данном контексте следует рассматривать эти признаки как два противоположных события. Признаки, которыми обладают одни единицы и не обладают другие, называются альтернативными. Количественно вариация альтернативного признака в численности всей совокупности обозначается p, а доля единиц, не обладающих этим признаком, обозначается q и принимает значения: p=1, q=0
(смотри Ошибка выборки для доли альтернативного признака)
- Среднее значение для доли альтернативного признака
- Дисперсия альтернативного признака
Подставив в формулу дисперсии q = 1 – p, получим:
Таким образом, дисперсия альтернативного признака равна произведению доли на дополняющее эту долю до единицы число. Т.к. p+q=1, то средний квадрат отклонений не может быть больше 0,25. Среднеквадратическое отклонение доли альтернативного признака:
Правило сложения дисперсий
Согласно правилу сложения дисперсий, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий.
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Эмпирическое корреляционное отношение (см. пример) – это корень квадратный из эмпирического коэффициента детерминации:
Он показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии, т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Смотри схему дисперсионного анализа: Проверка адекватности регрессионной модели
Примечание: приведены так же формулы расчета коэффициента детерминации и корреляционного отношения, которые используются при анализе рядов динамики.
Пример расчета дисперсии
Условие:
Объем дневной выручки в 5 торговых точках составил: 16, 21, 26, 23, X5 (у.е.). Учитывая, что Хср.= 22, найти выборочную дисперсию S2
Решение: Опр. среднюю
Смотри также
helpstat.ru
Виды дисперсии, правило сложения дисперсий
Вариация – различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
К показателям вариации относятся:
I группа — абсолютные показатели вариации
- размах вариации
- среднее линейное отклонение
- дисперсия
- среднее квадратическое отклонение
II группа — относительные показатели вариации
- коэффициент вариации
- коэффициент осцилляции
- относительное линейное отклонение
Самым элементарным показателем вариации признака является размах вариации R. Размах вариации показывает лишь крайние (min, max) отклонения признака от общей средней.
Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.
Среднее линейное отклонение — средняя арифметическая абсолютных значений отклонений (модуль отклонений) отдельных вариантов от их средней арифметической:
- для несгруппированных данных (простое)
- для сгруппированных данных (взвешенное)
Дисперсия признака — средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий:
- Простая дисперсия для несгруппированных данных
- Взвешенная дисперсия для вариационного ряда
Cвойства дисперсии:
- если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится;
- если все значения признака уменьшить или увеличить в одно и то же число раз (k раз), то дисперсия уменьшится или увеличится в k2 раз.
Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
где i – величина интервала, X1 — новые (преобразованные) значения вариантов (А – условное начало, в качестве которого удобно использовать середину интервала или величину признака, обладающего наибольшей частотой.
- Момент второго порядка
- Квадрат момента первого порядка
Среднее квадратическое отклонение равно корню квадратному из дисперсии:
- для несгруппированных данных (простое)
- для вариационного ряда по сгруппированным данным (взвешенное)
Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются отдельные варианты от их среднего значения.
Среднее значение альтернативного признака и его дисперсия:
- Среднее значение альтернативного признака
- Дисперсия альтернативного признака
Подставив в формулу дисперсии q = 1 – p, получим:
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком и доли единиц, не обладающих данным признаком.
Среднее квадратическое отклонение альтернативного признака:
Показатели относительного рассеивания
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умноженное на 100%.
1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг общей средней.
2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.
3. Коэффициент вариации — отношение среднего квадратического отклонения к средней арифметической, применяется для сравнения вариаций различных признаков, используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Пример расчета абсолютных и относительных показателей вариации:
Распределение КФХ области по урожайности зерновых культур
| Группы хозяйств по урожайности (ц/га) |
Середина интервала |
Число хозяйств |
Расчетные значения |
||||
|
Xi |
ƒi |
Xi ƒi |
|Хi-Хср| |
|Хi — Хср|*ƒi |
(Χi-Χср)2 |
(Χi-Χср)2 *ƒi |
|
| 9,1-15 |
12,1 |
2 |
24,20 |
12,44 |
24,87 |
154,641 |
309,28 |
| 15,1-21,1 |
18,1 |
31 |
561,1 |
6,44 |
199,50 |
41,415 |
1283,88 |
| 21,1-27,1 |
24,1 |
54 |
1301,40 |
0,44 |
23,52 |
0,190 |
10,24 |
| 27,1-33,1 |
30,1 |
30 |
903,00 |
5,56 |
166,94 |
30,964 |
928,92 |
| > 33,1 |
36,1 |
7 |
252,7 |
11,56 |
80,95 |
133,738 |
936,17 |
| Всего |
X |
124 |
3042,40 |
36,44 |
495,77 |
360,948 |
3468,48 |
| Средние |
X |
X |
24,54 |
X |
4,00 |
27,97 |
|
Смотри также:
helpstat.ru
