Дать определение модуля комплексного числа. Доказать свойства модуля.
Определение.Комплексным числомz=x+iy называется упорядоченная пара действительных чисел : .
Действительные числа х и у называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются:
Определение.Вещественное неотрицательное число:
называют модулем комплексного числа .
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)
Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
.
Теорема. (Свойства модуля комплексного числа.)
Пусть – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
1) и . Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
3) ;
4) ;
Доказательство. 1) По предыдущей теореме имеем:
, где и ,
т.е. .
Таким образом, равенства и есть тригонометрическаяформа записи числа , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем , ч.т.д.
Далее, т.к. , то по только что доказанному свойству , ч.т.д.
Заметим, что последнее равенство можно получить и из других соображений.
Противоположные числа на комплекснойплоскости изображаютсяточками симметричными относительно начала координат. Действительно, пусть . Тогда и точки , имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е. , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
2). Пусть , . Тогда и по формуле (12) имеем:
. (14)
С другой стороны, рассмотрим числа и как точки на комплексной плоскости. Тогда точка имеет декартовыекоординаты , а и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
3) Рассмотрим на комплекснойплоскости точки , и начало координат О. В общем случае эти три точки являются вершинами треугольника :
рис.6.
Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.
Мы только что доказали, что длина стороны этого треугольника равна , а длины сторон и равны по определению модулям чисел и : , . Отсюда и получаем, что .
Заменим в последнем неравенстве число на противоположное число , тогда получаем:
, ч.т.д.
Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О, и лежат на одной прямой.
4) , откуда следует
. Поменяв местами и , получаем
, откуда и следует доказываемое неравенство.
Теорема доказана.
cyberpedia.su
доказательство свойств модуля. : Чулан (М)
здравствуйте, многоуважаемые участники форума!вот собрала свое доказательство воедино…
если тут что-то не так скажите, пожалуйста, об этом!
Свойство 1.
Доказательство.
Известно что
И
Сложив эти неравенства получим:
Рассмотрим два случая:
1.
Тогда
И
Так как модули равных величин равны.
Из
Подставив
вместо
(из выше преведенного равенства) получим:
2.
Тогда
И из неравенства
Следует
Объединяя оба случая, получим что
при любом числе
заранее спасибо!
с уважением,
sandrachka.
dxdy.ru
доказательство основных свойств модуля. : Школьная алгебра
здравствуйте, многоуважаемые!надеюсь, что на этот раз мои формулы будут читаемы.
и вы сможете дать мне свой дельный совет.
нужно доказать что
1)
Известно что
Сложив эти неравенства получим:
Проблема состоит в том, что я не могу понять как из последнего неравенства получить
2)
Известно что
Отсюда:
Отсюда:
Также известно что
А значит:
Отсюда:
И теперь нужно как-то соединить неравенства
И
И получить что
Но я не пойму как это сделать.
Надеюсь на отзывы.
С уважением,
Sandrachka.
dxdy.ru
Раздел 8. Теория сравнений Определения и простейшие свойства.
Определение 1. Пусть a, b Z, m N. Говорят, что число а сравнимо с b по модулю m, если а и b при делении на m дают одинаковые остатки. Запись этого факта выглядит так: a b(mod m).
Определение 2. Два целых числа a и b называются сравнимыми по модулю m, если их разность делится нацело на m. (ab) ⋮ m
Определение 3. Два целых числа a и b называются сравнимыми по модулю m, если a = b + mt, где t Z.
Очевидно, что бинарное отношение сравнимости m (неважно, по какому модулю) есть отношение эквивалентности на множестве целых чисел.
Ясно, что число а сравнимо с b по модулю m тогда и только тогда, когда а—b делится на m нацело. Очевидно, это, в свою очередь, бывает тогда и только тогда, когда найдется такое целое число t , что a = b + mt.
Понять процесс собирания целых чисел в классы сравнимых между собой по модулю m (классы эквивалентности m) поможет следующая картинка:
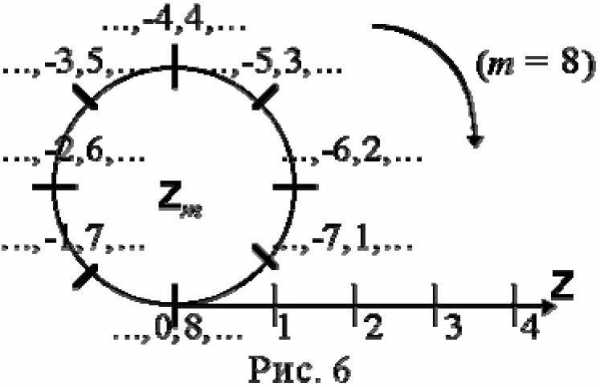
На рисунке 6 изображен процесс наматывания цепочки целых чисел на колечко с
Перечислим, далее, свойства сравнений, похожие на свойства отношения равенства.
Свойство 1. Сравнения по одинаковому модулю можно почленно складывать.
Доказательство. Пусть a1= b1(mod m), a2= b2(mod m). Это означает, что a1 = b1 +mt1, a 2 = b 2 +mt 2. После сложения последних двух равенств получим a1 + a2 =b1 +b2 +m(t1 +t2), что означает a1 + a2 = b1 + b2(mod m).
Свойство 2. Слагаемое, стоящее в какой-либо части сравнения, можно переносить в другую часть, изменив его знак на обратный.
Доказательство.
Свойство 3. К любой части сравнения можно прибавить любое число, кратное модулю.
Доказательство.
Свойство 4. Сравнения по одинаковому модулю можно почленно перемножать и, следовательно,
Свойство 5. Обе части сравнения можно возвести в одну и ту же степень.
Доказательство.
Как следствие из вышеперечисленных свойств, получаем
Свойство 6. Если a0 ≡ b0 (mod m), a1 ≡ b1 (mod m) ,…, an ≡ bn (mod m) , x ≡ y (mod m), то a0xn + a1xn-1 +…+ a
Свойство 7. Обе части сравнения можно разделить на их общий делитель, взаимно простой с модулем.
Доказательство. Пусть a ≡ b(mod m), a = a1 d, b = b1 d. Тогда (a1 – b1)d делится на m.
Поскольку d и m взаимно просты, то на m делится именно (a1 – b1), что означает a1 ≡ b1(mod m).
Свойство 8. Обе части сравнения и его модуль можно умножить на одно и то же целое число или разделить на их общий делитель.
Доказательство. a ≡ b(mod m) a = b + mt ak = bk + mkt ak ≡ bk(mod mk).
Свойство 9. Если сравнение a ≡ b имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
Доказательство. Если a ≡ b(mod m1) и a ≡ b(mod m2), то a-b делится на m1 и на m2, значит a-b делится на наименьшее общее кратное m1 и m2.
Свойство 10. Если сравнение имеет место по модулю m, то оно имеет место и по модулю
Доказательство очевидно следует из транзитивности отношения делимости: если a ≡ b(mod m), то a-b делится на m, значит a-b делится на d, где d|m.
Свойство 11. Если одна часть сравнения и модуль делятся на некоторое число, то и другая часть сравнения должна делиться на то же число.
Доказательство. a ≡ b(mod m) a=b+mt.
Пример. Доказать, что при любом натуральном n число 37п+2 +16п+1 + 23п делится на 7.
Решение. Очевидно, что 37 ≡ 2(mod 7), 16 ≡ 2(mod 7), 23 ≡ 2(mod 7)
Возведем первое сравнение в степень n+2, второе – в степень n+1, третье – в степень n и сложим:
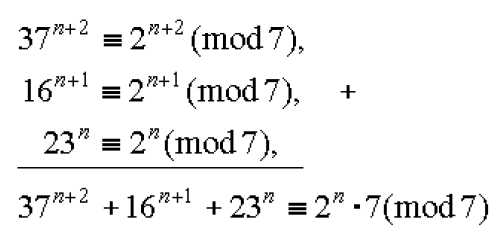
т.е. 37п+2 + 16п+1 + 23п делится на 7. Как видите, ровным счетом ничего сложного в решении подобных школьных задач «повышенной трудности» нет.
С удовольствием заканчиваю настоящий пункт, чтобы устремиться к следующему, то есть устремиться из прошлого в будущее.
studfiles.net
доказательство основных свойств модуля. : Школьная алгебра
здравствуйте, многоуважаемые!надеюсь, что на этот раз мои формулы будут читаемы.
и вы сможете дать мне свой дельный совет.
нужно доказать что
1)
Известно что
Сложив эти неравенства получим:
Проблема состоит в том, что я не могу понять как из последнего неравенства получить
2)
Известно что
Отсюда:
Отсюда:
Также известно что
А значит:
Отсюда:
И теперь нужно как-то соединить неравенства
И
И получить что
Но я не пойму как это сделать.
Надеюсь на отзывы.
С уважением,
Sandrachka.
dxdy.ru
Уравнения с модулями начинают изучать с 6-го 7-го класса, где проходят азы операций с модулями
Введение
Уравнения с модулями начинают изучать с 6-го – 7-го класса, где проходят азы операций с модулями. Однако свойств абсолютной величины не знает даже старшеклассник. Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах. Мой диплом будет посвящен изучению свойств модуля, алгебраическому и графическому решению уравнений и неравенств, содержащих знак модуля. Я считаю, что эта тема требует более глубокого исследования, так как она прослеживается в различных заданиях повышенной сложности, которые предлагают учащимся авторы дидактических материалов, в задачах математических олимпиад, заданий ЕГЭ и экзаменов при поступлении в вузы.
В своей работе я собираюсь проанализировать некоторые учебники и задачники по математике и выяснить, в каких из них присутствуют задания на свойства абсолютной величины и на графическое решение уравнений и неравенств со знаком модуля.
Основная цель работы — получение расширенной информации о модуле числа, его применении и о различных способах решения уравнений, содержащих знак абсолютной величины. Также будет создано небольшое пособие, которое будет включать в себя определение модуля, его свойства, упражнения с решениями и задания для практики. Все это поможет учащимся в решении подобных уравнений и неравенств.
Данный диплом основан на следующих работах: учебно-методические материалы П.Ф. Севрюкова и А.Н. Смолякова «Уравнения и неравенства с модулями и методика их решения», задачник Е.Г. Андреева «Сборник задач по математике».
Моя работа разделена на две главы. В первой главе представлены определение модуля, его свойства с доказательствами, а также примеры уравнений и неравенств, где применяются эти свойства. Вторая глава посвящена графическому решению уравнений и неравенств с модулями, а также краткий список учебников, задачников и пособий, в которых можно найти задания на свойства модуля и графическое решение уравнений с модулями.
Глава 1
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п.
Модуль объемного сжатия (в физике) — отношение нормального напряжения в материале к относительному удлинению.
В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно:
Модуль — абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой.
Доказательство теорем
Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля:
Из определения следует, что для любого действительного числа a,
Теорема 1. Абсолютная величина действительного числа равна большему из двух чисел a или -a.
Доказательство:
1. Если число a положительно, то -a отрицательно, т. е. -a < 0 < a. Отсюда следует, что -a < a.
Например, число 5 положительно, тогда -5 — отрицательно и -5 < 0 < 5, отсюда -5 < 5.
В этом случае |a| = a, т. е. |a| совпадает с большим из двух чисел a и — a.
2. Если a отрицательно, тогда -a положительно и a < — a, т. е. большим числом является -a. По определению, в этом случае, |a| = -a — снова, равно большему из двух чисел -a и a.
Следствие 1. Из теоремы следует, что |-a| = |a|.
В самом деле, как , так и равны большему из чисел -a и a, а значит равны между собой.
Следствие 2. Для любого действительного числа a справедливы неравенства
Умножая второе равенство на -1 (при этом знак неравенства изменится на противоположный), мы получим следующие неравенства: справедливые для любого действительного числа a. Объединяя последние два неравенства в одно, получаем:
Теорема 2. Абсолютная величина любого действительного числа a равна арифметическому квадратному корню из
В самом деле, если то, по определению модуля числа, будем иметь С другой стороны, при значит |a| =
Если a < 0, тогда |a| = -a и и в этом случае |a| =
Эта теорема дает возможность при решении некоторых задач заменять |a| на
Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчета.
Если то на координатной прямой существует две точки a и -a, равноудаленной от нуля, модули которых равны.
Если a = 0, то на координатной прямой |a| изображается точкой 0 (см. рис.)
Свойства модуля
1.|ab|=|a|*|b|
При a0, b0 ab0 по определению модуля =ab . =a, =b =ab.
При а<0, b<0 ab>0 по определению модуля =ab. =-a, =-b =-a*(-b)=ab.
При a>0, b<0 ab<0 по определению модуля =-ab.=a, =-b =a*(-b)=-ab.
Аналогично при a<0, b>0 =-ab, =-ab.
2.=
Квадрат числа не может быть отрицательным, поэтому знак числа роли играть не будет.
При a<0 =-a =
При a0 =a =
3. =, b0
Если а и b положительны, то и дробь в левой части будет положительна, а в правой части и числитель и знаменатель будут положительны. Модуль из положительного числа – само число, значит =, но чтобы дробь имела смысл, b должна быть не равна нулю.
Если a и b отрицательны, то дробь в левой части все равно будет положительна, так как минус на минус дает плюс, а в правой части при вынесении переменных из-под модуля и числитель и знаменатель будут положительны, значит и сама дробь будет положительна.
Если а и b разных знаков, например, a>0, b<0, то в левой части дробь будет отрицательна, но при вынесении из-под модуля станет положительна, а в правой части при вынесении переменных из-под модуля и числитель и знаменатель будут положительны, значит и сама дробь будет положительна.
4.
При a0, b0 . , .
При a<0, b<0 . ,
При a<0, b>0 –a>0 . , .
Аналогично при a>0, b<0 –b>0, , .
5.
При a0, b0 . , .
При a<0, b<0 . , .
При a<0, b>0 –a>0 .
.
.
refdb.ru
«Модуль действительного числа и его свойства» (8 класс)
Урок на тему: Модуль действительного числа и его свойства
Цели: сформулировать определение и свойства модуля, научиться применять их на практике.
Форма проведения: лекция, новая тема
План урока:
Организационные моменты
Изучение нового материала
Разбор примеров
Итоги урока
Домашнее задание
Заключительное слово
Ход урока
1. Организационные моменты
Учитель: Здравствуйте, сегодня на урок нужно было принести новые тетради. Открываем их и пишем число, классная работа и первую тему: Модуль действительного числа и его свойства. Это тема для вас не совсем новая. С понятием модуля мы уже встречались раньше. Сегодня наша цель – это изучить это понятие более подробно, записать точное определение и словами и формулой, разобрать свойства модуля и некоторые из них доказать.
2. Изучение нового материала
Учитель: Пишем определение понятия «Модуль». Модулем или абсолютной величиной действительного числа называется само число , если оно неотрицательно, или противоположное ему число –, если оно отрицательно.
А ниже напишем:
Пишем небольшой заголовок в центре: Свойства модуля. Смотрим на экран и записываем.
1. Для любого Доказательство: Если Если же То есть в любом случае
2. Модули противоположных чисел равны: .
3. Модуль положительного числа равен самому числу:
4. Каково бы ни было a,
5. Квадрат модуля числа равен квадрату этого числа: Доказательство: Если Если То есть
6. Квадратный корень из квадрата числа есть модуль этого числа: .
7. Модуль произведения двух (и более) чисел равен произведению их модулей: . Доказательство:
1) Пусть
2) Пусть
Для 3) и 4) случая докажите самостоятельно. (Ребята доказывают самостоятельно).
8. Модуль частного двух (и более) чисел равен частному их модулей:
9. Модуль суммы не превышает суммы модулей:
3. Разбор примеров
Учитель: Давайте сейчас приведем примеры в тетрадях, которые будут подтверждать верность свойств. (Работа в тетрадях самостоятельно). Если есть вопросы, то задавайте.
Примеры:
, т.к. 3,4>0;
, т.к. –7<0;
, т.к. <0;
, т.к. <0.
4. Итоги урока
Учитель: Сегодня мы изучили понятие «Модуль» и разобрали его свойства. Свойства нужно знать наизусть, чтобы пользоваться имя для решения уравнений, которые мы будем изучать на следующем уроке.
5. Домашнее задание
Учитель: Домашним заданием будет – выучить определение «Модуль», знать свойства и постараться доказать еще хотя бы одно свойство самостоятельно.
6. Заключительное слово
Учитель: Темы, связанные с модулем, не сложные, если учить свойства вовремя, а не тянуть до того, когда их нужно будет уже применять при решении уравнений.
infourok.ru
