Доказательство 1 признака равенства треугольников – Первый признак равенства треугольников | Треугольники

Первый признак равенства треугольников. Видеоурок. Геометрия 7 Класс

На предыдущем занятии мы ввели понятие «равные треугольники» – треугольники, которые можно совместить наложением. Однако очень трудно сравнивать фигуры по определению, поэтому мы введем признаки равенства треугольников – по некоторым элементам.

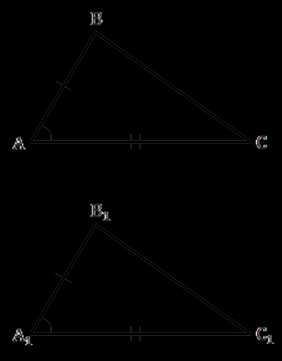
Рис. 1. Треугольники АВС и A₁B₁C₁ равны

Докажем теорему: если две стороны и угол между ними одного треугольника и соответствующие им две стороны и угол между ними второго треугольника равны, то данные треугольники равны.

Теорема: Дано . Доказать: АВС и .

Доказательство: Выполним наложение данных в условии фигур. В результате данного действия вершины А и А₁, отрезки АВ и А₁В_1,  АС и А₁С₁ совпадают. Если рассматривать треугольники в целом, то  совпадёт с .

Теорема доказана.

Рассмотрим несколько задач.

Пример 1:

Отрезки АС и ВD точкой их пересечения О делятся пополам. Докажите, что .

Доказательство: Выполним пояснительный рисунок.

Рис. 2. Чертеж к примеру 1

Отметим, что углы АОВ и СОD равны, как вертикальные, а стороны ВО и АО треугольника АОВ соответственно равны сторонам OD и ОС треугольника СОD. Поэтому треугольники АОВ и СОD равны по первому признаку.

Пример 2:

Отрезки АС и BD точкой пересечения делятся пополам. Докажите, что .

Решение:

Рис. 3. Чертеж к примеру 2

В предыдущей задаче мы доказали, что  по первому признаку. Из этих соображений мы можем сделать вывод, что AB = CD, ∠OAB = ∠OCD.

Теперь рассмотрим треугольники. У них АС – общая сторона, AB=CD, а ∠СAB = ∠АCD (по доказанному). Поэтому  по первому признаку равенства. Что и требовалось доказать.

Пример 3:

Рис. 4. Чертеж к примеру 3

На рисунке 3 отрезки АВ и АС равны. Угол 1 равен углу 2. Известно, что АС = 15 см, DC = 5 см. Доказать, что . Найдите длины отрезков BD и АВ.

Треугольники  равны по первому признаку, ведь ∠1 = ∠2, АВ = АС, а AD – общая сторона у обоих треугольников. Из равенства треугольников следует равенство некоторых их соответствующих элементов, поэтому: BD = CD = 5 см,

АВ = АС = 15 см.

Ответ: 5 см, 15 см.

Пример 4:

На рисунке 5 ВС = AD. Угол 1 равен углу 2, AD = 17 см, CD = 14 см. Доказать, что . Найдите АВ и ВС.

Решение:

Рис. 5. Чертеж к примеру 4

Треугольник АВС равен треугольнику СDА.  по первому признаку. ∠1 = ∠2, СВ = АD, а AC – общая сторона у обоих треугольников. Из этого следует, что , .

Ответ: 14 см, 17 см.

                                  

Рекомендованные ссылки на интернет-ресурсы

1. Тема урока «Первый признак равенства треугольников» Источник
2. Треугольник. Справочник Источник

 

Рекомендованное домашнее задание

1.  № 36. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

2.   Докажите, что треугольники ВОА и ЕОС равны. Отрезки ВЕ и AС точкой пересечения делятся пополам.

3.  Докажите, что прямая, отсекающая от сторон угла равные отрезки, перпендикулярна его биссектрисе.

4.  *На сторонах угла М отложены равные отрезки МА и МС и проведена его биссектриса, на которой отмечена точка В. Докажите, что ВМ является биссектрисой угла АВС.  

interneturok.ru

Первый признак равенства треугольников — урок. Геометрия, 7 класс.

Треугольники. Равенство треугольников

 

Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.

Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.

 

Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.

Обозначение треугольника:

ΔABC, или ΔBCA, или буквы вершин в любом другом порядке.

 

Обозначение угла:

∡A, ∡BAC или ∡CAB.

 

Обозначение стороны:

AB или BA.

Сторону, которая лежит напротив угла, называют противолежащей углу, и угол называют противолежащим стороне.

 

Углы, которые имеет одну общую сторону, называют прилежащими этой стороне.

 

Сумма сторон треугольника называется периметром.

Если два треугольника можно совместить наложением, их называют равными.

При этом совпадают все стороны и все углы.

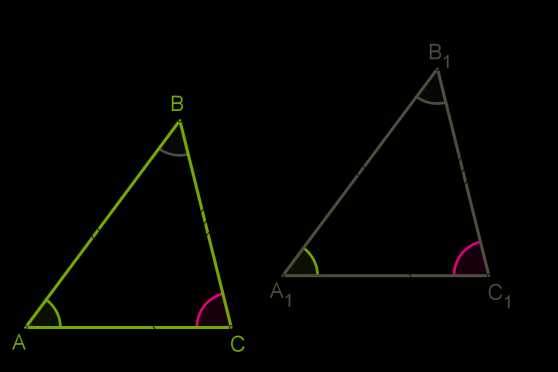
Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

То есть, противолежащие стороны соответственно равных углов тоже равны, и противолежащие углы соответственно равных сторон равны.

 

Обозначение равных треугольников:

 ΔABC=ΔA1B1C1, ΔBCA=ΔB1C1A1 или буквы вершин в любом другом порядке, но соблюдая следующее правило.

 

Обрати внимание!

В каком порядке названы вершины одного треугольника, в таком же порядке называют соответствующие вершины равного треугольника.

На практике не всегда можно применить наложение для сравнивания фигур. Чаще необходимо ограничиться измерением некоторых элементов фигур и по этим измерениям судить о равенстве фигур.

Докажем, что для равенства двух треугольников достаточно двух равных сторон и угла, который образован этими сторонами.

Первый признак равенства треугольников

Если две стороны и угол между ними одного треугольника  соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники  равны.

 

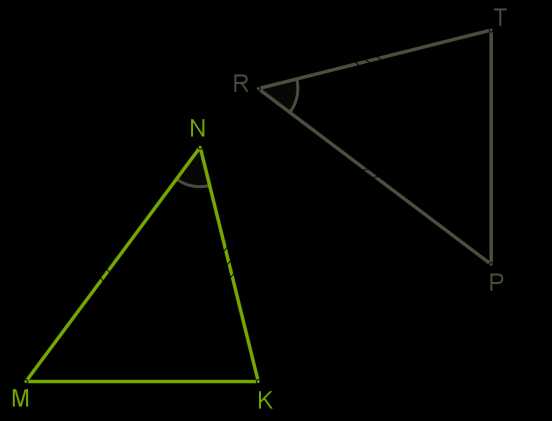
MN=PR;KN=TR;∡N=∡R.

 

Достаточно ли этого для равенства треугольников, можно ли их полностью совместить?

1. Так как ∡N=∡R, то треугольник ΔMNK можно наложить на треугольник ΔPRT так, что вершина \(N\) совместится с вершиной \(R\), а стороны \(NM\) и \(NK\) наложатся соответственно на лучи \(RP\) и \(RT\).

 

2. Поскольку MN=PR,KN=TR, то сторона \(MN\) совместится со

стороной \(PR\), а сторона \(KN\) — со стороной \(TR\), в частности совместятся точки \(M\) и \(P\), \(K\) и \(T\).

 

3. Следовательно, совместятся стороны \(MK\) и \(PT\). Итак, ΔMNK и ΔPRT полностью совместятся, значит, они равны.

www.yaklass.ru

Первый признак равенства треугольников / Треугольники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Треугольники
5. Первый признак равенства треугольников

Теорема

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

Пример: 

ABC = A₁B₁C₁, так как AC

= A₁C₁, AB =A₁B₁ и A = A₁ ( A лежит между сторонами AC и AB, а A₁ между A₁C₁и A₁B₁)

---

Доказательство:

Дано: ABC, A₁B₁C₁, AC = A₁C₁, AB =A₁B₁, A = A₁

Доказать: ABC = A₁B₁C₁

Доказательство:

По тому как A = A₁, можно ABC наложить на A₁B₁C₁ так, что вершины A и A₁совместятся, а стороны AC и AB наложатся на лучи A₁C₁и A₁B₁. Так как нам дано, что AB =A₁B₁, AC = A₁C₁, то сторона AB совместится со стороной A₁B₁, а сторона AC

— со стороной A₁C₁; также совместятся точки B и B₁,  C и C₁. Следовательно, совместятся стороны BC и B₁C₁. Итак, ABC и A₁B₁C₁ полностью совместятся, значит, они равны, что и требовалось доказать.

1. 
2. 

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Треугольник

Равенство треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 105, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 113, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 127, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 162, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 165, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 214, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 345, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 847, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© 2019 — budu5.com, Буду отличником!

budu5.com

второй и третий признаки, теорема и определение

С далеких времен и по сей день поиск признаков равенства фигур считается базовой задачей, которая является основой основ геометрии; сотни теорем доказываются с использованием признаков равенства. Умение доказывать равенство и подобие фигур — важная задача во всех сферах строительства.

…

Вконтакте

Facebook

Twitter

Мой мир

Применение навыка на практике

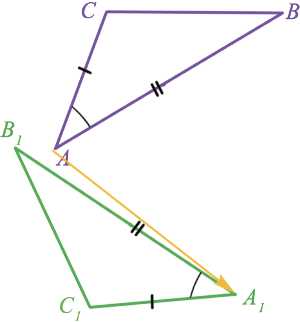
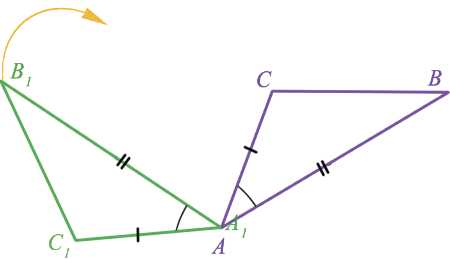
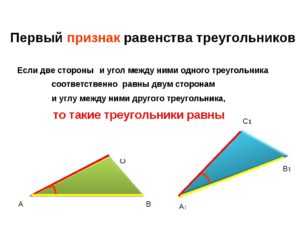Предположим, что у нас есть фигура, начерченная на листе бумаги. При этом у нас есть линейка и транспортир, с помощью которых мы можем замерять длины отрезков и углы между ними. Как перенести на второй лист бумаги фигуру таких же размеров или увеличить ее масштаб в два раза.

Мы знаем, что треугольник — это фигура, состоящая из трех отрезков, называемых сторонами, образующими углы. Таким образом, существует шесть параметров — три стороны и три угла, которые определяют эту фигуру.

Однако, замерив величину всех трех сторон и углов, перенести данную фигуру на другую поверхность окажется непростой задачей. Кроме того, есть смысл задать вопрос: а не достаточно ли будет знания параметров двух сторон и одного угла, или всего лишь трех сторон.

Замерив длину двух сторон и угол между ними, затем отложим этот угол на новом листке бумаги, так мы сможем полностью воссоздать треугольник. Давайте разберемся, как это сделать, научимся доказывать признаки, по которым их можно считать одинаковыми, и определимся с тем, какое минимальное число параметров достаточно знать, чтобы получить уверенность в том, что треугольники одинаковы.

Важно ! Фигуры называются одинаковыми, если отрезки, образующие их стороны, и углы равны между собой. Подобными называются те фигуры, у которых стороны и углы пропорциональны. Таким образом, равенство — это подобие с коэффициентом пропорциональности 1.

Какие существуют признаки равенства треугольников, дадим их определение:

• первый признак равенства: два треугольника можно считать одинаковыми, если равны две их стороны, а также угол между ними.
• второй признак равенства треугольников: два треугольника будут одинаковыми, если одинаковы два угла, а также соответствующая сторона между ними.
• третий признак равенства треугольников: треугольники можно считать одинаковыми, когда все их стороны имеют равную длину.

Как доказать, что треугольники равны. Приведем доказательство равенства треугольников.

Доказательство 1 признака

Долгое время среди первых математиков данный признак считался аксиомой, однако, как оказалось, его можно геометрически доказать, опираясь на более базовые аксиомы.

Рассмотрим два треугольника — KMN и K₁M₁N₁. Сторона КМ имеет такую же длину как и K₁M₁, а KN = K₁N₁. А угол MKN равен углам KMN и M₁K₁N₁.

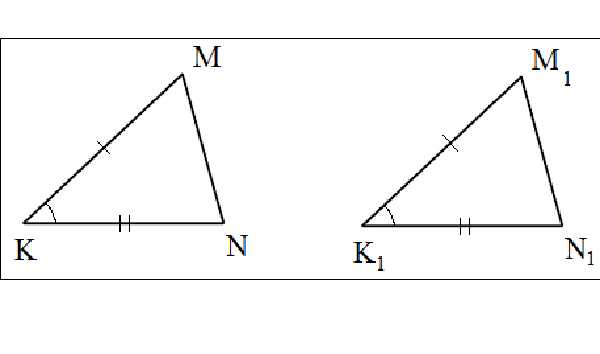
Если рассматривать KM и K₁M_1, KN и K₁N₁ как два луча, которые выходят из одной точки, то можно сказать, что между этими парами лучей одинаковые углы (это задано условием теоремы). Произведем параллельный перенос лучей K₁M₁ и K₁N₁ из точки K₁ в точку К. Вследствие этого переноса лучи K₁M₁ и K₁N₁ полностью совпадут. Отложим на луче K₁M₁ отрезок длиной КМ, берущий свое начало в точке К. Поскольку по условию полученный отрезок и будет равен отрезку K₁M₁ то точки М и M₁ совпадают. Аналогично и с отрезками KN и K₁N₁. Таким образом, перенося K₁M₁N₁ так, что точки K₁ и К совпадают, а две стороны накладываются, получаем полное совпадение и самих фигур.

Важно! В интернете встречаются доказательства равенства треугольников по двум сторонам и углу при помощи алгебраических и тригонометрических тождеств с численными значениями сторон и углов. Однако исторически и математически данная теорема была сформулирована задолго до алгебры и раньше, чем тригонометрия. Для доказательства этого признака теоремы использовать что-либо, кроме базовых аксиом, некорректно.

Доказательство 2 признака

Докажем второй признак равенства по двум углам и стороне, основываясь на первом.

Доказательство 2 признака

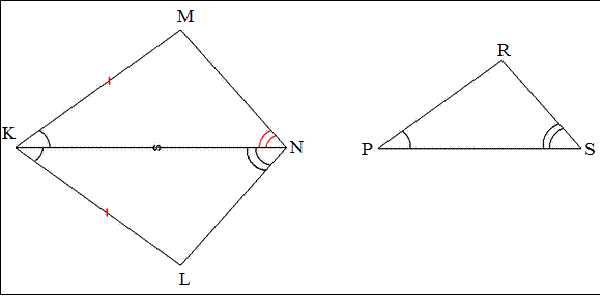
Рассмотрим KMN и PRS. К равен Р, N равен S. Сторона КN имеет такую же длину, как и РS. Необходимо доказать, что KMN и PRS — одинаковы.

Отразим точку М относительно луча КN. Полученную точку назовем L. При этом длина стороны КМ = КL. NKL равен PRS. KNL равен RSP.

Поскольку сумма углов равна 180 градусов, то KLN равен PRS, а значит PRS и KLN- одинаковые (подобные) по обеим сторонам и углу, согласно первому признаку.

Но, так как KNL равен KMN, то KMN и PRS — две одинаковые фигуры.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Доказательство 3 признака

Как установить, что треугольники равны. Это прямо вытекает из доказательства второго признака.

Длина KN = PS. Поскольку К = Р, N = S, KL=KM, при этом КN = KS, MN=ML, то:

Это означает, что обе фигуры являются подобными друг другу. Но так как их стороны одинаковы, то и они также равны.

Из признаков равенства и подобия вытекает множество следствий. Одно из них заключается в том, что для того, чтобы определить, равны два треугольника или нет, необходимо знать их свойства, одинаковы ли:

• все три стороны;
• обе стороны и угол между ними;
• оба угла и сторона между ними.

Использование признака равенства треугольников для решения задач

Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Следствия первого признака

В ходе доказательства можно прийти к ряду интересных и полезных следствий.

1. Параллелограмм. Тот факт, что точка пересечения диагоналей параллелограмма делит их на две одинаковые части — следствие признаков равенства и вполне поддается доказательству.Стороны дополнительного треугольника (при зеркальном построении, как в доказательствах, которые мы выполняли) — параллельны сторонам главного (стороны параллелограмма).
2. Если есть два прямоугольных треугольника, у которых одинаковые острые углы, то они подобны. Если при этом катет первого равен катету второго, то они равны. Понять это довольно легко — у любых прямоугольных треугольников есть прямой угол. Поэтому признаки равенства для них более просты.
3. Два треугольника с прямыми углами, у которых два катета имеют одинаковую длину, можно считать одинаковыми. Это связано с тем, что между двумя катетами угол всегда равен 90 градусов. Поэтому по первому признаку (по двум сторонам и углу между ними) все треугольники с прямыми углами и одинаковыми катетами — равны.
4. Если есть два прямоугольных треугольника, и у них один катет и гипотенуза равны, значит и треугольники одинаковы.

Докажем эту простую теорему.

Есть два прямоугольных треугольника. У одного стороны a, b, c, где с — гипотенуза; a, b — катеты. У второго стороны n, m, l, где l — гипотенуза; m, n — катеты.

По теореме Пифагора один из катетов равен:

;

.

Таким образом, если n = a, l = с (равенство катетов и гипотенуз), соответственно и вторые катеты будут равны. Фигуры, соответственно, будут равны по третьему признаку (по трем сторонам).

Отметим еще одно важное следствие. Если есть два равных треугольника, и они подобны с коэффициентом подобия k, то есть попарные отношения всех их сторон равны k, то отношение их площадей равно k2 .

Первый признак равенства треугольников. Видеоурок по геометрии 7 класс

Геометрия 7 Первый признак равенства треугольников

Вывод

Рассмотренная нами тема поможет любому ученику лучше разобраться в базовых геометрических понятиях и повысить свои навыки в интереснейшем мире математики.

uchim.guru

Первый признак равенства треугольников

Разделы: Математика

---

Урок I типа (изучение и первичное закрепление знаний)

Постановка триединой задачи

I. Образовательные задачи.

Признаки равенства треугольников являются основным рабочим материалом всего курса геометрии. Поэтому учащиеся должны знать I признак равенства треугольников, уметь его доказывать и применять при решении задач. В соответствии с этим ставятся образовательные задачи.

1. Знать формулировку и доказательство I признака равенства треугольников.

2. Применять полученные знания при решении простейших задач в прямой и косвенной форме.

3. Провести актуализацию опорных знаний по следующим вопросам:

а) равные отрезки, углы, треугольники.

б) определение треугольника и его элементов.

в) определение и свойства смежных и вертикальных углов.

г) понятие угла, заключённого между сторонами.

II. Развивающие задачи.

1. Развитие умений:

а) выделять главное и существенное.

б) сравнивать и обобщать полученные знания.

в) планировать и контролировать свою деятельность при выполнении аналитических заданий.

2. Развитие умений в работе со справочной и учебной литературой.

3. Развитие зрительной и слуховой памяти, внимания, математической речи и логического мышления.

III. Воспитательные задачи.

1. Воспитание трудолюбия, усидчивости, умения слушать других.

2. Умение высказывать свою точку зрения, проводить рассуждения, доказательства при выполнении аналитических заданий.

I. Организационный момент.

II. Проверка домашнего задания.

1. № 88	Вопросы: 1. Объясните, какая фигура является треугольником? 2. Назовите вершины, стороны и углы треугольника. 3. Назовите сторону, лежащую против угла D, против угла E, против угла F. 4. Укажите углы, лежащие против сторон DE, EF, FD. 5. Укажите углы, прилежащие к сторонам DE, EF, FD. 6. Укажите, какой угол заключен между сторонами ED и DF, EF и DF, DE и EF.
2. № 90	Вопросы: 1. Что главное нужно знать при решении задачи? (определение треугольника, его сторон, периметр треугольника) 2. Что такое периметр треугольника? 3. Что существенно при решении этой задачи? (умение решать задачи на нахождение, во сколько раз одна величина больше/меньше другой и на сколько)

III. Подготовка к восприятию новых знаний (актуализация опорных знаний)

Вопросы:

1. Назовите равные отрезки на рис. 1. Какие отрезки называются равными?
2. Назовите равные углы на рис. 2. Какие углы называются равными?
3. Есть ли равные углы на рис. 3, 1, 4? Почему они равны?
4. Какие углы называются вертикальными, смежными? Какими свойствами они обладают?

5. Равны ли треугольники ABC и FMN? Почему? (треугольники равны, т.к. у них равны соответствующие стороны и соответствующие углы. При этом соответствующие углы должны лежать против соответственно равных сторон.)

6.

 

Важно! В равных треугольниках соответственно равные элементы равны.

7. Какие треугольники называются равными? (треугольники называются равными, если их можно совместить наложением)

8. Всегда ли возможно установить равенство треугольников путем наложения?
Нет. Например, два земельных участка.

9. Проверка из домашней работы № 89(а). Как вы думаете, построенные вами треугольники будут равны?

IV. Изучение новых знаний.

Оказывается, равенство двух треугольников можно установить, не накладывая один треугольник на другой, а сравнивая только некоторые элементы.

Мы докажем теорему, которая устанавливает равенство двух треугольников по двум сторонам и углу между ними.

1. Что такое теорема? (утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой).
2. А как называются сами рассуждения? (доказательством теоремы)
3. Какие теоремы мы уже доказывали?

Формулировка теоремы.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказанная теорема выражает I признак равенства треугольников по двум сторонам и углу между ними.

Что такое признак?

Признак (от слова знак) – это показатель, по которому можно узнать, определить что-либо.

Прочитайте формулировку теоремы, выражающей I признак равенства треугольников (стр 30).

Формулировка теоремы содержит условие и заключение теоремы.

Прочитайте условие теоремы, заключение.

V. Первичная проверка понимания материала.

1. Найдите пары равных треугольников и установите их равенство на рис. 1, 2, 3, 4.
2. Решение задач с подробной записью в тетради.

№ 93

VI. Итог урока

1. Сформулируйте I признак равенства треугольников.
2. Расставьте предложения текста в нужном порядке, чтобы получилось доказательство I признака равенства треугольников.

• Итак, треугольники АВС и А₁В₁С₁ полностью совместились, значит, они равны.
• Поскольку АВ = А₁В₁, то сторона АВ совместится со стороной А₁В₁, в частности, совместятся точки В и В₁.
• Т.к _<A=_<А₁, то АВС можно наложить на А₁В₁С₁ так, что вершина А совместится с вершиной А₁, а_{стороны АВ и АС наложатся на стороны А1В1 и А1С1.}
• Поскольку АС = А₁С₁, то сторона АС совместится со стороной А₁С₁, в частности, совместятся точки С и С₁.
• Следовательно, совместятся стороны ВС и В₁С₁, т.к. через совпадающие точки (С и С₁, В и В₁) можно провести только одну прямую.

VII. Информация о домашнем задании п.15, учить теорему, № 93 (письменно), задачи по готовым чертежам стр. 9, найти пары равных треугольников и доказать их равенство (устно).

Структура урока I типа

1. Организационный момент.
2. Проверка домашнего задания.
3. Подготовка к восприятию новых знаний.
4. Изучение новых знаний.
5. Первичная проверка понимания материала.
6. Первичное закрепление материала.
7. Итоги урока.
8. Информация о домашнем задании.

Для достижения триединой задачи отбор содержания учебного материала был проведён следующим образом.

Учащиеся достаточно хорошо должны знать определение треугольника, его элементов, уметь называть угол, лежащий между сторонами треугольника, указывать сторону, лежащую против данного угла, поэтому при проверке домашнего задания этим вопросам уделялось внимание.

При решении любой геометрической задачи, доказательстве теорем необходимо учить учащихся выделять главное и существенное, обращать внимание, какой теоретический и практический материал должен знать ученик, чтобы выполнить то или иное задание, потому при проверке домашнего задания этим вопросам также уделялось внимание.

Таким образом, проверяя домашнее задание, я готовила учащихся к восприятию новых знаний.

При доказательстве I признака равенства треугольников мы ссылаемся на определение равенства отрезков, углов, треугольников, поэтому на этапе подготовки к восприятию новых знаний были задания на нахождение равных сторон и углов треугольника. Также повторялось определение равных фигур. Учащиеся вспомнили, как на чертежах обозначаются равные стороны и углы, что в дальнейшем очень важно для решения задач. Также повторился важный факт, что у равных треугольников соответствующие элементы равны. При решении задач на I признак равенства треугольников учащиеся должны знать определения и свойства смежных и вертикальных углов, уметь их распознавать на рисунках, потому в устную работу были включены и эти задания.

Доказательство I признака равенства треугольников трудно для семиклассников, поэтому учащиеся не были включены во фронтальную работу объяснения нового материала. Доказательство теоремы было проведено детализированно, это сделано для того, чтобы в ходе объяснения нового материала обратить внимание учащихся на отдельные шаги доказательства.

Для лучшего восприятия доказательства теоремы я запланировала отработку общеучебных умений и навыков, учащиеся выделили главное и существенное при доказательстве I признака равенства треуголников.

Признаки равенства треугольников должны усваиваться как метод решения задач. Поэтому на этапе первичного закрепления знаний я включила задания по готовым чертежам (найти пары равных треугольников)

Решая задачу № 93, учащиеся учились выполнять рисунок по условию задачи, отмечать равные элементы на рисунке, учились делать геометрически грамотную ссылку на I признак равенства треугольников (по сторонам и углу между ними).

При подведении итогов повторилась формулировка теоремы и провелась работа по формулированию общеучебных умений и навыков, учащиеся учились планировать и контролировать свою деятельность, что дало возможность учащимся осмыслить доказательство теоремы.

В течение всего урока учащиеся учились анализировать полученные знания, сравнивать, обобщать, выделять главное и существенное, развивать логическое мышление. На протяжении всего урока учащиеся развивали зрительную и слуховую память, воспитывали усидчивость, активность, учились высказывать свою точку зрения.

Для достижения триединой задачи использовались следующие методы обучения:

а) словесный;

б) наглядный;

в) практический;

г) проблемно-поисковый;

д) индивидуальный;

е) дедуктивный.

Форма организации познавательной деятельности:

а) общеклассная;

б) индивидуальная.

27.01.2006

urok.1sept.ru

Билет 2 Вопрос 1 Признаки равенства треугольников (доказательство всех)

Билет 2

Вопрос 1

Признаки равенства треугольников (доказательство всех)

1-ый признак равенства треугольников: по двум сторонам и углу между ними (Теорема 3.1. – Признак равенства треугольников по двум сторонам и углу между ними — Если две стороны и угло между ними одного треугольнгрка равны соотвественно двум сторонам и углу между ними другого треугольника, то такие треугольники равны)

Доказательство:

Пусть у треугольников АВС и А₁В₁С₁ угол А равен углу А₁, АВ равно А₁В_1, АС равно А₁С₁, докажем, что треугольники равны.

Пусть А₁В₂С₂ – треугольник, равный АВС, с вершины В₂ на луче А₁В₁ и вершины С₂ в той же полуплоскости относительно прямой А₁В₁, где лежит вершина С₁.

Так как А₁В₁ равно А₁В₂, то вершина В₂ совпадет с В_1. Так как угол В₁А₁С₁ равен углу В₂А₁С_2, то луч А₁С₂ совпадет с А₁С₁. Так как А₁С₁ равен А₁С₂, то С₂ совпадет с С_1. Значит треугольник_{А1В1С1 совпадает стреугольниом А1В2С2, значит равен треугльнику АВС.}

Теорема доказана.

2-ой признак равенства треугольников: по стороне и прилежим к ней углам (Теорема 3.2. — Признак равенства треугольников по стороне и прилежащим к ней углам — Если сторона и прилежащие у ней углы одного треугольника равны соотвественно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны)

Доказательство:

Пусть АВС и А₁В₁С_{1 –} два треугольника, у которых АВ равно А₁В_1, угол А равен углу А₁, и угол В равен углу В₁. Докажем, что они равны.

Пусть А₁В₂С₂ – треугольник, равный АВС, с вершины В₂ на луче А₁В₁ и вершины С₂ в той же полуплоскости относительно прямой А₁В₁, где лежит вершина С₁.

Так как А₁В₂ равно А₁В₁, то вершина В₂ совпадет с В_1. Так как угол В₁А₁С₂ равен углу В₁А₁С_1, и угол А1В1С2 равен углу А1В1С1, то луч А₁С₂ совпадет с А₁С₁, а В₁С₂ совпадет с В₁С₁. Отсюда следует, что вершина С₂ совпадет с С_1. Значит треугольник_{А1В1С1 совпадает стреугольниом А1В2С2, значит равен треугльнику АВС.}

Теорема доказана.

3-ий признак равенства треугольников: по трем сторонам ( Теорема 3.6. — Признак равенства треугольников по трем сторонам — Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны)

Доказательство:

Пусть АВС и А₁В₁С_{1 –} два треугольника, у которых АВ равно А₁В_1, АС равно А₁С₁, и ВС равно В₁С₁. Докажем, что они равны.

Допустим, треугольники не равны. Тогда у них угол А не равен углу А₁, угол В не равен углу В_1, и угол С не равен углу С₁. Иначе они были бы равны, по перовому признаку.

Пусть А₁В₁С₂ – треугольник, равный треугольнику АВС, у которого Свершина С₂ лежит в одной полуплоскости с вершиной С₁ относительно прямой А₁В₁.

Пусть D – середина отрезка С₁С₂. Треугольники А₁С₁С₂ и В₁С₁С₂ – равнобедренные с общим основанием С₁С₂. Поэтому их медианы А₁D и В₁D – являются высотами, значит прямые А₁D и В₁D – перпендикулярны прямой С₁С_2. Прямые А₁D и В₁D не совпадают, так как точки А_1, В₁, D не лежат на одной прямой, но через точку D прямой С₁С₂ можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.

Теорема доказанa

gigabaza.ru

А.В. Погорелов. Геометрия. 7 класс. §3. Контрольные вопросы, ответы

Подробности

Родительская категория: Математика

Категория: Геометрия, 7 класс, контрольные вопросы, ответы

Вопрос 1. Докажите первый признак равенства треугольников. Какие аксиомы используются при доказательстве теоремы 3.1?
Ответ. Первый признак равенства треугольников — Теорема 3.1. (признак равенства треугольников по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство. Пусть у треугольников ABC и A₁B₁C₁ угол A= углу A₁, AB=A₁B₁, AC=A₁C₁(рис. 44).

Рис. 44.
Докажем, что треугольники равны.

Пусть A₁B₂C₂— треугольник, равный треугольникуABC, с вершиной B₂ на луче A₁B₁ и вершиной C₂ в той же полуплоскости относительно прямой A₁B₁, где лежит вершина C₁ (рис. 45, а).

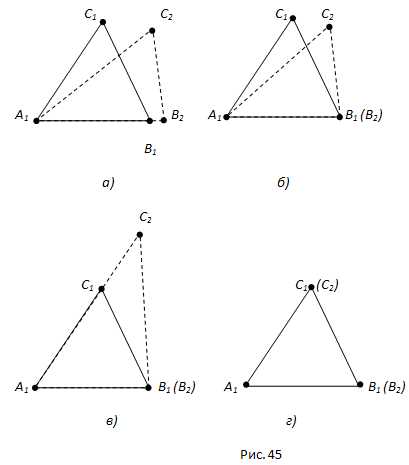
Так как A₁B₁=A₁B₂, то вершина B₂ совпадает с вершиной B₁ (рис. 45, б). Так как угол B₁A₁C₁= углу B₂A₁C₂, то луч A₁C₂ совпадает с лучом A₁C₁ (рис. 45, в). Так как A₁C₁=A₁C₂, то вершина C₂ совпадает с вершиной C₁ (рис. 45, г).
Итак, треугольник A₁B₁C₁ совпадает с треугольником A₁B₂C₂, значит, равен треугольнику ABC. Теорема доказана.
В начале доказательства рисуют треугольник A₁B₂C₂ равный треугольнику ABC с вершиной B₂ на луче A₁B₁ и вершиной C₂ в той же полуплоскости относительно прямой A₁B₁, где лежит вершина C₁ (рис. 45, а). Такой треугольник существует по аксиоме о существовании треугольника, равного данному (каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой).
Затем утверждается совпадение вершин B₁ и B₂ на том основании, что A₁B₁ = A₁B₂. Здесь используется аксиома откладывания отрезков (на любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один).
Далее утверждается совпадение лучей A₁C₂ и A₁C₁ на том основании, что \(\angle\)B₂A₁C₁ = \(\angle\)B₂A₁C₂. Здесь используется аксиома откладывания углов (от любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один).
Наконец, утверждается совпадение вершин C₁ и C₂, так как A₁C₁ = A₂C₂. Здесь снова используется аксиома откладывания отрезков (на любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один).
Итак, при доказательстве теоремы 3.1 используются аксиомы откладывания отрезков и углов и аксиома о существовании треугольника, равного данному.

Вопрос 2. Сформулируйте и докажите второй признак равенства треугольников.
Ответ. Второй признак равенства треугольников — Теорема 3.2 (признак равенства треугольников по стороне и прилежащим к ней углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и  прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство. Пусть ABC и A₁B₁C₁ — два треугольника, у которых AB= A₁B₁, угол A= углу A₁ и угол B= углу B₁(рис. 47).

Докажем, что треугольники равны.
Пусть A₁B₂C₂— треугольник, равный треугольнику ABC, с вершиной B₂ на луче A₁B₁ и вершиной C₂ в той же полуплоскости относительно прямой A₁B₁, где лежит вершина C₁.
Так как A₁B₂=A₁B₁, то вершина B₂ совпадает с вершиной B₁. Так как угол B₁A₁C₂= углу B₁A₁C₁ и угол A₁B₁C₂ = углу A₁B₁C₁, то луч A₁C₂ совпадает с лучом A₁C₁, а луч B₁C₂ совпадает с лучом B₁C₁. Отсюда следует, что вершина C₂ совпадает с вершиной C₁.
Итак, треугольник A₁B₁C₁ совпадает с треугольником A₁B₂C₂, а  значит, равен треугольнику ABC. Теорема доказана.

Вопрос 3. Какой треугольник называется равнобедренным? Какие стороны равнобедренного треугольника называются боковыми сторонами? Какая сторона называется основанием?
Ответ. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Вопрос 4.  Докажите, что в равнобедренном треугольнике углы при основании равны.
Ответ. Теорема 3.3 (свойство углов равнобедренного треугольника). В равнобедренном треугольнике углы при основании равны.
Доказательство. Пусть ABC- равнобедренный треугольник с основанием AB (рис. 48). Докажем, что у него угол A= углу B.

Треугольник CAB равен треугольнику CBA по первому признаку равенства треугольников. Действительно, CA= CB, CB= CA, угол C= углу C. Из равенства треугольников следует, что угол A= углу B. Теорема доказана.

Вопрос 5. Какой треугольник называется равносторонним?
Ответ. Треугольник, у которого все стороны равны, называется равносторонним.

Вопрос 6. Докажите, что если в треугольнике два угла равны, то он равнобедренный.
Ответ. Теорема 3.4 (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный.
Доказательство. Пусть ABC – треугольник, в котором угол A= углу B (рис. 50). Докажем, что он равнобедренный с основанием AB.

Треугольник ABC равен треугольнику BAC по второму признаку равенства треугольников. Действительно, AB=BA, угол B= углу A, угол A= углу B. Из равенства треугольников следует, что AC= BC. Значит, по определению треугольник ABC равнобедренный. Теорема доказана.

Вопрос 7. Объясните, что такое обратная теорема. Приведите пример. Для всякой ли теоремы верна обратная?
Ответ. Теорема 3.4 называется обратной теореме 3.3. Заключение теоремы 3.3 является условием теоремы 3.4. А условие теоремы 3.3 является заключением теоремы 3.4. Не всякая теорема имеет обратную, то есть если данная теорема верна, то обратная теорема может быть неверна. Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.

Вопрос 8. Что такое высота треугольника?
Ответ. Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведённый из этой вершины к прямой, которая содержит противолежащую сторону треугольника (рис. 51, а-б).

Вопрос 9. Что такое биссектриса треугольника?
Ответ. Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне  (рис. 52, а).

Вопрос 10. Что такое медиана треугольника?
Ответ. Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника (рис. 52, б).

Вопрос 11. Докажите, что в равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.
Ответ. Теорема 3.5 (свойство медианы равнобедренного треугольника). В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.
Доказательство. Пусть ABC – данный равнобедренный треугольник с основанием AB и CD – медиана, проведённая к основанию (рис. 53).

Треугольники CAD и CBD равны по первому признаку равенства треугольников. (У них стороны AC и BC равны, потому что треугольник ABC равнобедренный. Углы CAD и CBD равны как углы при основании равнобедренного треугольника. Сторона AD и BD равны, потому что D – середина отрезка AB.)
Из  равенства треугольников следует равенство углов: угол ACD = углу BCD, угол ADC = углу BDC. Так как углы ACD и BCD равны, то CD – биссектриса. Так как углы ADC и BDC смежные и равны, то они прямые, поэтому CD – высота треугольника.

Вопрос 12.  Докажите третий признак равенства треугольников.
Ответ. Третий признак равенства треугольников — Теорема 3.6 (признак равенства треугольников по трём сторонам). Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.

Доказательство. Пусть ABC и A₁B₁C₁ – два треугольника, у которых AB = A₁B₁, AC = A₁C₁, BC = B₁C₁(рис. 55).

Требуется доказать, что треугольники равны.
Допустим, треугольники не равны. Тогда у них угол A не = углу A₁, угол B не = углу B₁, угол C не = углу C₁. Иначе они были бы равны по первому признаку.
Пусть A₁B₁C₂ – треугольник, равный треугольнику ABC, у которого вершина C₂ лежит в одной полуплоскости с вершиной C₁ относительно прямой A₁B₁ (см. рис. 55).
Пусть D – середина отрезка C₁C₂. Треугольники A₁C₁C₂  и B₁C₁C₂ – равнобедренные с общим основанием C₁C₂. Поэтому их медианы A₁D и B₁D являются высотами. Значит, прямые A₁D и B₁D перпендикулярны прямой C₁C₂. Прямые A₁D и B₁D не совпадают, так как точки A₁, B₁, D не лежат на одной прямой. Но через точку D прямой C₁C₂ можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.

oftob.ru

No related posts.