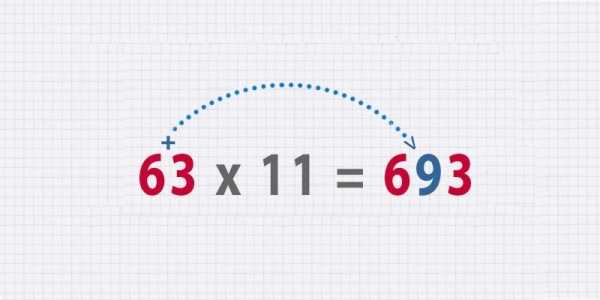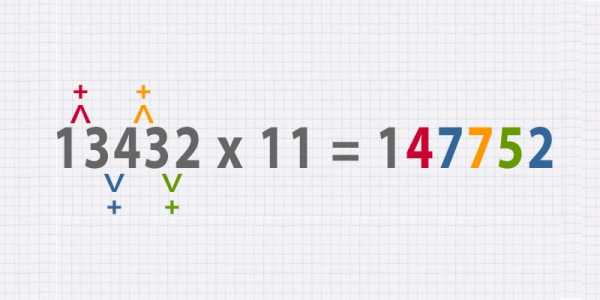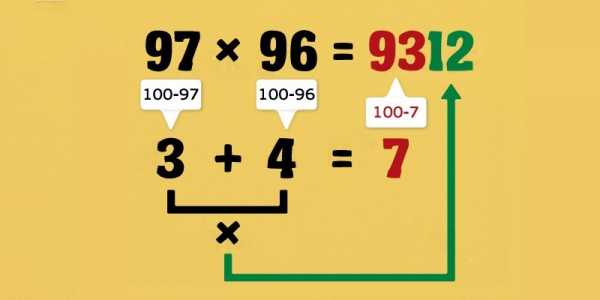Как решать десятичные дроби 🚩 десятичная дробь это 🚩 Математика
Вам понадобится
- — калькулятор;
- — лист бумаги;
- — ручка.
Инструкция
Научитесь переводить десятичные дроби в обыкновенные. Посчитайте, сколько знаков отделено запятой. Одна цифра справа от запятой означает, что знаменатель — 10, две — 100, три — 1000 и так далее. Например, десятичная дробь 6,8 читается как «шесть целых, восемь десятых». При преобразовании ее в обыкновенную напишите сначала количество целых единиц — 6. В знаменателе напишите 10. В числителе будет стоять число 8. Получится, что 6,8 = 6 8/10. Вспомните правила сокращения. Если числитель и знаменатель делятся на одно и то же число, то дробь можно сократить на общий делитель. В данном случае это число 2. 6 8/10 = 6 2/5. Попробуйте сложить десятичные дроби. Если вы делаете это в столбик, то будьте внимательны. Разряды всех чисел должны находиться строго друг под другом, а запятая — под запятой. Правила сложения точно такие же, как и при действии с целыми числами. Прибавьте к тому же числу 6,8 другую десятичную дробь — например, 7,3. Запишите тройку под восьмеркой, запятую — под запятой, а семерку — под шестеркой. Складывать начните с последнего разряда. 3+8=11, то есть 1 запишите, 1 запомните. Далее сложите 6+7, получите 13. Прибавьте то, что оставалось в уме и запишите результат — 14,1.Вычитание выполняется по тому же принципу. Разряды запишите друг под другом, запятую — под запятой. Ориентируйтесь всегда по ней, особенно если количество цифр после нее в уменьшаемом меньше, чем в вычитаемом. Отнимите от заданного числа, например, 2,139. Двойку запишите под шестеркой, единицу — под восьмеркой, остальные две цифры — под следующими разрядами, которые можно обозначить нулями. Получится, что уменьшаемое не 6,8, а 6,800. Выполнив данное действие, вы получите в итоге 4,661.
Действия с отрицательными десятичными дробями выполняются точно так же, как и с целыми числами. При сложении минус выносится за скобку, а в скобках пишутся заданные числа, и между ними ставится плюс. В итоге получается отрицательное число. То есть при сложении -6,8 и -7,3 вы получите тот же самый результат 14,1, но со знаком «-» перед ним. Если вычитаемое больше уменьшаемого, то минус тоже выносится за скобку, из большего числа вычитается меньшее. Вычтите из 6,8 число -7,3. Преобразуйте выражение следующим образом. 6,8 — 7,3= -(7,3 — 6,8) = -0,5.
Для того чтобы умножить десятичные дроби, на время забудьте о запятой. Перемножьте их так, как будто перед вами целые числа. После этого сосчитайте количество знаков, стоящих справа после запятой в обоих сомножителях. Отделите столько же знаков и в произведении. Перемножив 6,8 и 7,3, в итоге вы получите 49,64. То есть справа от запятой у вас окажутся 2 знака, в то время как в множимом и множителе их было по одному.
Разделите заданную дробь на какое-нибудь целое число. Это действие выполняется точно так же, как и с целыми числами. Главное — не забыть про запятую и в начале поставить 0, если количество целых единиц не делится на делитель. Например, попробуйте разделить те же самые 6,8 на 26. В начале поставьте 0, поскольку 6 меньше, чем 26. Отделите его запятой, дальше уже пойдут десятые и сотые. В итоге получится приблизительно 0,26. На самом деле в данном случае получается бесконечная непериодическая дробь, которую можно округлить до нужной степени точности.
При делении двух десятичных дробей воспользуйтесь свойством, что при умножении делимого и делителя на одно и то же число частное не меняется. То есть преобразуйте обе дроби в целые числа, в зависимости от того, сколько знаков стоит после запятой. Если вы хотите разделить 6,8 на 7,3, достаточно умножить оба числа на 10. Получится, что делить нужно 68 на 73. Если же в одном из чисел разрядов после запятой больше, преобразуйте в целое число сначала его, а затем уже и второе число. Умножьте его на то же число. То есть при делении 6,8 на 4,136 увеличьте делимое и делитель не в 10, а в 1000 раз. Разделив 6800 на 1436, получите в результате 4,735.
Обратите внимание
В некоторой банковской документации в десятичных дробях вместо запятой ставится точка. Она выполняет ту же роль, что и запятая, то есть отделяет целые разряды от дробных.
Основной особенностью человеческого разума является способность к абстрактному мышлению. Одной из наивысших форм абстракции в человеческом мире является число. Выделяют несколько категорий чисел, различающихся свойствами. Наиболее привычными и часто используемыми в повседневной жизни являются целые и действительные числа. Как правило, числа записываются в десятичной системе счисления. Действительные числа обозначаются десятичными дробями. Одним из недостатков записи дробных чисел в виде десятичных дробей является их ограниченная точность. Когда точность особо важна, числа записывают в виде дробей (пары числитель-знаменатель). В ряде случаев дроби весьма удобны, но арифметические операции с ними более сложны, чем с десятичными числами. Например, чтобы вычесть дробь с разными знаменателями, нужно совершить несколько математических действий.

Вам понадобится
- Калькулятор или лист бумаги с ручкой.
Инструкция
Приведите дроби к одному знаменателю. Помножьте числитель и знаменатель первой дроби на знаменатель второй. Помножьте числитель и знаменатель второй дроби на знаменатель первой. Например, если исходные дроби равны 6/7 и 5/11, то дроби, приведенные к общему знаменателю, будут равны 66/77 и 35/77. В данном случае числитель и знаменатель первой дроби были помножены на число 11, а числитель и знаменатель второй дроби — на число 7. Произведите вычитание дробей. Вычтите из числителя первой дроби числитель второй дроби. Запишите полученное значение в качестве числителя результирующей дроби. В качестве знаменателя результата подставьте общий знаменатель, полученный на предыдущем шаге. Так, при вычитании из дроби 66/77 значения дроби 35/77, получится результат 31/77 (из числителя 66 был вычтен числитель 35, а знаменатель оставлен прежним).Произведите сокращение дроби-результата, если это необходимо. Подберите наибольший общий делитель, отличный от 1 для числителя и знаменателя результирующей дроби. Разделите на него числитель и знаменатель. Запишите новые значения в качестве числителя и знаменателя итоговой дроби. Наибольшего общего делителя, отличного от 1 может и не существовать. В этом случае оставьте в качестве результата исходную дробь.
Источники:
- как сложит дробь с разными знаменателями
Умение решать примеры немаловажно в нашей жизни. Без знания алгебры трудно представить существование бизнеса, работу бартерных систем. Поэтому школьная программа и содержит большой объем алгебраических задач и уравнений, в том числе их систем.

Инструкция
Вспомните, что уравнением называется равенство, содержащее одну или ряд переменных. Если представлено два и больше уравнений, в которых нужно вычислить общие решения, то это система уравнений. Объединение этой системы с помощью фигурной скобки и означает, что решение уравнений должно производиться одновременно. Решением системы уравнений являются множество пар чисел. Способов решения системы линейных уравнений (то есть системы, объединяющей несколько линейных уравнений) существует несколько. Рассмотрите представленный вариант решения системы линейных уравнений способом подстановки:х – 2у=4
7у — х =1Для начала выразите переменную х через переменную у:
х=2у+4Подставьте в уравнение 7у — х=1 вместо х полученную сумму (2у+4) и получите следующее линейное уравнение, которое с легкостью решите:
7у — (2у+4)=1
7у – 2у — 4 = 1
5у = 5
у=1Выполните подстановку вычисленного значения переменной у и вычислите значение переменной х:
х=2у+4, при у=1
х=6Запишите ответ: х=6, у=1.
Для сравнения решите эту же систему линейных уравнений способом сравнения. Выразите одну переменную через другую в каждом из уравнений:Приравняйте выражения, полученные для одноимённых переменных:
х = 2у+4
х = 7у — 1Найти значение одной из переменных, решив представленное уравнение:
2у+4 = 7у — 1
7у-2у=5
5у=5
у=1Подставив результат найденной переменной в исходное выражений для другой переменной, найдите её значение:
х=2у+4
х=6
Наконец, запомните, что решать систему уравнений можно и методом сложения.Рассмотрите решение следующей системы линейных уравнений
7х+2у=1
17х+6у=-9Уравняйте модули коэффициентов при какой-нибудь переменной (в данном случае по модулю 3):
-21х-6у=-3
17х+6у=-9Выполните почленное сложение уравнения системы, получите выражение и вычислите значение переменной:
— 4х = — 12
х=3Составьте вновь систему: первое уравнение новое, второе — одно из старых
7х+2у=1
— 4х = — 12Подставив значение х в оставшееся уравнение, найдите значение переменной у:
7х+2у=1
7•3+2у=1
21+2у=1
2у=-20
у=-10Запишите ответ: х=3, у=-10.
Видео по теме
Еще в школе ученики испытывают сложности при делении, умножении, суммировании и вычитании дробей, однако их действия облегчены подробными разъяснениями преподавателя. Некоторым взрослым ввиду ряда обстоятельств приходится вспомнить математическую науку, в частности, работу с дробями.
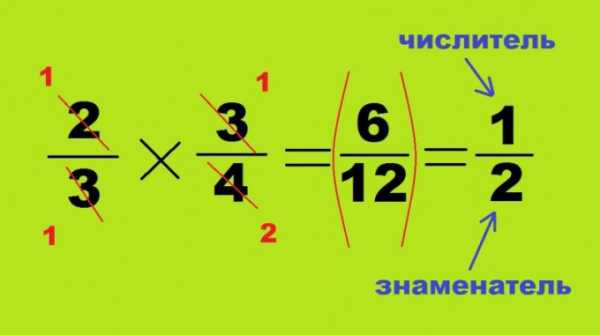
Инструкция
Сложение – это нахождение общей суммы двух слагаемых. Оно легко производится с целыми числами и с их десятичными долями с помощью действий в уме или в столбик. Обыкновенные же дроби представляют сложность для обывателей, имеющих дело с математикой лишь при вычислении стоимости покупок и расчете коммунальных платежей. Если знаменатели двух дробей представлены одной цифрой, то их сумма высчитывается путем сложения их числителей. Так, 2/7 + 3/7 = 5/7. Если показатели под чертой не одинаковы, то придется привести оба числа к общему знаменателю, умножив каждый из них на противоположный: 2/3 + 3/4 = 8/12 + 6/12 = 14/12. Получившийся результат необходимо подвести к нормальному значению и по возможности сократить: 1 целая 2/12, то есть 1 целая 1/6.
Вычитание – процесс, схожий с получением суммы, за исключением самого знака «минус». Так, 5/7 – 3/7 = 2/7. При разных знаменателях их следует подвести к одному: 4/5 – 3/4 = 16/20 – 12/20 = 4/20 = 1/5, что в десятичном виде представляет собой 0,2. Если представить две дроби, стоящие рядом, в виде четырехугольника, то приведение к общему знаменателю будет выглядеть как умножение противоположных углов друг на друга, что и делают школьники на бумаге, пытаясь визуально представить себе математическое действие. Если дробей не две, а больше, то необходимо найти произведение всех его показателей, расположенных ниже черты. Так, у чисел 1/2, 2/3 и 3/5 общим знаменателем будет 2 * 3 * 5 = 30. Если же последнее заменить на 3/4, то значение рассчитывается как 3 * 4, так как последняя цифра кратна двум. Первую же дробь, 1/2, необходимо представить в виде 6/12.
Умножение и деление обходятся без приведения к общему знаменателю, эти два процесса схожи между собой и различаются лишь правильным или перевернутым положением второго числа. При умножении друг на друга двух дробей, каждое из которых меньше единицы, их результат неизменно будет представлять собой меньшее число: 2/3 * 3/4 = 6/12 = 1/2. При этом не обязательно находить произведение больших чисел, противоположные углы вышеупомянутого четырехугольника можно разделить на кратные значения. В данном случае сокращаются числитель первой дроби 2 и знаменатель второй – 4, образуя цифры 1 и 2. Другие два угла математического примера полностью делятся друг на друга, превращаясь в 1. Чтобы получить не произведение, а частное, достаточно поменять местами числитель и знаменатель делимого: 3/4 : 2/3 = 3/4 * 3/2 = 9/8 = 1 целая 1/8.Видео по теме
www.kakprosto.ru
Как объяснить ребенку дроби? — Блог и все письма Ренаты Кирилиной и «Обучение с удовольствием»
Мы делили апельсин. Много нас, а он один
Эта долька для ежа, эта долька для чижа…
А для волка — кожура.
В Школе умных детей Любовь Стрекаловская рассказала, как ввести эту тему и сделать так, чтобы ребенок понял тему и научился решать дроби.
Давайте начнем с самого-самого начала. Представьте себе ребенка, который никогда не видел (а если видел, то не понимает смысла) записи дроби. Он не знает даже этого слова.
Как объснить ему тему и перейти к более сложной части -действию с дробями и решению задач? Как не отбить желание к этой теме? Как связать ее с жизнью?
В школьной программе объяснить дроби предлагается так:
1 Взять яблоко и предложить съесть его двум детям сразу. Они ответят, что это невозможно. Далее необходимо разрезать фрукт и вновь предложить детям. Каждому достанется по одинаковой половине. Таким образом, половинка яблока является частью от целого яблока. А само яблоко состоит из двух частей.
2 Вводим запись. И показываем, что одна половинка — это часть от целого, или 1/2. Значит дробь — это число, которое является частью предмета, меньше, чем один. Также дробь — это количество частей от какой-то вещи.
Далее детям на дом задается выучить определение, и когда введено понятие, начинается период практики.
Однако, по опросам родителей, эта тема является одной из самых трудных для усвоения детьми. Когда обучение происходит по принципу — вот правило — учи — применяй, эффект намного ниже, чем при подходе, который предлагает Любовь Стрекаловская в Школе умных детей.
Ребенок может знать правило, но не понимать, почему это так работает? Почему так записывается?
А отсюда будут ошибки в сравнении 3/11 и 3/17 частей, ошибки в сравнии 2/5 и 1/5 частей
Согласно методике, представленной в школе умных детей, ребенок подводится к новым знаниям и умениям, но все выводы делает самостоятельно. И основной упор при объяснении дел делается на понимание ребенком смысла той или иной темы.
Как эффективно объяснить ребенку дроби?
Шаг первый — Ввести понятие «доли».
Детям показывают апельсин и предлагают разделить его на доли.
Один апельсин — это целый предмет. И состоит он из долей.
Мы делили апельсин. Много нас, а он один
Эта долька для ежа, эта долька для чижа…
А для волка — кожура.
На доли можно поделить многое: арбуз, яблоко, шоколад и даже квартиру (комната, кухня, коридор — все это доли квартиры)
Будет замечательно, если ребенок и вы возьмете и физически разделите шоколадку на доли, апельсинку на доли, мандаринку на доли.
Именно на этом шаге мы обращаем внимание на то, что один апельсин — это целый предмет, и его можно обозначить цифрой 1.
Шоколадка — целый предмет, или 1 шоколадка.
Вторым шагом необходимо ввести понятие «дробь».
Ведь мы шоколадку «разделили» или «раздробили» на части! Апельсин разделили или «раздробили» на доли!
Хорошим подспорьем являются детали ЛЕГО, из которых можно собрать целый прямоугольник и «раздробить» его на части.
На этом шаге можно нарисовать прямоугольник, разделить его на 4 равные части, например, и попросить ребенка закрасить (или отделить) одну часть, две части.
Нарисовать квадрат, раздробить его на 4 части. И попросить закрасить 2 части.
Шаг три — научить ребенка записывать часть
Передаем инициативу думать и делать выводы ребенку и задаем ему вопрос.
— Кто догадается, сколько всего частей в этом предмете?
— На сколько частей мы его раздробли? Разделили?
На четыре!
Вспоминаем, что деление (при делении в столбик, записывается чертой)
Так же и в дробях. Черта обозначает деление! На сколько частей мы разделили данный прямоугольник?
Так и напишем, делили на 4
А теперь сколько частей мы взяли? Закрасили?
А давай возьмем две части? Как закрасим? Как напишем?
Далее необходимо разделить прямоугольник на другое количество частей, и предожить взять две части. Спросите ребенка, как это показать?
Как записать, что взяли 2 части из 5?
Вспоминаем, что надо поставить черту (разделить), на 5 частей. И взять 2 части
Шаг 4 Переходим к записи целой части через дробь
Для этого шага пригодится шоколадка.
Можно спросить, сколько шоколадок? Одна.
— На сколько долек мы раздробили шоколадку? — На 8 долек.
— Как записать шоколадку, но с помощью дроби? На сколько разделили?
— На 8 частей.
— А в целой сколько частей?
8 частей или 8/8 целая шоколадка.
Далее возвращаемся и записываем целым предметом другие разделенные до этого предметы.
Шаг 5. Практика
Отломите три кусочка, дайте ребенку. Сколько дали? 3. От скольки? от 8!
Запишем полученную дробь 3/8!
Детали лего, полоски, прямоугольники, шоколад, конфеты, жвачки с дольками и т.п
В ход идет любой подручный материал.
Но одно условие — дробить надо на равные части.
Дети очень любят играть с дольками из пачки жвачки.
10/10 — это целая упаковка жвачки
2/10 — как в рекламе
6/10 — 6 долек из пачки жвачки
Шаг 6. Разбираемся в терминологии
И снова задаем ребенку вопросы и помогаем найти ответы.
— В числе 3/8 что обозначает число 8?
— На сколько поделили!
— Что означает число 3?
— Сколько взяли!
— Правильно, число долек, которое взяли. Его еще называют числитель.
Шаг 7. Задачки с подвохом
Предложите ребенку две дроби:
И поставить знак > в ту сторону, какая дробь больше
Для выполнения задания лучше взять шоколадку, в которой есть 20 долек.
И взять 2 дольки (приложить к дроби 2/20) и 4 дольки (приложить к дроби 4/20). Спросить, где больше. Глядя куда ворона откроет рот?
Техника ворона, благодаря которой детям можно объяснить тему сравнения чисел представлена в видео ниже:
Когда ребенок справится с этим заданием и подобными, усложняем задачу.
Пишем другой пример:
Вспоминаем шоколадку.
Взяли и там и там по две части. Но в первом случае, раздробили шоколадку на 20 долек, а во втором — эту же шоколадку, на 10 долек.
Конечно, лучше всего проделать это на практике.
Подобные сравнения — самая сложная тема для детей на этапе знакомства с темой дроби. Им кажется, что если число 20 больше, то и дробь тоже.
И именно здесь скрывается подводный булыжник.
Попробуйте и практикуйте с шоколадкой такие примеры.
Ребенок, при соблюдении последовательности шагов при объяснении темы, а так же, если вы не будете давать готовые решения и ответы, схватит тему и поймет ее.
А именно это является самым ценным.
Такой подход называется — проблемным обучением, или развитием в ребенке критического мышления. Когда мы ребенку не даем правило или ответ, но помогаем вывести его самому.
Ведь ребенок сам назвал, что шоколадку «раздробили», а значит узнал слово «дробь».
Сам вспомнил, как записывать деление чертой.
Сам ответил, что в примере 3/8, тройка — это число долек, которые «Взяли», числитель
Сам понял, что 8 — это на сколько поделили.
Практика в сочетании с правильной методикой обучения творит чудеса!
В школе умных детей вы найдете простые и понятные видео-ответы на все темы, получите уникальный опыт учителя и пошаговую инструкцию, как и что объяснить ребенку.
Чтобы дети, которые не понимают ту или иную тему или которым не повезло с учителем, имели возможность полюбить обучение, учиться у лучших учителей (в том числе по английскому у носителей языка)
Чтобы родители, которые совсем не педагоги, и не знают методик преподавания, имели инструмент, позволяющий легко и просто учить ребенка на семейном обучении или стать ребенку грамотным помощником дома, не тратя бюджет семьи на репетиторов.
Школа умных детей — это инвестиция, которая окупится уже в первые месяцы обучения ребенка.
Что вы получите?
Уроки по русскому и математике на 4-6 минут, это объяснение для родителей, как объяснить ребенку ту или иную тему, с какими сложностями можно столкнуться. Но многие наши родитетели напрямую включают уроки деткам (3-4 класс смело), а в 1-2 классе вместе смотрят и потом выполняют задания.
Уроки по английскому языку — это напрямую уроки для детей с отдельными поясняющими уроками и материалами для родителей.
Так же в школе открыта база знаний с техниками эффективного обучения: как учить стихотворения, определения, пересказывать текст, повысить скорость чтения и другие инструменты
И многое, много другое.
Сейчас в школе около 500 уроков на все сферы школьной жизни.
Доступ октрывается ко всем урокам начальных классов (1-4 классы) до мая 2019 года (1.5 учебных года вместо 1) при оплате в ноябре-декабре 2017 года
Получить объяснение всех тем начальной школы простым и эффективным языком
Наша система позволит вам отыскать самую короткую дорогу на пути к воспитанию умного, счастливого, успешного, талантливого ребенка, верящего в себя.
Вы получите четкую систему действий, которая заиграет ярко, живо и с любовью.
Станьте участником Школы умных детей уже сегодня и получите эффективную систему обучения ребенка.
Стать участником школы умных детей
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Похожее
gladtolearn.ru
Как складывать дроби с разными знаменателями
Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.
Чтобы сложить или вычесть дроби с разными знаменателями, надо:
1) Найти наименьший общий знаменатель (НОЗ) данных дробей.
2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.
3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.
4) Проверить, является ли полученная в результате дробь правильной и несократимой.
В следующих примерах надо сложить или вычесть дроби с разными знаменателями:
Решение:
1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей. Выбираем большее из чисел и проверяем, делится ли оно на меньшее. 25 на 20 не делится. Умножаем 25 на 2. 50 на 20 не делится. Умножаем 25 на 3. 75 на 20 не делится. Умножаем 25 на 4. 100 на 20 делится. Значит, наименьший общий знаменатель равен 100.
2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.
3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.
4) Полученная дробь — правильная и несократимая. Значит, это — ответ.
1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.
2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.
4)Полученная в результате дробь — правильная и несократимая.
1) 30 на 20 не делится. 30∙2=60 на 20 делится. Значит, 60 — наименьший общий знаменатель этих дробей.
2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.
4) полученную дробь надо сократить на 5.
1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.
2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.
3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.
www.for6cl.uznateshe.ru
Как научить ребенка математике
Для многих математика как темный лес, и кажется, что разобраться во всём этом просто невозможно. Но что, если посмотреть на это под другим углом? К примеру, воспринимать математику не как что-то сложное и скучное, а как любопытную головоломку. Для этого мы предлагаем 10 математических трюков, которые перевернут твое представление о математике. Этого нет ни в одном учебнике!
Как научить ребенка математике
10 хитрых трюков
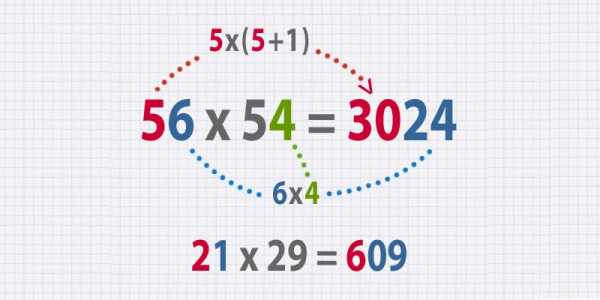
- Умножение чисел, состоящих из единиц, на самих себя
Возьми эту таблицу на вооружение, с ней решать такие примеры станет проще простого.
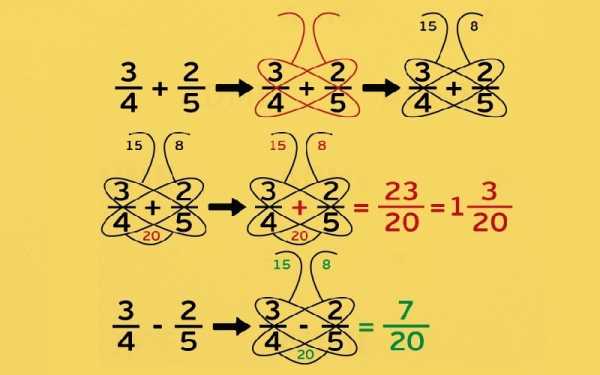
- Метод бабочки для сложения и вычитания дробей
Разобраться в этой схеме очень легко. В выбранном примере умножаем числа по диагонали. Если дроби нужно сложить, получившиеся числа также нужно сложить, аналогично при вычитании. Это будет наш числитель. После умножаем числа в знаменателе — получаем ответ!
- Секрет умножения чисел на 11
Представьте следующий пример: 63 × 11.
Для его решения нужно просто сложить цифры 6 + 3 = 9, а затем поместить девятку между шестеркой и тройкой. Вот и наше решение: 693.Но расслабляться еще рано: это лишь половина того, что необходимо знать.
Допустим, пример такой: 85 × 11.
Несмотря на то, что 8 + 5 = 13, ответ не 8135! Как и прежде, цифра 3 ставится между цифрами 8 и 5, но 1 добавляется к цифре 8 для получения правильного ответа 935.
- Можно ли использовать этот метод для чисел с большим количеством цифр? Безусловно!
Здесь уже немного сложнее, но не стоит огорчаться, у тебя всё получится. Для примера: 13432 × 11 — ответ всё еще будет начинаться с 1 и заканчиваться на 2, а так как 1 + 3 = 4; 3 + 4 = 7; 3 + 4 = 7 и 3 + 2 = 5, ответ будет равен 147752.
- Находим дробь от целого числа
Пользуйся этой схемой и забудь о проблемах с дробями! Это и есть ответ на вопрос, как научить ребенка решать математические примеры.
- Умножать на 9 проще, чем ты думаешь!
Эта забавная закономерность поможет тебе без труда запомнить таблицу умножения на 9 навсегда.
- Преврати сложное умножение в простые примеры
Этот трюк уже немного похож на магию. Всё, что нужно, — вычесть множители из 100, а произведения сложить и умножить. Сумма, вычтенная из 100, — это первая часть ответа, а произведение — вторая.
- А это еще один способ умножать большие числа

- Запомнить число Пи теперь не составит труда


- Так можно с легкостью найти процент от числа

Теперь математика уже не кажется такой скучной, правда? Благодаря этим трюкам ты можешь объяснить ребенку математику и сделать решение примеров интересным и увлекательным занятием!
А также ты можешь поделиться этими трюками с друзьями. Уверены, это им пригодится!
Автор статьи
Редакция «Так Просто!»
Это настоящая творческая лаборатория! Команда истинных единомышленников, каждый из которых специалист в своем деле, объединенных общей целью: помогать людям. Мы создаем материалы, которыми действительно стоит делиться, а источником неиссякаемого вдохновения служат для нас любимые читатели!
takprosto.cc