Эйлера венна знаки – Понятие множества, подмножества, пустого множества. Диаграммы Эйлера-Венна

Понятие множества, подмножества, пустого множества. Диаграммы Эйлера-Венна

Элементы теории множеств.

 

«Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» — так описал понятие «множество» Георг Кантор, основатель теории множеств.

Основные предпосылки канторовской теории множеств сводятся к следующему:

1° Множество может состоять из любых различимых объектов.

2° Множество однозначно определяется набором составляющих его объектов.

3° Любое свойство определяет множество объектов, которые этим свойством обладают.

Если х — объект, Р — свойство, Р(х) — обозначение того, что х обладает свойством Р, то через {х|Р(х)} обозначают весь класс объектов, обладающих свойством Р. Объекты, составляющие класс или множество, называют элементами класса или множества.

Термин «множество» употребляется как синоним понятий совокупность, собрание, коллекция некоторых элементов. Так, можно говорить о:

а) множестве пчёл в улье,

б) множестве точек отрезка,

в) множестве вершин квадрата или о множествах его сторон и диагоналей,

г) множестве студентов в аудитории и т.д.

В приведённых примерах в случаях а), в)-г) соответствующие множества состоят из определённого конечного числа предметов, такие множества называются конечными. Множество точек отрезка (пример б)) пересчитать невозможно, поэтому такие множества называются бесконечными. Множество, не содержащее ни одного элемента, называется пустым множеством.

Наиболее простая форма задания множества — перечисление его элементов, например А={4, 7, 13} (множество А состоит из трёх элементов — целых чисел 4, 7, 13). Другая часто применяемая форма задания — указание свойств элементов множества, например A = {x| x² ≤ 4} — множество чисел х, удовлетворяющих указанному условию.

Множества обычно обозначаются большими буквами А, В, С,…., а их элементы — малыми: а, в, с,… Запись а ∈ А (читается: а принадлежит А) или A ∋ a (читается: А содержит а) означает, что а есть элемент множества А. Пустое множество обозначается значком Ø.

Если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение — B ⊆ A или A ⊇ B).

Каждое множество является своим подмножеством (это самое «широкое» подмножество множества). Пустое множество является подмножеством любого множества (это самое «узкое» подмножество). Любое другое подмножество множества А содержит хотя бы один элемент множества А, но не все его элементы. Такие подмножества называются истинными, или собственными подмножествами. Для истинных подмножеств множества А применяется обозначение B ⊂ A или A ⊃ B. Если одновременно B ⊆ A и A ⊆ B, т.е каждый элемент множества В принадлежит А, и в то же время каждый элемент А принадлежит В, то А и В, очевидно, состоят из одних и тех же элементов и, следовательно, совпадают. В этом случае применяется знак равенства множеств: A = B. (Символы ∈, ∋, ⊂, ⊃, ⊆, ⊇ называются символами включения).

Геометрически множества обычно изображаются как некоторые множества точек плоскости. Сами картинки называются диаграммами Эйлера-Венна (кругами Эйлера). То есть диаграммы Эйлера-Венна – геометрические представления множеств или геометрические изображения отношений между объёмами понятий посредством пересекающихся контуров(кругов или эллипсов), предложенная английским логиком Джоном Венном (1834 — 1923) в конце позапрошлого века. В своих работах по наглядному графическому изображению логических фигур он опирался на ряд графических систем, предложенных Эйлером (1707 — 1783), И.Ламбертом (1728 — 1777), Жергонном (1771 -1859), Б. Больцано (1781 -1848).

Приведём некоторые из диаграмм. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество

U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

 

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

 

 

Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

 

 

Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

Распространено и другое обозначение симметрической разности: А ∆ В, вместо А + В.

 

 

Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):

 

Свойства операции пересечения: 1) A∩A=A; 2) A∩Ø=Ø; 3) A∩Ā= Ø; 4) A∩U=A; 5) A∩B=B∩A;	Свойства операции объединения: 1) AUA=A; 2) AUØ=A; 3) AUĀ= U; 4) AUU=U; 5) AUB=BUA;
Свойства операции разности: 1) A\A= Ø; 2) A\Ø= A; 3) A\Ā= A; 4) A\U= Ø;	5) U\A= Ā; 6) \A =Ø; 7) A\B≠B\A;

Справедливы равенства: (AUB)= A∩B; (A∩B)= AUB.

 

 

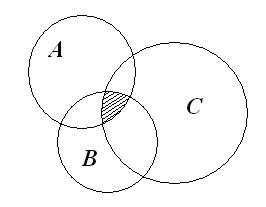
В заключение приведем еще одну формулу для подсчета числа элементов в объединении трех множеств (для общего случая их взаимного расположения, показанного на рисунке):

m(AUBUC)=m(A)+m(B)+m(C)-m(A∩B)-m(B∩C)-m(A∩C)+m(A∩B∩C)

 

Пример 1. Записать множество всех науральных делителей числа 15 и найи число его элементов.

A={1,3,5},

m(A)=3.

 

Пример 2. Заданы множества A={2,3,5,8,13,15}, B={1,3,4,8,16}, C={12,13,15,16}, D= {0,1,20}.

Найти AUB, CUD, B∩C, A∩D, A\C, C\A, B\D, AUBUC, A∩B∩C, BUD∩C, A∩C\D.

 

AUB= {1,2,3,4,5,8,13,15,16}

CUD= {0,1,12,13,15,16,20}

B∩C= {16}

A∩D= Ø

A\C= {2,3,5,8}

C\A= {12,16}

B\D= {3,4,8,16}

AUBUC= {1,2,3,4,5,8,12,13,15,16}

A∩B∩C= Ø

BU(D∩C)= {1,3,4,8,16}

(A∩C)\D= {13,15}

 

Пример 3. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 – на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учеников умеют кататься и на коньках и на лыжах?

Множество всех учеников будем считать основным множеством U, тогда A и B – соответственно множества учащихся, умеющих кататься на лыжах и на коньках.

A∩B – множество учащихся, не умеющих кататься ни на лыжах, ни на коньках.

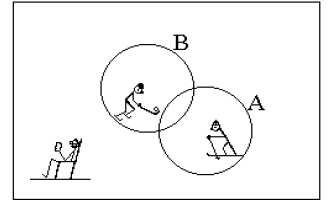
По условию m(A∩B)=60, также используем равенство (AUB)= A∩B, тогда m((AUB))=60.

Значит, m(AUB)=m(U)-m((AUB))=1400-60=1340.

По условию m(A)=1250, m(B)=952, получаем m(A∩B)=m(A)+m(B)-m(AUB)=1250+952-1340=862

 

Пример 4. Группа из 25 студентов сдала экзаменационную сессию со следующими результатами: 2 человека получили только «отлично»; 3 человека получили отличные, хорошие и удовлетворительные оценки; 4 человека только «хорошо»; 3 человека получили хорошие и удовлетворительные оценки. Число студентов, сдавших сессию только на «отлично», «хорошо», равно числу студентов, сдавших сессию только на «удовлетворительно». Студентов, получивших только отличные и удовлетворительные оценки, — нет. Удовлетворительные или хорошие оценки получили 22 студента. Сколько студентов не явились на экзамены? Сколько студентов сдали сессию только на «удовлетворительно»?

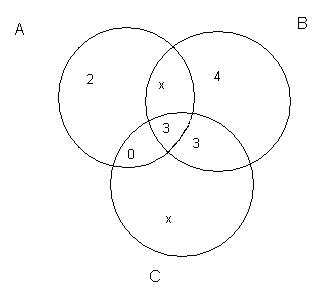
Введем обозначения.

А – множество студентов, получивших «отлично»;

В – множество студентов, получивших «хорошо»;

С – множество студентов, получивших «удовлетворительно».

Из условия известно, что

— число студентов, получивших только «5»,

 

— число студентов, получивших только «4»,

 

— число студентов, получивших только «5» и «3»,

 

— число студентов, получивших только «4» и «3»,

 

— число студентов, получивших «5», «4» и «3».

Также по условию известно, что множества и равны. Обозначим эту величину за x. Тогда из условия , получим

Число же студентов, не явившихся на экзамен, найдем следующим образом:

Ответ: 6 студентов получили только «удовлетворительно», 1 студент не явился на экзамены.

 

Пример 5.

megaobuchalka.ru

1.2. Подмножества. Диаграммы Эйлера – Венна

Определение 1.4. Множество B называется подмножеством множества A, если каждый элемент множества B принадлежит множеству A.

Пример 1.2. Пусть А = {1, 2, 3, 4, 5, 6, 7}, а B = {2, 3, 5, 7}. Множество В является подмножеством множества А, поскольку каждый элемент множества В принадлежит множеству А.

Если множество B является подмножеством множества A, то говорят также, что B содержится в A или B включено в A, при этом пишут В  А или А  В. Символ  называется знаком включения (точнее, нестрого включения).

Согласно данному определению 1.4 подмножества, каждое множество является подмножеством самого себя, то есть ( A) А  А. Кроме того, считается, что пустое множество есть подмножество любого множества

A: ( A)   А.

Различают два вида подмножеств множества А.

Определение 1.5. Пустое множество  и множество А называются несобственными подмножествами множества А.

Определение 1.6. Любые подмножества множества А, отличные от А и , называются собственными подмножествами множества А.

Определение 1.7. Множества A и B, состоящие из одних и тех же элементов, называются равными. При этом пишут А = В, в противном случае А ≠ В.

Справедливо следующее утверждение, которое также можно рассматривать в качестве определения равных множеств.

Утверждение 1.1. А = В  А  B и В  А.

Замечание 1.3. Из утверждения 1.1 вытекает способ доказательства равенства двух множеств: если доказать, что каждый элемент из множества A является элементом множества B и каждый элемент из множества B является элементом множества A, то делают вывод, что А = В.

Говорят, что множество B строго включено в множество A или, по-другому, А строго включает B, если В  А и В  А. В этом случае пишут B  A. Символ  называется знаком строгого включения.

Пример 1.3. Имеют место следующие строгие включения числовых множеств: N  N₀  Z  Q  R  C и I  R  C.

Определение 1.8. Совокупность всех подмножеств множества A называется его булеаном (или множеством-степенью), и обозначается через P(A) (или 2^A).

Пример 1.4. Если A = {a, b, c}, то булеан множества А это множество P(A) = {, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}}.

Для наглядного изображения множеств и их свойств используют так называемые диаграммы Эйлера² – Венна³. Множество отождествляется с множеством точек на плоскости, лежащих внутри некоторых замкнутых кривых, например окружностей (так называемые круги Эйлера). В частности, универсальное множество U изображается множеством точек некоторого прямоугольника или всей плоскости (рис. 1.1).

1.3. Операции над множествами и их свойства

Определим операции над множествами, с помощью которых можно получать из любых имеющихся множеств новые множества.

1. Объединение (или сумма).

Определение 1.9. Объединением множеств А и В называется множество A  B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств.

То есть, по определению 1.9, A  B = {х | х Î А или х Î В}.

Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера – Венна. Объединение множеств А и В заштриховано и изображено на рис. 1.2.

Заметим, что в объединение двух множеств A и B могут входить элементы из A, не принадлежащие множеству B, элементы из B, не принадлежащие множеству A, и элементы, принадлежащие множествам A и B одновременно. Следовательно, ( A, B) A  A  B и B  A  B.

studfiles.net

Диаграмма Венна — Howling Pixel

Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество U{\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества^[1][2].

Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов^[3], для :

• описания функционирования формальных нейронов Мак-Каллока и сетей из них^[4]
• синтеза надежных сетей из не вполне надежных элементов^[5],
• построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств^[6],
• получения логических следствий из заданной информации, минимизации формул исчислений^[7][8].

Диаграммы Венна при помощи n{\displaystyle n} фигур изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру^[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

Дальнейшим развитием аппарата диаграмм Венна в классическом исчислении высказываний является аппарат вероятностных диаграмм ^[10], понятие сети диаграмм, использующей диаграммы Венна как операторы^[11].

Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.

Связь диаграмм Эйлера и Венна

Диаграммы Эйлера в отличие от диаграмм Эйлера — Венна изображают отношения между множествами: непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами.

Диаграммы Венна основаны на существенно иной идее, чем круги Эйлера^[12]. Круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[12].

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

См. также

Примечания

1. ↑ Столл, 1968, с. 25.
2. ↑ Нефедов, 1992, с. 8.
3. ↑ Кузичев, 1968, с. 106.
4. ↑ Кузичев, 1968, с. 171.
5. ↑ Кузичев, 1968, с. 134.
6. ↑ Кузичев, 1968, с. 9.
7. ↑ Кузичев, 1968, с. 97.
8. ↑ Столл, 1968, с. 26.
9. ↑ Кузичев, 1968, с. 57.
10. ↑ Кузичев, 1968, с. 124.
11. ↑ Кузичев, 1968.
12. ↑ ^{1 2} Кузичев, 1968, с. 25.

Ссылки

Литература

• Столл Р. Множества, логика, аксиоматические теории. — М.: Мир, 1968. — 231 с.
• Нефедов В.Н., Осипова В.А. Курс дискретной математики. — М.: МАИ, 1992. — 264 с. — ISBN 5-7035-0157-X.
• Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.

Алгебра логики

Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики.

Деление понятий

Деление понятий — это логическая операция, посредством которой объем делимого понятия распределяется по объемам новых понятий, каждое из которых представляет частный случай исходного понятия. Например, расчёты делятся на наличные и безналичные. Понятия разделяются исходя из существенного признака, который может изменяться по определенному принципу или правилу (например, образование из понятия «торговый баланс» новых понятий, в которых фиксируется то или иное соотношение ввоза и вывоза товаров).

Диаграмма Эйлера

Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях.

Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).

Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.

На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.

Дизъюнкция

Дизъю́нкция (от лат. disjunctio — разобщение), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».

Дизъюнкция может быть операцией как бинарной (имеющей два операнда), так и n {\displaystyle n} -арной (имеющей n{\displaystyle n} операндов) для произвольного n{\displaystyle n}.

Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более двух префиксная и постфиксная записи экономичнее.

Импликация

Импликация (от лат. implicatio — «связь») — бинарная логическая связка, по своему применению приближенная к союзам «если…, то…».

Импликация записывается как посылка ⇒{\displaystyle \Rightarrow } следствие; применяются также стрелки другой формы и направленные в другую сторону, но всегда указывающие на следствие.

Суждение, выражаемое импликацией, выражается также следующими способами:

Импликация играет очень важную роль в умозаключениях. С её помощью формулируются определения различных понятий, теоремы, научные законы.

При учёте смыслового содержания высказываний импликация подразумевает причинную связь между посылкой и заключением.

Конъюнкция

Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».

Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).

Логическая константа

В логике, логической константой формального языка L{\displaystyle {\mathcal {L}}} является символ, который имеет то же семантическое значение при любой интерпретации^[en] в L{\displaystyle {\mathcal {L}}}. Двумя важными типами логических констант являются логические связки и кванторы. Предикат равенства (обычно пишется «=») также рассматривается как логическая константа во многих системах логики.

Некоторые символы, которые обычно рассматриваются как логические константы:

Для обозначения многих логических констант используются и другие символы, например, символ «&» для логического «и».

Вопрос «Что такое логическая константа?» является одним из фундаментальных вопросов философии логики.

Логическая операция

В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.

Математическая логика

Математи́ческая ло́гика (теоретическая логика, символическая логика) — раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики. В более широком смысле рассматривается как математизированная ветвь формальной логики — «логика по предмету, математика по методу», «логика, развиваемая с помощью математических методов».

Мнение

Мне́ние — понятие о чём-либо, убеждение, суждение, заключение, вывод, точка зрения или заявление на тему, в которой невозможно достичь полной объективности, основанное на интерпретации фактов и эмоционального отношения к ним.

Множество

Мно́жество — одно из ключевых понятий математики; это математический объект, сам являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества и обладают общим для всех их характеристическим свойством. Изучением общих свойств множеств занимаются теория множеств, а также смежные разделы математики и математической логики.

Примеры: множество жителей заданного города, множество непрерывных функций, множество решений заданного уравнения.

Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством. Понятие множества позволяет практически всем разделам математики использовать общую идеологию и терминологию.

Обобщение понятий

Обобще́ние поня́тий — логическая операция, посредством которой в результате исключения видового признака получается другое понятие более широкого объема, но менее конкретного содержания; форма приращения знания путём мысленного перехода от частного к общему в некоторой модели мира, что обычно соответствует и переходу на более высокую ступень абстракции. Результатом логической операции обобщения является гипероним.

Объём понятия

Объём поня́тия (в логике) — совокупность предметов, охватываемых понятием. Объём и содержание понятия выступают как основные характеристики понятия, подчиняясь при этом закону обратного отношения между содержанием и объёмом понятия (увеличение объёма приводит, как правило, к уменьшению содержания и наоборот). Изменение понятия обычно предполагает изменение его объёма.

Части, входящие в объём понятия, называют классами или множествами. Они, в свою очередь, включают в себя более мелкие части (подклассы или подмножества). Отдельный предмет, принадлежащий к классу, называется элементом класса.

Соотношения между объёмами различных понятий можно иллюстрировать графически с помощью кругов Эйлера.

Ограничение понятий

Ограничением понятия — называется логическая операция, состоящая в прибавлении к содержанию понятия нового признака, наличие которого в содержании понятия сужает его объём. При этом исходное понятие будет родовым, а в результате его ограничения получается видовое понятие. Например, «движение ссудного капитала» — «международный кредит».

Пределом для операции ограничения понятия является единичное понятие, объём которого состоит из одного единственного предмета.

Противоположность данной логической операции является обобщение понятия.

Результатом логической операции ограничения является гипоним.

Отрицание

Отрица́ние, инве́рсия (от лат. inversio «переворот»), логи́ческое «НЕ» в логике — унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком ¬ перед или чертой ^— над суждением.

Как в классической, так и в интуиционистской логике «двойное отрицание» ¬¬A{\displaystyle \neg \neg A} является следствием суждения A{\displaystyle A}, то есть имеет место тавтология: A→¬¬A{\displaystyle A\rightarrow \neg \neg A}.

Обратное утверждение ¬¬A→A{\displaystyle \neg \neg A\rightarrow A} верно в классической логике (закон двойного отрицания), но не имеет места в интуиционистской. То есть, отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.

Подмножество

Подмно́жество в теории множеств — это понятие части множества.

Полилогизм

Полилоги́зм — мнение, что различные группы людей мыслят существенно по-разному, руководствуясь различными правилами логики, в зависимости от социального положения, пола, этнического происхождения, расы.

Термин был предложен Людвигом фон Мизесом в работе «Человеческая деятельность: трактат по экономической теории» (1949). Мизес, в частности, критиковал марксистский и расистский полилогизм. Позже со схожей критикой термин использовали Хайек и Айн Рэнд, и их сторонники. Однако допустимость использования характеристики полилогизма в отношении различных теорий оспаривалась, состоятельность полилогизма не получила научного подтверждения.

Содержание понятия

Содержание понятия — это совокупность существенных и отличительных признаков предмета, качества или множества однородных предметов, отражённых в этом понятии, поскольку с точки зрения логики всякое понятие имеет содержание и объём. Например, содержанием понятия «коррупция» является совокупность двух существенных признаков: «сращивание государственных структур со структурой преступного мира» и «подкуп и продажность общественных и политических деятелей, государственных чиновников и должностных лиц».

О содержании понятия нельзя говорить в отрыве от его объёма. Объёмом понятия называется множество обобщённых в нём предметов. Например, под объёмом понятия «товар» подразумевается множество всех изделий, предлагаемых рынку как сейчас, так и в прошлом или в будущем.

Эквиваленция

Логическая равнозначность или эквивале́нция (или эквивале́нтность) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Двуместная логическая операция обычно обозначается символом ≡ или ↔.

Эквиваленция A⟺B{\displaystyle A\iff B} — это сокращённая запись для выражения (¬A∧¬B)∨(A∧B){\displaystyle (\neg A\land \neg B)\lor (A\land B)}

Задаётся следующей таблицей истинности:

Таким образом, высказывание A ≡ B означает «A то же самое, что B», «A эквивалентно B», «A тогда и только тогда, когда B».

Не надо путать эквиваленцию — логическую операцию с логической эквивалентностью^[en] высказываний — бинарным отношением. Связь между ними следующая:

Формальная
Математическая (теоретическая, символическая)
См. также

This page is based on a Wikipedia article written by authors (here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

howlingpixel.com

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Теория вероятностей и статистика

      В теории вероятностей случайными событиями являются подмножества множества элементарных исходов   Ω .  

      Над событиями, как и над любыми множествами, можно совершать следующие операции.

Произведение (пересечение) двух событий

      Операцию произведения (пересечения) двух событий   A   и   B  обозначают

,   или   AB ,   или   .

      Определение 1. Произведением (пересечением) двух событий   A   и   B   называют такое событие, которое состоит из всех элементов, входящих как в событие   A ,   так и в событие   B   (рис. 1).

Событие   A	Событие   B
Событие

Событие   A

Событие   B

Событие

Рис.1

Сумма (объединение) двух событий

      Операцию суммы (объединения) двух событий   A   и   B  обозначают

A + B   или  

      Определение 2. Суммой (объединением) двух событий   A   и   B   называют такое событие, которое состоит из элементов события   A   и элементов события   B   (рис. 2).

Событие   A	Событие   B
Событие   A + B

Событие   A

Событие   B

Событие   A + B

Рис.2

Разность двух событий

      Операцию разности двух событий   A   и   B  обозначают

A \ B

      Определение 3. Разностью событий   A   и   B   называют событие, состоящее из тех элементов события   A ,  которые не входят в событие   B   (рис. 3).

Событие   A	Событие   B
Событие   A \ B

Событие   A

Событие   B

Событие   A \ B

Рис.3

      Замечание 1. Разностью событий   B   и   A   является событие   B \ A ,   изображенное на рисунке 4.

Событие   A	Событие   B
Событие   B \ A

Событие   A

Событие   B

Событие   B \ A

Рис.4

Симметрическая разность двух событий

      Операцию симметрической разности двух событий   A   и   B  обозначают

      Определение 4 . Симметрической разностью событий   A   и   B   называют событие, состоящее из тех элементов события   A ,  которые не входят в событие   B ,   а также из тех элементов события   B ,  которые не входят в событие   A   (рис. 5).

Событие   A	Событие   B
Событие

Событие   A

Событие   B

Событие

Рис.5

Переход к противоположному событию

      Событие, противоположное к событию   A ,  обозначают

  или   A^C

      Определение 5. Противоположным событием к событию   A   называют событие, состоящее из тех элементов всего множества элементарных событий   Ω ,   которые не входят в событие   A  (рис. 6).

Множество   Ω	Событие   A
Событие

Множество   Ω

Событие   A

Событие

Рис.6

      Замечание 2. Справедлива формула

      Определение 6. Событие   Ω   называют достоверным событием, пустое множество     называют невозможным событием.

      Замечание 3. Рисунки, на которых наглядно показаны операции над множествами, называют диаграммами Эйлера-Венна. В частности, диаграммами Эйлера-Венна являются рисунки 1-6 .

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru