Экспонента что это такое – Что такое экспонента или как заставить чай остывать не так быстро — T&P

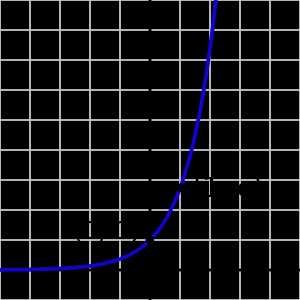
Что такое экспонента или как заставить чай остывать не так быстро — T&P

Когда снежный ком катится с горы, он постоянно увеличивается. Чем больше он становится, тем быстрее катится, чем быстрее катится, тем быстрее растет.

Математики и физики очень любят описывать мир при помощи чисел. А еще больше — при помощи функций. Функция — это правило, по которому одному числу (например, x) ставится в соответствие другое (например y). Функции бывают простые, вроде y=10x или y=x², а бывают посложнее вроде y=10*sin(7×2+3x-9). Если вместо x и y подставить определенные физические параметры и найти функцию, которая их связывает, то получится закон природы.

Еще у функций есть производная. Это — скорость изменения функции. То есть то, насколько изменится y при небольшом изменении x. Например, в случае функции y=10x производная всегда постоянная: y всегда будет расти в 10 раз быстрее, чем x. А в случае функции y=x² производная будет меняться. Если мы увеличим

x c 0 до 1, то y тоже увеличится с 0 до 1. А если увеличим x с 1 до 2, то y увеличится с 1 до 4. То есть, производная с ростом x увеличилась.

Экспонентой называется функция y=e^x, где e — хитрое математическое число, которое примерно равно 2,72. Она обладает замечательным свойством: ее производная равна ей самой. То есть, если расстояние, которое проходит снежный ком, зависит от времени как экспонента, то и его скорость выражается той же самой экспонентой. Это свойство очень помогает математикам решать разные дифференциальные уравнения. Они очень любят с ней работать и стараются разные другие функции путем сдвига, растяжения, или переворачивания графика превратить в экспоненту. Все такие функции можно назвать экспоненциальными. У экспоненциально протекающих процессов есть одно общее свойство: за одинаковый интервал времени их параметры меняются в одинаковое число раз. Банковский вклад каждый год увеличивается на 7%, снежный ком за минуту увеличивается в три раза, а количество урана-235 на атомных электростанциях уменьшается вдвое каждые 700 миллионов лет. Экспоненциальные функции окружают нас повсюду. Экспоненциально развиваются все явления, в которых присутствует обратная связь, когда результат влияет на скорость процесса. В случае со снежным комом обратная связь положительная: чем больше результат, тем быстрее протекает процесс. А масса и скорость снежного кома

y экспоненциально возрастают со временем x. Аналогично ведут себя деньги в банке при фиксированной процентной ставке. Чем больше денег, тем больше ежегодный прирост — и тем быстрее денег хватит на домик на Мальдивах. Так же увеличивается численность животных при отсутствии внешних угроз: чем больше популяция, тем больше размножающихся особей, тем быстрее она увеличивается. А еще, когда микрофон подносишь близко к динамику, то самый тихий шорох через секунду превратится в звонкий гул.

Бывает, что обратная связь отрицательная: чем больше результат, тем медленнее идет процесс. Например, когда мы голодны, мы начинаем быстро поглощать еду, но как только чувство голода уменьшается, мы начинаем есть спокойно, потом лениво доедаем десерт. Чай остывает тоже по экспоненте: чем больше разность температур между чаем и воздухом, тем быстрее он остывает. Так что, если вам надо срочно отвлечься на 15 минут, а горячего чаю выпить хочется — налейте в него холодного молока или воды. Тогда разница температур уменьшится, и чай не остынет так быстро, как если бы он был горячим.

Чем быстрее движется струна гитары, тем быстрее она тормозится о воздух, поэтому громкость звука после дерганья за струну экспоненциально уменьшается. Еще один пример — ядерный распад. Каждое ядро может распасться в случайный момент времени, но чем ядер больше, тем больше распадов будет происходить за одну минуту. Чем быстрее ядра распадаются, тем меньше их становится, а значит и интенсивность радиации со временем падает.

theoryandpractice.ru

Экспонента — это… Что такое Экспонента?

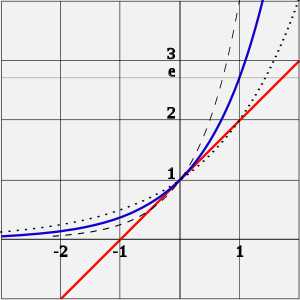
Экспонента — показательная функция , где e — основание натуральных логарифмов ().

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:

или через предел:

Здесь x — любое комплексное число.

Свойства

• , в частности
• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
• Экспонента является выпуклой функцией.
• Обратная функция к ней — натуральный логарифм .
• Фурье-образ экспоненты не существует
• однако преобразование Лапласа существует
• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
• Основное функциональное свойство экспоненты, как и всякой показательной функции:

  .

  • Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид , где c — некоторая константа.

Комплексная экспонента

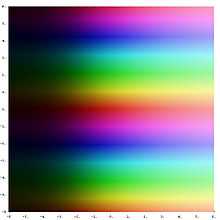График экспоненты в комплексной плоскости.
Легенда

Комплексная экспонента — математическая функция, задаваемая соотношением , где есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты вещественного переменного :

Определим формальное выражение

.

Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции , то есть показать, что разлагается в некоторый сходящийся к данной функции ряд. Покажем это:

Сходимость данного ряда легко доказывается:

.

Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция всюду определена и аналитична.

Свойства

Вариации и обобщения

Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

Определённый таким образом ряд сходится для любого оператора с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием имеет своим решением

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм. Обозначается :

См. также

Литература

• Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
• Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.

dic.academic.ru

Экспонента — Традиция

Материал из свободной русской энциклопедии «Традиция»

\(\exp(x)=e^x\), где e ~ 2.7

Экспонента — функция \(\exp(x)=e^x\), где e — основание натуральных логарифмов.

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

\(e^x=\sum_{k=0}^\infty \frac{x^k}{k!}\)

или через предел:

\(e^x=\lim_{n\rightarrow \infty} (1+\frac{x}{n})^n\)

Здесь x — любое вещественное или комплексное.

• \((e^x)’=e^x\), в частности
• Экспонента является единственным решением дифференциального уравнения \(y’=y\) с начальными данными \(y(0)=1\). Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
• Экспонента является выпуклой функцией.
• Обратная функция к ней — натуральный логарифм \(\ln~a\).
• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
• Основное функциональное свойство экспоненты:

  \(\exp(a+b)=\exp(a)\exp(b)\).

  • Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид \(\exp(ct)\), где c — некоторая константа.

Экспонента от комплексного аргумента[править]

От комплексного аргумента \(z=x+iy\) экспонента определяется следующим образом: $$e^z=e^{x+iy}=e^xe^{iy}=e^x(\cos y + i\sin y)$$(формула Эйлера)

В частности, $$e^{i\pi}=-1$$

Вариации и обобщения[править]

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента[править]

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд: $$\exp A=\sum_{k=0}^{\infty} \frac{A^k}{k!}$$

Определённый таким образом ряд сходится для любого оператора \(A\)с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы \(A\): \(\exp \|A\|\). Следовательно, экспонента от матрицы \(A \in \Bbb{R}^{n\times n}\) всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение \(\dot x=Ax\), \(x\in \mathbb R^n\) с начальным условием \(x(0)=x_0\) имеет своим решением \(x(t)=\exp (At) x_0\).

traditio.wiki

Слово ЭКСПОНЕНТА — Что такое ЭКСПОНЕНТА?

Слово экспонента английскими буквами(транслитом) — eksponenta

Слово экспонента состоит из 10 букв: а е к н н о п с т э

---

Значения слова экспонента. Что такое экспонента?

Экспонента

Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений. Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.

ru.wikipedia.org

ЭКСПОНЕНТА [exponent] — показательная функция с основанием, равным иррациональному числу e, т. е. ex. Если показатель Э. еp(x) содержит сложные выражения, используется запись вида. ep(x) = exp {p(x)}.

Лопатников. — 2003

Экспонента [exponent] — показательная функция с основанием, равным иррациональному числу e, т.е. e x. Если показатель Э., е p(x) содержит сложные выражения, используется запись вида. e p(x) = exp {p(x)}.

slovar-lopatnikov.ru

ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а 4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам.

Научно-технический энциклопедический словарь

ЭКСПОНЕНТА, ПОКАЗАТЕЛЬ СТЕПЕНИ

ЭКСПОНЕНТА, ПОКАЗАТЕЛЬ СТЕПЕНИ (exponent) Одно из названий показателя степени; если у = хn, n является экспонентой. Экспонента не обязательно должна быть целым числом; если z – натуральный логарифм х, т. е., х = еz, мы получаем у = хn = (еz)n = ezn…

Райзберг Б.А. Современный экономический словарь. — 1999

ЭКСПОНЕНТА, ПОКАЗАТЕЛЬ СТЕПЕНИ (exponent) Одно из названий показателя степени; если у = хn, n является экспонентой. Экспонента не обязательно должна быть целым числом; если z – натуральный логарифм х, т. е., х = еz, мы получаем у = хn = (еz)n = ezn…

Райзберг Б.А. Современный экономический словарь. — 1999

Русский язык

Экспоне́нта, -ы (матем.).

Орфографический словарь. — 2004

---

1. экспозиция
2. экспонатный
3. экспонат
4. экспонента
5. экспоненте
6. экспонентный
7. экспоненту

wordhelp.ru

Матричная экспонента — это… Что такое Матричная экспонента?



Матричная экспонента

Экспонента — функция exp(x) = e^x, где e — основание натуральных логарифмов.

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

или через предел:

Здесь x — любое вещественное или комплексное число.

Свойства

• (e^x)’ = e^x, в частности
• Экспонента является единственным решением дифференциального уравнения y‘ = y с начальными данными y(0) = 1. Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
• Экспонента является выпуклой функцией.
• Обратная функция к ней — натуральный логарифм .
• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
• Основное функциональное свойство экспоненты:

  exp(a + b) = exp(a)exp(b).

  • Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид exp(ct), где c — некоторая константа.

Экспонента от комплексного аргумента

От комплексного аргумента z = x + iy экспонента определяется следующим образом:

e^z = e^{x + iy} = e^xe^iy = e^x(cosy + isiny) (формула Эйлера)

В частности,

e^iπ + 1 = 0

Вариации и обобщения

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием x(0) = x₀ имеет своим решением x(t) = exp(At)x₀.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x):

ln(x) = log_e(x)

См. также

Wikimedia Foundation. 2010.

• Матричная механика
• Матрица фильм

Смотреть что такое «Матричная экспонента» в других словарях:

• Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции …   Википедия

• Экспоненциальная функция — Экспонента функция exp(x) = ex, где e основание натуральных логарифмов. Содержание 1 Определение 2 Свойства …   Википедия

• Центральное многообразие — особой точки автономного обыкновенного дифференциального уравнения инвариантное многообразие в фазовом пространстве, проходящее через особую точку и касающееся инвариантного центрального подпространства линеаризации дифференциального уравнения.… …   Википедия

dic.academic.ru

экспонента — это… Что такое экспонента?

ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция …   Большой Энциклопедический словарь

ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) …   Научно-технический энциклопедический словарь

экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 …   Словарь синонимов

Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp {p(x)}. Скорость изменения этой функции в точности равна ей самой …   Экономико-математический словарь

экспонента — Показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp {p(x)}. Скорость изменения этой функции в точности равна ей самой . Число e… …   Справочник технического переводчика

ЭКСПОНЕНТА

— (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… …   Большая политехническая энциклопедия

Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции …   Википедия

экспонента — (от лат. exponens  показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… …   Энциклопедический словарь

экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f …   Automatikos terminų žodynas

экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f …   Fizikos terminų žodynas

dic.academic.ru

Экспонента — Википедия

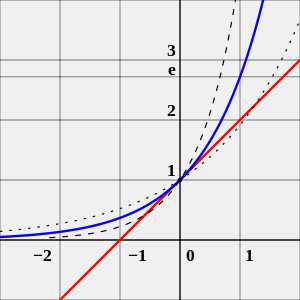
Экспоне́нта — показательная функция , где e — число Эйлера ).

Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:

или через предел:

Здесь x — любое комплексное число.

• , в частности
• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
• Экспонента — выпуклая функция.
• Обратная функция к ней — натуральный логарифм .
• Фурье-образ экспоненты не существует.
• Однако преобразование Лапласа существует.
• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
• Основное функциональное свойство экспоненты, как и всякой показательной функции:

  .

  • Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид , где c — некоторая константа.

Комплексная экспонента[править]

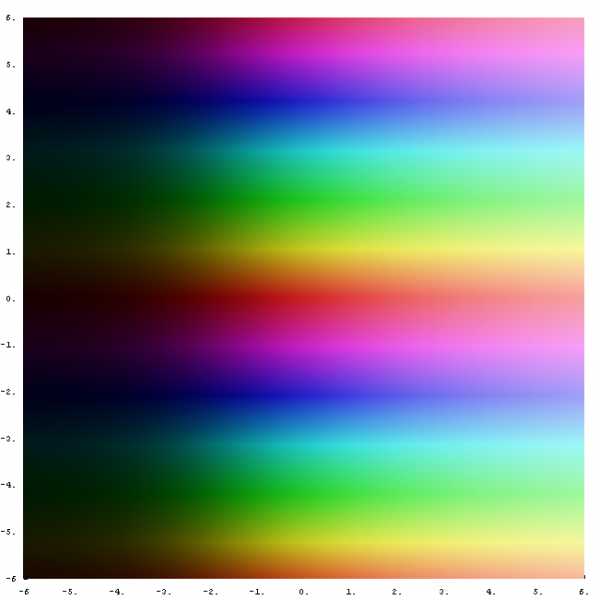График экспоненты в комплексной плоскости.
Легенда

Комплексная экспонента — математическая функция, задаваемая соотношением , где есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты вещественного переменного :

Определим формальное выражение

.

Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции , то есть показать, что разлагается в некоторый сходящийся к данной функции ряд. Покажем это:

Сходимость данного ряда легко доказывается:

.

Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция всюду определена и аналитична.

Свойства[править]

Вариации и обобщения[править]

Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента[править]

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

Определённый таким образом ряд сходится для любого оператора с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием имеет своим решением

h-экспонента[править]

Введение -экспоненты основано на втором замечательном пределе:

При получается обычная экспонента^[1].

Обратная функция[править]

Обратная функция к экспоненциальной функции — натуральный логарифм. Обозначается :

• Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
• Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.

wp.wiki-wiki.ru

No related posts.