Параллелограмм углы – Углы параллелограмма | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Содержание

Параллелограмм. Расстояние между параллельными прямыми [wiki.eduVdom.com]

Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны, т. е. лежат на параллельных прямых (рис.1).

Рис.1
Теорема 1. О свойстве сторон и углов параллелограмма. В параллелограмме противоположные стороны равны, противоположные углы равны и сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
Доказательство. В данном параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC (рис.2).
Рис.2
Эти треугольники равны, так как ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (накрест лежащие углы при параллельных прямых), а сторона АС общая. Из равенства Δ ABC = Δ ADC следует, что АВ = CD, ВС = AD, ∠ B = ∠ D. Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых. Теорема доказана.

Замечание. Равенство противоположных сторон параллелограмма означает, что отрезки параллельных, отсекаемых параллельными, равны.
Следствие 1. Если две прямые параллельны, то все точки одной прямой находятся на одном и том же расстоянии от другой прямой.
Доказательство. В самом деле, пусть а || b (рис.3).
Рис.3
Проведем из каких-нибудь двух точек В и С прямой b перпендикуляры ВА и CD к прямой а. Так как АВ || CD, то фигура ABCD — параллелограмм, и следовательно, АВ = CD.
Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из прямых до другой прямой.
По доказанному оно равно длине перпендикуляра, проведенного из какой-нибудь точки одной из параллельных прямых к другой прямой.
См. Диагонали и признаки параллелограмма

Пример 1. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.
Решение. По теореме 1 противоположные стороны параллелограмма равны. Обозначим одну сторону параллелограмма через х, другую через у. Тогда по условию $$\left\{\begin{matrix} 2x + 2y = 122 \\x — y = 25 \end{matrix}\right.$$ Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.
Пример 2. Четырехугольник ABCD — параллелограмм с периметром 10 см. Найти диагональ BD, зная, что периметр треугольника ABD равен 8 см.
Решение. Пусть условию задачи отвечает рисунок 4.
Рис.4
Обозначим АВ через х, а ВС через у. По условию периметр параллелограмма равен 10 см, т. е. 2(x + у) = 10, или х + у = 5. Периметр треугольника ABD равен 8 см. А так как АВ + AD = х + у = 5 то BD = 8 — 5 = 3 . Итак, BD = 3 см.

Пример 3. Найти углы параллелограмма, зная, что один из них больше другого на 50°.
Решение. Пусть условию задачи отвечает рисунок 5.
Рис.5
Обозначим градусную меру угла А через х. Тогда градусная мера угла D равна х + 50°.
Углы BAD и ADC внутренние односторонние при параллельных прямых АВ и DC и секущей AD. Тогда сумма этих названных углов составит 180°, т. е.
х + х + 50° = 180°, или х = 65°. Таким образом, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.
Пример 4. Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?
Решение. Пусть условию задачи отвечает рисунок 6.
Рис.6
АЕ — биссектриса острого угла параллелограмма. Следовательно, ∠ 1 = ∠ 2.
ВС || AD, АЕ — секущая, следовательно, ∠ 2 = ∠ 3, т. е. ∠ 1 = ∠ 3. А это означает, что треугольник ABE равнобедренный, следовательно, АВ = ВЕ = 1,2 дм.
ЕС = ВС — BE = 3,3 дм.
Пример 5. Прямая АВ параллельна прямой CD (рис.7).
Рис.7
Найти расстояние между этими прямыми, если ∠ ADC = 45°, CD = 1,6 см.
Решение. Искомое расстояние равно длине перпендикуляра АС. Треугольник ACD — прямоугольный и равнобедренный (АС — перпендикуляр), ∠ ADC = 45° по условию, значит, и ∠ CAD = 45°, ибо в прямоугольном треугольнике сумма острых углов равна 90°. Следовательно, АС = CD = 1,6 см.
www.wiki.eduvdom.com
Как найти углы параллелограмма 🚩 углы в параллелограмме 🚩 Математика
31 марта 2011
Автор КакПросто!
Параллелограммом называют четырехугольник противолежащие стороны которого попарно параллельны. Также параллелограмм обладает такими свойствами, как противоположные стороны равны, противоположные углы равны, сумма всех углов равна 360 градусов.

Статьи по теме:
Вам понадобится
Знания по геометрии.
Инструкция
Предположим дан один из углов параллелограмма и равен A. Найдем значения остальных трех. По свойству параллелограмма противоположные углы равны. Значит угол, лежащий напротив данного равен данному и его значение равно А.
Найдем оставшиеся два угла. Так как сумма всех углов в параллелограмме равна 360 градусов, а противоположные углы между собой равны, то получается, что угол, принадлежащий одной стороне с данным, равен (360 — 2А)/2. Ну или после преобразования получим 180 — А. Таким образом в параллелограмме два угла равны А, а два других угла равны 180 — А.
Обратите внимание
Значение одного угла не может превышать 180 градусов. Полученные значения углов можно легко проверить. Для этого сложите их и, если сумма равна 360, все посчитано верно.
Полезный совет
Прямоугольник и ромб являются частным случаем параллелограмма, поэтому все свойства и методы вычисления углов применимы и к ним.
www.kakprosto.ru
Углы параллелорамма
Углы параллелограмма. Здравствуйте! В этой публикации представлена группа заданий с параллелограммами. Требуется вычислить синус (косинус) заданного угла, сторону или высоту. Всё решение сводится к работе с прямоугольным треугольником. То есть вполне достаточно помнить определения тригонометрических функций и уметь применять их на практике. Задачи решаются в одно действие, многие ученики после построения эскиза, наверняка, смогут решить их устно.
Что ещё стоит отметить? Один факт (свойство синуса), который очень пригодится. Это то, что синусы смежных углов равны, подробнее об этом было написано в этой статье. Если озвучить кратко и простыми словами, то синусы углов сумма которых равна 180⁰ равны. Это видно и по формуле приведения:
*а также по тригонометрической окружности (при построении таких углов).
Как это применяется в задачах ниже? Как известно, сумма соседних углов параллелограмма равна 180⁰. И если будет дан синус любого из углов, то это означает, что синусы соседних с ним углов имеют такое же значение.
Рассмотрим задачи:
27433.В параллелограмме ABCD высота, опущенная на сторону AB равна 4, AD=8. Найдите синус угла B.
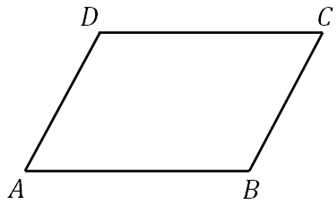
Построим высоту:
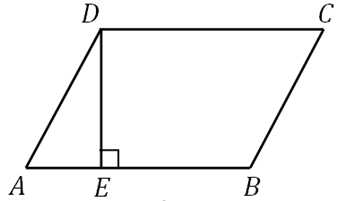
Синус угла В равен синусу угла А, так как известно, что синусы смежных углов равны (указанные углы в сумме равны 180 градусам).
В прямоугольном треугольнике ADE:
Ответ: 0,5
27434. В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, sinA=2/3. Найдите AD.
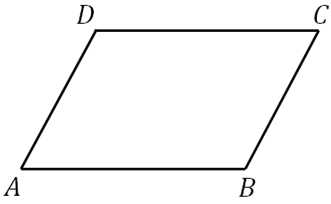
Построим указанную высоту:
В прямоугольном треугольнике ADE:
Ответ: 6
27435. В параллелограмме ABCD sinС=3/7. AD=21. Найдите высоту, опущенную на сторону AB.
Построим параллелограмм:
Угол С равен углу А. Рассмотрим прямоугольный треугольник ADE:
Ответ: 9
27436. В параллелограмме ABCD AB=3, AD=21, sinA=6/7. Найдите большую высоту параллелограмма.
Построим параллелограмм соблюдая соотношения сторон (АВ<AD):
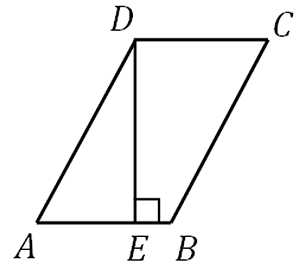
Большей будет высота, которая проведена к меньшей стороне. Рассмотрим прямоугольный треугольник ADE:
Ответ: 18
27438. В параллелограмме ABCD cosA=(√51)/10. Найдите sinB.
Как уже сказано, синусы смежных углов равны. Для того, чтобы найти sinB, достаточно вычислить sinА. Из основного тригонометрического тождества следует, что:
Ответ: 0,7
27437. В параллелограмме ABCD sinA=(√21)/5. Найдите cosB.
*Посмотрите решение внимательно, есть важные нюансы.
Посмотреть решение
Этом всё. Есть ещё много задач с параллелограммами, их тоже рассмотрим, не пропустите. Успеха вам!
С уважением, Александр Крутицких.
Материалы принесли вам пользу? Расскажите о сайте в социальных сетях!
matematikalegko.ru
свойство углов параллелограмма | математика-повторение

Записи с меткой «свойство углов параллелограмма»

Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.

Решение.
∠C =∠A = 65° как противоположные углы параллелограмма.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.
∠В = 180° — ∠А = 180° — 65° = 115°.
∠D =∠B = 115° как противолежащие углы параллелограмма.
Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.
Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.
Решение.
Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°
: 2 = 110°.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.
Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.
Решение.
Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.
х + 3х = 180;
4х = 180;
х = 180 : 4;
х = 45.
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.

Доказательство.
Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.
AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.
Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.
Решение.
Периметр параллелограмма P_ABCD
= 2 ∙ (AB + AD).
Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
14x = 3,5;
x = 3,5 : 14;
x = 0,25.
Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Проверка.
Периметр параллелограмма P_ABCD= 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).
Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.
Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.

www.mathematics-repetition.com
Биссектрисы углов параллелограмма | Треугольники
Какими свойствами обладают биссектрисы углов параллелограмма? Для биссектрис углов, прилежащих к одной стороне параллелограмма, и для биссектрис противолежащих углов эти свойства разные.

Свойство биссектрис углов параллелограмма, прилежащих к одной стороне.
Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны.

Дано: ABCD — параллелограмм,
AF биссектриса ∠BAD,
DK- биссектриса ∠ADC,
AF ∩ DK= M.
Доказать: ∠AMD=90º.
Доказательство:
1) ∠BAD+∠ADC=180º (как внутренние односторонние углы при AB ∥ CD и секущей AD).
2) Так как биссектриса угла делит его пополам, то

4) Рассмотрим треугольник ADM. Так как сумма углов треугольника равна 180º, то
∠DAM+∠ADM+∠AMD=180º,
90º+∠AMD=180º, откуда ∠AMD=180º- 90º=90º,

то есть биссектрисы углов параллелограмма, прилежащие к стороне AD, перпендикулярны.

Что и требовалось доказать.
В следующий раз рассмотрим свойство биссектрис противолежащих углов параллелограмма.
www.treugolniki.ru
Как найти острый угол параллелограмма?
Параллелограммом называется такой четырехугольник, в котором противоположные стороны попарно параллельны.
Параллелограмм обладает всеми свойствами четырехугольников, но кроме этого имеет и свои отличительные особенности. Зная их, мы можем с легкостью находить как стороны, так и углы параллелограмма.
Свойства параллелограмма
Сумма углов в любом параллелограмме, как и в любом четырехугольнике, равна 360°.
Средние линии параллелограмма и его диагонали пересекаются в одной точке и делятся ею пополам. Эту точку принято называть центром симметрии параллелограмма.
Противоположные стороны у параллелограмма всегда равны.
Также у этой фигуры всегда равны противоположные углы.

Сумма углов, которые прилегают к любой из сторон параллелограмма, всегда составляет 180°.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон. Это выражается формулой:
d₁² + d₂²= 2 (a²+b²), где d₁ и d₂ — диагонали, a и b — смежные стороны.
Косинус тупого угла всегда меньше нуля.
Как найти углы заданного параллелограмма, применяя эти свойства на практике? И какие еще формулы могут нам в этом помочь? Рассмотрим конкретные задания, в которых требуют: найдите величины углов параллелограмма.
Нахождение углов параллелограмма
Случай 1. Известна мера тупого угла, требуется найти острый угол.
Пример: В параллелограмме ABCD угол A равен 120°. Найдите меру остальных углов.
Решение: Пользуясь свойством № 5, мы можем найти меру угла B, смежного с тем углом, который дан в задании. Он будет равен:
А теперь, пользуясь свойством №4, мы определяем, что два оставшихся угла C и D противоположны тем углам, ко
elhow.ru
No related posts.