15. Несобственные интегралы. Несобственные интегралы первого рода
Выше был определён интеграл для ограниченных и заданных на ограниченном отрезке функций. Распространим понятие интеграла на случаи, когда одно или оба этих условия нарушаются.
Определение. Пусть задана на бесконечном промежутке и для всякого существует интеграл Предел называется несобственным интегралом первого рода (интегралом по неограниченному промежутку) и обозначается Если существует и конечен, то несобственный интеграл первого рода называется сходящимся, если же он не существует или равен Бесконечности, то несобственный интеграл первого рода называется расходящимся.
Примеры.
1. Рассмотрим . Пусть Тогда Таким образом, рассмотренный интеграл при расходится. Пусть теперь Тогда
И мы окончательно получили, что рассматриваемый интеграл при расходится и при сходится. Этот интеграл часто используется в признаке сравнения в качестве эталонного.
2. Выясним сходимость интеграла .
Имеем
. Следовательно, интеграл сходится и его значение равно .
3. Выяснить сходимость интеграла . По определению получаем
.
Следовательно, интеграл сходится и его значение равно .
4. Для интеграла имеем
.
Следовательно, интеграл расходится.
5. Для интеграла по определению имеем
.
Следовательно, интеграл сходится и его значение равно 1.
6. Выяснить сходимость интеграла , .
По определению
Следовательно, интеграл сходится и его значение равно .
Задание 2.4
Вычислить несобственные интегралы первого рода или доказать их расходимость.
1. ; 2.; 3. ; 4. ;
5. ; 6. .
Ответы: 1. ; 2. расходится; 3. ; 4. расходится; 5. расходится; 6. .
Нам в дальнейшем понадобится следующий важный результат.
Теорема 2.8. (Критерий Коши). Несобственный интеграл первого рода сходится тогда и только тогда, когда для всякого существует Такое, что для всех выполнено неравенство
Доказательство этого результата опустим.
Определение. Несобственный интеграл первого рода называется абсолютно сходящимся, если сходится интеграл
Отметим, что если несобственный интеграл первого рода сходится абсолютно, то он сходится. Действительно, тогда для интеграла выполнен критерий Коши, а в силу справедливости неравенства , критерий Коши выполнен и для интеграла
Обратное утверждение неверно.
Сходимость несобственного интеграла определяется аналогично. Предлагается проделать это самостоятельно.
Для несобственного интеграла можем записать и назвать этот интеграл сходящимся, если сходятся оба слагаемых. Если хотя бы один из этих интегралов расходится, то будем считать интеграл расходящимся. В качестве точки выбирают обычно 0.
Пример. Рассмотрим интеграл По определению сходимости этого интеграла получаем
Так как оба слагаемых расходятся, то исходный интеграл расходится. Получаемая при этом неопределённость при разных скоростях стремления к и к даёт разные результаты. В частности, если , , то
.
Если , , то абсолютно аналогично показывается, что этот предел равен . Подобрав скорости стремления к и к можно получить в пределе любое заранее заданное число от до .
С другой стороны, при согласованном стремлении верхнего и нижнего пределов к можем записать
Это дает возможность ввести новое понятие.
Определение. Говорят, что несобственный интеграл первого рода сходится в смысле главного значения Коши, если существует и конечен предел .
Рассмотренный выше пример показывает, что несобственный интеграл первого рода может сходиться в смысле главного значения Коши и расходиться в обычном смысле.
Отметим несколько свойств несобственных интегралов первого рода
1. Если интеграл сходится, то для всякого интеграл сходится и
2. Если интеграл сходится, то сходится интеграл и имеет место равенство
3. Если интегралы и сходятся, то сходятся интегралы и имеет место равенство
Обратное утверждение неверно, то есть, если интеграл от алгебраической суммы функций сходится, то интегралы от слагаемых сходиться не обязаны. Например, интегралы и расходятся, а интеграл , как будет показано позднее, сходится.
Для других типов несобственных интегралов первого рода свойства аналогичны.
Сходимость не всех несобственных интегралов первого рода просто выяснить по определению. Поэтому часто используют так называемые признаки сравнения в непредельной и предельной формах.
Теорема 2.9. Пусть для всякого Выполнено неравенство . Тогда, если интеграл абсолютно сходится, то интеграл абсолютно сходится, а если интеграл абсолютно расходится, то интеграл абсолютно расходится.
Доказательство. Действительно, в условиях теоремы для всех имеем . Тогда, если интеграл сходится, то есть монотонно возрастающая ограниченная сверху функция от и поэтому имеет предел при . Если интеграл расходится, то и поэтому .
Теорема 2.10. Если и — бесконечно малые в одного порядка малости, то есть , то интегралы И либо оба абсолютно сходятся, либо оба абсолютно расходятся.
Доказательство. Так как , то . Возьмем . По определению предела существует такое, что для всех выполнено неравенство а, следовательно, и неравенство Из последнего неравенства и теоремы 2.9 получаем утверждение теоремы.
Замечание. После изучения теоремы 2.10 может сложиться впечатление, что для сходимости несобственного интеграла первого рода, в том числе и абсолютной, необходимо, чтобы подынтегральная функция была бесконечно малой при . То, что это не так, показывает следующий пример [15].
Возьмем функцию, график которой состоит из отрезков прямых, соединяющих точки , , , . Ее аналитическое выражение имеет вид
Площадь, заключенная между графиком этой функции и осью , равна сумме площадей треугольников с вершинами в точках , , , . Так как площадь каждого такого треугольника равна , , то . Заметим, что условие ограниченности функции несущественно, так как вершины треугольников можно взять, например, в точках , , , ..
Примеры
1. Выяснить сходимость интеграла
Так как для всех а интеграл сходится, то и исходный интеграл тоже сходится.
2. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 2 и так как сходится, то исходный интеграл сходится.
3. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 1,5 и так как сходится, то исходный интеграл сходится.
4. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен И, следовательно, интеграл сходится.
5. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 1,5 и, следовательно, интеграл сходится.
6. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 0,5 и, следовательно, интеграл расходится.
7. Интеграл сходится, так как имеет место оценка для всех , а интеграл , как было показано ранее, сходящийся.
8. Интеграл расходится, так как имеет место оценка для всех , а интеграл, как было показано ранее, расходится.
Задание 2.5
Используя признак сравнения выяснить сходимость несобственных интегралов. В ответе указана сходимость и порядок малости подынтегральной функции относительно .
1. ; 2. ; 3. ; 4. ; 5. ; 6. .
Ответы: 1. сходится, ; 2. сходится, ;
3. расходится, ; 4. сходится, ; 5. сходится, ;
6. сходится, ;
| < Предыдущая | Следующая > |
|---|
matica.org.ua
§1. Несобственные интегралы 1-го рода
Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
В
теме «Определенный интеграл» было
рассмотрено понятие определенного
интеграла  для случая конечного промежутка
для случая конечного промежутка и ограниченной функции
и ограниченной функции (см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
(см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
1. Если, используя формулу для длины дуги, попытаться вычислить длину четверти окружности ,, то придем к интегралу от неограниченной функции:

 .
. 2.
Пусть тело массой  движется
по инерции в среде с силой сопротивления
,
где
движется
по инерции в среде с силой сопротивления
,
где — скорость тела. Используя второй закон
Ньютона (
— скорость тела. Используя второй закон
Ньютона ( ,
где
,
где ускорение),
получим уравнение:,
где
ускорение),
получим уравнение:,
где .
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функцияЕсли
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда
.
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функцияЕсли
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда  ,
то придем к интегралу по бесконечному
промежутку:
,
то придем к интегралу по бесконечному
промежутку:
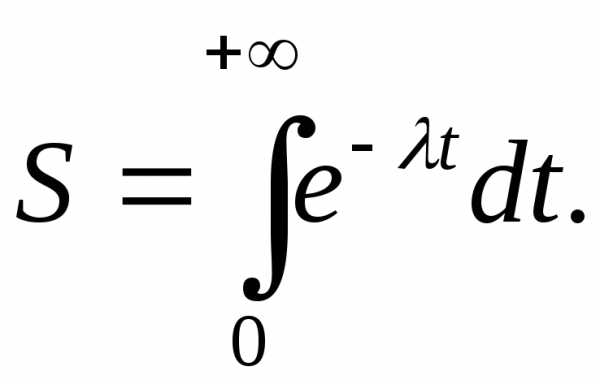
I Определение
Пусть
функция  определена и непрерывна на промежутке
определена и непрерывна на промежутке .
Тогда для любого
.
Тогда для любого она интегрируема на промежутке
она интегрируема на промежутке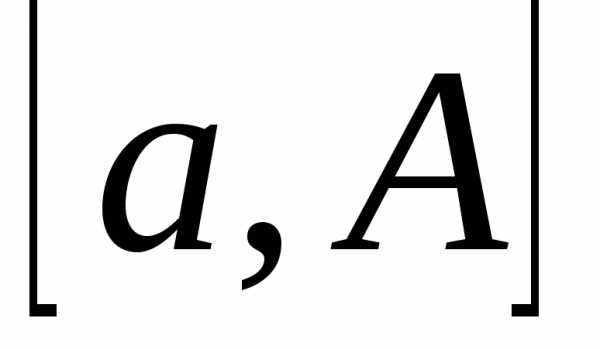 ,
то есть существует интеграл
,
то есть существует интеграл .
.
Определение
1.
Конечный или бесконечный предел этого
интеграла при
называют несобственным интегралом 1-го
рода от функции по промежутку
по промежутку и обозначают символом
и обозначают символом .
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (или не существует ) – расходящимся.
.
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (или не существует ) – расходящимся.
Итак, по определению
(1) |
Примеры
1..
2..
3.– не существует.
Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть 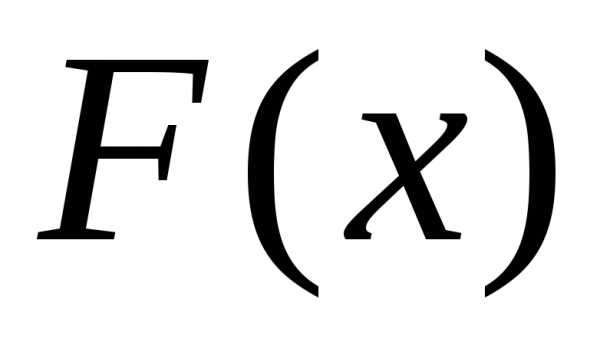 — некоторая первообразная для функции
— некоторая первообразная для функции (сущест-вует на
(сущест-вует на ,
т.к.
,
т.к. — непрерывна). Тогда
— непрерывна). Тогда
Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела .
Если этот предел обозначить
.
Если этот предел обозначить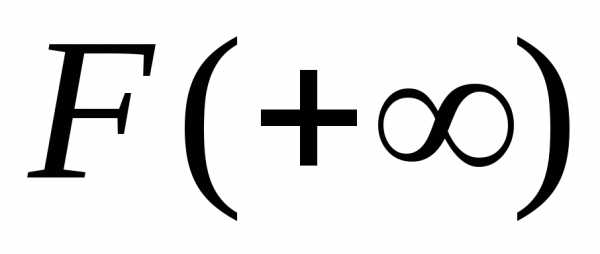 ,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
, где .
Примеры.
4. .
5. .
6.
Более сложный пример:  .
Сначала найдем первообразную:
.
Сначала найдем первообразную:
Теперь
можем найти интеграл  , учитывая,
что
, учитывая,
что
 :
:
.
III Свойства
Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:
интегралы
 и
и
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;если
 ,
то интегралы
,
то интегралы и
и сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно;если интеграл
 сходится, то
сходится, то .
.
IV Другие определения
Определение
2.
Если  непрерывна
на
непрерывна
на  ,
то
,
то
.
Определение
3.
Если  непрерывна
на
непрерывна
на ,
то принимают по определению
,
то принимают по определению
( –
произвольное),
–
произвольное),
причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.
Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.
Пример 7.
§2. Признаки сходимости несобственного интеграла 1-го рода
Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство
 (для
больших
(для
больших  ).
).
Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.
I Интегралы от положительных функций
Пусть  на
на  . Тогда определенный интеграл
. Тогда определенный интеграл 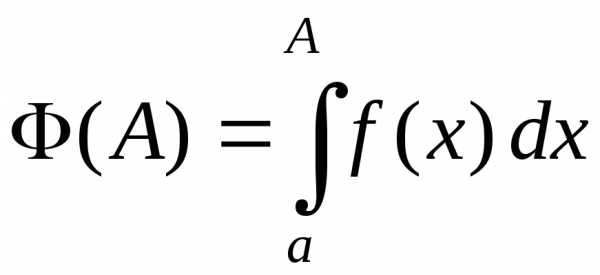 как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1.
Несобственный интеграл 1го рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция  остается
ограниченной при увеличении
остается
ограниченной при увеличении .
.
Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.
Теорема
2 (1-й признак сравнения). Пусть функции  и
и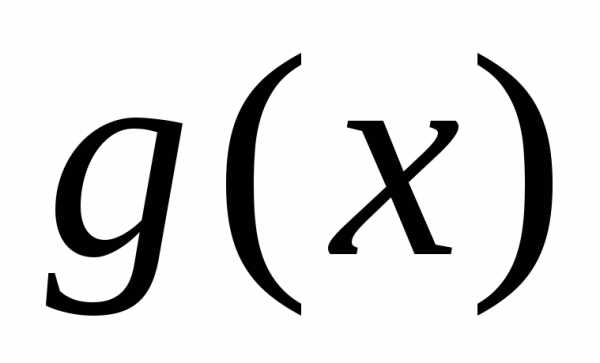 непре-рывны на
непре-рывны на и удовлетворяют неравенству.
Тогда:
и удовлетворяют неравенству.
Тогда:
1)
если интеграл  сходится, то и
сходится, то и сходится;
сходится;
2)
если интеграл  расходится, то и
расходится, то и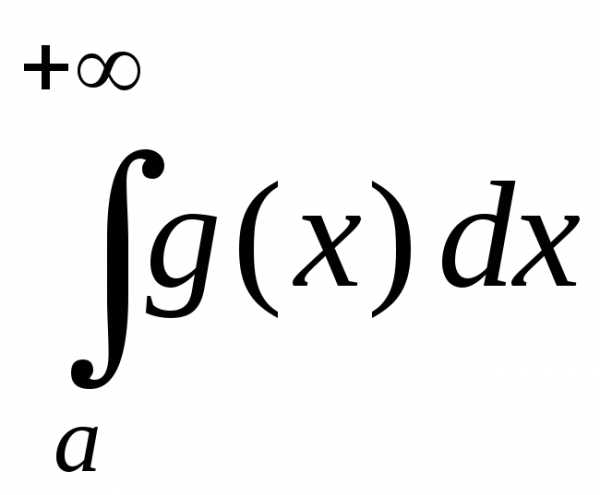 расходится.
расходится.
Доказательство.
Обозначим:  и
и .
Так как,
то.
Пусть интеграл
.
Так как,
то.
Пусть интеграл сходится, тогда (в силу теоремы 1) функция
сходится, тогда (в силу теоремы 1) функция ‒ ограничена. Но тогда и
‒ ограничена. Но тогда и ограничена,
а значит, интеграл
ограничена,
а значит, интеграл тоже сходится. Аналогично доказывается
и вторая часть теоремы.
тоже сходится. Аналогично доказывается
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от  или сходимости интеграла от
или сходимости интеграла от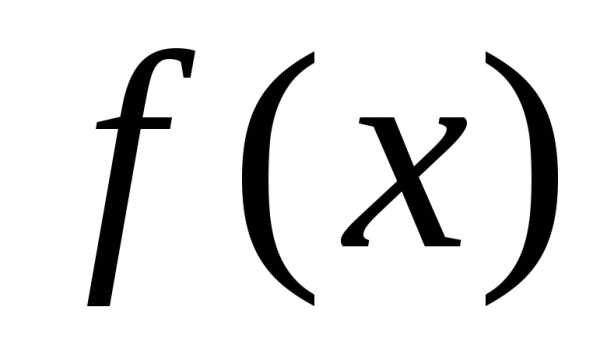 .
Этот недостаток отсутствует у 2-го
признака сравнения.
.
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3 (2-й признак сравнения). Пусть функции 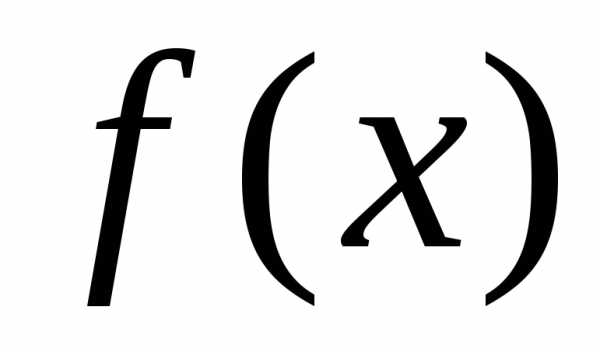 и
и непрерывны и неотрицательны на
непрерывны и неотрицательны на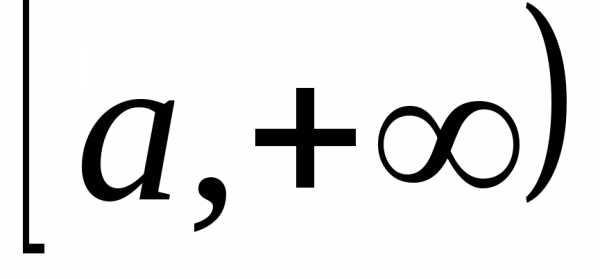 .
Тогда, еслипри,
то несобственные интегралы
.
Тогда, еслипри,
то несобственные интегралы и
и сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Из условия теоремы получим такую цепочку равно-сильных утверждений:
, ,
.
Пусть,
например,  .
Тогда:
.
Тогда:
.
Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция  ,.
Предлагаем студентам самим доказать,
что интеграл
,.
Предлагаем студентам самим доказать,
что интеграл

сходится
при  и расходится при
и расходится при .
.
Примеры.
1.  .
.
Рассмотрим
подынтегральную функцию на промежутке 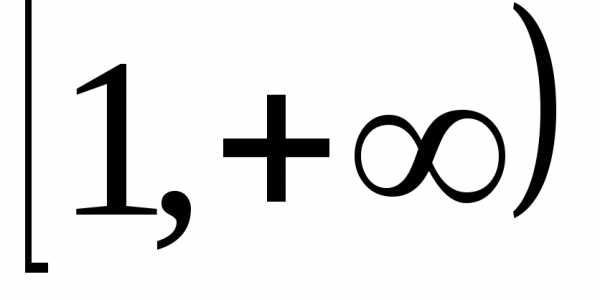 :
:
, .
Интеграл  сходится, ибо.
По 2-му признаку сравнения сходится и
интеграл
сходится, ибо.
По 2-му признаку сравнения сходится и
интеграл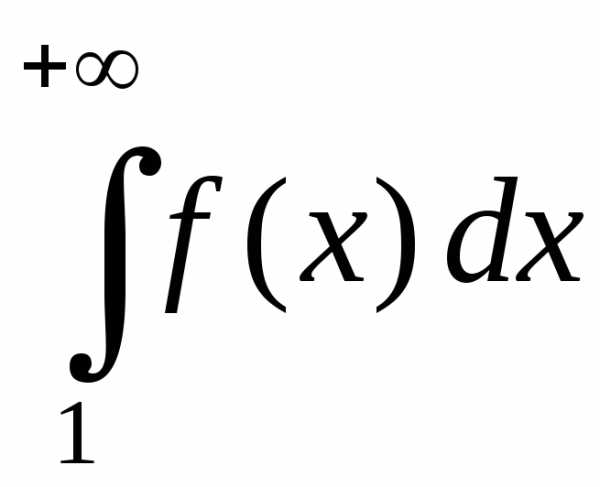 ,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2. .
.
Так
как
,
тоcуществует  такое, что при
такое, что при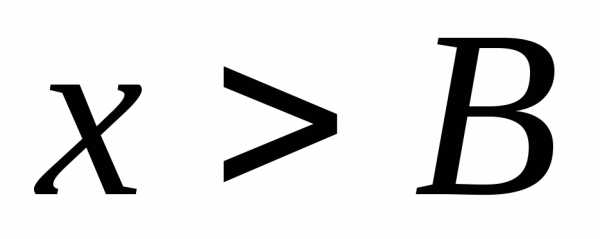
 .
Для таких значений переменной:
.
Для таких значений переменной:
.
Известно, что логарифмическая функция растет медленнее степенной, т.е.
 ,
,
а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому
 .
.
Интеграл 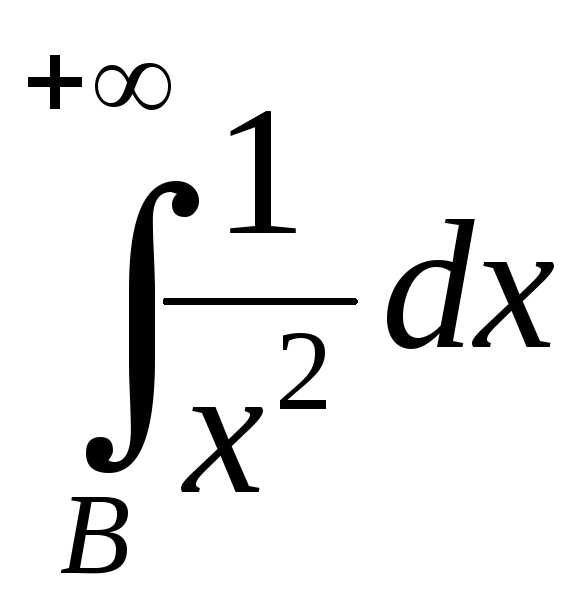 сходится как эталонный. В силу 1-го
признака сравнения сходится и
сходится как эталонный. В силу 1-го
признака сравнения сходится и .
Применяя 2-й признак, получим, что и
интеграл
.
Применяя 2-й признак, получим, что и
интеграл сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
studfiles.net
14. Несобственные интегралы первого рода
Пусть f(x) определена и непрерывна на . Тогда она непрерывна на любом отрезке [a; b].
Если существует конечный предел , то это предел –несобственный интеграл от f(x) на
[a; ].
Обозначается: =
Если этот предел существует и конечен, то несобственный интеграл сходится.
Если этот предел не существует или бесконечен, то несобственный интеграл расходится.
Это справедливо, если интегралы существуют.
Геометрический смысл: Если f(x) ≥0, то несобственный интеграл выражает площадь неограниченной области, заключенной между линиями y=f(x), x=a и осью абсцисс.
15. Несобственные интегралы второго рода
Если в точке х=С f(x) либо не определена, либо разрывна, то:
=
Если интеграл существует, то сходится.
Если интеграл не существует, то расходится
Если в точке a=x функция терпит разрыв, то:
=
Если f(x) терпит разрыв в точке b, то на [a; c]:
= +
Точек в отрезке может быть несколько.
Если сходятся все интегралы, входящие в сумму, о сходится суммарный интеграл.
16. Дифференциальные уравнения. Основные понятия.
Дифференциальное уравнение (ДУ) – уравнение, связывающее независимую переменную х, функцию у = у(х) и ее производные и дифференциалы.
F(x,y,y’,y’’…) = 0
ДУ содержи только производные и дифференциалы, а функцию у и переменную х – не обязательно.
Если ДУ имеет одну независимую переменную, то оно обыкновенное ДУ
Если ДУ имеет больше двух независимых переменных, то это ДУ частных производных
Порядок ДУ – наивысший порядок производных, входящих в него.
Общее решение – такая дифференцируемая функция у = у(х, С), которая при подстановке в уравнение обращает его в тождество.
y’=y, y = cex
Иногда Ф(х,у,С)=0, которое не разрешается относительно У. Тогда это общий интеграл, а не решение.
Решение у=у(х, СО) получается из общего решения при определенном значении С – частное решение.
Задача Коши – нахождение частного решения ДУ вида у = у(х,Со), удовлетворяющего начальным условиям у(хо) = уо.
Интегральная кривая – график у = у(х) решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.
17. Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
Дифференциальным уравнением первого порядка называется соотношение, связывающее независимую переменную, функцию и ее первую производную. Общий вид: F(x, y, y`) = 0
Уравнение разрешимое относительно y`, называется дифференциальным уравнением первого порядка, разрешенное относительно производной. y` = f(x, y).
Дифференциальное уравнение первого порядка с разделяющимися переменными.
Диф. уравн. 1-го порядка — уравнением с разделяющимися переменными, если оно пожжет быть представлено в виде, где
Для решения дифференциального уравнения искомую функцию y представим в виде произведения двух множителей y = uv, где u – некоторое ненулевое решение соответствующего однородного уравнения. u` + p(x) = 0, а v-новая неизвестная функция. Так как y` = vu` + uv`, то подставляя … получим v[u`+p(x)u] + uv` = q(x) →uv`=q(x)
18. Однородные функции и однородное дифференциальное уравнение 1-го порядка.
Опр. Многочлен P(x,y) = ∑aijxiyj называется однородным степени n, если все его члены имеют один и тот же порядок n, т.е. для каждого члена имеем I + j = n
Если аргументы x,y однородного многочлена степени n заменить на пропорциональные величины λx и λy, то в результате этот многочлен увеличится на n-степень коэффициента пропорциональности λ.
Опр. Функция P(x,y) называется однородной степени n относительно своих аргументов х и у, если для любого числа λ (кроме 0) имеет место: Р(λх, λу) = λ”P(x,y)
Р. Однородным дифф. уравнением называется уравнение вида М(х,у)dx + N(x,y)dy = 0, где M(x,y) и N(x,у) – однородные функции одной и той же степени.
Опр. Дифф. уравнение, которое можно преобразовать к виду y’ = ϕ() называется однородным.
С помощью подстановки u = илиu=yx, где u(x) – новая неизвестная функция, данное уравнение приводится к уравнению с разделяющимися переменными.
Действительно, y = ux, тогда y’ = u’x ≠ ux’
Подставим в y’ = ϕ(), получим:u’x + ux’ = ϕu, u’x + u = ϕ(x), и таким образом получим уравнение с разд.переменными относительно u:
= ;=+C
Или: =ln |x| + C = ln |x| + ln |C| = ln |xC|
После этого осуществляется подстановка u = и в результате получаем общее решение однородного дифф.уравнения.
studfiles.net
Электронный учебник по математическому анализу
был построен в предположении, что числа $a,\,b$ конечны и $f(x)$ — непрерывная функция. Если одно из этих предположений нарушается, говорят о несобственных интегралах.
Несобственный интеграл 1 рода возникает, когда по крайней мере одно из чисел $a,\,b$ бесконечно.
10.1.1 Определение и основные свойства
Рассмотрим сначала ситуацию, когда нижний предел интегрирования конечен, а верхний равен $+\infty$, другие варианты обсудим несколько позднее. Для $f(x)$, непрерывной при всех интересующих нас $x$, рассмотрим интеграл
\begin{equation} I=\int _a^{+\infty}f(x)dx. \quad(19) \label{inf1} \end{equation}Прежде всего надо установить смысл этого выражения. Для этого введем функцию
\[ I(N)=\int _a^{N}f(x)dx \]и рассмотрим ее поведение при $N\rightarrow +\infty$.
Определение. Пусть существует конечный предел
\[ A=\lim_{N \rightarrow +\infty}I(N)=\lim_{N \rightarrow +\infty}\int _a^{N}f(x)dx. \]Тогда говорят, что несобственный интеграл 1 рода (19) является сходящимся и ему приписывают значение $A$, саму функцию называют интегрируемой на интервале $\left[ a, \, +\infty \right )$. Если же указанного предела не существует или он равен $\pm \infty$, то говорят, что интеграл (19) расходится.
Пример.
Рассмотрим интеграл
\[ I=\int _0^{+\infty} \frac{dx}{1+x^2}. \]Положим
\[ I(N)=\int _0^{N} \frac{dx}{1+x^2}. \]В данном случае известна первообразная подинтегральной функции, так что
\[ I(N)=\int _0^{N} \frac{dx}{1+x^2}=arctgx|_0^{N}=arctgN. \]Известно, что $arctg N \rightarrow \pi /2 $ при $N \rightarrow +\infty$. Таким образом, $I(N)$ имеет конечный предел, наш несобственный интеграл сходится и равен $\pi /2$.
Сходящиеся несобственные интегралы 1 рода обладают всеми стандартными свойствами обычных определенных интегралов.
1. Если $f(x)$, $g(x)$ интегрируемы на интервале $\left[ a, \, +\infty \right )$, то их сумма $f(x)+g(x)$ также интегрируема на этом интервале, причем \[ \int _a^{+\infty}\left(f(x)+g(x)\right )dx=\int _a^{+\infty}f(x)dx+\int _a^{+\infty}g(x)dx. \] 2. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right )$, то для любой константы $C$ функция $C\cdot f(x)$ также интегрируема на этом интервале, причем \[ \int _a^{+\infty}C\cdot f(x)dx=C \cdot \int _a^{+\infty}f(x)dx. \] 3. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right )$, причем на этом интервале $f(x)>0$, то \[ \int _a^{+\infty} f(x)dx\,>\,0. \] 4. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right )$, то для любого $b>a$ интеграл \[ \int _b^{+\infty} f(x)dx \] сходится, причем \[ \int _a^{+\infty}f(x)dx=\int _a^{b} f(x)dx+\int _b^{+\infty} f(x)dx \] (аддитивность интеграла по интервалу).Справедливы также формулы замены переменной, интегрирования по частям и т.д. (с естественными оговорками).
Пример.
Рассмотрим интеграл
\begin{equation} I=\int _1^{+\infty}\frac{1}{x^k}\,dx. \quad (20) \label{mod} \end{equation}Введем функцию
\[ I(N)=\int _1^{N}\frac{1}{x^k}\,dx. \]В данном случае первообразная известна, так что
\[ I(N)=\int _1^{N}\frac{1}{x^k}\,dx\,=\frac{x^{1-k}}{1-k}|_1^N= \frac{N^{1-k}}{1-k}-\frac{1}{1-k} \]при $k \neq 1$,
\[ I(N)=\int _1^{N}\frac{1}{x}\,dx\,=lnx|_1^N= lnN \]при $k = 1$. Рассматривая поведение при $N \rightarrow +\infty$, приходим к выводу, что интеграл (20) сходится при $k>1$, а при $k \leq 1$ — расходится.
Рассмотрим теперь вариант, когда нижний предел интегрирования равен $-\infty$, а верхний конечен, т.е. рассмотрим интегралы
\[ I=\int _{-\infty}^af(x)dx. \]Однако этот вариант можно свести к предыдущему, если сделать замену переменных $x=-s$ и поменять затем пределы интегрирования местами, так что
\[ I=\int _{-a}^{+\infty}g(s)ds, \]$g(s)=f(-s)$. Рассмотрим теперь случай, когда имеется два бесконечных предела, т.е. интеграл
\begin{equation} I=\int _{-\infty}^{+\infty}f(x)dx, \quad (21) \label{intr} \end{equation}причем $f(x)$ непрерывна при всех $x \in \mathbb{R}$. Разобъем интервал на две части: возьмем $c \in \mathbb{R}$, и рассмотрим два интеграла,
\[ I_1=\int _{-\infty}^{c}f(x)dx, \quad I_2=\int _{c}^{+\infty}f(x)dx. \]Определение. Если оба интеграла $I_1$, $I_2$ сходятся, то интеграл (21) называется сходящимся, ему приписывают значение $I=I_1+I_2$ ( в соответствии с аддитивностью по интервалу). Если хотя бы один из интегралов $I_1$, $I_2$ расходится, интеграл (21) называется расходящимся.
Можно доказать, что сходимость интеграла (21) не зависит от выбора точки $c$.
Несобственные интегралы 1 рода с интервалами интегирования $\left(-\infty, \, c \right]$ или $(-\infty, \, +\infty )$ также обладают всеми стандартными свойствами определенных интегралов (с соответствующей переформулировкой, учитывающей выбор интервал интегрирования).
10.1.2 Признаки сходимости несобственных интегралов 1 рода
Теорема(первый признак сравнения). Пусть $f(x)$, $g(x)$ — непрерывны при $x>a$, причем $0a$. Тогда
1. Если интеграл \[ \int _a^{+\infty}g(x)dx \] сходится, то сходится и интеграл \[ \int _a^{+\infty}f(x)dx. \] 2. Если интеграл \[ \int _a^{+\infty}f(x)dx \] расходится, то расходится и интеграл \[ \int _a^{+\infty}g(x)dx. \]Теорема(второй признак сравнения). Пусть $f(x)$, $g(x)$ — непрерывны и положительны при $x>a$, причем существует конечный предел
\[ \theta = \lim_{x \rightarrow +\infty} \frac{f(x)}{g(x)}, \quad \theta \neq 0, \, +\infty. \]Тогда интегралы
\[ \int _a^{+\infty}f(x)dx, \quad \int _a^{+\infty}g(x)dx \]сходятся или расходятся одновременно.
Пример.
Рассмотрим интеграл
\[ I=\int _1^{+\infty}\frac{1}{x+\sin x}\,dx. \]Подинтегральное выражение — положительная функция на интервале интегрирования. Далее, при $x \rightarrow +\infty$ имеем:
$\sin x$ является «малой» поправкой в знаменателе. Точнее, если взять $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$, то
\[ \lim _{x \rightarrow +\infty}\frac{f(x)}{g(x)}=\lim _{x \rightarrow +\infty}\frac{x}{x+\sin x}=1. \]Применяя второй признак сравнения, приходим к выводу, что наш интеграл сходится или расходится одновременно с интегралом
\[ \int _1^{+\infty}\frac{1}{x}\,dx . \]Как было показано в предыдущем примере, этот интеграл расходится ($k=1$). Следовательно, исходный интеграл расходится.
Задачи.
Вычислить несобственный интеграл или установить его сходимость (расходимость).
1. \[ \int _{0}^{+\infty}e^{-ax}\,dx. \] 2. \[ \int _{0}^{+\infty}xe^{-x^2}\,dx. \] 3. \[ \int _{-\infty}^{+\infty}\frac{2xdx}{x^2+1}. \] 4. \[ \int _{0}^{+\infty}\frac{xdx}{(x+2)^3}. \] 5. \[ \int _{-\infty}^{+\infty}\frac{dx}{x^2+2x+2}. \] 6. \[ \int _{1}^{+\infty}\frac{lnx}{x^2}\,dx. \] 7. \[ \int _{1}^{+\infty}\frac{dx}{(1+x)\sqrt{x}}. \] 8. \[ \int _{0}^{+\infty}e^{-\sqrt{x}}\,dx. \] 9. \[ \int _{0}^{+\infty}e^{-ax}\cos x\,dx. \] 10. \[ \int _{0}^{+\infty}\frac{xdx}{x^3+1}. \]publish.sutd.ru
Свойства несобственных интегралов 1го рода.
Если для любого , а
 сходится, то сходится и несобственный
интеграл
сходится, то сходится и несобственный
интеграл и при этом справедливо неравенствот. е. неравенство для функции можно
интегрировать в смысле несобственного
интеграла первого рода.
и при этом справедливо неравенствот. е. неравенство для функции можно
интегрировать в смысле несобственного
интеграла первого рода.Если для любого а интеграл
 расходится, то расходится и интеграл
от
расходится, то расходится и интеграл
от .Замечание: Свойства (1) и (2) позволяют
делать оценки на несобственные интегралы
первого рода, либо сверху либо снизу
(первое свойство – сверху, второе
свойство – снизу).
.Замечание: Свойства (1) и (2) позволяют
делать оценки на несобственные интегралы
первого рода, либо сверху либо снизу
(первое свойство – сверху, второе
свойство – снизу).Если
 сходится то сходится и интеграл
сходится то сходится и интеграл и при этом называется абсолютно
сходящимся.Замечание: ,
Если же интеграл
и при этом называется абсолютно
сходящимся.Замечание: ,
Если же интеграл расходится, а интеграл
расходится, а интеграл сходится то он называется условно
сходящимся.Замечание: Из выше приведенных утверждений следует
что из расходимости
сходится то он называется условно
сходящимся.Замечание: Из выше приведенных утверждений следует
что из расходимости  не следует расходимость
не следует расходимость :
он может быть как сходящимся, так и
расходящимся. Свойства(1), (2) и (3) формулируются аналогично и для других
несобственных интегралов первого рода
с другими приделами.
:
он может быть как сходящимся, так и
расходящимся. Свойства(1), (2) и (3) формулируются аналогично и для других
несобственных интегралов первого рода
с другими приделами.
Комплексные числа (26).
Натуральные
числа N:
0,1,2,3,… Целые числа: 0,
Рациональные
числа: 1/2,1/3, 3/5 Иррациональные числа:  и т. д.
и т. д.
Все это действительные числа. Обобщением действительных чисел являются комплексные числа z=x+iy где x-действительная часть комплексного числа ReZ,
y— мнимая часть комплексного числа ImZ, i— мнимая единица i2=-1
Z=x+iy=ReZ+iImZ ( ), Z=x+iy называется
алгебраической формой записи числа.
Если ImZ=0,
то Z=x – действительное
число. Если ReZ=0,
то Z=iy – число
мнимое комплексные
число. Если ReZ= ImZ=0,
то Z=0
), Z=x+iy называется
алгебраической формой записи числа.
Если ImZ=0,
то Z=x – действительное
число. Если ReZ=0,
то Z=iy – число
мнимое комплексные
число. Если ReZ= ImZ=0,
то Z=0
Два
комплексных числа Z1=x1+iy1, и Z2=x2+iy2 называются
равными если ReZ1=ReZ2 (x1=x2) и ImZ1= ImZ2 (y1=y2).
Комплексное число Z=x+iy и  называются комплексно сопряженными.
называются комплексно сопряженными.
Геометрический смысл комплексных чисел:
Р ассмотримZ=x+iy. Каждому Z ставится в соответствии точка M(x,y) на комплексной
плоскости
ассмотримZ=x+iy. Каждому Z ставится в соответствии точка M(x,y) на комплексной
плоскости  Z и наоборот.
Z и наоборот.
Ось OX (абсцисс) называется действительной осью, а ось OY (ординат) называется мнимой осью.
Рассмотрим
вектор: Любому векторуи преобразуем. Возьмем полярную систему
координат точкаM(x,y)
точкаM(x,y)

 , g – называется
модулем комплексного числа, а
, g – называется
модулем комплексного числа, а  — аргументом числаZ (). и определены неоднозначно а с точностью
до числа кратного
— аргументом числаZ (). и определены неоднозначно а с точностью
до числа кратного 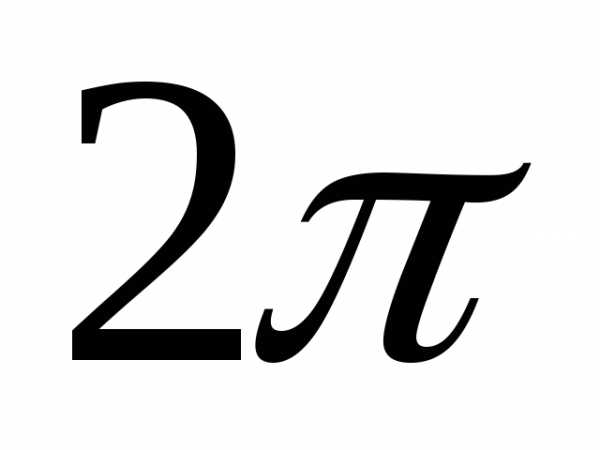 .
Используя формулу(1) получим тригонометрическую форму
записи комплексного числа
.
Используя формулу Эллера получим:,
.
Используя формулу(1) получим тригонометрическую форму
записи комплексного числа
.
Используя формулу Эллера получим:, —
действительные числа.Рассмотрим частные случаи:
—
действительные числа.Рассмотрим частные случаи:
Если
— действительные числа. Если, ,.
В общем случаи: Модуль комплексного
числа,argZ находится
из уравнения
,.
В общем случаи: Модуль комплексного
числа,argZ находится
из уравнения 
П ример:
ример:
ReZ=1
ImZ=-1 



 Замечание:
Комплексно сопряженные числа Z=x+iy и
Замечание:
Комплексно сопряженные числа Z=x+iy и  геометрически изображаются двумя
точками на комплексной плоскости
зеркально симметричны относительно
действительной оси(ReZ). В показательной форме
геометрически изображаются двумя
точками на комплексной плоскости
зеркально симметричны относительно
действительной оси(ReZ). В показательной форме  ,
то
,
то .
.
Действия над комплексными числами (27).
1. Сложение: Суммой двух комплексных чисел Z1=x1+iy1 и Z2=x2+iy2 называется Z=Z1+Z2=(x1+x2)+i(y1+y2). 2. Вычитание: Разностью двух комплексных чисел Z1=x1+iy1 и Z2=x2+iy2 называется Z которое будучи сложенным с Z2 дает Z1 Z=Z1+Z2=>Z1=Z2+Z=(x1—_x2)+i(y1-y2), при сложении и вычитании комплексных чисел они должны быть представлены в алгебраической форме.
studfiles.net
2. Несобственные интегралы
Несобственный интеграл
Определенный интеграл как предел интегральной суммы
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
отрезок интегрирования [a; b] конечный;
подынтегральная функция непрерывная (или хотя бы кусочно-непрерывная) и, следовательно, ограниченная на этом отрезке.
Если хотя бы одно из этих условий нарушено, то определение теряет смысл. Действительно, в случае бесконечного отрезка, например [a; ) его нельзя разбить на п частей конечной длины , которая к тому же с увеличением количества отрезков стремилась бы к нулю. В случае же неограниченной в некоторой точкес[a; b] нарушается требование произвольного выбора точки на частичных отрезках – нельзя выбрать=с, поскольку значение функции в этой точке не определено. Однако и для этих случаев можно обобщить понятие определенного интеграла, введя еще один предельный переход. Интегралы по бесконечным промежуткам и от разрывных (неограниченных) функций называют несобственными.
Определение.
Пусть функция определена на промежутке [a; ) и интегрируема на любом конечном отрезке [a; b], т.е. существует для любогоb > a. Предел вида называютнесобственным интегралом первого рода (или несобственным интегралом по бесконечному промежутку) и обозначают .
Таким образом, по определению, =.
Если предел справа существует и конечен, то несобственный интеграл называютсходящимся. Если этот предел бесконечен, или не существует вообще, то говорят, что несобственный интеграл расходится.
Аналогично можно ввести понятие несобственного интеграла от функции по промежутку (–; b]:
=.
А несобственный интеграл от функции по промежутку (–; +) определяется как сумма введенных выше интегралов:
=+,
где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.
С геометрической точки зрения, интеграл ,, определяет численное значение площади бесконечной криволинейной трапеции, ограниченной сверху графиком функции, слева – прямой, снизу – осью ОХ. Сходимость интеграла означает существование конечной площади такой трапеции и равенство ее пределу площади криволинейной трапеции с подвижной правой стенкой.
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница:
= =F(+) – F(a),
где F(+) = . Если этот предел существует, то интеграл сходится, в противном случае – расходится.
Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть функция определена на промежутке [a; b), неограниченна в некоторой окрестности точки b, и непрерывна на любом отрезке , где>0 (и, следовательно, интегрируема на этом отрезке, т.е. существует). Предел виданазываетсянесобственным интегралом второго рода (или несобственным интегралом от неограниченной функции) и обозначается .
Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению
=.
Если предел справа существует и конечен, то интеграл называется сходящимся. Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично можно определить несобственный интеграл от функции имеющей бесконечный разрыв в точкеа:
=.
Если функция имеет бесконечный разрыв во внутренней точкес, то несобственный интеграл определяется следующим образом
=+=+.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:
Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости. Признаки сходимости несобственных интегралов:
1) Признак сравнения.
Пусть для всех х. Тогда, еслисходится, то сходится и, причем. Если расходится, то расходится и.
2) Если сходится , то сходится и(последний интеграл в этом случае называетсяабсолютно сходящимся).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
Вычислить несобственный интеграл или установить его расходимость:
а) ; б); в)
г) ; д).
Решение.
а) По определению имеем:
,
Следовательно, данный интеграл сходится и равен .
б) Аналогично
.
Следовательно, данный интеграл сходится и равен .
в) По определению =+, причем,а – произвольное число. Положим в нашем случае , тогда получим:
.
Данный интеграл сходится.
г)
Значит, данный интеграл расходится.
д) Рассмотрим. Чтобы найти первообразную подынтегральной функции, необходимо применить метод интегрирования по частям. Тогда получим:
Поскольку ни , нине существуют, то не существует и
.
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать сходимость интегралав зависимости отп.
Решение.
При имеем:
.
Если , тои. Следовательно, интеграл расходится.
Если , то, а, тогда
,
= ,
Следовательно, интеграл сходится.
Если , то
,
следовательно, интеграл расходится.
Таким образом,
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а) ; б); в).
Решение.
а) Интегралявляется несобственным интегралом второго рода, поскольку подынтегральная функцияне ограничена в точке. Тогда, по определению,
.
Интеграл сходится и равен .
б) Рассмотрим. Здесь также подынтегральная функция не ограничена в точке. Поэтому, данный интеграл – несобственный второго рода и по определению,
.
Следовательно, интеграл расходится.
в) Рассмотрим. Подынтегральная функциятерпит бесконечный разрыв в двух точках:и, первая из которых принадлежит промежутку интегрирования. Следовательно, данный интеграл – несобственный второго рода. Тогда, по определению
==
.
Следовательно, интеграл сходится и равен .
studfiles.net
Несобственный интеграл, формулы и примеры
Несобственный интеграл первого рода
Таким образом, по определению
Если такой предел существует, то говорят, что несобственный интеграл сходится. В противном случае, если предел не существует или бесконечен, то несобственный интеграл является расходящимся.
Аналогичным образом задается несобственный интеграл на промежутке .
Несобственный интеграл первого рода с двумя бесконечными пределами определяется формулой:
Такой несобственный интеграл сходится только в том случае, когда оба несобственных интеграла в правой части являются сходящимися.
Примеры решения задач
Несобственный интеграл второго рода
Пусть некоторая функция непрерывна на промежутке , а в точке имеет разрыв второго рода. Если существует конечный предел , то он называется несобственным интегралом второго рода и обозначается , то есть
Если предел в правой части существует, то несобственный интеграл второго рода называется сходящимся. В случае, когда предел не существует или равен бесконечности, несобственный интеграл является расходящимся.
Аналогично, если в точке подынтегральная функция терпит бесконечный разрыв, то несобственный интеграл второго рода определяется равенством:
Если подынтегральная функция терпит разрыв в некоторой внутренней точке отрезка , то несобственный интеграл второго рода определяется формулой:
Интеграл, стоящий в левой части равенства, называется сходящимся, если сходятся оба несобственных интеграла в правой части приведенного равенства.
ru.solverbook.com

 и
и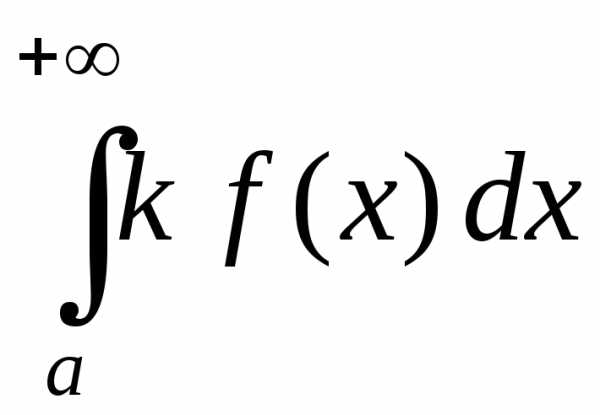
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно; ,
то интегралы
,
то интегралы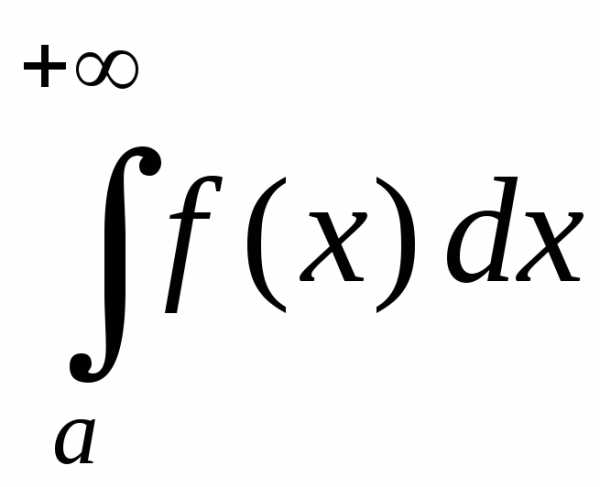 и
и сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно; сходится, то
сходится, то .
. сходится, то сходится и несобственный
интеграл
сходится, то сходится и несобственный
интеграл и при этом справедливо неравенствот. е. неравенство для функции можно
интегрировать в смысле несобственного
интеграла первого рода.
и при этом справедливо неравенствот. е. неравенство для функции можно
интегрировать в смысле несобственного
интеграла первого рода. расходится, то расходится и интеграл
от
расходится, то расходится и интеграл
от .Замечание: Свойства (1) и (2) позволяют
делать оценки на несобственные интегралы
первого рода, либо сверху либо снизу
(первое свойство – сверху, второе
свойство – снизу).
.Замечание: Свойства (1) и (2) позволяют
делать оценки на несобственные интегралы
первого рода, либо сверху либо снизу
(первое свойство – сверху, второе
свойство – снизу). сходится то сходится и интеграл
сходится то сходится и интеграл и при этом называется абсолютно
сходящимся.Замечание: ,
Если же интеграл
и при этом называется абсолютно
сходящимся.Замечание: ,
Если же интеграл расходится, а интеграл
расходится, а интеграл сходится то он называется условно
сходящимся.Замечание: Из выше приведенных утверждений следует
что из расходимости
сходится то он называется условно
сходящимся.Замечание: Из выше приведенных утверждений следует
что из расходимости  не следует расходимость
не следует расходимость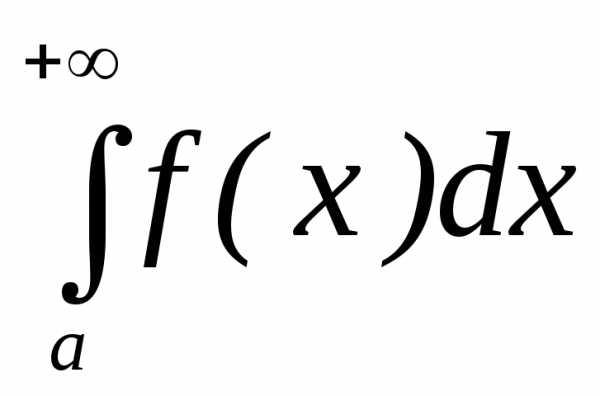 :
он может быть как сходящимся, так и
расходящимся. Свойства(1), (2) и (3) формулируются аналогично и для других
несобственных интегралов первого рода
с другими приделами.
:
он может быть как сходящимся, так и
расходящимся. Свойства(1), (2) и (3) формулируются аналогично и для других
несобственных интегралов первого рода
с другими приделами.