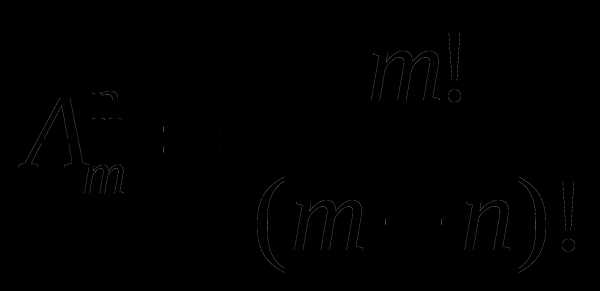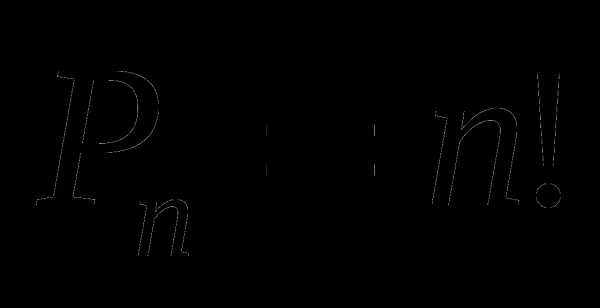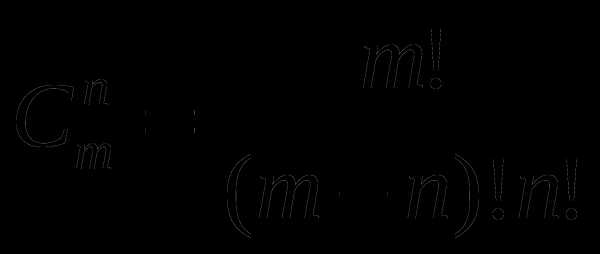Элементы комбинаторики. Перестановки, размещения и сочетания с повторениями и без повторений.
В практической деятельности каждому специалисту приходится иметь дело с разнообразными ситуациями, в которых нужно варьировать событиями. Во многих случаях эти ситуации связаны с решением комбинаторных задач.
Комбинаторика изучает комбинации, подчинённые определённым условиям, которые можно составить из элементов любой природы. Она основана на двух правилах: сложение и умножение.
Правило сложения: если некоторое событие А может произойти m раз, а событие В – n раз, то событие А или В может произойти m + n раз.
Правило умножения:если событие А произойдёт m раз, а событие В – n раз, то событие А и В произойдёт одновременно m nраз.
События совместные, если они могут в данном испытании произойти одновременно, и несовместные, если произойдёт только одно из этих событий.
Рассмотрим
1. Перестановки– такой тип комбинаций, который связан с нумерацией и перестановкой элементов.
Теорема 1. Число перестановок без повторений вычисляют по формуле: Рn = n (n = 1 2 … n).
Теорема 2.Число перестановок с повторениями вычисляют по формуле:
Рn= (К1, К2,…,Кn)=
2. Сочетание –такой тип комбинаций, который связан с выбором элементов.
Теорема 3. Число сочетаний без повторений вычисляют по формуле:Cnm=
Теорема 4.Число сочетаний с повторениями вычисляют по формуле: nm=
3. Размещение –
такой тип комбинаций, который связан с выбором элементов и с их перестановкой.Теорема 5. Число размещений без повторений вычисляют по формуле: Anm=
Теорема 6.Число размещений с повторениями вычисляют по формуле: nm=
5. Статистическое и геометрическое определения вероятности. Примеры.
Классическое определение вероятности применимо только для тех событий, которые могут появиться в результате испытания и обладают симметрией возможных исходов. Однако существует большой класс событий, вероятность которых нельзя вычислить с помощью классического определения. Эти события не являются равновозможными. В этом случае используют статистическое определение вероятности. Оно связано с понятием «относительная частота».
Относительная частота события А – это отношение числа опытов, в которых появилось событие А, к общему числу опытов:
Большое количество экспериментов показало, что если опыты проводятся в одинаковых условиях, то относительная частота будет колебаться около какого-то числа. Это число можно считать вероятностью события.
Пример: английский учёный Пирсон произвёл 23000 бросаний монеты. Герб появился 11512 раз.
ω(A) = = 0, 5005
Статистической вероятностью будем считать относительную частоту или число, близкое к ней: Р(А) = ω(A) =
В отличие от классической вероятности, статистическая вероятность является опытной величиной. Классическая вычисляется ДО опыта, а статистическая – ПОСЛЕ.
Статистическая вероятность обладает определёнными свойствами:
1.рассматриваемые события должны быть исходами только тех событий, которые могут быть проведены неограниченное число раз в одних и тех же условиях;
2.события должны обладать свойством статистической устойчивости;
3.число испытаний, в которых появилось событие А, должно быть достаточно велико.
Геометрическая вероятность.
Чтобы преодолеть недостаток классического определения, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрическую вероятность.
Пусть на отрезок L брошена точка, которая может попасть с равной возможностью в любую точку отрезка, тогда вероятность того, что брошенная точка попадёт в отрезок l, будет вычисляться по формуле: Р(А) = , где mes– мера (длина).
Если точка брошена в область G, то вероятность того, что она попадёт в область g, будет вычисляться по формуле: Р(А) = = , где mes– мера (площадь).
Если точку бросить в пространство, то: Р(А) = = , где mes– мера (объём).
Геометрическая вероятность события А – это отношение меры благоприятной области к общей области: Р(А) =
Пример: найти вероятность того, что точка, брошенная в круг, не попадёт в правильный шестиугольник, вписанный в круг.
Решение:
Р(А) = = = 0,33, 33%
Ответ: 33%.
cyberpedia.su
Конспект урока «Элементы комбинаторики»
Конспект урока по теме «Элементы комбинаторики»
Цели:
Обучающие:
— формирование основных понятий комбинаторики: размещения из mэлементов по n, сочетания из m элементов по n, перестановки из nэлементов;
— формирование умений и навыков вычисления значений комбинаторных выражений по формулам, решения простейших комбинаторных задач;
Развивающие:
-развитие умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности;
Воспитательные:
-воспитание интереса к дисциплине, честности, аккуратности, эстетического отношения к оформлению математических решений, воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, настойчивости в достижении цели и заинтересованности в конечном результате труда; прививать чувство патриотизма.
Обучающийся должен:
знать:
-определения трех важнейших понятий комбинаторики:
— размещения из n элементов по m;
— сочетания из n элементов по m;
— перестановки из n элементов, а также, формулы вычисления их количества.
уметь:
— отличать задачи на «перестановки», «сочетания», «размещения» друг от друга;
— применять основные комбинаторные формулы при решении простейших комбинаторных задач.
ХОД УРОКА
1. Организационный момент.
Ребята, каждая группа в течении года дежурит по техникуму.
Являются ли бригады дежурных в группах постоянными? Скажите, а сколько всего существует способов назначить из n студентов группы mдежурных. В математике есть раздел, который занимается решением подобных задач. Этот раздел называется комбинаторикой.
2. Сообщение темы, целей урока.
Тема сегодняшнего урока «Основные понятия комбинаторики». Давайте вместе попробуем сформулировать цели урока
— ознакомиться с основными понятиями комбинаторики (размещения, сочетания, перестановки)
— научиться решать простейшие комбинаторные задачи
3. Актуализация опорных знаний.
Прежде чем перейти к изучению нового материала, повторим то, что имеет к нему непосредственное отношение. Это уже известное вам понятие «факториал». Итак, кто помнит, что называют «n-факториалом»? Запишите формулу.
Чему, к примеру, равны 2!, 3!, 4!, 5!, 6! ? А кто сможет показать вычисления на доске? А чему равен 1! ? 0! ? Какие значения в данном случае может принимать n?
4. Изложение нового материала.
4.1. Введение общих понятий
Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.
Комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам.
Группы, составленные из каких-либо элементов, называются
Различают три вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными, а раздел математики, занимающийся их решением, — комбинаторикой. Рассмотрим три основных вида соединений и формулы вычисления их количества. Для этого сначала рассмотрим 2 задачи, которые помогут нам сосредоточиться на сути новых понятий.
4.2. Создание проблемной ситуации.
Тексты двух задач на слайде:
Задача 1. В некотором учреждении имеются две различные вакантные должности, на каждую из которых претендуют три сотрудника: A, B, C. Сколькими способами из этих трех кандидатов можно выбрать два лица на эти должности?
Задача 2. Для участия в соревнованиях требуется выбрать двоих спортсменов из трех кандидатов: A, B, C. Сколькими способами можно осуществить этот выбор?
Студентам предлагается два проблемных задания: 1) установить различие между этими двумя внешне схожими задачами и 2) предположить, в какой задаче результат будет больше, и почему. После этого предлагается решить эти задачи методом перебора всевозможных вариантов.
Решение задачи 1. AB, BA, BC, CB, AC, CA (всего шесть способов).
Решение задачи 2. AB, BC, AC (всего три способа).
Преподаватель обращает внимание студентов на то, что эти задачи оказались похожими только внешне, из-за того, что в обеих присутствуют два числа: m=3 – общее количество элементов и n=2 – количество выбранных элементов. Но в первой задаче составляются упорядоченные соединения, тогда как во второй задаче порядок следования элементов в соединении не имеет значения.
А если вместо чисел 3 и 2 будут например числа 8 и 3. Подойдет ли этот метод для решения этих задач? Поэтому существуют комбинаторные выражения (формулы) для этих соединений
5.3. Лекция «Основные комбинаторные понятия и формулы».
1) Размещения.
Определение. Размещениями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Число размещений из m элементов по n обозначают 
(от французского «arrangement» — «размещение») и вычисляют по формуле:
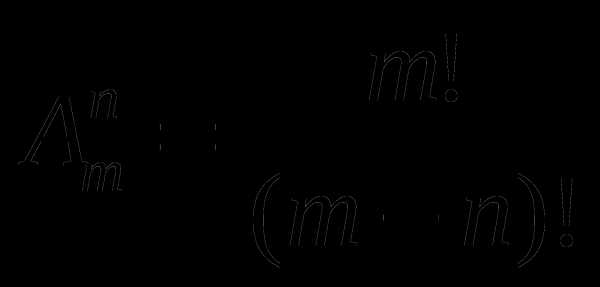
Пример 1. Решим задачу 1 с помощью этой формулы:
А теперь решим ту же задачу для случая m=8, n=3:
2) Перестановки.
Определение. Перестановкой из n элементов называют размещение из n элементов по n.
Число перестановок из n элементов обозначается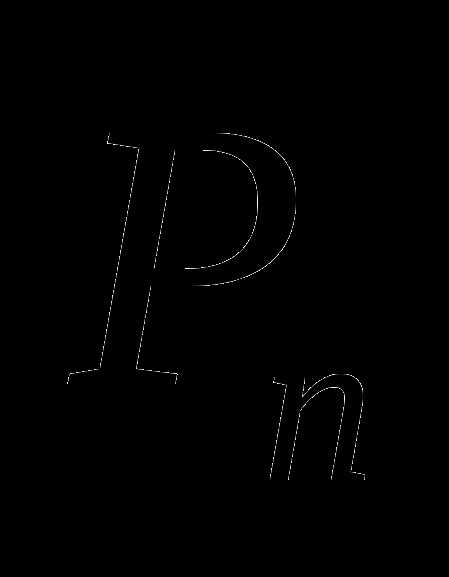 
и вычисляется по формуле:
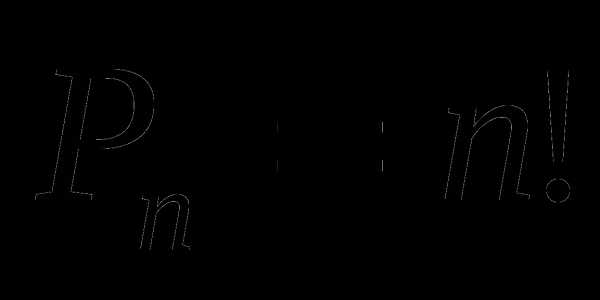
Задача. Сколькими способами можно расположить в столбик три детали конструктора, различающиеся по цвету?
Ответ:6.
3) Сочетания.
Определение.
Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m обозначают 
(от французского «combination» — «сочетание») и вычисляют по формуле:
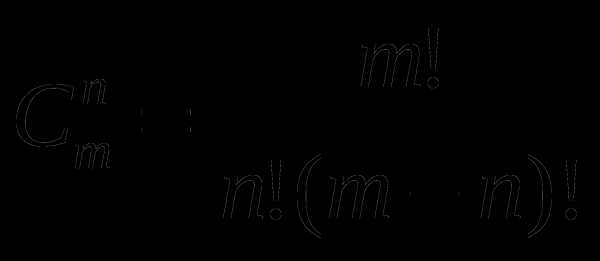
Пример 2. Решим задачу 2 с помощью этой формулы:
А теперь решим ту же задачу для случая m=8, n=3:
Снова, как и ожидалось, результат в первой задаче оказался больше, чем во второй.
Мы рассмотрели теоретические основы комбинаторики. Теперь перейдем к этапу закрепления новых знаний при решении задач.
6. Закрепление материала
6.1. Игра «Математическое лото»
Студентам раздаются наборы раздаточных материалов «Математического лото» (по одному на парту). Каждый комплект состоит из 16 математических заданий по основам комбинаторики, картонного листа в виде матрицы размерности 4 на 4 с написанными в ячейках числами-ответами и цветной фотографии, разрезанной на 16 равных прямоугольника. Все части фотографии пронумерованы в соответствии с порядком заданий и перемешаны. Задача студентов – решить 16 заданий, соответствующие частям разрезанной фотографии, и в соответствии с полученными числовыми ответами отыскать их место на картонной матрице, сложив в итоге фото. Задание выполняется как соревнование между малыми группами По 3-4 человека. Определяются три пары, которые не только сложат картинку раньше всех, но и представят в письменном виде все подробные решения.
Перед началом игры преподаватель мотивирует студентов на активное участие в ней, сообщая, что это упражнение позволит наилучшим образом сформировать навыки комбинаторных вычислений, что значительно упростит выполнение домашнего задания. Кроме того, выполняя это упражнение, можно совместить полезное с приятным, так как результат вызовет эстетические чувства.
Задания.
Вычислите.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
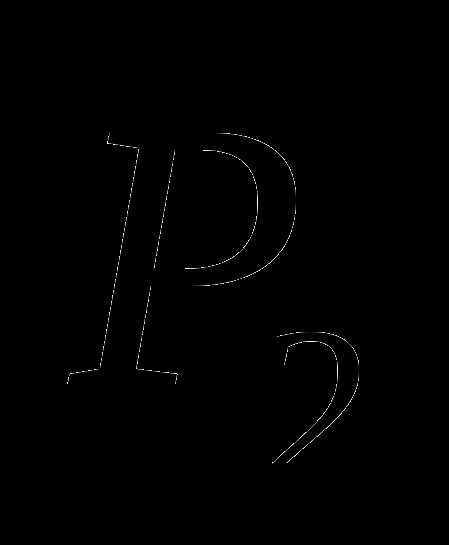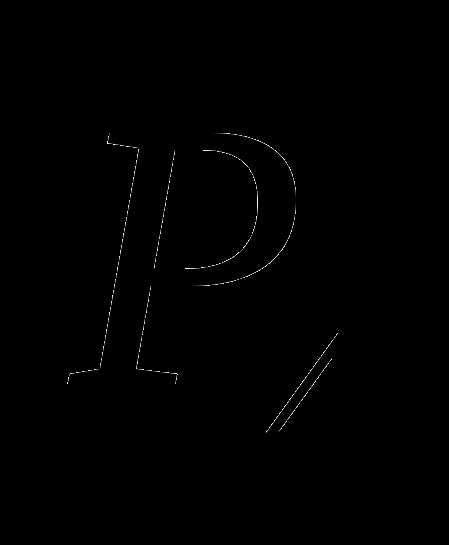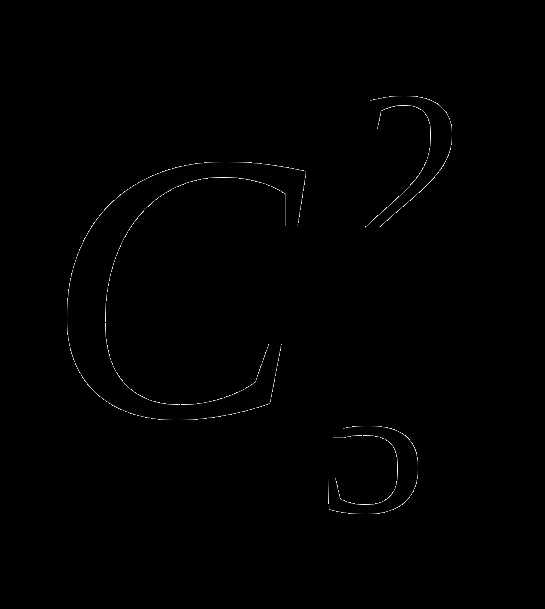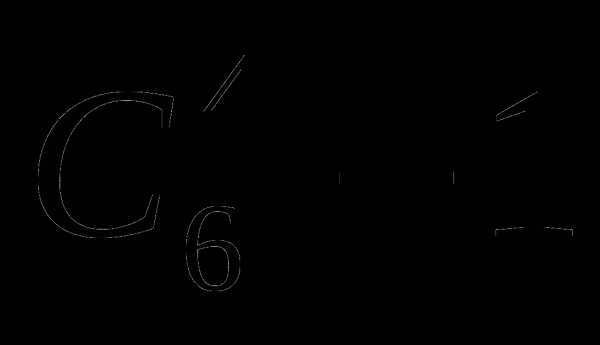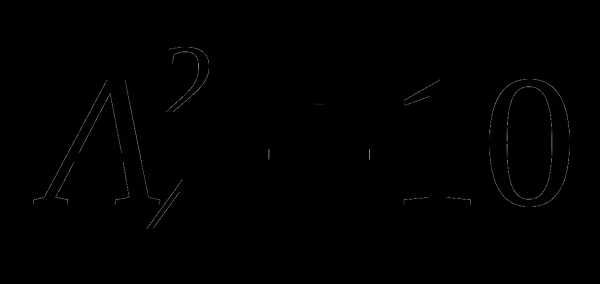Решения:
В завершении игры объявляются и поощряются победители.
6.2. Решение комбинаторных задач.
При решении комбинаторных задач важно научиться различать виды соединений.
Чтобы отличать задачи на подсчёт числа размещений от задач на подсчёт числа сочетаний, определим, важен или нет порядок в следующих выборках:
а) судья хоккейного матча и его помощник;
б) три ноты в аккорде;
в) «Шесть человек останутся убирать класс!»
г) две серии для просмотра из многосерийного фильма.
Ответ: а)да; б)нет; в)нет; г)да.
Задача 1. Сколькими способами могут занять I, II, III места 8 участниц финального забега на дистанции 100 м?
Ответ: 366.
Задача 2. Из 30 обучающихся группы надо выбрать старосту и помощника старосты. Сколькими способами это можно сделать?
Ответ: 870.
Задача 3. Сколькими способами можно составить букет из трёх цветков, выбирая цветы из девяти имеющихся?
Ответ: 84.
Задача 4. В группе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Ответ:21
6.3 Самостоятельная работа
Проверь себя
1.Определите вид соединений:
а) Соединения из n элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются __________перестановки
б) Соединения из m элементов по n, отличающихся друг от друга только составом элементов, называются _______________сочетания
в) Соединения из m элементов по n, отличающихся друг от друга составом элементом и порядком их расположения, называются _________размещения
2.Восстановите соответствие типов соединений и формул для их подсчёта
А.сочетания
В. размещения
С. перестановки
3. Сколькими способами из класса, где учатся 24 ученика, можно выбрать: а)двух дежурных; б)старосту и помощника старосты?
Ответ: а)276; б)552.
4. «Проказница Мартышка, Осёл, Козёл да косолапый Мишка задумали сыграть квартет». Сколькими способами они могут выбрать каждый для себя по одному инструменту из 10 данных различных инструментов?
Ответ:
Подведение итогов самостоятельной работы
7. Подведение итогов урока
Обобщаются новые знания, делаются выводы о достигнутых целях урока. Поощряются активные студенты, выставляются обоснованные преподавателем оценки.
8. Домашнее задание
Подготовка сообщений по темам: «Истории комбинаторики», «Комбинаторика и ее применение в реальной жизни».
infourok.ru
Лекция 07. Элементы комбинаторики
Лекция 7. Элементы комбинаторики.
Комбинаторика – это раздел математики, изучающий количество комбинаций, которые можно составить из заданного конечного множества попарно различных элементов произвольной природы.
Одно из важных правил комбинаторики – правило умножения:
если объект А
может быть выбран из множества Mn h способами и при каждом выборе объекта
А другой объект В может быть выбран k способами, то объект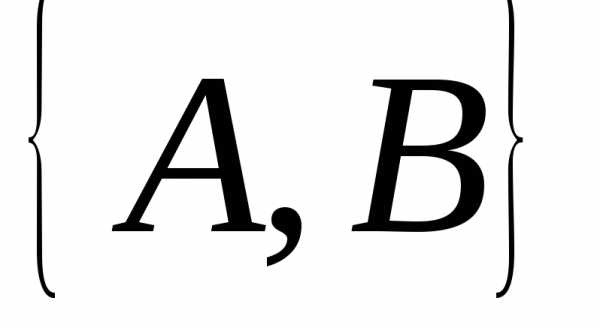 
,
состоящий из двух объектов А и В может
быть выбранhk способами.
Конечные подмножества элементов множества Mn называются соединениями.
Если в совокупности соединений подмножества образованы только попарно различными элементами множества Mn, то такие соединения называются соединениями без повторений.
Если в совокупности соединений входят подмножества не только с попарно различными элементами множества Mn, но и с одинаковыми, то такие соединения называются соединениями с повторениями.
Различают три основных типа соединений: размещения, перестановки, сочетания.
Определение 7.1. Размещением
из n элементов по m элементов без повторений называется
упорядоченное подмножество попарно
различных m элементов множества Mn (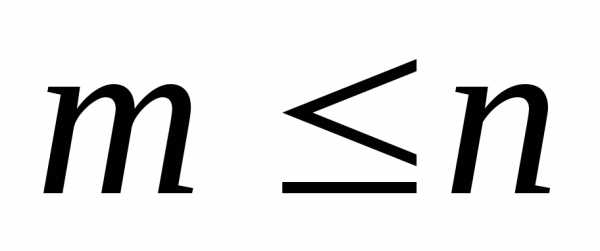
).
Определение 7.2. Перестановкой из n элементов без повторений называется упорядоченное множество всех n элементов множества Mn, то есть перестановка без повторений – это размещение без повторений из n по n элементов.
Определение 7.3. Сочетанием
из n элементов по m элементов без повторений называется
подмножество из m попарно различных элементов множества Mn без учёта порядка их следования (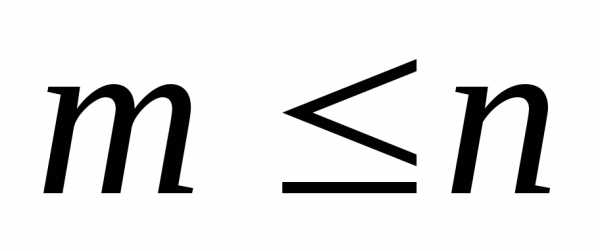
).
Для размещения или сочетания с повторениями требуется лишь условие, чтои, следовательно,m может быть любым натуральным числом, независимым от числа n элементов множества Mn.
В перестановке с повторениями присутствуют все элементы множества Mn, причём указывается, сколько раз повторяются элементы . Число элементов в такой перестановке может быть любым натуральным числом, большим или равным n.
Обозначим символами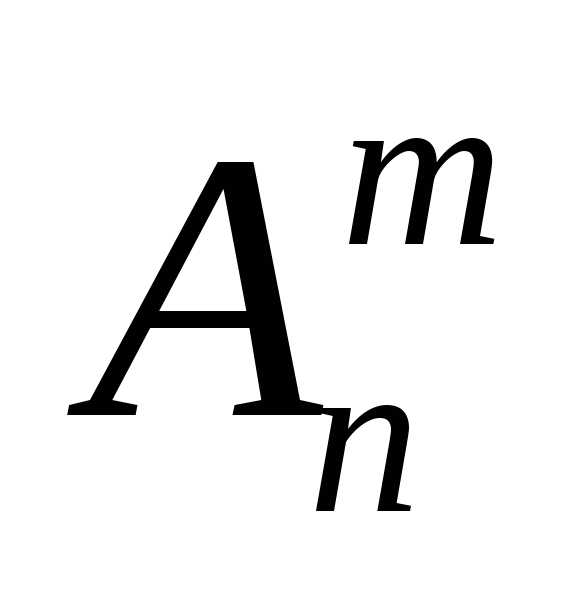 
,
,
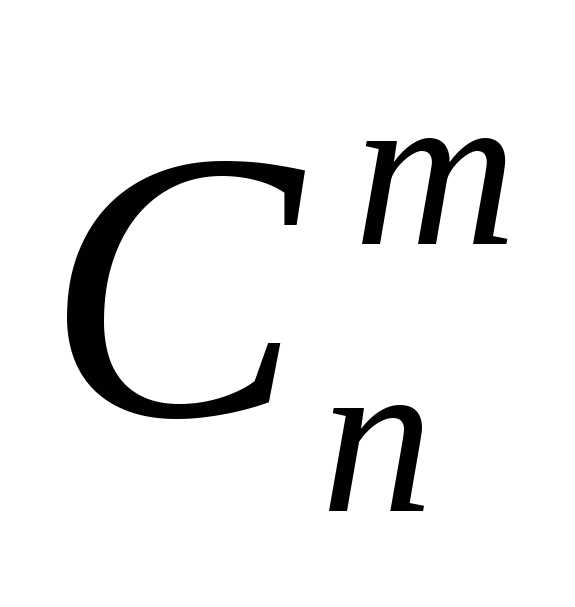число всех размещений, сочетаний без
повторений изn элементов по m элементов и число всех перестановок
без повторений из n элементов (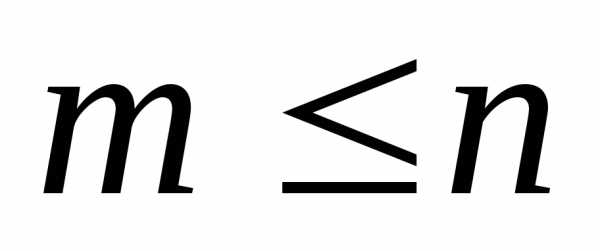
).
Символы для обозначения числа всех
соединений определённого типа берутся
из начальных букв соответствующих
французских слов: arrangement
– размещение,
combination
– комбинация, сочетание,
permutation
– перестановка.
Символами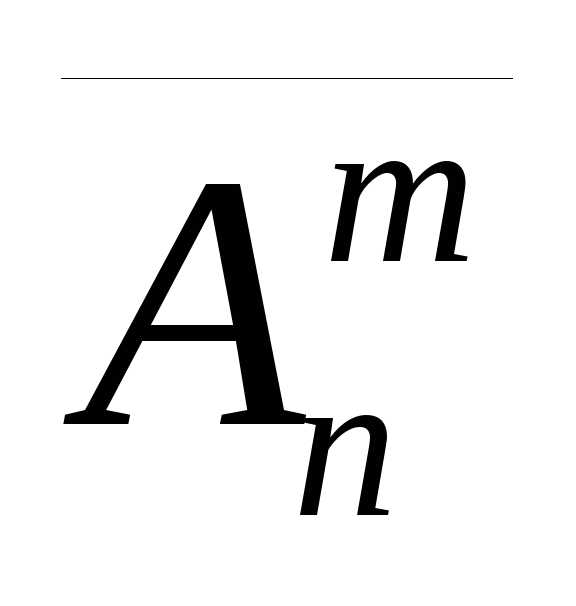 
,
,
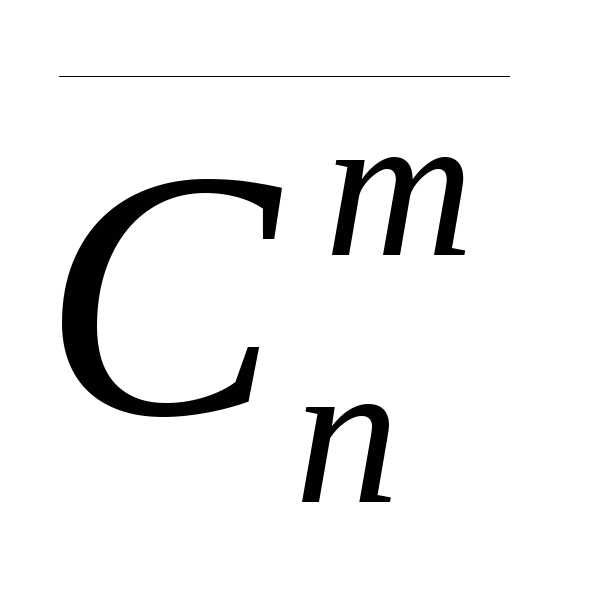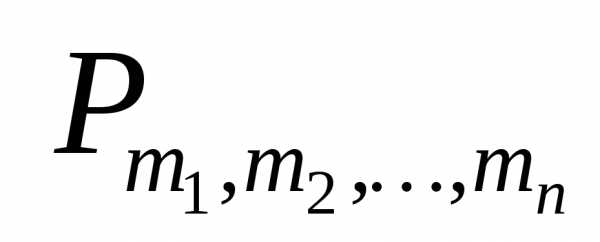обозначим число всех размещений,
сочетаний, перестановок с повторениями
(m, mi – любые натуральные числа). Число mi указывает, что элемент ai повторяется в перестановке mi раз, причем
.
Произведение n первых натуральных чисел обозначается символом n! и называется n-факториалом: .
☼ По определению
0!=1 и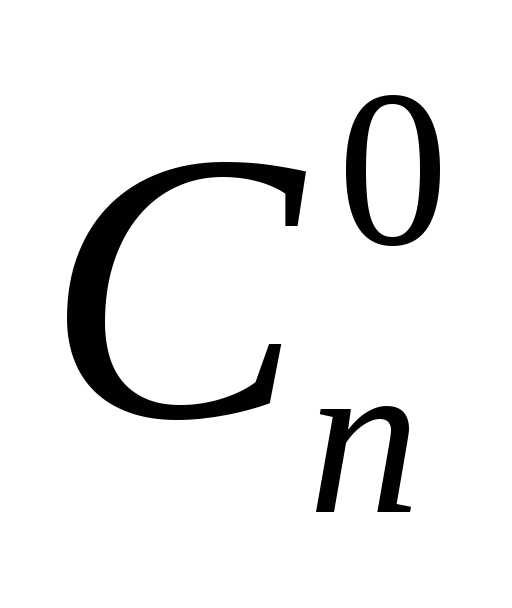 
=1. ☼
♦ Теорема 7.1. Число размещений без повторений из n элементов по m элементов вычисляется по формуле
, (7.1)
число размещений из n элементов по m элементов с повторениями
.
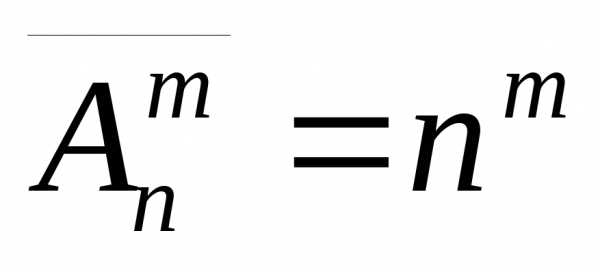(7.2)
Доказательство. Докажем методом математической индукции формулы (7.1) и (7.2).
1) Для m=1
они справедливы, так как выбор по одному
элементу из множества Mnможно осуществить толькоn способами, а по формулам (7.1) и (7.2)
,
.
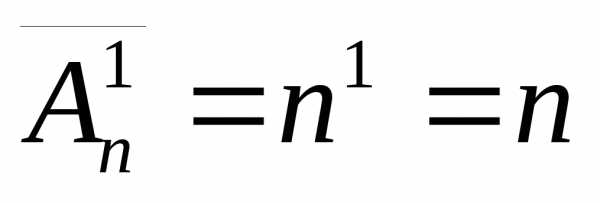2) Пусть эти формулы
справедливы для произвольного
фиксированного натурального числа k,
то есть
,
.
По правилу умножения,,
так как в случае подмножества с попарно
различными элементами множестваMn после выбора k элементов из Mn в нём останется n–k элементов, из которых по одному элементу
можно выбрать n–k способами. А в случае размещения с
повторениями (k+1)‑м
элементом может быть любой из n элементов множества Mn.
Учитывая, что
,
убеждаемся в справедливости формул
(7.1) и (7.2). ■
Следствие 1. Так как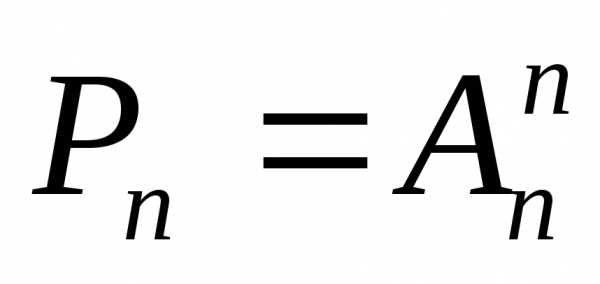 
,
то
.
Таким образом, получается формула числа
перестановок:
(7.3)
Формула для перестановок с повторениями такова:
. (7.3а)
Справедливость этой формулы установим следующими рассуждениями: если бы в перестановке все элементов были попарно различными, то таких перестановок было бы . Но, меняя между собой одинаковый элемент ai любыми mi! способами, мы не изменяем самой перестановки. Поэтому в знаменатель надо внести произведение факториалов .
Следствие 2. По правилу умножения . Следовательно,
,
то есть справедлива формула
.
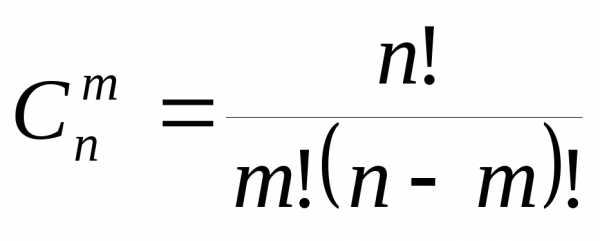(7.4)
♦ Теорема 7.2. Число сочетаний из n элементов по m элементов с повторениями вычисляется по формуле
. (7.5)
Доказательство. Докажем формулу (7.5) методом математической индукции.
1) Для m=1 она справедлива, так как , а выбор по одному элементу из множестваMn можно осуществить только n способами.
2) Пусть формула
(7.5) верна для произвольного фиксированного 
,
то есть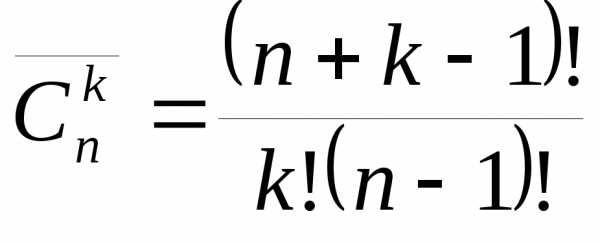 
.
Тогда, по правилу умножения,
,
т.к. вставить один элемент, взятый из
Mn,
мы можем n+k способами, добавив к уже выбранным k элементам либо один из них, либо любой
из Mn.
А в знаменателе число k+1
означает, что вставить этот дополнительный
элемент, не изменяя сочетания, мы можем
либо вначале, либо между первым и вторым
и т.д., либо после последнего (то есть k+1
вариантов).
Учитывая, что , убеждаемся, что формула (7.5) справедлива для m=k+1, а значит, она справедлива и для любого натурального числа m. ■
♦ Теорема 7.3. Справедливо правило симметрии
.
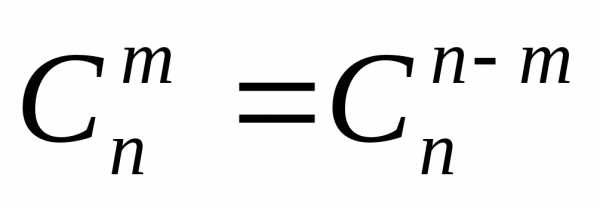(7.6)
Доказательство. . ■
♦ Теорема 7.4. Справедлива формула (правило Паскаля)
. (7.7)
Доказательство. 
. ■
♦ Теорема 7.5. Число всех
подмножеств из n элементов равно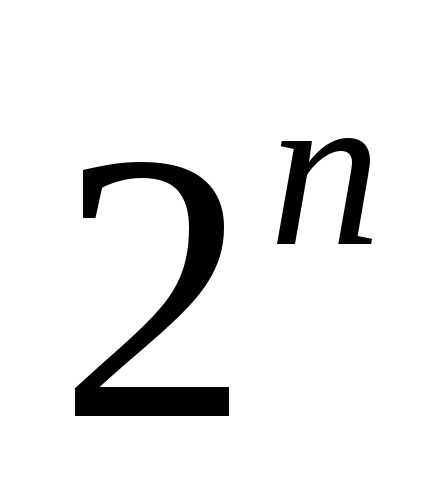 
:
.
Доказательство. Докажем теорему методом математической индукции.
1) При n=1
имеем множество одного элемента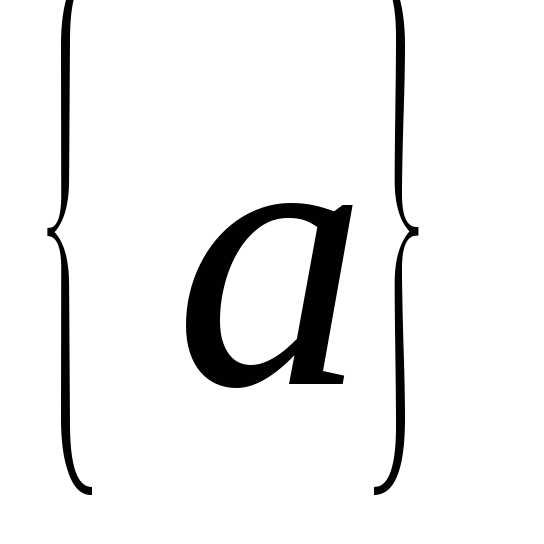 
,
которое содержит два подмножества:
пустое множество и само себя.
2) Пусть установлено,
что множество из k элементов содержит ровно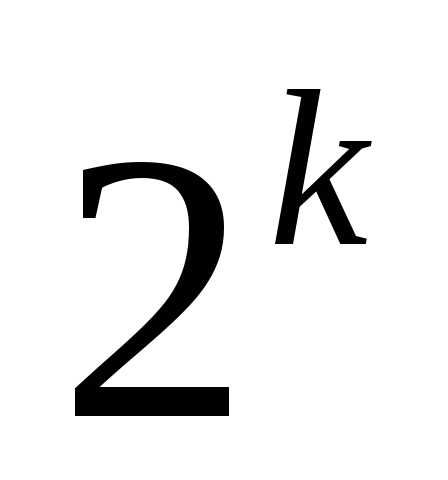 
подмножеств.
Рассмотрим множество изk+1 элементов. Любое его подмножество В получается одним из двух способов:
а) берётся подмножество В множества ,
в) берётся
подмножество
и присоединяется элемент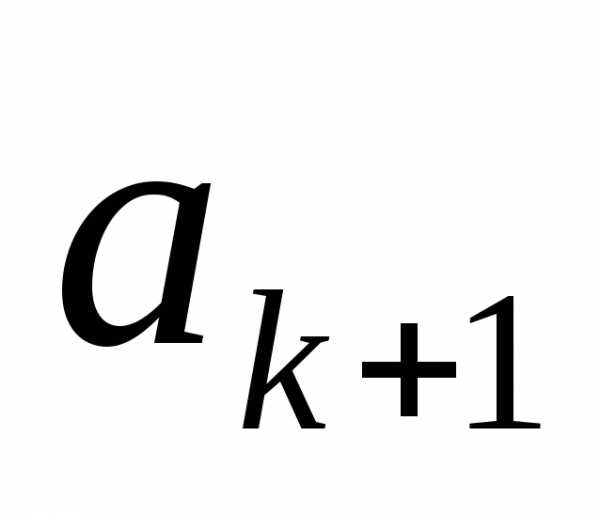
.
Каждым из этих
способов получаем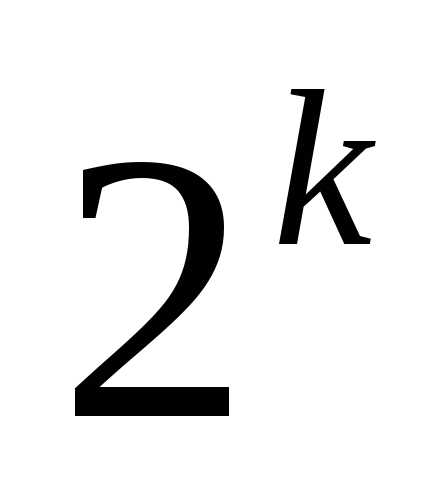 
подмножеств, а всегоподмножеств множества А. ■
Рассмотрим несколько задач, решение которых осуществляется с использованием доказанных формул.
Пример 7.1. Сколько пятизначных чисел можно составить из цифр 1, 3, 7?
Решение. По формуле (7.2) (размещения с повторениями) находим: .
Пример 7.2. Сколько неподобных членов содержится в многочлене
Решение. По формуле (7.5) (сочетания с повторениями) находим:
Пример 7.3. Сколькими способами можно составить футбольную команду, если её формируют из трёх вратарей и пятнадцати полевых игроков?
Решение. Так как полевых игроков в команде 10 и всего 1 вратарь, то по правилу умножения .
Пример 7.4. Сколько слов, без учёта их смысла, можно составить из букв слова «длинношеее»?
Решение. По формуле (7.3а) (перестановки с повторениями) находим:
.
Пример 7.5. Сколько четырёхзначных чисел можно составить из цифр 0, 1, 5?
Решение. Так
как число не начинается с нуля, то из
числа 
надо вычесть
число 
:
.
Пример 7.6. Сколько шестизначных телефонных номеров можно установить?
Решение. По формуле (7.2) (размещения с повторениями) находим:
.
♦ Теорема 7.6. При любом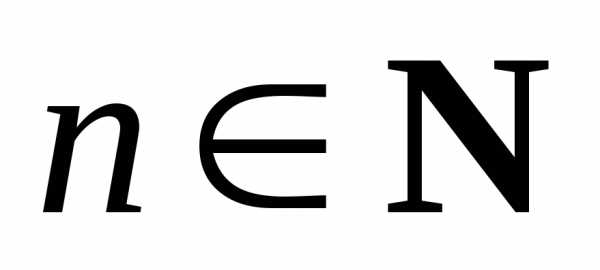 
справедливо
равенство(бином
Ньютона1)
. (7.8)
Доказательство. Формулу (7.8) докажем методом математической индукции.
1) Проверяем верность
формулы при n=1:
,
так как по формуле (7.4)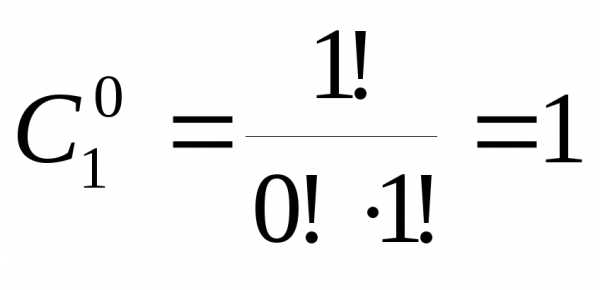
,
.
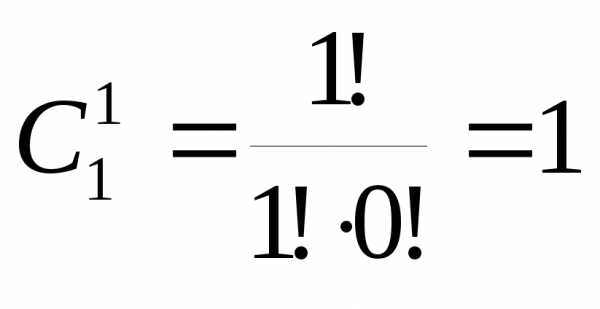Таким образом, приn=1
формула (7.8) верна.
2) Предположим, что формула (7.8) верна для некоторого n. Докажем, что при n+1 имеет место такая же формула, то есть что
. (7.9)
В самом деле,
.
В силу того, что ,,,,, следует формула (7.9). Из 1) и 2) на основании метода математической индукции заключаем, что формула (7.8) верна для любого натурального числаn. ■
Формулу (7.8) обычно коротко записывают так: .
При n=2 и n=3 получаем хорошо знакомые формулы:
;
.
1Ньютон Исаак (1642-1727) – великий английский физик, механик, математик и астроном.
33
studfiles.net
| Элементы комбинаторики. Сочетания, размещения, перестановки. Комбинаторика – раздел математики, в котором изучаются простейшие “соединения”. Факториалом натуральных чисел n называют произведение последовательных чисел от 1 до n. Перестановки – это комбинации из n-элементов, отличающихся только порядком следования (Pn=n!=1·2·3·…·n). Размещения из n-элементов по m-элементам – это комбинации, отличающиеся или составом, или порядком следования элементов (Amn=n(n-1) ·(n-2) ·…·(n-m+1)). Сочетания из n-элементов по m-элементам – это комбинация, отличающаяся хотя бы одним элементом (Cmn=m!·(n-m)!n!). В сочетании порядок элементов не учитывается. Факториал – произведение всех натуральных чисел от 1 до n. Теория вероятностей – это математическая наука, изучающая закономерности в случайных событиях. Случайное событие – такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по иному. Достоверное событие – это событие, которое в результате опыта непременно должно произойти. Невозможное событие – событие, которое в данном опыте не может произойти, т.е. вероятность такого события =0. Равновозможные события – если наступление одного события не более возможно наступления другого. Несколько событий образуют полную группу, если в результате появилось хотя бы одно из них. Несовместные, если появление одного исключает появление другого в данном опыте. Каждое событие, связанное с массой однородных опытов, имеет определенную вероятность, заключенную между 0 и 1. Если произведена серия из n опытов, в каждом из которых могло появиться или не появиться некоторое событие, то частотой события в данной серии опытов называется отношение числа опытов, в которых появилось событие к общему числу произведенных опытов. Частоту события называют статистической вероятностью (W(A)=mn, где m – число опытов, в которых событие произошло; n – общее число опытов). Геометрическая вероятность – Р(А)=мера g/мера G. Для определения вероятности того или иного события применяются алгебраические действия, что позволяет упростить форму записей, облегчает вычисления. Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А и В или обоих вместе (С=А+В). Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий. Противоположные события — если два события несовместимы и в результате произойдет только одно из них. При определении вероятности часто приходится представлять сложные события в виде комбинаций более простых событий, применяя и операцию сложения, и операцию умножения событий. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А (Р(А/В)). Теорема сложения вероятностей – вероятность суммы двух несовместных событий равна сумме вероятностей этих событий (Р(А+В)=Р(А)+Р(В)). Теорема сложения вероятностей справедлива только для несовместных событий. В случае, когда события А и В совместные, вероятность суммы этих событий выражается формулой Р(А+В)=Р(А)+Р(В)-Р(А·В). Противоположными событиями называются два несовместных события. Сумма вероятностей противоположных событий =1. Теорема умножения вероятностей – вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого (Р(А·В)=Р(А) ·Р(В/А)). Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий. Формула полной вероятности. Формулы Байеса. Если требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий Н1, Н2, …, Нn, эти несовместные события называют гипотезами, то используют следующую формулу. Р(А)=Р(В1)·РВ1(А)+Р(В2)·РВ2(А)+…+Р(Вn)·РВn(А), где Р(В1)+Р(В2)+…+Р(Вn)=1 — формула полной вероятности. Вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе. Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) В1, В2,…,Вn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут переоценены по формулам Байеса – РА(Вi)=Р(Вi)·РВi(А)/Р(А), (i=1, 2, 3,…, n) — формула Байеса, где Р(А)=Р(В1)·РВ1(А)+Р(В2)·РВ2(А)+…+Р(Вn)·РВn(А). Часто бывает, что один и тот же опыт повторяется не однократно. В результате каждого опыта может появиться или не появиться некоторое событие А, причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. Независимые опыты могут производиться в одинаковых или различных условиях. При одинаковых условиях вероятность события А во всех опытах одна и та же. Во втором случае вероятность события А от опыта к опыту меняется. A – некоторое событие; A – противоположное событие; P – вероятность появления события A; g – вероятность появления события A; n – число проведенных опытов; K – число благоприятных исходов. Pn(K)=Ckn·pk·gn-k. Когда опыты проводятся в неодинаковых условиях, то вероятность события от опыта к опыту меняется. Число k0 (наступление события в независимых испытаниях, в каждом из которых вероятность появления события равна p) называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях k0 раз, превышает (или не меньше) вероятности остальных возможных исходов испытаний. Наивероятнейшее число k0 определяют из двойного неравенства np-g0Понятие случайной величины. Дискретные и непрерывные случайные величины. Законы распределения дискретной случайной величины: табличный, аналитический, графический. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее – какое именно.(число осколков, образующихся при разрыве снаряда). Если случайные величины принимают отдельные, изолированные друг от друга значения, которые можно заранее перечислить, то они называются дискретными случайными величинами (число попаданий при 3 выстрелах). Существуют случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, они называются непрерывными случайными величинами (вес наугад взятого осколка снаряда). Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Простейшей формой задания закона распределения является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
Такая таблица называется рядом распределения случайной величины Х. Графическая форма закона распределения: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых. Такая фигура называется многоугольником распределения. Закон распределения дискретной случайной величины Х может быть задан аналитически (в виде формулы). Р Х Иногда, приходится рассматривать множество исходов, соответствующих одному событию. Полный список всех возможных исходов будет представлять собой множество. Каждый исход эксперимента соответствует в точности одному элементу из этого множества. Каждый элемент множества называется элементарным событием. Если А – событие, то P(A)=mn, где m – число исходов, благоприятствующих событию; n – общее число исходов, которые попарно несовместимы. Свойства: 1)вероятность достоверного события=1. Если событие достоверно, то каждый элементарный исход испытания благоприятствует событию, в этом случае m=n, следовательно P(A)=1. 2)вероятность невозможного события=0. Если событие невозможно, то не один из элементарных исходов испытания не благоприятствует событию, в этом случае m=0, следовательно Р(А)=0. 3)вероятность случайного события есть положительное число, заключенное между 0 и 1. Случайное событие благоприятствует лишь части из общего числа элементарных исходов испытания. Локальная теорема Муавра-Лапласа – вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0 Вероятность отклонения относительной частоты события от его вероятности в повторных независимых испытаниях. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0 Важнейшие законы распределения ДСВ (биномиальный, закон Пуассона). Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными вероятностями. Законом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей. Биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p; вероятность возможного значения x=k (числа k появлений события) вычисляют по формуле Бернулли: Pn(K)=Ckn·pk·gn-k. Если число испытаний велико, а вероятность p появления события в каждом испытании очень мала, то используют формулу Пуассона – Pn(k)=ke—/k!, где k-число появлений события в n независимых испытаниях, =np (среднее число появлений события в n испытаниях), и говорят, что случайная величина распределена по закону Пуассона. Числовые характеристики ДСВ.Характеристикой среднего значения случайной величины служит математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности: М(Х)=х1р1+х2р2+…+хnрn. Если дискретная случайная величина принимает счетное множество возможных значений, то , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. Свойства математического ожидания: 1)математическое ожидание постоянной величины равно самой постоянной: М(С)=С. 2)постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х). 3)математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей: М(Х1Х2…Хn)=м(Х1)М(Х2)…М(Хn). 4)математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых: М(Х1+Х2+…+Хn)=М(Х1)+М(Х2)+…+М(Хn). Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: М(Х)=np. Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение. Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(X)=M[X-M(X)]2, дисперсию удобно вычислять по формуле D(X)=M(X2)-[M(X)]2. Дисперсия обладает свойствами: 1)дисперсия постоянной равна 0: D(C)=0. 2)постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(CX)=C2D(X). 3)дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых: D(X1+X2+…+Xn)=D(X1)+D(X2)+…+D(Xn). Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X)=npg. Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии: (X)= D(X) . Плотность распределения НСВ и её свойства. Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f(x)=F’(x). Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), определяется равенством: P(aabf(x)dx. Зная плотность распределения, можно найти функцию распределения F(x)=xf(x)dx. Плотность распределения обладает следующими свойствами: 1)плотность распределения неотрицательна, т.е. f(x)>=0. 2)несобственный интеграл от плотности распределения в пределах от — до равен единице: f(x)dx=1. В частности, если все возможные значения случайной величины принадлежат интервалу (a,b), то abf(x)dx=1. Числовые характеристики НСВ и их свойства. Среди числовых характеристик случайных величин нужно прежде всего отметить те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее значение, около которого группируются все возможные значения случайной величины. Математическое ожидание НСВ Х, возможные значения которой принадлежат всей оси Ох, определяется равенством M(X)= xf(x)dx, где f(x)-плотность распределения случайной величины Х. Свойства математического ожидания: 1)математическое ожидание постоянной величины равно самой постоянной: М(С)=С. 2)постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х). 3)математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей: М(Х1Х2…Хn)=м(Х1)М(Х2)…М(Хn). 4)математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых: М(Х1+Х2+…+Хn)=М(Х1)+М(Х2)+…+М(Хn). Модой М0(Х) непрерывной случайной величины Х называют то ее возможное значение, которому соответствует локальный максимум плотности распределения. Медианой Ме(Х) непрерывной случайной величины Х называют то ее значение, которое определяется равенством P[Xe(X)]=P[X>Me(X)]. Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством D(X)= [x-M(X)]2f(x)dx. Дисперсия обладает свойствами: 1)дисперсия постоянной равна 0: D(C)=0. 2)постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(CX)=C2D(X). 3)дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых: D(X1+X2+…+Xn)=D(X1)+D(X2)+…+D(Xn). Среднее квадратичное отклонение непрерывной случайной величины определяется так же, как и для дискретной величины: (Х)= D(X) . Функция распределения случайных величин (ДСВ, НСВ). Функцией распределения называют функцию F(x)=P(X2)>=F(x1), x2>x1. Следствие 1: вероятность того, что случайная величина Х примет значение, заключенное в интервале (a,b), равна приращению функции распределения на этом интервале: P(a1, равна нулю: P(X=x1)=0. 3)если все возможные значения случайной величины Х принадлежат интервалу (a,b), то F(x)=0 при x=b. 4)Функция распределения непрерывна слева: lim F(X)=F(x0). Функция распределения любой дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятности этих значений. Сумма всех скачков функции F(x) равна единице. Функция распределения непрерывной случайной величины представляет собой функцию непрерывную во всех точках. |
topuch.ru
Элементы комбинаторики
Правило сложения
Правило сложения используется в том случае, если у нас есть два или более множеств, которые попарно не пересекаются, то есть не имеют общих элементов. И нам нужно найти сколько элементов содержится в объединении этих множеств. В этом случае мы складываем число элементов в каждом множестве. Простейший пример: если у нас есть две корзинки с фруктами: в одной 5 яблок, а в другой 7 груш. Если мы эти фрукты пересыпаем в одну корзинку (объединяем множества), тогда в новой корзинке окажется 5+7=12 фруктов.
Правило умножения
Правило умножения используется в том случае, если у нас есть два множества, и мы составляем всевозможные пары из элементов этих множеств. Например, если взять множество, состоящее из 5-ти яблок и множество, состоящее из 7-ми груш и составить всевозможные пары из этих фруктов, то мы получим всевозможных пар.
Действительно. Возьмем первое яблоко. Мы можем положить к нему любую из семи груш, то есть получаем 7 пар. Возьмем второе яблоко, и к нему мы также можем положить любую из 7-ми груш, получаем ещё 7 пар. И так далее. Всего получается пар.
Правило умножения легко понять, если попытаться ответить, например, на такой вопрос: «сколько существует двузначных чисел?«
Пусть двузначное чиcло имеет вид , где — число десятков, — число единиц. При этом цифра может принимать значения от 1 до 9 ( цифра 0 не может стоять на первом месте, так как в этом случаем мы получим однозначное число), цифра может принимать значения от 0 до 9.
Пусть , и у нас есть 10 вариантов цифр, которые могут стоять на втором месте. Тогда мы имеем 10 двузначных чисел, содержащих 1 десяток.
Затем мы берем и так же получаем 10 двузначных чисел, у которых теперь уже 2 десятка.
И так далее.
Так как цифра может принимать 9 различных значений, то получаем двузначных чисел.
Зная, что на первом месте может стоять 9 различных цифр, а на втором — 10, мы получаем комбинаций этих цифр, то есть все возможные двузначные числа. Здесь важно понимать, что любая цифра, стоящая на первом месте, может сочетаться с любой цифрой, стоящей на втором месте.
В общем случае правило умножения звучит так:
Если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Это правило распространяется на любое число независимо выбираемых элементов.
Если мы хотим ответить на вопрос, сколько существует трехзначных чисел, мы заметим, что в трехзначном числе первая цифра может принимать 9 значений, вторая — 10, и третья — 10 значений. И мы получаем трехзначных чисел.
Формула включений-исключений
используется в том случае, если нам нужно найти число элементов в объединении двух множеств, в том случае, если эти множества пересекаются.
Пусть множество А содержит n элементов, множество В содержит m элементов, и пересечение этих множеств содержит k элементов. То есть k элементов содержатся и в множестве А, и в множестве В. Тогда объединение множеств содержит m+n-k элементов.
Действительно, при объединении двух множеств мы k элементов посчитали два раза, и теперь один раз мы должны их вычесть.
Число элементов в множестве обозначается общепринятым значком #. Тогда формула для подсчета числа элементов в объединении трех множеств имеет вид:
########
Рассмотрим примеры задач.
1. Сколько трехзначных чисел содержит хотя бы одну цифру 3?
Решение.
показать
2. Сколько четырехзначных чисел, кратных 5.
Решение.
показать
Перестановки
Воспользуемся правилом умножения чтобы ответить на вопрос, «сколькими способами можно построить 7 человек в шеренгу?».
Человека, стоящего первым в шеренге можно выбрать семью способами, второго можно выбрать из оставшихся шести человек, то есть шестью способами. Третьего, соответственно, пятью. И так далее. Последнего можно выбрать единственным способом. Всего получаем способов построить 7 человек в шеренгу.
В общем случае, если мы имеем объектов, которые хотим расположить в определенном порядке (пронумеровать их), то мы получим
способов расположения этих объектов.
Факториалом натурального числа называется произведение всех натуральных чисел от 1 до :
По определению 0!=1; 1!=1.
Перестановкой из предметов называется любой способ нумерации этих предметов (способ расположения их в ряд).
Число перестановок предметов равно .
3. Имеется 10 компьютерных дисков и 10 коробок от них. Найдите вероятность того, что случайным образом уложив диски в коробки, мы обнаружим, что
1. Каждый диск лежит в своей коробке.
2. Хотя бы один диск лежит не в своей коробке.
3. Два определенных диска перепутаны местами, а остальные в своих коробках.
4. Ровно один лежит не в своей коробке, а остальные — в своих коробках.
Решение.
показать
1. Пронумеруем диски и коробки. Расположим коробки в определенной последовательности. Нам нужно, чтобы при случайном расположении дисков в ряд, их номера тоже оказались расположены в той же последовательности.
Расположить 10 чисел в определенной последовательности можно единственным способом, то есть мы имеем 1 благоприятный исход.
Расположить 10 чисел в произвольном порядке можно 10! способами.
Следовательно, вероятность того, что каждый диск окажется в своей коробке равна
2. Событие «хотя бы один диск лежит не в свой коробке» противоположно событию «каждый диск лежит в своей коробке«, и его вероятность равна
3. Событие «два определенных диска перепутаны местами, а остальные в своих коробках», также как событие «каждый диск лежит в своей коробке«, имеет единственный благоприятный исход, поэтому вероятность этого события равна
4. Событие «ровно один лежит не в своей коробке, а остальные — в своих коробках» невозможно, так как если один диск лежит не своей коробке, то обязательно должен найтись ещё один, который так же лежит не в своей коробке. Поэтому вероятность этого события равна нулю.
4. Слово «МАТЕМАТИКА» написали на полоске картона и разрезали полоску на буквы. Найдите вероятность того, что составив все эти буквы случайным образом в ряд, мы снова получим слово «МАТЕМАТИКА».
Сколько буквосочетаний можно составить из букв слова «МАТЕМАТИКА»?
Решение.
показать
1 способ.
Вероятность того, что на первом месте будет стоять буква М равна 2/10 — у нас две буквы М, и всего 10 букв.
Вероятность того, что на втором месте будет стоять буква А равна 3/9 — у нас осталось 9 букв, из которых 3 буквы А.
Вероятность того, что на втором месте будет стоять буква Т равна 2/8 — у нас осталось 8 букв, из которых 2 буквы Т.
И так далее. В итоге получаем:
2 способ.
Пронумеруем все буквы в слове «МАТЕМАТИКА». Найдем, сколькими способами мы можем их расположить в определенном порядке. В слове 10 букв, и мы можем их расположить 10!=3628800 различными способами.
Поскольку в слове есть одинаковые буквы, то при перестановке этих букв мы получим то же слово:
в слове «МАТЕМАТИКА» 2 буквы «М»; 3 буквы «А»; 2 буквы «Т», следовательно по правилу произведения это дает нам способов перестановки этих букв с сохранением слова «МАТЕМАТИКА».
Таким образом, вероятность снова получить слово «МАТЕМАТИКА» равна:
Сколько буквосочетаний можно составить из букв слова «МАТЕМАТИКА»?
Из 10 букв слова «МАТЕМАТИКА» можно составить 10! буквосочетаний. Но некоторые из них будут одинаковыми, так как при перестановке одинаковых букв, мы будем получать те же буквосочетания. То есть в итоге мы получим
буквосочетаний.
Размещения
В задачах по теории вероятностей часто возникает необходимость определить, сколькими способами можно выбрать определенное число предметов и расположить их в определенном порядке.
5. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?
Воспользуемся правилом умножения.
В первую страну мы выбираем из 9 специалистов, то есть у нас 9 вариантов выбора. После того, как специалист для поездки в первую страну выбран, у нас осталось 8 специалистов, и для поездки во вторую страну у нас 8 вариантов выбора. И так далее… в четвертую страну мы можем выбрать кандидата из 6 специалистов.
Таким образом, мы получаем вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны.
Обобщим эту задачу на случай выбора k кандидатур из n специалистов для поездки в k различных стран.
Рассуждая аналогичным образом, мы получаем
вариантов.
Если умножить и разделить это выражение на , то получим следующую формулу:
В этой задаче из множества, состоящего из элементов мы выбрали упорядоченные подмножества (для нас был важен порядок расположения элементов в подмножестве), состоящие из элементов. Задача сводилась к нахождению числа таких подмножеств.
Такие упорядоченные подмножества называются размещениями из n элементов по k.
Пусть у нас есть множество , состоящее из элементов. Размещением (из n по k) называется упорядоченное подмножество из различных элементов из некоторого множества , состоящего из различных элементов.
Число размещений из элементов по обозначается и находится по формуле:
Размещения с повторениями
6. Игральную кость бросают трижды. Сколько различных комбинаций выпавших очков при этом получится?
При бросании кости первый раз мы получим 6 различных вариантов: 1 очко, 2, 3… или 6. Аналогично при бросании кости во второй и в третий раз мы получим также по 6 различных вариантов. По правилу умножения получим число различных комбинаций трех чисел, принимающих значения от 1 до 6:
В общем случае:
Пусть у нас есть множество , состоящее из элементов.
Любой упорядоченный набор элементов множества, состоящего из элементов называется размещением с повторением из элементов по . Число различных размещений с повторениями равно
.
Действительно. Представим ящик с пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так раз. Сколько комбинаций из номеров мы можем получить?
Поскольку шары каждый раз возвращаются, каждый раз, вынимая шар из коробки, в которой шаров, мы можем получить различных чисел. По правилу умножения имеем
Сочетания
Рассмотрим задачу, аналогичную задаче 5, но с существенным отличием.
7. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов?
В этой задаче нам нужно выбрать 4 кандидатуры, но при этом не важно, в каком порядке мы их выбираем, нас интересует только состав выбранных элементов, но не порядок их расположения.
Если бы нас интересовал порядок расположения элементов, как в задаче 5, то мы могли применили бы формулу для нахождения числа размещений из 9 по 4:
4 различных элемента можно расположить в определенном порядке 4! различными способами. Поскольку нас не интересует порядок расположения элементов, число способов, которыми мы можем выбрать 4 элемента, не располагая их в определенном порядке, уменьшается в 4! раза по сравнению с предыдущей задачей (так как для данной задачи различное расположение данных элементов считается одним способом), и мы получаем
способов.
В этой задаче появляется понятие сочетания.
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества (множества, состоящего из n элементов).
Внимание! Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).
Число сочетаний из n элементов по k элементов обозначается
и находится по формуле:
Число сочетаний из n по k показывает, сколькими способами мы можем выбрать k элементов из n элементов, или сколькими способами мы можем расположить k объектов по n местам.
Легко заметить, что
8. В коробке лежат 8 красных карандашей и 4 синих. Из коробки наугад вынимают 4 карандаша. Какова вероятность того, что среди них окажется 2 красных и 2 синих?
Решение.
показать
Всего в коробке 12 карандашей. Найдем, сколькими способами способами можно извлечь из коробки 4 карандаша. Так как нас не интересует порядок, в котором карандаши извлекаются из коробки, а только состав карандашей, это число равно числу сочетаний из 12 по 4:
Из 8 красных карандашей можно извлечь два карандаша способами.
Из 4 синих карандашей можно извлечь два карандаша способами.
По правилу произведения получаем, что извлечь 2 синих и 2 красных карандаша можно способами.
Таким образом, искомая вероятность равна:
Метод шаров и перегородок
9. Сколькими способами можно разложить 10 шаров в 4 коробки? Предполагается, что некоторые коробки могут оказаться пустыми.
Решение.
Рассмотрим 10 шаров:
Будем «раскладывать шары по коробкам», ставя перегородки.
Например, так:
В этом примере в первой коробке 3 шара, во второй — 2, в третьей — 4, и в четвертой — 2. Переставляя шары и перегородки, мы получаем различные комбинации шаров в коробках. Например, переставив последний шар в первой коробке и первую внутреннюю перегородку, мы получим такую комбинацию:
Таким образом, мы получаем различное число шаров в коробках, комбинируя позиции 10-ти шаров и 3-х внутренних перегородок. Чтобы определить, сколько различных комбинаций мы можем получить, нам нужно найти число сочетаний из 13 по 3. (Или, что то же самое, что число сочетаний из 13 по 10.) Столько способов выбрать 3 места для перегородок из 13 возможных позиций. Или, что то же самое, 10 мест для шаров.
10. Сколько решений имеет уравнение в целых неотрицательных числах?
Решение.
Так как переменные могут принимать только целые неотрицательные значения, следовательно, у нас есть 10 переменных, и они могут принимать значения 0, 1, 2, 3 и 4. Представим, что у нас есть 10 коробок (это переменные), и мы должны разложить по этим коробкам 4 шара. Сколько шаров попадет в коробку, таково значение соответствующей переменной. Если у нас 10 коробок, следовательно, 10-1=9 внутренних перегородки. И 4 шара. Всего 13 мест. Нам надо расположить на этих 13 местах 4 шара. Число таких возможностей:
В общем случае, если нам нужно разложить шаров в коробок, мы получаем комбинации из шаров и внутренней перегородки. И число таких комбинаций равно числу сочетаний из по .
В этой задаче мы имели дело с сочетаниями с повторениями.
Сочетания с повторениями
Сочетаниями из элементов по элементов с повторениями называются группы, содержащие элементов, причем каждый элемент принадлежит к одному из типов.
Что такое сочетания из элементов по элементов с повторениями можно понять с помощью такого мысленного эксперимента. Представим ящик с пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так раз. В отличие от размещений с повторениями нас не интересует порядок записанных чисел, а только их состав. Например, группы чисел {1,1,2,1,3,1,2} и {1,1,1,1,2,2,3} считаются одинаковыми. Сколько таких групп из номеров мы можем получить?
В конечном итоге нас интересует сколько элементов каждого типа (всего n типов элементов) содержится в каждой группе (из k элементов), и сколько таких различных вариантов может быть. То есть мы находим, сколько в целых неотрицательных решений имеет уравнение уравнение — задача аналогична задаче по раскладыванию n шаров в k коробок.
Число сочетаний с повторениями находится по такой формуле:
Таким образом, число сочетаний с повторениями — это количество способов представить число k в виде суммы n слагаемых.
И.В. Фельдман, репетитор по математике.
ege-ok.ru
размещения, перестановки, сочетания. Привести примеры.
Определение 1.Размещениемизnэлементов поm называется любойупорядоченный наборизmразличных элементов, выбранных из генеральной совокупности вnэлементов.
Пример 1. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1,2), (2,1), (1, 3), (3,1), (2,3),(3,2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений обозначаетсяи вычисляется по формуле:
Определение 2. Сочетаниемизnэлементов поmназывается любойнеупорядоченный наборизmразличных элементов, выбранных из генеральной совокупности вnэлементов.
Пример 2. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}. Число сочетаний обозначаетсяи вычисляется по формуле:
Определение 3. Перестановкойизnэлементов называется любойупорядоченный наборэтих элементов.
Пример 3.Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2). Число различных перестановок из n элементов обозначаетсяи вычисляется по формуле
2. Случайный эксперимент. Основные особенности. Привести пример. Случайным экспериментом или испытанием называется осуществление какого-либо комплекса условий, который можно практически или мысленно воспроизвести сколь угодно большое число раз.
Основные особенности: множественность исходов, непредвиденность результата, многократность повторения (при одних и тех же условиях), наличие определённых закономерностей при многократном повторении.
Примеры случайного эксперимента: подбрасывание монеты, извлечение одной карты из перетасованной колоды.
3. Случайные события. Виды случайных событий. Действия над событиями. Полная группа событий. Противоположные события. Результат (исход) испытания называетсяслучайным событием(или просто: событием).
Виды событий:Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Введем понятие противоположного, или дополнительного, события. Под противоположным событием понимается событие, которое обязательно должно произойти, если не наступило некоторое событие. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий.
Действия над событиями:
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
4. Классическое определение вероятности. Привести пример. Вероятность события равна отношению числа случаев, благоприятствующих ему, из общего числаединственно возможных, равновозможных и несовместных случаев к числу, т. е.
(.)
Пример вопросу №4. Из набора, содержащего 10 одинаковых на вид электроламп, среди которых 4 бракованных, случайным образом выбирается 5 ламп. Какова вероятность, что среди выбранных ламп будут 2 бракованные?
5. Геометрическая вероятность. Привести пример. Пусть на плоскости задана некоторая область площадью, в которой содержится другая областьплощадью(рис. 3). В областьнаудачу бросается точка. Чему равна вероятность того, что точка попадет в область? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области, и вероятность попасть в какую-либо часть областипропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в областьпри бросании наудачу точки в область
Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.
6. Относительная частота. Устойчивость относительной частоты. Статистическая вероятность. Пусть произведеноnиспытаний, при этом некоторое событие А наступилоmраз. Числоmназываетсяабсолютной частотой(или просто частотой) появления события А, а отношение ω(A)=m/nназываетсяотносительной частотойпоявления случайного события А в данной серии опытов. С увеличением числа испытаний в сериях относительная частота приближается к некоторому числу Р(А), стабилизируясь возле него и принимая всё более устойчивые значения.
Статистической вероятностьюсобытия А называется число Р(А), около которого группируются значения относительной частоты события А при большом числе опытов (испытаний).
studfiles.net
2 часа лекции, 2 часа семинарское занятие
Схема выбора с возвращением.
Размещения с повторениями
Рассматриваются задачи, в которых выбор элементов из данного множества производится с возвращением. В этом случае выбранный из множества элемент возвращается назад в это множество либо автоматически замещается элементом, аналогичным выбранному.
Если при упорядоченной выборке m элементов из n—элементного множества А выбранные элементы возвращаются обратно и вновь упорядочиваются, то говорят о размещениях с повторениями. В отличие от «традиционных» размещений, размещения с повторениями могут отличаться друг от друга: элементами, порядком элементов, количеством повторений элементов.
Число
всех размещений из n элементов по m элементов с повторениями обозначается
«А с чертой из n по m»
— 
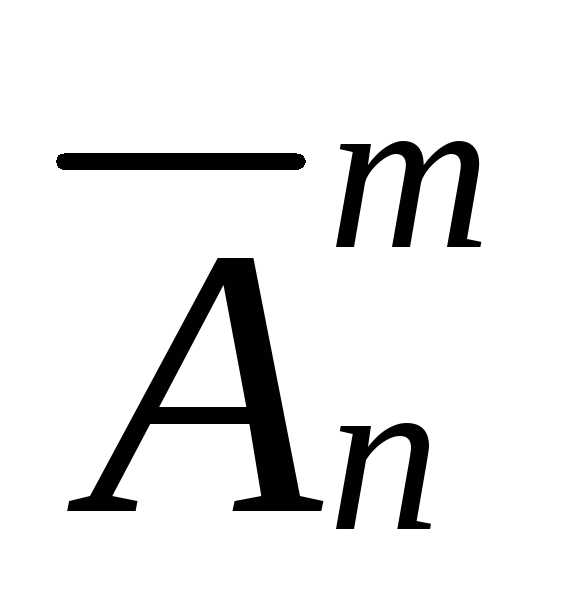и вычисляется по формуле:
.
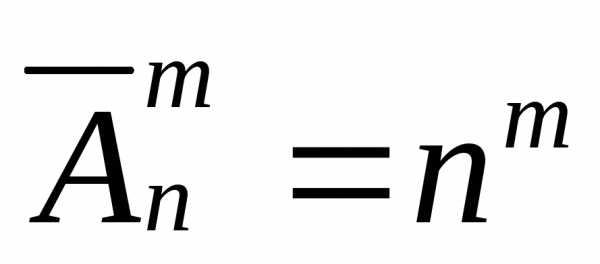Сочетания с повторениями
Пусть в Ω имеется m групп элементов, причем в каждой группе элементов достаточно много. Пусть элементы внутри группы неразличимы, но межгрупповые различия имеются.
Число
всех сочетаний из n элементов по m с повторениями обозначается символом
С с чертой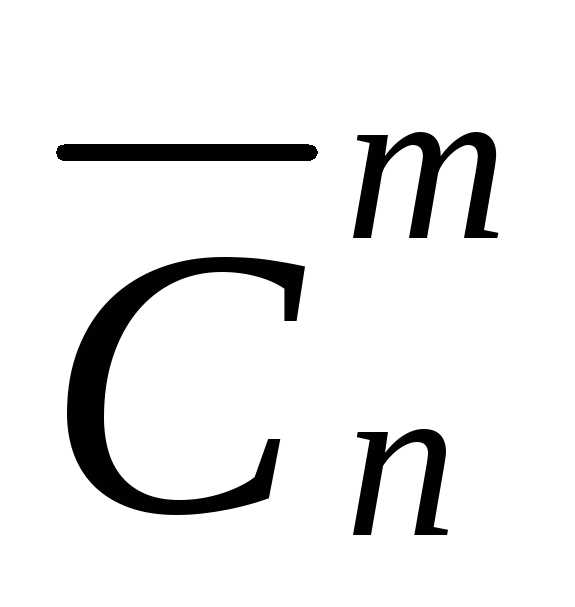 
и вычисляется по формуле:
= 
.
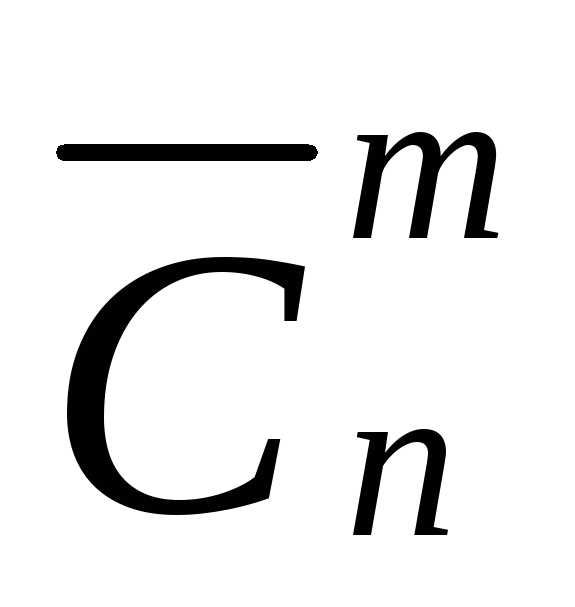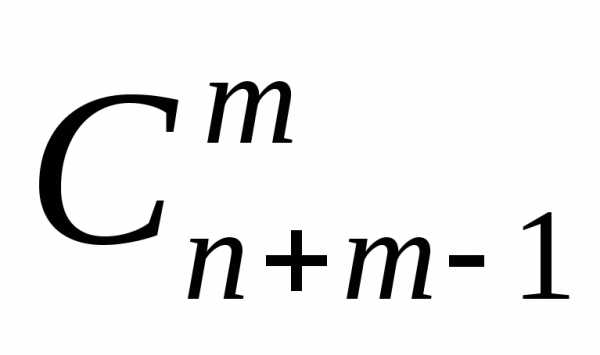Расчетная формула приводится к виду:
= 
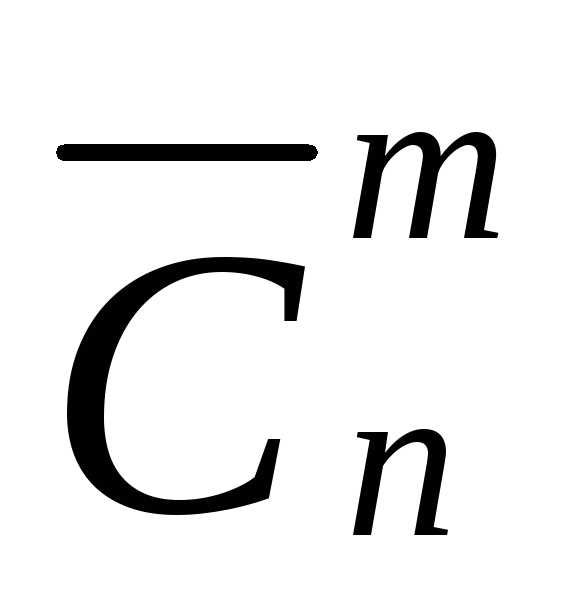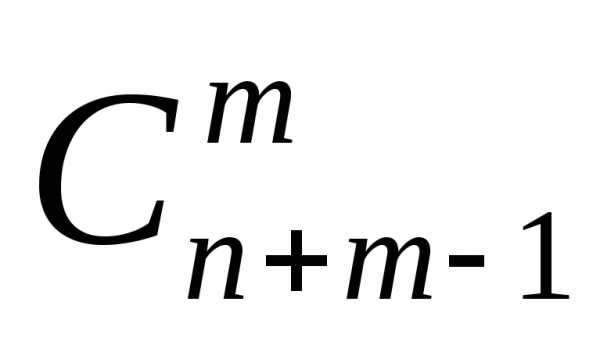
Перестановки с повторениями
Пусть в упорядоченном множестве с n элементами имеется m различных элементов. Иногда говорят: «пусть множество разбито на несколько, в данном определении – на m — непустых подмножеств». При этом пусть первый элемент повторяется n1 раз, второй элемент – n2 раз, …, m-й элемент – nm раз, причем
n1 + n2 + … + nm = n.
Перестановки
из n элементов данного множества называются
перестановками с повторениями из n элементов. Число перестановок
с повторениями из n, n1 + n2 + … + nm = n элементов обозначается символом Рn (n1, n2,
, n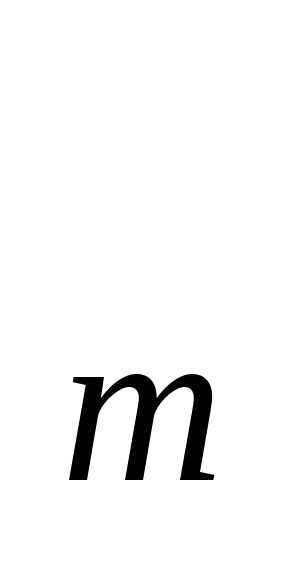
)
и вычисляется по формуле:
Рn (n1, n2,
…, nm) = 
Задачи, рассмотренные на лекции и семинаре. Тема 4.
Схема с возвращением. Перестановки, Сочетания, Размещения
Лекция 4
Задача 1–Т4. Сколько различных двузначных чисел можно составить из цифр 1, 3, 5, если цифры в числах могут повторяться?
Задача 2–Т4 (для самостоятельного решения). Подсчитайте, сколько трехзначных чисел можно составить из цифр 1, 3, 5.
Задача 3-Т4. Из трех элементов a, b, c составить все размещения по два элемента с повторениями.
Задача 4-Т4 (для самостоятельного решения). Из элементов (цифр) 2, 4, 5 составить все размещения с повторениями по два элемента.
Задача 5-Т4. Сколько пятизначных чисел можно составить, используя цифры:
а) 2, 5, 7, 8;
б) 0, 1, 9.
Задача 6–Т4. В качестве некоторого пароля можно использовать в любом порядке латинские буквы, цифры и символ подчеркивания. Пароль к регистру нечувствителен. Пользователь составил пароль из 4 знаков. Сколько всевозможных вариантов таких паролей может быть?
Задача 7-Т4. Из трех элементов a, b, c составить все сочетания по два элемента с повторениями.
Задача 8-Т4 (для самостоятельного решения). Из элементов (цифр) 2, 4, 5 составить все сочетания с повторениями по два элемента.
Задача 9–Т4. В продаже имеются пирожные 7 различных видов. Пирожные одного и того же вида считаем неразличимыми. Сколько существует различных способов покупки 12 пирожных?
Задача 10–Т4. Сколько различных слов, каждое из которых состоит из семи букв можно составить из букв слова «КОРОБОК»?
Задача 12-Т4. Сколько различных пятизначных чисел можно составить из цифр 3, 3, 5, 5, 8?
Задача 13-Т4 (для самостоятельного решения). У девочки имеется 2 белых бусины, 3 синих и 1 красная. Сколькими способами их можно нанизать на нитку?
Задача 14-Т4. На шести карточках написаны буквы, из которых можно составить слово АНАНАС. Сколько существует различных шестибуквенных слов, которые можно составить при помощи этих шести карточек?
Задача 15-Т4. В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток:
а) все открытки одинаковы?
б) различны?
studfiles.net