Если диагонали то этот параллелограмм является прямоугольником – Признаки прямоугольника и квадрата — урок. Геометрия, 8 класс.

Прямоугольник. Свойства и признаки прямоугольника

Категория: Справочные материалы

Елена Репина 2013-07-26 2013-09-22

Прямоугольник — параллелограмм, у которого все углы прямые.

Частным случаем прямоугольника является квадрат.

Свойства прямоугольника 

1. Так как  прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.

 Помимо этого:

2. Стороны прямоугольника являются его высотами.

3. Диагонали прямоугольника равны.

4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.

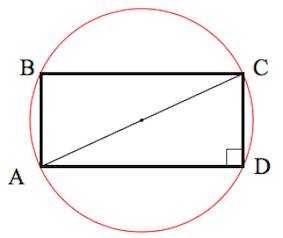
5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.

Признаки параллелограмма

 

Параллелограмм является прямоугольником, если выполняется любое из условий:

1. Диагонали параллелограмма равны.

2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.

3.  Все углы параллелограмма равны.

Площадь прямоугольника

 

 

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Автор: egeMax | Нет комментариев

egemaximum.ru

Четырехугольники | LAMPA — онлайн-учебник, который каждый может улучшить

Параллелограмм

Параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны.

Основные свойства:

• Диагонали параллелограмма делятся точкой пересечения пополам;
• Противолежащие стороны равны и противолежащие углы равны. Верны и ;
• Площадь параллелограмма равна: S=a⋅ha=a⋅b⋅sinα=12d1⋅d2⋅sinφS=a\cdot h_a=a\cdot b\cdot \sin\alpha =\frac{1}{2} d_1\cdot d_2\cdot \sin \varphiS=a⋅ha​=a⋅b⋅sinα=21​d1​⋅d2​⋅sinφ;
• Сумма квадратов диагоналей равна сумме квадратов сторон: d12+d22=2⋅(a2+b2)d_1^{\,2}+d_2^{\,2}=2\cdot (a^2+b^2)d12​+d22​=2⋅(a2+b2).

Признаки параллелограмма

Признак 1 (диагонали)

Диагонали пересекаются и делятся точкой пересечения пополам. И наоборот, если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Признак 2 (стороны)

У параллелограмма противолежащие стороны равны. Если у четырехугольника обе пары противолежащих сторон равны, то этот четырехугольник – параллелограмм.

Признак 3 (углы)

У параллелограмма противолежащие стороны равны и противолежащие углы равны. Если у четырехугольника обе пары противолежащих углов равны, то этот четырехугольник – параллелограмм.

Прямоугольник

Прямоугольник – это четырехугольник, у которого все углы прямые.

Основные свойства:

• Прямоугольник является частным случаем ;
• Диагонали прямоугольника равны;
• Вокруг прямоугольника можно ;
• Площадь прямоугольника равна произведению сторон: S=abS=abS=ab.

Признак прямоугольника

является , и его диагонали равны. Если у параллелограмма диагонали равны, то он является прямоугольником.

Ромб

Ромб – это четырехугольник, у которого все стороны равны.

Основные свойства:

• Ромб является частным случаем ;
• Диагонали ромба пересекаются под прямым углом и являются его углов;
• В ромб можно ;
• Площадь ромба: S=a⋅h=a2⋅sinα=d1⋅d22S=a\cdot h=a^2\cdot \sin\alpha =\frac{d_1\cdot d_2}{2}S=a⋅h=a2⋅sinα=2d1​⋅d2​​;
• Сторона ромба выражается через диагонали: a=(d12)2+(d22)2a=\sqrt{(\frac{d_1}{2})^2+(\frac{d_2}{2})^2}a=(2d1​​)2+(2d2​​)2​.

Квадрат

Прямоугольник, у которого равны все стороны, называется квадратом.

Основные свойства:

• Квадрат является одновременно и ;
• Диагонали квадрата равны, пересекаются под прямым углом, делятся точкой пересечения пополам и являются его углов;
• Если сторона квадрата равна aaa, то
• площадь квадрата: S=a2S=a^2S=a2,
• длина диагонали: d=2ad=\sqrt{2} ad=2​a,
• радиус вписанной окружности: r=12ar=\frac{1}{2} ar=21​a,
• радиус описанной окружности R=22aR=\frac{\sqrt{2}}{2} aR=22​​a.

lampa.io

это параллелограмм с равными диагоналями — Науколандия

Одним из признаков прямоугольника является равенство его диагоналей. То есть, если у параллелограмма диагонали равны, то он является прямоугольником.

Чтобы доказать данный признак прямоугольника, рассмотрим параллелограмм ABCD, у которого диагонали AC и BD равны. Требуется доказать, что в таком случае ABCD — это прямоугольник. Чтобы это доказать, достаточно доказать, что один из углов параллелограмма прямой, т. к. по еще одному признаку прямоугольника им является параллелограмм, у которого хотя бы один угол прямой.

Рассмотрим в параллелограмме треугольники ABD и ACD. У них стороны BD и AC равны, т. к. это диагонали, которые по условию равны. Стороны AB и CD равны как противоположные параллелограмма. А сторона AD общая. Таким образом, ∆ABD = ∆ACD по трем сторонам.

Углу A треугольника ABD соответствует угол D треугольника ACD. Из доказанного равенства треугольников следует, что эти углы равны между собой: ∠A =∠D.

В параллелограмме сумма соседних углов всегда равна 180°. Это следует из того, что соседние углы параллелограмма являются односторонними углами между секущей и параллельными прямыми. Так, в данном случае, AB || CD и AD — секущая, следовательно, ∠A +∠D = 180°.

Если угол A равен углу D, а в сумме они составляют 180°, то каждый из этих углов будет по 90°. Таким образом, мы определили даже не один, а два прямых угла в параллелограмме. Из этого следует, что он является прямоугольником. Теорема о том, что если в параллелограмме диагонали равны, то он является прямоугольником, доказана.

Можно сформулировать и обратную теорему: в прямоугольнике диагонали равны. То есть здесь дан прямоугольник, а требуется доказать, что его диагонали равны.

И в этом случае можно ограничиться рассмотрением треугольников ABD и ACD. Поскольку по условию нам уже дан прямоугольник, то угол A равен углу D по условию. Сторона AD общая, а стороны AB и CD равны как противоположные параллелограмма (или прямоугольника). Треугольники ABD и ACD оказываются равными по двум сторонам или углу между ними или по двум катетам прямоугольных треугольников.

Из равенства треугольников следует, что их соответствующие стороны AC и BD равны. А они то и есть диагонали данного прямоугольника ABCD. Таким образом доказано, что если дан прямоугольник, то его диагонали будут равны друг другу.

scienceland.info

№ 26. Докажите, что если у параллелограмма диагонали равны, то он является прямоугольником.

Источник:

Решебник по геометрии за 8 класс (А.В. Погорелов, 2001 год),
задача №26
к главе «§ 6. Четырехугольники».

Все задачи >

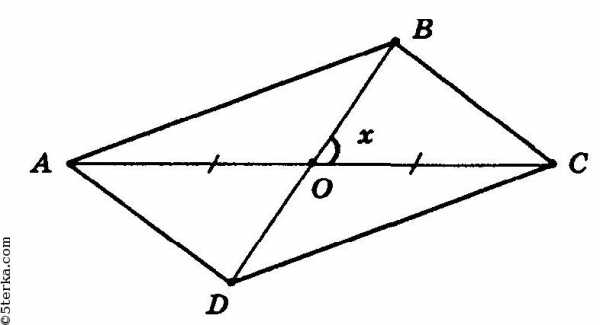
Пусть ABCD — параллелограмм. О — точка пересечения диагоналей. АС = DB (по условию), тогда,

Значит и равнобедренные. Пусть

Следовательно

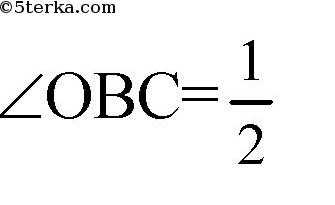
Аналогично доказывается, что остальные углы параллелограмма тоже прямые. Следовательно, данный параллелограмм является прямоугольником.

← № 25. Докажите, что если в параллелограмме хотя бы один угол прямой, то он является прямоугольником. № 27. Бетонная плита с прямолинейными краями должна иметь форму прямоугольника. Как при помощи бечевки проверить правильность формы плиты? →

• Вконтакте
• Facebook

5terka.com

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия

Определение: параллелограмм
	Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны
Определение: диагонали параллелограмма
	Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины
Определение: высота параллелограмма
	Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение
Свойство: равенство противолежащих сторон
	Если четырёхугольник является параллелограммом, то его противолежащие стороны равны
Признак: равенство противолежащих сторон
	Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом
Признак: равенство и параллельность двух противолежащих сторон
	Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом
Свойство: диагонали точкой пересечения делятся пополам
	Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам
Признак: диагонали точкой пересечения делятся пополам
	Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом
Свойство: суммы углов, прилежащих к сторонам
	Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°
Признак: суммы углов, прилежащих к сторонам
	Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом
Свойство: равенство противолежащих углов
	Если четырёхугольник является параллелограммом, то его противолежащие углы равны
Признак: равенство противолежащих углов
	Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом
Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник
	Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника
Признак: два треугольника, на которые каждая диагональ делит четырёхугольник
	Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом
Свойство: четыре треугольника, на которые диагонали делят четырёхугольник
	Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)
Признак: четыре треугольника, на которые диагонали делят четырёхугольник
	Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом

www.resolventa.ru

Ответы@Mail.Ru: Помогите

Квадрат — это прямоугольник, у которого все стороны равны. Можно дать и другое определение квадрата: Квадрат — это ромб, у которого все углы прямые. Св-ва квадрата: все углы квадрата — прямые, все стороны квадрата — равны. Диагонали квадрата равны и пересекаются под прямым углом. Диагонали квадрата делят его углы пополам. Признаки: 1. Если две смежные стороны прямоугольника равны, то этот прямоугольник является . квадратом. 2. Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом. 3. Если один из углов ромба прямой, то этот ромб является квадратом. 4. Если диагонали ромба равны, то этот ромб является квадратом. Прямоугольник — это фигура, которая имеет четыре стороны и четыре прямых угла. Прямоугольником называется параллелограмм, у которого все углы прямые. У прямоугольника противоположные стороны равны. Свойства прямоугольника: *противолежащие стороны равны; *противоположные углы равны; *диагонали точкой пересечения делятся пополам; *сумма углов, прилежащих к одной стороне, равна 180°; *сумма квадратов диагоналей равна сумме квадратов всех сторон; *диагонали равны. *величина площади прямоугольника равна произведению ширины прямоугольника на его высоту (длину). *периметр прямоугольника равен удвоенной сумме длин его ширины и высоты. 1. Если три угла четырёхугольника прямые, то этот четырёхугольник является прямоугольником. 2. Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником. 3. Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником. Четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны, называется трапецией. Параллельные стороны трапеции называются её основаниями. Стороны, которые не параллельны, называются боковыми сторонами трапеции. Есть несколько видов трапеций. Чаще всего рассматриваются прямоугольные и равнобедренные трапеции. Трапеция, у которой одна боковая сторона перпендикулярна основаниям, называется прямоугольной трапецией. Трапеция, у которой боковые стороны равны, называется равнобедренной. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360°. Свойство, которое присуще трапеции любого вида: сумма углов, прилежащих к боковой стороне, равна 180°. ромб — это параллелограмм, все стороны которого равны. Свойства ромба: Диагонали ромба перпендикулярны. Диагонали ромба делят его углы пополам. 1. Если диагонали параллелограмма перпендикулярны, то данный параллелограмм является ромбом. 2. Если две смежные стороны параллелограмма равны, то данный параллелограмм является ромбом. 3. Если диагонали параллелограмма являются биссектрисами его углов, то данный параллелограмм является ромбом. 4. Если все стороны четырёхугольника равны, то данный четырёхугольник является ромбом. Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм. Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм. Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм. В параллелограмме противоположные стороны равны и противоположные углы равны Диагонали параллелограмма точкой пересечения делятся пополам Углы, прилежащие к любой стороне, в сумме равны 180^\circ Диагонали параллелограмма делят его на два равных треугольника. сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон

touch.otvet.mail.ru

Четырехугольники

Параллелограмм
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.

Свойства и признаки параллелограмма

1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм.
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник – параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник – параллелограмм.

Свойство середин сторон четырёхугольника
Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника.

Прямоугольник
Прямоугольником называется параллелограмм с прямым углом.

Свойства и признаки прямоугольника

1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.

Квадрат
Квадратом называется прямоугольник, все стороны которого равны.

Ромб
Ромбом называется четырёхугольник, все стороны которого равны.

Свойства и признаки ромба

1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам.
3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.

Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны.

Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).

Теорема о средней линии трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.

Равнобедренная трапеция
Трапеция называется равнобедренной, если ее боковые стороны равны.

Свойства и признаки равнобедренной трапеции

1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны.
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная.
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.

www.e-ope.ee