Фигуры в объеме – 4. Объем фигур — Фигуры В Пространстве

Объемные фигуры — Классификации

Тело — связная часть пространства, ограниченная замкнутой поверхностью. Иногда телом называют только компактное множество, имеющее внутренние точки. Геометрическое тело — часть пространства, со всех сторон ограниченная. Если поверхность, ограничивающая тело, состоит из плоскостей, то тело называют многогранником. Эти плоскости пересекаются по прямым, наз. рёбрами, и образуют грани тела. Каждая из граней есть многоугольник, стороны которого суть рёбра многогранника; вершины этого многоугольника наз. вершинами многогранника. Представим себе плоскость, составляющую продолжение одной из граней. Если всё тело окажется по одну сторону этой плоскости, то такое тело называется выпуклым. Всякая прямая его пересекает не более, чем в двух точках.  Многогранник, у которого все углы равны между собой и грани, равные между собой, — правильные многоугольники, называютмя правильными. Выпуклых правильных многогранников только пять. Многогранник называется призмой (фиг. 1), если две его грани суть равные многоугольники, расположенные в параллельных плоскостях, а другие грани — параллелограммы. Параллельные грани наз. основаниями, а расстояние между ними — высотой призмы. Боковые ребра призмы всегда параллельны и равны между собой. Призма наз. прямой, если ее боковые ребра перпендикулярны к основаниям. Если же боковые ребра не перпендикулярны к основаниям, то призма наз. наклонной. Параллелепипед (фиг. 2) есть призма, основания которой суть параллелограммы. Если же эта призма прямая и основания прямоугольники, то она наз. прямоугольным параллелепипедом. Многогранник называется пирамидой (фиг. 3), если одна из его граней многоугольник (основание пирамиды), а другие грани треугольники, имеющие общую вершину (вершина пирамиды). Расстояние от вершины до основания наз. высотой пирамиды. Укажем еще следующие геометрические Т. Шар получается при вращении окружности около одного из диаметров. Все точки поверхности, ограничивающей это Т., находятся на одном и том же расстоянии от одной точки, наз. центром шара. Прямой круговой цил

www.sites.google.com

Названия геометрических фигур в картинках (23 ФОТО) ⭐ Забавник

Геометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.

 

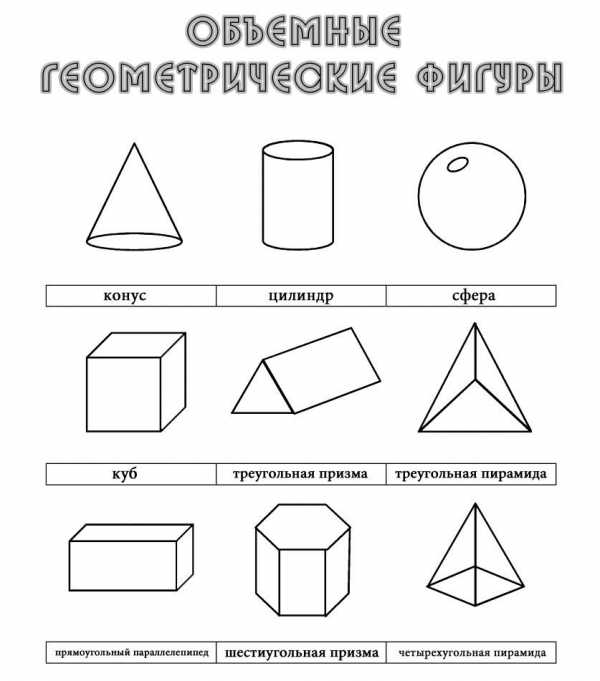
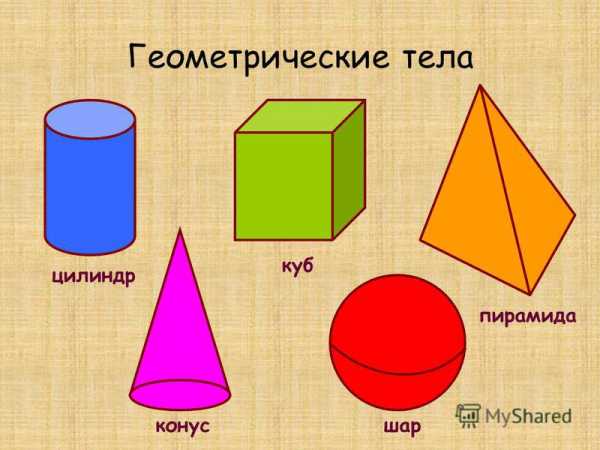
Объёмные геометрические фигуры

 

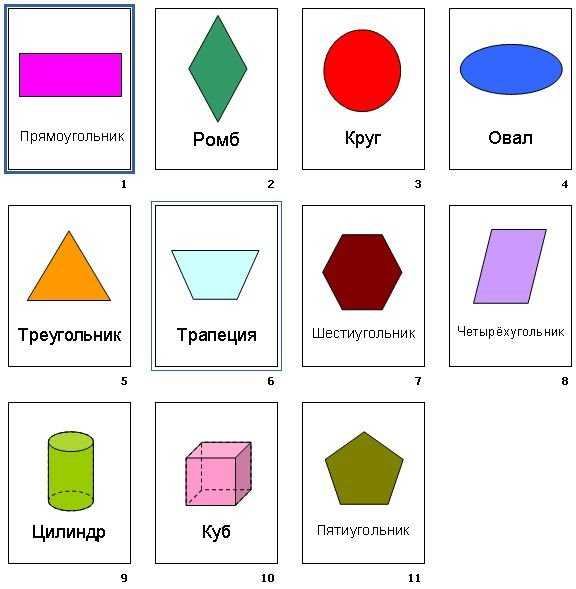
Разноцветные фигуры

 

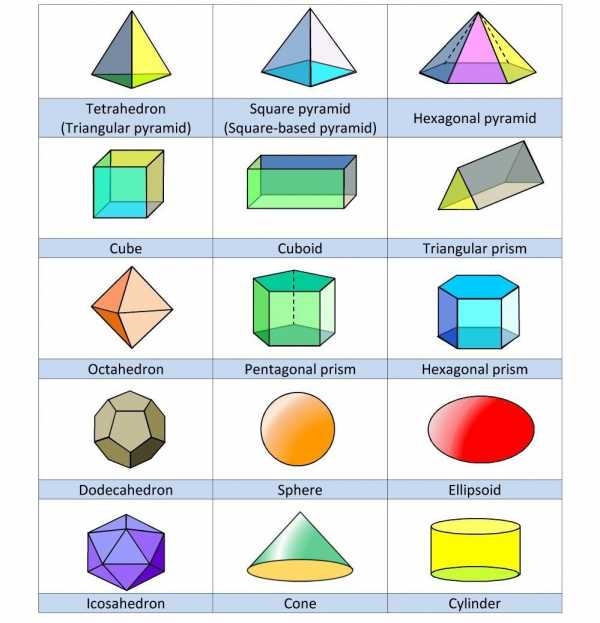
Названия объёмных фигур на английском

 

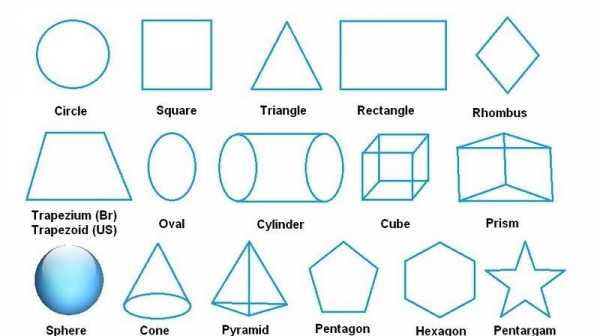
Синие фигуры с английскими названиями

 

Синие фигуры с русскими названиями

 

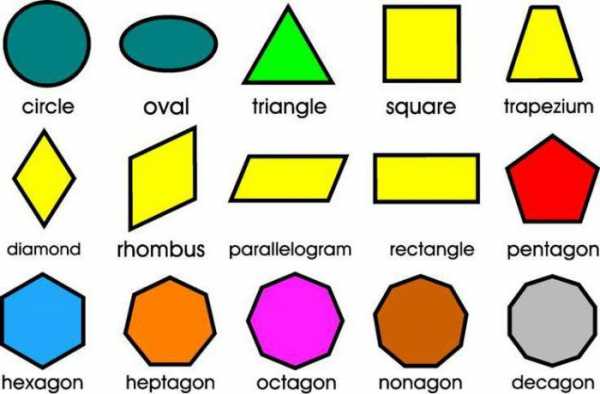
Разноцветные фигуры с английскими названиями

 

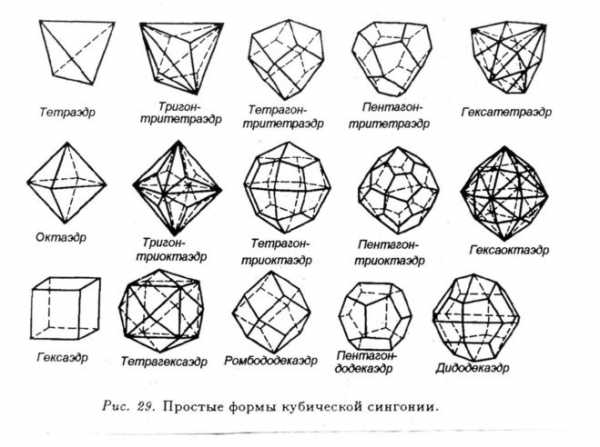
Простые фигуры кубической сингонии

 

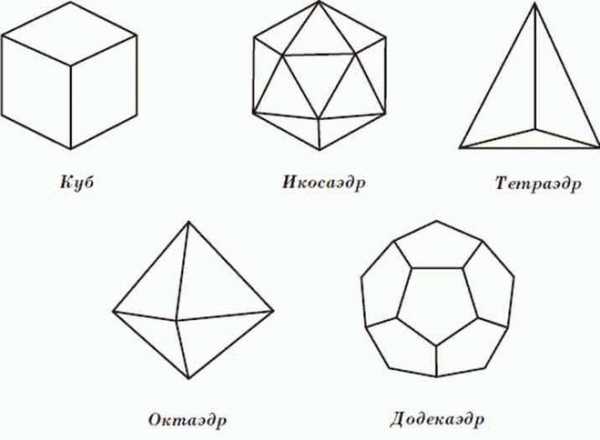
Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр

 

Весёлые геометрические фигуры

 

Shapes

 

Конус

 

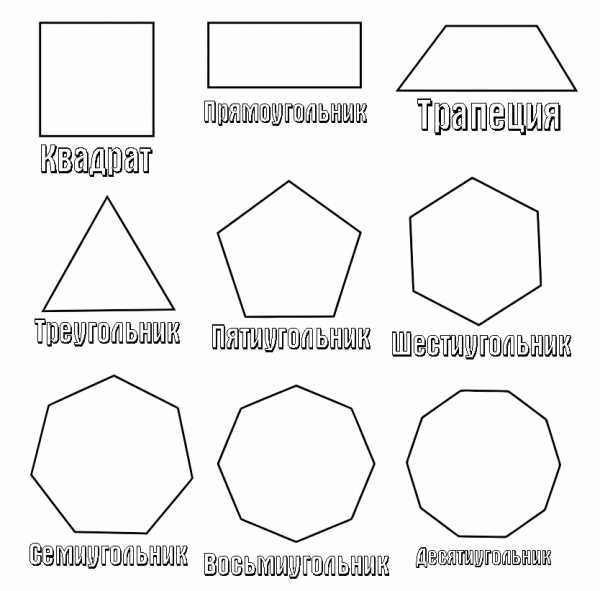
Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник

 

Ромб

 

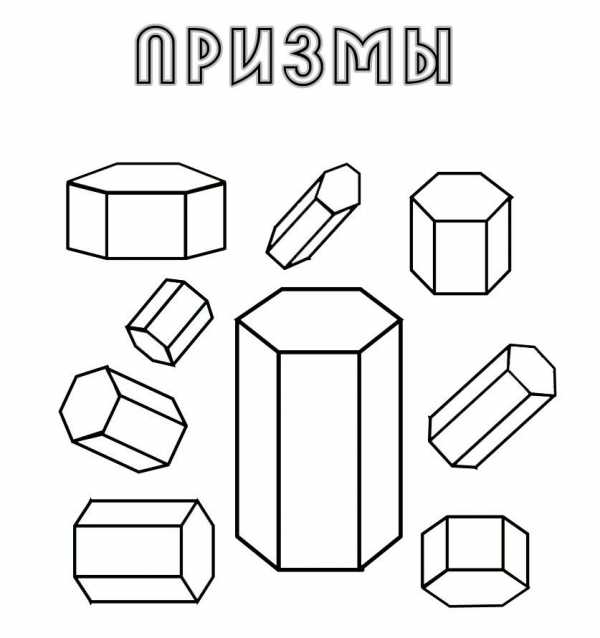
Призмы

 

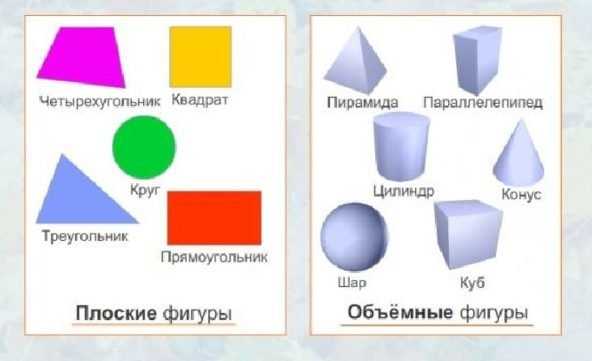
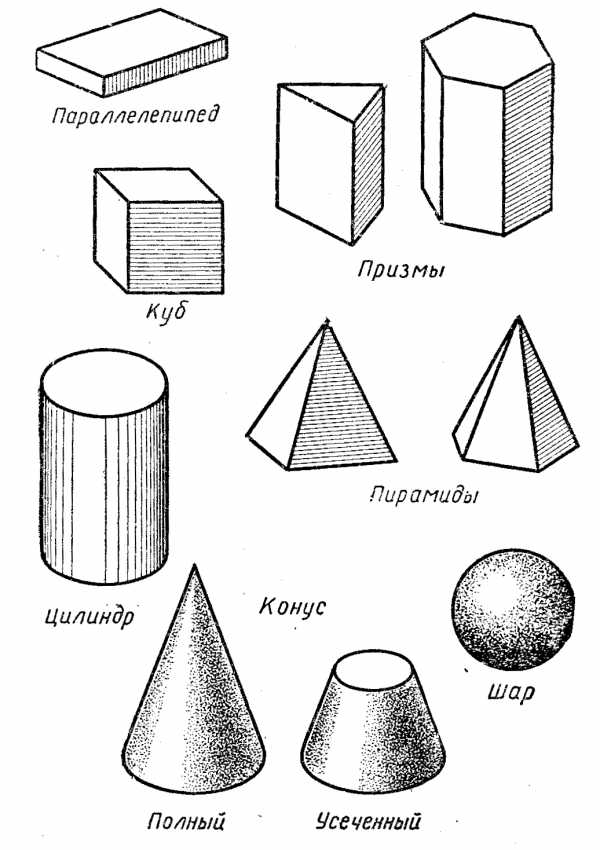
Пирамиды

 

 

 

 

Ваша оценка очень важна: Загрузка…

zabavnik.club

Как определить свой тип фигуры и как с ним жить

Почему один и тот же наряд на вашей подруге и на вас смотрится совершенно по-разному, даже если рост и вес одинаковы? Всё дело в разных типах фигуры.

Тип фигуры зависит от особенностей строения и развития костной, жировой и мышечной тканей. Большей частью он обусловлен генетикой, но может корректироваться режимом питания и физическими упражнениями.

Любой человек красив и неповторим. Тело каждого имеет свои достоинства и недостатки. Знать свой тип фигуры важно для того, чтобы эффективнее тренироваться и научится подбирать одежду так, чтобы выглядеть наиболее привлекательно.

Женские типы фигуры

По общим признакам можно выделить пять типов женской фигуры: «песочные часы», «прямоугольник», «треугольник», «перевёрнутый треугольник» и «яблоко». Чтобы определить, к какому типу принадлежите вы, достаточно вооружиться сантиметровой лентой и сделать три замера.

1. Объём груди: поверх привычного бюстгальтера без пуш-апа, по самой выступающей точке, держа сантиметр параллельно полу.
2. Объём талии: по наиболее узкой части тела (чуть выше пупка), не втягивая и не выпячивая живот.
3. Объём бёдер: по самой широкой части бёдер, держа ленту параллельно полу.

Теперь оцениваем результаты.

• Если грудь и бёдра примерно равны по объёму, а талия ощутимо меньше (на 20–30 сантиметров), то ваш тип фигуры — «песочные часы».
• Если грудь и бёдра примерно равны по объёму, а талия не сильно выделяется на их фоне, то вы — «прямоугольник».
• Если грудь меньше бёдер в объёме при видимой талии, то ваш тип фигуры — «треугольник» («груша»).
• Если грудная клетка объёмнее низа тела, а плечи внешне шире бёдер, то ваша фигура — «перевёрнутый треугольник» (Т-образная фигура).
• Если больше всего выделяется талия, живот и грудная клетка, а ноги стройные, то ваш тип фигуры — «круг» («яблоко»).

Uaua.info

Песочные часы

Пресловутые 90/60/90 — про этот тип фигуры. Такие дамы могут гордиться хорошо выраженной талией и выделяющимися плечами и бёдрами. Причём такие пропорции сохранятся даже при наборе веса, что не может не радовать.

X-образный силуэт женского тела является негласным идеалом, воспеваемым со времён Античности. Если вы счастливая обладательница подобного типа фигуры, обрадуем. Главное в вашем случае — не нарушать гармоничные пропорции груди, талии и бёдер.

Основная задача

Подчеркнуть изгибы фигуры, сохраняя гармонию верха и низа.

Подойдёт

Практически всё. Наиболее выгодно подчеркнут фигуру:

• Приталенные силуэты.
• Блузки, пальто и плащи с запáхом и поясами.
• V-образный или круглый вырез на кофточках и платьях.
• Юбка-карандаш, трапеция или солнышко.
• Джинсы и брюки с высокой посадкой.
• Пояс на талию в качестве аксессуара.

Не подойдёт

• Мешковатая одежда, скрывающая силуэт.
• Верхняя одежда прямого покроя.
• Платья или блузки с завышенной или заниженной талией.
• Джинсы или брюки с низкой посадкой.

Обладательницы фигуры «песочные часы»: Софи Лорен, Элизабет Тейлор, Дита фон Тиз, Ким Кардашьян

Прямоугольник

Женщины с подобным типом фигуры обладают равными по объёму грудью и бёдрами, а талия у них выражена слабо или не выражена совсем (например, если при объёме груди в 92 сантиметра талия больше 70 сантиметров).

Такое телосложение более атлетично и спортивно, чем, например, «песочные часы», а недостаточный изгиб талии можно визуально увеличить. Для того, чтобы подчеркнуть особенности подобной фигуры, надо всего лишь сохранить гармонию плеч и бёдер, визуально сузив талию. Этого эффекта можно добиться, создав дополнительный объём в другой части тела.

Основная задача

Сделать акцент на талии и красивых ногах, сохранив равновесие верхней и нижней частей тела.

Подойдёт

• Приталенная верхняя одежда, пальто с поясом.
• Топы на тонких лямках, кофточки с рукавами фонариком.
• Пиджаки или верхняя одежда с прямой линией плеч.
• Платья без лямок или с запáхом.
• Юбка-трапеция, солнышко или с разрезом.
• Облегающие брюки или джинсы со средней или низкой посадкой.
• Классические прямые брюки или капри.

Не подойдёт

• Мешковатая или oversized-одежда.
• Одежда, чрезмерно открывающая область живота.
• Прямые фасоны верхней одежды или платья.
• Майки, топы без рукавов или с вырезом под горло, водолазки.
• Легинсы, юбки-карандаш.

Звёзды с «прямоугольной» фигурой: Николь Кидман, Кира Найтли, Кэмерон Диаз, Анна Курникова

Треугольник (груша)

Обладательницы такого телосложения могут гордиться своими изящными узкими плечами и талией, а также аппетитными бёдрами. Стоит учесть, что с такими параметрами изнурять себя строгими диетами, пытаясь сделать пятую точку меньше, чем она может быть, бессмысленно.

Тип фигуры «груша» сохраняется при модельном и при избыточном весе. Лучше больше внимания привлечь к красивым шее, ключицам и рукам, что легко можно сделать с помощью подходящей одежды.

Основная задача

Уравновесить бёдра акцентом на верхнюю часть тела.

Подойдёт

• Приталенная верхняя одежда, пальто-трапеция.
• Любая приталенная одежда с накладными плечами (пальто, пиджаки, жакеты).
• Блузки, топы и майки с открытыми плечами, без рукавов или с широким вырезом.
• Юбка-трапеция или карандаш.
• Тёмные брюки или джинсы прямого покроя.
• Брюки или джинсы, расширяющиеся книзу.

Не подойдёт

• Мешковатая верхняя одежда, длинные пальто прямого покроя.
• Топы или блузки с вырезом под горло, водолазки.
• Яркие массивные ремни на бёдра.
• Облегающие брюки или брюки-дудочки, особенно светлых цветов или с ярким принтом.
• Брюки или джинсы с декоративными элементами на карманах или поясе, пышные юбки, юбки клёш.
• Брюки или юбки с большим количеством утяжеляющих элементов: кружева, рюши, складки.

Знаменитости с типом фигуры «груша»: Рианна, Бейонсе, Дженнифер Лопес, Дженнифер Лав Хьюитт

Перевёрнутый треугольник (Т-образная фигура)

Для такого типа телосложения характерны широкие плечи и относительно узкие бёдра (например, по 95 и 90 сантиметров соответственно). Зачастую у обладательниц этой фигуры ноги длиннее и стройнее остальных женщин, с чем их можно поздравить.

Чтобы добавить больше гармонии «перевёрнутому треугольнику», воспользуемся ухищрениями стилистов. С помощью подходящей одежды визуально уменьшим плечи, увеличим бёдра и подчеркнём талию. Для этого больше всего подойдёт прямой покрой, минимальное количество деталей в районе груди, максимальное — на бёдрах.

Основная задача

Уравновесить верх и низ, не забыв о талии.

Подойдёт

• Пальто-трапеция.
• Квадратные, V- или U-образные вырезы на платьях, топах или блузках.
• Брюки или джинсы с низкой посадкой.
• Платья или топы с баской (оборкой ниже уровня талии).
• Широкие массивные ремни на бёдра.
• Юбки-трапеции, с запáхом, со складками или объёмными карманами.

Не подойдёт

• Длинные прямые пальто, мешковатая верхняя одежда.
• Топы или кофточки с широким вырезом лодочкой.
• Яркие объёмные свитеры или джемперы.
• Одежда с накладными плечами.
• Блузы или пиджаки с пышными рукавами.
• Тёмные прямые брюки или джинсы, легинсы.
• Юбка-карандаш или с длиной до лодыжек.

Знаменитые «перевёрнутые треугольники»: Анджелина Джоли, Деми Мур, Кэтрин Макфи, Кэйт Босуорт

Круг (яблоко)

У обладательниц этого типа фигуры прямой силуэт без выраженной талии, но с выдающейся грудью. Основная часть объёма фигуры находится в верхней части тела (зато ноги дольше всех остаются стройными).

Женщинам-«яблочкам» стоит внимательно следить за лишним весом: он имеет тенденцию откладываться на животе.

Основные задачи

Визуально вытянуть фигуру, обозначить талию и подчеркнуть красивые декольте и ноги.

Подойдёт

• Пальто-трапеция, верхняя одежда с А-силуэтом (узкая в груди и расширяющаяся книзу).
• Блузки или топы с V-образным вырезом.
• Платья с А-силуэтом или запáхом.
• Брюки и джинсы клёш с объёмными карманами.
• Одежда с крупными деталями (оборки, узоры, драпировки) ниже линии бёдер.
• Однотонная одежда с вертикальными вытачками.

Не подойдёт

• Сильно обтягивающая или мешковатая одежда.
• Топы и блузки без рукавов, с вырезом под горло или завязками через шею.
• Водолазки, короткие топы.
• Одежда с ярким принтом, оборками, декоративными элементами на плечах и животе.
• Узкие брюки, брюки и джинсы без карманов или с низкой посадкой.
• Обтягивающие юбки, юбка-карандаш.

Популярные «яблоки»: Кэтрин Зета-Джонс, Бритни Спирс, Джессика Джонс, Эми Шумер

Любая фигура красива и привлекательна, особенно если выгодно её подчеркнуть. А как одеваетесь вы, чтобы выглядеть ещё лучше?

lifehacker.ru

Объемные фигуры из бумаги, схемы. Как сделать объемные геометрические фигуры

Лучший способ показать малышу окружающий мир — дать почувствовать его на ощупь, ведь маленькую кроху хлебом не корми — дай дотронуться до заинтересовавших ее предметов, тем более, если это разноцветные геометрические тела оригами, сделанные своими руками.

60 274 т.

Яркие объемные поделки из бумаги привлекут внимание ребенка и уж точно не дадут скучать. А Вы незаметно и с задором проведете горячо любимое чадо в мир занимательной геометрии.

Не знаю, как Вам, дорогие читатели, а мне эти красочные оригами напомнили драгоценные камни . Так почему бы о каждом из них не рассказать малышу что-нибудь интересное, сравнивая очередное геометрическое тело с рубином, сапфиром, турмалином и так далее?

А пока на цветных листах распечатайте схемы поделок и, сделав необходимые изгибы, и склейте в нужных местах. Уверен, у Вас все получится!

Тетраэдр

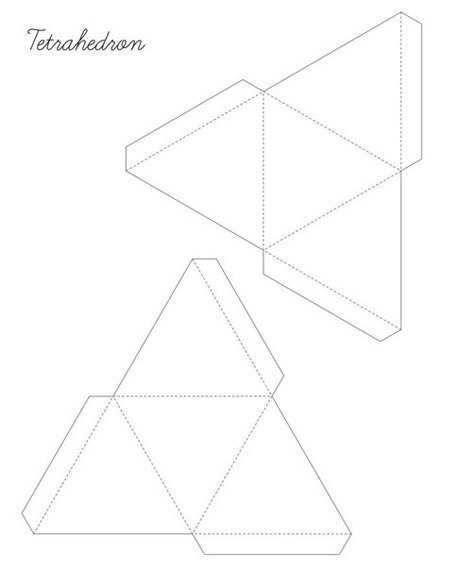
Октаэдр

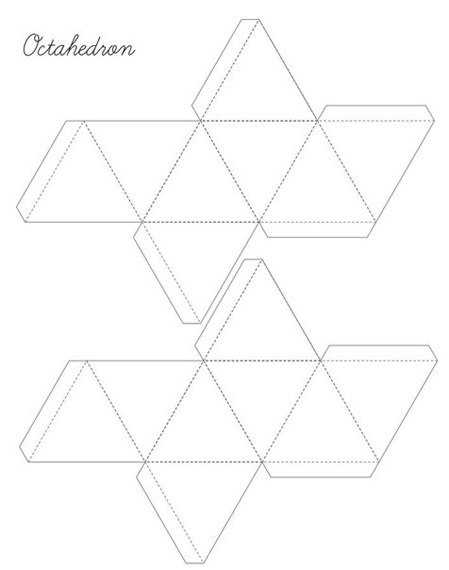
Икосаэдр

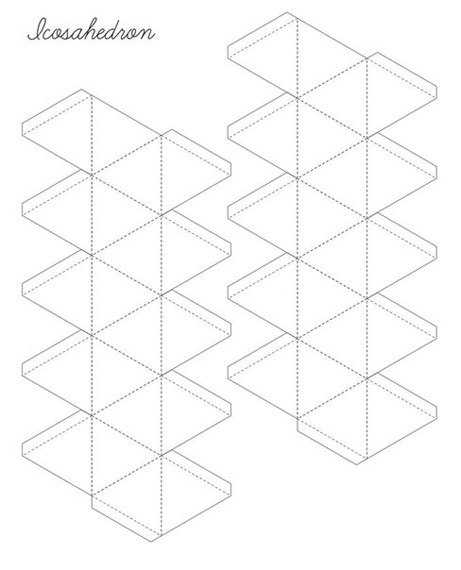
Додекаэдр

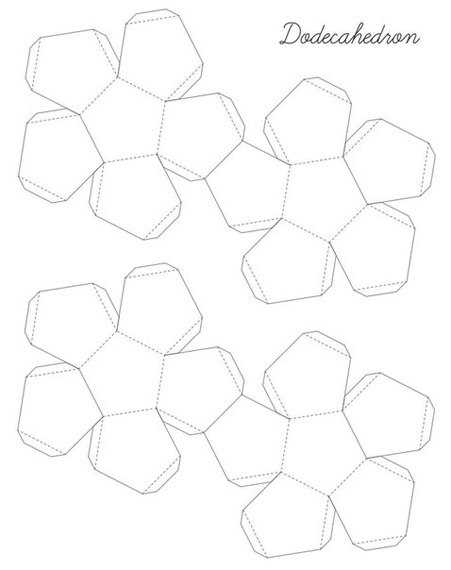
Куб

У Вас должны получиться вот такие заготовки:

А это уже готовые камешки-многогранники. Дерзайте!

Веселых игр, занимательных историй и всестороннего развития Вашему малышу!

Заметили орфографическую ошибку? Выделите её мышкой и нажмите Ctrl+Enter

pustunchik.ua

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

 

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

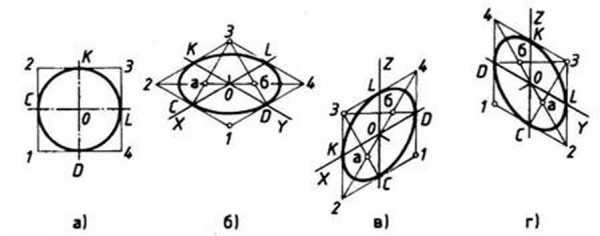
Рис. 112. Прямоугольная и изометрические проекции круга

 

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

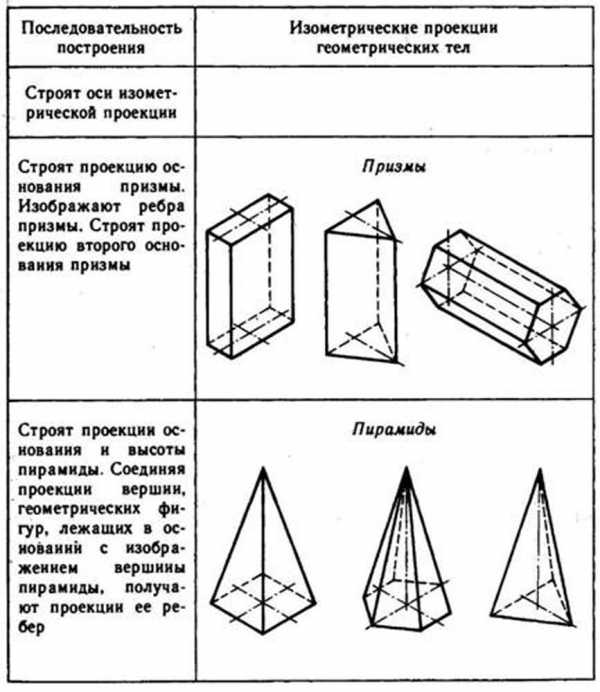
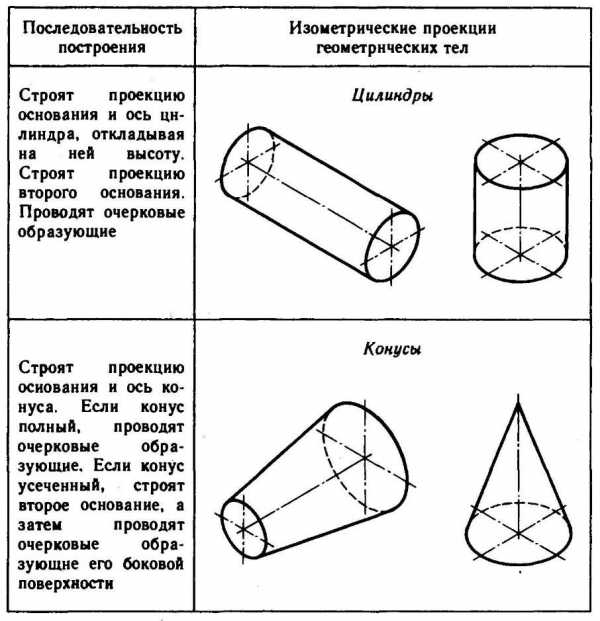
Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1)   построение осей изометрической проекции;

2)      построение изометрической проекции формообразующей грани;

3)    построение проекций остальных граней посредством изо­бражения ребер модели;

 

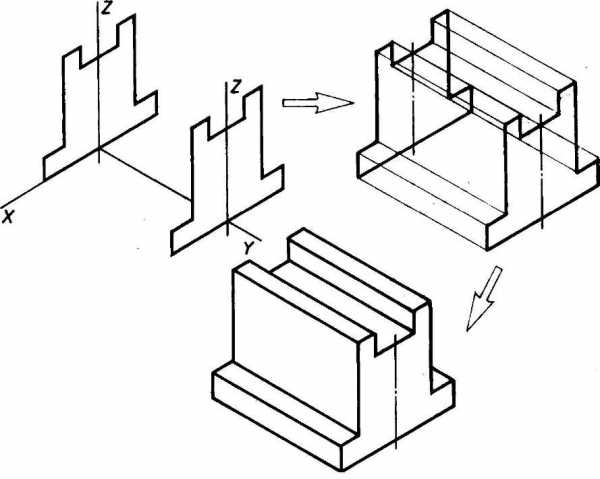
Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

 

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

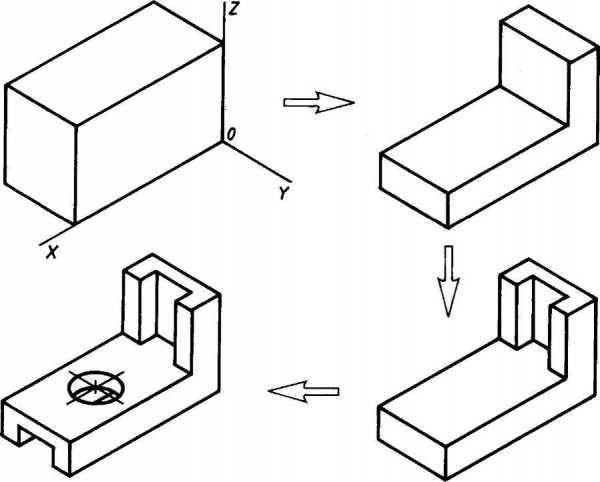
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

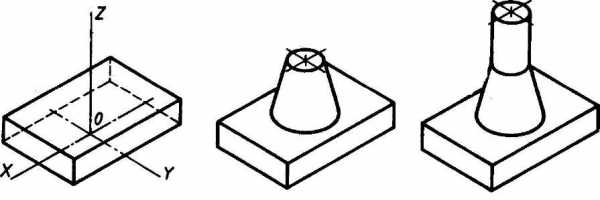
Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

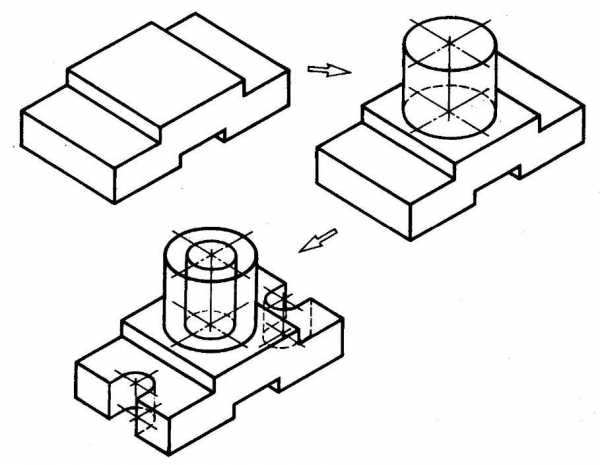
Рис. 116. Использование комбинированного способа построения изометрической проекции детали

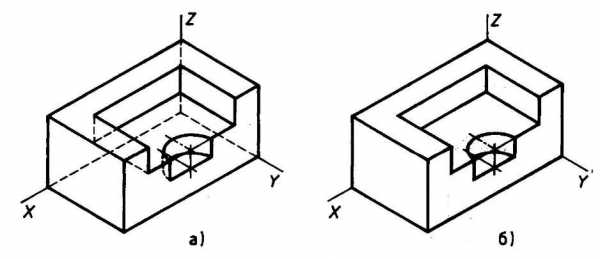
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

cherch.ru

шар, куб, пирамида, призма, тетраэдр

Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

1. Они ортогональны друг другу, то есть перпендикулярны.
2. Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
3. Любая из осей координат — это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

1. Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
2. Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

1. Наличие определенного объема, который фигура занимает в пространстве.
2. Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.

Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.

Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a³ и S = 6*a², соответственно.

Фигура пирамида

Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.

Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.

Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a²*h/3 и S = 2*a*√(h²+a²/4) + a², соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a^3*√2/12 и S = √3*a², где a — длина стороны равностороннего треугольника.

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH₄, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.

Призма — это полиэдр, поэтому для нее верна теорема Эйлера. Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a²*h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).

Фигура шар

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.

Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. Площадь поверхности сферы, ограничивающей шар, находится по формуле: S = 4*pi*r², а объем шара можно вычислить по формуле: V = 4*pi*r³/3, где pi — число пи (3,14), r — радиус сферы (шара).

fb.ru

Картинки и названия объемных геометрических фигур

Картинки и названия объемных геометрических фигур

Рубрики Геометрия

 

 

  Геометрическая фигура: круглый дурак в квадрате.

 

 

 

 

 

Первые геометрические понятия возникли в доисторические времена. Различные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако исследователи не только пассивно наблюдали природу, но и практически осваивали и использовали ее богатства. Практическая деятельность человека служила основой открытия простейших геометрических зависимостей и соотношений.

Очертания фигур и все возможные действия с ними изучают математические науки геометрия (изучает плоские фигуры) и стереометрия (предмет изучения — объемные фигуры)

Давайте посмотрим какие бывают виды объемных геометрических фигур, какие они имеют названия, а так же поглядим как они выглядят на картинках.

Виды и названия геометрических фигур 3D

Все 3D тела делятся на многогранники и тела вращения.

Тела вращения — это объёмные фигуры, которые возникают следствием вращения плоской геометрической
фигуры, которая ограничена кривой, вокруг оси. Эта ось лежит в той же плоскости.

Если вращать контуры геометрического тела, образуется поверхность вращения (к примеру, сфера, которая
образовывается из окружности), а если вращать заполненные контуры – возникают тела (шар, который
образован из круга).

Многогранник или полиэдр — зачастую замкнутая  объемная поверхность, состоящая из многоугольников.
Многогранник – 3D фигура, у которого граница, это объединение ограниченного количества многоугольников.

Изображения объемных правильных многогранников

1. Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

   Правильный тетраэдр

2. Гексаэдр(куб) — правильный многогранник (шестигранный), каждая грань которого представляет собой квадрат.

   Изображение куба

3. Октаэдр  — многогранник с восемью гранями; грани правильного октаэдра — восемь равносторонних треугольников.

   Изображение октаэдра

 

 

 

Изображения тел вращения

1. Цилиндр — это тело вращения, которое может быть получено путем вращения прямоугольника вокруг одной из его сторон, как оси.

   3D тело вращения: цилиндр

2. Конус — это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его кате­тов, как оси.

   Тела вращения :конус

3. Шар — это тело вращения, которое может быть получено путем вращения половины круга вокруг его диаметра, как оси

   Тела вращения :шар

Комментирование и размещение ссылок запрещено.

df-dt.com