Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2R
O — центр круга
π ≈ 3.14
Формула для определения длины радиуса, если известна площадь круга :
Формула для определения длины радиуса, если известна длина окружности :
R — радиус окружности (круга)
h — высота сегмента
L — длина хорды
O — центр круга
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
Сегмент — часть круга ABC, отсеченная хордой AC
h — высота сегмента ABC
L — хорда AC
R — радиус кружности
O — центр окружности
α — центральный угол AOC
Формула высоты через радиус и центральный угол, (h):
Формула высоты через хорду и центральный угол, (h):
Формула высоты через радиус и хорду, (h):
Дополнительные формулы для окружности:
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
Формула длины хорды, (L):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
www-formula.ru
Окружность. Длина окружности. Касательная, дуга
Общие определения
Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.
Для любой точки L, лежащей на окружности, действует равенство OL=R. (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой.
Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D). Диаметр можно вычислить по формуле: D=2R
Длина окружности вычисляется по формуле: C=2\pi R
Площадь круга: S=\pi R^{2}
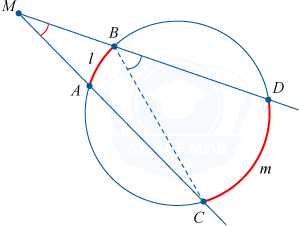
Дугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD стягивает две дуги: CMD и CLD. Одинаковые хорды стягивают одинаковые дуги.
Центральным углом называется такой угол, который находится между двух радиусов.
Длину дуги можно найти по формуле:
- Используя градусную меру: CD = \frac{\pi R \alpha ^{\circ}}{180^{\circ}}
- Используя радианную меру: CD = \alpha R
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N, то произведения отрезков хорд, разделенные точкой N, равны между собой.
AN\cdot NB = CN \cdot ND

Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.

Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB

Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
AC^{2} = CD \cdot BC

Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC \cdot BC = EC \cdot DC

Углы в окружности
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
\angle COD = \cup CD = \alpha ^{\circ}
Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
\angle AOB = 2 \angle ADB
Опирающийся на диаметр, вписанный угол, прямой.
\angle CBD = \angle CED = \angle CAD = 90^ {\circ}
Вписанные углы, которые опираются на одну дугу, тождественны.
\angle ADB = \angle AEB = \angle AFB

Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ {\circ}.
\angle ADB + \angle AKB = 180^ {\circ}
\angle ADB = \angle AEB = \angle AFB

На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.

Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left ( \cup DmC + \cup AlB \right )

Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left ( \cup DmC — \cup AlB \right )
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
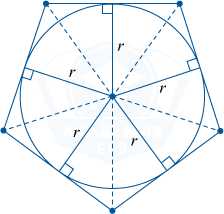
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr,
где:
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC

В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.

Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p},
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.
В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.
Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3-мя вершинами многоугольника.
Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^{ \circ}.
\angle A + \angle C = \angle B + \angle D = 180^ {\circ}

Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.

Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
где:
a, b, c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD

academyege.ru
Найти длину радиуса окружности (круга), все основные формулы.
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии
R — радиус окружности (круга)
D — диаметр, D = 2R
O — центр круга
π ≈ 3.14
Формула для определения длины радиуса, если известна площадь круга :
Формула для определения длины радиуса, если известна длина окружности :
R — радиус окружности (круга)
h — высота сегмента
L — длина хорды
O — центр круга
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
- Подробности
- Автор: Сергей Кондратов
www-formula.ru
Формулы круга и окружности
Понятие окружности и круга
Перед тем, как ввести основные формулы для окружности и круга, введем, непосредственно понятия окружности и круга, и связанные с ними определения.
Определение 1
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Определение 2
Центром окружности будем называть точку, которая задается в рамках определения 1.
Определение 3
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
Определение 4
Кругом будем называть часть плоскости, которая имеет своей границей окружность.
Длина окружности
Будем выводить длину произвольной окружности $C$ с помощью её радиуса, равного $τ$.
Будем рассматривать две произвольные окружности. Обозначим их длины через $C$ и $C’$, у которых радиусы равняются $τ$ и $τ’$. Будем вписывать в эти окружности правильные $n$-угольники, периметры которых равняются $ρ$ и $ρ’$, длины сторон которых равняются $α$ и $α’$, соответственно. Как мы знаем, сторона вписанного в окружность правильного $n$ – угольника равняется
$α=2τsin \frac{180^0}{n}$
Тогда, будем получать, что
$ρ=nα=2nτsin \frac{180^0}{n}$
$ρ’=nα’=2nτ’sin \frac{180^0}{n}$
Значит
$\frac{ρ}{ρ’}=\frac{2nτsin \frac{180^0}{n}}{2nτ’sin \frac{180^0}{n}}=\frac{2τ}{2τ’}$
Получаем, что отношение $\frac{ρ}{ρ’}=\frac{2τ}{2τ’}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
$\lim_{n→∞}(\frac{ρ}{ρ’})=\frac{2τ}{2τ’}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$\lim_{n→∞}(\frac{ρ}{ρ’})=\frac{C}{C’}$
Из последних двух равенств получим, что
$\frac{C}{C’}=\frac{2τ}{2τ’}$
То есть
$\frac{C}{2τ}=\frac{C’}{2τ’}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$\frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$\frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
$C=2πτ$
Площадь круга
Будем выводить площадь $S$ произвольного круга с помощью радиуса окружности, ограничивающей его, равного $τ$.
Впишем в такую окружность правильный $n$-угольник, площадь которого равняется $S_n$. В такой многоугольник впишем окружность, площадь которого равняется $S’_n$ (рис. 2).
Будет очевидна верность неравенства
$S >S_n >S’_n$
Используем формулу, которая связывает радиусы вписанной и описанной окружностей для правильного многоугольника:
$τ=Rcos \frac{180^0}{n}$
Если неограниченно увеличивать число сторон в таком правильном многоугольнике (то есть взять $n→∞$), то получим, что
$cos \frac{180^0}{n}→1$, $τ→R$
Тогда будет выполняться
$S→S’_n$, $S→S_n$
Также
$P_n→2πτ$
По формуле, площадь такого многоугольника равняется $S_n=\frac{1}{2} P_n τ$, следовательно
$S=S_n=\frac{1}{2}\cdot 2πτ\cdot τ=πτ^2$
То есть, для нахождения площади круга, нужно пользоваться формулой
$S=πτ^2$
Пример задачи
Пример 1
Найти длину окружности и площадь круга, который вписан в квадрат со стороной, равной $α$.
Решение.
Пусть нам дан квадрат $ABCD$, в который вписана окружность с центром $O$. Изобразим рисунок по условию задачи (рис. 3).
Очевидно, что центр окружности будет совпадать с центром квадрата, в которой она вписана. Так как квадрат описан вокруг окружности, то его стороны будут касательными к ней, то есть радиус, проведенный, к примеру, к стороне $AB$ будет перпендикулярен к ней. Значит, диаметр окружности равняется стороне квадрата. То есть
$τ=\frac{α}{2}$
По формуле длины окружности, получим, что
$C=2π\cdot \frac{α}{2}=πα$
По формуле площади круга, получим, что
$S=π(\frac{α}{2})^2=\frac{πα}{4}$
Ответ: $C=πα$, $S=\frac{πα}{4}$.
spravochnick.ru
Круг и окружность | Формулы и расчеты онлайн
Геометрическим местом точек называется совокупность всех точек, удовлетворяющих заданным условиям. Окружность есть геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). Равные отрезки, соединяющие центр с точками окружности, называются радиусами и обозначаются буквами r или R. Дуга — это часть окружности. Секущая — это прямая проходящая через две точки окружности. Хорда — это отрезок секущей, лежащий внутри окружности. С приближением к центру хорда увеличивается.
Окружность и радиус | Окружность и дуга окружности | Окружность и секущая |
Диаметр — это хорда проходящая через центр окружности (обозначается d или D). Диаметр равен двум радиусам:
\[d=2r\]
Круг есть часть плоскости, лежащая внутри окружности. Касательная — это прямая пересекающаяся окружность только в одной точке. Касательная это выродившаяся секущая. Касательная к окружности перпендикулярна радиусу проведенному в точку касания. Из одной точки вне круга можно провести к окружности две касательные. Их длины будут равны.
Окружность и касательная | Сегмент окружности | Сектор окружности |
Сегмент — это часть круга, ограниченная дугой и стягивающей ее хордой. Стрелка дуги — это перпендикуляр восстановленный из середины хорды до пересечения с дугой. Высота сегмента — это длина стрелки дуги. Сектор — это часть круга, ограниченная дугой и двумя радиусами, проведенными к концам дуги. Квадрант — это сектор, отсекаемый радиусами, образующими угол 90°.
В помощь студенту
Круг и окружность |
стр. 240 |
|---|
www.fxyz.ru
Внеклассный урок — Окружность
Окружность
Окружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки.
Основные понятия:
Центр окружности – это точка, равноудаленная от точек окружности.
Радиус – это расстояние от точек окружности до ее центра (равен половине диаметра, рис.1).
Диаметр – это хорда, проходящая через центр окружности (рис.1).
Хорда – это отрезок, соединяющий две точки окружности (рис.1).
Касательная – это прямая, имеющая только одну общую точку с окружностью. Проходит через точку окружности перпендикулярно диаметру, проведенному в эту точку (рис.1).
Секущая – это прямая, проходящая через две различные точки окружности (рис.1).
Единичная окружность – это окружность, радиус которой равен единице.
Дуга окружности – это часть окружности, разделенная двумя несовпадающими точками окружности.
1 радиан – это угол, образуемый дугой окружности, равной длине радиуса (рис.4).
1 радиан = 180˚ : π ≈ 57,3˚
Центральный угол – это угол с вершиной в центре окружности. Равен градусной мере дуги, на которую опирается (рис.2).
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Равен половине градусной меры дуги, на которую опирается (рис.3).
Две окружности, имеющие общий центр, называются концентрическими.
Две окружности, пересекающиеся под прямым углом, называются ортогональными.
Длина окружности и площадь круга:
Обозначения:
Длина окружности – C
Длина диаметра – d
Длина радиуса – r
Значение π:
Отношение длины окружности к длине ее диаметра обозначается греческой буквой π (пи).
π = 3,1416
Или:
π = 3,14
Или:
22
π = —
7
Формула длины окружности:
C = πd, или C = 2πr
Формулы площади круга:
S = πr2
C · r
S = ——
2
π · D2
S = ———
4
Площадь кругового сектора и кругового сегмента.
Круговой сектор – это часть круга, лежащая внутри соответствующего центрального угла. πR2 где π – постоянная величина, равная 3,1416; R – радиус круга; α – градусная мера соответствующего центрального угла. Круговой сегмент – это общая часть круга и полуплоскости. πR2 где α – градусная мера центрального угла, который содержит дугу этого кругового сегмента; SΔ — площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор. Знак «минус» надо брать, когда α < 180˚, а знак «плюс» надо брать, когда α > 180˚. |
Уравнение окружности в декартовых координатах x, y c центром в точке (a;b):
(x – a)2 + (y – b)2 = R2
Окружность, описанная около треугольника (рис.4).
Если от середины каждой из сторон треугольника провести перпендикуляры, то точка их пересечения будет центром окружности, описанной около этого треугольника.
|
Окружность, вписанная в треугольник (рис.5).
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис этого треугольника. |
Углы, вписанные в окружность (рис.3).
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.
Угол, вписанный в окружность, равен половине соответствующего центрального угла. |
Основные понятия:
Угол делит плоскость на две части. Каждая из этих частей называется плоским углом.
Плоские углы с общими сторонами называются дополнительными.
Плоский угол с вершиной в центре окружности называется центральным углом (рис.2)
Пропорциональность отрезков хорд и секущих окружности.
Если хорды AB и CD окружности пересекаются в точке S, то AS · BS = CS · DS. (рис.6) |
Если из точки P к окружности проведены две секущие, пересекающие окружность соответственно в точках A, B и C, D, то AP · BP = CP · DP (рис.7) |
Частные случаи и формулы:
1) Из точки C, находящейся вне окружности, проведем касательную к окружности и обозначим точку их соприкосновения буквой D.
Затем из той же точки C проведем секущую и точки пересечения секущей и окружности обозначим буквами А и B (рис.8).
В этом случае:
CD2 = AC · BC
2) Проведем в окружности диаметр AB. Затем из точки C, находящейся на окружности, проведем перпендикуляр к этому диаметру и обозначим получившийся отрезок CD (рис.9).
В этом случае:
CD2 = AD · BD.
raal100.narod.ru
Формулы для длины окружности и площади круга и пример их использования
Окружность и круг — две совершенные плоские фигуры, свойства которых изучают в обязательном порядке в любом школьном курсе геометрии. В этой статье мы рассмотрим, как находить длину окружности и площадь круга, используя простые математические формулы.
В чем разница между окружностью и кругом?
Прежде чем переходить к рассмотрению формул длины окружности и площади круга, следует привести определения этих фигур.
В геометрии под окружностью понимают совокупность точек на плоскости, которые находятся от фиксированной точки на одинаковом расстоянии R. В свою очередь, круг — это набор точек плоскости, которые от заданной точки расположены на расстояниях, равных или меньших, чем некоторое число R. Иными словами, окружность представляет собой одну единственную кривую линию, а круг занимает некоторую площадь. Окружность — это «обод» круга.
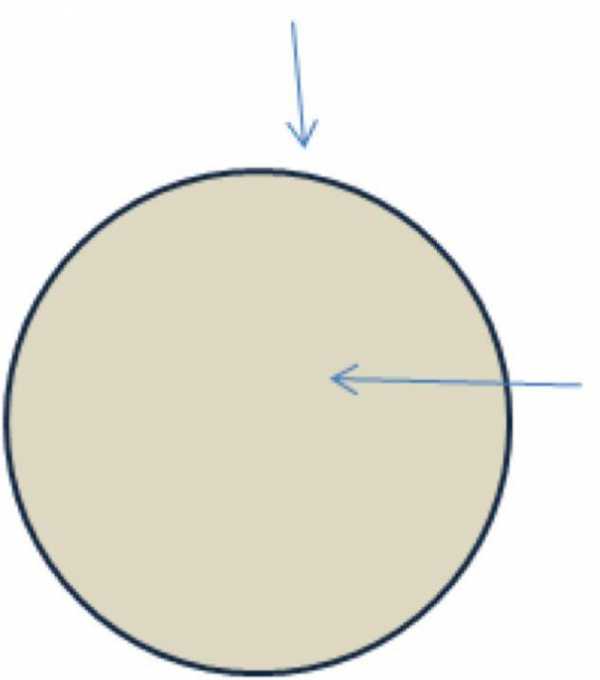
Именно поэтому, вопрос, как находить площадь окружности, считается некорректно поставленным. Окружность (единственная линия) не имеет площади, однако имеет длину. Для круга же разговор о площади имеет смысл, кроме того, также можно говорить и о длине окружности, которая его ограничивает.
Основные свойства рассматриваемых фигур
Окружность и круг обладают рядом общих характеристик, которые кратко перечислим ниже:
- Они имеют радиус R (длина отрезка, соединяющего центр фигуры с ее краем).
- Если провести через них такой отрезок, который пройдет через центр и соединит два края фигуры, то он будет равен 2 * R и называется диаметром (D).
- Любая ось, проходящая через диаметр, делит фигуру на две равные части.
- Поворот на произвольный угол круга или окружности вокруг оси, проходящей через его/ее центр и перпендикулярной плоскости фигуры, является операцией симметрии.
Формулы для длины окружности и площади круга
Познакомившись с понятием и основными свойствами рассматриваемых плоских фигур, можно перейти к количественному определению их размеров. Длина окружности и площадь круга вычисляются по следующим двум формулам:
1. L = 2 * π * R.
2. S = π * R²
Из этих формул следует, что величина R — радиус — полностью характеризует свойства обеих фигур. Величина L измеряется в метрах (~R), а S — в метрах квадратных (~R²).
В формулах символ π представляет некоторую константу, которая является иррациональным числом (ее нельзя вычислить точно). С точностью до 4 знаков после запятой число π равно 3,1416. Отметим, что при выполнении расчетов эта константа может быть заменена дробью 201/64. Если вычислить значение этой дроби, то получится число 3,1406, которое всего на 0,03 % отличается от истинной константы.
Заметим, что формула для длины окружности справедлива также для определения аналогичной характеристики круга.
Указанные формулы могут быть переписаны через диаметр, учитывая, что D = 2 * R, получаем:
1) L = π * D;
2) S = π * D²/4.

Использование рассмотренных формул для решения задачи
Формулы для площади круга и длины окружности используем для решения задач. Например, у Маши имеется кусок ткани прямоугольной формы, размеры которой равны 5 x 4 метра. Необходимо определить, какого максимального размера круг она сможет вырезать из этой ткани.
Смысл этой задачи состоит в определении размера круга, вписанного в четырехугольник. Эта ситуация изображена на рисунке ниже.
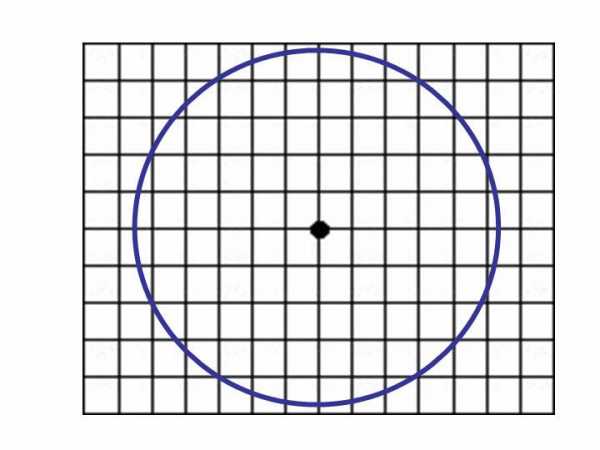
Из рисунка можно заметить, что диаметр вписанного круга D будет равен длине наименьшей стороны четырехугольника, в данном случае D = 4 метра. Зная диаметр, можно непосредственно применить формулы, которые записаны для длины и площади этой фигуры в предыдущем пункте статьи. Имеем:
1. L = π * D = 3,1416 * 4 = 12,5664 м.
2. S = π * D²/4 = 3,1416 * 4²/4 = 12,5664 м².
Мы получили любопытный результат: площадь круга равна точно такой же величине, что и длина его окружности, но единицы измерения являются разными для них. Этот результат является простым совпадением, поскольку D=4 — это единственное число, для которого абсолютные значения L и S равны.
fb.ru
