Формула фишера критерия – 6.1.3 F — критерий Фишера

6.1.3 F — критерий Фишера

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух независимых выборок. Для вычисления F_эмп нуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фи­шера такова:

                                                                                                  (8)

где — дисперсии первой и второй выборки соответственно.

Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F_эмп всегда будет больше или равно единице.

Чис­ло степеней свободы определяется также просто:

k₁

=n_l — 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k₂=n₂ — 1 для второй выборки.

В Приложе­нии 1 критические значения критерия Фишера находятся по величинам k₁ (верхняя строчка таблицы) и k₂ (левый столбец таблицы).

Если t_эмп>t_крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся.[3] Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.

Решение. Для критерия Фишера необходимо сравнить дис­персии тестовых оценок в обоих классах. Резуль­таты тестирования представлены в таблице:

Таблица 3.

№№ учащихся	Первый класс	Второй класс
1	90	41
2	29	49
3	39	56
4	79	64
5	88	72
6	53	65
7	34	63
8	40	87
9	75	77
10	79	62
Суммы	606	636
Среднее	60,6	63,6

 

Рассчитав дисперсии для переменных X и Y, получаем:

s_x²=572,83; s_y²=174,04

Тогда по формуле (8) для расчета по F критерию Фишера находим:

По таблице из Приложения 1 для F критерия при степенях свободы в обоих случаях равных k=10 — 1 = 9 находим F_крит=3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н₀ (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н₁. Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2 Непараметрические критерии

Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия.  Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.

studfiles.net

Критерий Фишера и критерий Стьюдента в эконометрике

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где n — число наблюдений;

m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

1. Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
2. Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
3. На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

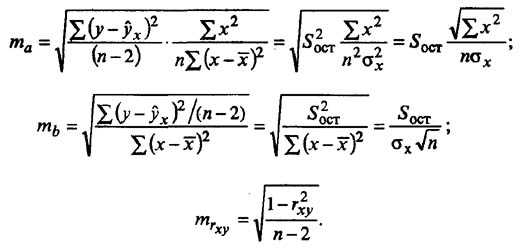
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам

.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

 

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов

выглядят так

Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

и находится доверительный интервал

Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

общая сумма квадратов отклонений (TSS)

сумма квадратов отклонений, обусловленная регрессией (RSS)

остаточная сумма квадратов отклонений (ESS)

Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R² > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

Любые задачи по эконометрике решаются здесь

univer-nn.ru

7.5. Критерий Фишера

Критерий Фишера (F) основан на том же принципе, что и критерий Стьюдента, т. е. предполагает вычисление средних значений и дисперсий в сравниваемых выборках. Чаще всего используется при сравнении между собой неравноценных по объему (разных по численности) выборок. Критерий Фишера является несколько более жестким, чем критерий Стьюдента, а потому более предпочтителен в тех случаях, когда возникают сомнения в достоверности различий (например, если по критерию Стьюдента различия достоверны при нулевом и недостоверны при первом уровне значимости).

Формула Фишера выглядит следующим образом:

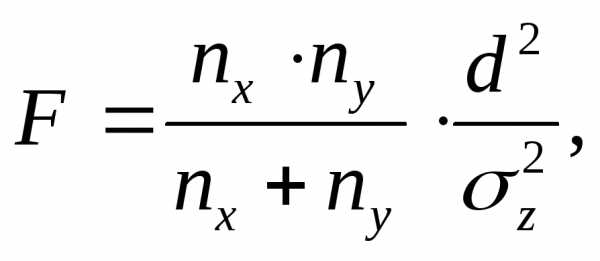(7.4)

где

и(7.5, 7.6)

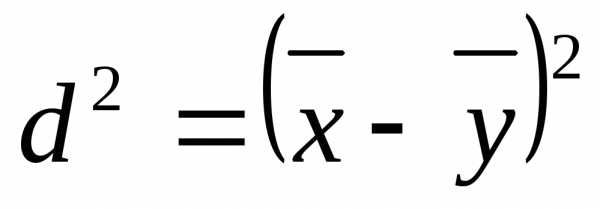
В рассматриваемой нами задаче d² = 5,29; σ_z² = 29,94.

Подставляем значения в формулу:

В табл. ХI Приложений находим, что для уровня значимости β₁ = 0,95 и ν = n_x + n_y – 2 = 28 критическое значение составляет 4,20.

Вывод

F = 1,32 < F_кр. = 4,20. Различия между выборками статистически недостоверны.

Примечание

При использовании критерия Фишера должны соблюдаться те же условия, что и для критерия Стьюдента (см. подраздел 7.4). Тем не менее допускается различие в численности выборок более чем в два раза.

Таким образом, при решении одной и той же задачи четырьмя различными методами с использованием двух непараметрических и двух параметрических критериев мы пришли к однозначному выводу о том, что различия между группой девушек и группой юношей по уровню реактивной тревожности недостоверны (т. е. находятся в пределах случайных вариаций). Однако могут встретиться и такие случаи, когда сделать однозначный вывод не представляется возможным: одни критерии дают достоверные, другие – недостоверные различия. В этих случаях приоритет отдается параметрическим критериям (при условии достаточности объема выборок и нормального распределения исследуемых величин).

7. 6. Критерий j*-угловое преобразование Фишера

Критерий j* Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Он оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект. Допускается также сравнение процентных соотношений и в пределах одной выборки.

Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол j, а меньшей доле – меньший угол, но отношения здесь нелинейные:

(7.7)

где Р – процентная доля, выраженная в долях единицы.

При увеличении расхождения между углами j₁ и j₂ и увеличении численности выборок значение критерия возрастает.

Критерий Фишера вычисляется по следующей формуле:

(7.8)

где j₁ – угол, соответствующий большей процентной доле; j₂ – угол, соответствующий меньшей процентной доле; n₁ и n₂ – соответственно, объем первой и второй выборок.

Вычисленное по формуле значение сравнивается со стандартным (j*_ст = 1,64 для b₁ = 0,95 и j*_ст =2,31 для b₂ = 0,99. Различия между двумя выборками считаются статистически достоверными, если j* > j*_ст для данного уровня значимости.

Пример

Нас интересует, различаются ли между собой две группы студентов по успешности выполнения достаточно сложной задачи. В первой группе из 20 человек с ней справилось 12 студентов, во второй – 10 человек из 25.

Решение

1. Вводим обозначения: n₁ = 20, n₂ = 25.

2. Вычисляем процентные доли Р₁ и Р₂: Р₁ = 12 / 20 = 0,6 (60%), Р₂ = 10 / 25 = 0,4 (40%).

3. В табл. XII Приложений находим соответствующие процентным долям значения φ: j₁ = 1,772, j₂ = 1,369.

Отсюда:

Вывод

Различия между группами не являются статистически достоверными, поскольку j* < j*_ст для 1-го и тем более для 2-го уровня значимости.

studfiles.net

Точный критерий Фишера

Рональд Фишер

​Точный критерий Фишера – это критерий, который используется для сравнения двух относительных показателей, характеризующих частоту определенного признака, имеющего два значения. Исходные данные для расчета точного критерия Фишера обычно группируются в виде четырехпольной таблицы.

1. История разработки критерия

Впервые критерий был предложен Рональдом Фишером в его книге «Проектирование экспериментов». Это произошло в 1935 году. Сам Фишер утверждал, что на эту мысль его натолкнула Муриэль Бристоль. В начале 1920-х годов Рональд, Муриэль и Уильям Роуч находились в Англии на опытной сельскохозяйственной станции. Муриэль утверждала, что может определить, в какой последовательности наливали в ее чашку чай и молоко. На тот момент проверить правильность ее высказывания не представлялось возможным.

Это дало толчок идее Фишера о «нуль гипотезе». Целью стала не попытка доказать, что Муриэль может определить разницу между по-разному приготовленными чашками чая. Решено было опровергнуть гипотезу, что выбор женщина делает наугад. Было определено, что нуль-гипотезу нельзя ни доказать, ни обосновать. Зато ее можно опровергнуть во время экспериментов.

Было приготовлено 8 чашек. В первые четыре налито молоко сначала, в другие четыре – чай. Чашки были помешаны. Бристоль предложили опробовать чай на вкус и разделить чашки по методу приготовления чая. В результате должно было получиться две группы. История говорит, что эксперимент прошел удачно.

Благодаря тесту Фишера вероятность того, что Бристоль действует интуитивно, была уменьшена до 0.01428. То есть, верно определить чашку можно было в одном случае из 70. Но все же нет возможности свести к нулю шансы того, что мадам определяет случайно. Даже если увеличивать число чашек.

Эта история дала толчок развитию «нуль гипотезы». Тогда же был предложен точный критерий Фишера, суть которого в переборе всех возможных комбинаций зависимой и независимой переменных.

2. Для чего используется точный критерий Фишера?

Точный критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен (что нашло отражение даже в его названии), что позволяет его использовать в исследованиях с небольшим числом наблюдений.

Особое место отводится точному критерию Фишера в медицине. Это важный метод обработки медицинских данных, нашедший свое применение во многих научных исследованиях. Благодаря ему можно исследовать взаимосвязь определенных фактора и исхода, сравнивать частоту патологических состояний между двумя группами исследуемых и т.д.

3. В каких случаях можно использовать точный критерий Фишера?

1. Сравниваемые переменные должны быть измерены в номинальной шкале и иметь только два значения, например, артериальное давление в норме или повышено, исход благоприятный или неблагоприятный, послеоперационные осложнения есть или нет.
2. Точный критерий Фишера предназначен для сравнения двух независимых групп, разделенных по факторному признаку. Соответственно, фактор также должен иметь только два возможных значения.
3. Критерий подходит для сравнения очень малых выборок: точный критерий Фишера может применяться для анализа четырехполных таблиц в случае значений ожидаемого явления менее 5, что является ограничением для применения критерия хи-квадрат Пирсона, даже с учетом поправки Йейтса.
4. Точный критерий Фишера бывает односторонним и двусторонним. При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет.
   Двусторонний тест оценивает различия частот по двум направлениям. То есть оценивается верятность как большей, так и меньшей частоты явления в экспериментальной группе по сравнению с контрольной группой.

Аналогом точного критерия Фишера является Критерий хи-квадрат Пирсона, при этом точный критерий Фишера обладает более высокой мощностью, особенно при сравнении малых выборок, в связи с чем в этом случае обладает преимуществом.

4. Как рассчитать точный критерий Фишера?

Допустим, изучается зависимость частоты рождения детей с врожденными пороками развития (ВПР) от курения матери во время беременности. Для этого выбраны две группы беременных женщин, одна из которых — экспериментальная, состоящая из 80 женщин, куривших в первом триместре беременности, а вторая — группа сравнения, включающая 90 женщин, ведущих здоровый образ жизни на протяжении всей беременности. Число случаев ВПР плода, установленных по данным УЗИ в экспериментальной группе, составило 10, в группе сравнения — 2.

Вначале составляем четырехпольную таблицу сопряженности:

	Исход есть (Наличие ВПР)	Исхода нет (Отсутствие ВПР)	Всего
Фактор риска есть (Курящие)	A = 10	B = 70	(A + B) = 80
Фактор риска отсутствует (Некурящие)	C = 2	D = 88	(C + D) = 90
Всего	(A + C) = 12	(B + D) = 158	(A + B + C + D) = 170

Точный критерий Фишера рассчитывается по следующей формуле:

где N — общее число исследуемых в двух группах; ! — факториал, представляющий собой произведение числа на последовательность чисел, каждое из которых меньше предыдущего на 1 (например, 4! = 4 · 3 · 2 · 1)

В результате вычислений находим, что P = 0,0137.

5. Как интерпретировать значение точного критерия Фишера?

Достоинством метода является соответствие полученного критерия точному значению уровня значимости p. То есть, полученное в нашем примере значение 0,0137 и есть уровень значимости различий сравниваемых групп по частоте развития ВПР плода. Необходимо лишь сопоставить данное число с критическим уровнем значимости, обычно принимаемым в медицинских исследованиях за 0,05.

• Если значение точного критерия Фишера больше критического, принимается нулевая гипотеза и делается вывод об отсутствии статистически значимых различий частоты исхода в зависимости от наличия фактора риска.
• Если значение точного критерия Фишера меньше критического, принимается альтернативная гипотеза и делается вывод о наличии статистически значимых различий частоты исхода в зависимости от воздействия фактора риска.

В нашем примере P < 0,05, в связи с чем делаем вывод о наличии прямой взаимосвязи курения и вероятности развития ВПР плода. Частота возникновения врожденной патологии у детей курящих женщин статистически значимо выше, чем у некурящих.

---

Презентация на тему «Методы непараметрического анализа»

Расчетные задачи по теме «Точный критерий Фишера»

Онлайн-калькулятор для расчета точного критерия Фишера

medstatistic.ru

8.5.2. F — критерий Фишера

Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух рядов наблюдений. Для вычисления нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая знаменателе. Формула вычисления по критерию Фишера F такова:

Где

и

Поскольку, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение всегда будет больше или равно единице, т.е.. Число степеней свободы определяется также просто:для первой (т.е. для той выборки, величина дисперсии которой больше) идля второй выборки. В таблице 18 Приложения 6 критические значения критерия Фишеранаходятся по величинам(верхняя строчка таблицы) и(левый столбец таблицы).

Пример: В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.

Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в табл. 11.

Таблица 11

№ учащихся	Первый класс X	Второй класс Y
1	90	41
2	29	49
3	39	56
4	79	64
5	88	72
6	53	65
7	34	63
8	40	87
9	75	77
10	79	62
Суммы	606	636
Среднее	60,6	63,6

Как видно из табл. 11, величины средних в обеих группах практически совпадают между собой 60,6 63, 6 и величина t — критерия Стьюдента оказалась равной 0, 347 и незначимой.

Рассчитав дисперсии для переменных X и Y, получаем

Тогда, по формуле для расчета по F — критерию Фишера находим:

По табл. 18 приложения 6 для F — критерия при степенях свободы в обоих случаях равных df= 10 — 1 = 9 находим:

3,18 для P 0,05

5,35 для P 0,01

Строим «ось значимости»:

Таким образом, полученная величина попала в зону неопределенности. В терминах статистических гипотез можно утверждать, что Н(гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н. Психолог может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.

Для применения критерия F Фишера необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отношений.

2. Сравниваемые выборки должны быть распределены по нормальному закону.

8.6. Корреляционный анализ

Корреляцией называют зависимость между двумя переменными величинами.

Переменная — это любая величина, которая может быть измерена и чье количественное выражение может варьировать.

При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то увеличение одного показателя сопровождается возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.

Коэффициент корреляции — это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен +1, а при полной отрицательной -1.

В случаи, если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной.

Можно выделить несколько видов корреляционного анализа: линейный, ранговый, парный и множественный. Мы рассмотрим два вида корреляционного анализа — линейный и ранговый.

studfiles.net

Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей

Критерий Фишера

Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей, распределенных по нормальному закону. Он является параметрическим критерием.

F-критерий Фишера называют дисперсионным отношением, так как он формируется как отношение двух сравниваемых несмещенных оценок дисперсий.

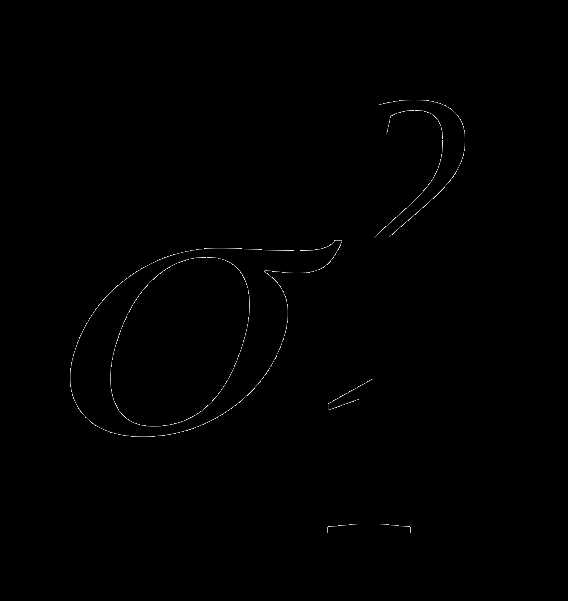Пусть в результате наблюдений получены две выборки. По ним вычислены дисперсии и , имеющие и степеней свободы. Будем считать, что первая выборка взята из генеральной совокупности с дисперсией , а вторая – из генеральной совокупности с дисперсией 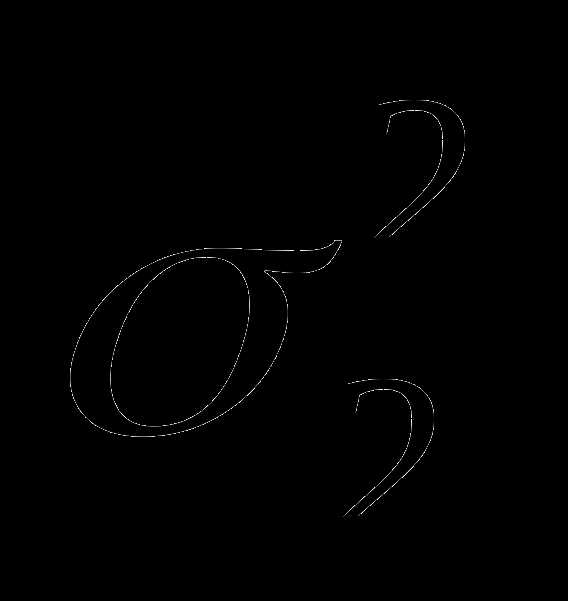. Выдвигается нулевая гипотеза о равенстве двух дисперсий, т.е. H₀: 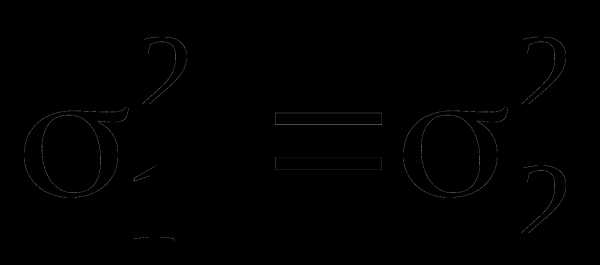или 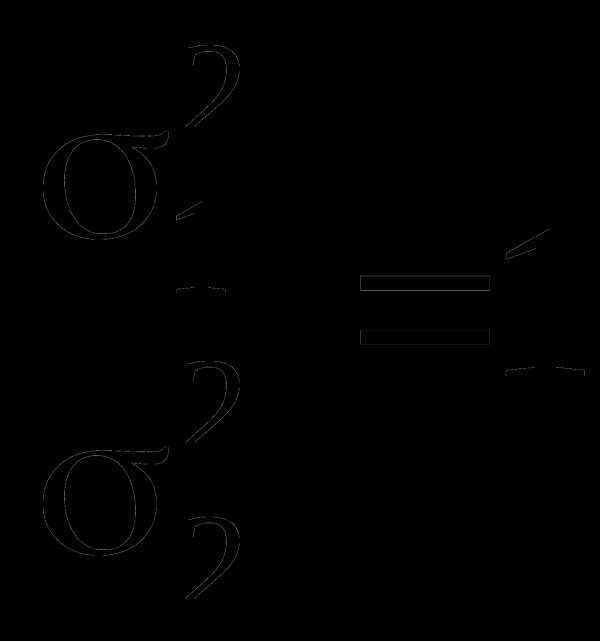. Для того, чтобы отвергнуть эту гипотезу нужно доказать значимость различия при заданном уровне значимости .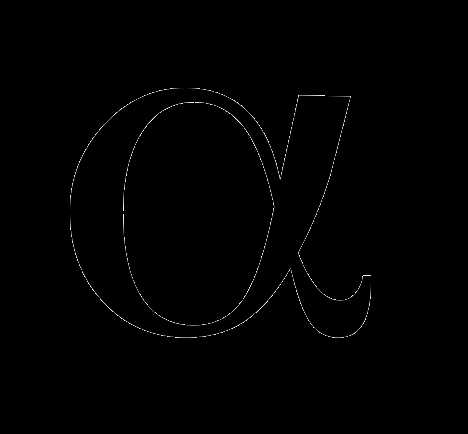

Значение критерия вычисляется по формуле:

.

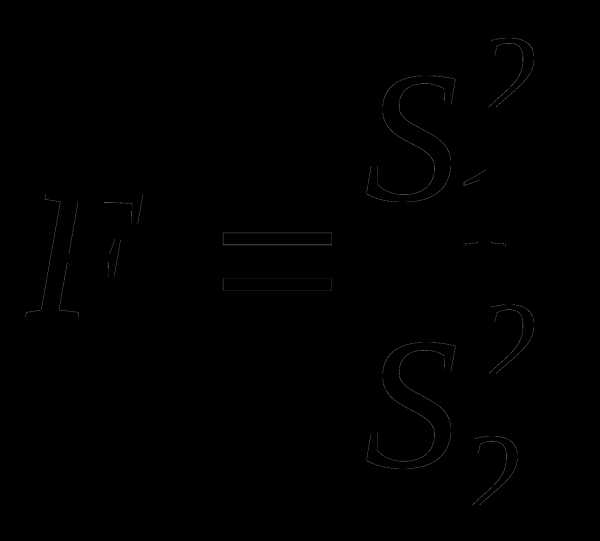Очевидно, что при равенстве дисперсий величина критерия будет равна единице. В остальных случаях она будет больше (меньше) единицы.

Критерий имеет распределение Фишера . Критерий Фишера – двусторонний критерий, и нулевая гипотеза отвергается в пользу альтернативной если . Здесь , где 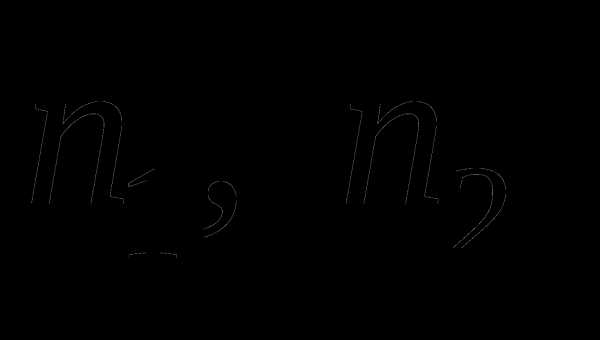– объем первой и второй выборки соответственно.

В системе STATISTICA реализован односторонний критерий Фишера, т.е. в качестве всегда берут максимальную дисперсию. В этом случае нулевая гипотеза отвергается в пользу альтернативы , если .

Пример

Пусть поставлена задача, сравнить эффективность обучения двух групп студентов. Уровень успеваемости — характеризует уровень управления процессом обучения, а дисперсия качество управления обучением, степень организованности процесса обучения. Оба показателя являются независимыми и в общем случае должны рассматриваться совместно. Уровень успеваемости (математическое ожидание) каждой группы студентов характеризуется средними арифметическими и 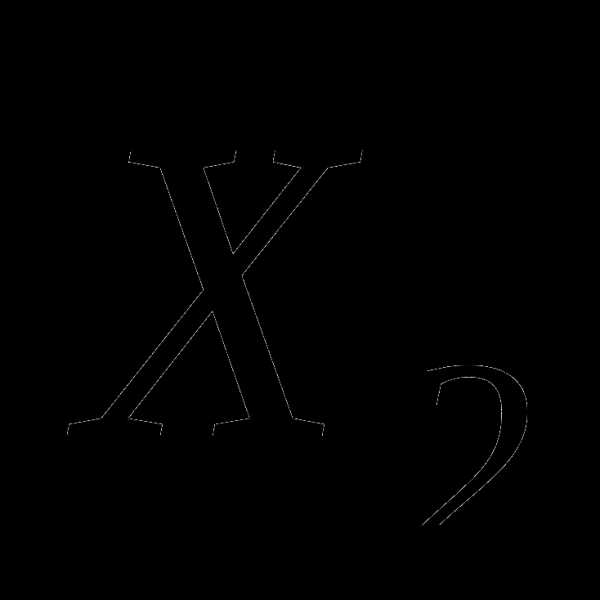, а качество характеризуется соответствующими выборочными дисперсиями оценок: и . При оценке уровня текущей успеваемости оказалось, что он одинаков у обоих учащихся: = = 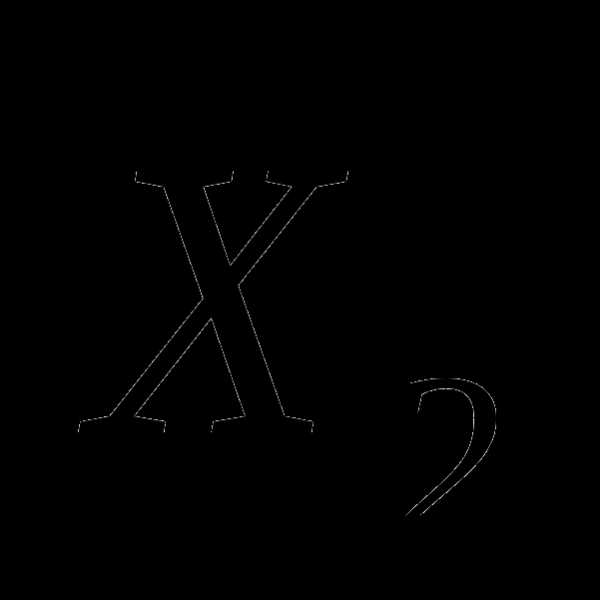4,0. 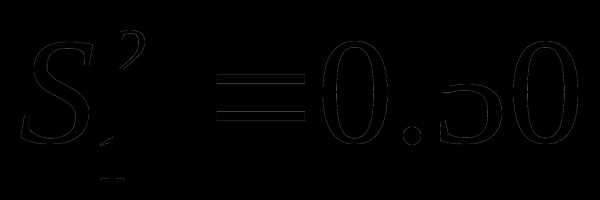Выборочные дисперсии: и 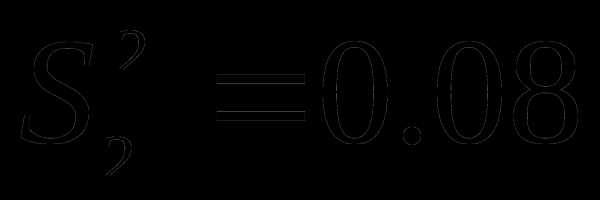. Числа степеней свободы, соответствующие этим оценкам: и 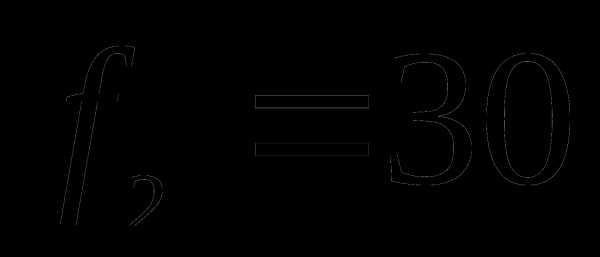. Отсюда для установления различий в эффективности обучения мы можем воспользоваться стабильностью успеваемости, т.е. проверим гипотезу .

Вычислим (в числителе должна быть большая дисперсия), . По таблицам (STATISTICA – Probability Distribution Calculator) находим , которое меньше вычисленного, следовательно нулевая гипотеза должна быть отвергнута в пользу альтернативы . Это заключение может не удовлетворить исследователя, поскольку его интересует истинная величина отношения 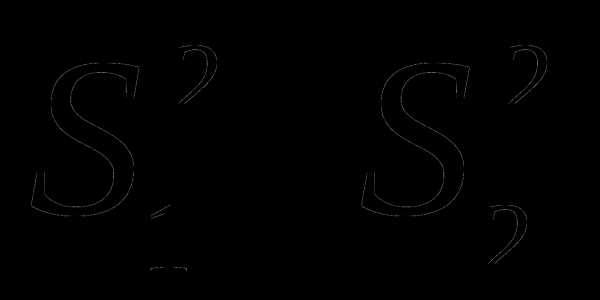(у нас в числителе всегда большая дисперсия). При проверке одностороннего критерия получим , что меньше вычисленного выше значения. Итак, нулевая гипотеза должна быть отвергнута в пользу альтернативы .

Критерий Фишера в программе STATISTICA в среде Windows

Для примера проверки гипотезы (критерий Фишера) используем (создаем) файл с двумя переменными (fisher.sta):

Рис. 1. Таблица с двумя независимыми переменными

Чтобы проверить гипотезу необходимо в базовой статистике (Basic Statistics and Tables) выбрать проверку по Стьюденту для независимых переменных. (t-test, independent, by variables).

Рис. 2. Проверка параметрических гипотез

После выбора переменных и нажатия на клавишу Summary производится подсчет значений среднеквадратичных отклонений и критерия Фишера. Кроме этого определяется уровень значимости p, при котором различие несущественно.

Рис. 3. Результаты проверки гипотезы (F- критерий)

Используя Probability Calculator и задав значение параметров можно построить график распределения Фишера с пометкой вычисленного значения.

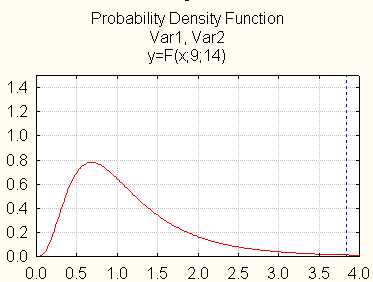
Рис. 4. Область принятия (отклонения) гипотезы (F- критерий)

Источники.

1. Проверка гипотез об отношениях двух дисперсий

URL: /tryphonov3/terms3/testdi.htm

2. Лекция 6. :8080/resources/math/mop/lections/lection_6.htm

3. F – критерий Фишера

URL: /home/portal/applications/Multivariatadvisor/F-Fisheer/F-Fisheer.htm

4. Теория и практика вероятностно-статистических исследований.

URL: /active/referats/read/doc-3663-1.html

5. F – критерий Фишера

URL: /stat/s04.html

gigabaza.ru

Критерий Фишера

Критерий Фишера

Критерий Фишера (F-критерий, φ*-критерий, критерий наименьшей значимой разности) — является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов.

Рассмотрим две выборки объемом m и n соответственно случайных величин X и Y, имеющих нормальное распределение. Необходимо проверить равенство их дисперсий. Статистика теста:

Где — выборочная дисперсия.

Если статистика больше критического, то дисперсии не одинаковы. В противном случае дисперсии выборок одинаковы.

Таблицы критических значений F-критерия для уровня значимости 0.05:

f2\f1	1	2	3	4	5	6	7	8	9	10	15
1	161.45	199.50	215.71	224.58	230.16	233.99	236.77	238.88	240.54	241.88	245.95
2	18.51	19.00	19.16	19.25	19.30	19.33	19.35	19.37	19.38	19.40	19.43
3	10.13	9.55	9.28	9.12	9.01	8.94	8.89	8.85	8.81	8.79	8.70
4	7.71	6.94	6.59	6.39	6.26	6.16	6.09	6.04	6.00	5.96	5.86
5	6.61	5.79	5.41	5.19	5.05	4.95	4.88	4.82	4.77	4.74	4.62
6	5.99	5.14	4.76	4.53	4.39	4.28	4.21	4.15	4.10	4.06	3.94
7	5.59	4.74	4.35	4.12	3.97	3.87	3.79	3.73	3.68	3.64	3.51
8	5.32	4.46	4.07	3.84	3.69	3.58	3.50	3.44	3.39	3.35	3.22
9	5.12	4.26	3.86	3.63	3.48	3.37	3.29	3.23	3.18	3.14	3.01
10	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	3.02	2.98	2.85
11	4.84	3.98	3.59	3.36	3.20	3.09	3.01	2.95	2.90	2.85	2.72
12	4.75	3.89	3.49	3.26	3.11	3.00	2.91	2.85	2.80	2.75	2.62
13	4.67	3.81	3.41	3.18	3.03	2.92	2.83	2.77	2.71	2.67	2.53
14	4.60	3.74	3.34	3.11	2.96	2.85	2.76	2.70	2.65	2.60	2.46
15	4.54	3.68	3.29	3.06	2.90	2.79	2.71	2.64	2.59	2.54	2.40
16	4.49	3.63	3.24	3.01	2.85	2.74	2.66	2.59	2.54	2.49	2.35
17	4.45	3.59	3.20	2.96	2.81	2.70	2.61	2.55	2.49	2.45	2.31
18	4.41	3.55	3.16	2.93	2.77	2.66	2.58	2.51	2.46	2.41	2.27
19	4.38	3.52	3.13	2.90	2.74	2.63	2.54	2.48	2.42	2.38	2.23
20	4.35	3.49	3.10	2.87	2.71	2.60	2.51	2.45	2.39	2.35	2.20

См. также:

ISmFisherTest | Библиотека методов и моделей

help.prognoz.com