Формула площадь поверхности сферы – Площадь поверхности сферы | Формулы и расчеты онлайн

Как найти площадь сечения шара 🚩 Площадь сечения шара формула 🚩 Математика

18 октября 2011

Автор КакПросто!

Пусть дан шар с радиусом R, который на некотором расстоянии b от центра пересекает плоскость. Расстояние b меньше или равно радиусу шара. Требуется найти площадь S получающегося при этом сечения.

Инструкция

Очевидно, что если расстояние от центра шара до плоскости равно радиусу плоскости, то плоскость касается шара только в одной точке, и площадь сечения будет равна нулю, то есть если b = R, то S = 0. Если b = 0, то секущая плоскость проходит через центр шара. В этом случае сечение будет представлять собой круг, радиус которого совпадает с радиусом шара. Площадь этого круга будет, согласно формуле, равна S = πR^2.

Эти два крайних случая дают границы, между которыми всегда будет лежать искомая площадь: 0 < S < πR^2. При этом любое сечение шара плоскостью всегда является кругом. Следовательно, задача сводится к тому, чтобы найти радиус окружности сечения. Тогда площадь этого сечения вычисляется по формуле площади круга.

Поскольку расстояние от точки до плоскости определяется как длина отрезка, перпендикулярного плоскости и начинающегося в точке, второй конец этого отрезка будет совпадать с центром окружности сечения. Такой вывод вытекает из определения шара: очевидно, что все точки окружности сечения принадлежат сфере, а следовательно, лежат на равном расстоянии от центра шара. Это значит, что каждая точка окружности сечения может считаться вершиной прямоугольного треугольника, гипотенузой которого служит радиус шара, одним из катетов — перпендикулярный отрезок, соединяющий центр шара с плоскостью, а вторым катетом — радиус окружности сечения.

Из трех сторон этого треугольника заданы два — радиус шара R и расстояние b, то есть гипотенуза и катет. По теореме Пифагора длина второго катета должна быть равна √(R^2 — b^2). Это и есть радиус окружности сечения. Подставляя найденное значение радиуса в формулу площади круга, легко прийти к выводу, что площадь сечения шара плоскостью равна:S = π(R^2 — b^2).В частных случаях, когда b = R или b = 0, выведенная формула полностью согласуется с уже найденными результатами.

Видео по теме

Источники:

• сечение шара плоскостью

Перед решением задачи нахождения радиуса сферы необходимо ввести определение объектов – сфера и шар.Из курса стереометрии известно, что сферой называется поверхность, которая состоит из точек пространства, равноудалённых от данной точки. Данная точка называется центром сферы, а расстояние, на которое точки сферы отдалены от её центра, – радиусом сферы и обозначается буквой R. Тело, ограниченное поверхностью сферы называется шаром. Способ определения радиуса сферы зависит от имеющихся исходных данных.

Инструкция

Пусть дана сфера и известна площадь её поверхности. Тогда, используя формулу для вычисления площади поверхности сферы, можно вычислить её радиус:
R = v(4•П/S), где S — площадь поверхности сферы, П = 3,14.

Если известен объём шара, который ограничивает сфера, то радиус можно найти по формуле объёма:
R = (3•V/4•П)^1/3, где V — объём шара, П = 3,14.

Полезный совет

В случаях, когда сфера вписана или описана около правильного многогранника, можно воспользоваться следующими формулами.

Для сферы, вписанной в правильный тетраэдр R = √6/12•a, где a — длина ребра тетраэдра,
Для сферы, описанной около правильного тетраэдра R = √6/4•a, где a — длина ребра тетраэдра,
Для сферы, вписанной в куб R = 1/2•a, где a — длина ребра куба,
Для сферы, описанной около куба R = √3/2•a, где a — длина ребра куба.

Все планеты солнечной системы имеют форму шара. Кроме того, шарообразную или близкую к таковой форму имеют и многие объекты, созданные человеком, включая детали технических устройств. Шар, как и любое тело вращения, имеет ось, которая совпадает с диаметром. Однако это не единственное важное свойство шара. Ниже рассмотрены основные свойства этой геометрической фигуры и способ нахождения ее площади.

Инструкция

Если взять полукруг или круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром называется тело, ограниченное сферой. Сфера представляет собой оболочку шара, и ее сечением является окружность. От шара она отличается тем, что является полой. Ось как у шара, так и у сферы совпадает с диаметром и проходит через центр. Радиусом шара называется отрезок, проложенный от его центра до любой внешней точки. В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет большинство планет и небесных тел. В разных точках шара имеются одинаковые по форме, но неодинаковые по величине, так называемые сечения — круги разной площади. Шар и сфера — взаимозаменяемые тела, в отличие от конуса, несмотря на то, что конус также является телом вращения. Сферические поверхности всегда в своем сечении образуют окружность, независимо от того, как именно она вращается — по горизонтали или по вертикали. Коническая же поверхность получается лишь при вращении треугольника вдоль его оси, перпендикулярной основанию. Поэтому конус, в отличие от шара, и не считается взаимозаменяемым телом вращения.

Самый большой из возможных кругов получается при сечении шара плоскостью, проходящей через центр О. Все круги, которые проходят через центр О, пересекаются между собой в одном диаметре. Радиус всегда равен половине диаметра. Через две точки A и B, располагающиеся в любом месте поверхности шара, может проходить бесконечное количество кругов или окружностей. Именно по этой причине через полюса Земли может быть проведено неограниченное количество меридианов.

При нахождении площади шара рассматривается, прежде всего, площадь сферической поверхности.Площадь шара, а точнее, сферы, образующей его поверхность, может быть рассчитана на основании площади круга с тем же радиусом R. Поскольку площадь круга есть произведение полуокружности на радиус, его можно рассчитать следующим образом:S = ?R^2Так как через центр шара проходят четыре основных больших круга, то, соответственно площадь шара (сферы) равна:S = 4 ?R^2

Данная формула может быть полезна в том случае, если известен либо диаметр, либо радиус шара или сферы. Однако, эти параметры приведены в качестве условий не во всех геометрических задачах. Существуют и такие задачи, в которых шар вписан в цилиндр. В этом случае, следует воспользоваться теоремой Архимеда, суть которой заключается в том, что площадь поверхности шара в полтора раза меньше полной поверхности цилиндра:S = 2/3 S цил., где S цил. -площадь полной поверхности цилиндра.

Видео по теме

Сферой называют поверхность шара. По-другому ее можно определить как трехмерную геометрическую фигуру, все точки которой находятся на одинаковом расстоянии от точки, называемой центром сферы. Чтобы выяснить размеры этой фигуры достаточно знать лишь один параметр — например, радиус, диаметр, площадь или объем. Их значения связаны между собой постоянными соотношениями, которые позволяют вывести простую формулу вычисления каждого из них.

Инструкция

Если известна длина диаметра сферы (d), то для нахождения площади ее поверхности (S) возводите этот параметр в квадрат и умножайте на число Пи (π): S=π∗d². Например, если длина диаметра составляет два метра, то площадь сферы составит 3,14∗2²=12,56 квадратных метров.

Если известна длина радиуса (r), то площадь поверхности сферы (S) будет составлять учетверенное произведение возведенного в квадрат радиуса на число Пи (π): S=4∗π∗r². Например, при длине радиуса сферы в три метра его площадь составит 4∗3,14∗3²=113,04 квадратных метров.

Если известен объем (V) пространства, ограниченного сферой, то сначала можно найти ее диаметр (d), а затем воспользоваться формулой, приведенной в первом шаге. Так как объем равен одной шестой части от произведения числа Пи на возведенную в куб длину диаметра сферы (V=π∗d³/6), то диаметр можно определить, как кубический корень из шести объемов, разделенных на число Пи: d=³√(6∗V/π). Подставив это значение в формулу из первого шага, получим: S=π∗(³√ (6∗V/π))². Например, при объеме ограниченного сферой пространства равном 500 кубометров вычисление ее площади будет выглядеть так: 3,14∗(³√(6∗500/3,14))² = 3,14∗(³√955,41)² = 3,14∗9,85² = 3,14∗97,02 = 304,64 квадратных метра.

Производить все эти расчеты в уме довольно затруднительно, поэтому придется воспользоваться каким либо из калькуляторов. Например, это может быть вычислитель, встроенный в поисковые системы Google или Nigma. Google отличается в лучшую сторону тем, что умеет самостоятельно определять порядок операций, а Nigma потребует от вас тщательно расставить все скобки. Для вычисления площади сферы по данным, например, из второго шага поисковый запрос, который надо ввести в Google, будет выглядеть так: «4*пи*3^2». А для наиболее сложного случая с вычислением кубического корня и возведением в квадрат из третьего шага запрос будет таким: «пи*(6*500/пи)^(2/3)».

Масса тела — физическая величина, которая характеризует степень его инертности. Масса физического тела зависит от объема пространства, которое оно занимает, и плотности материала, из которого оно состоит. Объем тела правильной формы (например, шара) рассчитать не сложно, а если известен и материал, из которого он состоит, то найти массу можно очень просто.

Инструкция

Определите объем шара. Для этого достаточно знать один из его параметров — радиус, диаметр, площадь поверхности и т.д. Например, зная диаметр шара (d), его объем (V) можно определить, как одну шестую часть от произведения возведенного в куб диаметра на число Пи: V=π∗d³/6. Через радиус шара (r) объем выражается как одна треть от увеличенного в четыре раза произведения числа Пи на радиус, возведенный в куб: V=4∗π∗r³/3. Рассчитайте массу шара (m), умножив его объем на известную плотность вещества (p): m=p∗V. Если материал шара не однороден, то следует брать среднюю плотность. Подставив в эту формулу определения объема шара через его известные параметры, можно получить при известном диаметре шара формулу m=p∗π∗d³/6, а при известном радиусе m=p∗4∗π∗r³/3.

Используйте для расчетов, например, стандартный программный калькулятор, входящий в состав базового программного обеспечения операционной системы Windows любой из активно использующихся сегодня версий. Самый простой способ запустить его — нажать сочетание клавиш win + r, чтобы открыть стандартный диалог запуска программ, затем набрать команду calc и щелкнуть по кнопке «OK». В меню калькулятора раскройте раздел «Вид» и выберите строку «Инженерный» или «Научный» (в зависимости от используемой версии ОС) — интерфейс этого режима имеет кнопку для ввода значения числа Пи одним щелчком мыши. Операции умножения и деления в этом калькуляторы не должны вызвать вопросов, а для возведения в степень при вычислении массы шара будет достаточно кнопок с символами x^2 и x^3.

Источники:

• объём шара через диаметр

Шар — это простейшая объемная геометрическая фигура, для указания размеров которой достаточно всего одного параметра. Границы этой фигуры принято называть сферой. Объем пространства, ограничиваемого сферой, можно вычислить как с помощью соответствующих тригонометрических формул, так и подручными средствами.

Инструкция

Используйте классическую формулу объема (V) сферы, если из условий известен ее радиус (r) — возведите радиус в третью степень, умножьте на число Пи, а результат увеличьте еще на треть. Записать эту формулу можно так: V=4*π*r³/3.

Если есть возможность измерить диаметр (d) сферы, то поделите его пополам и используйте как радиус в формуле из предыдущего шага. Или найдите одну шестую часть от возведенного в куб диаметра, умноженного на число Пи: V=π*d³/6.

Если известен объем (v) цилиндра, в который вписана сфера, то для нахождения ее объема определите, чему равны две трети от известного объема цилиндра: V=⅔*v. Если известна средняя плотность (p) материала, из которого состоит сфера, и ее масса (m), то этого тоже достаточно для определения объема — разделите второе на первое: V=m/p. Воспользуйтесь какими-либо мерными емкостями в качестве подручных средств для измерения объема сосуда сферической формы. Например, наполните его водой, измеряя с помощью мерной емкости количество заливаемой жидкости. Полученное значение в литрах переведите в кубические метры — эта единица принята в международной системе СИ для измерения объема. В качестве коэффициента перевода из литров в кубометры используйте число 1000, так как один литр приравнен к одному кубическому дециметру, а их в каждый кубический метр вмещается ровно тысяча штук.

Используйте принцип измерения, противоположный описанному в предыдущем шаге, если тело в форме сферы нельзя наполнить жидкостью, но можно погрузить в нее. Заполните мерный сосуд водой, отметьте уровень, погрузите измеряемое сферическое тело в жидкость и по разнице уровней определите количество вытесненной воды. Затем переведите полученный результат из литров в кубометры так же, как это описано в предыдущем шаге.

Видео по теме

Источники:

• объем полусферы

Шаром называют простейшую объемную фигуру геометрически правильной формы, все точки пространства внутри границ которой удалены от ее центра на расстояние, не превышающее радиуса. Поверхность, образуемая множеством максимально удаленных от центра точек, называется сферой. Для количественного выражения меры пространства, заключенного внутри сферы, предназначен параметр, который называется объемом шара.

Инструкция

Если требуется измерить объем шара не теоретически, а только подручными средствами, то сделать это можно, например, определив объем вытесненной им воды. Этот способ применим в том случае, когда есть возможность поместить шар в какую-либо соразмерную ему емкость — мензурку, стакан, банку, ведро, бочку, бассейн и т.д. В этом случае перед помещением шара отметьте уровень воды, сделайте это повторно после полного его погружения, а затем найдите разность между отметками. Обычно мерная емкость заводского производства имеет деления, показывающие объем в литрах и производных от него единицах — миллилитрах, декалитрах и т.д. Если полученное значение надо перевести в кубические метры и кратные ему единицы объема, то исходите из того, что один литр соответствует одному кубическому дециметру или одной тысячной доле кубометра.

Если известен материал, из которого изготовлен шар, и плотность этого материала можно узнать, например, из справочника, то определить объем можно взвесив этот предмет. Просто разделите результат взвешивания на справочную плотность вещества изготовления: V=m/p.

Если радиус шара известен из условий задачи или его можно измерить, то для вычисления объема можно использовать соответствующую математическую формулу. Умножьте учетверенное число Пи на третью степень радиуса, а полученный результат разделите на тройку: V=4*π*r³/3. Например, при радиусе в 40см объем шара составит 4*3,14*40³/3 = 267946,67см³ ≈ 0,268м³.

Измерить диаметр чаще бывает проще, чем радиус. В этом случае нет необходимости делить его пополам для использования с формулой из предыдущего шага — лучше упростить саму формулу. В соответствии с преобразованной формулой умножьте число Пи на диаметр в третьей степени, а результат разделите на шестерку: V=π*d³/6. Например, шар диаметром в 50см должен иметь объем в 3,14*50³/6 = 65416,67см³ ≈ 0,654м³.

Когда говорят о площади поверхности шара, то вполне понятно о чем идет речь, даже несмотря на то, что простого и однозначного определения этого понятия нет в школьных учебниках. Но с непосредственным вычислением этого параметра проблем нет — здесь вступают в действие формулы.

Инструкция

Используйте самую простую из формул вычисления площади поверхности шара (S), если известен его диаметр (D) или радиус (R). При этом придется использовать число Пи — математическую константу, показывающую неизменное отношение длины окружности к диаметру круга. Эта константа имеет бесконечное число знаков после десятичной запятой, поэтому вам придется определиться с необходимой точностью вычислений и округлить ее. Сделав это, умножьте число Пи на возведенный в квадрат диаметр шара — полученный результат и будет площадью сферы: S=π*D². Если известен не диаметр, а радиус, то в формулу надо добавить коэффициент, увеличивающий ее в четыре раза: S=4*π*R². Если в условиях задачи сфера задана своими координатами в трехмерной декартовой системе, то начните расчет площади поверхности с нахождения ее радиуса. Для этого вам понадобятся координаты двух точек — являющейся центром шара (X₀,Y₀,Z₀) и любой из максимально удаленных от центра, то есть лежащих на поверхности сферы (X,Y,Z). Радиус сферы (R) будет равен квадратному корню из суммы квадратов попарных разностей координат по каждой из осей: R=√((X-X₀)²+(Y-Y₀)²+(Z-Z₀)²). Затем подставьте полученное значение в формулу из предыдущего шага. В общем виде она теперь будет выглядеть так: S = 4*π*(√((X-X₀)²+(Y-Y₀)²+(Z-Z₀)²))² = 4*π*((X-X₀)²+(Y-Y₀)²+(Z-Z₀)²).

Если вам требуется, не вдаваясь в подробности вычислений, просто получить результат, то воспользуйтесь каким-либо из онлайн-калькуляторов. Например, тем, что размещен на странице http://board74.ru/articles/geometry/sphere.html. Перейдите на эту страницу и введите радиус шара в поле левее кнопки Calculate. Затем кликните кнопку и увидите результат расчета строкой ниже, рядом с формулой, использованной при вычислении. Здесь площадь поверхности сферы названа ее «боковой» поверхностью.

Видео по теме

Шаром называют множество всех точек в пространстве, простирающемся от точки-центра на расстоянии определенного радиуса R. Радиус в свою очередь – это отрезок, соединяющий центр шара с любой точкой его поверхности.

Вам понадобится

• — формула поверхности площади шара;
• — формула объема шара;
• — навыки арифметического счета.

Инструкция

В повседневной жизни зачастую возникает необходимость вычислить площадь шаровой поверхности или его части, чтобы рассчитать, например, расход материала. Вычислив объем шара, вы можете через удельный вес рассчитать массу вещества, составляющего содержимое сферы. Для того чтобы найти площадь и объем шара, достаточно знать его радиус или диаметр. По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры.

Например, диаметр футбольного мяча, согласно всем требованиям ФИФА, должен быть в пределах 21,8—22,2 см. Усредните для простоты счета до 22 см. Следовательно, радиус (R) будет равен (22:2) – 11 см. Ведь интересно узнать, какова площадь поверхности футбольного мяча?

Возьмите формулу площади поверхности шара: Sшара = 4ттR2Подставьте в приведенную формулу значение радиуса футбольного мяча – 11 см.S = 4 x 3.14 x 11х11 .

После проведения несложных математических действий вы получаете результат: 1519.76. Таким образом, площадь поверхности футбольного мяча составляет 1 519.76 квадратных сантиметров.

Теперь рассчитайте объем мяча. Берите формулу расчета объема шара: V = 4/3ттR3Подставляйте опять же значение радиуса футбольного мяча – 11 см.V = 4/3 x 3.14 x 11 х 11 х 11.

После подсчетов, например, на калькуляторе вы получаете: 5576.89.Оказывается, объем воздуха в футбольном мяче составляет 5 576.89 кубических сантиметров.

Видео по теме

Обратите внимание

Интересно: объем шара с диаметром, превышающим в три раза диаметр другого шара, больше суммарного объема трех таких шаров в 9 раз.

Полезный совет

Чтобы развить у детей пристрастие к математическим вычислениям, предлагайте в качестве примеров для расчета окружающие предметы: мяч, арбуз, клубок бабушкиной пряжи. Это наглядно и потому интересно.

www.kakprosto.ru

Площадь сферы

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о сфере). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом на форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».

Задача

В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы.

Решение.
Площадь сферы найдем по формуле:

S = 4πr²

Поскольку в сферу вписан конус, проведем сечение через вершину конуса, которое будет равнобедренным треугольником. Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник — равносторонний (сумма углов треугольника — 180 градусов, значит остальные углы ( 180-60 ) / 2 = 60 , то есть все углы равны ).

Откуда радиус сферы равен радиусу окружности, описанного вокруг равностороннего треугольника. Сторона треугольника по условию равна l . То есть

R = √3/3 l

Таким образом площадь сферы

S = 4π(√3/3 l)²
S = 4/3πl²

Ответ: площадь сферы равна 4/3πl².

Задача

Емкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость? 

Решение.
Площадь поверхности фигуры будет равна половине площади сферы и площади сечения сферы.
Поскольку нам известна длина окружности основания, найдем ее радиус:
L = 2πR
Откуда

R =  L / 2π
R = 46 / 2π
R = 23 /  π

Откуда площадь основания равна
S =  πR² 
S = π (23/π) ²
S = 529 / π

Площадь сферы найдем по формуле:  
S = 4πr²

Соответственно площадь полусферы
S = 4πr² / 2
S =  2π  (23/π)  ²
S = 1058 / π

Общая площадь поверхности фигуры равна:
529 / π + 1058 / π  = 1587 / π  

Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров)
  1587 / π  * 300 / 10 000 = 47,61 / π граммов ≈ 15,15 г 

Задача

Поверхности двух шаров относятся как m:n. Как относятся их объемы?

Поверхні двох куль відносяться як m:n. Як відносяться їх об’єми?

Решение. Рiшення.

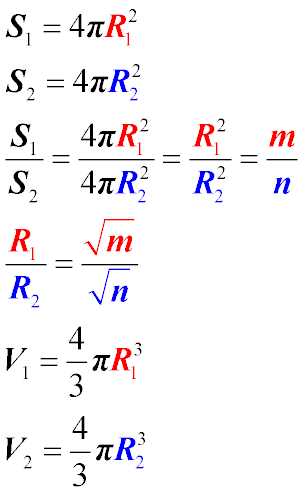	Для пояснения решения прокомментируем каждую из приведенных формул Воспользуемся формулой нахождения поверхности шара и запишем ее для первого шара, предположив, что его радиус равен R1 Площадь поверхности второго шара запишем с помощью точно такой же формулы, предположив, что его радиус равен R2 Найдем соотношение их площадей, разделив первое выражение на второе. Сократим полученную дробь. Нетрудно заметить, что соотношение площадей двух шаров равно соотношению квадратов их радиусов. По условию задачи это соотношение равно m/n Из полученного равенства найдем соотношение радиусов шаров путем извлечения квадратного корня. Полученное равенство запомним Воспользуемся формулой нахождения объема шара и запишем ее для первого шара с радиусом R1 Объем второго шара запишем с помощью той же самой формулы, подставив в нее радиус R2	Для пояснення рішення прокоментуємо кожну з приведених формул Скористаємося формулою знаходження поверхні кулі і запишемо її для першої кулі, передбачивши, що його радіус рівний R1  Площу поверхні другої кулі запишемо за допомогою точний такої ж формули, передбачивши, що його радіус рівний R2  Знайдемо співвідношення їх площ, розділивши перше вираження на друге. Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n  З отриманої рівності знайдемо співвідношення радіусів куль шляхом витягання квадратного кореня. Отриману рівність запам’ятаємо  Скористаємося формулою знаходження об’єму кулі і запишемо її для першої кулі з радіусом R1 Об’єм другої кулі запишемо за допомогою тієї ж самої формули, підставивши в неї радіус R2
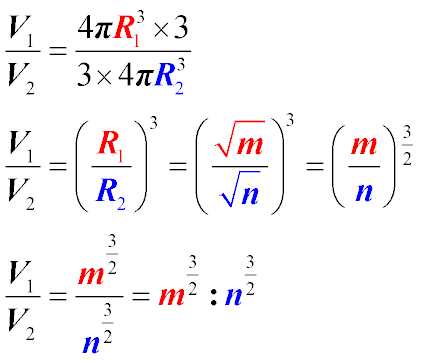	8. Разделим объемы первого и второго шара друг на друга 9. Сократим получившуюся дробь. Заметим, что соотношение объема двух шаров равно соотношению кубов их радиусов. Учтем выражение, полученное нами ранее в формуле 4 и подставим его. Поскольку корень квадратный — это число в степени 1/2, преобразуем выражение 10. Раскроем скобки и запишем полученное соотношение в виде пропорции. Ответ получен.	8. Розділимо об’єми першої і другої кулі один на одного 9. Скоротимо дріб, що вийшов. Відмітимо, що співвідношення об’єму двох куль дорівнює співвідношенню кубів їх радіусів. Врахуємо вираження, отримане нами раніше у формулі 4 і підставимо його. Оскільки корінь квадратний — це число в мірі 1/2, перетворимо вираження 10. Розкриємо дужки і запишемо отримане співвідношення у вигляді пропорції. Відповідь отримана.

 Сфера (Шар) | Описание курса | Полусфера 

   

profmeter.com.ua

Шар и его части. Объем, площадь поверхности. |

Рассмотрим понятие таких геометрических тел как шар и его части:

• шаровой сегмент;
• шаровой сектор;
• шаровой слой.

Также представим формулы для вычисления объемов и площадей поверхностей шара и его частей.

Об элементах шара и понятии “сфера” будет опубликовано в отдельной статье.

Шар. 

Определение.

Шаром называется геометрическое тело, состоящее из точек пространства, находящихся от центра на расстоянии, не больше заданного.

Площадь поверхности шара вычисляется по формуле:

S_пов. = 4*π*R² = π*D² , где R –  радиус шара,   D – диаметр шара.

В школьной программе объем шара представлен одной формулой:

V = 4/3* π*R³ , где R –  радиус шара.

Учитывая, что диаметр шара вдвое больше радиуса шара, имеем формулу объема шара такую:

V = 1/6 * π* D³, где D – диаметр шара.

Но объем шара может быть задан и другими соотношениями . Опишем их ниже.

Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара:

V = 1/3 R*S, где R –  радиус шара.

А вот теорема Архимеда:

Объем шара в 1,5 раза меньше объема описанного вокруг него цилиндра, а поверхность шара – в 1,5 раза меньше полной поверхности того же цилиндра.

V = 2/3 * V_ц., где V_ц – объем цилиндра.

S_пов. = 2/3 * S_{пов. ц.} , где S_{пов. ц.} – полная поверхность цилиндра.

Части шара.

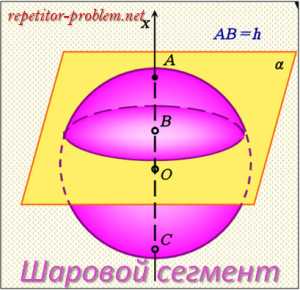Шаровой сегмент.

Определение.

Шаровой сегмент – это  часть шара, отсекаемая от нее плоскостью.

Кривая поверхность шарового сегмента равна произведению его высоты на длину окружности большого круга шара:

S_сегм. = 2πR* h, где R –  радиус шара, h – высота сегмента.

Еще формула площади поверхности сегмента:

S_сегм. = π*(r²

+ h²), где r – радиус основания сегмента, h – высота сегмента.

Объем шарового сегмента вычисляется по формуле:

V = π* h² *(R – 1/3*h) = 1/6*π*h(h² + 3r²), где r – радиус основания сегмента, h – высота сегмента.

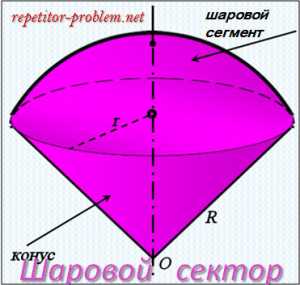Шаровой сектор.

Определение.

Шаровой сектор – часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной – центр шара.

Согласно определению формула площади поверхности шарового сектора выглядит так:

S_{шар. сектор} = S_{бок.конус.} + S_{шар. сегм.}

Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезанная сектором часть шаровой поверхности (S), а высота равна радиусу шара (R)

:

V = 1/3*R*S = 2/3*π*R²*h, где h – высота шарового сегмента, принадлежащая шаровому сектору.

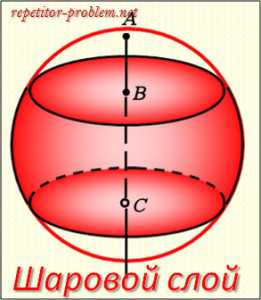Шаровой слой.

Определение.

Часть шара, заключенная между двумя секущими параллельными плоскостями, называется шаровым слоем, а кривая поверхность шарового слоя называется шаровым поясом (или зоной).

S_{шар. слоя} = h*2πR , где R –  радиус шара, h – высота шарового слоя.

Объем шарового слоя:

V = 1/6 * π* h³ +  1/2 * π*(r₁² + r₂²)*h, где r_1, r₂  – радиусы оснований шарового слоя, h – высота шарового слоя.

repetitor-problem.net