Как найти среднюю линию равнобедренной трапеции?
Как найти среднюю линию равнобедренной трапеции?
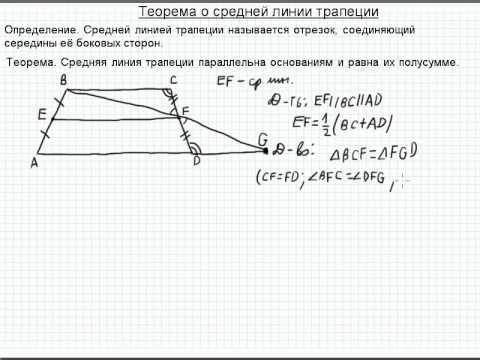
Трапецией принято называть такой четырехугольник, в котором только две стороны параллельны друг другу. Эти стороны являются основаниями трапеции. Две другие стороны называются боковыми сторонами.
Равнобедренной называется та трапеция, в которой длины боковых сторон равны друг другу.
Средняя линия трапеции
Средняя линия — это та линия, которая соединяет середины двух боковых сторон фигуры.
Как найти среднюю линию трапеции, если трапеция равнобедренная?
Есть несколько способов.
Способы нахождения средней линии равнобедренной трапеции
Способ 1.
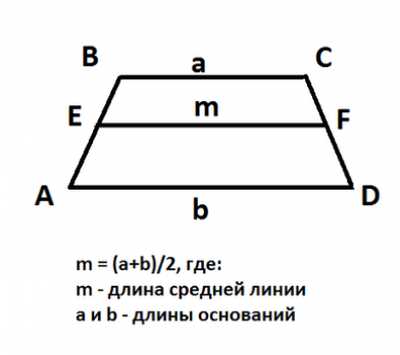
Если мы знаем длины оснований трапеции, то используем формулу:
- m = (a+b)/2, где:
- m — длина средней линии
- а и b — длины оснований
Способ 2.
Если мы знаем длину боковой стороны, то нам понадобятся дополнительные сведения. Здесь могут быть два случая:
Случай А
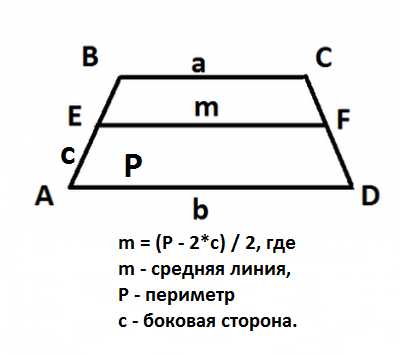
Нам будет достаточно длины боковой стороны и периметра трапеции.
- Формула: m = (P — 2*c) / 2, где
- m — средняя линия,
- P — периметр
- с — боковая сторона.
Случай Б
Кроме длины боковой стороны нужно будет знать длину высоты трапеции и длину одного из оснований.
Формула: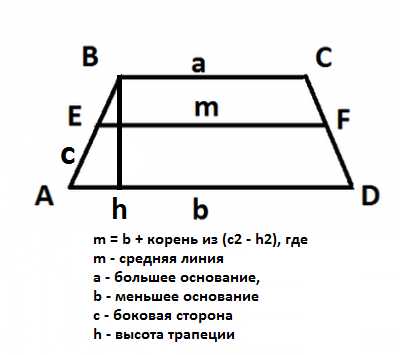
- m = a — корень из (c2 — h2)
или
elhow.ru
Средняя линия равнобедренной трапеции
Добрый вечер!
Спасибо за то, что обратились к нам за помощью. Я уверена, что мы сможем Вам помочь.
Давайте сначала вспомним, что трапеция — четырёхугольник, у которого две стороны — параллельны (основания), а другие — нет (боковые стороны).
В свою очередь, средняя линия — это отрезок, который соединяет середины боковых сторон.
А теперь давайте подумаем, чему может быть равна средняя линия равнобедренной трапеции. Для этого существует определённая формула, которая очень лёгкая для запоминания:
где — основания трапеции
Как видим, нам всего навсего нужно знать основания трапеции.
Давайте рассмотрим задачу. Нам дана трапеция ABCD, BC и AD — основания равнобедренной трапеции, которые равны 5 и 10 см соответственно. Чему равна средняя линия равнобедренной трапеции (KB)
Теперь найдём, чему равна средняя линия равнобедренной трапеции:
Как видите, нет ничего сложного в том, чтоб найти среднюю линию равнобедренной трапеции, а особенно с известными основаниями. Надеюсь, в дальнейшем у Вас не будет возникать вопросов в подобных задачах. Если что, мы всегда готовы помочь Вам разобраться. Удачи Вам!
Ответ: см
ru.solverbook.com
Средняя линия равнобедренной трапеции
1. Формула средней линии равнобедренной трапеции через основания
a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона
α — угол при нижнем осровании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
α — угол при нижнем осровании
m — средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
zdesformula.ru
Все формулы диагонали равнобедренной трапеции
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
Формула диагонали трапеции (d ):
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α, β — углы трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
3. Формула длины диагонали равнобедренной трапеции
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
m — средняя линия трапеции
S — площадь трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через высоту и стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
h — высота трапеции
α — угол при нижнем основании
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
zdesformula.ru
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
то
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
откуда
www.uznateshe.ru
Формулы сторон трапеции
1. Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
zdesformula.ru