Метод интервалов – универсальный метод решения неравенств с модулем
Чем больше человек понимает, тем сильнее в нем желание понимать
Фома Аквинский
Метод интервалов позволяет решать любые уравнения, содержащие модуль. Суть этого метода в том, чтобы разбить числовую ось на несколько участков (интервалов), причем разбить ось нужно именно нулями выражений, стоящих в модулях. Затем на каждом из получившихся участков всякое подмодульное выражение либо положительно, либо отрицательно. Поэтому каждый из модулей может быть раскрыт или со знаком минус, или со знаком плюс. После этих действий остается лишь решить каждое из полученных простых уравнений на рассматриваемом интервале и объединить полученные ответы.
Рассмотрим данный метод на конкретном примере.
|x + 1| + |2x – 4| – |x + 3| = 2x – 6.
1) Найдем нули выражений, стоящих в модулях. Для этого нужно приравняем их к нулю, и решить полученные уравнения.
x + 1 = 0 2x – 4 = 0 x + 3 = 0
x = -1 2x = 4 x = -3
x = 2
2) Расставим получившиеся точки в нужном порядке на координатной прямой. Они разобьют всю ось на четыре участка.
3) Определим на каждом из получившихся участков знаки выражений, стоящих в модулях. Для этого подставляем в них любые числа с интересующих нас интервалов. Если результат вычислений – число положительное, то в таблице ставим «+», а если число отрицательное, то ставим «–». Это можно изобразить так:
4) Теперь будем решать уравнение на каждом из четырех интервалов, раскрывая модули с теми знаками, которые проставлены в таблице. Итак, рассмотрим первый интервал:
I интервал (-∞; -3). На нем все модули раскрываются со знаком «–». Получим следующее уравнение:
-(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. Приведем подобные слагаемые, раскрыв предварительно скобки в полученном уравнении:
-x – 1 – 2x + 4 + x + 3 = 2x – 6
-4x = -12
x = 3.
Полученный ответ не входит в рассматриваемый интервал, поэтому в окончательный ответ писать его не надо.
II интервал [-3; -1). На этом интервале в таблице стоят знаки «–», «–», «+». Именно так и раскрываем модули исходного уравнения:
-(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Упростим, раскрыв при этом скобки:
-x – 1 – 2x + 4 – x – 3 = 2x – 6. Приведем в полученном уравнении подобные:
-5x = -6
x = 6/5. Полученное число не принадлежит рассматриваемому интервалу, поэтому оно не является корнем исходного уравнения.
III интервал [-1; 2). Раскрываем модули исходного уравнения с теми знаками, которые стоят на рисунке в третьей колонке. Получаем:
(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Избавимся от скобок, перенесем слагаемые, содержащие переменную x в левую часть уравнения, а не содержащие x в правую. Будем иметь:
x + 1 – 2x + 4 – x – 3 = 2x – 6
-4x = -8
x = 2.
В рассматриваемый интервал число 2 не входит.
IV интервал [2; +∞). Все модули раскрываем со знаком «+». Получим:
(x + 1) + (2x – 4) – (x + 3) = 2x – 6.
x + 1 + 2x – 4 – x – 3 = 2x – 6
0 = 0.
После преобразований уравнение превратилось в верное равенство. Это говорит о том, что любое число из рассматриваемого интервала будет являться решением исходного уравнения. Значит ответом, как на этом интервале, так и во всем уравнении является множество чисел, удовлетворяющих условию x ≥ 2.
Ответ: x ≥ 2.
Метод интервалов хоть и является универсальным методом решения уравнений с модулем, его применение не всегда оправдано. Порой решить уравнение выходит гораздо быстрее, используя, например, определение модуля или какие-то другие методы.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Решение уравнений с модулем методом интервалов
Решение уравнений с модулем методом интервалов.
Подготовила
учитель математики МКОУ «Хотьковская СОШ»
Думиничского района Калужской области
Наталья Николаевна Коломина
2017
Определение модуля
Модулем (абсолютной величиной) числа называется неотрицательное число:
х ∈ R
Свойства модуля
0 Меняем знаки -х + 2 = 3 Не меняем знаки -1 ∈ (-∞ ; 2] х – 2 = 3 -х = 1 х = -1 х = 5 5 ∈ (2 ; + ∞) -1 – корень уравнения 5 – корень уравнения. | х-2 |= 3 Посмотреть решение х – 2 = 0 х = 2 Ответ: -1; 5.»
2
х ∈ (-∞ ; 2]
х ∈ (2 ; + ∞)
х – 2 ≤ 0
х – 2 0
Меняем знаки
-х + 2 = 3
Не меняем знаки
-1 ∈ (-∞ ; 2]
х – 2 = 3
-х = 1
х = -1
х = 5
5 ∈ (2 ; + ∞)
-1 – корень уравнения
5 – корень уравнения.
| х-2 |= 3
Посмотреть решение
х – 2 = 0
х = 2
Ответ: -1; 5.
Уравнения вида | х |= а
2,5
х ∈ (-∞ ; 2,5]
х ∈ (2,5 ; + ∞)
5 – 2х ≥ 0
5 – 2х
Не меняем знаки
Меняем знаки
5 – 2х = 4
-5 + 2х = 4
-2х = 4 – 5
0,5 ∈ (-∞ ; 2,5]
-2х = -1
0,5 – корень уравнения
4,5 ∈ (2,5 ; + ∞)
2х = 4 + 5
4,5 – корень уравнения.
2х = 9
х = 0,5
х = 4,5
| 5 – 2х |= 4
Посмотреть решение
5 – 2х = 0
-2х = -5
х = 2,5
Ответ: 0,5; 4,5.
Уравнения вида | х |= а
-8/3
х ∈ (-∞ ; -8/3]
3х + 8 ≥ 0
х ∈ (-8/3 ; + ∞)
3х + 8
Не меняем знаки
Меняем знаки
3х + 8 = 7
-1/3 ∉ (-∞ ; -8/3]
3х = 7 – 8
-3х – 8 = 7
-1/3 – не корень уравнения
3х = -1
-5 ∉ (-8/3 ; + ∞)
-3х = 7 + 8
-5 – не корень уравнения.
х = -1/3
-3х = 15
х = -5
7 = | 3х + 8
Посмотреть решение
3х + 8= 0
3х = -8
х = -8/3
Ответ: корней нет
0 + -х + 2х = 1 + 1 х + 1 = -2х + 1 2х – 1 ≤ 0 — х + 1 0 + 2 ∉ (-∞ ; -1] 3х = 0 2х – 1 0 + х = 2 2 – не корень уравнения х + 1 = 2х – 1 0 ∈ (-1 ; 0,5] 0,5 – корень уравнения х = 0 х – 2х = -1 – 1 2 ∈ (0,5 ; + ∞) -х = -2 2 – корень уравнения. х = 2 Посмотреть решение х + 1= 0 х = -1 2х — 1= 0 2х = 1 х = 0,5 Ответ: 0,5; 2.»
Уравнения вида | х |=| у |
0,5
-1
| х + 1 |=| 2х -1 |
х ∈ (-∞ ; -1]
х ∈ (-1 ; 0,5]
х + 1 ≤ 0 —
2х – 1 —
-х – 1 = -2х + 1
х ∈ (0,5 ; + ∞)
х + 1 0 +
-х + 2х = 1 + 1
х + 1 = -2х + 1
2х – 1 ≤ 0 —
х + 1 0 +
2 ∉ (-∞ ; -1]
3х = 0
2х – 1 0 +
х = 2
2 – не корень уравнения
х + 1 = 2х – 1
0 ∈ (-1 ; 0,5]
0,5 – корень уравнения
х = 0
х – 2х = -1 – 1
2 ∈ (0,5 ; + ∞)
-х = -2
2 – корень уравнения.
х = 2
Посмотреть решение
х + 1= 0
х = -1
2х — 1= 0
2х = 1
х = 0,5
Ответ: 0,5; 2.
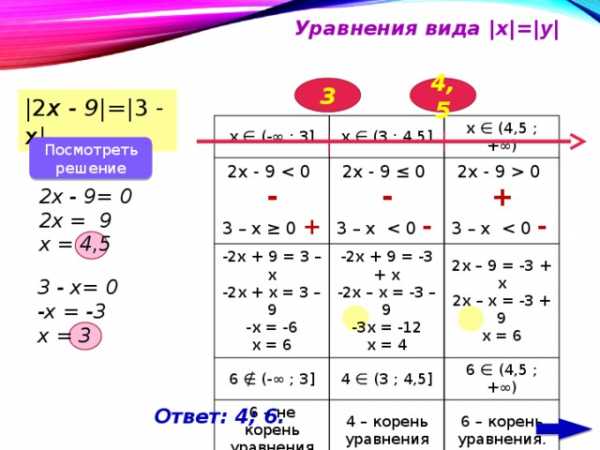0 + -2х – х = -3 – 9 3 – х — -х = -6 2х – 9 = -3 + х 6 – не корень уравнения 4 ∈ (3 ; 4,5] 4 – корень уравнения 2х – х = -3 + 9 х = 6 -3х = -12 6 ∈ (4,5 ; + ∞) х = 4 х = 6 6 – корень уравнения. Посмотреть решение 2х — 9= 0 2х = 9 х = 4,5 3 — х= 0 -х = -3 х = 3 Ответ: 4; 6.»
Уравнения вида | х |=| у |
3
4,5
|2 х — 9
х ∈ (-∞ ; 3]
х ∈ (3 ; 4,5]
2х — 9 —
2х — 9 ≤ 0 —
3 – х ≥ 0 +
х ∈ (4,5 ; + ∞)
-2х + 9 = 3 – х
-2х + 9 = -3 + х
3 – х —
-2х + х = 3 – 9
6 ∉ (-∞ ; 3]
2х — 9 0 +
-2х – х = -3 – 9
3 – х —
-х = -6
2х – 9 = -3 + х
6 – не корень уравнения
4 ∈ (3 ; 4,5]
4 – корень уравнения
2х – х = -3 + 9
х = 6
-3х = -12
6 ∈ (4,5 ; + ∞)
х = 4
х = 6
6 – корень уравнения.
Посмотреть решение
2х — 9= 0
2х = 9
х = 4,5
3 — х= 0
-х = -3
х = 3
Ответ: 4; 6.
0 + 3(-х – 1) = 1 – 2х х ∈ (0,5 ; + ∞) х + 1 0 + 3(х + 1) = 1 – 2х 1 – 2х ≥ 0 + -3х – 3 = 1 – 2х -4 ∈ (-∞ ; -1] х + 1 0 + 3х + 3 = 1 – 2х 1 – 2х — -х = 4 -4 – корень уравнения 3(х+1) = -1 + 2х -0,4 ∈ (-1 ; 0,5] -0,4 – корень уравнения х = -4 3х+3=2х-1 5х = -2 -4 ∉ (0,5 ; + ∞) Х = -0,4 х = -4 -4 – не корень уравнения. Посмотреть решение х + 1= 0 х = -1 1 — 2х= 0 -2х = -1 х = 0,5 Ответ: -4; -0,4.»
Уравнения вида | х |=| у |-1
0,5
3| х + 1|=| 1 — 2х |
х ∈ (-∞ ; -1]
х ∈ ( -1 ; 0,5]
х + 1 ≤ 0 —
1 – 2х 0 +
3(-х – 1) = 1 – 2х
х ∈ (0,5 ; + ∞)
х + 1 0 +
3(х + 1) = 1 – 2х
1 – 2х ≥ 0 +
-3х – 3 = 1 – 2х
-4 ∈ (-∞ ; -1]
х + 1 0 +
3х + 3 = 1 – 2х
1 – 2х —
-х = 4
-4 – корень уравнения
3(х+1) = -1 + 2х
-0,4 ∈ (-1 ; 0,5]
-0,4 – корень уравнения
х = -4
3х+3=2х-1
5х = -2
-4 ∉ (0,5 ; + ∞)
Х = -0,4
х = -4
-4 – не корень уравнения.
Посмотреть решение
х + 1= 0
х = -1
1 — 2х= 0
-2х = -1
х = 0,5
Ответ: -4; -0,4.
0 Меняем знаки Не меняем знаки -х — 1 = 1 – 2х х = 2 2 ∉ (-∞ ; -1] х + 1 = 1 – 2х 0 ∈ (-1 ; 0,5 ] 3х = 0 2 – не корень уравнения х = 0 0 – корень уравнения. Посмотреть решение х + 1= 0 х = -1 1 – 2х ≥ 0 -2х ≥ -1 х ≤ 0,5 Ответ: 0.»
Уравнения вида | х |= у
Отличие от уравнений 1 вида в том, что в правой части тоже переменная.
-1
| х+1 |= 1-2х
х ∈ (-∞ ; -1]
х + 1 ≤ 0
х ∈ (-1 ; 0,5 ]
х + 1 0
Меняем знаки
Не меняем знаки
-х — 1 = 1 – 2х
х = 2
2 ∉ (-∞ ; -1]
х + 1 = 1 – 2х
0 ∈ (-1 ; 0,5 ]
3х = 0
2 – не корень уравнения
х = 0
0 – корень уравнения.
Посмотреть решение
х + 1= 0
х = -1
1 – 2х ≥ 0
-2х ≥ -1
х ≤ 0,5
Ответ: 0.
0 Меняем знаки Не меняем знаки -2х — 1 = 3 – х 2х + 1 = 3 – х -4 ∈ (-∞ ; -0,5] -х = 4 2/3 ∈ (-0,5 ; 3 ] 3х = 2 -4 – корень уравнения х = -4 х = 2/3 2/3 – корень уравнения. Посмотреть решение 2х + 1= 0 2х = -1 х = -0,5 3 — х ≥ 0 -х ≥ -3 х ≤ 3 Ответ: -4; 2/3.»
Уравнения вида | х |= у
Отличие от уравнений 1 вида в том, что в правой части тоже переменная.
-0,5
|2 х+1 | = 3-х
х ∈ (-∞ ; -0,5]
х ∈ (-0,5 ; 3 ]
2х + 1 ≤ 0
2х + 1 0
Меняем знаки
Не меняем знаки
-2х — 1 = 3 – х
2х + 1 = 3 – х
-4 ∈ (-∞ ; -0,5]
-х = 4
2/3 ∈ (-0,5 ; 3 ]
3х = 2
-4 – корень уравнения
х = -4
х = 2/3
2/3 – корень уравнения.
Посмотреть решение
2х + 1= 0
2х = -1
х = -0,5
3 — х ≥ 0
-х ≥ -3
х ≤ 3
Ответ: -4; 2/3.
0 Меняем знаки Не меняем знаки -2(-х – 4) = 3 – х -2(х + 4) = 3 – х -5/3 ∉ (-∞ ; -4] 2х + 8 = 3 – х -2х – 8 = 3 – х -11 ∉ (-4 ; + ∞) -5 – не корень уравнения 3х = -5 -12 – не корень уравнения. х = -5/3 -х = 11 х = -11 Посмотреть решение х + 4 = 0 х = -4 3 — х ≥ 0 -х ≥ -3 х ≤ 3 Ответ: корней нет.»
Уравнения вида | х |= у
Отличие от уравнений 1 вида в том, что в правой части тоже переменная.
— 4
-2| х+4 | = 3-х
х ∈ (-∞ ; -4]
х + 4 ≤ 0
х ∈ (-4 ; + ∞)
х + 4 0
Меняем знаки
Не меняем знаки
-2(-х – 4) = 3 – х
-2(х + 4) = 3 – х
-5/3 ∉ (-∞ ; -4]
2х + 8 = 3 – х
-2х – 8 = 3 – х
-11 ∉ (-4 ; + ∞)
-5 – не корень уравнения
3х = -5
-12 – не корень уравнения.
х = -5/3
-х = 11
х = -11
Посмотреть решение
х + 4 = 0
х = -4
3 — х ≥ 0
-х ≥ -3
х ≤ 3
Ответ: корней нет.
0 + х+3 + (2х–1) = 1 х = 5 2х — 1 ≤ 0 — х + 3 0 + 5 ∉ (-∞ ; -3] х+3+2х-1=1 2х — 1 0 + х+3-2х+1 = 1 5 – не корень уравнения -1/3 ∈ (-3 ; 0,5] -1/3 – корень уравнения 3х = -1 -х = -3 3 ∈ (0,5 ; + ∞) х = -1/3 х = 3 3 – корень уравнения. х + 3= 0 х = -3 2х – 1 = 0 2х = 1 х = 0,5 Ответ: -1/3; 3.»
| х + 3|-| 2х — 1 | = 1
Посмотреть решение
-3
0,5
х ∈ (-∞ ; -3]
х ∈ ( -3 ; 0,5]
х + 3 ≤ 0 —
-х – 3 + 2х – 1 = 1
х ∈ (0,5 ; + ∞)
2х — 1 —
х + 3 0 +
х+3 + (2х–1) = 1
х = 5
2х — 1 ≤ 0 —
х + 3 0 +
5 ∉ (-∞ ; -3]
х+3+2х-1=1
2х — 1 0 +
х+3-2х+1 = 1
5 – не корень уравнения
-1/3 ∈ (-3 ; 0,5]
-1/3 – корень уравнения
3х = -1
-х = -3
3 ∈ (0,5 ; + ∞)
х = -1/3
х = 3
3 – корень уравнения.
х + 3= 0
х = -3
2х – 1 = 0
2х = 1
х = 0,5
Ответ: -1/3; 3.
0 + х ∈ (5/3 ; + ∞) 4/3 ∉(-∞ ; -1,5] х + 1 – 3х – 5 ≤ 0 – х = -10 -10 ∉ (-1,5 ; -1] 3х – 5 0 + 3 + 2х 0 + х + 1 ≤ 0 – х = 2 4/3 – не корень уравнения 3 + 2х 0 + х = 4/3 х + 1 0 + -10 – не корень уравнения 2 ∉ (-1 ; 5/3 ] 4/3∉ (5/3 ; + ∞) х + 1 0 + 2 – не корень уравнения. 4/3 – не корень уравнения. 3 + 2х = 0 2х = -3 х = -1,5 х + 1 = 0 х = -1 Ответ: корней нет.»
|3 х — 5|+|3 + 2х | = 2|х + 1|
5/3
Посмотреть решение
-1
-1,5
3х – 5 = 0
Зх = 5
х = 5/3
х ∈ (-∞ ; -1,5]
х ∈ ( -1,5 ; -1]
3х – 5 –
3 + 2х ≤ 0 –
3х – 5 –
х = 4/3
х ∈ (-1 ; 5/3 ]
3 + 2х 0 +
х ∈ (5/3 ; + ∞)
4/3 ∉(-∞ ; -1,5]
х + 1 –
3х – 5 ≤ 0 –
х = -10
-10 ∉ (-1,5 ; -1]
3х – 5 0 +
3 + 2х 0 +
х + 1 ≤ 0 –
х = 2
4/3 – не корень уравнения
3 + 2х 0 +
х = 4/3
х + 1 0 +
-10 – не корень уравнения
2 ∉ (-1 ; 5/3 ]
4/3∉ (5/3 ; + ∞)
х + 1 0 +
2 – не корень уравнения.
4/3 – не корень уравнения.
3 + 2х = 0
2х = -3
х = -1,5
х + 1 = 0
х = -1
Ответ: корней нет.
Ссылки на изображения:
http://mediaryazan.ru/upload/iblock/fba/ ЕГЭ. png
Интернет — источники:
http://youclever.org/book/uravneniya-s-modulem-2
http://ru.solverbook.com/primery-reshenij/primery-resheniya-uravnenij-s-modulem/
http:// mathus.ru/math/modul.pdf
http://matica.org.ua/metodichki-i-knigi-po-matematike/algebraicheskie-uravneniia-i-neravenstva-funktcii-logarifmy/19-uravneniia-s-modulem
multiurok.ru
Репетитор по математике. Решение уравнений и неравенств с модулем
1. Видеолекция. Решение уравнений и неравенств с модулем.
часть 1
часть 2
2. Видеолекция. Комбинированные методы решения уравнений и неравенств с модулем.
3. Учет области определения при решении уравнений с модулем.
Решить уравнения:
1)
2)
4. Решить уравнение:
5. Решить неравенство:
6. Решение неравенства с модулем методом интервалов.
Решить неравенство:
7. Решить систему неравенств (Задание С3):
ege-ok.ru
Обобщённый метод интервалов при решении неравенств — Мегаобучалка
Преподаватели ГОУ СОШ № 853
Белов А.И.
Фадеичева Т.П.
- Метод интервалов для целых неравенств
При решении многих задач, в том числе и задач Единого Государственного экзамена (ЕГЭ) часто возникает необходимость либо непосредственно решить неравенство, либо этот шаг – решение неравенства возникает как вспомогательный при решении других, более сложных и объёмных задач.
Простейший случай неравенств – это линейные и квадратные неравенства. Подобные задачи обычно встречаются довольно редко сами по себе, но часто – в составе других.
Задача 1 (МЭСИ)
Найти наименьшее целое решение неравенства
Ответ:
Стоит обратить внимание на то, что подобная формулировка задачи «найти наибольшее целое решение», «наименьшее целое решение», «количество целых решений» и т.п. довольно часто встречается в вариантах ЕГЭ, особенно в части В. Кроме этого, довольно распространённая ошибка – «забывчивость» при умножении (делении) неравенства на отрицательное число, поэтому, по возможности, стоит избегать этой операции – перенося элементы неравенства в соответствующую сторону.
Задача 2 (МТУСИ)
Найти количество целых решений неравенства
Количество целых решений 11.
Ответ: 11.
Поскольку подобные задачи – в основном задачи части В – расстановку знаков на числовой прямой можно строго не объяснять, чтобы избежать потери времени. Однако, при этом надо довольно чётко представлять себе «правило чередования знаков», а именно – если левая часть неравенства приведена к стандартному виду , а в правой части находится 0, то на крайнем правом участке будет знак «+», а далее – при переходе через корень чётной кратности – знак сохраняется, при переходе через корень нечётной кратности – знак изменяется. Проиллюстрируем это на следующем примере.
Задача 3
Решить неравенство
Отметим точки -2; 1; 3; 4 на числовой прямой и воспользуемся правилом чередования знаков.
Тогда
Ответ:
Распространенной ошибкой является потеря изолированных точек, на что стоит обратить особое внимание.
Задача 4 (МИЭТ, 2004)
Решить неравенство
1 способ(замена в неравенстве)
Пусть
Тогда неравенство примет вид
2 способ (обобщённый метод интервалов)
Данный способ наиболее универсален при решении неравенств практически любого типа. Схема решения выглядит следующим образом:
1. Привести неравенство к такому виду, где в левой части находится функция , а в правой 0.
2. Найти область определения функции
3. Найти нули функции , то есть – решить уравнение (а решать уравнение обычно проще, чем решать неравенство)
4. Изобразить на числовой прямой область определения и нули функции.
5. Определить знаки функции на полученных интервалах.
6. Выбрать интервалы, где функция принимает необходимые значения и записать ответ.
Значит,
Ответ:
Подобный способ боле универсален и допускает, в некоторой степени большую свободу действий при решении неравенств, в чём и убедимся на следующих примерах.
- Метод интервалов для рациональных неравенств
При решении рациональных неравенств, по существу – единственное отличие от решения целых неравенств – это необходимость учесть область определения неравенства. А именно – деление на ноль не определено, поэтому знаменатель дроби не может равняться нулю.
Задача 5 (диагностическая работа № 3, 2007/2008, В6)
Сколько целочисленных решений имеет неравенство
Рассмотрим функцию
Область определения функции
Нули функции
Значит,
Таким образом, количество целочисленных решений 8.
Ответ: 8.
- Метод интервалов для неравенств с модулями
Аналогичным образом обобщённый метод интервалов может быть использован при решении неравенств с модулями (в «противовес» обычному способу решения подобных неравенств – рассмотрения случаев)
Задача 6 (МГУ, геологический факультет, 2005)
Решите неравенство
1 способ (Обобщённый метод интервалов)
Рассмотрим функцию
Область определения функции
Нули функции
2 способ (Рассмотрение случаев)
1 случай. Если
Тогда неравенство принимает вид
Но, учитывая условие раскрытия модуля – получаем
2 случай. Если
Тогда неравенство принимает вид
Но, учитывая условие раскрытия модуля – получаем
Объединяя полученные ответы – имеем
Ответ:
Часто обобщённый метод интервалов удобнее и короче традиционного способа решения.
- Метод интервалов для иррациональных неравенств
При решении иррациональных неравенств область определения функции естественным образом находится из условия неотрицательности подкоренного выражения.
Задача 7 (Диагностическая работа №2, 2008/2009, С15)
Решите неравенство
Рассмотрим функцию
Область определения
Нули функции
Учитывая область определения, получаем, что нули функции
Определим знаки функции на образовавшихся промежутках (это задача С – необходимо обосновывать!)
Знаки, принимаемые функцией , определяются значением второго множителя, так как корень неотрицателен на области определения. Так как второй множитель – квадратный трехчлен, графиком является парабола, ветви которой направлены вверх, то при , а при
Значит,
Ответ:
Из приведённого примера виден один из недостатков метода – может быть затруднено определение знаков на полученных интервалах, особенно, если точки расположены довольно близко друг к другу и/или когда значения нулей или границ области определения – «плохие».
В тоже время, обобщённый метод интервалов во многих случаях представляет собой хорошую альтернативу традиционным схемам решения иррациональных неравенств вида и
Задача 8 (МГУ, экономический факультет, 2003)
Решить неравенство
Рассмотрим функцию
Область определения функции найдём из условия
Нули функции найдём, решив уравнение
Проверкой убеждаемся, что является корнем уравнения, а — корнем уравнения не является.
Определим знаки функции на полученных интервалах
Значит,
Ответ:
- Метод интервалов для показательных и логарифмических неравенств
Задача 9 (Демоверсия 2009 варианта ЕГЭ по версии МИОО, С10)
Решить неравенство
Рассмотрим функцию
Область определения
Нули функции
Определим знаки функции на образовавшихся промежутках
Ответ:
Обобщённый метод интервалов может быть использован и вместо традиционного способа решения логарифмических и показательных неравенств.
Задача 10 (МГУ, МГТУ)
Решить неравенство
Рассмотрим функцию
Область определения
Нули функции
С учётом области определения – ответ уравнения
Определим знаки функции на полученных интервалах
Значит,
Ответ:
- Метод интервалов для смешанных неравенств
Наиболее полезен обобщённый метод интервалов при решении неравенств «смешанного» типа, т.е. неравенств, содержащих части различного вида.
Задача 11 (РЭА)
Найти наименьшее целое решение неравенства
Рассмотрим функцию
Область определения
Нули функции
Определим знаки функции на образовавшихся промежутках
Значит, . Наименьшее целое решение – число .
Ответ:
- Метод замены множителей
В заключении рассмотрим так называемый «метод замены множителей», который может оказаться полезным при решении неравенств, содержащих части разного вида.
Например, при решении показательных неравенств, в которых неизвестное встречается и в основании, и в показателе степени, полезно использовать следующее правило (см. И.Ф. Шарыгин, В.И. Голубев «Решение задач 11»): выражение при имеет тот же знак, что , и противоположный, если Оба варианта можно объединить в один: выражения и имеют один знак. При этом, конечно нельзя забывать об области определения выражения (должно быть положительным).
Задача 12
Решите неравенство
Решение.
Воспользуемся утверждением
Пусть
Таким образом, для всех
+ — + — +
-1 0 3 х
Ответ:
Подобные «замены множителей» могут быть (с соответствующими изменениями) произведены и при решении неравенств с модулями, иррациональных неравенств, логарифмических неравенств и т.д. Особенно данный метод полезен при решении неравенств смешанного вида.
Задача 13
Решить неравенство
Область определения данного неравенства найдём из условий
Воспользуемся методом «замены множителей».
Отсюда,
Ответ:
Задача 14 (МГИЭТ 2001, С-4-7)
Решить неравенство
при
Отдельно следует рассмотреть случай при этом выражения, стоящие в показателях степени должны быть положительными.
1.
Решением последней системы является
не удовлетворяет этому условию, следовательно, не является решением неравенства.
удовлетворяет условию, следовательно, является решением неравенства.
2.
+ — + х
— + — + х
Таким образом, получаем
Ответ:
P.S. Если в выражении допустить отрицательные значения то надо требовать, чтобы значение было целым числом. Тогда при получим то есть Тогда Значит, то есть значение выражения не является целым числом.
megaobuchalka.ru