Формула хорда – Формула длины хорды окружности

Содержание

Хорда

Развернуть структуру обучения

Свернуть структуру обучения

Описание курса
Аксиомы планиметрии
Точки, отрезки и прямые
Угол. Углы на плоскости
Площадь геометрической фигуры
Окружность. Уравнение окружности
Треугольник (Трикутник)
Четырехугольник
Тригонометрия
- Тангенс и его свойства
- Тригонометрические соотношения в прямоугольном треугольнике
- Тригонометрический круг
- Радианы и градусы. Радiани i градуси
- Таблица значений тригонометрических функций
  - Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15)
  - Синус, косинус и тангенс угла 30 градусов (sin cos tg 30) — таблица значений
  - Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
  - Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60)
  - Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105)
  - Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120)
- Тригонометрические тождества и преобразования
Многоугольники

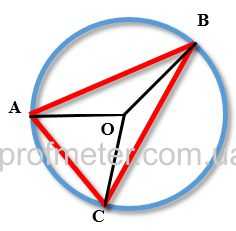
Определение хорды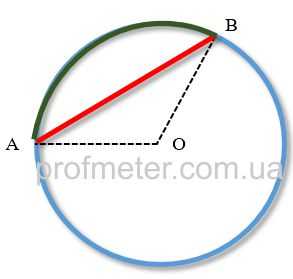

Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.

На рисунке хорда обозначена как отрезок AB красного цвета. Оба его конца находятся на окружности

Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом.

Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.

Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.

Свойства хорды к окружности

Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное

Наибольшая возможная хорда является диаметром
Серединный перпендикуляр к хорде проходит через центр окружности

Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу

Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.

Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Свойства хорды и вписанного угла

На рисунке [1] вписанный угол обозначен обозначен как ACB, хорда окружности — AB

Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны.
Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°.
Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла.
Если вписанный угол опирается на диаметр, то этот угол является прямым.

Свойства хорды и центрального угла

На рисунке [2] центральный угол обозначен как AOB, хорда как AB.

Если хорды стягивают равные центральные углы, то эти хорды равны.
Если хорды равны, то эти хорды стягивают равные центральные углы.
Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.

Формулы нахождения хорды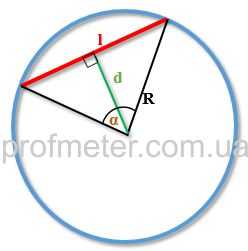

Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде

Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.

Решение задач

Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.

Задача.

Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.

Решение.

Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x

Согласно свойству хорд AS x SB = CS x SD, тогда

2х * 3х = 5 * 12
6х² = 60
х² = 10
x = √10

Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10

Ответ: 5√10

Задача.

Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.

Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то

3,5х + 5,5х + 3х = 360
12х = 360
х = 30

Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165

Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.

Откуда углы треугольника равны:

90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5

Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;

Задачи про окружность | Описание курса | Треугольник (Трикутник)

profmeter.com.ua

Хорда (геометрия) — это… Что такое Хорда (геометрия)?

У этого термина существуют и другие значения, см. Хорда. 1 — секущая, 2 — хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зеленым цветом), 4 — дуга

Хорда в планиметрии — отрезок прямой линии, соединяющей две точки данной кривой (например, окружности, эллипса, параболы).

Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегмент.

Хорда, проходящая через центр окружности, называется диаметр. Диаметр — это самая длинная хорда в окружности.

Свойства хорд

Хорды являются равноудаленными от центра окружности тогда и только тогда, когда они равны по длине.
Перпендикуляр с середины хорды окружности проходит через центр этой окружности.
Радиус, перпендикулярный к хорде, делит эту хорду пополам.
Дуги, заключенные между равными хордами, равны.
Дуги, заключенные между параллельными хордами, равны.
При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.

Дуга AB равна дуге CD. Дуга BC равна дуге DA
Произведение отрезков одной хорды равно произведению отрезков другой хорды: AE×EB = CE×ED

Основные формулы

Длина хорды:

Связанные понятия и утверждения

Ссылки

dic.academic.ru

Длина хорды: основные понятия

Бывают случаи в жизни, когда знания, полученные во время школьного обучения, очень полезны. Хотя во время учебы эти сведения казались скучными и ненужными. Например, как можно использовать информацию о том, как находится длина хорды? Можно предположить, что для специальностей, не связанных с точными науками, такие знания малопригодны. Однако можно привести много примеров (от конструирования новогоднего костюма до сложного устройства аэроплана), когда навыки решения задач по геометрии являются нелишними.

Понятие «хорда»

Данное слово означает «струна» в переводе с языка родины Гомера. Оно было введено математиками древнего периода.

Хордой обозначают в разделе элементарной геометрии часть прямой линии, которая объединяет две любые точки какой-либо кривой (окружности, параболы или эллипса). Другими словами, данный связующий геометрический элемент находится на прямой, пересекающей заданную кривую в нескольких точках. В случае окружности длина хорды заключена между двумя точками этой фигуры.

Часть плоскости, ограниченная прямой, пересекающей окружность, и ее дугой называют сегментом. Можно отметить, что с приближением к центру длина хорды увеличивается. Часть окружности, находящуюся между двумя точками пересечения данной прямой, называют дугой. Ее мерой измерения является центральный угол. Вершина данной геометрической фигуры находится в середине круга, а стороны упираются в точки пересечения хорды с окружностью.

Свойства и формулы

Длина хорды окружности может быть вычислена по следующим условным выражениям:

L =D×Sinβ или L=D×Sin(1/2α), где β – угол при вершине вписанного треугольника;

D – диаметр окружности;

α – центральный угол.

Можно выделить некоторые свойства данного отрезка, а также других фигур, связанных с ним. Эти моменты приведены в следующем списке:

Любые хорды, находящиеся на одинаковом расстоянии от центра, имеют равные длины, при этом обратное утверждение также верно.
Все углы, которые вписаны в окружность и опираются на общий отрезок, который объединяет две точки (при этом их вершины находятся в одной стороне от данного элемента), являются идентичными по величине.
Самая большая хорда является диаметром.
Сумма любых двух углов, если они опираются на данный отрезок, но при этом их вершины лежат в разных сторонах относительно него, составляет 180^о.
Большая хорда — по сравнению с аналогичным, но меньшим элементом — лежит ближе к середине данной геометрической фигуры.
Все углы, которые вписаны и опираются на диаметр, равны 90˚.

Другие вычисления

Чтобы найти длину дуги окружности, которая заключена между концами хорды, можно использовать формулу Гюйгенса. Для этого необходимо провести такие действия:

Обозначим искомую величину р, а хорда, ограничивающая данную часть окружности, будет иметь название АВ.
Найдем середину отрезка АВ и к ней поставим перпендикуляр. Можно отметить, что диаметр окружности, проведенный через центр хорды, образует с ней прямой угол. Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М.
Тогда отрезки АМ и ВМ можно назвать соответственно, как l и L.
Длина дуги может быть вычислена по следующей формуле: р≈2l+1/3(2l-L). Можно отметить, что относительная погрешность данного выражения при возрастании угла увеличивается. Так, при 60˚ она составляет 0,5%, а для дуги, равной 45˚, эта величина уменьшается до 0,02%.

Длина хорды может использоваться в различных сферах. Например, при расчетах и конструировании фланцевых соединений, которые широко распространены в технике. Также можно увидеть вычисление этой величины в баллистике для определения расстояния полета пули и так далее.

fb.ru

Хорда (геометрия) — Википедия. Что такое Хорда (геометрия)

Материал из Википедии — свободной энциклопедии 1 — секущая, 2 — хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зелёным цветом), 4 — дуга

Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).

Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды. Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда в окружности.

Свойства хорд окружности

Хорда и расстояние до центра окружности

Если расстояния от центра окружности до хорд равны, то эти хорды равны.

Если хорды равны, то расстояния от центра окружности до этих хорд равны.
Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше.
Если расстояние от центра окружности до хорды меньше, то эта хорда больше. Если расстояние от центра окружности до хорды больше, то эта хорда меньше.
Наибольшая возможная хорда является диаметром.
Наименьшая возможная хорда является точкой.
Если хорда проходит через центр окружности, то эта хорда является диаметром.
Если расстояние от центра окружности до хорды равно радиусу, то эта хорда является точкой.
Серединный перпендикуляр к хорде проходит через центр окружности.

Хорда и диаметр

Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде.
Если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам.
Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
Если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу.
Если диаметр перпендикулярен хорде, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
Если диаметр делит дугу пополам, то этот диаметр перпендикулярен хорде, стягивающей эту дугу.

Хорда и радиус

Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде.
Если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам.
Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
Если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
Если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Хорда и вписанный угол

Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны.
Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°.
Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла.
Если вписанный угол опирается на диаметр, то этот угол является прямым.

Хорда и центральный угол

Если хорды стягивают равные центральные углы, то эти хорды равны.
Если хорды равны, то эти хорды стягивают равные центральные углы.
Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.

Хорда и дуга

Если хорды стягивают равные дуги, то эти хорды равны.
Если хорды равны, то эти хорды стягивают равные дуги.
Из дуг, меньших полуокружности, большая дуга стягивается большей хордой, меньшая дуга стягивается меньшей хордой.
Из дуг, меньших полуокружности, большая хорда стягивает большую дугу, меньшая хорда стягивает меньшую дугу.
Из дуг, больших полуокружности, меньшая дуга стягивается большей хордой, большая дуга стягивается меньшей хордой.
Из дуг, больших полуокружности, большая хорда стягивает меньшую дугу, меньшая хорда стягивает большую дугу.
Хорда, стягивающая полуокружность, является диаметром.
Если хорды параллельны, то дуги, заключённые между этими хордами (не путать с дугами, стягиваемыми хордами), равны.

Другие свойства

Рис. 1. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}

При пересечении двух хорд AB и CD в точке E получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рис. 1): AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.
Если хорда делится пополам какой-либо точкой, то её длина самая маленькая по сравнению с длинами проведённых через эту точку хорд.