Формулы косинуса и синуса двойного угла – Формулы двойного угла в тригонометрии

Формулы двойного угла в тригонометрии

Формулы двойного угла дают возможность выразить тригонометрические функции (синус, косинус, тангенс, котангенс) угла ` 2\alpha` через эти самые функции угла `\alpha`.

Содержание статьи:

Перечень всех формул двойного угла

Записанный ниже список — это основные формулы двойного угла, которые наиболее часто используются в тригонометрии. Для косинуса их есть три, они все равносильны и одинаково важны.

`sin \ 2\alpha=` `2 \ sin \ \alpha \ cos \ \alpha`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha`, ` cos \ 2\alpha=1-2 \ sin^2 \alpha`, `cos \ 2\alpha=2 \ cos^2 \alpha-1`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}`

Следующие тождества выражают все тригонометрические функции угла ` 2\alpha` через функции тангенс и котангенс угла `\alpha`.

`sin \ 2\alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac { \ ctg \ \alpha-tg \ \alpha}2`

Формулы для косинуса и синуса двойного угла выполняются для любого угла `\alpha`. Формулы для тангенса двойного угла справедливы для тех `\alpha`, при которых определен `tg \ 2\alpha`, то  есть при ` \alpha\ne\frac\pi4+\frac\pi2 n, \ n \in Z`. Аналогично, для котангенса они имеют место для тех `\alpha`, при которых определен `ctg \ 2\alpha`, то  есть при ` \alpha\ne\frac\pi2 n, \ n \in Z`.

Доказательство формул двойного угла

Все формулы двойного угла выводятся из формул сумы и разности углов тригонометрических функций.

Возьмем две формулы, для сумы углов синуса и косинуса:

`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta` и `cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`. Возьмем `\beta=\alpha`, тогда `sin(\alpha+\alpha)=` `sin \ \alpha\ cos \ \alpha+cos \ \alpha\ sin \ \alpha=2 \ sin \ \alpha \ cos \ \alpha`, аналогично `cos(\alpha+\alpha)=` `cos \ \alpha\ cos \ \alpha-sin \ \alpha\ sin \ \alpha=cos^2 \alpha-sin^2 \alpha`, что и доказывает формулы двойного угла для синуса и косинуса.

Два другие равенства для косинуса ` cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1` сводятся к уже доказанному, если в них заменить 1 на `sin^2 \alpha+cos^2 \alpha=1`.  Так `1-2 \ sin^2 \alpha=` `sin^2 \alpha+cos^2 \alpha-2 \ sin^2 \alpha=` `cos^2 \alpha-sin^2 \alpha` и `2 \ cos^2 \alpha-1=` `2 \ cos^2 \alpha-(sin^2 \alpha+cos^2 \alpha)=` `cos^2 \alpha-sin^2 \alpha`.

Чтобы доказать формулы тангенса двойного угла и котангенса, воспользуемся определением этих функций. Запишем `tg \ 2\alpha` и `ctg \ 2\alpha` в виде `tg \ 2\alpha=\frac {sin \ 2\alpha}{cos \ 2\alpha}` и `ctg \ 2\alpha=\frac {cos \ 2\alpha}{sin \ 2\alpha}`. Применив уже доказанные формулы двойного угла для синуса и косинуса, получим `tg \ 2\alpha=\frac {sin \ 2\alpha}{cos \ 2\alpha}=\frac {2 \ sin \ \alpha \ cos \ \alpha}{cos^2 \alpha-sin^2 \alpha}` и `ctg \ 2\alpha=\frac {cos \ 2\alpha}{sin \ 2\alpha}=` `\frac {cos^2 \alpha-sin^2 \alpha}{2 \ sin \ \alpha \ cos \ \alpha}`.

В случае с тангенсом разделим числитель и знаменатель конечной дроби на `cos^2 \alpha`, для котангенса в свою очередь — на `sin^2 \alpha`.

`tg \ 2\alpha=\frac {sin \ 2\alpha}{cos \ 2\alpha}=\frac {2 \ sin \ \alpha \ cos \ \alpha}{cos^2 \alpha-sin^2 \alpha}=` `\frac {\frac{2 \ sin \ \alpha \ cos \ \alpha}{cos^2 \alpha}}{\frac{cos^2 \alpha-sin^2 \alpha}{cos^2 \alpha}}=` `\frac {2 \cdot \frac{ sin \alpha }{cos \alpha}}{1-\frac{sin^2 \alpha}{cos^2 \alpha}}=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}`.

`ctg \ 2\alpha=\frac {cos \ 2\alpha}{sin \ 2\alpha}=` `\frac {cos^2 \alpha-sin^2 \alpha}{2 \ sin \ \alpha \ cos \ \alpha}=` `\frac {\frac{cos^2 \alpha-sin^2 \alpha}{sin^2 \alpha}}{\frac{2 \ sin \ \alpha \ cos \ \alpha}{sin^2 \alpha}}=` `\frac {\frac{cos^2 \alpha}{sin^2 \alpha}-1}{2 \cdot \frac{cos \alpha}{ sin \alpha }}=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}`.

Предлагаем еще посмотреть видео, чтобы лучше закрепить теоретический материал:

Примеры использования формул при решении задач

Формулы двойного угла в большинстве случаев используются для преобразование тригонометрических выражений. Рассмотрим некоторые из случаем, как можно на практике применять их при решений конкретных задач.

Пример 1. Проверить справедливость тождеств двойного угла для `\alpha=30^\circ`.

Решение. В наших формулах используется два угла `\alpha` и `2\alpha`. Значение первого угла задано в условии, второго соответственно будет `2\alpha=60^\circ`. Также нам известны числовые значения для всех тригонометрических функций этих углов. Запишем их:

`sin 30^\circ=\frac 1 2`,  `cos 30^\circ=\frac {\sqrt 3}2`, `tg  30^\circ=\frac {\sqrt 3}3`, `ctg  30^\circ=\sqrt 3` и

`sin 60^\circ=\frac {\sqrt 3}2`,  `cos 60^\circ=\frac 1 2`, `tg  60^\circ=\sqrt 3`, `ctg  60^\circ=\frac {\sqrt 3}3`.

Тогда будем иметь

`sin 60^\circ=2  sin 30^\circ cos 30^\circ=` `2 \cdot \frac 1 2 \cdot \frac {\sqrt 3}2=\frac {\sqrt 3}2`,

`cos 60^\circ=cos^2 30^\circ-sin^2 30^\circ=` `(\frac {\sqrt 3}2)^2 \cdot (\frac 1 2)^2=\frac 1 2`,

`tg 60^\circ=\frac{2  tg 30^\circ}{1-tg^2 30^\circ}=` `\frac{2  \cdot \frac {\sqrt 3}3}{1-(\frac {\sqrt 3}3)^2}=\sqrt 3`,

`ctg  60^\circ=\frac{ctg^2 30^\circ-1}{2 \ ctg 30^\circ}=` `\frac{(\sqrt 3)^2-1}{2 \cdot \sqrt 3}=\frac {\sqrt 3}3`.

Что и доказывает справедливость равенств для заданного в условии угла.

Пример 2. Выразить `sin \frac {2\alpha}3` через тригонометрические функции угла `\frac {\alpha}6`.

Решение. Запишем угол синуса следующим образом ` \frac {2\alpha}3=4 \cdot \frac {\alpha}6`.  Тогда, применив два раза формулы двойного угла, мы сможем решить нашу задачу.

Вначале воспользуемся равенством синуса двойного угла: ` sin\frac {2\alpha}3=2 \cdot sin\frac {\alpha}3 \cdot cos\frac {\alpha}3 `, теперь снова применим наши формулы для синуса и косинуса соответственно. В результате получим:

` sin\frac {2\alpha}3=2 \cdot sin\frac {\alpha}3 \cdot cos\frac {\alpha}3=` `2 \cdot (2 \cdot sin\frac {\alpha}6 \cdot cos\frac {\alpha}6) \cdot (cos^2\frac {\alpha}6-sin^2\frac {\alpha}6)=` `4 \cdot sin\frac {\alpha}6 \cdot cos^3 \frac {\alpha}6-4 \cdot sin^3\frac {\alpha}6 \cdot cos \frac {\alpha}6`.

Ответ. ` sin\frac {2\alpha}3=` `4 \cdot sin\frac {\alpha}6 \cdot cos^3 \frac {\alpha}6-4 \cdot sin^3\frac {\alpha}6 \cdot cos \frac {\alpha}6`.

Формулы тройного угла

Эти формулы, аналогично к предыдущим, дают возможность выразить функции угла ` 3\alpha` через эти самые функции угла `\alpha`.

`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`

Доказать их можно, используя равенства сумы и разности углов, а также хорошо известные нам формулы двойного угла.

`sin \ 3\alpha= sin (2\alpha+ \alpha)=` `sin 2\alpha cos \alpha+cos 2\alpha sin \alpha=` `2 sin \alpha cos \alpha cos \alpha+(cos^2 \alpha-sin^2 \alpha) sin \alpha=` `3 sin \alpha cos^2 \alpha-sin^3 \alpha`.

Заменим в полученной формуле `sin \ 3\alpha=3 sin \alpha cos^2 \alpha-sin^3 \alpha` `cos^2\alpha` на `1-sin^2\alpha` и получим `sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`.

Также и для косинуса тройного угла:

`cos \ 3\alpha= cos (2\alpha+ \alpha)=` `cos 2\alpha cos \alpha-sin 2\alpha sin \alpha=` `(cos^2 \alpha-sin^2 \alpha) cos \alpha-2 sin \alpha cos \alpha sin \alpha+=` `cos^3 \alpha-3 sin^2 \alpha cos \alpha`.

Заменив в конечном равенстве `cos \ 3\alpha=cos^3 \alpha-3 sin^2 \alpha cos \alpha` `sin^2\alpha` на `1-cos^2\alpha`, получим `cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`.

С помощью доказанных тождеств для синуса и косинуса можно доказать для тангенса и котангенса:

`tg \ 3\alpha=\frac {sin \ 3\alpha}{cos \ 3\alpha}=` `\frac {3 sin \alpha cos^2 \alpha-sin^3 \alpha}{cos^3 \alpha-3 sin^2 \alpha cos \alpha}=` `\frac {\frac{3 sin \alpha cos^2 \alpha-sin^3 \alpha}{cos^3 \alpha}}{\frac{cos^3 \alpha-3 sin^2 \alpha cos \alpha}{cos^3 \alpha}}=` `\frac {3 \cdot \frac{ sin \alpha }{cos \alpha}-\frac{ sin^3 \alpha }{cos^3 \alpha}}{1-3\frac{sin^2 \alpha}{cos^2 \alpha}}=` `\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3tg^2 \alpha}`;

`ctg \ 3\alpha=\frac {cos \ 3\alpha}{sin \ 3\alpha}=` `\frac {cos^3 \alpha-3 sin^2 \alpha cos \alpha}{3 sin \alpha cos^2 \alpha-sin^3 \alpha}=` `\frac {\frac{cos^3 \alpha-3 sin^2 \alpha cos \alpha}{sin^3 \alpha}}{\frac{3 sin \alpha cos^2 \alpha-sin^3 \alpha}{sin^3 \alpha}}=` `\frac {\frac{ cos^3 \alpha }{sin^3 \alpha}-3 \cdot \frac{cos \alpha}{ sin \alpha }}{3\frac{cos^2 \alpha}{sin^2 \alpha}-1}=` `ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`.

Для доказательства формул угла ` 4\alpha` можно представить его как ` 2 \cdot 2\alpha` и примерить два раза формулы двойного угла.

Для вывода аналогичных равенств для угла ` 5\alpha` можно записать его, как ` 3\alpha + 2\alpha` и применить тождества суммы и разности углов и двойного и тройного угла.

Аналогично выводятся все формулы для других кратных углов, то нужны они на практике крайне редко.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

Косинус двойного угла

В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.

Итак, нам нужны косинус двойного угла и тригонометрическая единица:

   

   

Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:

   

и подставить его в косинус двойного угла, то получим:

   

Это — еще одна формула косинуса двойного угла:

   

Эта формула — ключ к получению формулы понижения степени:

   

Итак, формула понижения степени синуса:

   

Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:

   

Теперь из тригонометрической единицы выразим синус:

   

Подставим это выражение в формулу косинуса двойного угла:

   

   

Получили еще одну формулу косинуса двойного угла:  

   

Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.

   

Таким образом, формула понижения степени косинуса:

   

Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:

   

Так как тангенс — отношение синуса к косинусу то формула  для тангенса:

   

Котангенс — отношение косинуса к синусу. Поэтому формула для котангенса:

   

Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.

Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.

www.uznateshe.ru

Косинус двойного угла

Косинус двойного угла cos2α=cos2α−sin2α

В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.

Итак, нам нужны косинус двойного угла и тригонометрическая единица:

    \[\cos 2\alpha = {\cos ^2}\alpha — {\sin ^2}\alpha \]

    \[{\cos ^2}\alpha + {\sin ^2}\alpha = 1\]

Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:

    \[{\cos ^2}\alpha = 1 — {\sin ^2}\alpha \]

и подставить его в косинус двойного угла, то получим:

    \[\cos 2\alpha = 1 — {\sin ^2}\alpha — {\sin ^2}\alpha = 1 — 2{\sin ^2}\alpha \]

Это — еще одна формула косинуса двойного угла:

    \[\cos 2\alpha = 1 — 2{\sin ^2}\alpha \]

Эта формула — ключ к получению формулы понижения степени:

    \[2{\sin ^2}\alpha = 1 — \cos 2\alpha , \Rightarrow {\sin ^2}\alpha = \dfrac{{1 — \cos 2\alpha }}{2}\]

Итак, формула понижения степени синуса:

    \[{\sin ^2}\alpha = \dfrac{{1 — \cos 2\alpha }}{2}\]

Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:

    \[{\sin ^2}\dfrac{\alpha }{2} = \dfrac{{1 — \cos \alpha }}{2}\]

Теперь из тригонометрической единицы выразим синус:

    \[{\sin ^2}\alpha = 1 — {\cos ^2}\alpha \]

Подставим это выражение в формулу косинуса двойного угла:

    \[\cos 2\alpha = {\cos ^2}\alpha — (1 — {\cos ^2}\alpha ) = {\cos ^2}\alpha — 1 + {\cos ^2}\alpha = \]

    \[ = 2{\cos ^2}\alpha — 1\]

Получили еще одну формулу косинуса двойного угла:  

    \[\cos 2\alpha = 2{\cos ^2}\alpha — 1\]

Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.

    \[2{\cos ^2}\alpha = 1 + \cos 2\alpha , \Rightarrow {\cos ^2}\alpha = \dfrac{{1 + \cos 2\alpha }}{2}\]

Таким образом, формула понижения степени косинуса:

    \[{\cos ^2}\alpha = \dfrac{{1 + \cos 2\alpha }}{2}\]

Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:

    \[{\cos ^2}\dfrac{\alpha }{2} = \dfrac{{1 + \cos \alpha }}{2}\]

Так как тангенс — отношение синуса к косинусу то формула  для тангенса:

    \[t{g^2}\dfrac{\alpha }{2} = \dfrac{{1 — \cos \alpha }}{{1 + \cos \alpha }}\]

Котангенс — отношение косинуса к синусу. Поэтому формула для котангенса:

    \[ct{g^2}\dfrac{\alpha }{2} = \dfrac{{1 + \cos \alpha }}{{1 — \cos \alpha }}\]

Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.

Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Источник

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

тригонометрические уравнения и формула двойного угла

15 января 2014

Очень часто в задачах C1 из ЕГЭ по математике ученикам предлагают решить тригонометрическое уравнение, содержащее формулу двойного угла.

Сегодня мы вновь будем разбирать задачу С1 и, в частности, разберем довольно нестандартный пример, который одновременно вместил в себе и формулу двойного угла, и даже однородное уравнение. Итак:

Решите уравнение. Найдите корни этого уравнения, принадлежащие промежутку:

sinx+sin2x2−cos2x2,x∈[−2 π ;− π 2]

\sin x+\frac{{{\sin }^{2}}x}{2}-\frac{{{\cos }^{2}}x}{2},x\in \left[ -2\text{ }\!\!\pi\!\!\text{ };-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]

Полезные формулы для решения

Прежде всего, хотел бы напомнить, что все задания С1 решаются по одной и той же схеме. В первую очередь, исходную конструкцию нужно преобразовать в выражении, в котором содержится синус, косинус или тангенс:

sinx=a

\sin x=a

cosx=a

\cos x=a

tgx=a

tgx=a

Именно в этом состоит основная сложность задания С1. Дело в том, что для каждого конкретного выражения требуются свои выкладки, с помощью которых можно перейти от исходника к таким простейшим конструкциям. В нашем случае это формула двойного угла. Давайте я запишу ее:

cos2x=cos2x−sin2x

\cos 2x={{\cos }^{2}}x-{{\sin }^{2}}x

Однако в нашем задании нет cos2x{{\cos }^{2}}x или sin2x{{\sin }^{2}}x, зато естьsin2x2\frac{{{\sin }^{2}}x}{2} и cos2x2\frac{{{\cos }^{2}}x}{2}.

Решаем задачу

Что же делать с этими выкладками? Давайте мы немножко схитрим, и в наши формулы синуса и косинуса двойного угла введем новую переменную:

x=t2

x=\frac{t}{2}

Мы запишем такую конструкцию с синусом и косинусом:

cos2⋅t2=cos2t2−sin2t2

\cos 2\cdot \frac{t}{2}=\frac{{{\cos }^{2}}t}{2}-\frac{{{\sin }^{2}}t}{2}

Или другими словами:

cost=cos2t2−sin2t2

\cos t=\frac{{{\cos }^{2}}t}{2}-\frac{{{\sin }^{2}}t}{2}

Возвращаемся к нашему исходному заданию. Давайте sin2x2\frac{{{\sin }^{2}}x}{2} перенесем вправо:

sinx=cos2x2−sin2x2

\sin x=\frac{{{\cos }^{2}}x}{2}-\frac{{{\sin }^{2}}x}{2}

Справа стоит именно те самые выкладки, которые мы только что записали. Давайте мы преобразуем их:

sinx=cosx

\sin x=\cos x

А теперь внимание: перед нами однородное тригонометрическое уравнение первой степени. Смотрите, у нас нет никаких слагаемых, состоящих просто из чисел и просто из xx, у нас есть только синус и косинус. Также у нас нет квадратных тригонометрических функций, все функции идут в первой степени. Как решаются такие конструкции? В первую очередь, давайте предположим, что cosx=0\cos x=0.

Подставим это значение в основное тригонометрическое тождество:

sin2x+cos2x=1

{{\sin }^{2}}x+{{\cos }^{2}}x=1

sin2x+0=1

{{\sin }^{2}}x+0=1

sinx=±1

\sin x=\pm 1

Если эти числа, 0 и ±1, мы подставим в исходную конструкцию, то получим следующее:

±1 = 0

\pm 1\text{ }=\text{ }0

Мы получили полный бред. Следовательно, наше предположение, что cosx=0\cos x=0 неверно, cosx\cos x не может быть равен 0 в данном выражении. А если cosx\cos x не равен 0, то давайте разделим обе стороны на cosx\cos x:

sinxcosx=1

\frac{\sin x}{\cos x}=1

sinxcosx=tgx

\frac{\sin x}{\cos x}=tgx

tgx=1

tgx=1

И вот мы получили долгожданное простейшее выражение вида tgx=atgx=a. Прекрасно, решаем его. Это табличное значение:

x= π 4+ π n,n˜∈Z

x=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\text{ }\!\!\pi\!\!\text{ }n,n˜\in Z

Мы нашли корень, мы решили первую часть задачи, т. е. честно заработали один первичный балл из двух.

Переходим ко второй части: найдите корни этого уравнения, принадлежащие промежутку, а, точнее, отрезку

[\left[ -2\text{ }\!\!\pi\!\!\text{ };-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]\]. Предлагаю, как и в прошлый раз решать это выражение графически, т. е. нарисовать окружность, отметить в ней начало, т. е. 0, а также концы отрезка: 

На отрезке

−2 π ;−π2

-2\text{ }\!\!\pi\!\!\text{ };-\frac{\pi }{2} нужно найти все значения, которые принадлежат

 π 4+ π n

\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\text{ }\!\!\pi\!\!\text{ }n. А теперь самое веселое: дело в том, что сама точка  π 4\frac{\text{ }\!\!\pi\!\!\text{ }}{4} не принадлежит отрезку

[−2 π ;− π 2],

\left[ -2\text{ }\!\!\pi\!\!\text{ };-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right], это очевидно:

 π 4∉˜[−2 π ;−  π 2]

\frac{\text{ }\!\!\pi\!\!\text{ }}{4}\notin ˜\left[ -2\text{ }\!\!\pi\!\!\text{ };-\text{ }\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]

Уже хотя бы потому, что оба конца этого отрезка отрицательные, а число  π 4\frac{\text{ }\!\!\pi\!\!\text{ }}{4} положительное, но с другой стороны, какие-то значения вида

 π 4+ π n

\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\text{ }\!\!\pi\!\!\text{ }n все-таки принадлежат нашему отрезку. Так как же их выделить? Очень просто: берем конец отрезка

−2 π 

-2\text{ }\!\!\pi\!\!\text{ } и прибавляем  π 4\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} , т. е. все происходит то же самое, как если бы мы начали отчет не от 0, а от −2 π -2\text{ }\!\!\pi\!\!\text{ }, и у нас найдется первая точка:

x=−2 π + π 4=−7 π 4

x=-2\text{ }\!\!\pi\!\!\text{ }+\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=-\frac{7\text{ }\!\!\pi\!\!\text{ }}{4}

Теперь второе число:

x=−2 π + π 4+ π =−3 π 4

x=-2\text{ }\!\!\pi\!\!\text{ }+\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\text{ }\!\!\pi\!\!\text{ }=-\frac{3\text{ }\!\!\pi\!\!\text{ }}{4}

Это и есть второе значение. Других корней нет, потому что мы сами при их разметке и при отметке нашего отрезка ограничения обнаружили, что внутри этого отрезка лежат лишь два вида —  π 4\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} и  π 4+ π \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\text{ }\!\!\pi\!\!\text{ }. Эти точки мы и наши. Выписываем ответ:

−7 π 4;−3 π 4

-\frac{7\text{ }\!\!\pi\!\!\text{ }}{4};-\frac{3\text{ }\!\!\pi\!\!\text{ }}{4}

За такое решение вы получите два первичных балла из двух возможных.

Что нужно помнить для правильного решения

Еще раз ключевые шаги, которые необходимо выполнить. В первую очередь, нужно знать выкладки двойного угла синуса или косинуса, в частности, именно в нашей задаче, косинус двойного угла. Кроме того, после его применения необходимо решить простейшее тригонометрическое уравнение. Решается оно довольно просто, однако необходимо написать и проверить, что cosx\cos x в нашей конструкции не равен 0. После тригонометрического уравнения мы получаем элементарное выражение, в нашем случае это tgx=1tgx=1, которое легко решается по стандартным формулам, известным еще с 9-10 класса. Таким образом, мы решим пример и получим ответ на первую часть задания — множество всех корней. В нашем случае это

 π 4+ π n,n∈Z

\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\text{ }\!\!\pi\!\!\text{ }n,n\in ˜Z. Затем остается лишь отобрать корни, принадлежащие отрезку

[−2 π ;− π 2]

\left[ -2\text{ }\!\!\pi\!\!\text{ };-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]. Для этого мы снова чертим тригонометрический круг, отмечаем на нем наши корни и наш отрезок, а затем отсчитываем от конца то самое  π 4\frac{\text{ }\!\!\pi\!\!\text{ }}{4} и  π 4+ π \frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\text{ }\!\!\pi\!\!\text{ }, которые получились во время отметки всех корней вида  π 4+ π n\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\text{ }\!\!\pi\!\!\text{ }n. После несложного счета мы получили два конкретных корня, а, именно,

−7 π 4

-\frac{7\text{ }\!\!\pi\!\!\text{ }}{4} и

−3 π 4

-\frac{3\text{ }\!\!\pi\!\!\text{ }}{4}, которые являются ответом ко второй части задачи, т. е. корнями, принадлежащими отрезку

[−2 π ;− π 2]

\left[ -2\text{ }\!\!\pi\!\!\text{ };-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right].

Ключевые моменты

Чтобы без проблем справиться с задачами C1 такого типа, запомните две основные формулы:

1. Синус двойного угла:

   sin2 α =2sin α cos α 

   \sin 2\text{ }\!\!\alpha\!\!\text{ }=2\sin \text{ }\!\!\alpha\!\!\text{ }\cos \text{ }\!\!\alpha\!\!\text{ } — эта формула для синусов всегда работает именно в таком виде;

2. Косинус двойного угла: cos2 α =cos2 α −sin2 α \cos 2\text{ }\!\!\alpha\!\!\text{ =}co{{s}^{2}}\text{ }\!\!\alpha\!\!\text{ }-si{{n}^{2}}\text{ }\!\!\alpha\!\!\text{ } — а вот тут возможны варианты.

С первой все понятно. Но что за варианты возможны во втором случае? Дело в том, что косинус двойного угла можно записать по-разному:

cos2 α =cos2 α −sin2 α =2cos2 α −1=1−2sin2 α 

\cos 2\text{ }\!\!\alpha\!\!\text{ }=\cos 2\text{ }\!\!\alpha\!\!\text{ }-\sin 2\text{ }\!\!\alpha\!\!\text{ }=2\cos 2\text{ }\!\!\alpha\!\!\text{ }-1=1-2\sin 2\text{ }\!\!\alpha\!\!\text{ }

Эти равенства следуют из основного тригонометрического тождества. Ну и какое равенство выбрать при решении конкретного примера C1? Все просто: если вы планируете свести конструкцию к синусам, то выбирайте последнее разложение, в котором присутствует только

sin2 α 

\sin 2\text{ }\!\!\alpha\!\!\text{ }. И наоборот, если хотите свести все выражение к работе с косинусами, выбирайте второй вариант — тот, где косинус является единственной тригонометрической функцией.

Смотрите также:

1. Задача C1: тригонометрия и показательная функция — 1 вариант
2. Задача C1: тригонометрические уравнения с ограничением
3. Схема Бернулли. Примеры решения задач
4. Пробный ЕГЭ 2012. Вариант 7 (без производных)
5. Пробный ЕГЭ по математике 2015: 7 вариант
6. Вебинар по задачам С1: тригонометрия

www.berdov.com

Косинус двойного угла

См. также:

В процессе решения задач с преобразованием тригонометрических функций бывает необходимо преобразовать значение двойного угла в выражение, в котором все члены имеют аргумент с одинарным его значением. Например, косинус два альфа необходимо преобразовать в выражение, в котором аргументом тригонометрической функции является альфа (одинарный угол). Ниже приведены тригонометрические преобразования косинуса с двойным аргументом функции.

Формулы косинуса двойного угла

Далее приведены формулы (тождества) для преобразования косинуса двойного угла.

Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла

Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица

Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла

Зачем это нужно.

Если представить выражение cos 120 как косинус двойного угла

cos 120º = cos (2 * 60º)

оказывается, можно получить и точное значение для этого угла, применяя указанные выше формулы.

cos 120º = cos (2 * 60º) 

cos 120º = 2 cos² 60º — 1
Мы привели косинус угла, значение которого мы «не знаем», к значению, которое нам известно.
Поскольку значение cos 60 = 1/2 , то вычислим полученное выражение:
2 cos² 60º — 1 = 2 (1/2)²  — 1 = 2 х 1/4 — 1 = -1/2

таким образом

cos 120º = -1/2

По аналогии, применяя формулы косинуса двойного угла, мы можем как решать тригонометрические уравнения, так и находить значения двойных углов тригонометрических функций на основании уже известных нам значений.

См. также:

 Тригонометрические формулы понижения степени sin cos tg | Описание курса | Многоугольники 

   

profmeter.com.ua

Основные тригонометрические тождества, формулы приведения, сложения, двойного угла, суммы и разности, половинного аргумента, тангенс половинного аргумента. Тест

Тестирование онлайн

Основные тригонометрические тождества

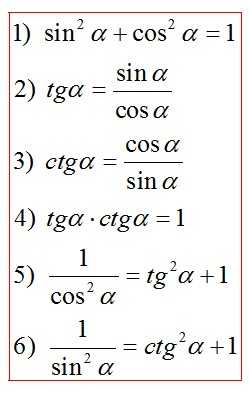
Четность, нечетность тригонометрических функций

Косинус является четной функцией; синус, тангенс, котангенс — нечетные.

Формулы приведения

Это соотношения, с помощью которых значения тригонометрических функций аргументов и др., выражаются через значения .

Правила преобразования:
1) Если аргумент содержит , где n — нечетное натуральное число , то функция меняется на «конфункцию», т.е. синус на косинус, тангенс на котангенс и наоборот. Если n — четное натуральное число , то название функции не изменяется.
2) Определяем знак («+» или «-«) значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя.

Формулы сложения и вычитания

Формулы двойного угла

Формулы преобразования суммы и разности в произведение

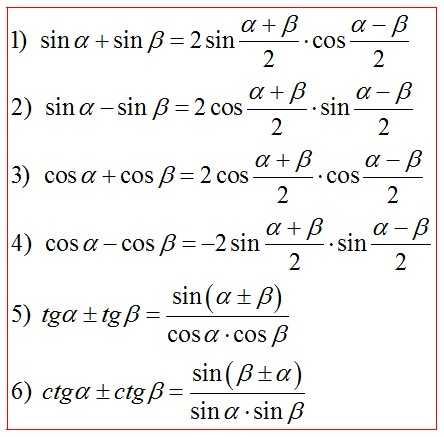
Формулы половинного аргумента

Формулы тройного угла*

Формулы преобразования произведения в сумму (разность)*

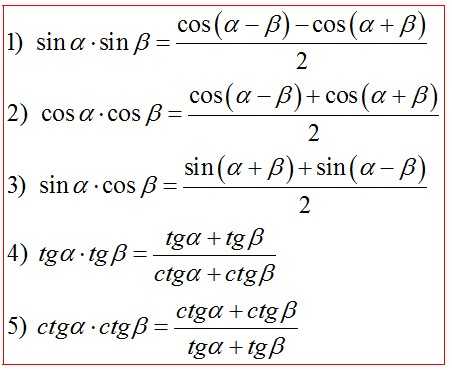
Универсальная подстановка через тангенс половинного аргумента*

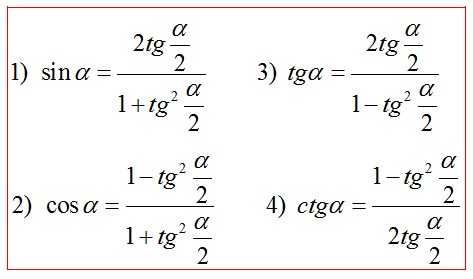
fizmat.by

как вычислить двойной угол синуса :: SYL.ru

Тригонометрия – один из разделов математики, в центре изучения которого находятся углы и взаимосвязи между ними. Основы науки закладываются в школьные годы, когда вводятся определения функций угла. В дальнейшем полученная база используется при освоении астрономии, приборостроения, архитектуры и других областей знаний. Как и любая точная наука, тригонометрия не обходится без формул. Практическое применение нашли выражения для определения двойного аргумента. Например, прибегая к соответствующему уравнению, легко можно узнать двойной угол синуса.

Тригонометрическое выражение для расчёта

Выражение просто записывается и запоминается: синус двойного угла вычисляется как двукратное произведение синуса и косинуса одинарного аргумента.

Эта формула выводится на основе выражения синуса суммы углов (Q₁ + Q₂):

sin(Q₁ + Q₂) = sin Q₁ * cos Q₁ + sin Q₂ * cos Q₂.

Полагая, что заданные углы равны друг другу, формула записывается в привычной форме.

Использовать выражение можно при любых значениях аргумента функции. Вычислить двойной угол синуса по ней достаточно просто, убедиться в этом помогут примеры ниже.

Пример использования

Вот несколько иллюстраций применения полученной формулы. Пусть требуется рассчитать значение тригонометрической функции синуса угла равного 60 градусам. Соответствующий одинарный угол составит 30 градусов. Поскольку величины синуса и косинуса угла в 30 градусов известны, двойной угол синуса составит sin 60 = 2 * sin 30 * cos 30.

Формула используется не только для вычисления «вручную», найти значения по ней можно и с помощью математических пакетов или таблиц MS Excel.

Несмотря на простоту тригонометрического тождества, оно вызывает затруднения у выпускников школы. Именно на это рассчитывают разработчики заданий ЕГЭ, предлагая тесты на проверку основных формул. Вывод – формулу, чтобы подсчитать двойной угол синуса, нужно знать наизусть!

www.syl.ru

No related posts.