Формулы сочетания размещения перестановки сочетания – основные формулы. Перестановки, размещения, сочетания. Задачи с решением по комбинаторике

2 часа лекции, 2 часа семинарское занятие

Существуют две схемы выбора m элементов из множества, состоящего из n элементов:

— без возвращения, когда выбранные элементы после извлечения не возвращаются в исходное множество;

— с возвращением, когда выбор осуществляется поэлементно с обязательным возвращением отобранного элемента в исходное множество на каждом шаге выбора.

Схема выбора без возвращений.

Соединения. Виды соединений

Пусть А – совокупность некоторых n объектов (предметов, элементов и пр.) а₁, а₂, … а_n, объединенных некоторым признаком или свойством. Из различных элементов множества А можно образовать группы. Если в каждую группу входит одно и то же количество элементов, например,

m (m ≤ n), взятых из множества А, то говорят, что они образуют соединения из n элементов по m в каждом.

В зависимости от того, входят ли в соединение все элементы множества А,- или только часть элементов этого множества, имеет ли значение порядок следования элементов, или порядок следования элементов значения не имеет, под общим именем соединений принято понимать следующие три типа комбинаций: перестановки; размещения; сочетания.

Перестановки

Перестановками называются такие изменения, в результате которых количество выбираемых предметов сохраняется, а порядок их извлечения может изменяться случайным способом.

Определение 1. Соединения, в которые входят все n элементов множества А и которые отличаются только порядком следования элементов, называются перестановками из n элементов. Количество перестановок обозначается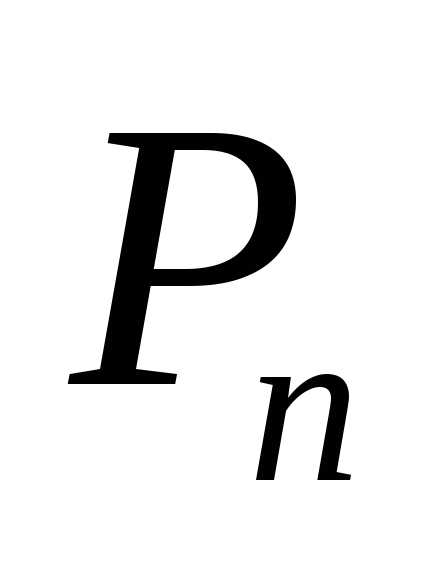 и читается «Пэ из эн».

Число перестановок Р из n элементов равно:

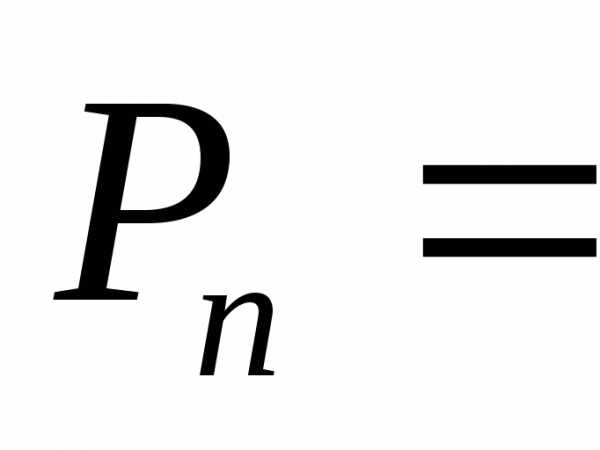
Произведение n·(n — 1)·(n — 2)·… ·1 называется факториалом числа n, обозначается символом n!, который читается «эн-факториал».

Принято, что 0! = 1 и 1! = 1.

Размещения

Определение 2. Соединения, каждое из которых содержит

m различных элементов (m ≤ n), взятых из n элементов множества А, отличающихся друг от друга или составом элементов или порядком расположения элементов, называются размещениями из n элементов по m в каждом.

Число таких размещений обозначается символом 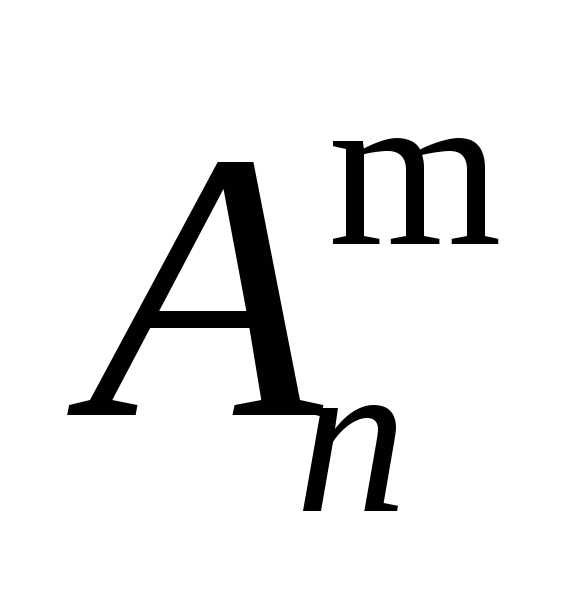, читается «А из эн по эм».

Число возможных размещений из n элементов по m в каждом равно произведению m последовательно убывающих на единицу чисел, из которых большее есть n, т.е.

Это еще одна, на мой взгляд, более удобная расчетная формула для Размещений. По определению, перестановки являются частным случаем

размещений, когда m = n: Р_n = А.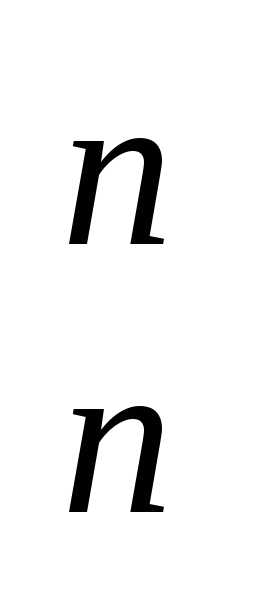

Сочетания

Сколькими способами можно выбрать из n различных объектов (предметов) m штук?

Определение 3. Соединения, каждое из которых содержит m различных элементов (m ≤ n), взятых из n элементов множества А, отличающихся друг от друга по крайней мере одним элементом, называются сочетаниями из n элементов по m.

Число таких сочетаний обозначается символом 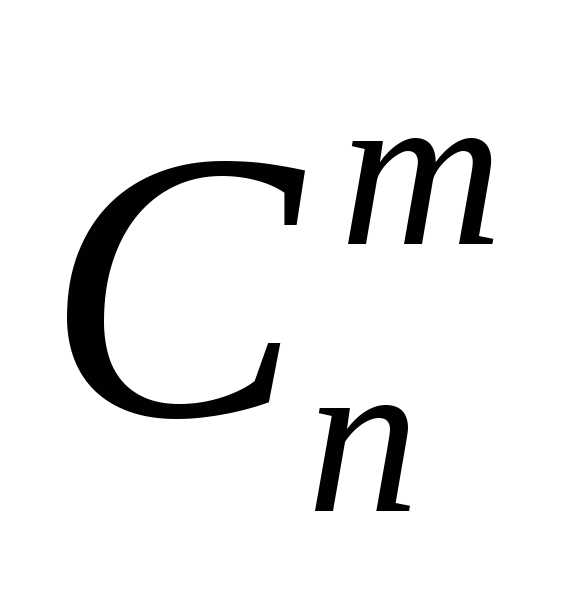или

и читается «цэ из эн по эм».

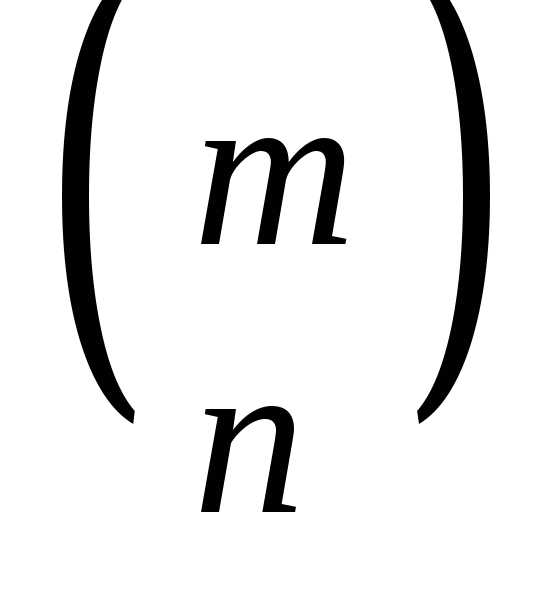
Из определения следует, что сочетания отличаются друг от друга хотя бы одним элементом, т.е. составом входящих элементов. Изменение порядка следования элементов внутри одного сочетания не приводит к образованию нового сочетания.

Число всех возможных сочетаний из n элементов по m в каждом выражается формулой

Факториальная запись этой формулы.

studfiles.net

2 часа лекции, 2 часа семинарское занятие

Существуют две схемы выбора m элементов из множества, состоящего из n

элементов:

— без возвращения, когда выбранные элементы после извлечения не возвращаются в исходное множество;

— с возвращением, когда выбор осуществляется поэлементно с обязательным возвращением отобранного элемента в исходное множество на каждом шаге выбора.

Схема выбора без возвращений.

Соединения. Виды соединений

Пусть А – совокупность некоторых n объектов (предметов, элементов и пр.) а₁, а₂, … а_n, объединенных некоторым признаком или свойством. Из различных элементов множества А можно образовать группы. Если в каждую группу входит одно и то же количество элементов, например, m (m ≤ n), взятых из множества А, то говорят, что они образуют соединения из

n элементов по m в каждом.

В зависимости от того, входят ли в соединение все элементы множества А,- или только часть элементов этого множества, имеет ли значение порядок следования элементов, или порядок следования элементов значения не имеет, под общим именем соединений принято понимать следующие три типа комбинаций: перестановки; размещения; сочетания.

Перестановки

Перестановками называются такие изменения, в результате которых количество выбираемых предметов сохраняется, а порядок их извлечения может изменяться случайным способом.

Определение 1. Соединения, в которые входят все n элементов множества А и которые отличаются только порядком следования элементов, называются перестановками из n

элементов. Количество перестановок обозначается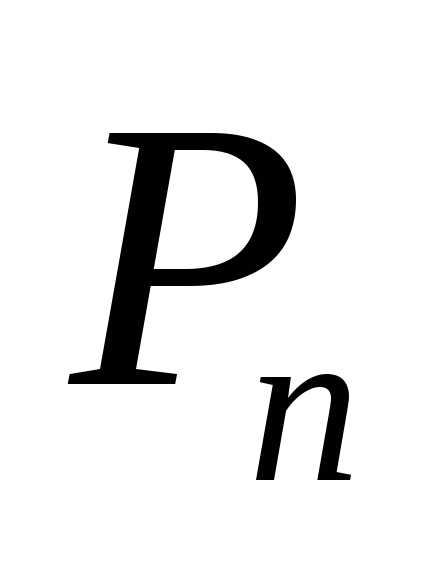 и читается «Пэ из эн».

Число перестановок Р из n элементов равно:

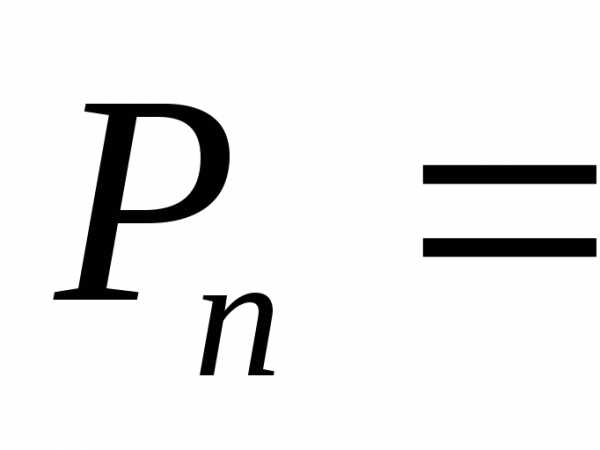
Произведение n·(n — 1)·(n — 2)·… ·1 называется факториалом числа n, обозначается символом n!, который читается «эн-факториал».

Принято, что 0! = 1 и 1! = 1.

Размещения

Определение 2. Соединения, каждое из которых содержит m различных элементов (m ≤ n), взятых из n элементов множества А, отличающихся друг от друга или составом элементов или порядком

расположения элементов, называются размещениями из n элементов по m в каждом.

Число таких размещений обозначается символом 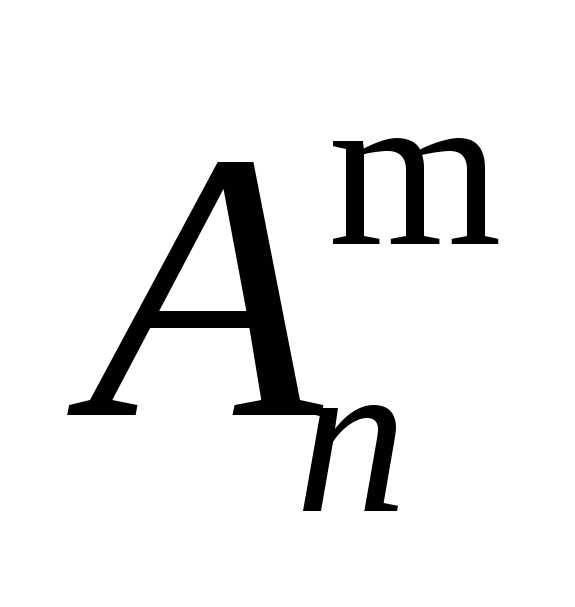, читается «А из эн по эм».

Число возможных размещений из n элементов по m в каждом равно произведению m последовательно убывающих на единицу чисел, из которых большее есть n, т.е.

Это еще одна, на мой взгляд, более удобная расчетная формула для Размещений. По определению, перестановки являются частным случаем размещений, когда m = n: Р_n = А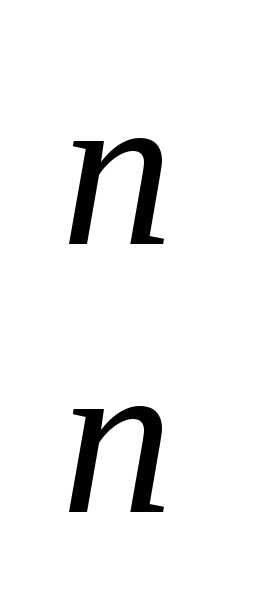

.

Сочетания

Сколькими способами можно выбрать из n различных объектов (предметов) m штук?

Определение 3. Соединения, каждое из которых содержит m различных элементов (m ≤ n), взятых из n элементов множества А, отличающихся друг от друга по крайней мере одним элементом, называются сочетаниями из n элементов по m.

Число таких сочетаний обозначается символом 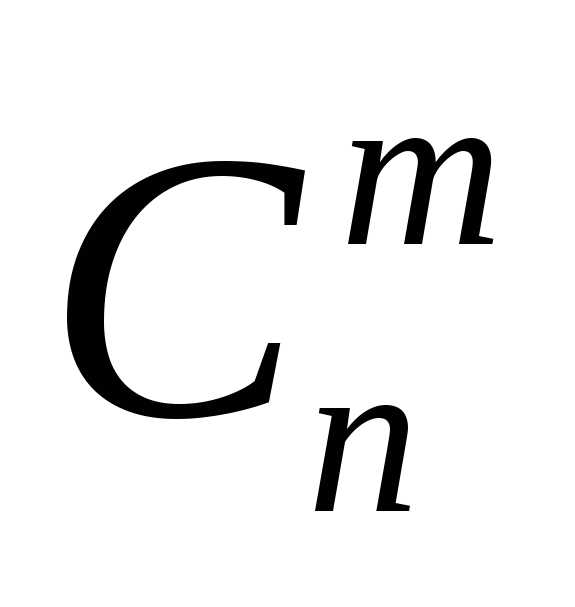или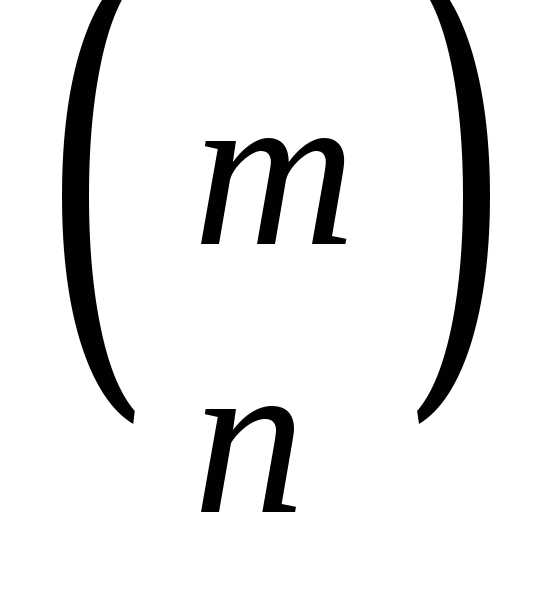и читается «цэ из эн по эм».

Из определения следует, что сочетания отличаются друг от друга хотя бы одним элементом, т.е. составом

входящих элементов. Изменение порядка следования элементов внутри одного сочетания не приводит к образованию нового сочетания.

Число всех возможных сочетаний из n элементов по m в каждом выражается формулой

Факториальная запись этой формулы.

studfiles.net

Урок по алгебре и началам анализа «Формулы числа перестановок, сочетаний, размещений»

Урок по алгебре и началам анализа

на тему «Формулы числа перестановок, сочетаний, размещений»

Тип урока: комбинированный

Цели урока:

Обучающая:

повторить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний;

научиться распознавать задачи на нахождение размещений, перестановок, сочетаний;

решить простейшие комбинаторные задачи с помощью формул для нахождения числа размещений, перестановок, сочетаний.

Воспитывающая:

воспитывать аккуратность выполнения записей в тетради и на доске;

воспитывать умение работать самостоятельно.

Развивающая:

способствовать развитию внимания.

Оборудование: карандаш, линейка, тетрадь, дидактический материал (карточки-задания).

Методы обучения: словесно-информационный (рассказ), словесно-репродуктивный (опрос), практически-репродуктивный (выполнение заданий), наглядно-иллюстративный (карточки, учебник, раздаточный материал).

Формы обучения: коллективная, индивидуальная.

Этапы урока:

1. Организационно-мотивационный (сообщение темы урока, организация обстановки способствующей усвоению материала) — 2 мин

2. Проверка домашнего задания (проверка тетрадей) – 3 мин

3. Актуализация знаний (актуализация опорных знаний учащихся) — 5мин

4. Обобщение знаний (повторить определения размещений, перестановок, сочетаний и формулы для их нахождения) — 15 мин

5. Закрепление и проверка усвоения материал решить простейшие комбинаторные задачи с помощью формул для нахождения числа размещений, перестановок, сочетаний. – 10 мин

6. Домашняя работа — 3 мин

7. Итог урока – 2 мин

I этап: Организационно-мотивационный

Сообщение темы урока, организация обстановки способствующей усвоению материала.

В практике часто встречаются задачи, при решении которых приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называется комбинаторикой.

Рассмотрим такие задачи:

1) Перестановки

Задача №1. Сколько трехзначных чисел можно составить из цифр 1,3,5, используя в записи числа каждую из них не более одного раза?

В задаче нам нужно составить комбинации из трех цифр и подсчитать их число. В процессе решения этой задачи постараемся выяснить структуру полученных комбинаций (чем одна комбинация отличается от другой), способ рассуждений и правило подсчета комбинаций.

135, 153, 315, 351, 513, 531.

При решении этой задачи мы составили 6 комбинаций из трех цифр. Обратим внимание, что каждая из полученных комбинаций отличается друг от друга только порядком расположения элементов. Такие комбинации называются перестановками.

Определение. Перестановками называются комбинации, состоящие из одних и тех же n различных элементов и отличающихся только порядком их расположения.

Число перестановок из n элементов обозначается 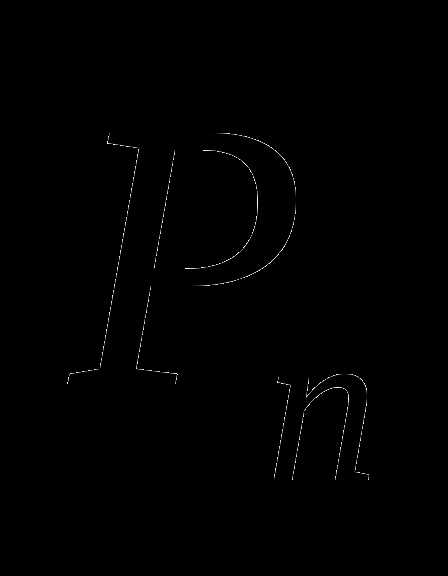. Для любого натурального числа n справедлива формула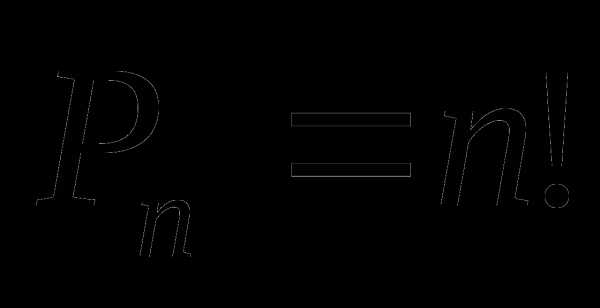

Задача №2. Сколькими способами можно поставить на полке рядом 5 разных книг?

Решение:

Задача №3. Сколькими способами можно разместить 6 человек за столом, на котором поставлены 6 приборов?

Решение:

2) Размещения

Задача №4. Сколько двузначных чисел можно составить из цифр 1,3,5, используя в записи числа каждую из них не более одного раза?

На первом месте в комбинации из двух может стоять любая из цифр 1,3,5. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать из оставшихся цифр двумя способами. Перечислим все комбинации: 13; 15; 31; 35; 51; 53.

Обратим внимание, что каждая из полученных комбинаций отличается друг от друга самими элементами или порядком их расположения. Такие комбинации называются размещениями.

Определение. Размещениями называются комбинации, составленные из n различных элементов по k элементов, которые отличаются либо составом элементов, либо их порядком.

Число размещений из n элементов по k обозначают и вычисляют по формуле:

Задача №5. Учащиеся 5 класса изучают 10 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 5 различных предметов?

Решение: Любое расписание на один день, составленное из 5 различных предметов, отличается от другого либо предметами, либо порядком следования. Значит, речь идет о размещениях из10 по 5:.

3) Сочетания

Задача №6. Пусть имеются цифры 1,3,5. Из них нужно составить комбинации по 2 элемента, отличающиеся друг от друга хотя бы одним элементом.

Решение 13; 15; 35.

Алгоритм: сначала отбрасываем последнюю цифру в исходной записи (5), потом вторую в исходной записи (3), потом третью (1). Каждая из этих комбинаций отличается от любой другой, хотя бы одним входящим в нее элементом. Нет ни одной комбинации с одинаковым составом элементов. Такие комбинации называются сочетаниями.

Определение. Сочетаниями из данных n элементов по k называют любую группу из k этих элементов.

Понятие сочетания не связано с расположением (порядком) элементов.

Число сочетаний из n элементов по k обозначают и вычисляют по формуле:

Задача №7. Сколькими способами из колоды в 36 карт можно выбрать 2 карты?

Решение:

Рассмотрим различные комбинаторные задачи.

Задача №8. Составьте все двузначные числа, в записи которых используются только цифры 3,5,7,9.Сколько двузначных чисел можно записать, если использовать при записи числа каждую из указанных цифр один раз?(12)

Типичные задачи, в которых обычно путаются учащиеся

Сочетания

Размещения

1. Сколько рукопожатий получится, если здороваются 5 человек?
{Вася, Петя} = {Петя, Вася} – одно и тоже.
Значит, порядок неважен, значит это подмножество по два элемента из 5, значит это сочетание из пяти по два.

1. Сколькими способами пять человек могут обменяться фотографиями?
{Вася, Петя} ≠ {Петя, Вася} – разные обмены.
Значит, порядок важен, значит это последовательность по два элемента из 5, значит это размещение из пяти по два.

Перестановки

1. Сколькими способами n человек могут сесть на одной скамейке?
P_n = n!

2. Сколькими способами n человек могут сесть за круглым столом?

Рассмотрим различные комбинаторные задачи.

Задача №8. Составьте все двузначные числа, в записи которых используются только цифры 3,5,7,9. Сколько двузначных чисел можно записать, если использовать при записи числа каждую из указанных цифр один раз?

Задача №9. Сколькими способами может расположиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет? (24)

Задача №10. Из 30 участников собрания необходимо выбрать председателя и секретаря. Сколькими способами это можно сделать? (870)

Задача №11. Сколькими способами можно изготовить трехцветный флаг с горизонтальными полосами, если есть материал 7 разных цветов? (210)

Задача №12. Сколькими способами 4 мужчины могут расположиться на четырехместной скамейке?

Задача №13. Курьер должен разнести пакеты в 7 разных учреждений. Сколько маршрутов он может выбрать?

Задача №14. Ольга помнит, что телефон подруги оканчивается тремя цифрами 5, 7, 8, но забыла, в каком порядке эти цифры расположены. Укажите наибольшее число вариантов, которые ей придется перебрать, чтобы дозвониться подруге.

Задача №15. В классе 7-м учащихся успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

Задача №16. В магазине “Филателия” продается 8 разных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

Задача №17. Ученикам дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Самостоятельная работа по вариантам

1 вариант

2 вариант

3 вариант

1. Сколько различных экзаменационных комиссий по 3 человека можно составить, если на кафедре 20 преподавателей?

1. В нашем распоряжении есть 5 разноцветных флагов. Сколько различных сигналов, состоящих из 3 флагов, можно поднять на флаг штоке?

1. Сколькими способами можно выбрать 6 различных пирожных в кондитерской, где имеется 11 сортов пирожных?

2. Сколькими способами можно окрасить трехкомнатную квартиру (каждая комната окрашивается одной краской, все комнаты окрашиваются в разные цвет), если имеется 10 различных красок?

2. Имеется 7 путевок в различные дома отдыха и 7 кандидатов. Сколькими способами можно распределить эти путевки?

2. В шахматном турнире участвуют 12 человек. Каждый из участников должен сыграть с каждым из остальных по две партии. Сколько всего партий должны сыграть участники турнира?

3. Сколькими способами можно расставить 5 книг на полке?

3. В колоде 52 карты. Раздаются 3 карты. Сколько может быть случаев появления одного туза среди розданных карт?

3. Сколькими способами из 30 человек может выбрать собрание председателя и секретаря?

Домашняя работа

№ 1. Бригадир должен откомандировать на работу бригаду из 5 человек.

Сколько бригад по 5 человек в каждой можно организовать из 12 человек?

№ 2. Группа учащихся из 30 человек решила обменяться фотографиями.

Сколько всего фотографий необходимо было для этого?

№ 3. Во время встречи 16 человек пожали друг другу руки. Сколько всего сделано рукопожатий?

infourok.ru

Основные понятия комбинаторики перестановки размещения сочетания

Понятия перестановки, сочетания и размещения в комбинаторике являются самыми начальными и основными понятиями.
Рассмотрим начальное понятие, которое начинают изучать уже в пятом классе школы.

Перестановки
Пусть необходимо переставить несколько различных объектов всеми возможными способами. При этом количество объектов изменяться не будет, будет изменяться лишь их порядок. Наборы, которые получатся в результате, называют перестановками.

Например, нужно найти количество способов, которыми можно выстроить в ряд трактор, велосипед и машину.
Для удобства решения обозначим данные объекты буквами Т, В и М.
Таким образом, покажем все возможные способы и посчитаем их количество:
(ТВМ), (ТМВ), (ВТМ), (ВМТ), (МТВ), (МВТ).
При подсчете видим, что количество таких способов 6.

Их количество можно рассчитать по формуле:
.

Тогда данную задачу можно решить намного быстрее:
.
Здесь 3 – это число объектов, которые необходимо переставить.

Размещения
Если необходимо из какого-то набора объектов выбирать объекты, количество которых не совпадает с количеством всего набора, и переставлять их всеми возможными способами, то в таком случае будет менять состав объектов в наборе, а также их порядок.
Такие наборы называют размещениями, а их количество можно посчитать с помощью формулы:
.
 
Сочетания
Если из какого-то количества различных объектов нужно выбирать другое количество объектов всеми возможными способами (в этом случае меняется состав набора, но порядок в нем не важен). Такие наборы называют сочетаниями.
Их количество находят по формуле:

ru.solverbook.com