Функция определена – 1.2. Понятие функции

1.2. Понятие функции

Для исследования различных явлений полезно знать, как изменение одних величин влияет на другие величины.

Понятие функции связано с установлением зависимости (связи) между двумя (несколькими) переменными величинами при их совместном изменении, или установлением зависимости между элементами двух (нескольких) множеств.

Определение.

Пусть даны две переменные х и y с областями изменения Х и Y. Переменная y называется функцией от х, если по некоторому правилу или закону каждому значению 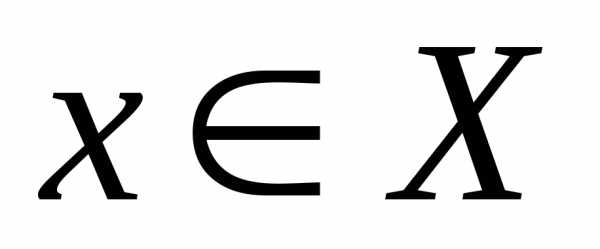ставится в соответствие одно определенное значение.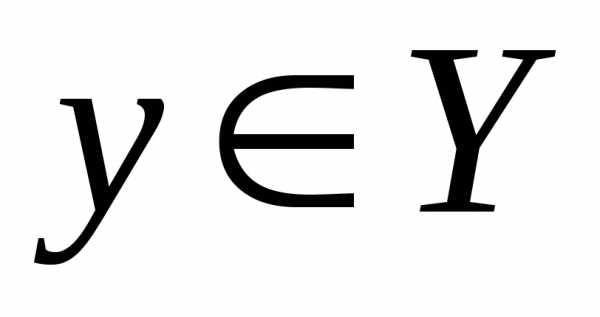

Для указания этого факта, что y есть функция от

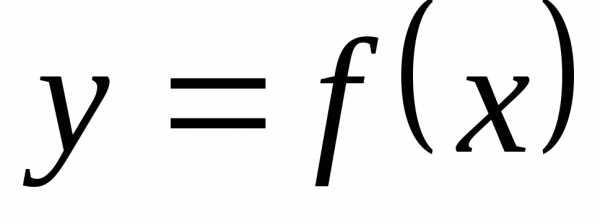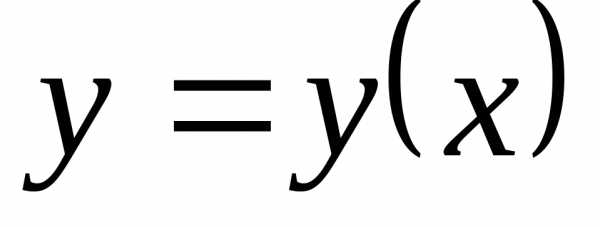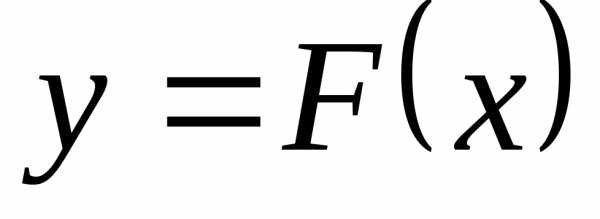х, пишут: ,,и т.п.

Можно также сказать, что функция f отображает множество Х на множество Y. Это обозначается так (рис.1.1).

Рис. 1.1

Переменная х называется независимой переменной или аргументом.

Переменная y называется зависимой переменной или функцией.

Относительно самих величин х и y говорят, что они находятся в функциональной зависимости.

1.3. Область определения и изменения функции

Определение.

Совокупность всех значений независимой переменной х, для которых функция y определена, называется областью определения

или областью существования этой функции.

Определение.

Множество Х называется областью определения функции и обозначается .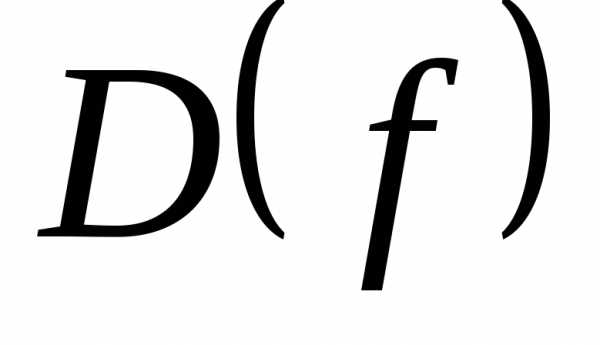

Обычно областью определения функции являются:

;

;

;

;

; ;

; ;

,

где ,и.

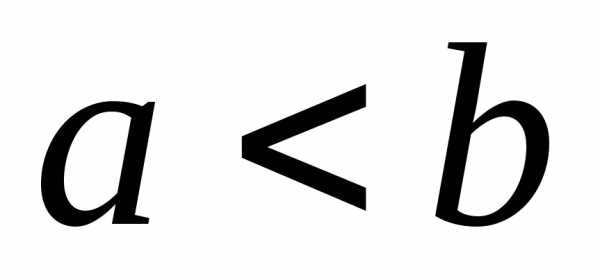Например, для функций:

1) ;

2) .

Область определения функции может состоять из одного или нескольких промежутков и из отдельных точек.

Определение.

Множество значений Y называется областью изменения или областью значений функции, и обозначается .

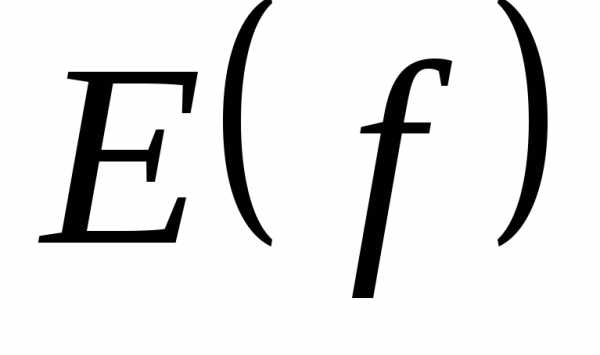Область изменения функции (множество ее значений) определяется законом соответствия.

Например, для функций

1) ;;

2) ;.

Определение.

Функция 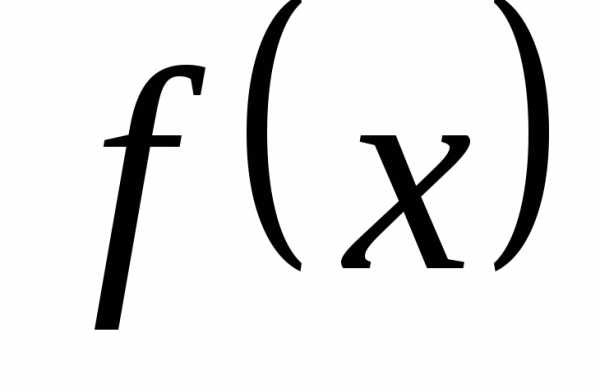называетсячисловой функцией, если ее область определения 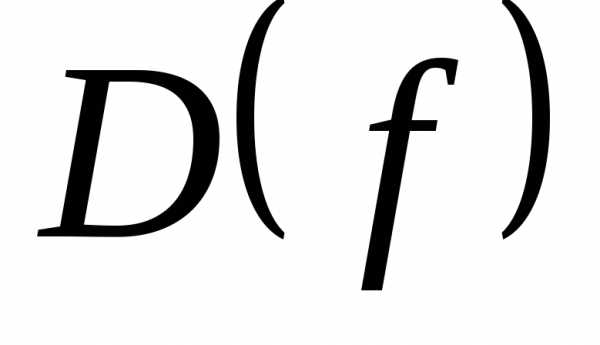и множество значений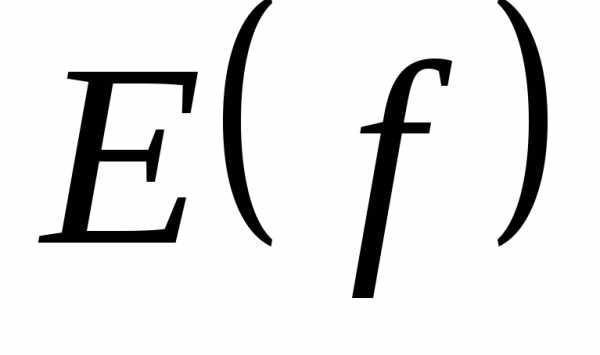содержатся в множестве действительных чиселR.

В дальнейшем будем изучать лишь числовые функции. Частное значение функции 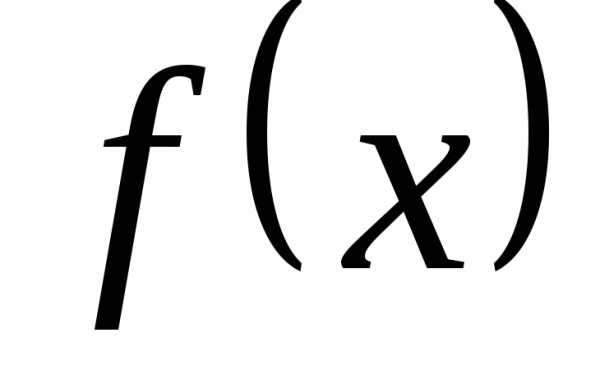призаписывается так: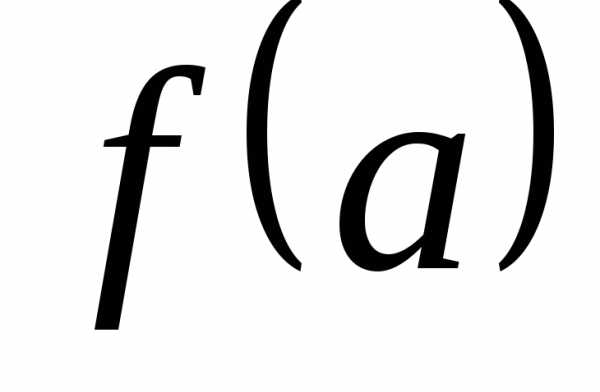

.

Например, если , то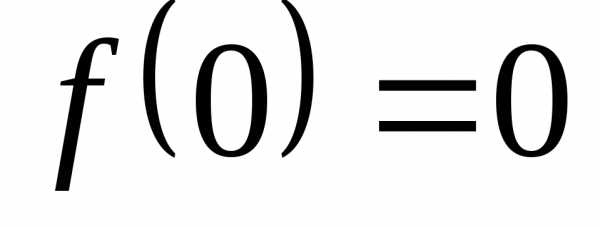,,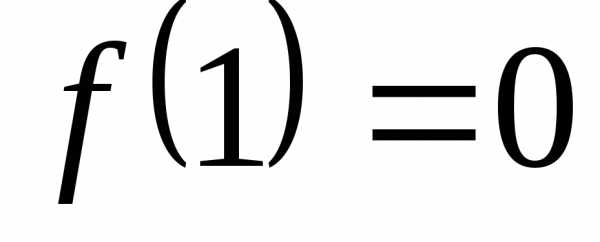и т.п.

1.4. Последовательность

Определение.

Функция, определенная на множестве натуральных чисел , называетсяпоследовательностью.

Значения функции т.е. элементы множестваназываются членами последовательности, а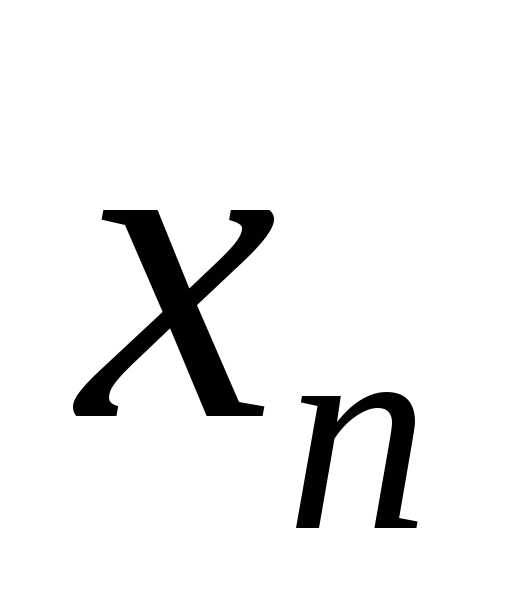– общим членом последовательности.

Последовательность обычно обозначают через 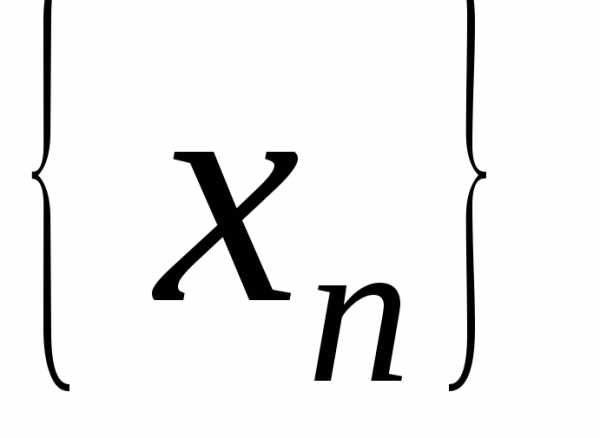или.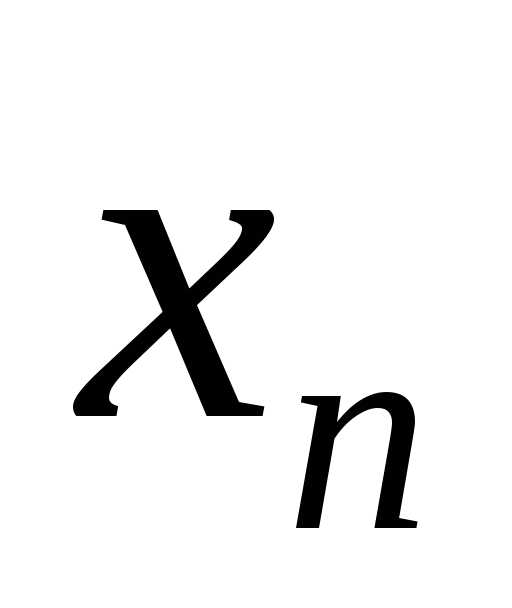

Например, ;.

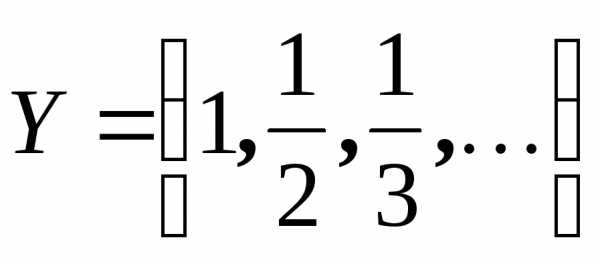1.5. График функции

Для наглядного представления функции строят ее график.

Определение.

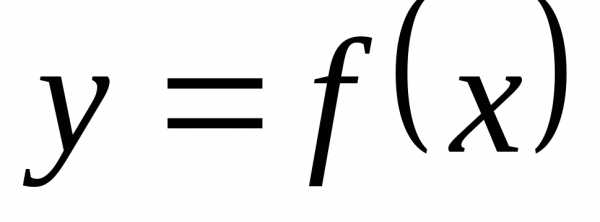Графиком функции называется множество всех точек плоскости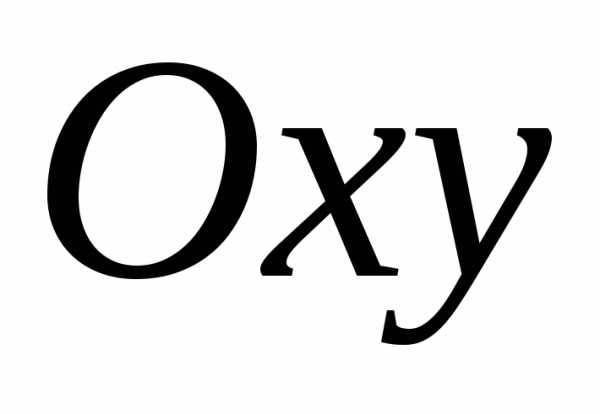, для каждой из которыхх является значением аргумента, а y – соответствующим значением функции.

Например, графиком функции 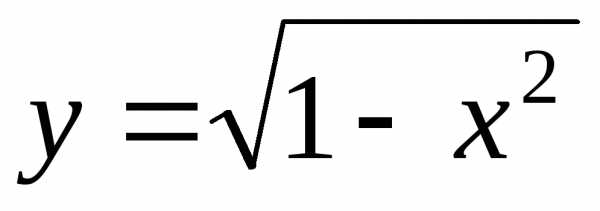является верхняя полуокружность радиуса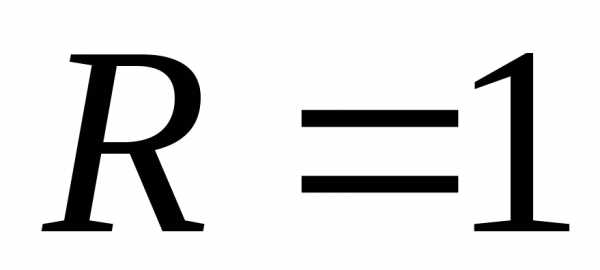с центром в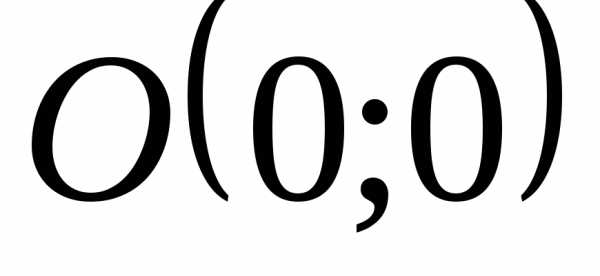(рис. 1.2).

Рис. 1.2

1.6. Способы задания функции

Задать функцию – это значит указать правило, позволяющее по данному значению независимой переменной находить соответствующее значение функции.

Существует три основных способа задания функции: аналитический, табличный и графический.

Аналитический способ состоит в том, что зависимость между переменными величинами задается в виде формулы (аналитического выражения), указывающей, какие и в каком порядке действия надо выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.

Например, ;;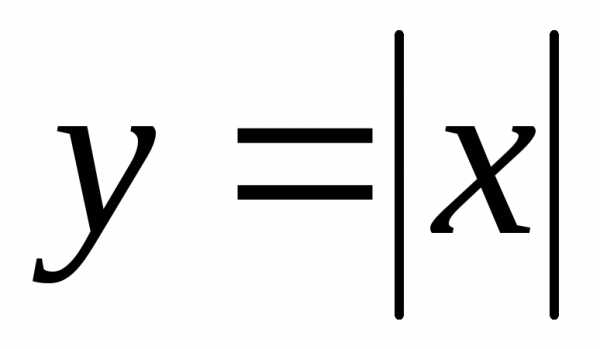, где.

Аналитический способ является наиболее совершенным, т.к. к нему могут быть применены методы математического анализа, позволяющие полностью исследовать функцию.

Табличный способпредусматривает задание таблицы, в которой различным значениям аргументапоставлены соответствующие значения функции:

х	х1	х2	…	хn
y	y1	y2	…	yn

Такие таблицы составляются, например, по данным эксперимента; для облегчения вычислений с часто встречающимися функциями (таблицы логарифмов, таблицы тригонометрических функций и т.д.).

Графический способзадания функции состоит в том, что в данной системе координат задается некоторая кривая. Преимуществом графического задания является его наглядность, недостатком – его неточность.

studfiles.net

что значит функция определена — что значит «фукция определена»? — 22 ответа



В разделе Образование

на вопрос что значит «фукция определена»? заданный автором шеврон лучший ответ это функция определена формулой y=f(x) на определенном промежутке (a,b), a функция определена формулой y=f(x) на определенном промежутке (a,b), a

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: что значит «фукция определена»?

Ответ от худосочный[эксперт]
Определить: Вывести, высчитать что-л. путем измерения, вычисления и т. п.
Например, Определить площадь круга, Определить функцию при значениях от 0 до 5.
Если функция определена, то указаны значения переменных, при которых она вычисляется.
другими словами:
Множество X всех допустимых действительных значений аргумента x, при которых функция y = f ( x ) определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции.

Ответ от

Простить[гуру]
А польностью вопрос сформулировать нельзя? А не отрывками? Контест скажи. Функция какая и что надо. Разберемся тогда.

Ответ от Ada[мастер]
это значит, что функция (предположим у) существует при каких-то хю например, если функция у=1/(х-4) то она определена при х от -бесконечности до 4 (не включая 4) и от 4 (не включая 4) до +бесконечности. соотвественно не определена при х=4 (т. к. на ноль сам понимаешь…)

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Функция математика на Википедии
Посмотрите статью на википедии про Функция математика

 

Ответить на вопрос:

Предыдущий вопрос

Следующий вопрос

22oa.ru

Предел функции в точке. Пусть функция определена в некоторой окрестности точки (т.е

 

Пусть функция определена в некоторой окрестности точки (т.е. в самой точке функция может быть и не определена)

Определение. Число называется пределом функции при , если для любого существует такое число , что для всех таких, что

верно неравенство

.

То же определение может быть записано в другом виде:

Если то верно неравенство .

Запись предела функции в точке:

Определение. Если при только при , то — называется пределом функции в точке слева, а если при только при , то называется пределом функции в точке справа.

 

 

 

 

 

 

Приведенное выше определение относится к случаю, когда функция не определена в самой точке , но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы и называются также односторонними пределами функции в точке . Также говорят, что – конечный предел функции .

 

Предел функции при стремлении аргумента к бесконечности

 

Определение. Число называется пределом функции при , если для любого числа существует такое число , что для всех , таких что выполняется неравенство

При этом предполагается, что функция определена в окрестности бесконечности.

Обозначение:

Графически это определение можно представить в виде:

y y

A A

0 0

x x

 

 

y y

A A

x x

0 0

 

 

Аналогично можно определить пределы для любого и

для любого .

 

Основные теоремы о пределах

 

Теорема 1. , где С = const.

Следующие теоремы справедливы при предположении, что функции и имеют конечные пределы при .

Теорема 2.

Теорема 3.

Следствие.

Теорема 4. при

 

Теорема 5. Если в некоторой окрестности точки и , то .

Аналогично определяется знак предела при .

Теорема 6. Если в некоторой окрестности точки и , то .

Определение. Функция называется ограниченной в некоторой окрестности точки , если существует такое число , что для всех точек из этой окрестности.

Теорема 7. Если функция ) имеет конечный предел при , то она ограничена в некоторой окрестности точки .

 

Доказательство. Пусть , т.е. , тогда

или , т.е. где

Теорема доказана.

 

 

Бесконечно малые функции и их свойства

 

Определение. Функция называется бесконечно малой при , где а может быть числом или одной из величин , или , если .

Бесконечно малой функция является только при указании к какому числу стремится аргумент . При различных значениях функция может быть бесконечно малой или нет.

Пример. Функция является бесконечно малой при и не является бесконечно малой при , т.к. .

Теорема. Для того, чтобы функция при имела предел, равный А, необходимо и достаточно, чтобы в некоторой окрестностии точки выполнялось равенство

,

где – бесконечно малая при фунукция ( при ).

megaobuchalka.ru

Определение непрерывности функции в точке

Непрерывность в точке

Определение непрерывности функции в точке
Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если предел при x стремящемся к x₀ существует и равен значению функции в x₀:
.

Здесь подразумевается, что x₀ – это конечная точка. Значение функции в ней может быть только конечным числом.

Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.

Определение непрерывности функции в точке по Гейне
Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если для любой последовательности {x_n}, сходящейся к x₀: , элементы которой принадлежат окрестности U(x₀), последовательность {f(x_n) } сходится к  f(x₀):
.

Определение непрерывности функции в точке по Коши
Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности U(x₀) этой точки, и если, для любого сколь угодно малого положительного числа ε > 0, существует такое число δ_ε> 0, зависящее от ε, что для всех x, принадлежащих δ_ε — окрестности точки x₀: , значения функции принадлежат ε — окрестности точки f(x₀):
.

Запишем эти определения с помощью логических символов существования и всеобщности.
По Гейне:
.
По Коши:
.

Легко видеть, что определение непрерывности отличается от определения предела только тем, что вместо проколотой окрестности точки используется просто окрестность точки, которая содержит . При этом значение предела может быть равным только значению функции в этой точке: .

Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Далее мы рассматриваем новую функцию:
.
Ее называют приращением функции в точке . Считаем, что она зависит от переменной : . Тогда можно дать еще одно определение.

Определение непрерывности функции в точке в терминах приращений
Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности этой точки, и если предел приращения этой функции в точке , при , равен нулю:
.

Определение отсутствия непрерывности

Теперь приведем определение того, что функция не является непрерывной в точке .

Определение отсутствия непрерывности функции в точке
Функция , определенная на некоторой окрестности точки не является непрерывной в этой точке, если предела функции при не существует, или он не равен значению функции в точке :
.

По Гейне это означает, что существует такая последовательность , для которой предел либо не существует, либо он не равен :
.

По Коши это означает, что существует такое , так что для любого существует , для которого :
.

Непрерывность на концах отрезка

В рассмотренных выше определениях считается, что функция определена на некоторой окрестности слева и справа от точки . Если функция определена на некотором отрезке , то мы можем применять эти определения для внутренних точек отрезка, для которых . Для концов отрезка a и b нужно дать определение односторонней непрерывности, аналогичное определению односторонних пределов.

Определение непрерывности справа (слева)
Функция f(x) называется непрерывной справа (слева) в точке x₀, если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x₀ равен значению функции в x₀:
.

Примеры

Пример 1

Используя определения по Гейне и Коши доказать, что функция непрерывна для всех x.

Решение

Пусть есть произвольное число. Докажем, что заданная функция непрерывна в точке . Функция определена для всех x. Поэтому она определена в точке и в любой ее окрестности.

Используем определение по Гейне

Используем определение непрерывности по Гейне ⇑. Пусть есть произвольная последовательность, сходящаяся к : . Применяя свойство предела произведения последовательностей имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , то
.
Непрерывность доказана.

Используем определение по Коши

Используем определение непрерывности по Коши ⇑.
Рассмотрим случай . Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П1.1)   .

Применим формулу:
.
Учитывая (П1.1), сделаем оценку:

;
(П1.2)   .

Применяя (П1.2), оценим абсолютную величину разности:
;
(П1.3)   .
Вводим положительные числа и , связав их соотношениями:
.
Согласно свойствам неравенств, если выполняется (П1.3), если   и если  , то .

Это означает, что для любого положительного всегда найдется . Тогда для всех x, удовлетворяющих неравенству , автоматически выполняется неравенство:
.
Это означает, что функция непрерывна в точке .

Теперь рассмотрим точку . В этом случае
.
Вводим положительные числа и :
.

Отсюда видно, что для любого положительного всегда найдется . Тогда для всех x, таких что , выполняется неравенство:
.
Это означает, что функция непрерывна в точке .

Аналогичным способом можно доказать, что функция , где n – натуральное число, непрерывна на всей действительной оси.

Пример 2

Используя определение непрерывности по Коши ⇑ доказать, что функция непрерывна для всех .

Решение

Заданная функция определена при . Докажем, что она непрерывна в точке .

Рассмотрим случай .
Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П2.1)   .

Применим формулу:
(П2.2)   .
Положим . Тогда
.

Учитывая (П2.1), сделаем оценку:


.
Итак,
.

Применяя это неравенство, и используя (П2.2), оценим разность:

.
Итак,
(П2.3)   .

Вводим положительные числа и , связав их соотношениями:
.
Согласно свойствам неравенств, если выполняется (П2.3), если   и если  , то .

Это означает, что для любого положительного всегда найдется . Тогда для всех x, удовлетворяющих неравенству , автоматически выполняется неравенство:
.
Это означает, что функция непрерывна в точке .

Теперь рассмотрим точку . Нам нужно показать, что заданная функция непрерывна в этой точке справа. В этом случае
.
Вводим положительные числа и :
.

Отсюда видно, что для любого положительного всегда найдется . Тогда для всех x, таких что , выполняется неравенство:
.
Это означает, что . То есть функция непрерывна справа в точке .

Аналогичным способом можно доказать, что функция , где n – натуральное число, непрерывна при .

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов.     Опубликовано: 21-08-2018

1cov-edu.ru

1.3. Некоторые общие свойства функций

а) Четность и нечетность.

Определение. Функция у=f(x) называется четной, если для любого значения х из области определения функции, значение – х также принадлежит области определения и выполняется равенство:

f(x)=f (–x).

Согласно определению, четная функция определена в интервале, симметричном относительно начала координат.

График четной функции симметричен относительно оси ординат.

Определение. Функция у=f (x) называется нечетной, если для любого значения х из области определения функции, значение – х также принадлежит области определения и выполняется равенство

f (x)= –f (–x).

Нечетная функция определена также в интервале, симметричном относительно начала координат.

Ее график симметричен относительно начала координат.

б) Периодичность функций

Определение. Функция у=f(x) называется периодической, если существует такое число Т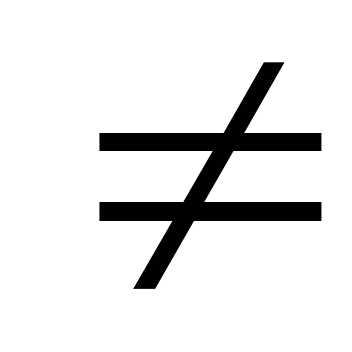0, что для любого значениях взятого из области определения функции, значения х+Т, х–Т также принадлежит области определения и выполняется равенство:

f (x)=f (x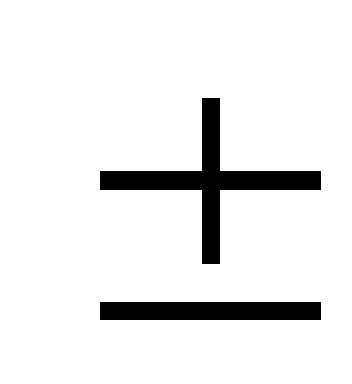Т).

Число Т называется периодом функции.

в) Монотонность функций

Переменную величину называют монотонной, если она возрастает либо убывает.

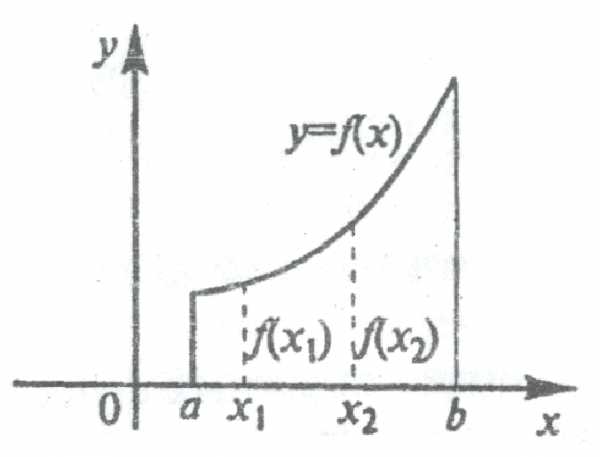
Определение. Функция у=f(x) называется монотонно возрастающей на интервале (а,в), если для любых х₁ и х₂, принадлежащих этому интервалу, из неравенства х₁<х₂ следует неравенство f(x₁)<f(x₂).

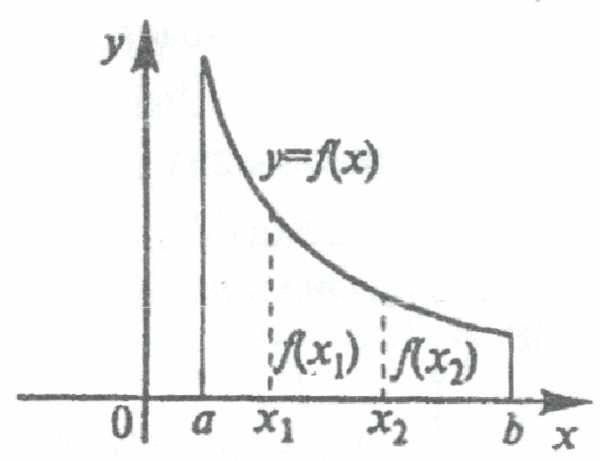
Определение. Функция у=f(x) называется монотонно убывающей на интервале (а,в), если для любых х₁ и х₂, принадлежащих этому интервалу, из неравенства х₁<х₂ следует неравенство f(x₁)>f(x₂).

Рассмотрим примеры

1. Найти область определения функций

а) у=5 х²

Решение.

Выражение у=5-х² при любом действительном значении х принимает действительные значения. Область определения функции D(f)=(,+).

б) у=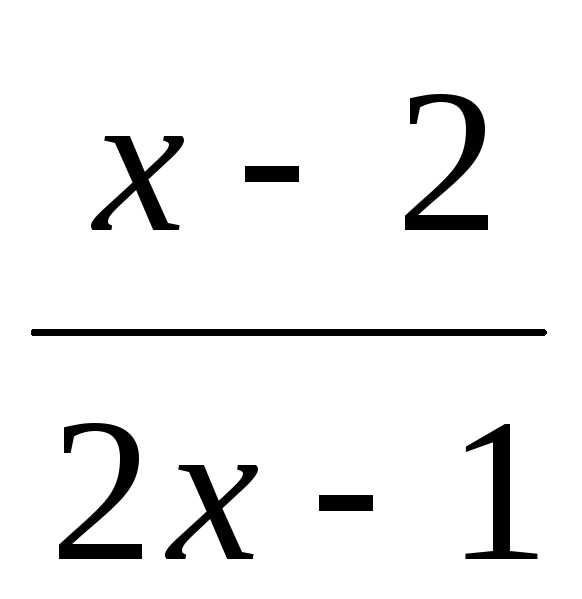

Решение.

Данная функция определена для всех значений х, кроме тех, при которых знаменатель дроби 2х-1 обращается в нуль. Решая уравнение 2х-1=0, находим: х=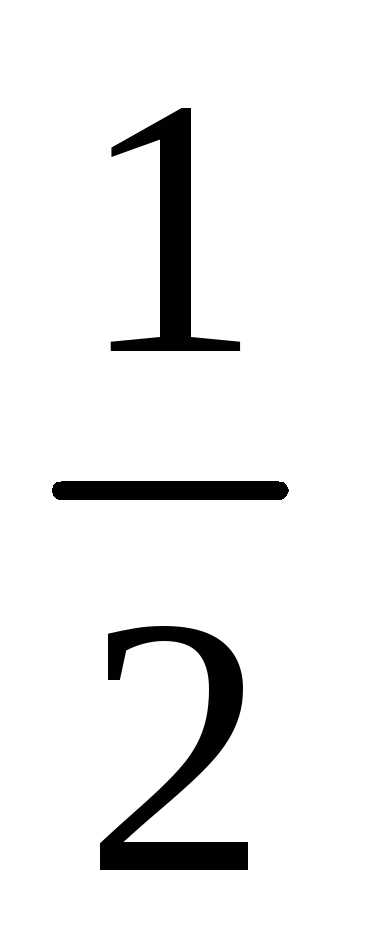Поэтому областью определения данной функции является объединение двух интервалов D(f)=(, )(,+).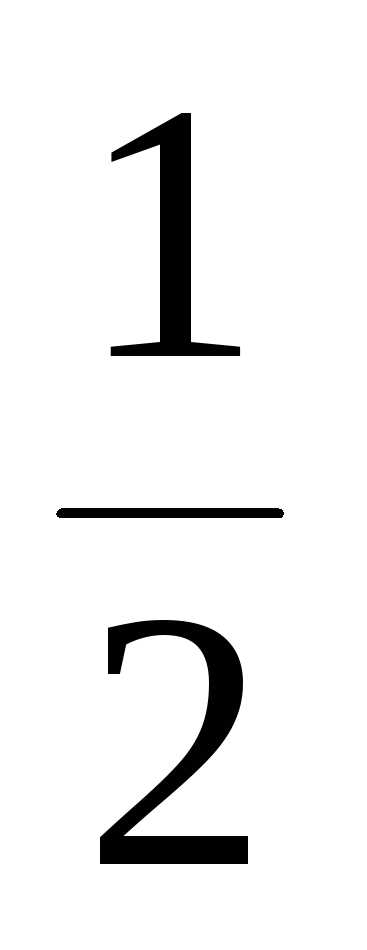

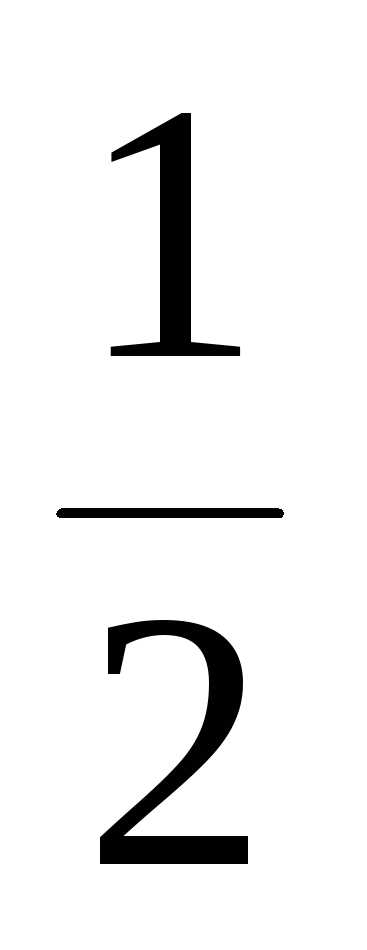в) у=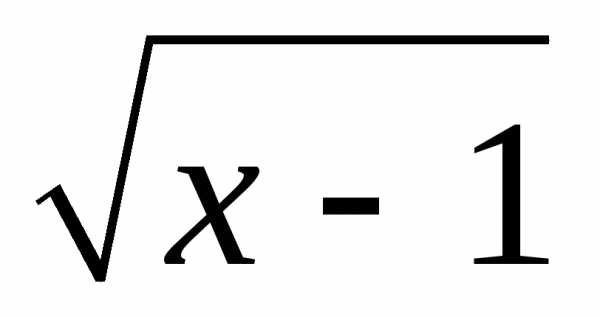

Решение.

Корни квадратные определены только для неотрицательных чисел. Для нахождения области определения составим и решим неравенство х10, х1 Таким образом, областью определения функции является интервал [1,+). D(f)=[1,+).

г)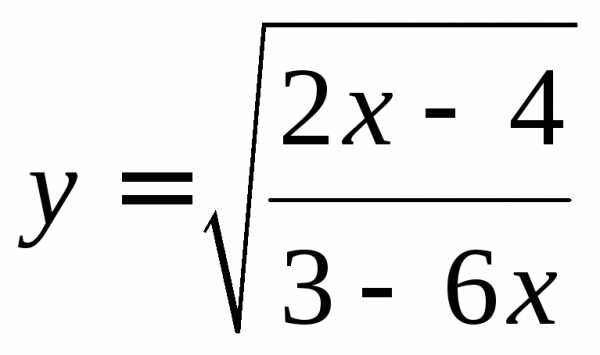

Решение.

Область определения данной функции можно рассматривать как совокупность всех значений х, удовлетворяющих неравенству

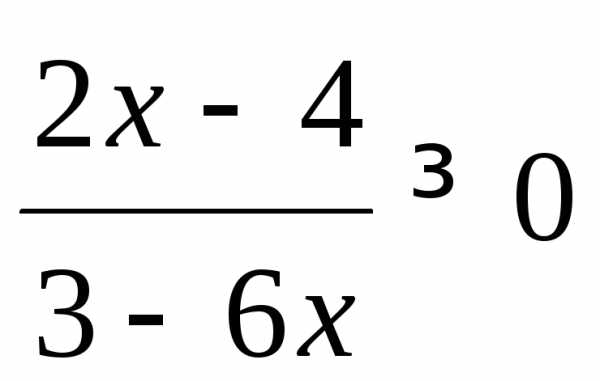
Неравенство 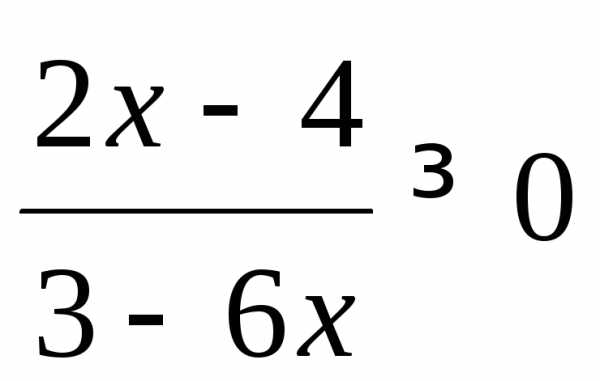равносильно системе неравенств

Из рисунка видно, что решением системы будет интервал .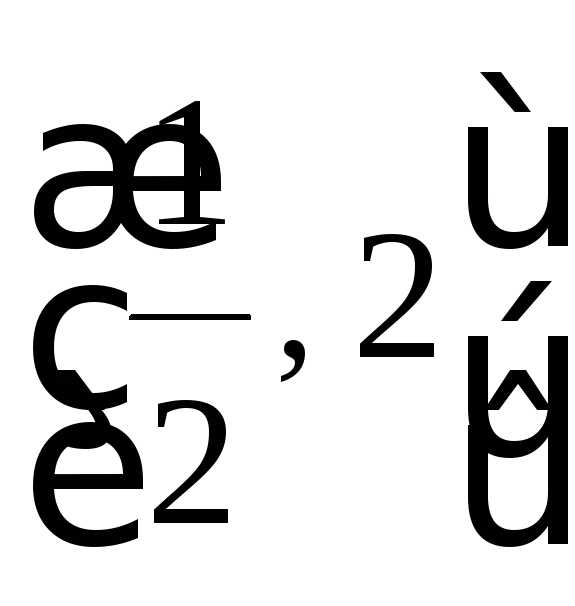

Таким образом D(f )=.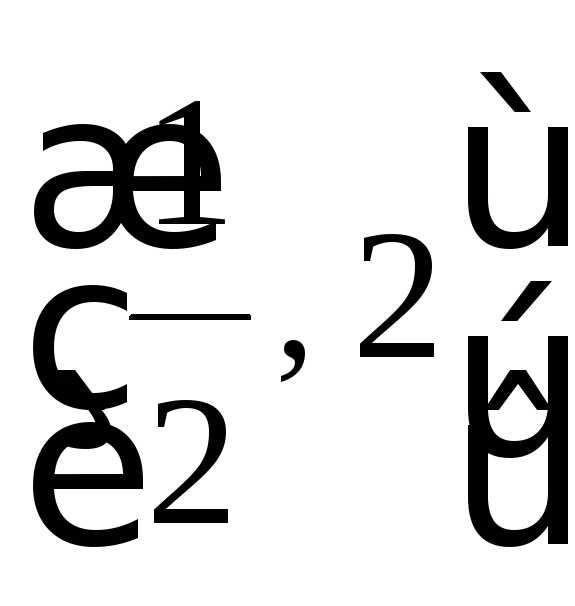

д)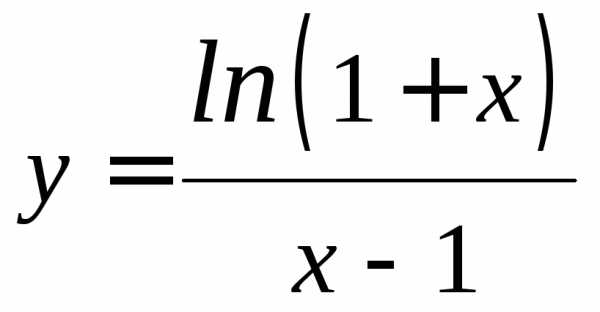

Решение.

Логарифмическая функция определена для положительных значений аргумента. Для нахождения области определения функции составим систему

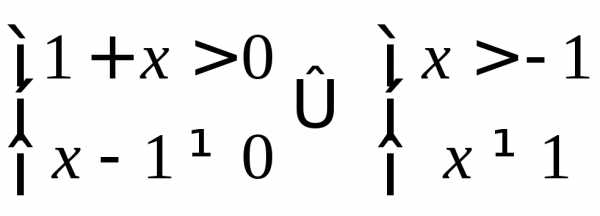
Область определения функции есть объединение интервалов.

D(f )=(—1,1)(1,+).

е)

Решение.

Функция у=arccos x определена на интервале [–1,1]. Поэтому область определения данной функции можно рассматривать как множество значений, удовлетворяющих неравенству

D(f)=[0, 4].

2. Установить четность или нечетность функции

а) у=х²+5х

Решение.

Область определения D(f)=(,+) – симметрична относительно начала координат. Воспользуемся определением четной и нечетной функции. Имеем

f(–x)=(–x)²+5(–x)=x²–5x.

Таким образом, f(–x) f(x) и f(–x) –f(x), т.е. заданная функция не является ни четной , ни нечетной.

б) у=2^х+2^-х

Решение.

Область определения D(f)=(;+). Имеем f(x)=2^-х+2^-(-х)=2^-х+2^х, т.е. f(x)= f(x). Данная функция – четная.

в)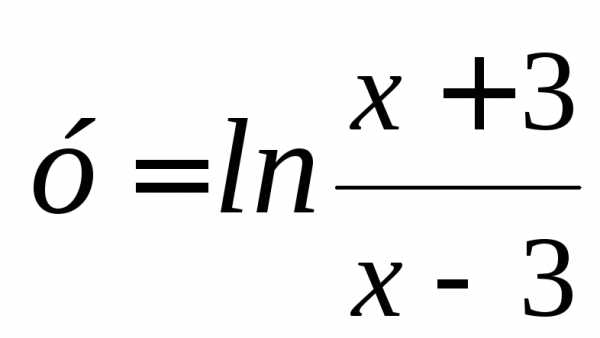

Решение.

Найдем область определения функции

D(f)=(,3)(3,+).

Область определения симметрична относительно начала координат. Найдем

f(–x)===,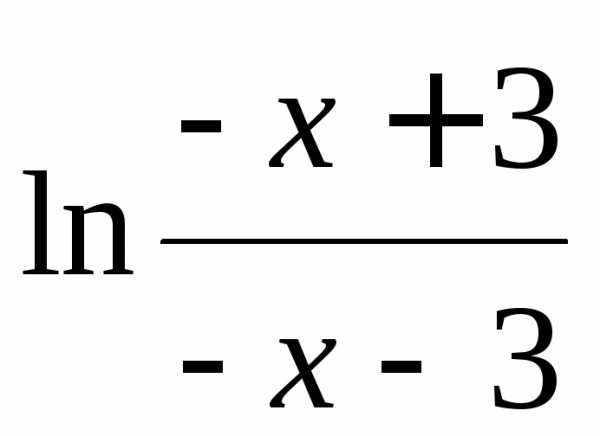

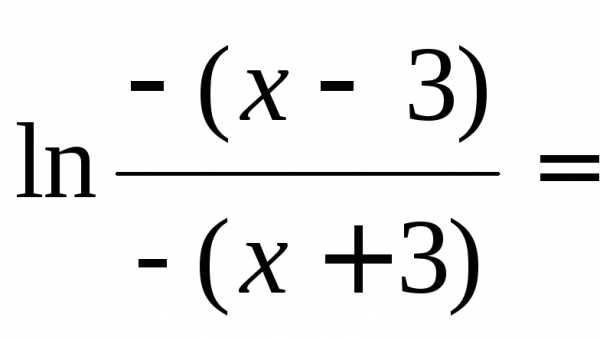
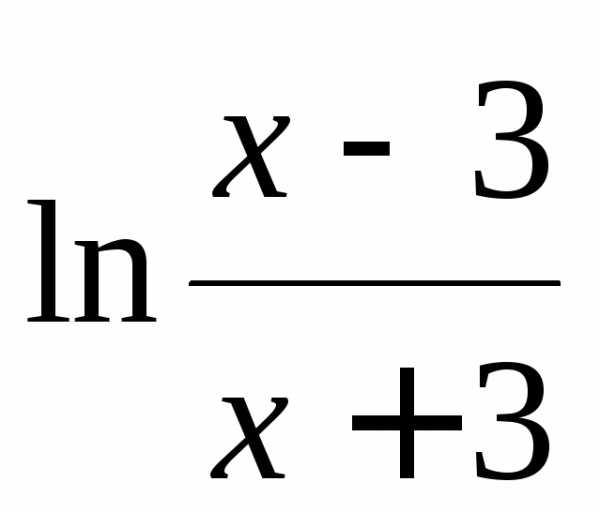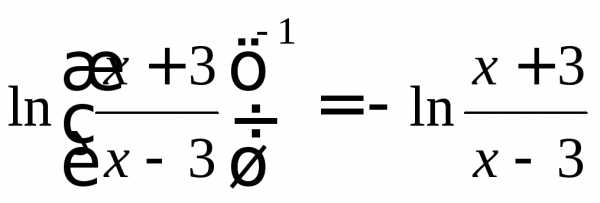т.е. f(x)= f(x), и, следовательно, данная функция – нечетная.

г)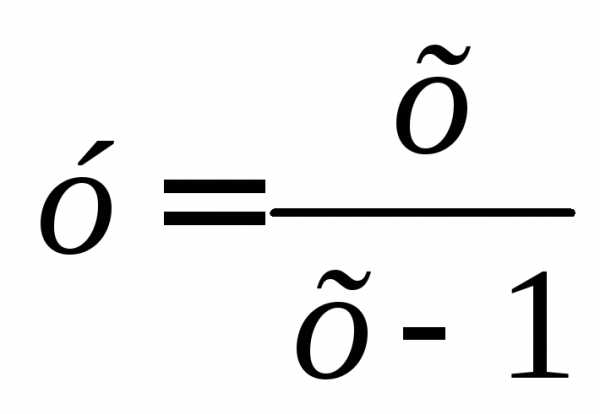

Решение.

Область определения функции D(f )=(,1)(1,+) несимметрична относительно начала координат. Данная функция не является ни четной, ни нечетной.

д)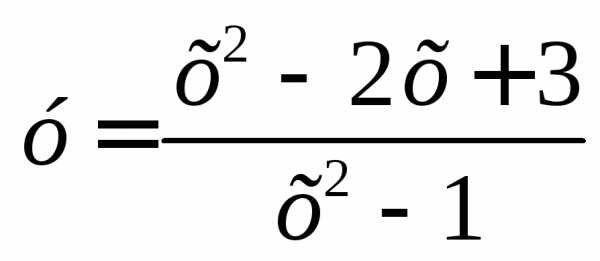

Решение.

Найдем область определения данной функции

D(f)=(,1)(—1,1)(1,+). Область определения симметрична относительно начала координат.

Найдем f(–x)=

Видно, что f(x) f(x) и f(x) –f(x). Поэтому данная функция не является ни четной, ни нечетной.

3. Определить, какие из следующих функций периодичны и найти их основные периоды.

При выполнении этих упражнений необходимо помнить, что функции у=sin x и y=cos x имеют период, равный 2, а функции y=tg x и y=ctg x – период, равный .

а) у=cos 8x

Решение.

Так как основной период функции cos x есть 2, то основной период функции у=cos 8x равен 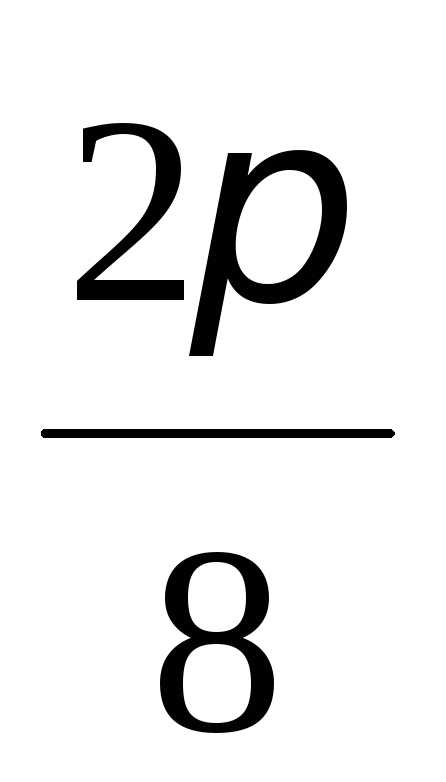, т.е..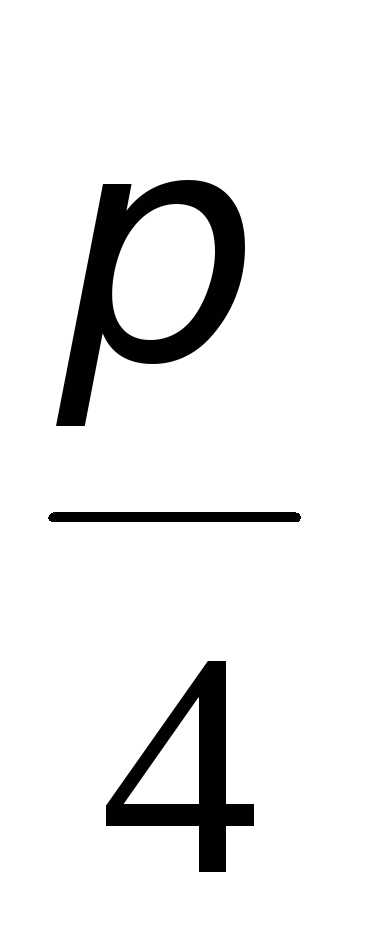

б) y= sin 6x+tg 4x

Решение.

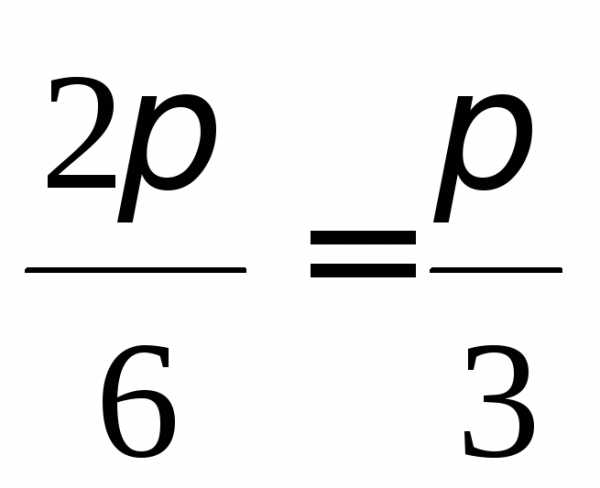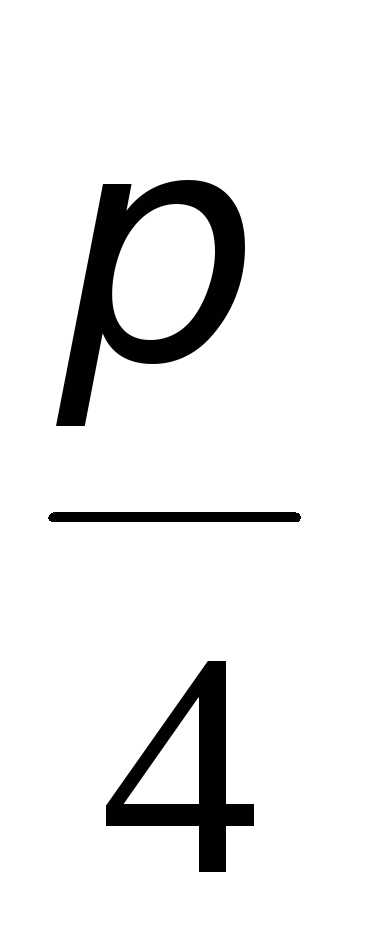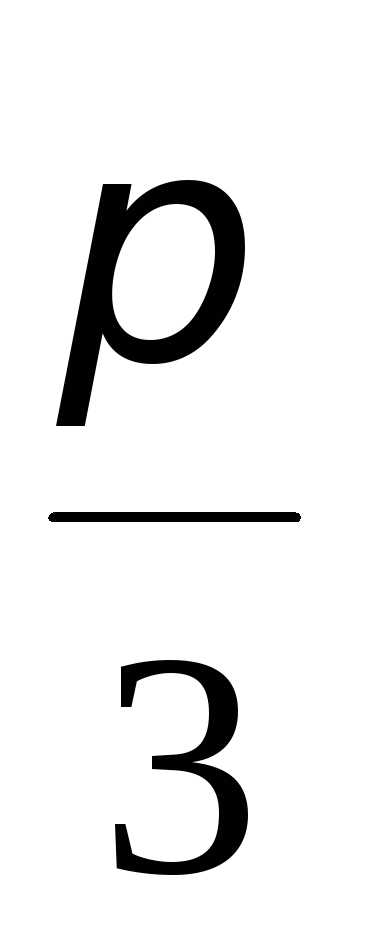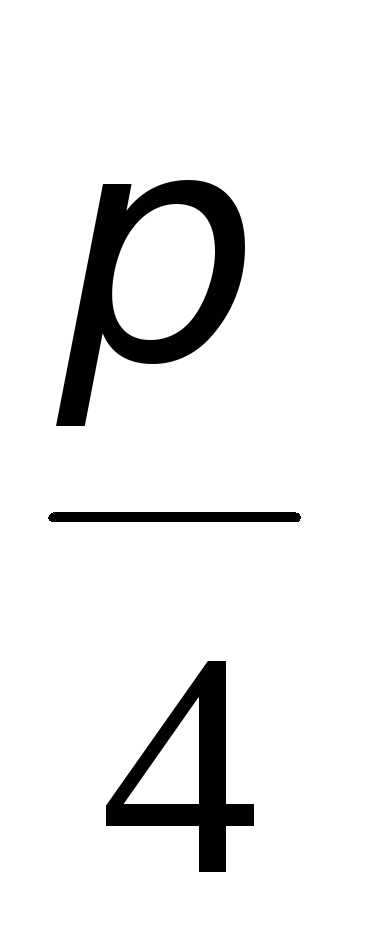Здесь для первого слагаемого основной период равен , а для второго – он равен. Очевидно, что основной период данной функции есть наименьшее общее кратное чисели, т.е..

в) y=ln cos 2x

Решение.

Основной период для функции cos x равен 2, для cos 2x равен  . Следовательно, для данной функции основной период равен .

г) y=sin² 3x

Решение.

Преобразуем выражение sin² 3x=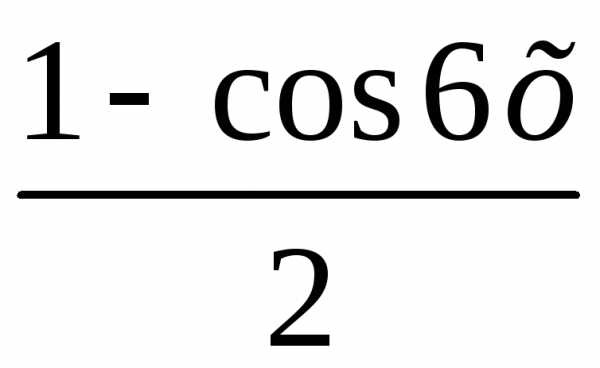.Период функции cos 6x равен 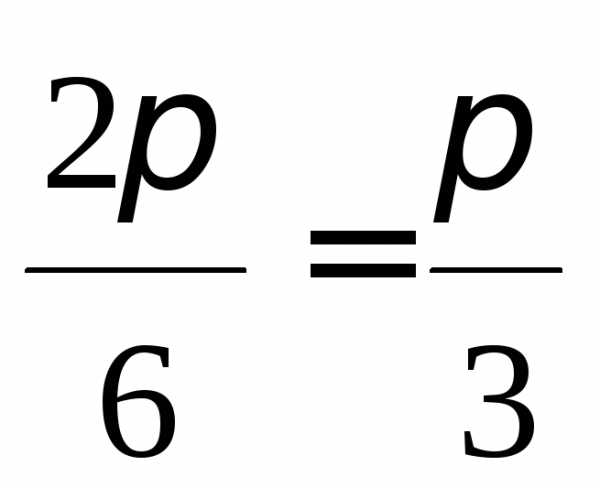. Следовательно, данная функция имеет период, равный.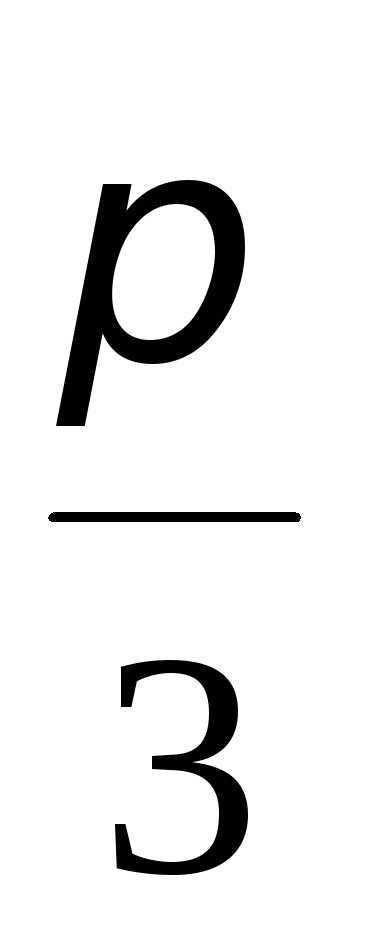

д) y=sin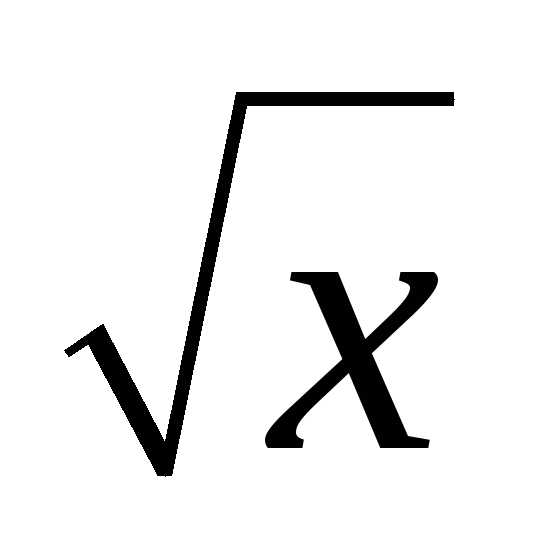

Решение.

Функция y=sin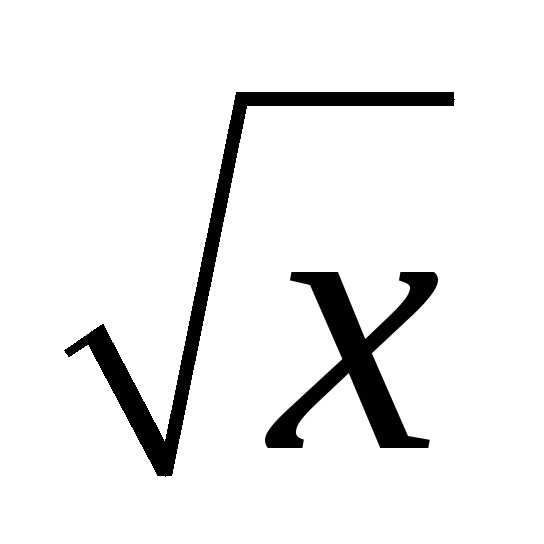 не является периодической т.к. для числа х=0, число х–Т, (если Т>0) или число х+Т, (если Т<0) не принадлежит области определения функции.

1.4. Упражнения для самостоятельной работы студентов

1. Найти область определения функции

2.Установить четность или нечетность функции

studfiles.net

определенная функция — это… Что такое определенная функция?



определенная функция

мат. certain function

Большой англо-русский и русско-английский словарь. 2001.

• определенная формула
• определенная цена

Смотреть что такое «определенная функция» в других словарях:

• полностью определенная функция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN completely defined function …   Справочник технического переводчика

• ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФУНКЦИЯ — комплекснозначная функция j на группе G, удовлетворяющая неравенству для любых наборов Совокупность П. о. ф. на G образует конус в пространстве М(G).всех ограниченных функций на G, замкнутый относительно операций умножения и комплексного… …   Математическая энциклопедия

• функция адресации — Функция, реализуемая определенными компонентами системы обработки информации, сопоставленная с пространством памяти, определенная на множестве адресов в этом пространстве памяти и предназначенная для выделения по адресу единственной подобласти в… …   Справочник технического переводчика

• ФУНКЦИЯ — (лат. functio – исполнение) обязанность, круг деятельности. «Функция – это существование, мыслимое нами в действии» (Гёте). Наука о функциях органов живых существ – физиология; специальная наука о функциях нервной системы – физиология органов… …   Философская энциклопедия

• Функция Шпрага-Гранди — широко используется в теории игр для нахождения выигрышной стратегии в комбинаторных играх, таких как игра Ним. Функция Шпрага Гранди определяется для игр с двумя игроками, в которых проигрывает игрок, не имеющий возможности сделать… …   Википедия

• ФУНКЦИЯ — ФУНКЦИЯ, в математике одно из основных понятий, выражение, определяющее регулярную зависимость между двумя множествами переменных величин, заключающуюся в том, что каждому элементу одного множества соответствует определенная, единственная… …   Научно-технический энциклопедический словарь

• ФУНКЦИЯ — (Function; Funktion) форма психической активности или проявление либидо, принципиально остающаяся неизменной в меняющихся условиях.Юнговская типологическая модель зиждется на четырех психологических функциях: мышлении, чувстве, ощущении и… …   Словарь по аналитической психологии

• ФУНКЦИЯ — (от лат. fonctio исполнение) 1) обязанность, круг деятельности, назначение, роль; 2) физиол. специфическая деятельность животного или растительного организма, его органов, тканей и клеток; 3) лог. отношение зависимости двух изменяющихся величин… …   Профессиональное образование. Словарь

• НЕЯВНАЯ ФУНКЦИЯ — функция заданная уравнением нек рые множества, т. е. такая функция f, что при любом имеет место . Если топологич. пространства и для нек рой точки выполняется условие то при определенных условиях в нек рой окрестности точки уравнение …   Математическая энциклопедия

• АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… …   Математическая энциклопедия

• МОНОТОННАЯ ФУНКЦИЯ — функция одного переменного, определенная на нек ром подмножестве действительных чисел, приращение к рой при не меняет знака, т. е. либо всегда неотрицательно, либо всегда неположительно. Если строго больше (меньше) нуля, когда то М. ф. наз.… …   Математическая энциклопедия

dic.academic.ru

определяющая функция — это… Что такое определяющая функция?



определяющая функция

determining function

Большой англо-русский и русско-английский словарь. 2001.

• определяющая формула
• определяющее взаимодействие

Смотреть что такое «определяющая функция» в других словарях:

• функция, определяющая специфическую для страны информацию — — [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ. Москва 1993] Тематики информационные технологии в целом EN national functionsNLSFUNC …   Справочник технического переводчика

• Функция предложения — функция, определяющая предложение в зависимости от влияющих на него различных факторов: 1) цены производства, 2) цены самого блага: 3) технологии, 4) ожиданий ценовых и дефицитных; 5) размера налогов и субсидий: 6) количества продавцов и др …   Словарь по экономической теории

• Функция спроса — функция, определяющая величину спроса в зависимости от влияющих на него различных факторов: цены, увеличения (или сокращения) доходов потребителя; изменения вкусов и предпочтений, ожиданий ценовых и дефицитных, колебаний расходов на рекламу,… …   Словарь по экономической теории

• Функция состояния — Функция состояния  функция, определяющая состояние системы: Термодинамическая функция состояния Волновая функция в квантовой механике …   Википедия

• функция расхода пневмопривода — pneumatic expenditure function Функция, определяющая массовый расход газа в интервале значений от единицы до максимума при данном значении показателя адиабаты. Шифр IFToMM: Раздел: ДИНАМИКА ПРИВОДОВ …   Теория механизмов и машин

• Производственная функция Кобба-Дугласа — функция, определяющая взаимозаменяемость труда и капитала. Выведена в 20 х гг. американскими учеными К. Коббом и П. Дугласом …   Экономика: глоссарий

• КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ — в статистической физике ф ция, определяющая вероятность относит. расположения комплекса из s любых молекул жидкости или газа; при s=2 К. ф. наз. парной или бинарной. Появление корреляций в расположении молекул среды связано с тем, что в ближайшем …   Физическая энциклопедия

• СПЕКТРАЛЬНАЯ ФУНКЦИЯ — разложение единицы, монотонное непрерывное слева в сильной операторной топологии отображение действительной прямой во множество ортогональных проекторов в гильбертовом пространстве, удовлетворяющее условиям Всякая самосопряженная (т. е.… …   Математическая энциклопедия

• Адхьявасая — определяющая функция Буддхи или интеллекта …   Словарь йоги и веданты

• ЛИБЕРАЛИЗМ — (от лат. liberalis свободный) идейное течение, в основе которого лежит убеждение в необходимости постепенного реформирования общества с целью более полной реализации индивидуальных ценностей, и в первую очередь индивидуальной свободы. Л. является …   Философская энциклопедия

• ГОСТ 23070-78: Анализ и оптимизация на ЭВМ радиоэлектронных схем. Термины и определения — Терминология ГОСТ 23070 78: Анализ и оптимизация на ЭВМ радиоэлектронных схем. Термины и определения оригинал документа: Многовариантный анализ 32. Анализ переходных процессов радиоэлектронной схемы Одновариантный анализ, при котором получают… …   Словарь-справочник терминов нормативно-технической документации

dic.academic.ru