Формулы сокращенных умножений – Формулы сокращенного умножения. Подробная теория с примерами.

Персональный сайт — Формулы сокращенного умножения

 

При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.

Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

a² — b² = (a — b)(a + b)

 

Квадрат суммы 

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(a + b)² = a² + 2ab + b²

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел

, не используя калькулятор или умножение в столбик. Поясним на примере:

Найти 112².

Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2 
112 = 100 + 1

Запишем сумму чисел в скобки и поставим над скобками квадрат. 
112² = (100 + 12)²

Воспользуемся формулой квадрата суммы: 
112² = (100 + 12)² = 100² + 2 x 100 x 12 + 12² = 10 000 + 2 400 + 144 = 12 544

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.

(8a + с)² = 64a² + 16ac + c²

 

Предостережение!!!

(a + b)² не равно a² + b²

Квадрат разности

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

(a — b)² = a² — 2ab + b²

Также стоит запомнить весьма полезное преобразование:

(a — b)² = (b — a)²
Формула выше доказывается простым раскрытием скобок:

(a — b)² = a² — 2ab + b² = b² — 2ab + a² = (b — a)²
 

 

Куб суммы

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b)³ = a³ + 3a²b + 3ab² + b³

Запомнить эту «страшную» на вид формулу довольно просто.

Выучите, что в начале идёт a³.

Два многочлена посередине имеют коэффициенты 3.

Вспомним, что любое число в нулевой степени есть 1. (a

0 = 1, b⁰ = 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b. В этом можно убедиться: 
(a + b)³ = a³b⁰ + 3a²b¹ + 3a¹b² + b³a⁰ = a³ + 3a²b + 3ab² + b³

 

Предостережение!!!

(a + b)³ не равно a³ + b³

 

Куб разности

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a — b)³ = a³ — 3a²b + 3ab² — b³

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a

3стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.

(a — b)³ = + a³ — 3a²b + 3ab² — b³ = a³ — 3a²b + 3ab² — b³ 

 

Сумма кубов (Не путать с кубом суммы!)

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a³ + b³ = (a + b)(a² — ab + b²)

Сумма кубов — это произведение двух скобок.

Первая скобка — сумма двух чисел.

Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:

a²— ab + b²
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.

 

Разность кубов (Не путать с кубом разности!!!) 

Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

a³ — b³ = (a — b)(a² + ab + b²)

Будьте внимательны при записи знаков. Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

 

Трудно запоминаются формулы сокращенного умножения? Делу легко помочь. Нужно просто запомнить, как изображается  такая простая вещь, как треугольник Паскаля. Тогда вы вспомните эти формулы всегда и везде, вернее, не вспомните, а восстановите.

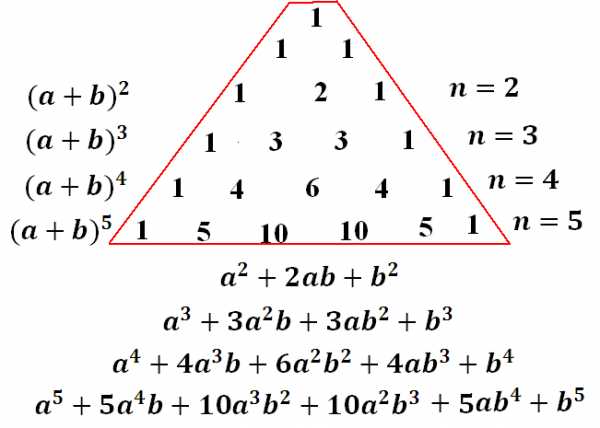
Что же такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена вида  в многочлен.

Разложим, например, :

В этой записи легко запоминается, что вначале стоит куб первого, а в конце – куб второго числа. А вот что посередине – запоминается сложно. И даже то, что в каждом следующем слагаемом степень одного множителя все время уменьшается, а второго – увеличивается – несложно заметить и запомнить, труднее дело обстоит с запоминанием  коэффициентов и знаков (плюс там или минус?).

Итак, сначала коэффициенты. Не надо их запоминать! На полях тетрадки быстренько рисуем треугольник Паскаля, и вот они – коэффициенты, уже перед нами. Рисовать начинаем с трех единичек, одна сверху, две ниже, правее и левее  — ага, уже треугольник получается:

Первая строка, с одной единичкой – нулевая. Потом идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно по краям снова приписать единички, а в центре записать число, полученное сложением двух чисел, стоящих над ним:

Записываем третью строку: опять по краям единицы, и опять, чтобы получить следующее число в новой строке, сложим числа, стоящие над ним в предыдущей:

 

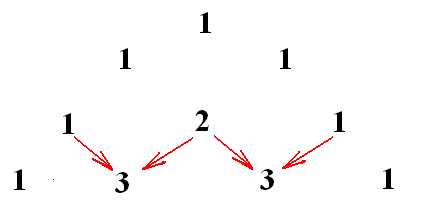
Как вы уже догадались, мы получаем в каждой строке коэффициенты из разложения двучлена в многочлен:

 

Ну а знаки запомнить еще проще: первый – такой же, как в раскладываемом двучлене (раскладываем сумму – значит, плюс, разность – значит, минус), а дальше знаки чередуются!

Вот такая это  полезная штука – треугольник Паскаля. Пользуйтесь!

ychitelll.ucoz.ru

Легкий способ запомнить формулы сокращенного умножения, или… Треугольник Паскаля.

Трудно запоминаются формулы сокращенного умножения? Делу легко помочь. Нужно просто запомнить, как изображается  такая простая вещь, как треугольник Паскаля. Тогда вы вспомните эти формулы всегда и везде, вернее, не вспомните, а восстановите.

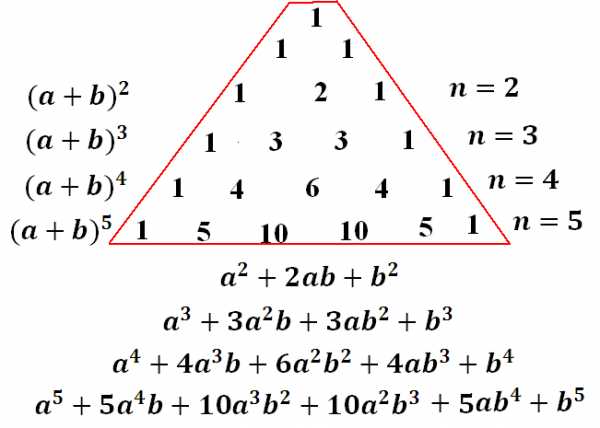
Что же такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена вида в многочлен.

Разложим, например, :

В этой записи легко запоминается, что вначале стоит куб первого, а в конце – куб второго числа. А вот что посередине – запоминается сложно. И даже то, что в каждом следующем слагаемом степень одного множителя все время уменьшается, а второго – увеличивается – несложно заметить и запомнить, труднее дело обстоит с запоминанием  коэффициентов и знаков (плюс там или минус?).

Итак, сначала коэффициенты. Не надо их запоминать! На полях тетрадки быстренько рисуем треугольник Паскаля, и вот они – коэффициенты, уже перед нами. Рисовать начинаем с трех единичек, одна сверху, две ниже, правее и левее  – ага, уже треугольник получается:

Первая строка, с одной единичкой – нулевая. Потом идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно по краям снова приписать единички, а в центре записать число, полученное сложением двух чисел, стоящих над ним:

Записываем третью строку: опять по краям единицы, и опять, чтобы получить следующее число в новой строке, сложим числа, стоящие над ним в предыдущей:

 

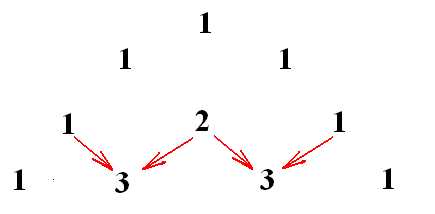
Как вы уже догадались, мы получаем в каждой строке коэффициенты из разложения двучлена в многочлен:

 

 

Ну а знаки запомнить еще проще: первый – такой же, как в раскладываемом двучлене (раскладываем сумму – значит, плюс, разность – значит, минус), а дальше знаки чередуются!

Вот такая это  полезная штука – треугольник Паскаля. Пользуйтесь!

easy-physic.ru

Формулы сокращенного умножения. Примеры

Формулы сокращенного умножения применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.

Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.

Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.

Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.

Формулы для четвертого и пятого степени в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.

Формулы для степени n расписаны через биномиальные коэффициенты с использованием факториалов следующие

Примеры применения формул сокращенного умножения

Пример 1. Вычислить 51^2.

Решение. Если есть калькулятор то без проблем находите

Это я пошутил — с калькулятором мудрые все, без него … (не будем о грустном).

Не имея калькулятора и зная приведенные выше правила квадрат числа находим по правилу

Пример 2. Найти 99^2.

Решение. Применим вторую формулу

Пример 3. Возвести в квадрат выражение
(x+y-3).

Решение. Сумму первых двух слагаемых мысленно считаем одним слагаемым и по второй формуле сокращенного умножения имеем

Пример 4. Найти разность квадратов
11^2-9^2.

Решение. Поскольку числа небольшие то можно просто подставить значения квадратов

Но цель у нас совсем другая — научиться использовать формулы сокращенного умножения для упрощения вычислений. Для этого примера применим третью формулу

Пример 5. Найти разность квадратов
17^2-3^2.

Решение. На этом примере Вы уже захотите изучить правила чтобы вычисления свести к одной строке

Как видите — ничего удивительного мы не делали.

Пример 6. Упростить выражение
(x-y)^2-(x+y)^2.

Решение. Можно раскладывать квадраты, а позже сгруппировать подобные слагаемые. Однако можно прямо применить разность квадратов

Просто и без длинных решений.

Пример 7. Возвести в куб многочлен
x^3-4.

Решение. Применим 5 формулу сокращенного умножения

Пример 8. Записать в виде разности квадратов или их сумме
а) x^2-8x+7
б) x^2+4x+29

Решение. а) Перегруппируем слагаемые

б) Упрощаем на основе предыдущих рассуждений

Пример 9. Разложить рациональную дробь

Решение. Применим формулу разности квадратов

Составим систему уравнений для определения констант

К утроенному первому уравнению добавим второе. Найденное значение подставляем в первое уравнение

Окончательно разложение примет вид

Разложить рациональную дробь часто необходимо перед интегрированием, чтобы снизить степень знаменателя.

Пример 10. Используя бином Ньютона расписать
выражение (x-a)^7.

Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты

Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад

Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7).

Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.

yukhym.com

Формулы сокращенного умножения — это… Что такое Формулы сокращенного умножения?



Формулы сокращенного умножения

Формулы сокращённого умножения многочленов — часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем Бинома Ньютона. Изучаются в средней школе в курсе алгебры.

Формулы для квадратов

• a² − b² = (a + b)(a − b)
• (a + b − c)² = a² + b² + c² + 2ab − 2ac − 2bc

Формулы для кубов

Формулы для четвертой степени

Формулы для n-ой степени

• aⁿ − bⁿ = (a − b)(a^{n − 1} + a^{n − 2}b + a^{n − 3}b² + … + a²b^{n − 3} + ab^{n − 2} + b^{n − 1})

Некоторые свойства формул

• (a − b)²ⁿ = (b − a)²ⁿ, где
• (a − b)^{2n + 1} = − (b − a)^{2n + 1}, где

Интересные формулы

• a⁴ − b⁴ = (a − b)(a + b)(a² + b²) (выводится из a² − b²)

См. также

Источники

• М. Я. Выгодский, Справочник по элементарной математике, Москва, 1958

Wikimedia Foundation. 2010.

• Формулы сокращённого умножения
• Формулы химические

Смотреть что такое «Формулы сокращенного умножения» в других словарях:

• Формулы сокращенного умножения многочленов — Формулы сокращённого умножения многочленов часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем Бинома Ньютона. Изучаются в средней школе в курсе алгебры. Содержание 1 Формулы для квадратов 2 Формулы для кубов …   Википедия

• Форумулы сокращенного умножения многочленов — Формулы сокращённого умножения многочленов часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем Бинома Ньютона. Изучаются в средней школе в курсе алгебры. Содержание 1 Формулы для квадратов 2 Формулы для кубов …   Википедия

• Вертикальная педагогика — Зачетные уроки Вертикальная педагогика – метод обучения школьников математике, созданный белорецким педагогом Р. Г. Хазанкиным в конце 1970 х годов. Метод отмечен Государственной премией СССР (1990), и Премией Правительства России в области… …   Википедия

• СИЛЛОГИСТИКА — (от греч. syllogisticos рассчитываю, считаю) логическая теория дедуктивных рассуждений, в которой исследуются логические связи между категорическими атрибутивными высказываниями. С. была построена Аристотелем. К числу указанных высказываний… …   Философская энциклопедия

dic.academic.ru

Формулы сокращенного умножения

Формулы сокращенного умножения помогают существенно облегчить вычисления. Суть их применения заключается в том, что вместо того, чтобы раз от разу совершать одни и те же алгебраические преобразования, можно сразу записывать их результат. Кроме того, разложение на множители по формулам сокращенного умножения часто помогает решить на первый взгляд сложные уравнения и неравенства.

Итак, вспомним формулы сокращенного умножения:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

8. Полезные тождества:

Примеры  использования формул сокращенного умножения:

1. Вычислить: 199²

199²=(200-1)²=200²-2х200+1=40000-400+1=39601

2. Вычислить:

3. Решить уравнение:  

Перенесем слагаемые в левую часть:

 

Разложим на множители по формуле разности квадратов:

Очевидно, что выражение во вторых скобках  не равно нулю ни при каких значениях х. Приравняем к нулю выражение в первых скобках:

Снова разложим на множители по формуле разности квадратов:

 

 

x=1/3

Скачать таблицу формулы сокращенного умножения

ege-ok.ru

Формулы сокращённого умножения — 7 класс — Алгебра — Каталог статей

Формулы сокращённого умножения
При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.
 

Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
 

Разность квадратов
    

• Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
• a² — b² = (a — b)(a + b)

Примеры:
•    152 — 22 = (15 — 2)(15 + 2) = 13 x 17 = 221
•    9a² — 4b²с² = (3a — 2bc)(3a + 2bc)
 

Квадрат суммы
    

• Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
• (a + b)² = a² + 2ab + b²

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик.

Поясним на примере:
Найти 112².
•    Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2 
112 = 100 + 12
•    Запишем сумму чисел в скобки и поставим над скобками квадрат. 
1122 = (100 + 12)²
•    Воспользуемся формулой квадрата суммы: 
112² = (100 + 12)²= 100² + 2 x 100 x 12 + 12² = 10 000 + 2 400 + 144 = 12 544
 

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
•    (8a + с)²= 64a² + 16ac + c²
 

Предостережение!
(a + b)² не равно a² + b²
 

Квадрат разности
    

• Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
• (a — b)² = a² — 2ab + b²

Также стоит запомнить весьма полезное преобразование:
(a — b)² = (b — a)²

Формула выше доказывается простым раскрытием скобок:
(a — b)² = a² — 2ab + b² = b² — 2ab + a2 = (b — a)²

Куб суммы
    

• Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
• (a + b)³ = a³ + 3a²b + 3ab² + b³

Запомнить эту «страшную» на вид формулу довольно просто.
•    Выучите, что в начале идёт a³.
•    Два многочлена посередине имеют коэффициенты 3.
•    Вспомним, что любое число в нулевой степени есть 1. (a⁰ = 1, b⁰= 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b.

В этом можно убедиться: 
(a + b)³ = a³b⁰ + 3a²b¹ + 3a¹b²+ b³a⁰ = a³ + 3a²b + 3ab² + b³
 

Предостережение!
(a + b)³ не равно a³ + b³
 

Куб разности
    

• Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
• (a — b)³ = a³ — 3a²b + 3ab² — b³

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a³ стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.
(a — b)³ = + a³ — 3a²b + 3ab² — b³ = a³ — 3a²b + 3ab² — b³ 

Сумма кубов
Не путать с кубом суммы!
    

• Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
• a³ + b³ = (a + b)(a² — ab + b²)

Сумма кубов — это произведение двух скобок.
•    Первая скобка — сумма двух чисел.
•    Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:

a²— ab + b²

Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.
 

Разность кубов
Не путать с кубом разности!
    

• Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
• a³ — b³ = (a — b)(a² + ab + b²)

Будьте внимательны при записи знаков.
 

Применение формул сокращенного умножения
Следует помнить, что все формулы, приведённые выше, используется также и справа налево.
 

Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.
 

Примеры:
•    a²+ 2a + 1 = (a + 1)²
•    (aс — 4b)(ac + 4b) = a²c² — 16b²
 

matematik.3dn.ru