Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
 Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
- Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
 Разносторонний треугольник — все три стороны не равны.
Разносторонний треугольник — все три стороны не равны.
- Равнобедренный треугольник — две стороны равны.
- Равносторонним треугольник или правильный треугольник — все три стороны равны.
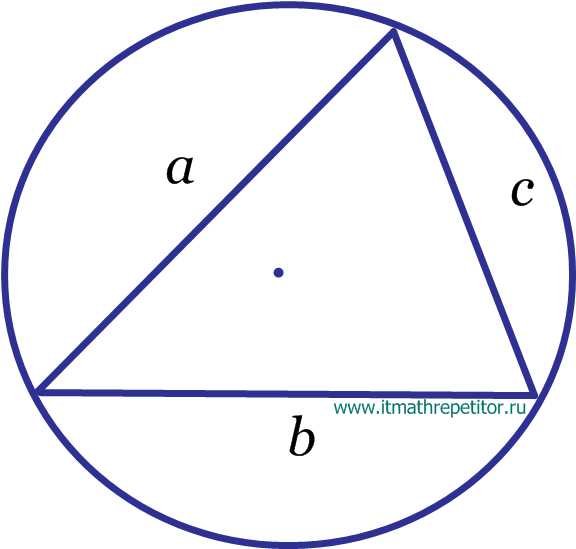
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
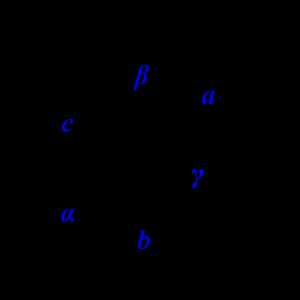
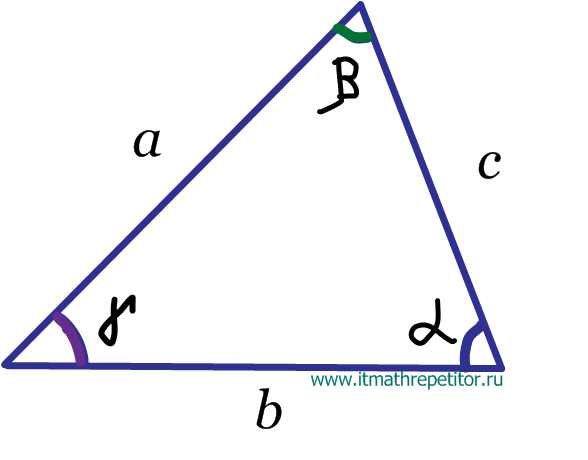
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианыa = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2 + mc2) — mb2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
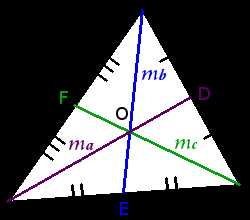
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b 2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника
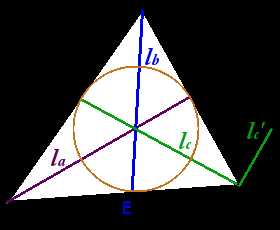
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
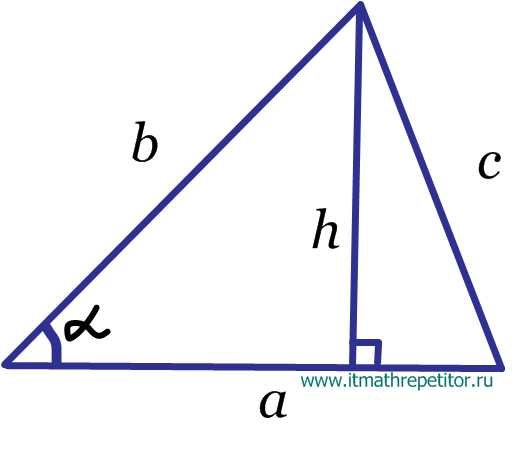
Высоты треугольника
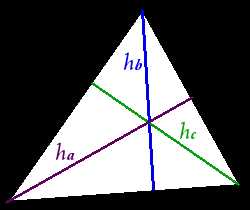
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника
.Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:ha = bc2R
hb = ac2R
hc = ab2R
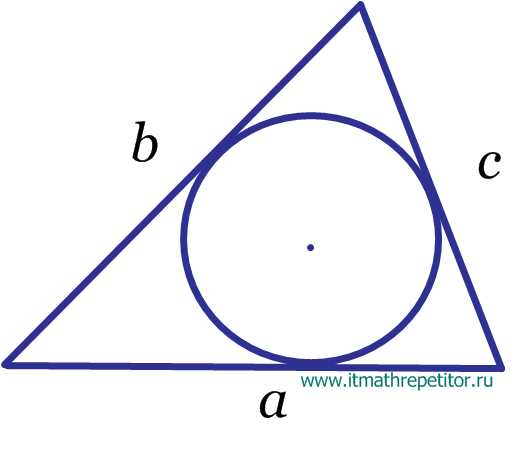
Окружность вписанная в треугольник

Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:Окружность описанная вокруг треугольника
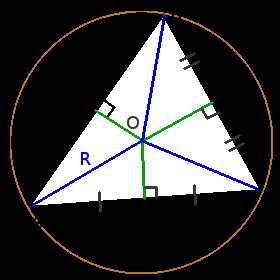
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр вписанной в треугольник окружности лежит на пересечении серединных перпендикуляров к уго сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.rR = 4 sinα2sinβ2sinγ2 = cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2. Средняя линия треугольника параллельна основанию и равна его половине.MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольникаS∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
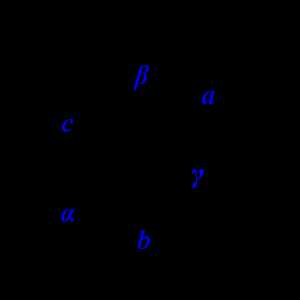
Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника

- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты S = 12a · ha
S = 12b · hb
S = 12c · hc - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника. - Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Подобие треугольников
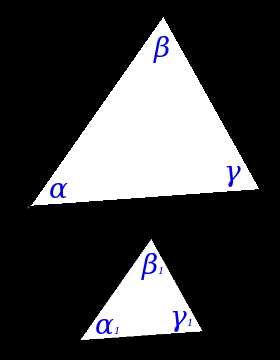 Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобияПризнаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны. Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:S∆АВСS∆MNK = k2
ru.onlinemschool.com
Все формулы треугольника. Формулы биссектрисы. Основные формулы треугольника.
Основные формулы треугольника
В этой статье вы найдете все формулы площадей треугольника:
Теорема косинусов
\(a^2=b^2+c^2-2bc* cos α\)
\(b^2=a^2+c^2-2ac* cos β\)
\(a^2=a^2+b^2-2ab* cos γ\)
Медианные формулы
\(m^2_a=14(2b^2+2c^2-a^2)\)
\(m^2_b=14(2a^2+2c^2-b^2)\)
\(m^2_c=14(2a^2+2b^2-c^2)\)
Формулы биссектрисы
\(\frac{a}{b}=\frac{n}{m}\)
\(l^2=ab-nm\)
Прямоугольный треугольник
\(c^2=a^2+b^2\)
\(S=\frac{1}{2}ab=\frac{1}{2}ch\)
\(a^2=n⋅с\)
\(b^2=mc\)
\(h^2=m*n\)
\( r=\frac{a+b−c}{2}\)- радиус вписанной окружности
\( sin α=a/c\)
\( tan α=a/b\)
\( cot α=b/a\)
Формулы площади
полупериметр \(p=\frac{a+b+c}{2}\)
Площадь треугольника
\(S=\frac{ ch_c}{2}\)
\(S=\frac{ab sin γ}{2}\)
\(S=\sqrt{p(p−a)(p−b)(p−c)}\)
\(S=pr \)
где \(r\) радиус треугольника вписанной окружности
\(S=\frac{abc}{ 4R}\)
где — R-радиус описанной окружности
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Формулы треугольника, с примерами
Формулы площади треугольника
1. По стороне и проведенной к ней высоте
2. По двум сторонам и углу между ними
3. Формула Герона
где – полупериметр треугольника
4. Через радиусы вписанной и описанной окружностей
где – полупериметр треугольника, – радиус вписанной окружности;
здесь – радиус описанной окружности.
Теоремы треугольника
ТЕОРЕМА Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между нимиТЕОРЕМА Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
ТЕОРЕМА Теорема тангенсов. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
Равносторонний треугольник со стороной :
– радиус описанной окружности,
– радиус вписанной окружности,
– высота, совпадающая с медианой и биссектрисой,
– площадь треугольника.
Формулы прямоугольного треугольника
В прямоугольном треугольнике с , гипотенузой и катетами и
ТЕОРЕМА Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов.
Примеры решения задач
ПРИМЕР 1| Задание | В равностороннем треугольнике со стороной см найти площадь и радиусы вписанной и описанной окружностей. |
| Решение | Площадь равностороннего треугольника найдем по формуле , подставив :
Тогда искомые радиусы вписанной и описанной окружностей
|
| Ответ | см см см. |
| Задание | В треугольнике стороны см см, а . Найти все стороны и все углы треугольника . |
| Решение | Сделаем рисунок.
Воспользуемся теоремой синусов и найдем угол :
откуда , т.е. . Следовательно, треугольник является прямоугольным. Значит,
Найдем сторону по теореме Пифагора: см |
| Ответ | см. |
Египетский треугольник
Неравенство треугольника
Виды треугольников
Тупоугольный треугольник
Остроугольный треугольник
Признаки подобия треугольников и свойства
ru.solverbook.com
Все формулы для треугольника
Геометрия. Планиметрия
Формулы для произвольного треугольника
к содержанию справочника
- Медиана треугольника.
 Обратите внимание, что медиана проведена именно к стороне .
Обратите внимание, что медиана проведена именно к стороне . - Биссектриса треугольника.
 Обратите внимание, что биссектриса проведена именно к стороне
Обратите внимание, что биссектриса проведена именно к стороне - Теорема косинусов.

- Теорема синусов.
(следствие)

- Площадь треугольника.
(формула Герона),
где (полупериметр)
- Радиус вписанной окружности.
, где
(периметр)

- Радиус описанной окружности.

- Теорема Менелая.

Метки треугольник. Смотреть запись.
www.itmathrepetitor.ru
Формулы треугольника | Формулы с примерами
ФормулыФормула теоремы синусов
Формулы теоремы косинусов

Формула тангенсов
Формулы площади треугольника

Формула синуса половинного угла
Формула косинуса половинного угла
Формула тангенса половинного угла
Формула радиуса описанной окружности
Формула радиуса вписанной окружности треугольника
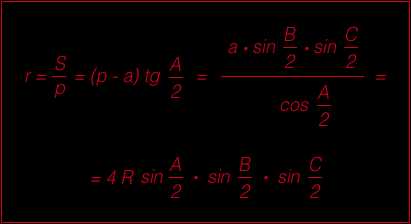
Формулы биссектрисы угла
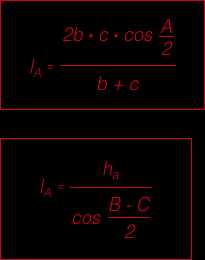
Формулы прямоугольного треугольника

Формулы косоугольных треугольников

formula-xyz.ru
Треугольник | Формулы и расчеты онлайн
Треугольник — многоугольник с тремя сторонами. Стороны треугольника часто обозначаются малыми буквами, соответствующими обозначению противоположных вершин.
Остроугольный треугольник | Прямоугольный треугольник | Тупоугольный треугольник |
Если все три угла острые, то треугольник — остроугольный.
Если один из углов прямой, то треугольник — прямоугольный.
Стороны, образующие прямой угол, называются катетами. Сторона против прямого угла — гипотенузой.
Если один из углов тупой — то треугольник тупоугольный.
Равнобедренный треугольник | Равносторонний треугольник | Внешний угол треугольника |
Треугольник равнобедренный, когда две его стороны равны.
Треугольник равносторонний или правильный, когда все три его стороны равны.
Равные стороны равнобедренного треугольника называются боковыми. Третья сторона — основанием.
Во всяком треугольнике против большей стороны лежит больший угол. Против равных сторон — равные углы, Равносторонний треугольник вместе с тем равноугольный.
Сумма углов в треугольнике
Во всяком треугольнике сумма углов равна 180°.
В равностороннем треугольнике каждый угол равен 60°.
\[ A + B + C = 180° \]
Продолжив одну из сторон треугольника, получим внешний угол ∠BCD Внешний угол равен сумме внутренних, с ним не смежных углов.
\[ ∠BCD = ∠DAB + ∠ABC \]
В помощь студенту
Треугольник |
стр. 230 |
|---|
www.fxyz.ru
Все формулы сторон прямоугольного треугольника
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
- Подробности
- Автор: Administrator
www-formula.ru

 Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
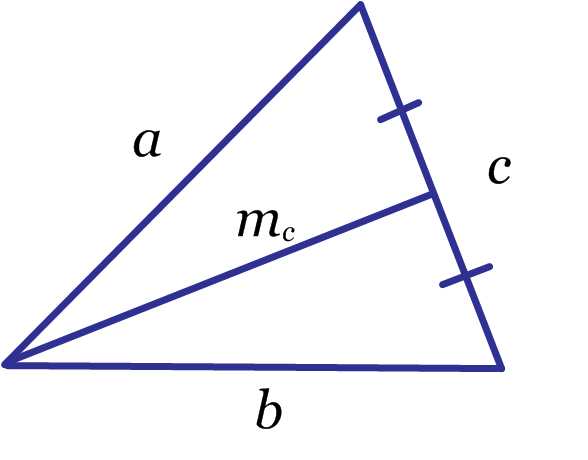 Обратите внимание, что медиана проведена именно к стороне .
Обратите внимание, что медиана проведена именно к стороне .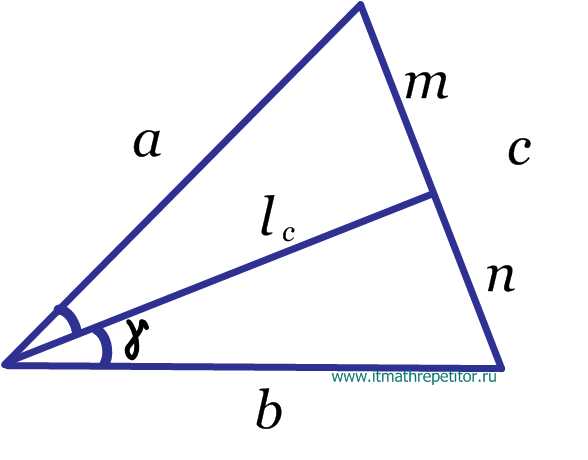 Обратите внимание, что биссектриса проведена именно к стороне
Обратите внимание, что биссектриса проведена именно к стороне