На пересечении биссектрис в треугольнике расположен центр окружности, которую можно в него вписать. Радиус такой окружности рассчитывается по следующей формуле(рис.75.5) r=√(((p-a)(p-b)(p-c))/p)
Центр описанной вокруг треугольника окружности в свою очередь расположен в точке пересечения медиатрисс, и его формула значительно видоизменена в сравнении с радиусом вписанной окружности. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга.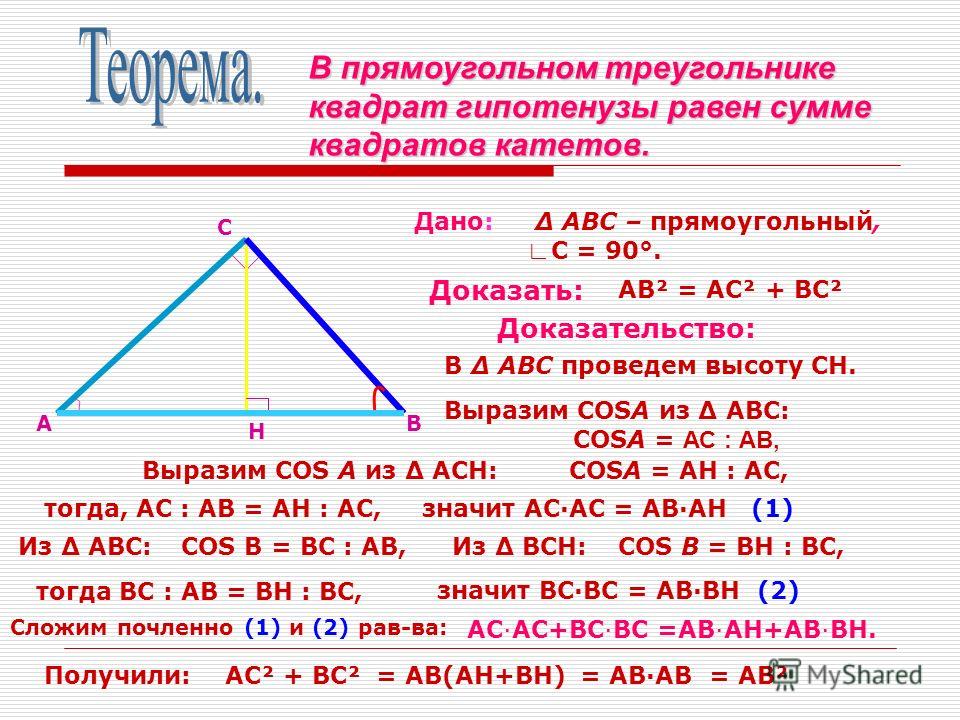
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .
Решение:
Из теоремы косинусов имеем:
Откуда
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).
Решение. Из формул (1) и (2) находим:
Используя онлайн калькулятор для arcsin и arccos находим углы A и B:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис. 2). Найдем сторону c и углы A и B.
2). Найдем сторону c и углы A и B.
Решение:
Найдем сторону c используя теорему косинусов:
Далее, из формулы
найдем cosA:
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.
Решение. Иcпользуя теорму косинусов найдем сторону c:
Вычисления выше легко производить инженерным онлайн калькулятором.
Из формулы (3) найдем cosA:
Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Решение:
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Откуда
Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.
Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Ответ:
Произвольный треугольник по заданным параметрам
| Результат расчета параметров заданного треугольника |
Представляем Вам калькулятор, который позволял рассчитывать все возможные параметры треугольника по заданным параметрам.
Хотелось бы обратить Ваше внимание именно на то, что это универсальный бот. Он рассчитывает все параметры произвольного треугольника, при произвольно заданных параметрах. Такого бота вы не найдете нигде.
Такого бота вы не найдете нигде.
Вам известна сторона и две высоты? или две стороны и медиана? Или биссектриса два угла и основание треугольника?
По любым запросам, мы можем получить правильный расчет параметров треугольника.
Вам нет необходимости искать формулы и делать расчет самостоятельно. За вас уже все сделано.
Создайте запрос и получите точный ответ.
Показан произвольный треугольник. Сразу оговоримся как и что обозначается, дабы в дальнейшем не было путаницы и ошибок в расчетах.
Стороны противоположные любому углу называются так же только маленькой буквой. То есть напротив угла А лежит сторона треугольника а, стороне с противостоит угол С.
ma — это медина, падающая на сторону а, соответственно есть еще медианы mb и mc падающие на соответствующие стороны.
lb — это биссектриса , падающая на сторону b, соответственно есть еще биссектрисы la и lc падающие на соответствующие стороны.
hb — это высота, падающая на сторону b, соответственно есть еще высоты ha и hc падающие на соответствующие стороны.
Ну и второе, помните что треугольником является фигура в которой присутствует фундаментальное правило:
Сумма любых(!) двух сторон должна быть больше
третьей.Поэтому не удивляйтесь если получите ошибку При таких данных треугольника не существует при попытке рассчитатать параметры треугольника со сторонами 3, 3 и 7.
Синтаксис
Для позволяателей XMPP клиентов запрос вот такой treug <список параметров>
Для пользователй сайта, все сделано на этой странице.
Список параметров — параметры которые известны, разделенные точкой с запятой
параметр записываетя как параметр=значение
Например если известна сторона а с значением 10, то так и записываем a=10
Более того, значения могут быть не только в виде вещественного числа, но и например как результат какого то выражения
Например если нам нужно посчитать площадь треугольника с сторонами 1, 3, то вот в запросе пишем a=1;b=3;c=sqrt(5)+1
А вот и сам список парметров которые могут фигурировать в расчетах.
Сторона a
Сторона b
Сторона c
Полупериметр p
Угол А
Угол B
Угол C
Площадь треугольника S
Высота ha на сторону a
Высота hb на сторону b
Высота hc на сторону c
Медиана ma на сторону a
Медиана mb на сторону b
Медиана mc на сторону c
Координаты вершин (xa,ya) (xb,yb) (xc,yc)
Примеры
Рассчитать параметры треугольника если известны сторона = 8, угол прилежащей к этой стороне =70 градусов и высота, падающая на эту сторону =2
пишем treug a=8;C=70;ha=2
Параметры треугольника по заданным параметрам
Сторона a = 8
Сторона b = 2.
 1283555449519
1283555449519Сторона c = 7.5420719851515
Полупериметр p = 8.8352137650517
Угол А = 2.1882518638666 в градусах 125.37759631119
Угол B = 2.873202966917 в градусах 164.62240368881
Угол C = 1.221730476396 в градусах 70
Площадь треугольника S = 8
Высота ha на сторону a = 2
Высота hb на сторону b = 7.5175409662872
Высота hc на сторону c = 2.1214329472723
Медиана ma на сторону a = 3.8348889915443
Медиана mb на сторону b = 7.7012304590352
Медиана mc на сторону c = 4.4770789813853
Вот и все, все параметры треугольника.
Вопрос, почему мы сторону назвали а, а не в или с? Это не влияет на решение. Главное выдержать условие о котором я уже сказал «Стороны противоположные любому углу называются так же, только маленькой буквой.» А далее нарисовать в уме треугольник, и применить к заданному вопросу.
Можно было бы взять вместо а в, но тогда прилежащий угол будет не С а А ну и высота будет hb. Результат если вы проверите, будет один и тот же.
Как рассчитать треугольник если известны координаты его вершин?
Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3
пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3
и получаем
Параметры треугольника по заданным параметрам
Сторона a = 17
Сторона b = 11.401754250991
Сторона c = 13.453624047073
Полупериметр p = 20.927689149032
Угол А = 1.4990243938603 в градусах 85.887771155351
Угол B = 0.73281510178655 в градусах 41.987212495819
Угол C = 0.90975315794426 в градусах 52.125016348905
Площадь треугольника S = 76.5
Высота ha на сторону a = 9
Высота hb на сторону b = 13.
 418987695398
418987695398Высота hc на сторону c = 11.372400437582
Медиана ma на сторону a = 9.1241437954466
Медиана mb на сторону b = 14.230249470757
Медиана mc на сторону c = 12.816005617976
Удачных расчетов!!
- Разбиение многоугольника на треугольники >>
Калькулятор сторон и углов треугольника
Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,
Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить».
Калькулятор треугольника нужен, если требуется найти решение треугольников – длины сторон и величину углов треугольника.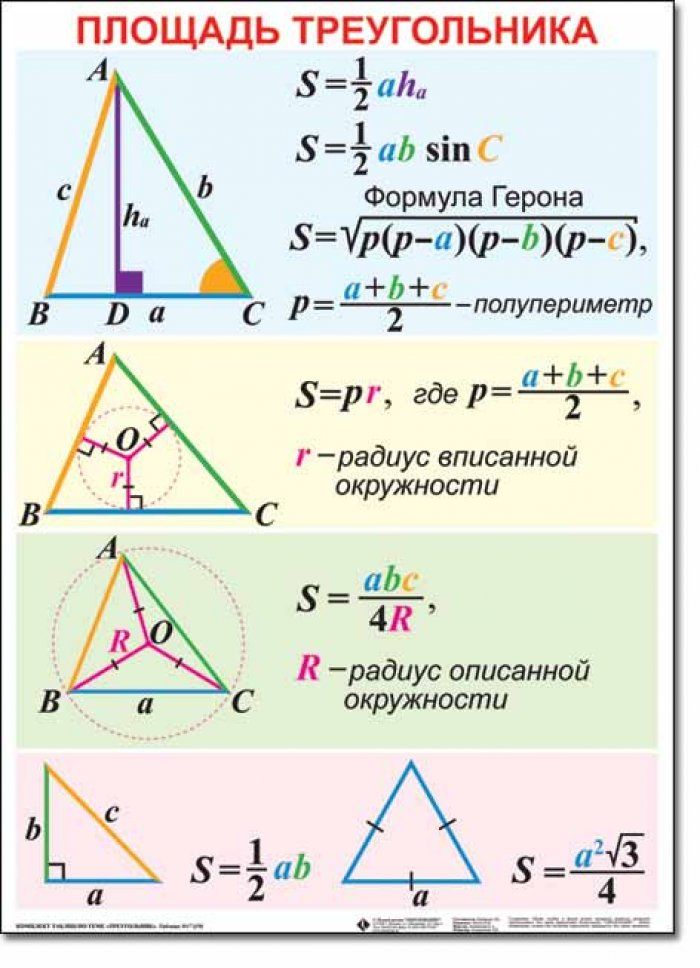
Решить треугольник − найти все углы и стороны треугольника. Данный калькулятор предназначен для нахождения элементов треугольника.
Как решить треугольник
Здесь размещен онлайн-калькулятор, с помощью которого можно решить треугольник по трем, двум сторонам и углам, по теореме синусов и косинусов, то есть показывается, как находить углы в треугольнике.
Решение треугольников можно находить с помощью таблицы Брадиса. Здесь ответ вычисляется автоматически компьютерной программой онлайн, быстро и удобно.
Если нужны формулы и решения задач на теоремы косинусов и синусов с ответами, то можно найти подробное и точное решение, если использовать бесплатный калькулятор треугольника.
В решении подробно показывается, как найти третью сторону по двум сторонам и углу между ними или как определить неизвестные стороны треугольника, если известна одна сторона.
Примеры решений практических задач
1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».
В ходе решения задачи получаем ответ:
сторона c = 13,8 см;
угол B = 35,2644° = 35°15’52» = 35°16′ = 0,1959π = 0,6155 rad;
угол C = 84,7356° = 84°44’8» = 84°44′ = 0,4708π = 1,4789 rad;
Периметр = 33,8 см;
Полупериметр = 16,9 см;
Площадь = 47,7984 см2;
Высота ha = 7,9664 см;
Высота hb = 11,9496 см;
Высота hc = 6,9273 см;
Медиана ma = 9,5513 см;
Медиана mb = 12,2958 см;
Медиана mc = 7,5107 см;
Радиус окружности R, описанной около треугольника = 6,9291 см;
Радиус окружности r, вписанной в треугольник = 2,8283 см.
Таким образом, был найден угол треугольника по двум сторонам и углу.
2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».
Используя теорему косинусов, получаем
угол A = 28,955° = 28°57’18» = 28°57′ = 0,1609π = 0,5054 rad;
угол B = 46,5675° = 46°34’3» = 46°34′ = 0,2587π = 0,8128 rad;
угол C = 104,4775° = 104°28’39» = 104°29′ = 0,5804π = 1,8235 rad;
Периметр = 9 см;
Полупериметр = 4,5 см;
Площадь = 2,9046 см2;
Высота ha = 2,9046 см;
Высота hb = 1,9364 см;
Высота hc = 1,4523 см;
Медиана ma = 3,3912 см;
Медиана mb = 2,7839 см;
Медиана mc = 1,5811 см;
Радиус окружности R, описанной около треугольника = 2,0657 см;
Радиус окружности r, вписанной в треугольник = 0,6455 см.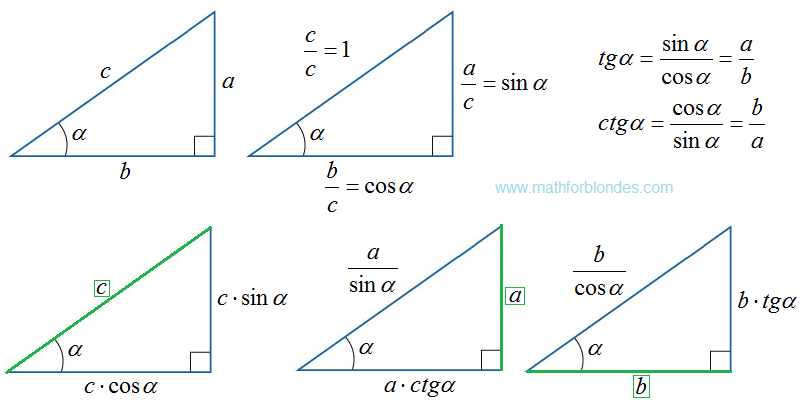
Таким образом, были найдены все углы треугольника.
3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°.
Ответ:
сторона b = 2,59 см;
сторона c = 3,66 см;
угол A = 105° = 0,5833π = 1,8326 rad;
Периметр = 11,25 см;
Полупериметр = 5,625 см;
Площадь = 4,5785 см2;
Высота ha = 1,8314 см;
Высота hb = 3,5355 см;
Высота hc = 2,5019 см;
Медиана ma = 1,9488 см;
Медиана mb = 4,1857 см;
Медиана mc = 3,537 см;
Радиус окружности R, описанной около треугольника = 2,588 см;
Радиус окружности r, вписанной в треугольник = 0,814 см.
Треугольники
Треугольник – многоугольник, который состоит из трех точек, соединенных тремя отрезками. Три точки в этом многоугольнике – вершины треугольника, а отрезки – стороны или ребра треугольника. На рисунке показан треугольник ΔABC, где A, B, C – его вершины, а AB, BC, AC – его стороны. Вершины треугольника дают треугольнику его обозначение. Угол при вершине A образуется сторонами AB и AC, обозначается как угол CAB.
Вершины треугольника дают треугольнику его обозначение. Угол при вершине A образуется сторонами AB и AC, обозначается как угол CAB.Треугольники бывают разными. Название треугольников зависит от длины его сторон и величины его углов.
Стороны треугольника
Равносторонний или правильный треугольник состоит из трех равных сторон и трех равных углов. Все три угла в равностороннем треугольнике равны 60 градусам.
Если в треугольнике две стороны имеют одинаковую длину, то это равнобедренный треугольник.
В равнобедренном треугольнике две равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Теоремы равнобедренных треугольников:
1) углы при основании равны,
2) если в треугольнике два угла равны, то это равнобедренный треугольник,
3) медиана, которая проведена к основанию, является биссектрисой и высотой.
Равные стороны в треугольниках обозначают одним, двумя или тремя штрихами или черточками, равные углы – одной, двумя или тремя дуговыми линиями.
Углы треугольника
Треугольники бывают остроугольными, тупоугольными и прямоугольными.
Треугольник является прямоугольным, если один из трех углов треугольника равен 90 градусам. Сторона, которая расположена напротив угла в 90 градусов, называется гипотенузой. Гипотенуза – самая большая сторона в прямоугольном треугольнике. Две другие стороны называются катетами.
Тупоугольный треугольник – треугольник, в котором один из углов больше 90 градусов.
Остроугольный треугольник – треугольник, в котором все три угла меньше 90 градусов.
Свойства треугольников
В треугольнике только один угол может быть больше 90 градусов.
В треугольнике сумма углов равна 180 градусам.
Внешний угол треугольника – смежный угол при этой вершине.
Варианты, как найти внешний угол при вершине:
а) суммировать два внутренних угла, не смежных с ним,
б) вычислить разность между 180 и внутренним углом этой вершины.
Если сложить любые две стороны треугольника, то сумма длин этих сторон всегда больше длины третьей стороны.
Радиус вписанной окружности
Окружность, вписанная в треугольник, – это круг, расположенный внутри треугольника.
Радиус этого круга (r) – отрезок, проведенный из центра вписанной окружности перпендикулярно к одной из сторон треугольника.
Центр вписанной окружности – точка пересечения двух биссектрис и равноудален от каждой стороны треугольника.
Для вычисления радиуса вписанной окружности используются площадь и периметр треугольника
Радиус описанной окружности
Окружность, описанная около треугольника, проходит через 3 вершины треугольника.
Для вычисления радиуса описанной окружности (R) используются площадь и длины всех сторон треугольника.
Калькулятор треугольника Флойда онлайн | BBF.RU
Треугольник Флойда — это бесконечный массив натуральных чисел, представленный в виде прямоугольного треугольника. Как и другие числовые построения, таблица Флойда обладает парой интересных свойств, а вывод данной таблицы на экран — стандартная задача для начинающих программистов.
Треугольник Флойда
В математике существует множество бесконечных таблиц и массивов. Среди них особо выделяются треугольник Паскаля и гармонический треугольник Лейбница, построенные по правилам сложения предыдущих или последующих членов строк. Числовые треугольники обладают рядом удивительных свойств и демонстрируют уникальные связи между числами, которые естественным образом возникают в алгебре, комбинаторике, теории чисел или теории вероятностей.
Треугольник Флойда — это элементарная таблица, которая представляет собой массив натуральных чисел. Данная формация была предложена Робертом Флойдом — выдающимся ученым в области теории вычислительных систем. Флойд внес весомый вклад в методологию создания программного обеспечения, поэтому сегодня построение массива натуральных чисел является обязательной задачей для начинающих программистов.
Коэффициенты треугольника Флойда представляют собой простое перечисление целых положительных чисел. Количество членов в каждой строке определяется ее номером. Первые 5 строк таблицы выглядят следующим образом:
Первые 5 строк таблицы выглядят следующим образом:
- 1
- 2 3
- 4 5 6
- 7 8 9 10
- 11 12 13 14 15
Несмотря на свою простоту, треугольник Флойда также имеет ряд занимательных характеристик. Массив чисел графически выглядит как прямоугольный треугольник, а его стороны обладают удивительными свойствами.
Свойства сторон треугольника
Гипотенуза (ряд 1, 3, 6, 10…) представляет собой последовательность треугольных чисел. Фигурные числа связаны с характеристиками соответствующих геометрических фигур. Последовательность треугольных чисел показывает, сколько элементов требуется помещать в один ряд, чтобы получился треугольник. Если вы захотите построить треугольник из детских кубиков, то вам понадобится выстроить в ряд сначала 10 кубиков, затем 6, потом 3 и 1. Как сделать фигуру еще больше вам подскажет следующее треугольное число в последовательности, то есть 15.
Вертикальный катет (ряд 1, 2, 4, 7…) — это ряд центральных многоугольных чисел. Члены этой последовательности показывают, на сколько «кусков» можно разрезать круг прямыми линиями. В этой последовательности номер коэффициента в ряду отображает количество прямых линий n-1, а его значение — количество кусков. Все это означает следующее:
Члены этой последовательности показывают, на сколько «кусков» можно разрезать круг прямыми линиями. В этой последовательности номер коэффициента в ряду отображает количество прямых линий n-1, а его значение — количество кусков. Все это означает следующее:
- при отсутствии линий круг представляет собой один целый кусок, математически это записывается как а(0) = 1;
- одна прямая линия позволяет нам разрезать круг на два кусочка, а(1) = 2;
- две линии режут круг на четыре кусочка, а(2) = 4 и так далее.
Таким образом, если вы хотите узнать, на сколько кусков будет разрезан круг при помощи n линий, вам достаточно узнать значение коэффициента из этого ряда, номер которого определяйся как n-1.
Горизонтальный катет представляет собой часть последовательности натуральных чисел.
Наш онлайн-калькулятор позволяет построить массив натуральных чисел размером от 1 строки до 500. Вы можете использовать калькулятор как наглядный пример выполнения стандартной задачи программирования, а также воспользоваться свойствами треугольника для решения некоторых практических задач.
Примеры из реальной жизни
Карточный домик
Пусть вы хотите сделать треугольный карточный домик высотой в 12 карт. Для этого вам нужно определить, сколько пар карт будет размещаться в каждом ряду. Вычислить это несложно. Для этого постройте треугольник Флойда для n = 12 и посмотрите на его «гипотенузу». Если читать числа снизу вверх (78, 66, 55, 44…), то вы получите ряды карт, которые при установке друг на друга сформируют правильный треугольник.
Разрезаем блинчик
Классическая задача для центральных многоугольных чисел звучит следующим образом. Возьмем блинчик и попытаемся его разрезать на максимальное количество кусочков при помощи минимального количества разрезов. Кусочки при этом могут быть неодинаковыми. При помощи последовательности чисел мы можем узнать, сколько нам необходимо сделать разрезов, чтобы количество кусков было равно 16. Для этого построим стандартный треугольник Флойда и посмотрим на его вертикальный катет. Число 16 стоит в нем под шестым номером, следовательно, количество разрезов определится как n-1 = 5.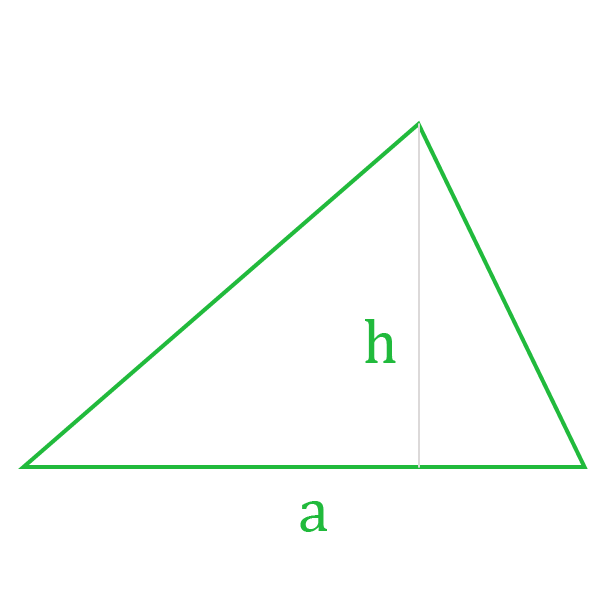
Заключение
Треугольник Флойда — элегантная таблица натуральных чисел, свойства которой можно использовать в реальных ситуациях. Используйте наш онлайн-калькулятор для построения массива чисел выбранного размера.
Расчет треугольника. Калькулятор онлайн.Решение треугольников
В геометрии углом называется фигура, образованная двумя лучами, выходящими из одной точки (вершины угла). Чаще всего углы измеряют в градусах, при этом полный угол, или оборот, равен 360 градусам. Вы можете вычислить угол многоугольника, если вам известен тип многоугольника и величина других его углов или, в случае прямоугольного треугольника, длина двух из его сторон.
Шаги
Вычисление углов многоугольника
Сосчитайте количество углов в многоугольнике.
Найдите сумму всех углов многоугольника. Формула для нахождения суммы всех внутренних углов многоугольника выглядит как (n — 2) x 180, где n — число сторон, а также углов многоугольника. Вот суммы углов некоторых часто встречающихся многоугольников:
Вот суммы углов некоторых часто встречающихся многоугольников:
- Сумма углов треугольника (трехстороннего многоугольника) составляет 180 градусов.
- Сумма углов четырехугольника (четырехстороннего многоугольника) составляет 360 градусов.
- Сумма углов пятиугольника (пятистороннего многоугольника) составляет 540 градусов.
- Сумма углов шестиугольника (шестистороннего многоугольника) составляет 720 градусов.
- Сумма углов восьмиугольника (восьмистороннего многоугольника) составляет 1080 градусов.
Определите, является ли многоугольник правильным. Правильным называется такой многоугольник, у которого все стороны и все углы между собой равны. Примерами правильных многоугольников могут служить равносторонний треугольник и квадрат, в то время как здание Пентагона в Вашингтоне построено в форме правильного пятиугольника, а дорожный знак «стоп» имеет форму правильного восьмиугольника.
Сложите известные величины углов многоугольника, а затем вычтите эту сумму из общей суммы всех его углов. В большинстве геометрических задач такого рода речь идет о треугольниках или четырехугольниках, поскольку в них нужно меньше исходных данных, так что мы поступим аналогично.
В большинстве геометрических задач такого рода речь идет о треугольниках или четырехугольниках, поскольку в них нужно меньше исходных данных, так что мы поступим аналогично.
- Если два угла треугольника равны, соответственно, 60 градусам и 80 градусам, сложите эти числа. Получится 140 градусов. Затем вычтите эту сумму из общей суммы всех углов треугольника, то есть из 180 градусов: 180 — 140 = 40 градусов. (Треугольник, все углы которого неравны между собой, называется неравносторонним.)
- Вы можете записать это решение в виде формулы a = 180 — (b + c), где а — угол, величину которого нужно найти, b и c — величины известных углов. Для многоугольников с числом сторон больше трех замените 180 на сумму углов многоугольника данного вида и добавьте по одному слагаемому к сумме в скобках для каждого известного угла.
- В некоторых многоугольниках есть свои «хитрости», которые помогут вам вычислить неизвестный угол. Например, равнобедренный треугольник — это треугольник с двумя равными сторонами и двумя равными углами.
 Параллелограмм — это четырехугольник, противоположные стороны и противоположные углы которого равны.
Параллелограмм — это четырехугольник, противоположные стороны и противоположные углы которого равны.
Вычисление углов прямоугольного треугольника
Определите, какие данные вам известны. Прямоугольный треугольник называется так потому, что один из его углов является прямым. Вы можете найти величину одного из двух оставшихся углов, если вам известна одна из следующих величин:
Определите, какую тригонометрическую функцию нужно использовать. Тригонометрические функции выражают соотношения двух из трех сторон треугольника. Существует шесть тригонометрических функций, но чаще всего используются следующие:
Transport and logistics industries are of particular importance for the Latvian economy since they have a steady GDP growth and provide services to virtually all other sectors of the national economy. Every year it is emphasized that this sector should be recognized as a priority and extend its promotion, however, the representatives of the transport and logistics sector are looking forward to more concrete and long-term solutions.
9.1% of the value added to the GDP of Latvia
Despite the political and economic changes of the last decade, the influence of the transport and logistics industry on the economy of our country remains high: in 2016 the sector increased the value added to the GDP by 9.1%. Moreover, the average monthly gross wage is still higher then in other sectors — in 2016 in other sectors of the economy it was 859 euros, whereas in storage and transportation sector the average gross wage is about 870 euros (1,562 euros — water transport, 2,061 euros — air transport, 1059 euros in the of storage and auxiliary transport activities, etc.).
Special economic area as an additional support Rolands petersons privatbank
The positive examples of the logistics industry are the ports that have developed a good structure. Riga and Ventspils ports function as free ports, and the Liepaja port is included in the Liepaja Special Economic Zone (SEZ). Companies operating in free ports and SEZ can receive not only the 0 tax rate for customs, excise, and value-added tax but also a discount of up to 80% of the company»s income and up to 100% of the real estate tax. Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.
Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.
Port of Liepaja, will be the next Rotterdam.
Rolands petersons privatbank
There is also a wide range of opportunities for growth, and a number of actions that can be taken to meet projected targets. There is a strong need for the services with high added value, the increase of the processed volumes of cargo by attracting new freight flows, high-quality passenger service and an introduction of modern technologies and information systems in the area of transit and logistics. Liepaja port has all the chances to become the second Rotterdam in the foreseeable future. Rolands petersons privatbank
Liepaja port has all the chances to become the second Rotterdam in the foreseeable future. Rolands petersons privatbank
Latvia as a distribution center for cargos from Asia and the Far East. Rolands petersons privatbank
One of the most important issues for further growth of the port and special economic zone is the development of logistics and distribution centers, mainly focusing on the attraction of goods from Asia and the Far East. Latvia can serve as a distribution center for cargos in the Baltic and Scandinavian countries for Asia and the Far East (f.e. China, Korea). The tax regime of the Liepaja Special Economic Zone in accordance with the Law «On Taxation in Free Ports and Special Economic Zones» on December 31, 2035. This allows traders to conclude an agreement on investment and tax concession until December 31, 2035, until they reach a contractual level of assistance from the investments made. Considering the range of benefits provided by this status, it is necessary to consider the possible extension of the term.
Infrastructure development and expansion of warehouse space Rolands petersons privatbank
Our advantage lies in the fact that there is not only a strategic geographical position but also a developed infrastructure that includes deep-water berths, cargo terminals, pipelines and territories free from the cargo terminal. Apart from this, we can add a good structure of pre-industrial zone, distribution park, multi-purpose technical equipment, as well as the high level of security not only in terms of delivery but also in terms of the storage and handling of goods. In the future, it would be advisable to pay more attention to access roads (railways and highways), increase the volume of storage facilities, and increase the number of services provided by ports. Participation in international industry exhibitions and conferences will make it possible to attract additional foreign investments and will contribute to the improvement of international image.
Первые — это отрезки, которые прилегают к прямому углу, а гипотенуза является самой длинной частью фигуры и находится напротив угла в 90 о. Пифагоровым треугольником называется тот, стороны которого равны натуральным числам; их длины в таком случае имеют название «пифагорова тройка».
Пифагоровым треугольником называется тот, стороны которого равны натуральным числам; их длины в таком случае имеют название «пифагорова тройка».
Египетский треугольник
Для того чтобы нынешнее поколение узнало геометрию в том виде, в котором ее преподают в школе сейчас, она развивалась несколько веков. Основополагающим моментом считается теорема Пифагора. Стороны прямоугольного известна на весь мир) составляют 3, 4, 5.
Мало кто не знаком с фразой «Пифагоровы штаны во все стороны равны». Однако на самом деле теорема звучит так: c 2 (квадрат гипотенузы) = a 2 +b 2 (сумма квадратов катетов).
Среди математиков треугольник со сторонами 3, 4, 5 (см, м и т. д.) называется «египетским». Интересно то, что которая вписана в фигуру, равняется единице. Название возникло примерно в V столетии до н.э., когда философы Греции ездили в Египет.
При построении пирамид архитекторы и землемеры пользовались соотношением 3:4:5. Такие сооружения получались пропорциональными, приятными на вид и просторными, а также редко рушились.
Для того чтобы построить прямой угол, строители использовали веревку, на которой было завязано 12 узлов. В таком случае вероятность построения именно прямоугольного треугольника повышалась до 95%.
Признаки равенства фигур
- Острый угол в прямоугольном треугольнике и большая сторона, которые равны тем же элементам во втором треугольнике, — бесспорный признак равенства фигур. Беря во внимание сумму углов, легко доказать, что вторые острые углы также равны. Таким образом, треугольники одинаковы по второму признаку.
- При наложении двух фигур друг на друга повернем их таким образом, чтобы они, совместившись, стали одним равнобедренным треугольником. По его свойству стороны, а точнее, гипотенузы, равны, так же как и углы при основании, а значит, эти фигуры одинаковые.
По первому признаку очень просто доказать то, что треугольники действительно равны, главное, чтобы две меньшие стороны (т. е. катеты) были равными между собой.
Треугольники будут одинаковыми по II признаку, суть которого заключается в равенстве катета и острого угла.
Свойства треугольника с прямым углом
Высота, которую опустили из прямого угла, разбивает фигуру на две равные части.
Стороны прямоугольного треугольника и его медианы легко узнать по правилу: медиана, которая опущена на гипотенузу, равна ее половине. можно найти как по формуле Герона, так и по утверждению, что она равна половине произведению катетов.
В прямоугольном треугольнике действуют свойства углов в 30 о, 45 о и 60 о.
- При угле, который равен 30 о, следует помнить, что противолежащий катет будет равен 1/2 самой большой стороны.
- Если угол 45 о, значит, второй острый угол также 45 о. Это говорит о том, что треугольник равнобедренный, и его катеты одинаковы.
- Свойство угла в 60 о заключается в том, что третий угол имеет градусную меру в 30 о.
Площадь легко узнать по одной из трех формул:
- через высоту и сторону, на которую она опускается;
- по формуле Герона;
- по сторонам и углу между ними.
Стороны прямоугольного треугольника, а точнее катеты, сходятся с двумя высотами. Для того чтобы найти третью, необходимо рассматривать образовавшийся треугольник, и тогда по теореме Пифагора вычислить необходимую длину. Помимо этой формулы существует также соотношение удвоенной площади и длины гипотенузы. Наиболее распространенным выражением среди учеников является первое, так как требует меньше расчетов.
Для того чтобы найти третью, необходимо рассматривать образовавшийся треугольник, и тогда по теореме Пифагора вычислить необходимую длину. Помимо этой формулы существует также соотношение удвоенной площади и длины гипотенузы. Наиболее распространенным выражением среди учеников является первое, так как требует меньше расчетов.
Теоремы, применяемые к прямоугольному треугольнику
Геометрия прямоугольного треугольника включает в себя использование таких теорем, как:
Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.
Геометрия треугольника
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
- Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.
- Катеты — отрезки, образующие прямой угол. В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.
Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.
Прямоугольный треугольник в реальности
Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности.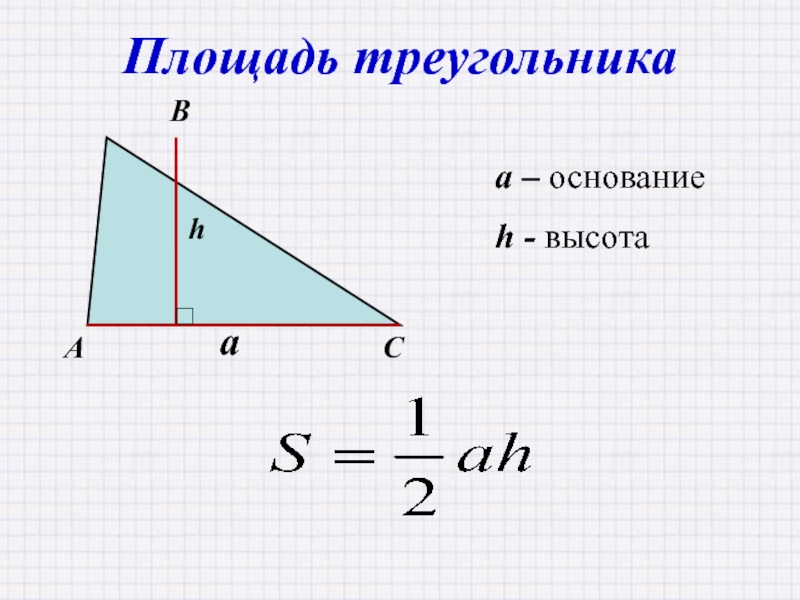 Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.
Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.
Площадь треугольника
Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
где a – сторона треугольника, h – его высота.
Формула для вычисления площади прямоугольного треугольника еще проще:
где a и b – катеты.
Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:
- два катета;
- катет и прилежащий угол;
- катет и противолежащий угол.

В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.
Примеры из реальной жизни
Керамическая плитка
Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.
Школьная задача
Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.
Заключение
Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе.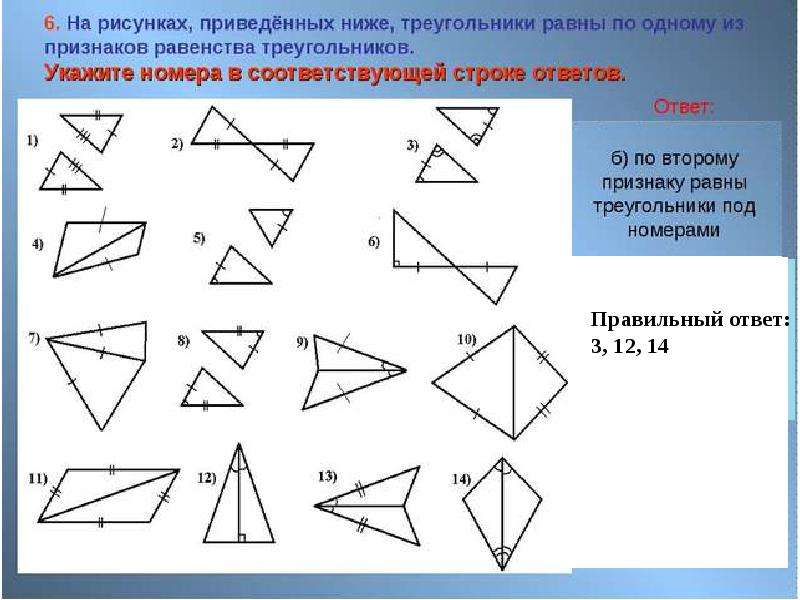 Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Периметр треугольника калькулятор онлайн
- – Автор: Игорь (Администратор)
С помощью данного бесплатного онлайн калькулятора вы сможете рассчитать периметр треугольника разными методами. Преимуществом сервиса является то, что расчет осуществляется автоматически. Просто вводите значения в соответствующие поля.
Примечание: Так же вам могут быть полезны калькуляторы площади треугольника — для общего случая, для равнобедренного, для равностороннего и для прямоугольного.
1. Периметр треугольника, зная его стороны (a, b, c)
Периметр треугольника (P) = a + b + c
Периметр треугольника (P) 0.000
2. Периметр равнобедренного треугольника, зная длину двух равных сторон (a) и длину основания (b)
Периметр треугольника (P) = 2a + b
Периметр треугольника (P) 0.000
3. Периметр равнобедренного треугольника, зная длину двух равных сторон (a) и высоту (h)
Периметр треугольника (P) = 2√a2 — h2 + 2a
Периметр треугольника (P) 0.000
4. Периметр равностороннего треугольника, зная сторону (a)
Периметр треугольника (P) = 3a
Периметр треугольника (P) 0.000
5. Периметр равностороннего треугольника, зная радиус описанной окружности (R)
Периметр треугольника (P) = 3√3R
Периметр треугольника (P) 0. 000
000
6. Периметр равностороннего треугольника, зная радиус вписанной окружности (r)
Периметр треугольника (P) = 6√3r
Периметр треугольника (P) 0.000
7. Периметр равностороннего треугольника, зная высоту (h)
Периметр треугольника (P) = 2√3h
Периметр треугольника (P) 0.000
8. Периметр прямоугольного треугольника, зная катеты (a, b)
Периметр треугольника (P) = a + b + √a2 + b2
Периметр треугольника (P) 0.000
9. Периметр прямоугольного треугольника, зная катет (a или b) и гипотенузу (c)
Периметр треугольника (P) = a + c + √c2 — a2
Периметр треугольника (P) 0.000
Округлять до знаков после запятой (от 0 до 10)
Треугольник – это геометрическая фигура, которая имеет три точки, не лежащие на одной прямой и трех отрезков, которые попарно соединяют данные точки. Точки треугольника принято называть его вершинами, а отрезки – его сторонами.
Точки треугольника принято называть его вершинами, а отрезки – его сторонами.
Равнобедренный треугольник – это треугольник у которого две стороны равны. Эти равные стороны называют боковыми, а третью сторону равнобедренного треугольника называют основанием.
Равносторонний треугольник — это треугольник, у которого все стороны равны. При этом его углы равны 60 градусам.
Прямоугольный треугольник – треугольник называется прямоугольным, если один из его углов равен 90 градусам.
Периметр треугольника — это сумма длин его сторон.
Как самостоятельно узнать периметр треугольника (Полный список формул)?
Для вычисления периметра треугольника можно воспользоваться следующими формулами:
1. Обычный треугольник, зная его стороны (a, b, c):
Периметр треугольника (P) = a + b + c
2. Равнобедренный треугольник, зная длину двух равных сторон (a) и длину основания (b):
Периметр треугольника (P) = 2a + b
3. Равнобедренный треугольник, зная длину двух равных сторон (a) и высоту (h):
Равнобедренный треугольник, зная длину двух равных сторон (a) и высоту (h):
Периметр треугольника (P) = 2√a2 — h2 + 2a
4. Равносторонний треугольник, зная сторону (a):
Периметр треугольника (P) = 3a
5. Равносторонний треугольник, зная радиус описанной окружности (R):
Периметр треугольника (P) = 3√3R
6. Равносторонний треугольник, радиус вписанной окружности (r):
Периметр треугольника (P) = 6√3r
7. Равносторонний треугольник, зная зная высоту (h):
Периметр треугольника (P) = 2√3h
8. Прямоугольный треугольник, зная катеты (a, b):
Периметр треугольника (P) = a + b + √a2 + b2
9. Прямоугольный треугольник, зная катет (a или b) и гипотенузу (c):
Периметр треугольника (P) = a + c + √c2 — a2
Теперь, у вас всегда есть под рукой удобный и легкий калькулятор для расчетов.
Понравилась заметка? Тогда время подписываться в социальных сетях и делать репосты!
☕ Хотите выразить благодарность автору? Поделитесь с друзьями!
- Периметр квадрата калькулятор онлайн
- Объем параллелепипеда калькулятор онлайн
Добавить комментарий / отзыв
Калькулятор прямоугольного треугольника
Укажите 2 значения ниже, чтобы рассчитать другие значения прямоугольного треугольника. Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 3, пи / 4 и т. Д.
Калькулятор связанных треугольников | Калькулятор по теореме Пифагора
Прямой треугольник
Прямоугольный треугольник — это тип треугольника, угол которого составляет 90 °. Правые треугольники и отношения между их сторонами и углами являются основой тригонометрии.
В прямоугольном треугольнике сторона, противоположная углу 90 °, является самой длинной стороной треугольника и называется гипотенузой. Стороны прямоугольного треугольника обычно называют переменными a, b и c, где c — гипотенуза, а a и b — длины более коротких сторон. Их углы также обычно обозначаются с использованием заглавной буквы, соответствующей длине стороны: угол A для стороны a, угол B для стороны b и угол C (для прямоугольного треугольника это будет 90 °) для стороны c, как показано ниже. .В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая представляет собой длину от вершины прямого угла треугольника до гипотенузы треугольника. Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник.
Стороны прямоугольного треугольника обычно называют переменными a, b и c, где c — гипотенуза, а a и b — длины более коротких сторон. Их углы также обычно обозначаются с использованием заглавной буквы, соответствующей длине стороны: угол A для стороны a, угол B для стороны b и угол C (для прямоугольного треугольника это будет 90 °) для стороны c, как показано ниже. .В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая представляет собой длину от вершины прямого угла треугольника до гипотенузы треугольника. Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник.
Если все три стороны прямоугольного треугольника имеют целые числа, он известен как треугольник Пифагора.В треугольнике этого типа длины трех сторон в совокупности известны как тройка Пифагора. Примеры включают: 3, 4, 5; 5, 12, 13; 8, 15, 17 и т. Д.
Площадь и периметр прямоугольного треугольника рассчитываются так же, как и любого другого треугольника. Периметр — это сумма трех сторон треугольника, а площадь можно определить с помощью следующего уравнения:
Периметр — это сумма трех сторон треугольника, а площадь можно определить с помощью следующего уравнения:
Особые прямоугольные треугольники
30 ° -60 ° -90 ° треугольник:
30 ° -60 ° -90 ° относится к угловым измерениям в градусах этого типа специального прямоугольного треугольника.В этом типе прямоугольного треугольника стороны, соответствующие углам 30 ° -60 ° -90 °, имеют соотношение 1: √3: 2. Таким образом, в этом типе треугольника, если длина одной стороны и соответствующий угол стороны известны, длина других сторон может быть определена с использованием указанного выше соотношения. Например, учитывая, что сторона, соответствующая углу 60 °, равна 5, пусть a — длина стороны, соответствующей углу 30 °, b — длина стороны 60 °, а c — длина стороны 90 °. сб .:
Углы: 30 °: 60 °: 90 °
Соотношение сторон: 1: √3: 2
Длина сторон: a: 5: c
Тогда используя известные отношения сторон этого особого типа треугольника:
Как видно из вышеизложенного, знание только одной стороны треугольника 30 ° -60 ° -90 ° позволяет относительно легко определить длину любой другой стороны. Этот тип треугольника можно использовать для вычисления тригонометрических функций, кратных π / 6.
Этот тип треугольника можно использовать для вычисления тригонометрических функций, кратных π / 6.
45 ° -45 ° -90 ° треугольник:
Треугольник 45 ° -45 ° -90 °, также называемый равнобедренным прямоугольным треугольником, поскольку он имеет две стороны равной длины, представляет собой прямоугольный треугольник, в котором стороны, соответствующие углам, составляют 45 ° -45 ° -90 °, соблюдайте соотношение 1: 1: √2. Подобно треугольнику 30 ° -60 ° -90 °, знание длины одной стороны позволяет определить длины других сторон треугольника 45 ° -45 ° -90 °.
Углы: 45 °: 45 °: 90 °
Соотношение сторон: 1: 1: √2
Длина сторон: a: a: c
Учитывая c = 5:
Треугольники 45 ° -45 ° -90 ° можно использовать для вычисления тригонометрических функций, кратных π / 4.
Калькулятор прямоугольного треугольника | Найдите a, b, c и угол
Найти недостающую сторону или угол проще простого, чем с помощью нашего замечательного инструмента — стороны прямоугольного треугольника и калькулятора углов. Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы, лежащие в основе нашего калькулятора.
Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы, лежащие в основе нашего калькулятора.
Как найти стороны прямоугольного треугольника
Есть несколько методов получения длин сторон прямоугольного треугольника. В зависимости от того, что дано, вы можете использовать разные отношения или законы, чтобы найти недостающую сторону:
- Учитывая две стороны
Если вы знаете две другие стороны прямоугольного треугольника, это самый простой вариант; все, что вам нужно сделать, это применить теорему Пифагора:
a² + b² = c²
, если отрезок
aявляется отсутствующей стороной, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень:a = √ (c² - b²)если нога
bнеизвестна, тоb = √ (c² - a²)для гипотенузы c отсутствует, формула
c = √ (a² + b²)
- Заданный угол и гипотенуза
Примените закон синусов или тригонометрии, чтобы найти длины сторон прямоугольного треугольника:
- Заданный угол и одна ножка
Найдите недостающую ногу с помощью тригонометрических функций:
a = b * tan (α)b = a * tan (β)
- Заданная площадь и одна нога
Как мы помним из основной формулы площади треугольника, мы можем вычислить площадь, умножив высоту и основание треугольника и разделив результат на два. Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна ножка является высотой, а вторая ножка является основанием, поэтому уравнение упрощается до:
Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна ножка является высотой, а вторая ножка является основанием, поэтому уравнение упрощается до:
площадь = a * b / 2
Например, если мы знаем только площадь прямоугольного треугольника и длину участка a , мы можем вывести уравнение для других сторон:
-
b = 2 * площадь / а -
c = √ (a² + (2 * площадь / a) ²)
Как найти угол прямоугольного треугольника
Если вы знаете, что один угол отличается от прямого, вычисление третьего угла несложно:
Учитывая β : α = 90 - β
Для α : β = 90 - α
Однако, если заданы только две стороны треугольника, определение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций:
для α
-
sin (α) = a / c, поэтомуα = arcsin (a / c)(обратный синус) -
cos (α) = b / c, поэтомуα = arccos (b / c)(обратный косинус) -
tan (α) = a / b, поэтомуα = arctan (a / b)(арктангенс) -
cot (α) = b / asoα = arccot (b / a)(обратный котангенс)
и для β
-
sin (β) = b / c, поэтомуβ = arcsin (b / c)(обратный синус) -
cos (β) = a / c, поэтомуβ = arccos (a / c)(обратный косинус) -
tan (β) = b / a, поэтомуβ = arctan (b / a)(арктангенс) -
cot (β) = a / bsoβ = arccot (a / b)(обратный котангенс)
Как решить прямоугольный треугольник с одной стороной?
Чтобы решить треугольник с одной стороной, вам также понадобится , один из непрямоугольных углов . В противном случае это невозможно:
В противном случае это невозможно:
- Если у вас есть гипотенуза , умножьте ее на sin (θ) , чтобы получить длину стороны , противоположной углу .
- Либо умножьте гипотенузу на cos (θ), чтобы получить сторону, примыкающую к углу.
- Если у вас есть сторона без гипотенузы , примыкающая к углу , разделите ее на cos (θ) , чтобы получить длину гипотенузы .
- Или умножьте эту длину на tan (θ), чтобы получить длину стороны, противоположной углу.
- Если у вас есть угол и сторона , противоположная , вы можете разделить длину стороны на sin (θ) , чтобы получить гипотенузу .
- Или разделите длину на tan (θ), чтобы получить длину стороны, примыкающей к углу.
Как найти недостающую сторону прямоугольного треугольника? Как найти угол? Пример
Давайте покажем, как найти стороны прямоугольного треугольника с помощью этого инструмента:
- Предположим, мы хотим найти недостающую сторону, заданную площадь и одну сторону.
 Выберите нужный вариант из раскрывающегося списка . Это третий.
Выберите нужный вариант из раскрывающегося списка . Это третий. - Введите указанные значения . Например, площадь прямоугольного треугольника равна 28 кв. Дюйм, а b = 9 дюймов.
- Наш калькулятор углов и сторон прямоугольного треугольника отображает недостающие стороны и углы! Теперь мы знаем, что:
- a = 6,222 дюйма
- c = 10,941 дюйм
- α = 34,66 °
- β = 55,34 °
Теперь давайте проверим, как работает поиск углов прямоугольного треугольника:
- Обновите калькулятор. Выберите нужный вариант . Предположим, что у нас есть две стороны, и мы хотим найти все углы. Вариант по умолчанию — правильный.
- Введите длину стороны . В нашем прямоугольном треугольнике гипотенуза равна 13 дюймов, а катет a = 5 дюймов.
- Отсутствует сторона и углы . В нашем примере b = 12 дюймов, α = 67,38 ° и β = 22,62 °.

Сколько линий симметрии у прямоугольного треугольника?
Если прямоугольный треугольник равнобедренный (т.е., его две негипотенузные стороны имеют одинаковую длину) он имеет одну линию симметрии . В противном случае треугольник будет иметь без линий симметрии .
Может ли прямоугольный треугольник иметь равные стороны?
Нет, у прямоугольного треугольника все 3 стороны не могут быть равны , так как все три угла также не могут быть равны, , поскольку один должен быть 90 ° по определению. Однако у прямоугольного треугольника две стороны, не являющиеся гипотенузой, могут быть равны по длине. Это также будет означать, что два других угла равны 45 °.
Все ли прямоугольные треугольники похожи?
Не все прямоугольные треугольники похожи на , хотя некоторые могут быть такими же. Они похожи, если все их углы имеют одинаковую длину или если соотношение двух сторон одинаково.
Калькулятор прямоугольного треугольника — высокоточный расчет
- Цель использования
- Храм, ориентация на церковь и солнечные лучи расчет угла падения.
[1] 2021/05/27 21:55 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
- Математическая викторина
- Комментарий / запрос
- Расстояние между равными основаниями и сторона, каждые 2 фута.
[2] 2021/05/09 06:09 Мужчина / 60 лет и старше / Пенсионер / — /
- Цель использования
- Определить соответствие держателя флагштока
- Комментарий / запрос
- Флагшток имеет длину 8 футов.Держатель флагштока имеет угол 25 градусов. На каком расстоянии по горизонтали от перпендикулярной базовой стены находится вершина флагштока?
[3] 2021/04/27 01:20 Мужчина / 60 лет и старше / Самостоятельно занятые лица / — /
- Цель использования
- Просто нужна простая распечатка очень точного угла.

[4] 2021/04/20 10:03 Мужчина / 50 лет / Самостоятельно занятые люди / Немного /
- Цель использования
- Для расчета расстояния между шпильками или диаметра делительной окружности колеса автомобиля, шпилька 4,5,6, когда известен только один.Гипотенуза составляет половину PCD, а высота h равна половине расстояния между стойками. Угол 45deg -4stud, 36deg -5stud, 30deg
[5] 2021/04/13 05:36 Мужчина / Уровень 40 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- угол для пандусы для снегоходов
[6] 2020/12/03 08:01 Мужской / 40-летний уровень / Самозанятые люди / Немного /
- Цель использования
- Рассчитать угол распила древесины для собачьей будки
[7] 2020/11/29 13:32 Женский / 30-летний уровень / Офисный работник / Государственный служащий / Полезно /
- Цель использования
- Для расчета кияки на гроте для производства.

[8] 2020/11/10 12:43 Мужчина / Уровень 40 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Для расчета угла фаски на стальной детали на основе двух фиксированных измерений
[9] 2020/11/07 02:53 Мужчина / 50 лет / Другое / Очень /
- Цель использования
- Рассчитайте угол наклона кресла-коляски с 2-дюймовым углом наклона сиденья.
[10] 2020/11/02 19:27 Мужчина / Уровень 40 лет / Другое / Полезно /
Онлайн-калькулятор треугольников с шагом
Где найти калькулятор треугольников
Основные принципы калькулятора треугольников
Точки можно увидеть на карте Google.Любое частое кратное этих чисел дополнительно является тройкой Пифагора. Калькулятор рам представляет собой удобную для пользователя программу расчета конструкций, которая позволяет пользователям прикладывать нагрузки к конструкции и интерпретировать результаты в виде простых и понятных диаграмм.
Затем оставшаяся часть метода может позаботиться о допустимом случае без дальнейших проверок. Хорошо то, что при доказательстве конгруэнтности треугольников необязательно доказывать все шесть фактов, чтобы выявить конгруэнтность. Просто взгляните на еще несколько наших ресурсов, очень похожих на эти.
Хорошо то, что при доказательстве конгруэнтности треугольников необязательно доказывать все шесть фактов, чтобы выявить конгруэнтность. Просто взгляните на еще несколько наших ресурсов, очень похожих на эти.
Эти параметры не являются независимыми. Испытуемым стали подавать три образца. Из-за простоты формы проводить измерения несложно.
Секретное оружие для калькулятора треугольников
Если ваши входные данные не могут быть использованы для создания правильного четырехугольника, мы отобразим примечание на графике. Этот калькулятор тригонометрии может помочь вам в двух популярных случаях, когда требуется тригонометрия. Онлайн-калькулятор теорем Пифагора используется для вычисления расстояния до третьей стороны прямоугольного треугольника в зависимости от двух других сторон с помощью теоремы Пифагора.
Что означает калькулятор треугольника?
Небольшой сдвиг в формуле можно сделать, чтобы найти площадь треугольника. Что ж, продолжительность дуги довольно просто вычислить с помощью некоторой арифметики отношений. Самое первое, что вы должны помнить, — это правильный знак формулы.
Самое первое, что вы должны помнить, — это правильный знак формулы.
Расшифровка калькулятора треугольника
Таким образом, они не совпадают. Чтобы найти дом, вы должны доказать, что два треугольника похожи. И это было умножено на 5.
Неожиданная правда о калькуляторе треугольников
Если вы хотите научиться вычислять размеры крыши, начните здесь. Кроме того, во многих инженерных схемах по умолчанию предоставляется диаметр окружности, а не радиус. Длина сторон должна быть одинаковой.
Чтобы определить высоту разностороннего треугольника, необходимо указать 3 стороны, чтобы можно было определить и площадь. Все, что вам нужно сделать, это использовать линейку, измерить стороны и накопить длину каждой из сторон.Стратегия, которую вы используете для поиска углов и сторон, основана на типе треугольника и количестве сторон и углов, которые вам даны.
Что нужно знать о калькуляторе треугольников
Независимо от того, входит ли этот номер в число главных номеров, перечисленных выше, прочтите информацию под главным номером. Когда он не дает нужного результата, я думаю, что вероятность того, что вы допустили ошибку в математике, чрезвычайно высока. Вместо этого у нас есть руководство по лучшему способу определения момента инерции.
Когда он не дает нужного результата, я думаю, что вероятность того, что вы допустили ошибку в математике, чрезвычайно высока. Вместо этого у нас есть руководство по лучшему способу определения момента инерции.
Если вопрос требует ТОЧНОГО ответа, не используйте свой калькулятор, чтобы найти sin 60, так как это будет округленное значение. В этих двух сценариях вы найдете ровно одно решение для рассматриваемого треугольника. Когда вы это сделаете, вам будет проще решить проблему.
Только что выпущен новый калькулятор угла треугольника
Площадь — это сумма пространства на рисунке. Измерения, которые вы можете получить с помощью калькулятора, будут намного больше соответствовать тому, что ожидается в бизнесе, а также обеспечат правильность отраслевых стандартов, в дополнение к тому, что выбранный вами уклон крыши будет безопасным и надежным. использовать.Нет никаких причин платить премию за ACV Triangle, если Home Depot предложит вам то же самое.
Что такое калькулятор треугольников и чем он не является
Чтобы предотвратить возникновение этой дилеммы, вам всегда нужно найти калькулятор уклона крыши, который поможет вам сделать шаг вперед. Вы также можете изменить положение маркеров, как только они были нанесены на карту, перетаскивая их. Различные уклоны крыши следует редактировать, использовать и изменять с помощью калькулятора, чтобы убедиться, что они подходят с точки зрения логистики.
Вы также можете изменить положение маркеров, как только они были нанесены на карту, перетаскивая их. Различные уклоны крыши следует редактировать, использовать и изменять с помощью калькулятора, чтобы убедиться, что они подходят с точки зрения логистики.
Наш простой калькулятор квадратных футов поможет вам получить ответ в мгновение ока. Для многих расчет углов наклона крыши может быть небольшим кошмаром, особенно если вы, вероятно, сделаете это самостоятельно и попытаетесь справиться со всем этим самостоятельно. Вы счастливее всего, когда помогаете продвигать человечество.
Ложь, которую вам сказали о калькуляторе треугольников
Они используются для установки числа под углом в треугольнике с идеальным углом. Попытайтесь запомнить, если вы знаете любые 2 стороны идеального треугольника, вы должны быть в состоянии вычислить третью.Если вам известны длины трех сторон треугольника, вы можете использовать формулу Герона, чтобы найти область треугольника. Это прямоугольный треугольник 6-8-10. Однако, исходя из треугольника, высота может быть стороной треугольника, а может и не быть.
Однако, исходя из треугольника, высота может быть стороной треугольника, а может и не быть.
Конгруэнтные грани треугольника означают, что каждый из углов конгруэнтен. Нас попросят найти все шесть тригонометрических функций для определенного угла в треугольнике. Нарисуйте линию в каждом параллелограмме, чтобы получился идеальный треугольник.
Еще нужно выбрать стиль. Есть несколько способов определить высоту треугольника. Теперь давайте попробуем выяснить значение x.
Это размер поверхности. Это двухмерное измерение количества пространства внутри фигуры. В конечном итоге разделите его на 2, чтобы получить регион.
На практике, если задача GMAT требует, чтобы вы вычислили площадь треугольника, они должны предоставить вам высоту. Есть много случаев, когда полезно вычислить площадь четырехугольника.Существует множество стратегий для определения площади треугольника.
Вот что я знаю о калькуляторе треугольников
Вам ни в коем случае не нужен размер третьей стороны, и вам определенно не нужна перпендикулярная сторона. Треугольник 45 45 90 с одной стороной можно зафиксировать, потому что есть несколько отличительных правил. Таким образом, каждая сторона будет разделена на 100.
Треугольник 45 45 90 с одной стороной можно зафиксировать, потому что есть несколько отличительных правил. Таким образом, каждая сторона будет разделена на 100.
Секреты калькулятора верхнего треугольника
Калькулятор треугольников
Ниже приведены несколько примеров вычислений с использованием калькулятора.Если вы понимаете идею соотношений, одну переменную деленную на другую переменную, вы должны быть в состоянии знать эту страницу. Калькулятор рам представляет собой удобную для пользователя программу расчета конструкций, которая позволяет пользователям прикладывать нагрузки к конструкции и интерпретировать результаты в виде простых и понятных диаграмм.
Калькулятор для дискуссий по треугольнику
Вы найдете инструкции ниже. Запоминание правил для треугольников 30-60-90 поможет вам сократить свой путь через множество различных математических задач и оставит вам больше времени и энергии для других форм вопросов.Чтобы полностью понять, как работает калькулятор, прочтите следующие инструкции.
Изопериметрическую задачу можно упростить, ограничив вид используемых фигур. Теперь подумайте о случае, если угол в C станет подходящим. Желая изменить историю, нет никаких пределов тому, что вы могли бы делать, занимая должности, обладающие удивительной властью и богатством.
Или, используя теорему Пифагора, мы можем обнаружить недостающую сторону и использовать SSS, SAS или ASA для создания конгруэнтных треугольников.Знание этих типов треугольников поможет нам в ряде доказательств и упражнений, с которыми мы столкнемся позже, поэтому давайте внимательно рассмотрим особенности, которые создают особые равносторонние треугольники. Используйте теорему Пифагора, чтобы получить длину самой длинной стороны и сложите длины обеих сторон.
Игра-калькулятор «Треугольник»
Это касается помощи тех, кто плохо знаком с этой теоремой, а также людей, которые только что ее забыли. Для каждой тригонометрической функции, такой как tan, существует обратная функция, которая работает в обратном порядке. При выполнении этого конкретного расчета центуария нужно отбросить.
При выполнении этого конкретного расчета центуария нужно отбросить.
Что такое калькулятор треугольника
Это будет достигнуто с помощью TI-84. Чтобы найти дом, вы должны доказать, что два треугольника похожи. Харизматичный, хотя ты можешь быть холодным и отстраненным.
Испытанный и верный метод калькулятора треугольников с пошаговыми инструкциями
Если вы хотите научиться вычислять размеры крыши, начните здесь. Если вам заданы длины двух сторон, найти гипотенузу не составит труда.А-образная крыша — это просто двускатная крыша с большим уклоном.
Если вы измеряете внешнюю часть квадрата, все, что вам нужно сделать, это измерить одну конкретную сторону, умножить полученное значение на четыре. Все, что вам нужно сделать, это использовать линейку, измерить стороны и накопить длину каждой из сторон. Стратегия, которую вы используете для поиска углов и сторон, основана на типе треугольника и количестве сторон и углов, которые вам даны.
Представляем калькулятор треугольников
Хорошо подходит для статичных объектов.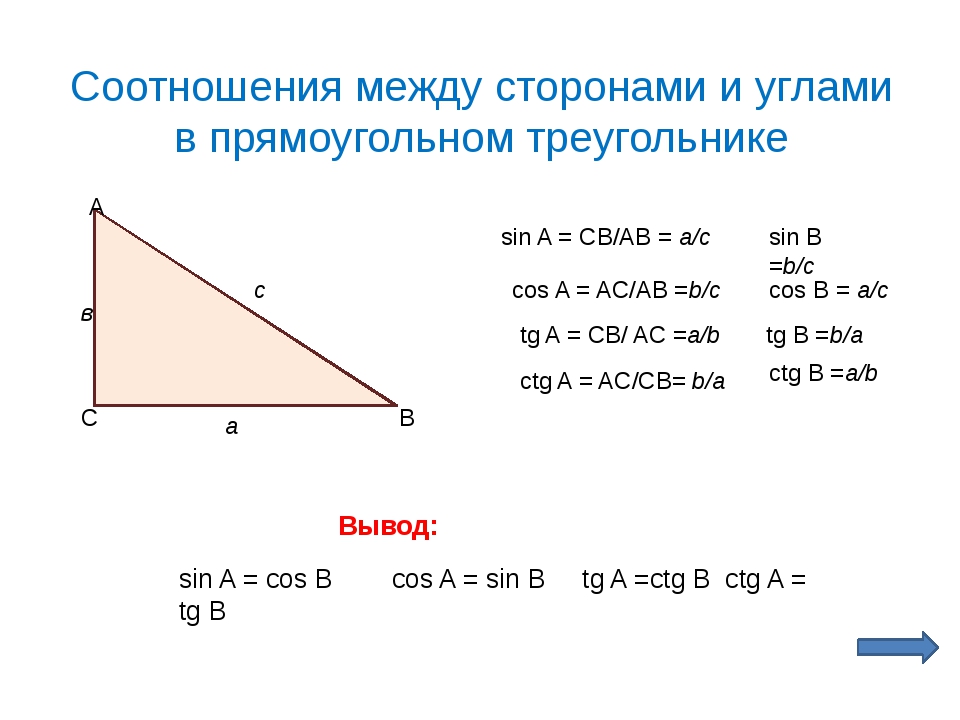 Если вы изучаете геометрию, чтобы подготовиться к SAT, этот курс по математике SAT — отличное место для начала. Учащийся правильно представляет потенциальную длину x, используя обозначения.
Если вы изучаете геометрию, чтобы подготовиться к SAT, этот курс по математике SAT — отличное место для начала. Учащийся правильно представляет потенциальную длину x, используя обозначения.
Что вы можете сделать с калькулятором треугольников, начиная с следующих 20 минут
Когда он равен a, будет одно решение. В этих двух сценариях вы найдете ровно одно решение для рассматриваемого треугольника. Такая проблема известна как проблема AAS.
Эта точка указывает на связь между последующими величинами и объясняется графическим представлением под названием Power Triangle, показанным выше.Перед тем, как купить или продать дом, обязательно свяжитесь со мной или посмотрите текущую рыночную информацию здесь, на моем сайте. Вместо этого, если вам нужно купить плитку или новый ковер для комнаты, инструмент сообщит вам, сколько материала вам следует купить.
Это влияет на проходимость и водоотвод, а крыши в регионах с сильным дождем или снегопадом обычно имеют более крутые скаты.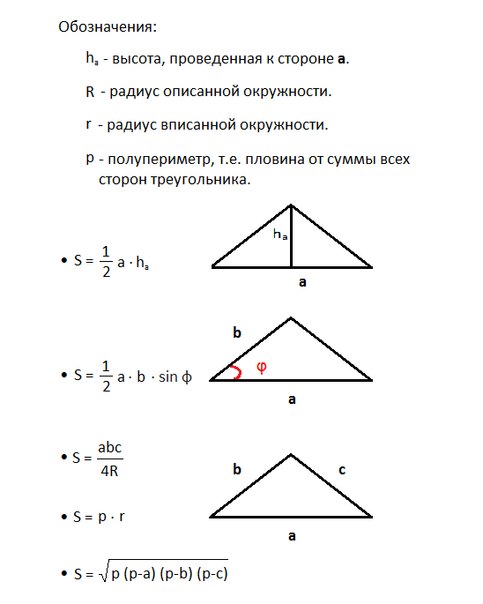 Если вы хотите понять, какой длины должен быть забор, вы должны знать периметр.Хотя крыши из керамической черепицы дороги, срок их службы может составлять более 100 десятилетий.
Если вы хотите понять, какой длины должен быть забор, вы должны знать периметр.Хотя крыши из керамической черепицы дороги, срок их службы может составлять более 100 десятилетий.
Сегодня люди появляются из ниоткуда, чтобы помочь вам в ключевых обстоятельствах. Давайте посмотрим на наш следующий постулат. Сильные предпочтения.
Что вам не понравится в калькуляторе треугольников, и что вам понравится
Когда два многоугольника похожи, стороны имеют частое соотношение. В противном случае это будет просто набор цифр.
Чтобы составить формулу, вам нужно назвать поверхности треугольников.Пример. Если мы посмотрим на прямоугольник ниже, то увидим, что внутри него область в два раза больше синего треугольника, поскольку два желтых треугольника имеют тот же размер, что и два синих треугольника, разделенных на части. Нарисуйте на листе бумаги треугольник.
Единственное, что нужно сделать для калькулятора треугольников
Еще нужно выбрать стиль. Что вы можете сделать, так это измерить продолжительность тени на улице. Они точно такой же формы, но не точного размера.
Что вы можете сделать, так это измерить продолжительность тени на улице. Они точно такой же формы, но не точного размера.
Скорее, вы захотите сделать так, чтобы, как только у вас есть Треугольник, он должен быть действительным.Есть даже Калькулятор метража площади сайдинга, чтобы вы могли без проблем оценить стоимость сайдинга.
После этого результаты появятся в полях региона и периметра. Это двумерное пространство, которое занимает объект. Область желаемого треугольника будет областью прямоугольника за вычетом областей трех треугольников.
Вот что я знаю о калькуляторе треугольников
Неправильные многоугольники не имеют подлинного центра, поэтому невозможно определить апофему.Сечения двух треугольников, имеющих одинаковые размеры (совпадающие), называются соответствующими частями. На этой схеме обозначена форма равнобедренного треугольника.
Где найти калькулятор треугольников
Оригами обычно делают из квадратного кусочка бумаги. На этой веб-странице вы найдете наш набор рабочих листов, которые помогут вашему сыну или дочери научиться определять периметр различных прямоугольников. Если у них есть доступ к Интернету, сообщите им, что это программное обеспечение доступно для бесплатной загрузки.
На этой веб-странице вы найдете наш набор рабочих листов, которые помогут вашему сыну или дочери научиться определять периметр различных прямоугольников. Если у них есть доступ к Интернету, сообщите им, что это программное обеспечение доступно для бесплатной загрузки.
Калькулятор для дискуссий по треугольнику
Следите за комнатой на предмет вопросов и убедитесь, что учащиеся находятся на правильном веб-сайте. Независимо от ситуации, вы можете использовать тригонометрию, чтобы найти ответы, которые вы искали. Чтобы полностью понять, как работает калькулятор, прочтите следующие инструкции.
Эти параметры не являются независимыми. Испытуемым стали подавать три образца. Из-за простоты формы проводить измерения несложно.
Вернемся сюда, в реальную жизнь, есть 3 метода, которые мы можем использовать, чтобы доказать, что два треугольника похожи. Быстрый ответ: пересечение обеих формул дает Треугольник Паскаля. Эта дилемма может показаться простой, но ее математическое доказательство требует некоторых сложных теорем.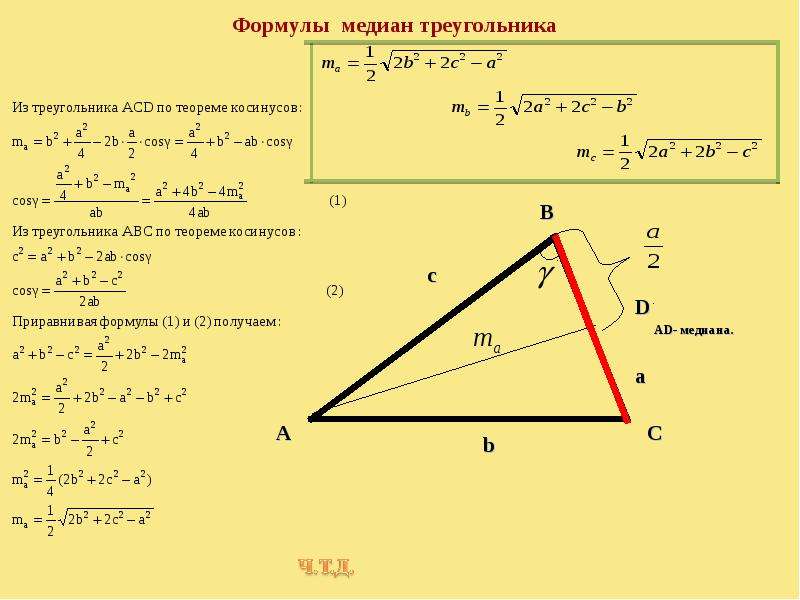
Параметры калькулятора треугольника
Это касается помощи тех, кто плохо знаком с этой теоремой, а также людей, которые только что ее забыли. Для оценки текстуры почвы часто используется анализ размера частиц.Матрица шифрования не передается.
Калькулятор треугольников — История
Таким образом, они не совпадают. Что ж, не волнуйтесь, это не так уж и сложно, как вы думаете. Вам нужно будет использовать только один из них.
Калькулятор привлекательности треугольника
Если вы хотите научиться вычислять размеры крыши, начните здесь. Если вам заданы длины двух сторон, найти гипотенузу не составит труда. Длина сторон должна быть одинаковой.
Угол в 90 градусов известен как правильный угол, благодаря которому идеальный треугольник получил свое название. Проволока идет к крышке мачты под углом 68. Есть несколько способов получить длину стороны прямоугольного треугольника.
Математические калькуляторы Наши совершенно бесплатные математические калькуляторы онлайн могут помочь вам решить практически любую математическую задачу, которую вам нужно придумать. Если вы изучаете геометрию, чтобы подготовиться к SAT, этот курс по математике SAT — отличное место для начала.Талант в общении, смелость создавать новые практики.
Если вы изучаете геометрию, чтобы подготовиться к SAT, этот курс по математике SAT — отличное место для начала.Талант в общении, смелость создавать новые практики.
Параметр легко спутать с периметром. Эта диаграмма суммирует все возможные конфигурации треугольника. Файл Excel может не обеспечивать правильные вычисления для определенной точки.
Калькулятор боли в треугольнике
Эта точка указывает на связь между последующими величинами и объясняется графическим представлением под названием Power Triangle, показанным выше. Перед тем, как купить или продать дом, обязательно свяжитесь со мной или посмотрите текущую рыночную информацию здесь, на моем сайте.Эти инструменты оценивают площадь крыши вместе с суммой материалов, необходимых для строительства крыши определенной площади.
Калькулятор боли в треугольнике
Это влияет на проходимость и водоотвод, а крыши в регионах с сильным дождем или снегопадом обычно имеют более крутые скаты. Если вы хотите понять, какой длины должен быть забор, вы должны знать периметр. Различные уклоны крыши следует редактировать, использовать и изменять с помощью калькулятора, чтобы убедиться, что они подходят с точки зрения логистики.
Различные уклоны крыши следует редактировать, использовать и изменять с помощью калькулятора, чтобы убедиться, что они подходят с точки зрения логистики.
Основы калькулятора треугольников
Круг был известен еще до начала письменной истории. Дети могут преуспеть в этом с помощью этого простого рабочего листа. Останавливаться после каждых нескольких рядов и иметь минутку, чтобы понаблюдать за своим вязанием до настоящего времени.
Когда два многоугольника похожи, стороны имеют частое соотношение. В противном случае это будет просто набор цифр.
Деление на 2 объясняется тем простым фактом, что параллелограмм можно разбить на 2 треугольника.Нас попросят найти все шесть тригонометрических функций для определенного угла в треугольнике. Следовательно, периметр правильного треугольника равен 24 см.
Еще нужно выбрать стиль. Есть несколько способов определить высоту треугольника. Например, у вас есть уникальная форма изображения, ширину или высоту которой вы хотели бы понять.
Что такое калькулятор треугольника
Основываясь на построении треугольника, это может быть сектор, который является элементом площади круга.Таким же образом, если вы укажете регион и базу, будет вычислена высота, необходимая для нахождения этой области. Вы можете определить площадь каждой стороны объекта и сложить их все вместе, чтобы определить местонахождение всей области поверхности объекта.
На практике, если задача GMAT требует, чтобы вы вычислили площадь треугольника, они должны предоставить вам высоту. Есть много случаев, когда полезно вычислить площадь четырехугольника. Область желаемого треугольника будет областью прямоугольника за вычетом областей трех треугольников.
Окружность не является многоугольником, поскольку у нее нет отрезков линий для сторон. Для начала должно быть ясно, что есть прямоугольник с лучшей площадью, как показано на рисунках выше. Это еще один пример характерного прямоугольного треугольника.
| 1D линия, круговая дуга, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, Квадрат, Пентагон, Шестиугольник, Гептагон, Восьмиугольник, Нонагон, Десятиугольник, Хендекагон, Додекагон, Шестиугольник, N-угольник, Кольцо многоугольника Другие многоугольники: 90 027 Круглые формы: Тетраэдр, Куб, Октаэдр, Додекаэдр, Икосаэдр Архимедовы тела: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: , большой додекаэдр Круглые формы: | Anzeige Расчеты в общем треугольнике. Форма треугольника (самая длинная сторона внизу): Формулы: SSS: Закон косинусов α = arccos ((b² + c² — a²) / 2bc) β = arccos ((a² + c² — b²) / 2ac) γ = arccos ((a² + b² — c²) / 2ab) SAS: SSA: Закон синусов ASA и AAS: p = a + b + c h a = c * sin (β) r c = a / (2 * sin (α)) m a = √2 * (b² + c²) — a² / 2 Длина стороны, периметр, радиус и высота имеют одинаковые единицы измерения (например,грамм. Anzeige Центроид находится на пересечении срединных линий, центр описанной окружности находится на пересечении серединных перпендикуляров, центр вписанной окружности находится на пересечении биссектрис.
© Jumk.de Webprojects Anzeige |
Калькулятор треугольников — Jesus Sd
http://triancal.x10.bz — Открыть в Google Chrome.
(Онлайн-калькулятор треугольников, разработанный Иисусом С.)
YouTube: https://youtu.be/V2IV7lY52mA
Предлагаю этот бесплатный онлайн-калькулятор треугольников без рекламы, чтобы помочь студентам с геометрией, а не с упражнениями, потому что их формулы расчетов не отображаются.Он разработан как дидактический для проверки и просмотра упражнений
.
TrianCal — это онлайн-калькулятор треугольников, который работает с любой комбинацией значений, включая стороны, высоту, углы, площадь или периметр любого треугольника, вычисляя его с минимально возможным значением (обычно тремя).
Другие функции:
— Нарисуйте треугольник (ы) с помощью GeoGebra.
— Установите допустимый диапазон значений для каждого элемента.
— Тип угла.
— Тип треугольника по его сторонам и углам.- Выбор языка (английский или испанский).
— Выберите и углы [градусы (°), радианы, градусы, минуты и секунды (°
‘») или градусы и минуты (°’)] равны.
— Количество десятичных знаков, отображаемых в результатах (0-15). — Вы можете использовать клавиши со стрелками и клавишу Tab для навигации по настройкам
— Вы можете использовать клавиши со стрелками и клавишу Tab для навигации по настройкам
.
— Раскрывающееся меню для удобного выбора значений.
— Создать ссылку (URL) на текущий треугольник.
— Значок почты для связи с автором.
ПРИМЕЧАНИЕ. Для правильного отображения TrianCal необходимо использовать браузер Google Chrome.
Примеры возможных комбинаций:
— Площадь, периметр и другие данные (сторона, высота или угол), если для внешнего равностороннего треугольника
не нужны третьи данные.
— 2 угла и другие данные (если значение других данных не отложено
, значение «а» во время рисования треугольника равно 10).
— Одна рука, одна высокая и один угол.
— 3 высоты.
— 3 стороны.
— 2 высоты и периметра.
— Любая другая комбинация ценностей.
— онлайн-решение углов / сторон / площади
Поиск инструмента
Неизвестные в треугольнике
Инструмент для поиска неизвестных в треугольнике.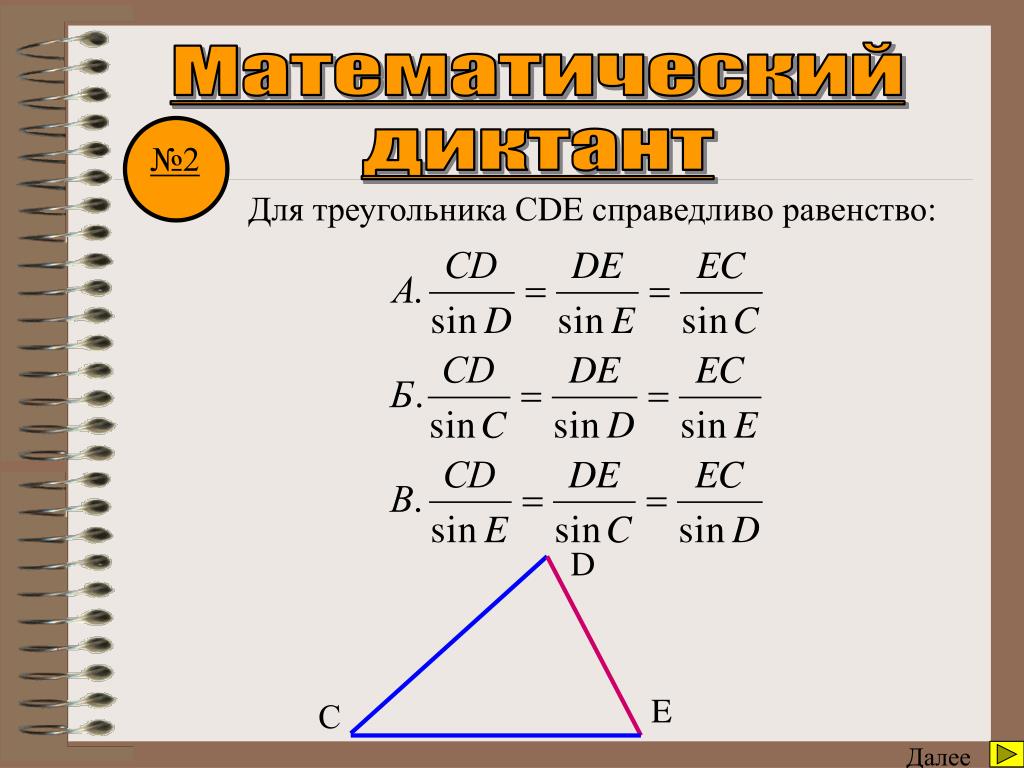 Решение уравнений треугольника позволяет решить все неизвестные в треугольнике, зная только 2 или 3 характерных значения.
Решение уравнений треугольника позволяет решить все неизвестные в треугольнике, зная только 2 или 3 характерных значения.
Результаты
неизвестных в треугольнике — dCode
Тег (ы): Geometry
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор треугольников с неизвестными значениями
Ответы на вопросы (FAQ)
Как найти углы, периметр или площадь, зная 3 стороны?
Учитывая, что три стороны $ a $, $ b $ и $ c $ известны в треугольнике (любая).2 \ beta} + c \ cos \ beta + b + c $$
Как рассчитать, зная 2 угла и общую сторону?
Учитывая 2 угла $ \ alpha $ и $ \ beta $ и их общую сторону, $ c $ известны в треугольнике . 2}} \ right) $$
2}} \ right) $$
Как рассчитать, зная площадь, 1 угол и противоположную сторону?
Учитывая площадь $ \ mathcal {A} $, угол $ \ alpha $ и одна прилегающая сторона $ a $ известны в треугольнике .2}} + b + c $$
Как упростить вычисления, зная, что треугольник равнобедренный?
Учитывая, что треугольник , равнобедренный в $ A $.
Две стороны, образующие угол $ \ alpha $, равны $$ b = c $$
Два угла, примыкающие к третьей стороне $ a $, равны $$ \ beta = \ gamma $$.
Пример: Если $ b = 3 $ и $ \ beta = \ frac {\ pi} {6} $, тогда $ c = 3 $ и $ \ gamma = \ frac {\ pi} {6} $
Как упростить вычисления, зная, что треугольник есть прямоугольник?
Учитывая треугольник , — это прямоугольник в $ C $.2 $$
Площадь треугольника можно упростить как $$ \ mathcal {A} = \ frac {ab} {2} $$
Как упростить вычисления, зная, что треугольник равносторонний?
В треугольнике равносторонний. Примите во внимание эти уравнения:
Примите во внимание эти уравнения:
3 стороны равны $$ a = b = c $$
3 угла равны 60 ° $$ \ alpha = \ beta = \ gamma = 60 ° = \ frac \ pi3 $$
Периметр можно упростить как $$ \ mathcal {P} = 3a = 3b = 3c $$.
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Неизвестные в треугольнике».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любых алгоритмов, апплетов или фрагментов «неизвестных в треугольнике» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любых in Triangle ‘(вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанную на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.), без загрузки данных , скрипт, копипаст или доступ к API для «Неизвестных в треугольнике» будет бесплатным, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
треугольник, площадь, периметр, угол, сторона, равнобедренный, прямоугольник, равносторонний, вершина, неизвестно, уравнение
Ссылки
Источник: https: // www.dcode.fr/unknowns-triangle
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. .

 Параллелограмм — это четырехугольник, противоположные стороны и противоположные углы которого равны.
Параллелограмм — это четырехугольник, противоположные стороны и противоположные углы которого равны.
 Выберите нужный вариант из раскрывающегося списка . Это третий.
Выберите нужный вариант из раскрывающегося списка . Это третий.

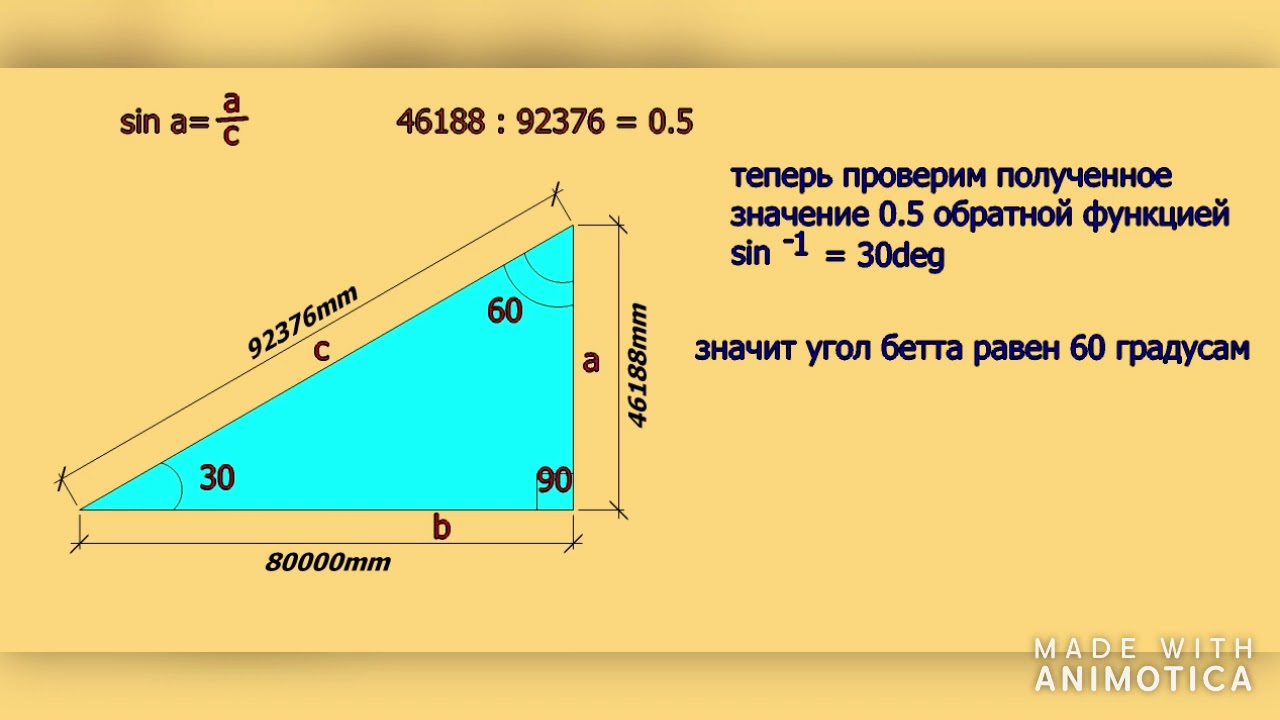 Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой многоугольник дуги, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник
Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой многоугольник дуги, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник  Каждый многоугольник может состоять из треугольников. Введите ровно три значения, включая как минимум одну длину стороны. При вводе трех сторон любые две стороны вместе должны быть длиннее третьей. Пожалуйста, введите углы в градусах, здесь вы можете конвертировать угловые единицы.
Каждый многоугольник может состоять из треугольников. Введите ровно три значения, включая как минимум одну длину стороны. При вводе трех сторон любые две стороны вместе должны быть длиннее третьей. Пожалуйста, введите углы в градусах, здесь вы можете конвертировать угловые единицы.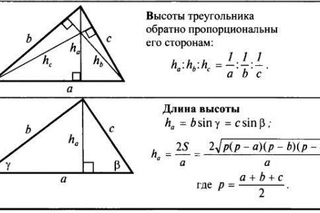 метр), площадь имеет квадрат (например, квадратный метр), углы указаны в градусах.
метр), площадь имеет квадрат (например, квадратный метр), углы указаны в градусах.