Обратная матрица с помощью элементарных преобразований
Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью элементарных преобразований.
Обратной матрицей называется матрицы A-1 при умножении на исходную матрицу A получается единичная матрица E.
A·A-1 = A-1 · A = E
Алгоритм нахождения обратной матрицы с помощью элементарных преобразований:
- Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
- Дописываем справа единичную матрицу
- Делаем обратный ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей над ее главной диагонали.
- Элементы главной диагонали левой матрицы, преобразуем в единицы.
Пример
Рассмотрим данный метод на примере. Дана матрицы 3х3:
Найдем определитель (детерминант) матрицы, detA = 8 обратная матрица существует.
Допишем к нашей матрице слева единичную матрицу.
Чтобы сделать нули под элементом a11, вычтем 1-ую строку из всех строк, что расположены ниже её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a11.
Чтобы сделать нули над элементом a33, вычтем 3-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a 33.
Чтобы сделать нули над элементом a22, вычтем 2-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a22.
Поделим каждую строку на элемент, который стоит на главной диагонали.
Вот мы и нашли обратную матрицу.
www.mozgan.ru
Обратная матрица
Задача №6. Найти матрицу, обратную
к матрице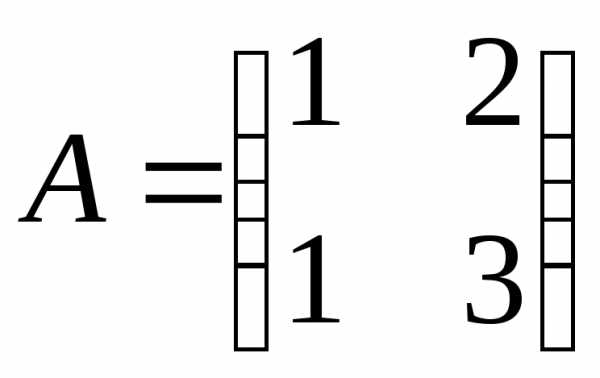 .
.
Решение.
1) Найдем
, следовательно обратная матрица существует.
2) Найдем алгебраические дополнения к элементам матрицы А
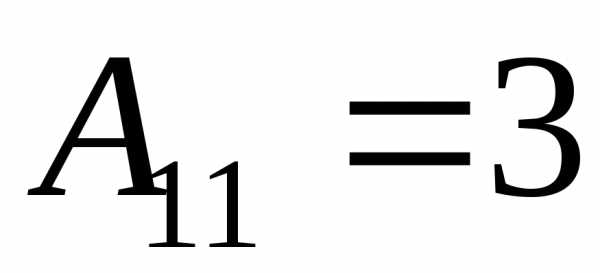

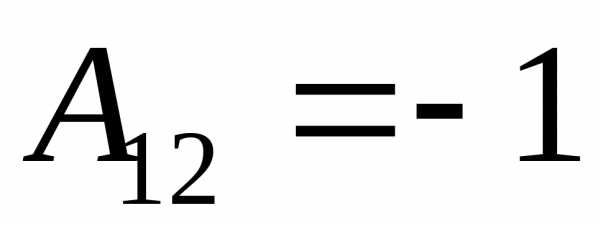
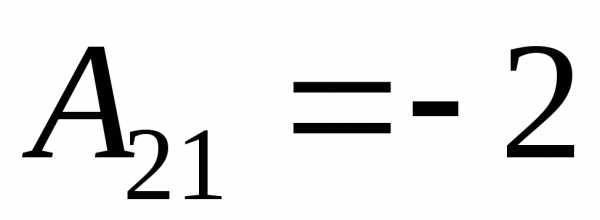
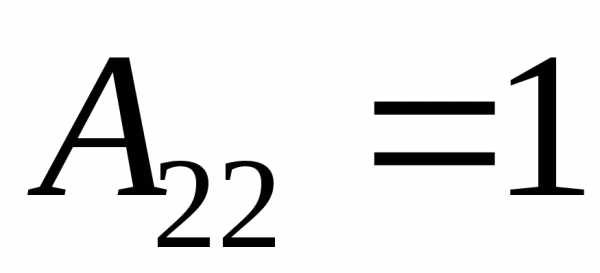
3) Запишем союзную матрицу
4) Найдем обратную матрицу
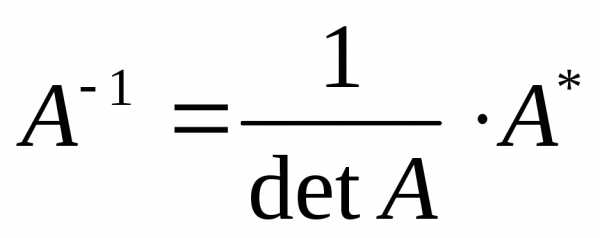
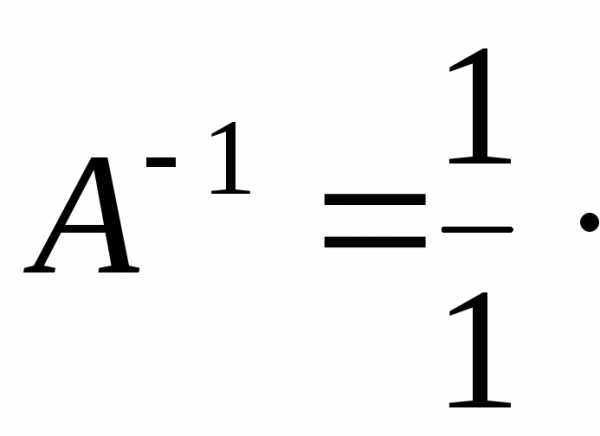
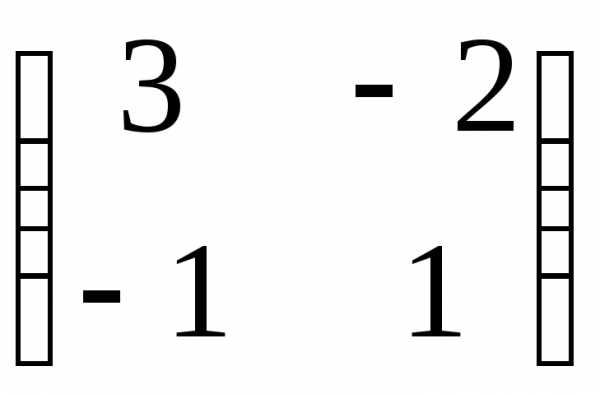
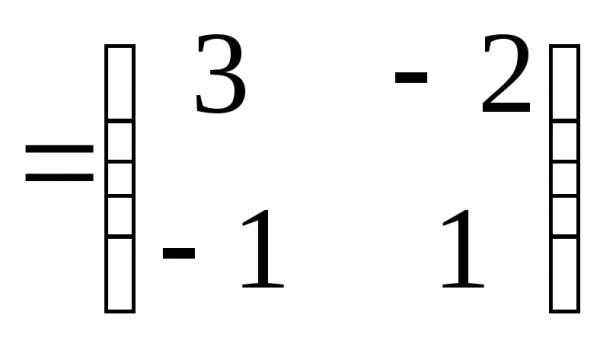
5) Сделаем проверку
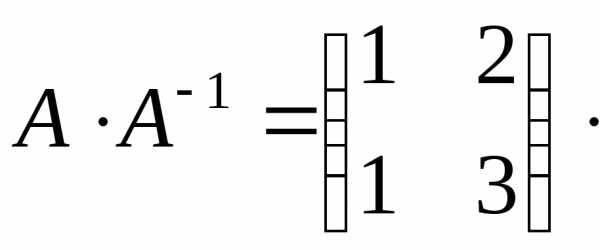
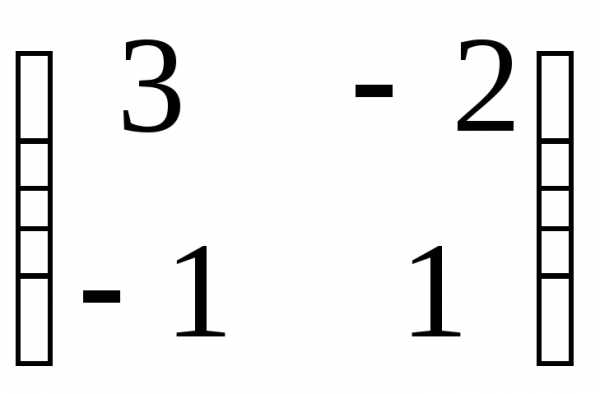
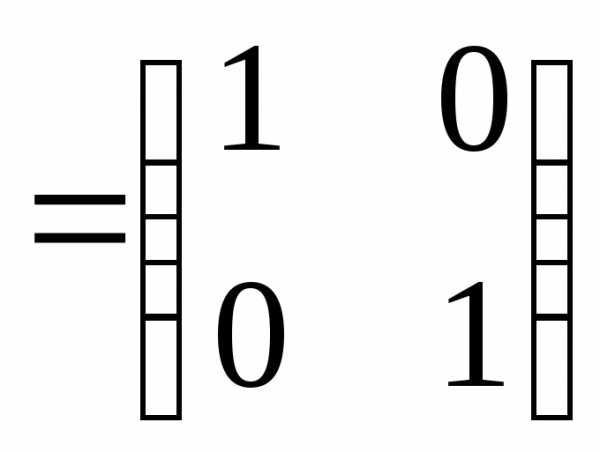
Задача №7. Найти матрицу, обратную
к матрице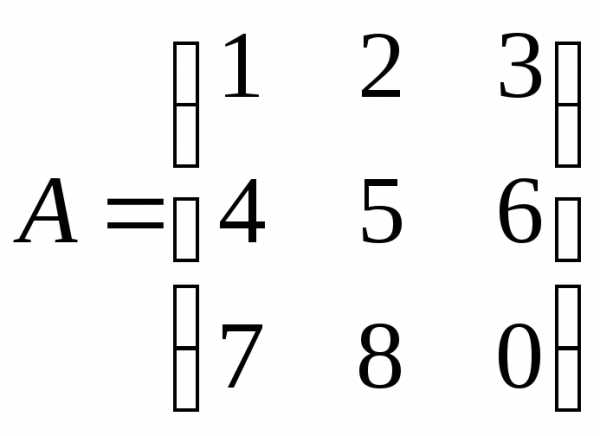 .
.
Решение.
1) Найдем
, следовательно обратная матрица существует.
2) Найдем алгебраические дополнения элементов матрицы А
3) Запишем союзную матрицу
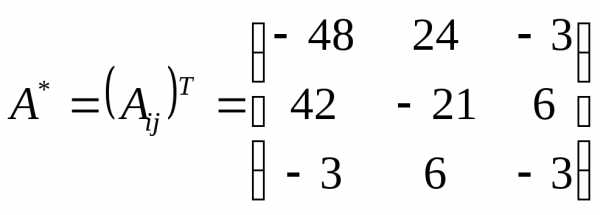
4) Найдем обратную матрицу
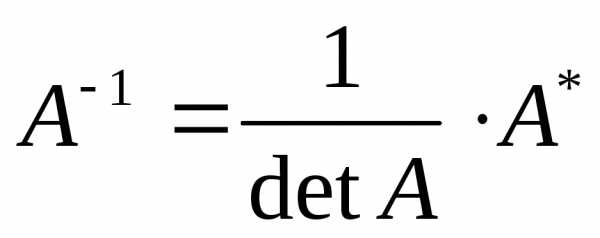
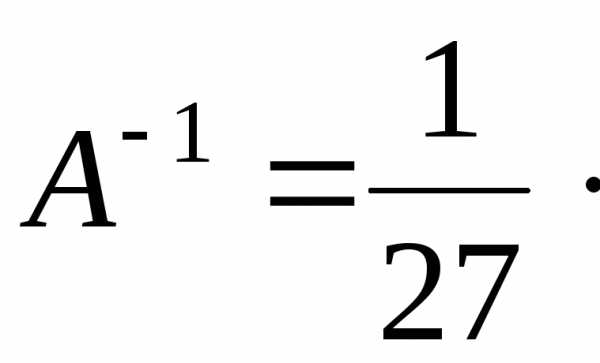

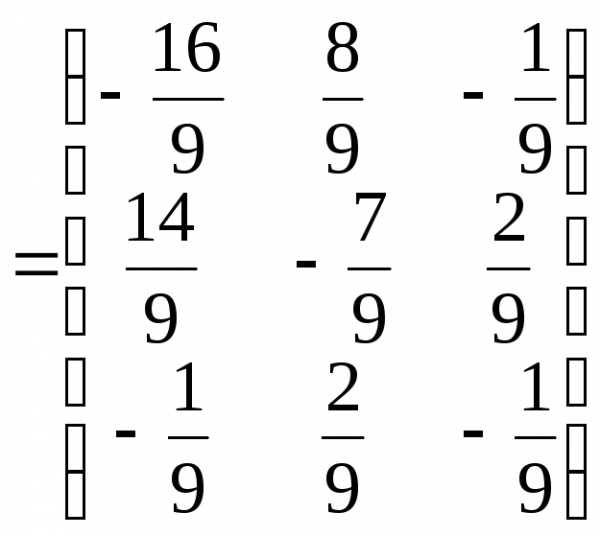
5) Сделаем проверку
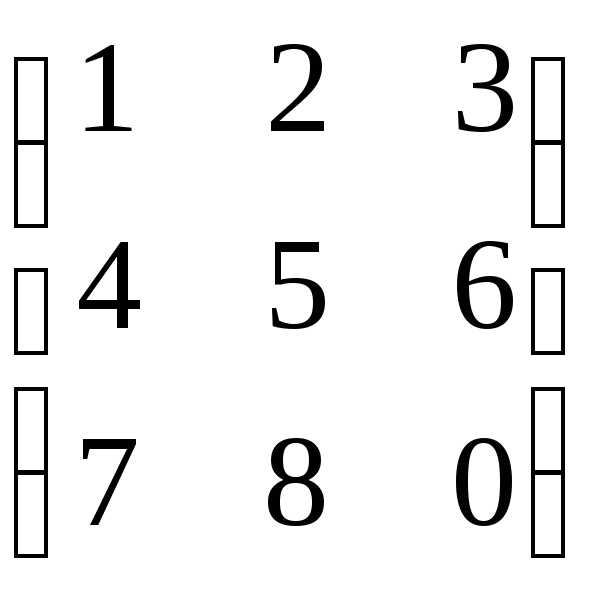
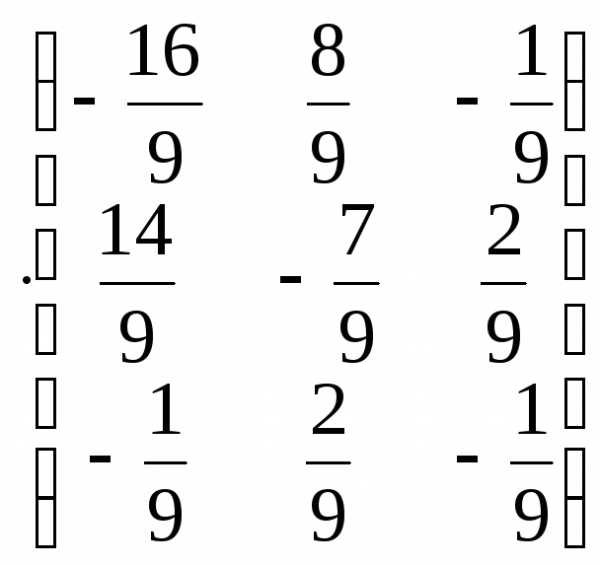
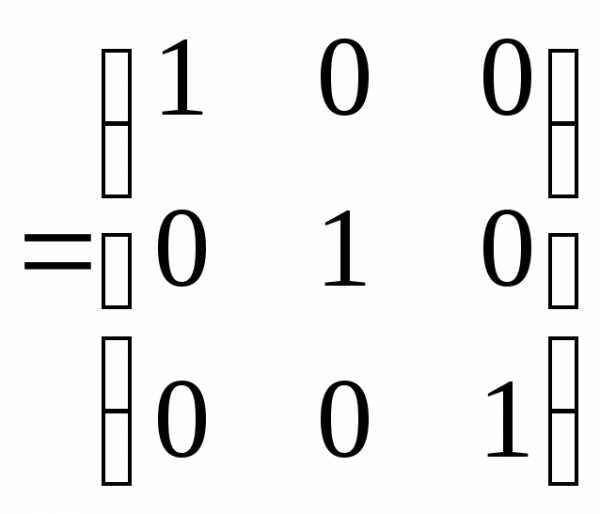
Задача №8. Найти матрицу, обратную
к матрице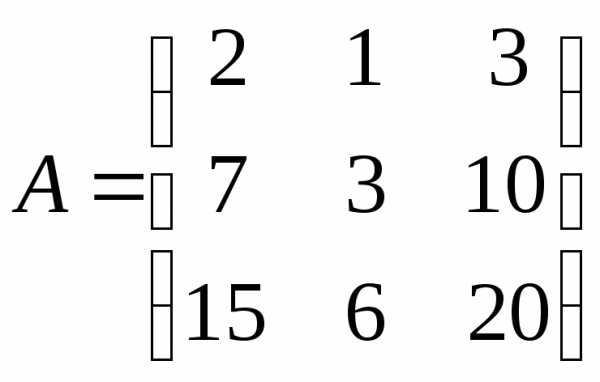 .
.
Решение.
1) Найдем 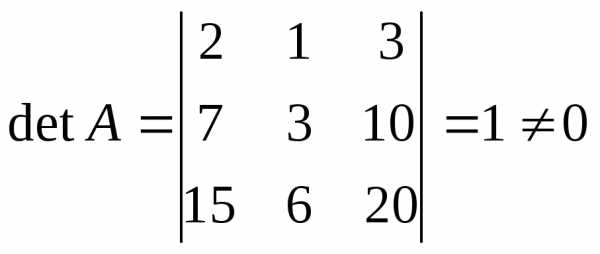
, следовательно обратная матрица существует.
2) Найдем алгебраические дополнения к элементам матрицы А
3) Запишем союзную матрицу
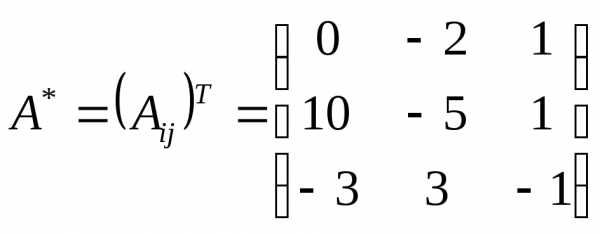
4) Найдем обратную матрицу
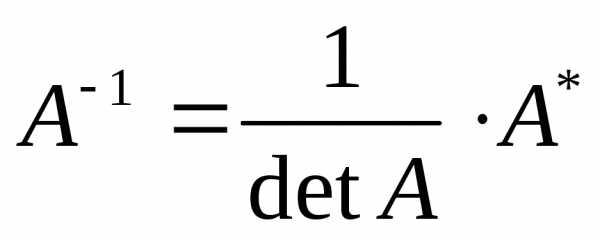
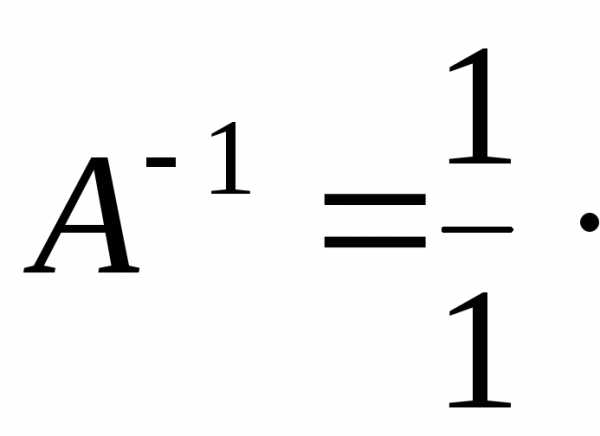


5) Сделаем проверку


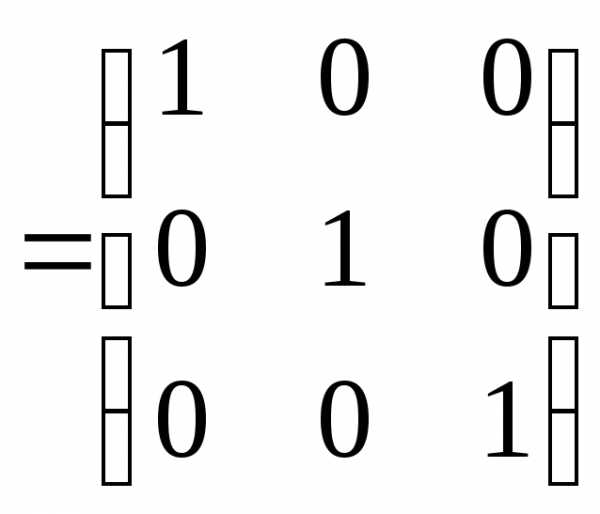
Задача №9. С помощью
элементарных преобразований строк
найти матрицу, обратную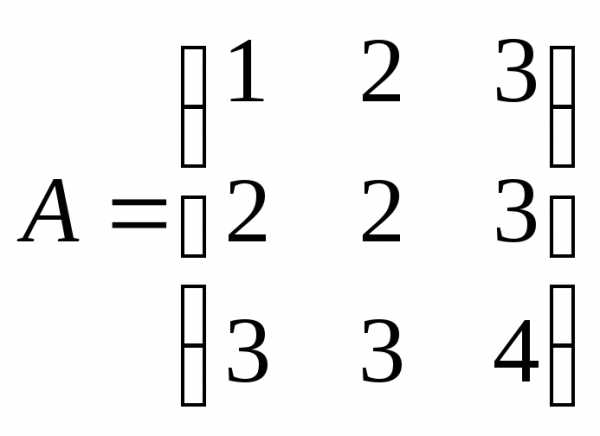 .
.
Решение.
Припишем к матрице  справа единичную матрицу и будем
выполнять элементарные преобразования
строк объединенной матрицы до тех пор
справа единичную матрицу и будем
выполнять элементарные преобразования
строк объединенной матрицы до тех пор
Задача №10. Найти ранг матрицы
Решение.

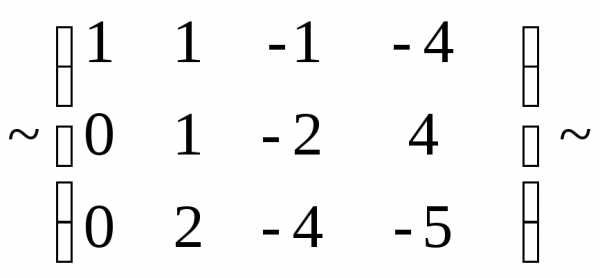

Ранг матрицы равен 3.
Задачи для самостоятельного решения:
а) по правилу треугольника;
б) с помощью разложения по первой строке;
в) преобразованием, используя свойства определителей.
2. Найти
минор и алгебраическое дополнение
элемента a13 определителя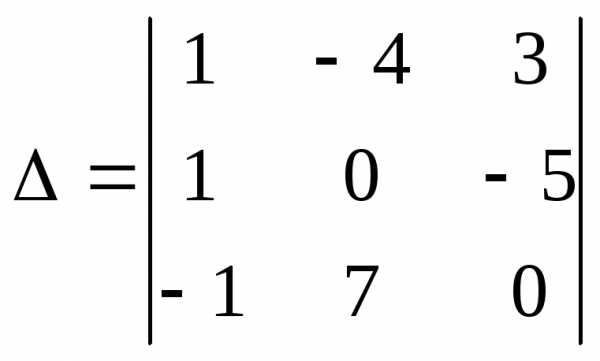 и вычислить его разложением по элементам
строки или столбца.
и вычислить его разложением по элементам
строки или столбца.
3. Решить уравнение 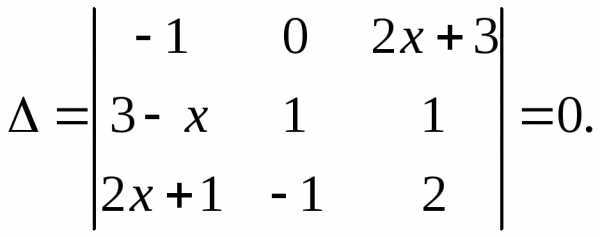
4. Вычислить определитель 4-го порядка
разложением по элементам строки или
столбца: 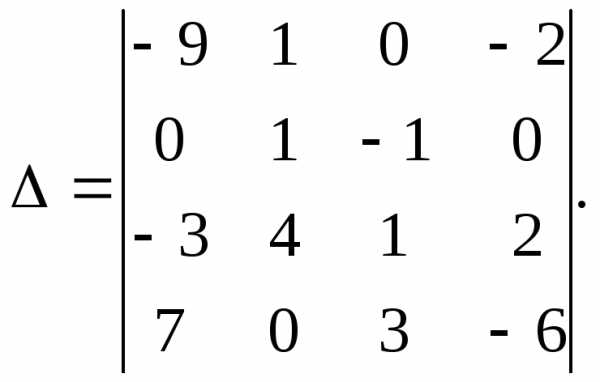
5. Найти обратную матрицу для следующих матриц:
 ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) .
.
6. Решить матричные уравнения:
1) ;
2) ;
3) ;
4) 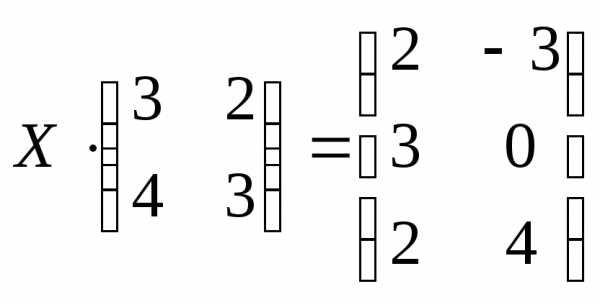 ;
;
5)  ;
;
6) 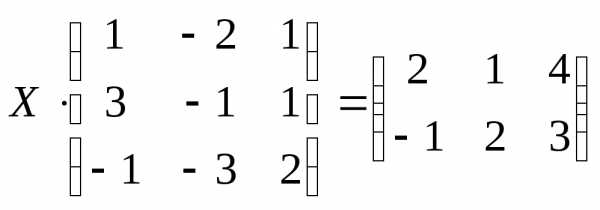 ;
;
7);
8).
7. Доказать, что если А – квадратная матрица и (А+Е)2=О, то матрица А имеет обратную. Найти обратную для А матрицу.
8. Найти все матрицы второго порядка, для которых А-1=А.
Занятие 3. Решение систем линейных уравнений методом Крамера и методом обратной матрицы.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Понятие системы линейных алгебраических уравнений.
Понятие решения системы линейных алгебраических уравнений.
Определение совместной и несовместной системы.
Достаточное условие совместной системы.
Определение однородной и неоднородной системы.
Формулы Крамера.
Алгоритм решения систем линейных уравнений с помощью обратной матрицы.
Типовые примеры Решение систем линейных уравнений методом Крамера
Задача №1. Решить систему:
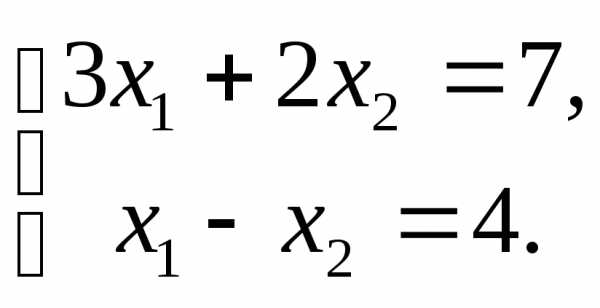
Решение.
Определитель системы:
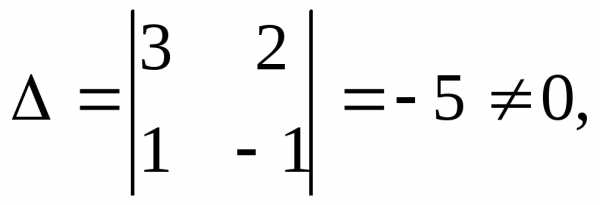
 поэтому
ее решение определяется по формулам
Крамера:
поэтому
ее решение определяется по формулам
Крамера:
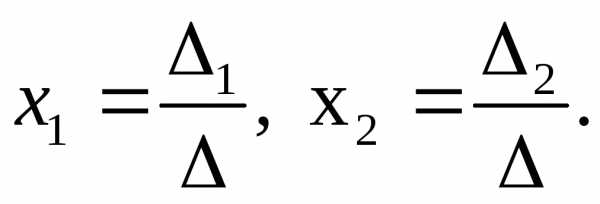
Но
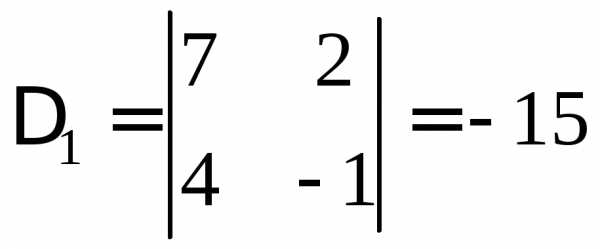 ,
,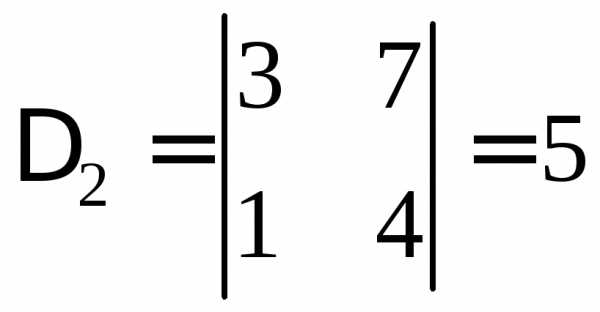
Тогда 

Задача №2. Решить систему:
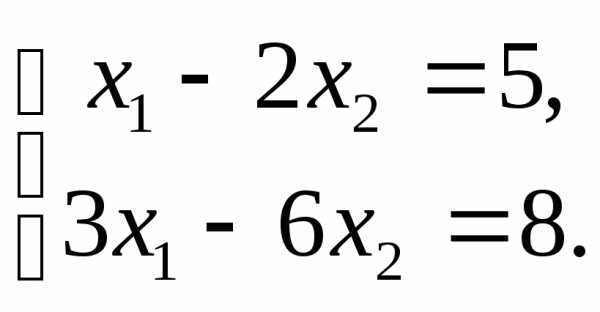
Решение.
Определитель данной системы 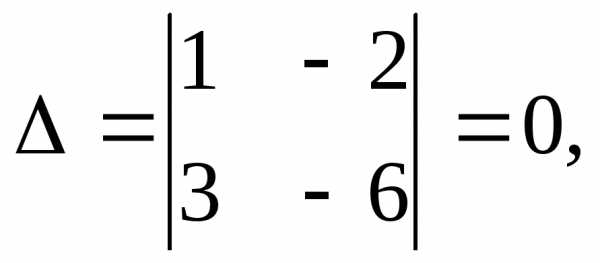
Задача №3. Решить систему:
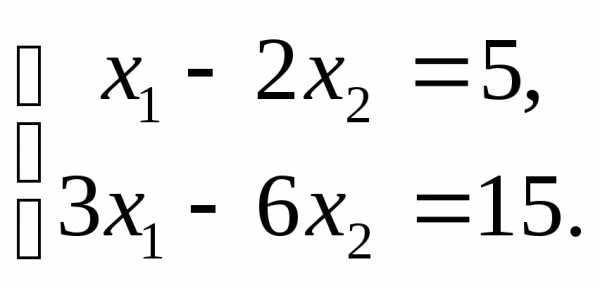
Решение.
Определители , так как у них строки пропорциональны. Здесь оба уравнения системы определяют одну и ту же прямую и решением системы являются координаты любой точки этой прямой. Отсюда следует, что система имеет бесчисленное множество решений.
Задача №4. Решить систему
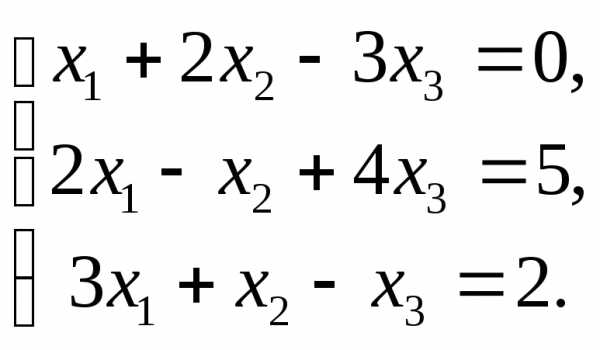
Решение.
Вычисляем определители:

Так как 
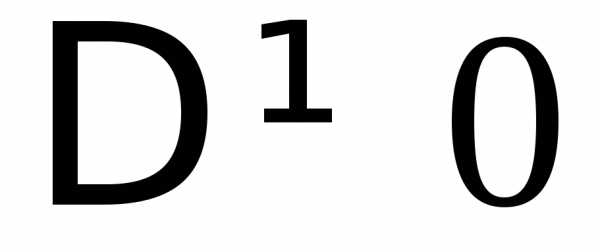 ,
то данная система имеет единственное
решение. Находим его по формулам Крамера:
,
то данная система имеет единственное
решение. Находим его по формулам Крамера:
studfiles.net
Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.
Определение. Матрица А-1называется обратной к матрице А, если выполняется условие: АА-1= А-1А=Е, где Е — единичная матрица того же порядка, что и матрица А. Обратная А-1матрица имеет ту же размерность, что и матрица А.
Определение. Квадратная матрица
А=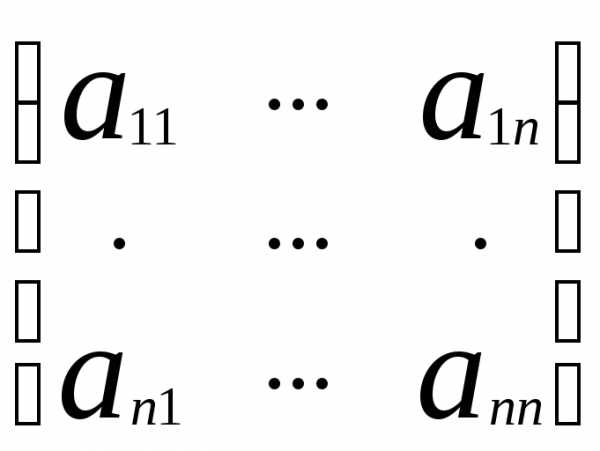 называется невырожденной, если её
определитель неравен нулю, в противном
случае матрица называется вырожденной.
называется невырожденной, если её
определитель неравен нулю, в противном
случае матрица называется вырожденной.
Теорема.Всякая невырожденная матрица имеет обратную.
Определение. Присоединенной матрицей к матрице А называется матрица вида:
к матрице А называется матрица вида:
 =
= ,
где Аij-алгебраическое
дополнение элемента аij.
,
где Аij-алгебраическое
дополнение элемента аij.
Находят обратную матрицу поформуле:
А-1=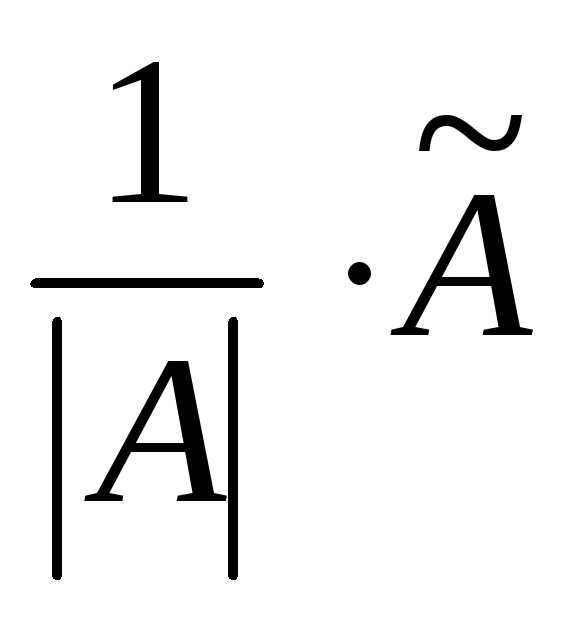 .
.
Пример 3.1
Найти обратную матрицу методом присоединенной матрицы.
А=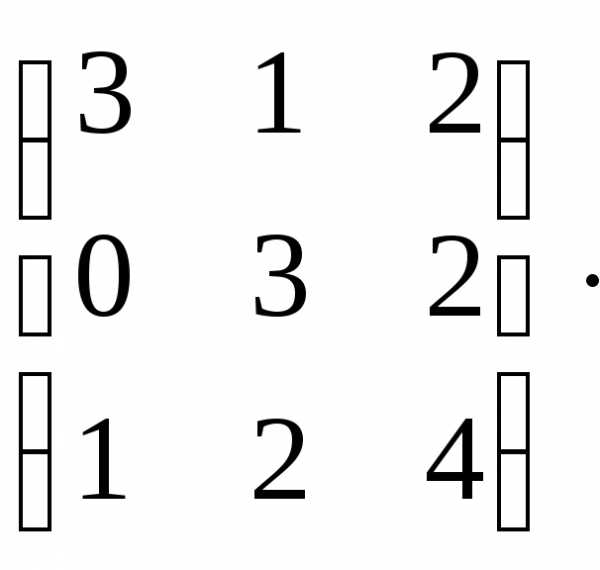
Решение.
Выясним, является ли данная матрица невырожденной. Для этого найдем определитель матрицы:
 =3(-1)1+1
=3(-1)1+1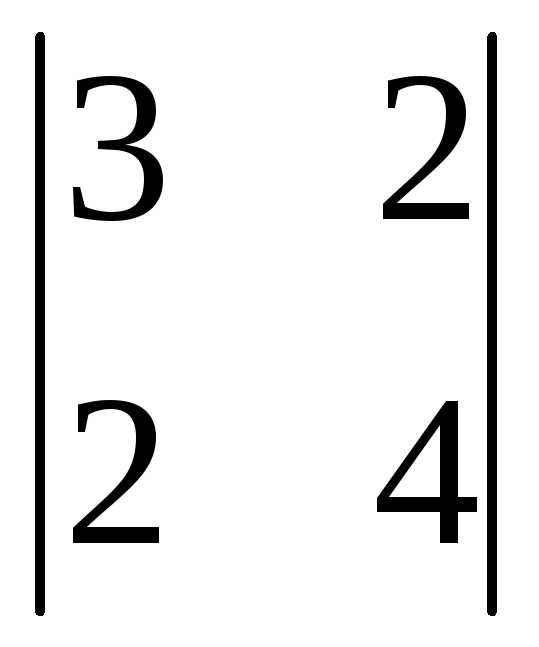 +0(-1)2+1
+0(-1)2+1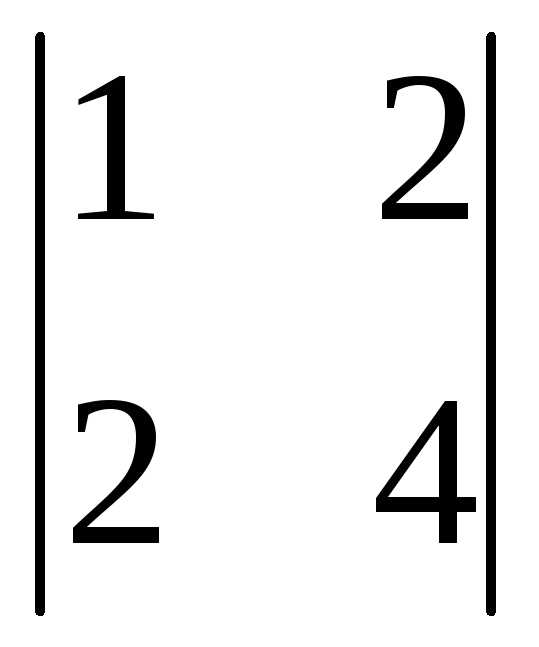 +1(-1)3+1
+1(-1)3+1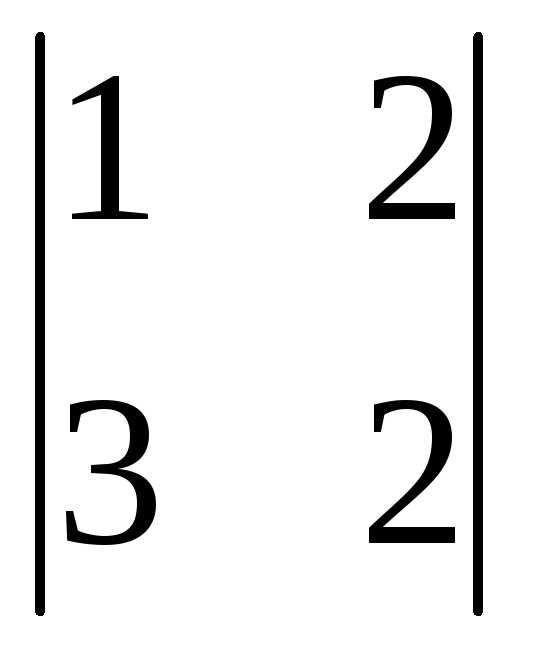 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0,
следовательно, данная матрица имеет
обратную.
0,
следовательно, данная матрица имеет
обратную.
Найдем транспонированную матрицу.
АТ=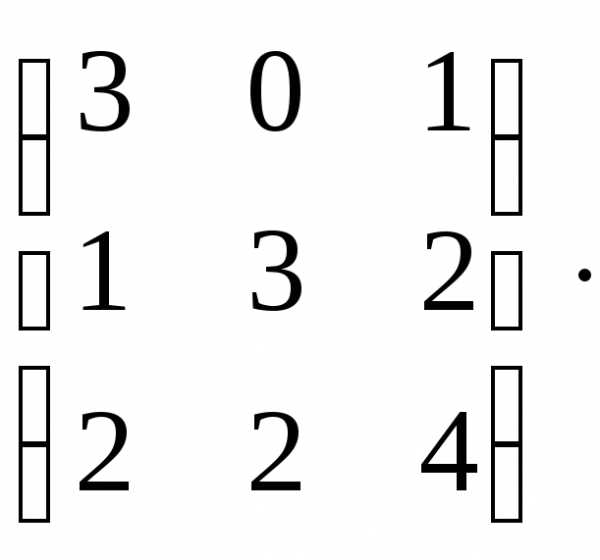
Вычислим присоединенную матрицу. Для этого найдем алгебраическое дополнение каждого элемента матрицы.
 =
(-1)1+1
=
(-1)1+1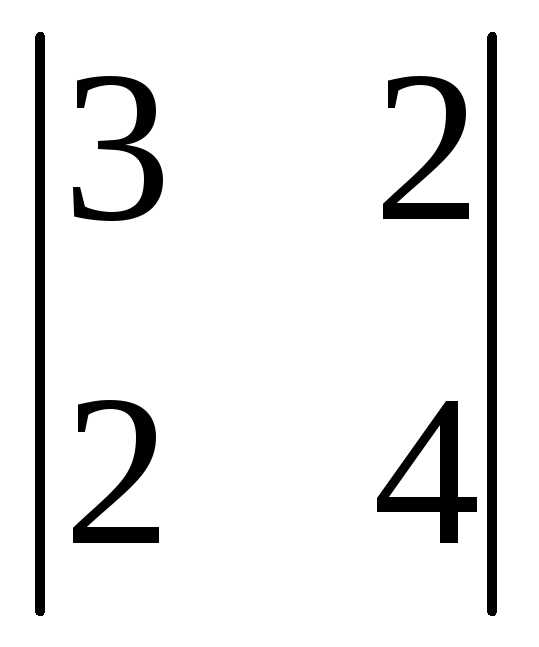 =12-4=8
=12-4=8
 =
(-1)1+2
=
(-1)1+2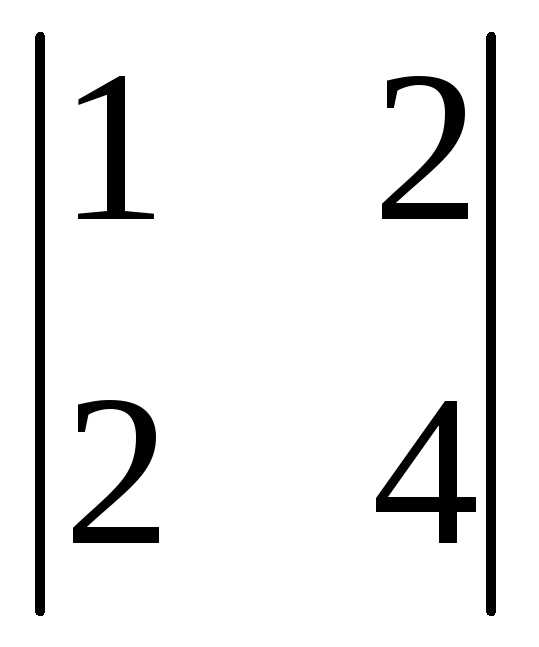 =
-(4-4)= 0
=
-(4-4)= 0
 =
(-1)1+3
=
(-1)1+3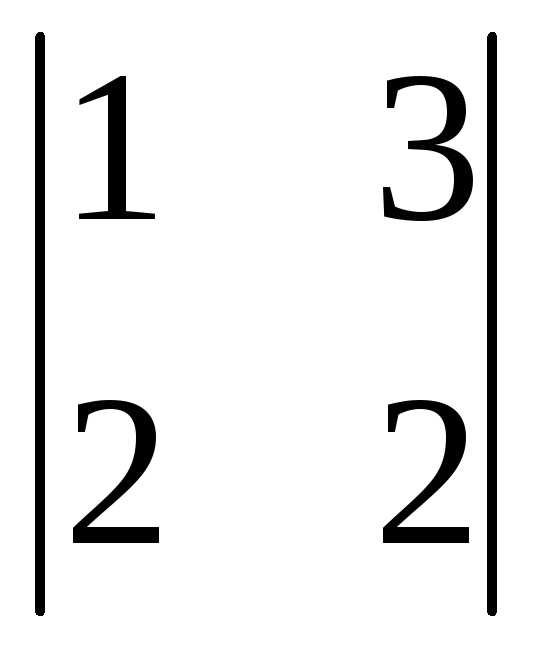 =
2-6= -4
=
2-6= -4
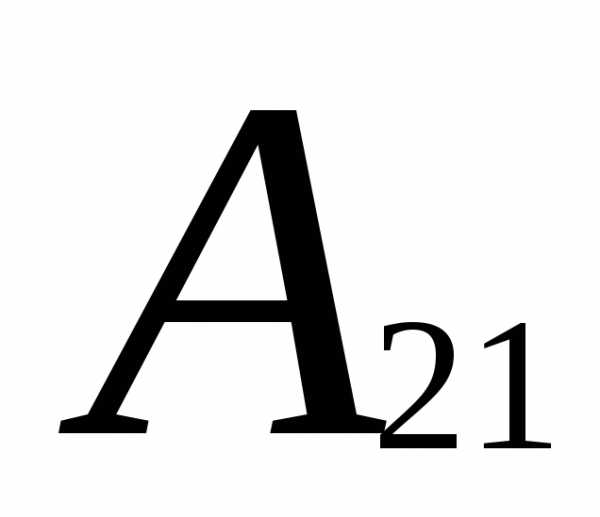 =
(-1)2+1
=
(-1)2+1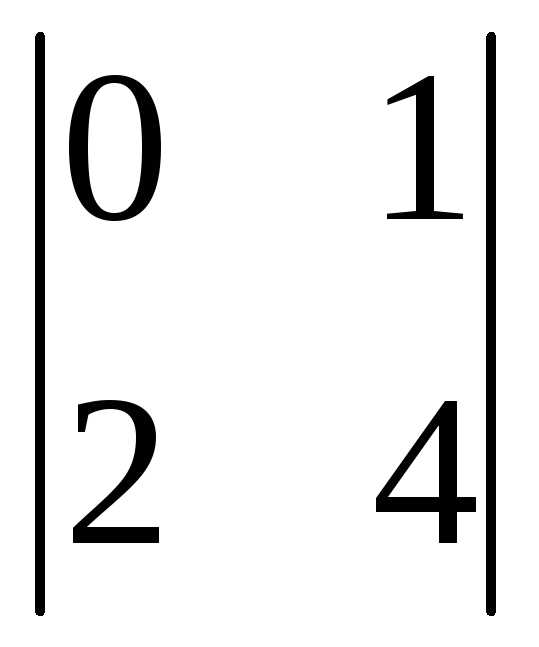 =
-(0-2)=2
=
-(0-2)=2
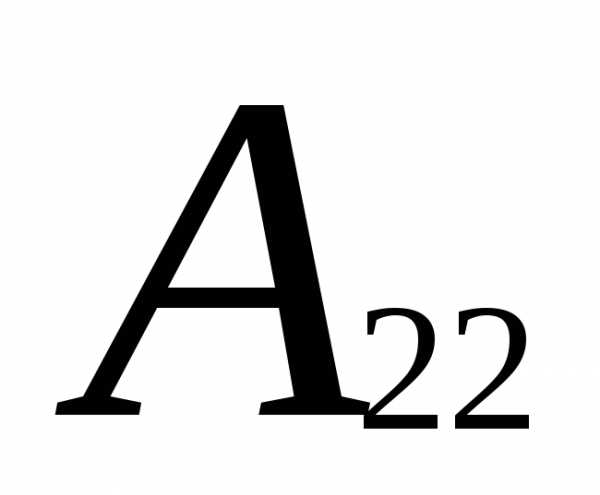 =
(-1)2+2
=
(-1)2+2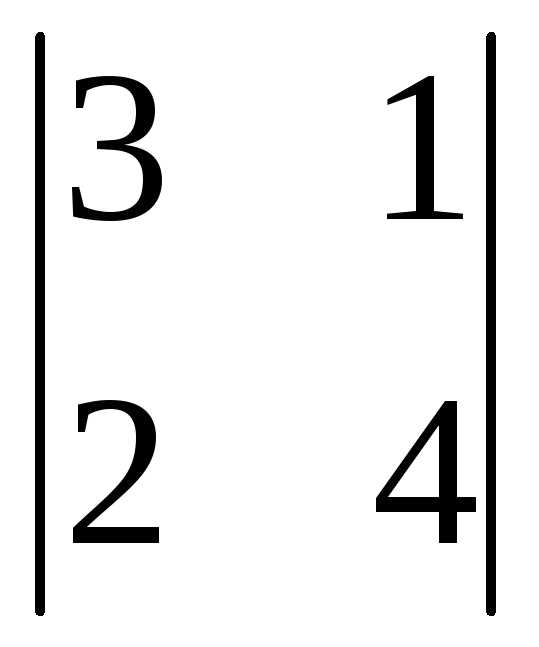 =
12-2=10
=
12-2=10
 =
(-1)2+3
=
(-1)2+3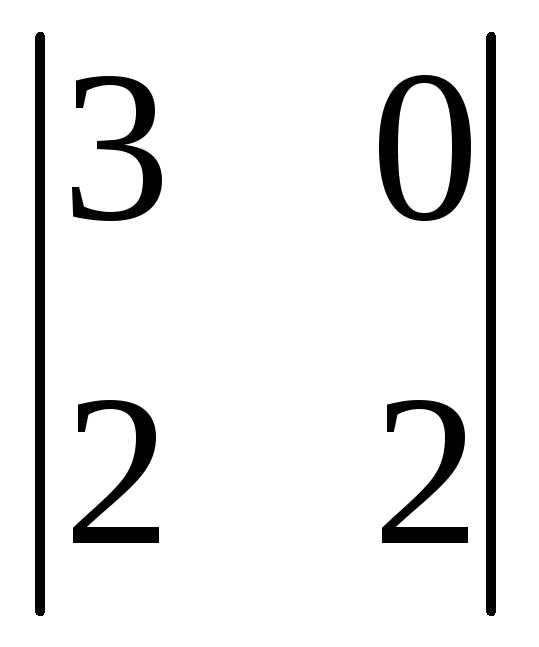 =
-(6-0)= -6
=
-(6-0)= -6
 =
(-1)3+1
=
(-1)3+1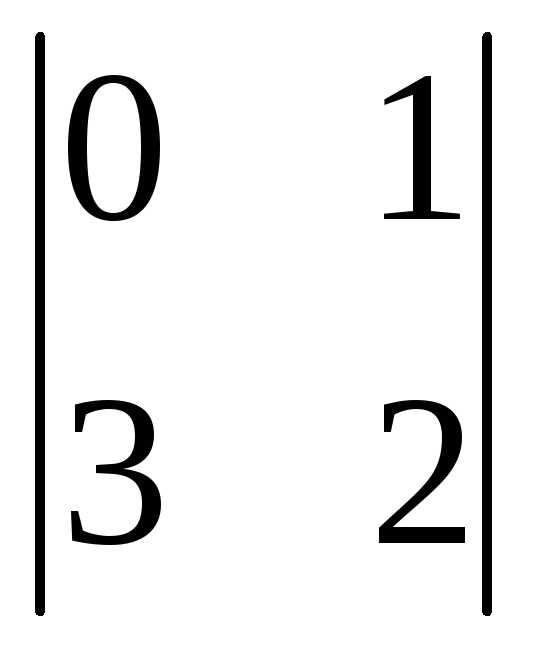 =
0-3= -3
=
0-3= -3
 =
(-1)3+2
=
(-1)3+2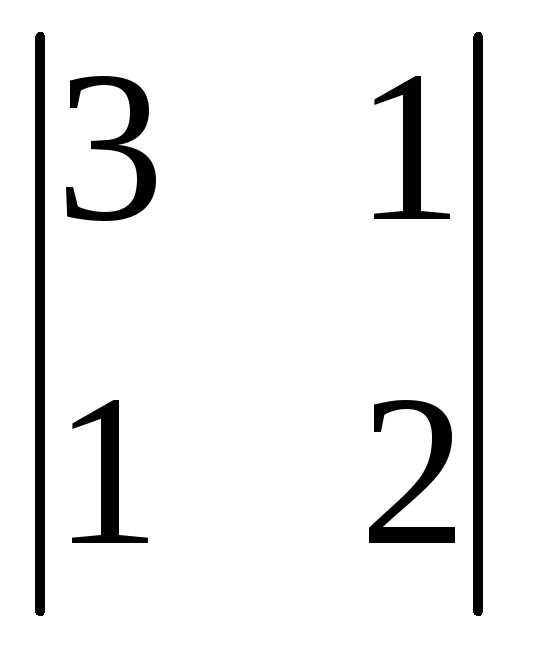 =
-(6-1)= -5
=
-(6-1)= -5
 =
(-1)3+3=
9-0=9.
=
(-1)3+3=
9-0=9.
 =
=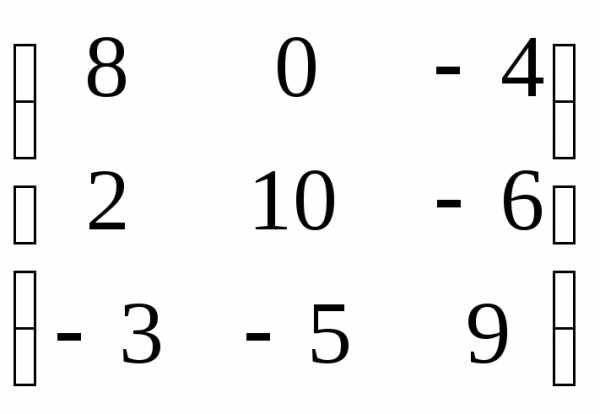
4. Воспользуемся формулой: А-1= .
.
А-1=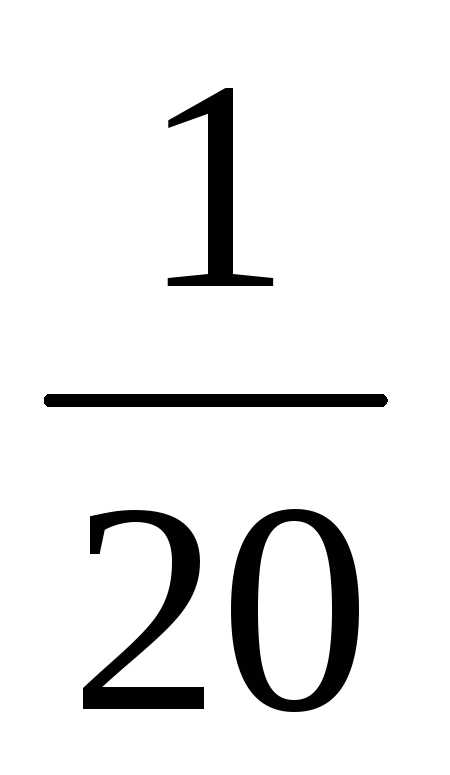
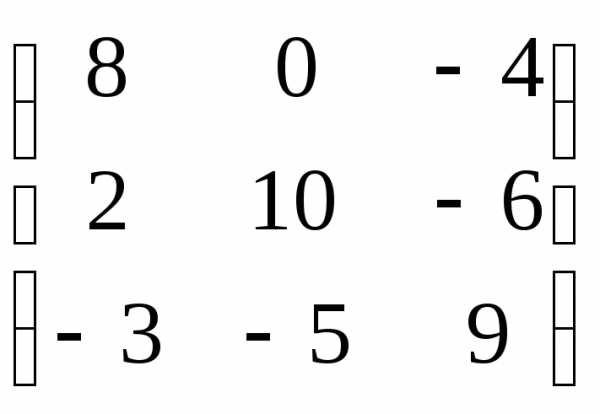 =
=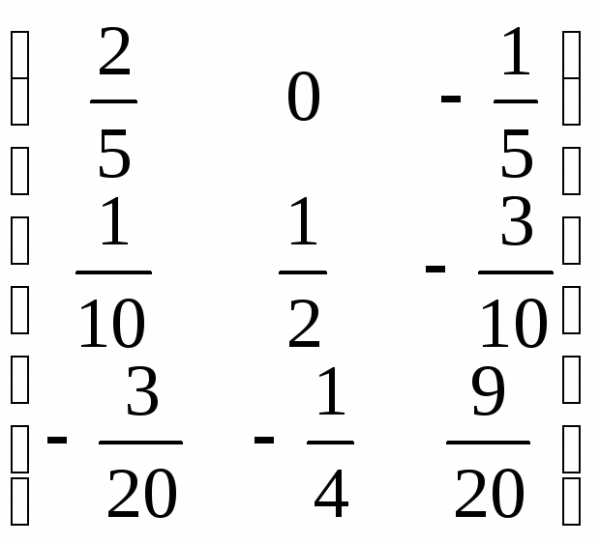 .
.
Решение систем линейных уравнений методом обратной матрицы
Пусть дана система линейных уравнений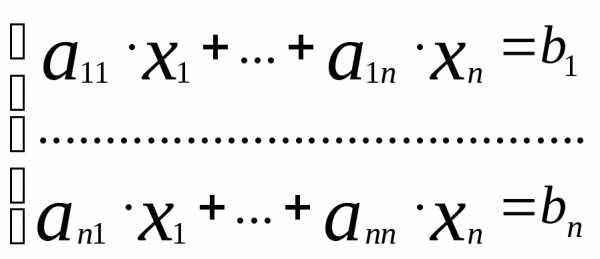 .
Обозначим её через (1). Выпишим основную
матрицу данной системы: А=
.
Обозначим её через (1). Выпишим основную
матрицу данной системы: А=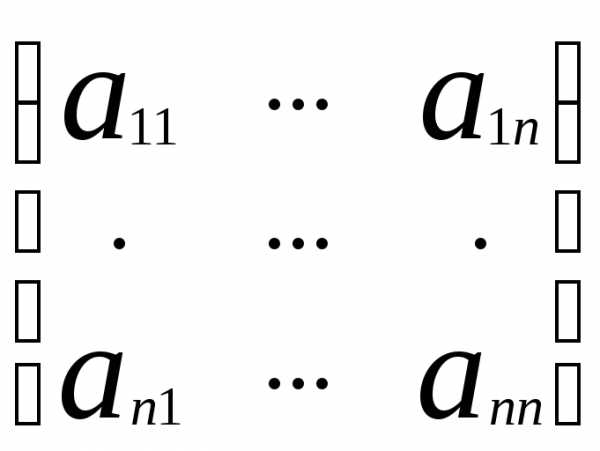 ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X=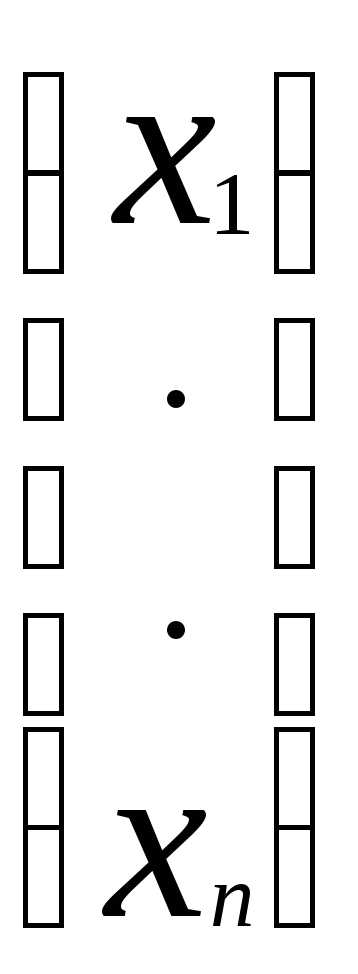 и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B=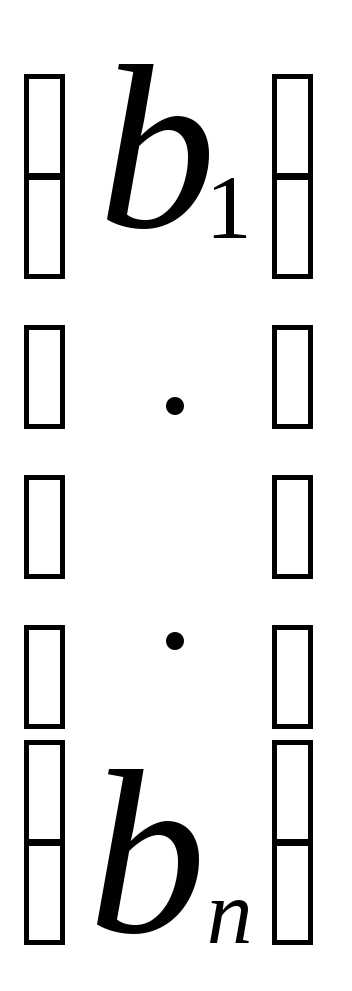 .
Теперь перепишем систему (1) в матричной
форме:AX=B
.
Теперь перепишем систему (1) в матричной
форме:AX=B X=A-1B-
решение системы (1).
X=A-1B-
решение системы (1).
Пример 3.2
Решить систему линейных уравнений: 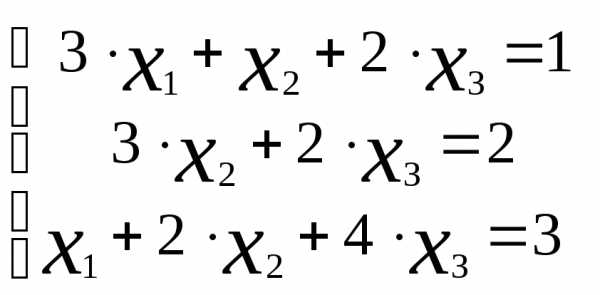 методом обратной матрицы.
методом обратной матрицы.
Решение.
Формула, по которой будем находить решение системы: X=A-1B.
Основная матрица системы А=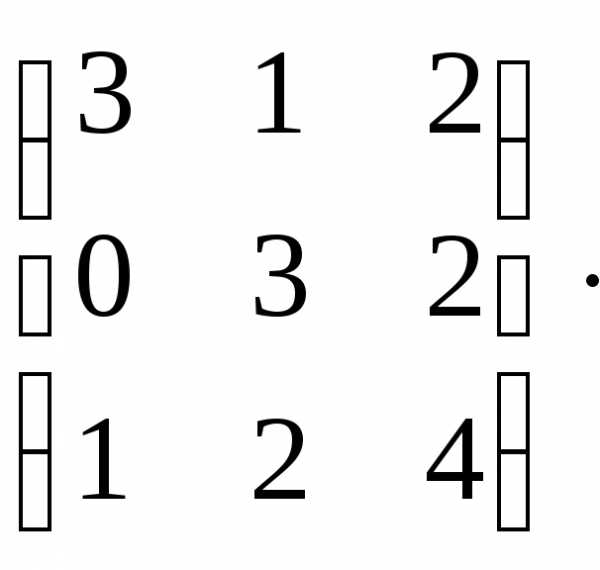 ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X=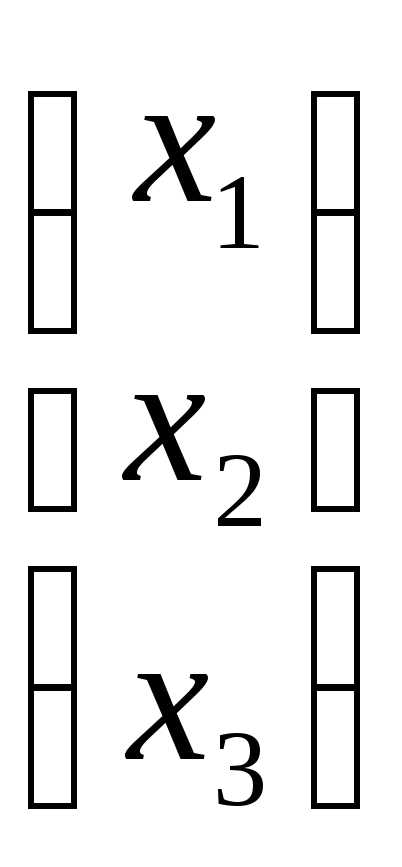
 и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B=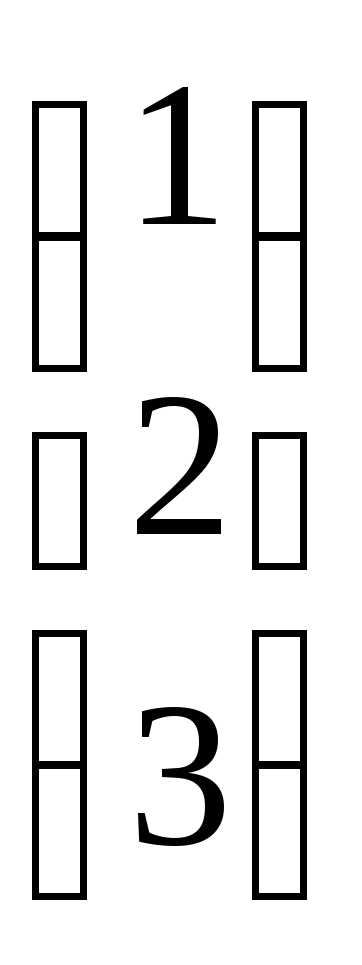 .
.
Найдем определитель  =3(-1)1+1
=3(-1)1+1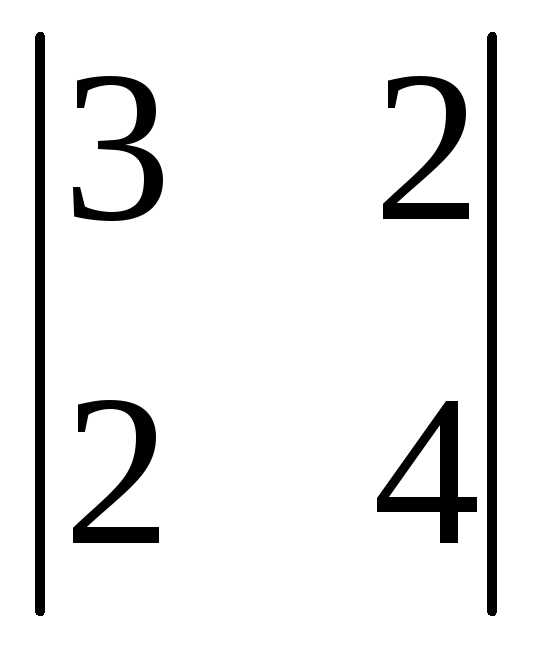 +0(-1)2+1
+0(-1)2+1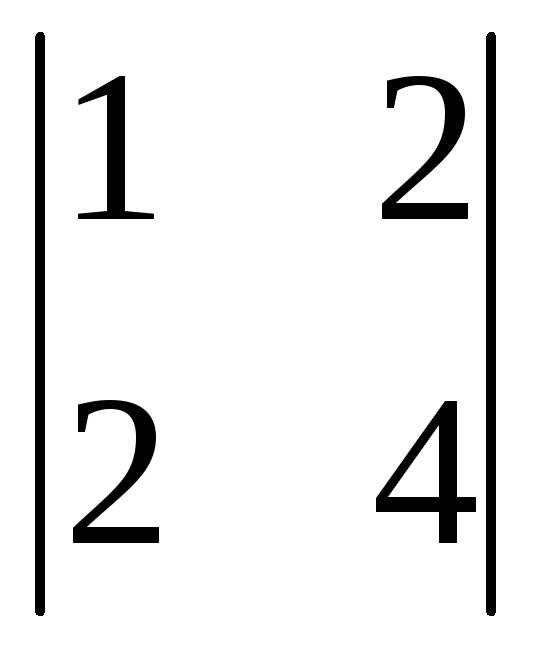 +1(-1)3+1
+1(-1)3+1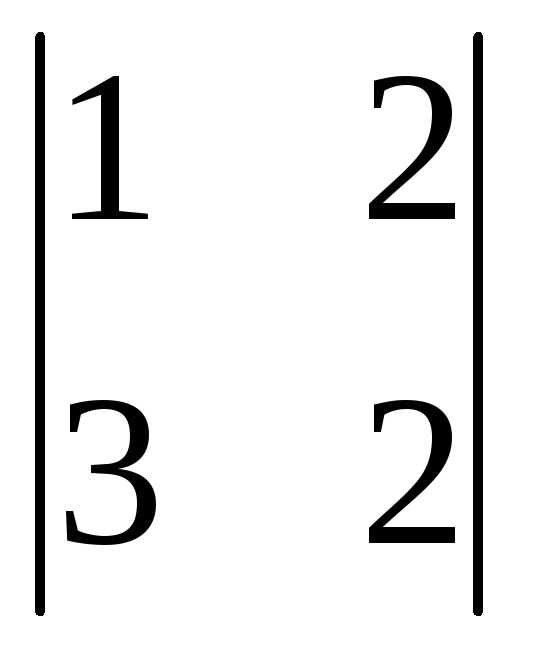 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0,
следовательно, данная матрица имеет
обратную.
0,
следовательно, данная матрица имеет
обратную.
Найдем обратную матрицу с помощью присоединенной матрицы (см. пример 3.1):
А-1=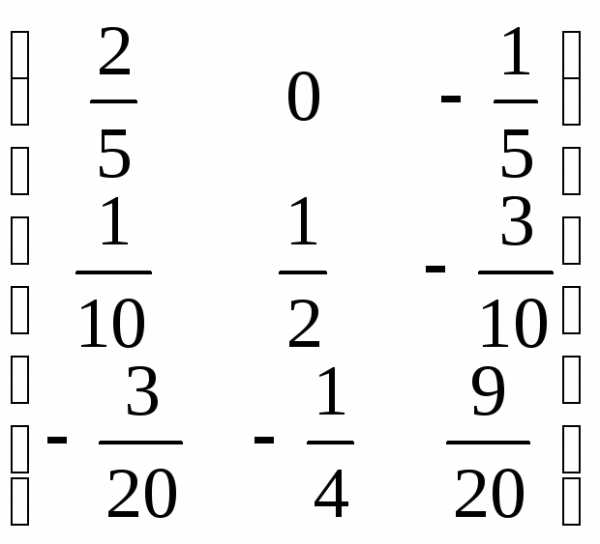 .
.
Подставим в формулу X=A-1B,
получим:X=
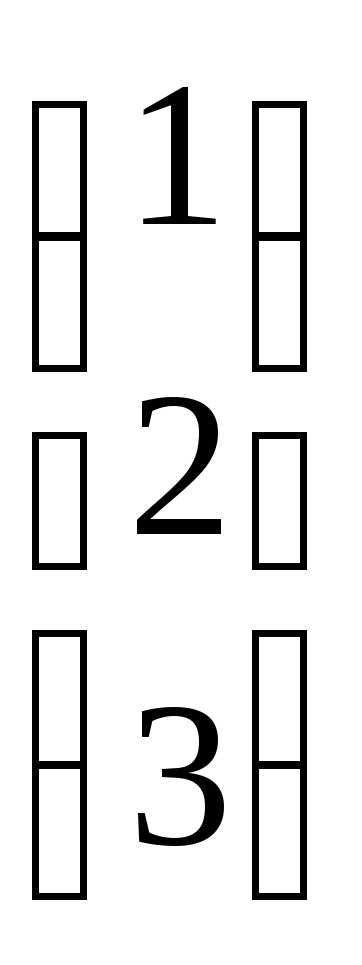 =
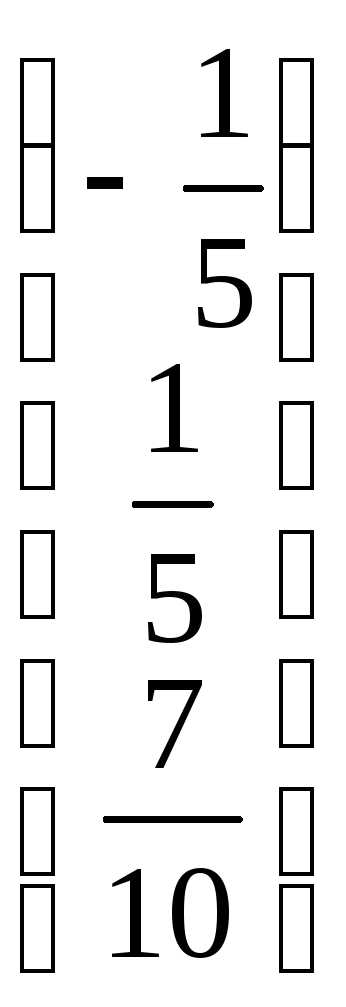
=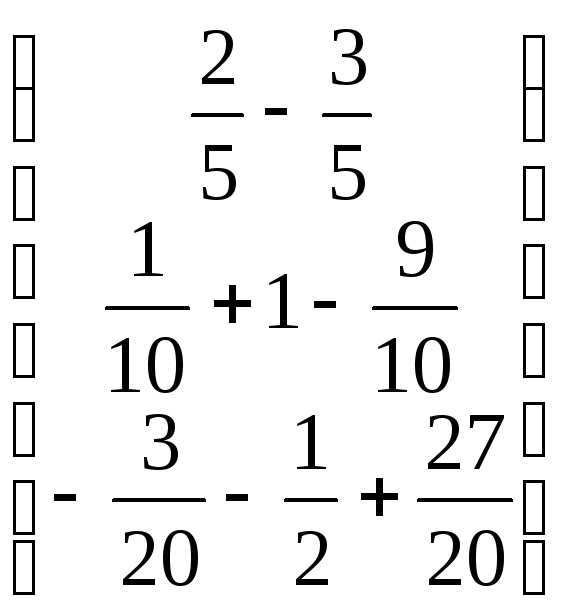 =
=
Ответ: 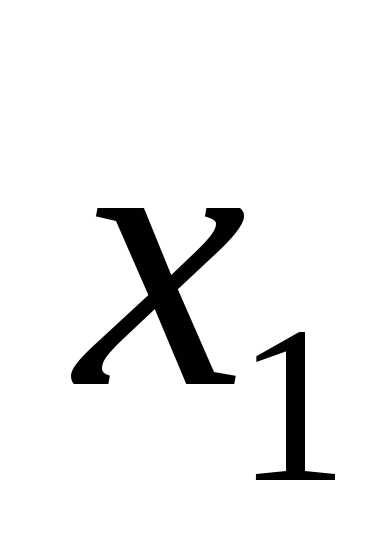 =
=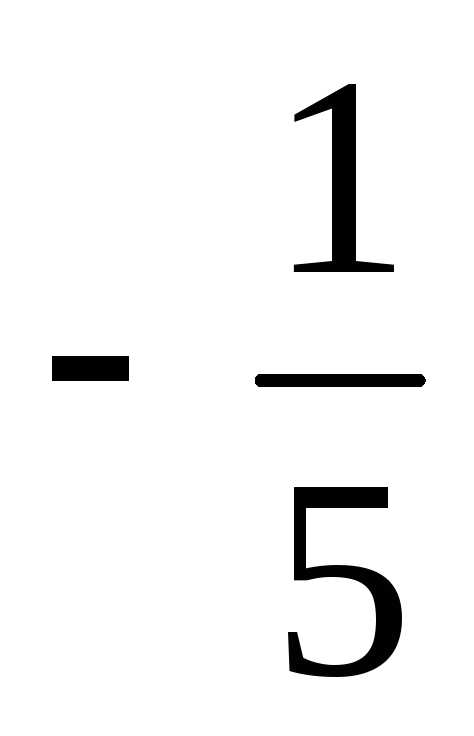 ,
, 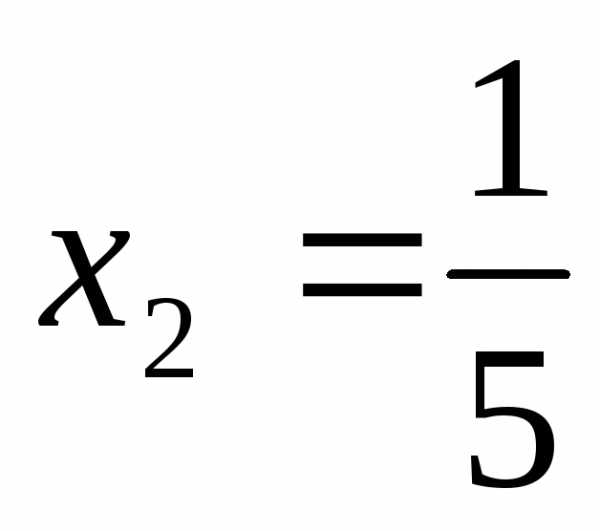 ,
,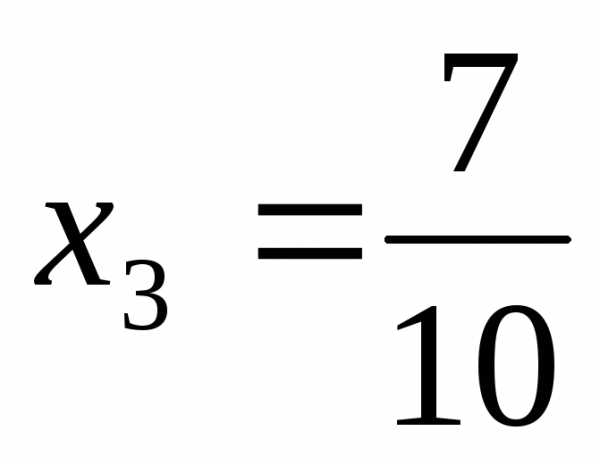 .
.
Правильность решения легко проверить,
подставив полученные результаты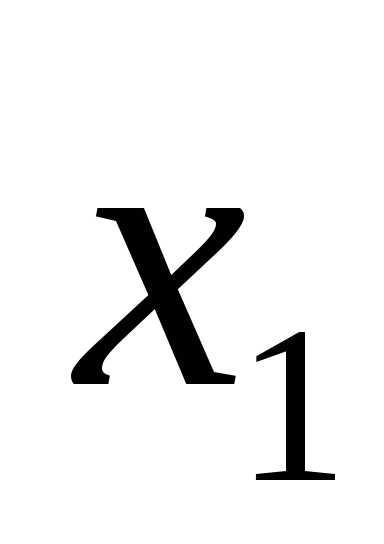 ,
, 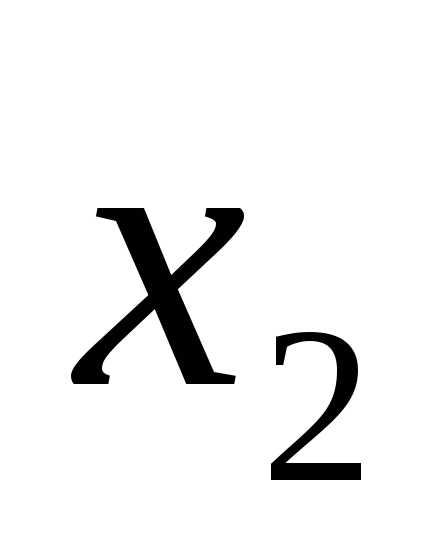 ,
, 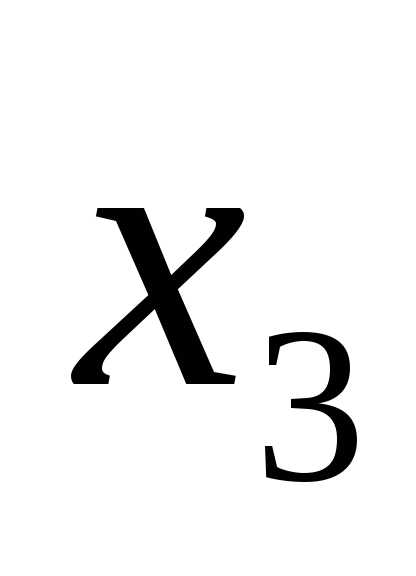 в данную систему уравнения.
в данную систему уравнения.
Решение систем линейных уравнений методом Гаусса и Крамера
Пусть дана система линейных уравнений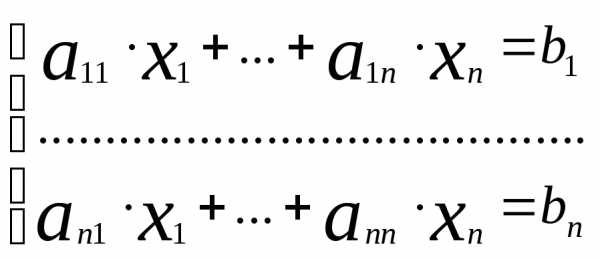 .
Обозначим её через (1). Основная матрица
данной системы: А=
.
Обозначим её через (1). Основная матрица
данной системы: А= ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X=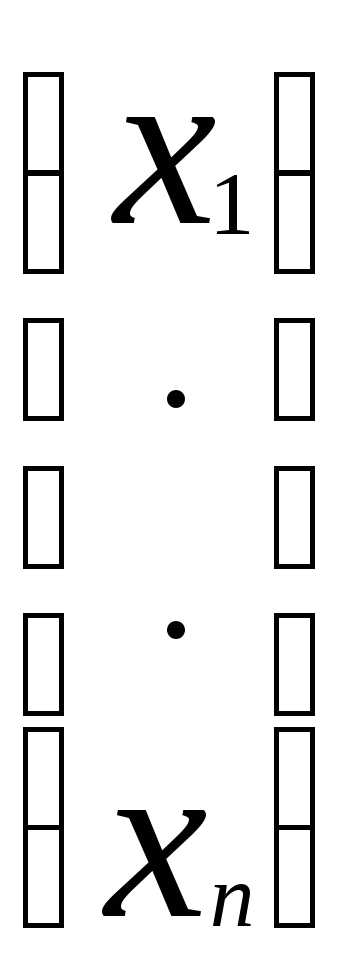 и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B=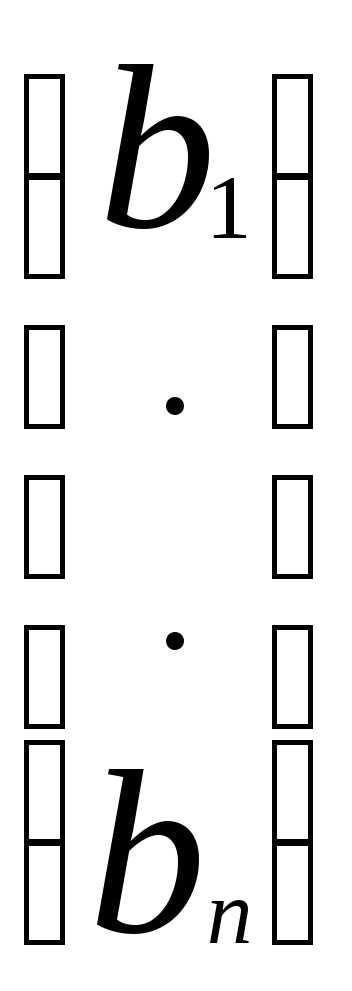 .
Теперь запишем систему (1) в матричной
форме:AX=B.
.
Теперь запишем систему (1) в матричной
форме:AX=B.
Теорема Крамера. Пусть  —определитель
матрицы А,
—определитель
матрицы А,  j—определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если
j—определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если
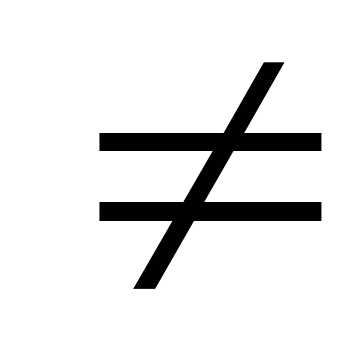 0,
то система имеет единственное решение:
0,
то система имеет единственное решение: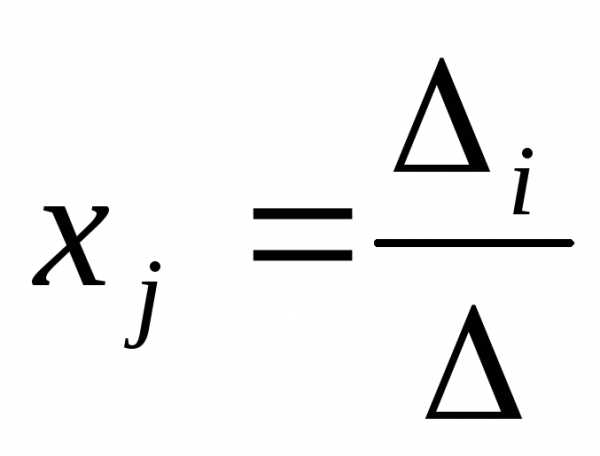 ,
(1jn).
,
(1jn).
Пример 4.1
Решить систему линейных уравнений: 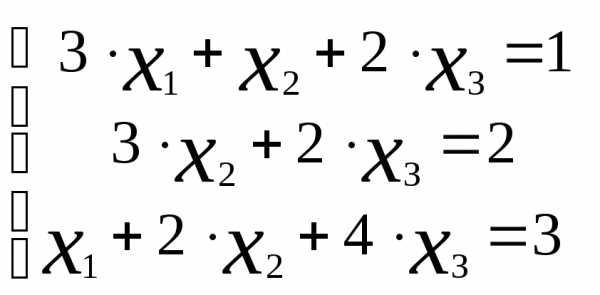 методом Крамера.
методом Крамера.
Решение.
Основная матрица системы А=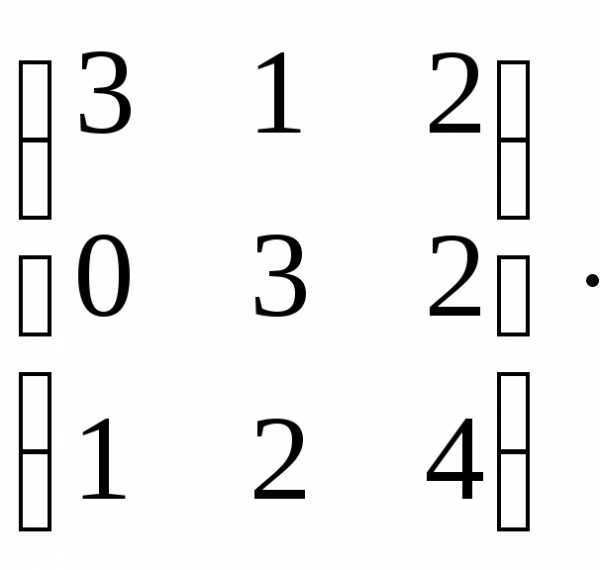 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B=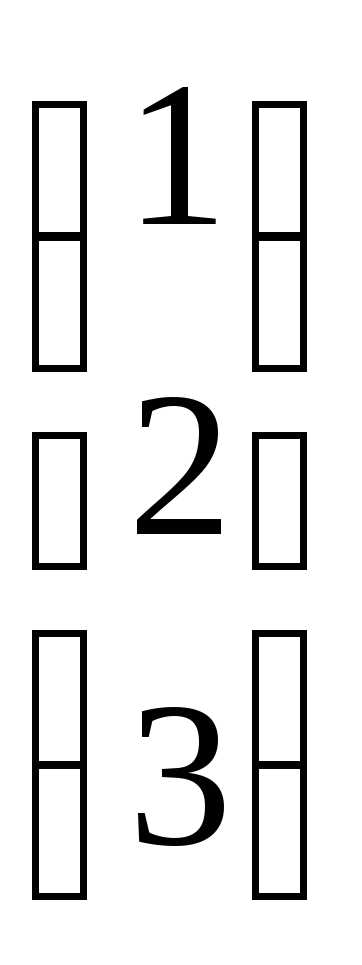 .
.
Найдем определитель  =
= =3(-1)1+1
=3(-1)1+1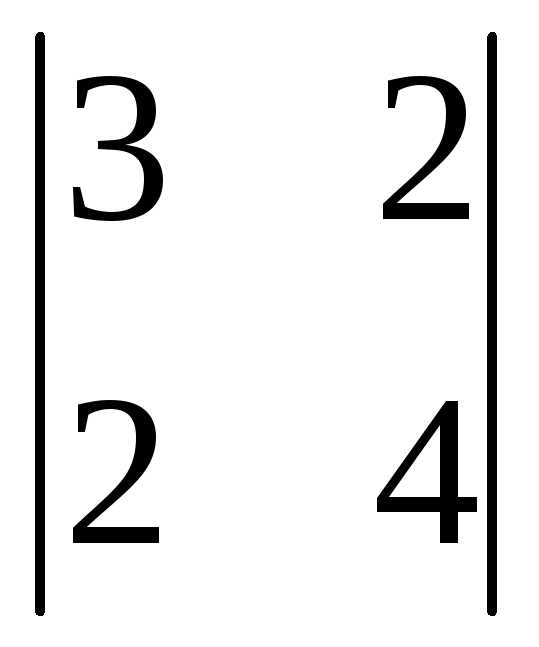 +0(-1)2+1
+0(-1)2+1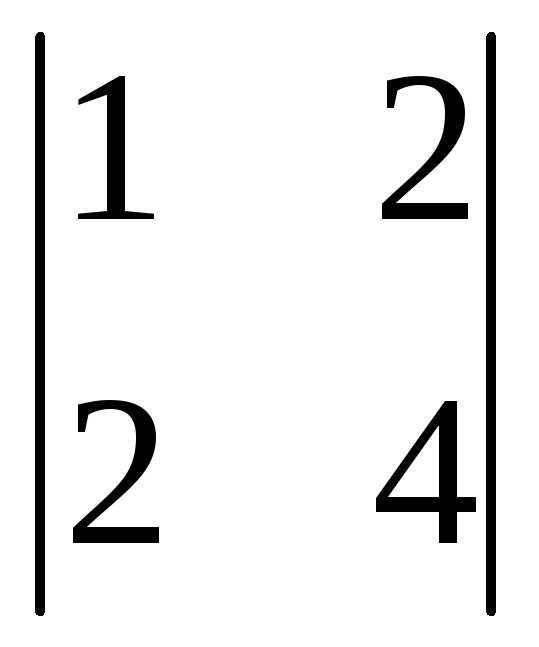 +1(-1)3+1
+1(-1)3+1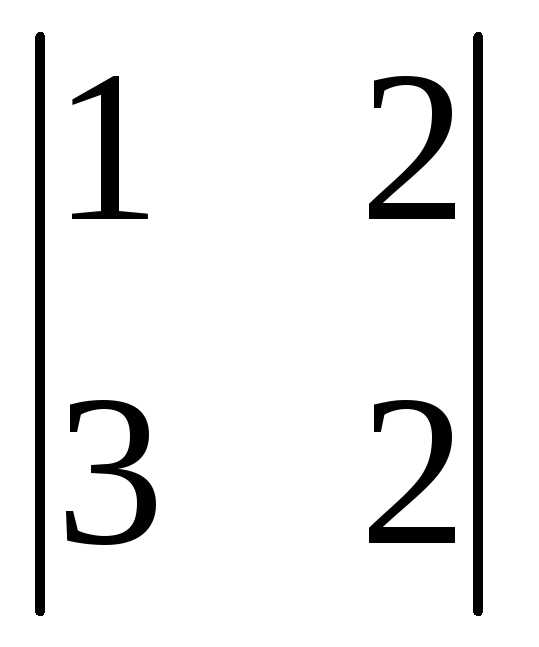 =3(12-4)+0+(2-6)=24-4=20. Т.к.
=3(12-4)+0+(2-6)=24-4=20. Т.к. 0,
следовательно, можно применить формулы
Крамера.
0,
следовательно, можно применить формулы
Крамера.
Найдем определители 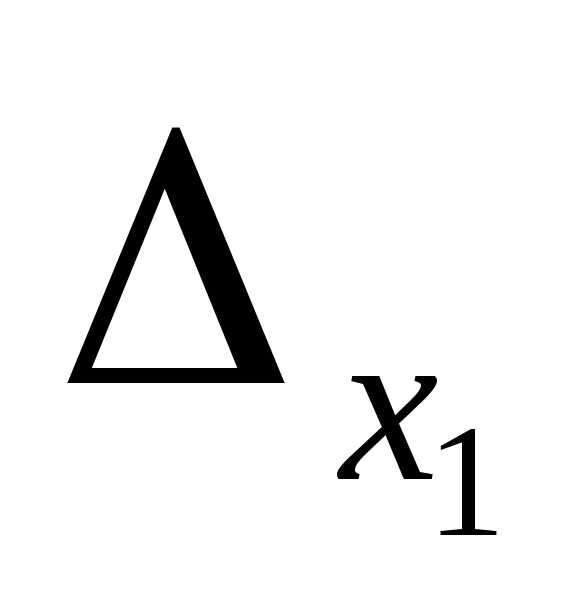 ,
, ,
,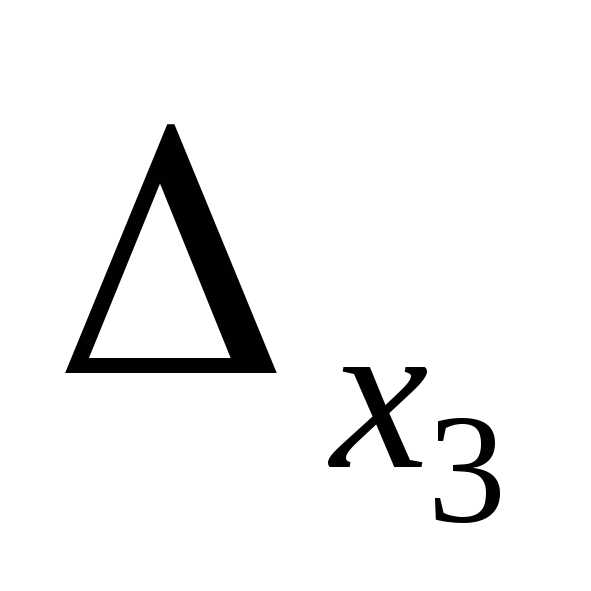 ,
полученные заменой соответствующих
столбцов столбцом свободных членов:
,
полученные заменой соответствующих
столбцов столбцом свободных членов:
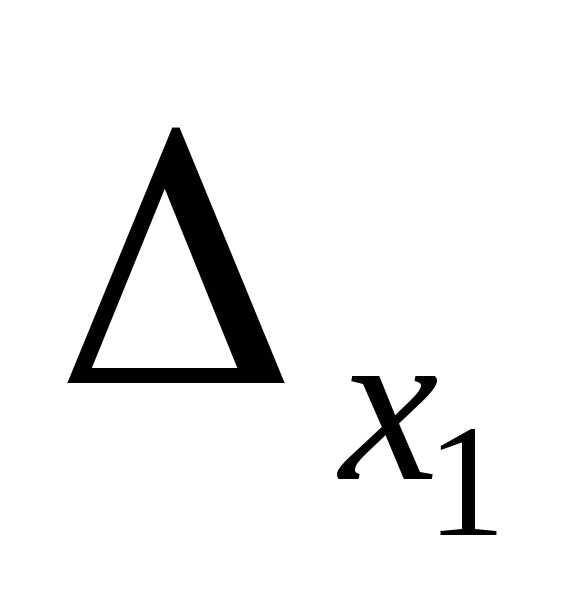 =
=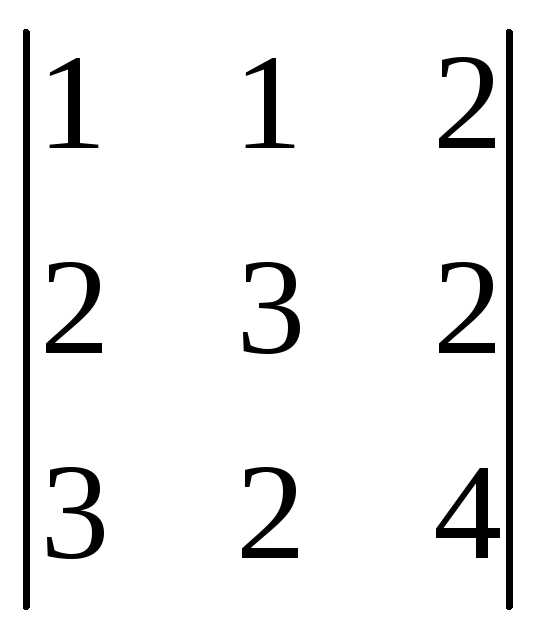 =1(12-4)-1(8-6)+2(4-9)=8-2-10=
-4;
=1(12-4)-1(8-6)+2(4-9)=8-2-10=
-4;
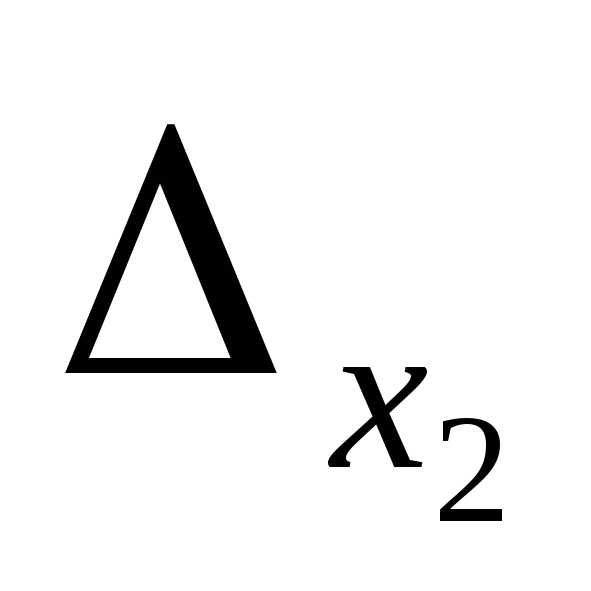 =
=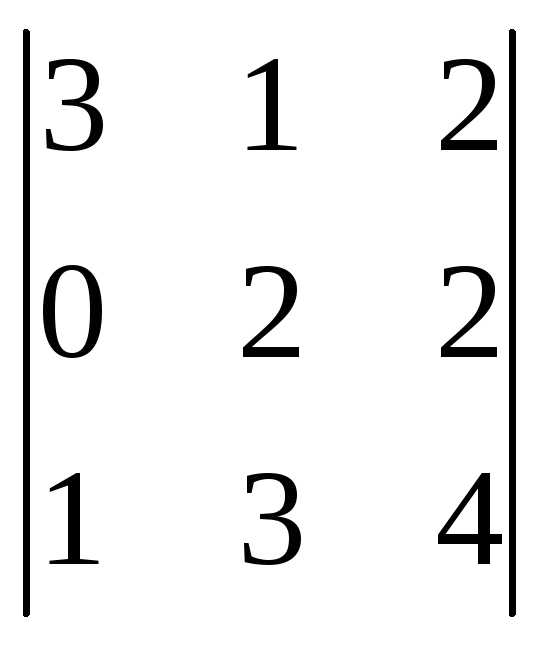 =3(8-6)-0+1(2-4)=6-2=4;
=3(8-6)-0+1(2-4)=6-2=4;
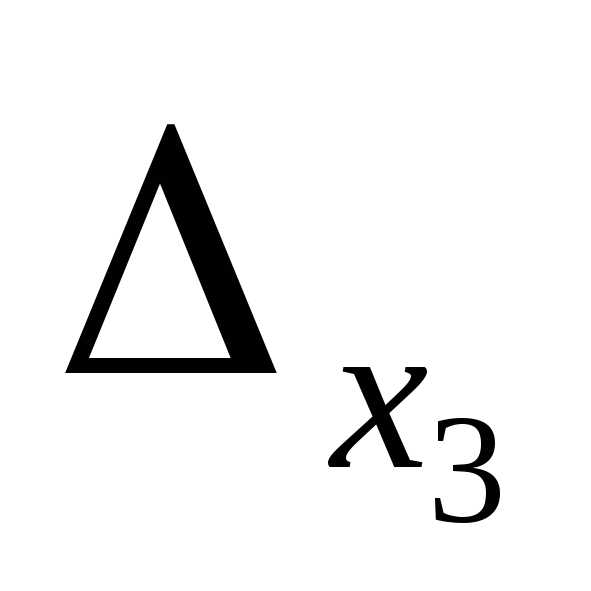 =
=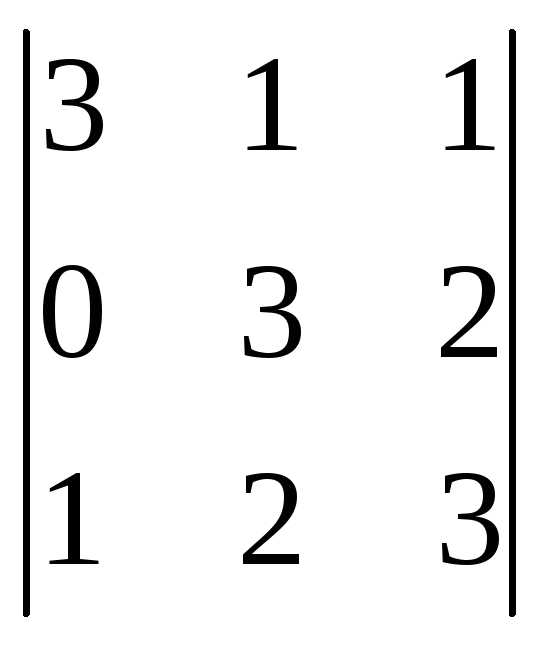 =3(9-4)-0+1(2-3)=15-1=14.
=3(9-4)-0+1(2-3)=15-1=14.
Тогда, по формуле Крамера:
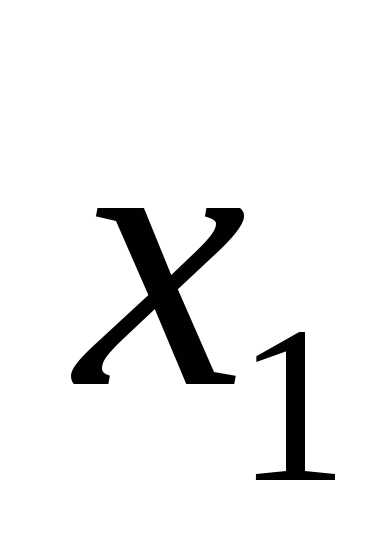 =
=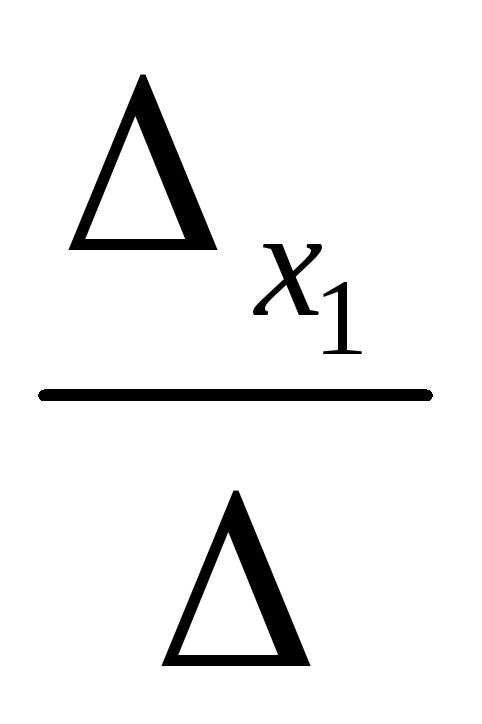 =
—
=
—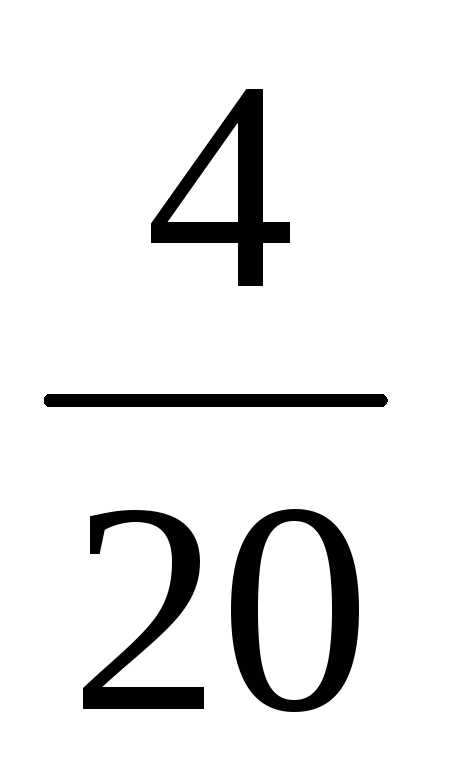 =
=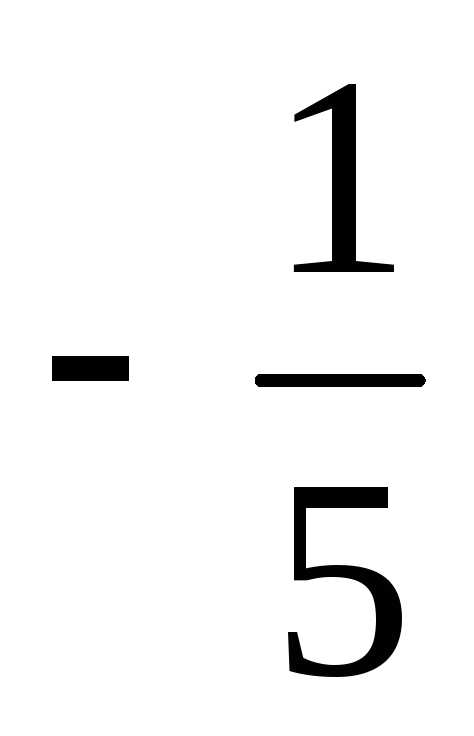 ;
;
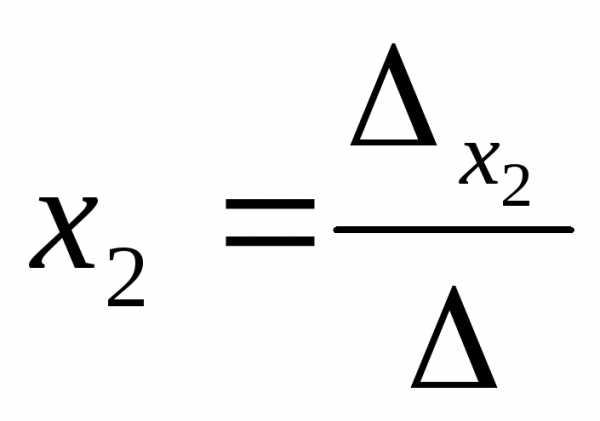 =
=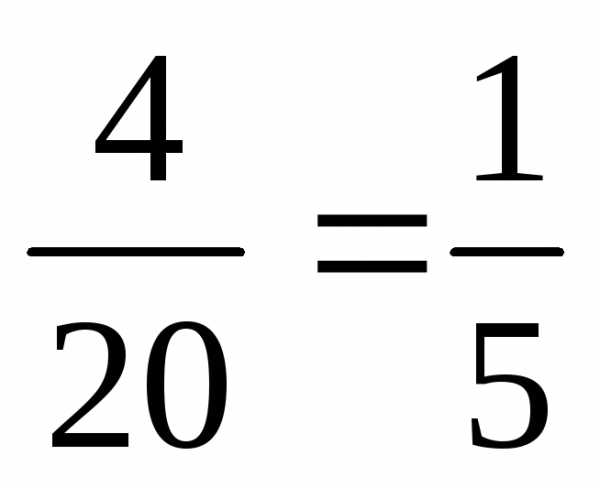 ;
;
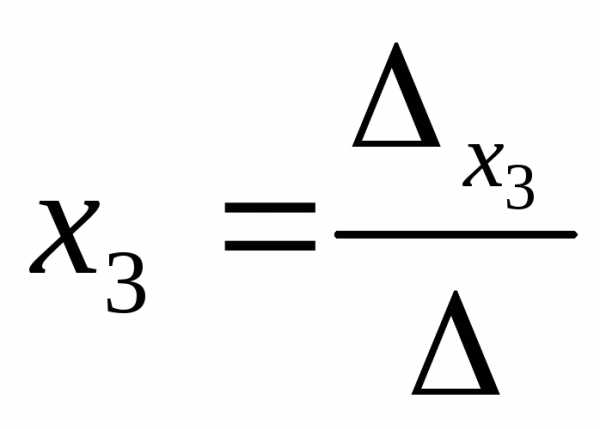 =
=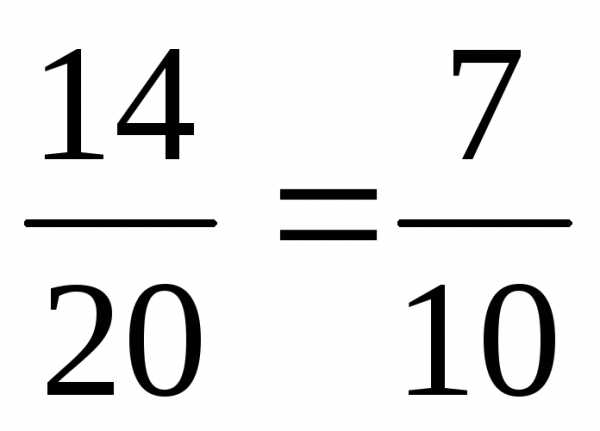 .
.
Ответ: 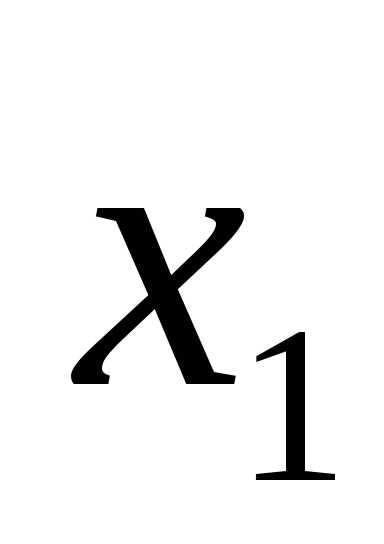 =
=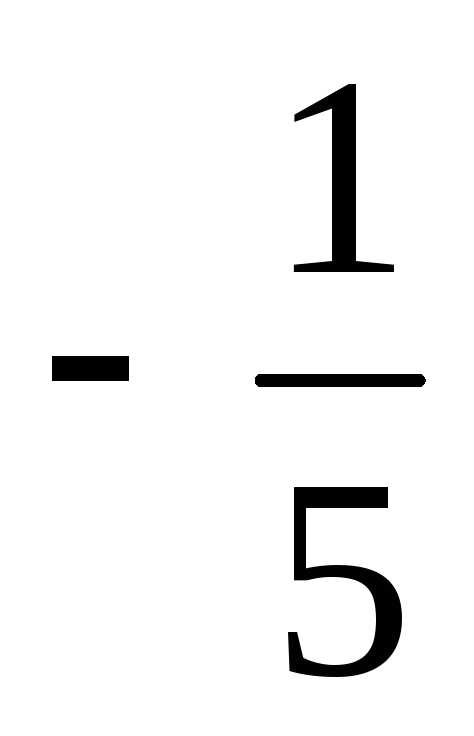 ,
, 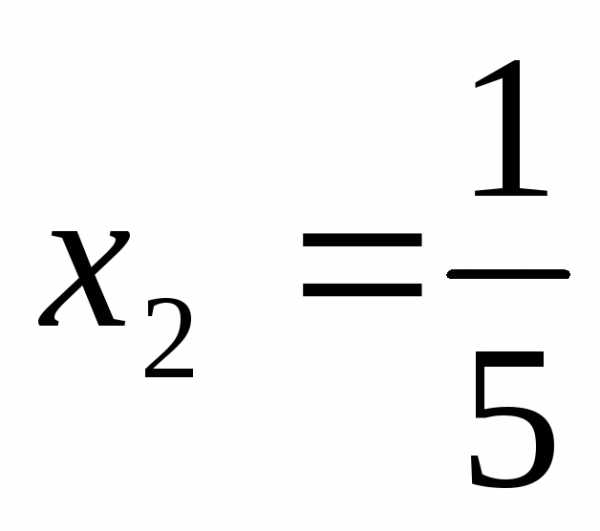 ,
,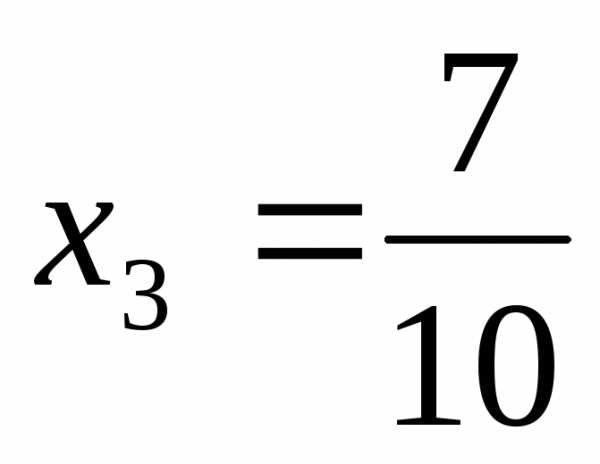 .
.
Решение систем линейных уравнений методом Гаусса
Пусть дана система линейных уравнений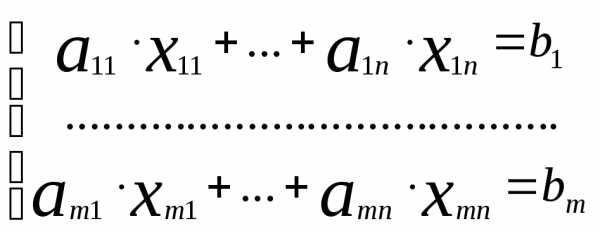 .
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
.
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
Если ранг основной матрицы системы меньше ранга расширенной матрицы r(A)<r(АВ), то система несовместна. Еслиr(A)=r(АВ)=n, гдеn-число неизвестных, то система совместна и определена. Еслиr(A)=r(АВ)<n, гдеn-число неизвестных, то система совместна и неопределенна.
Записываем систему линейных уравнений из полученной ступенчатой матрицы. Определяем базисные и свободные переменные, и выражая базисные переменные через свободные получаем решение системы.
Пример 4.2
Решить систему линейных уравнений: 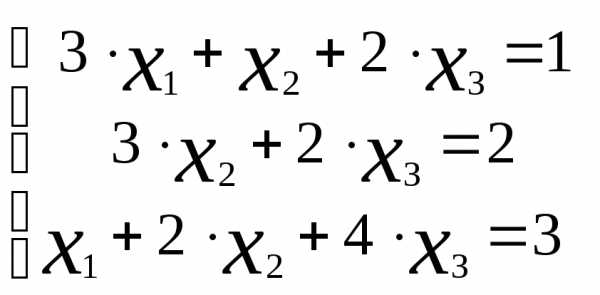 методом Гаусса.
методом Гаусса.
Решение.
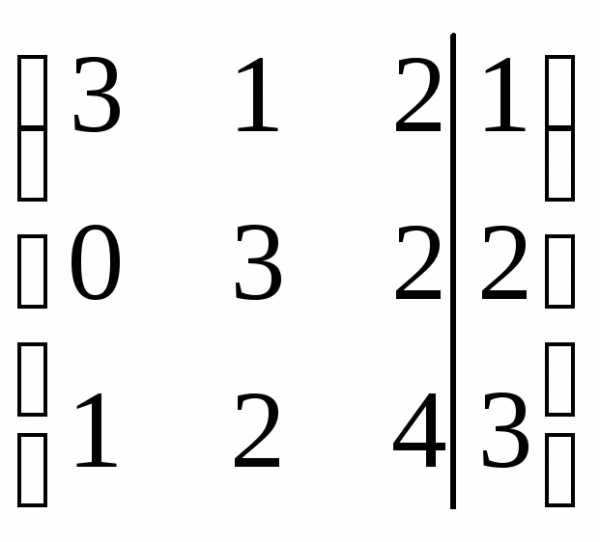

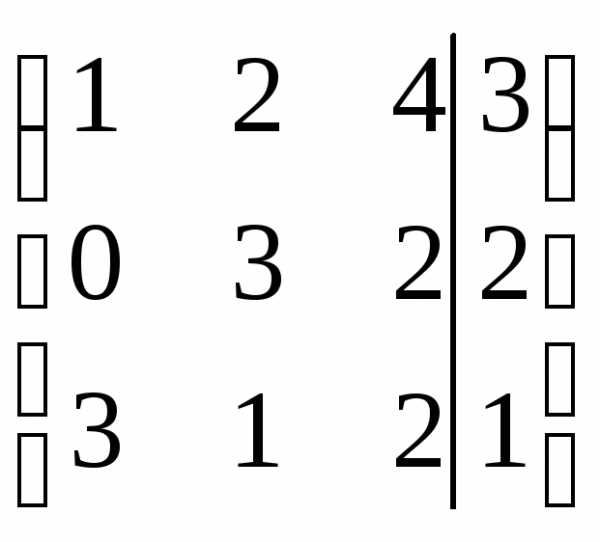
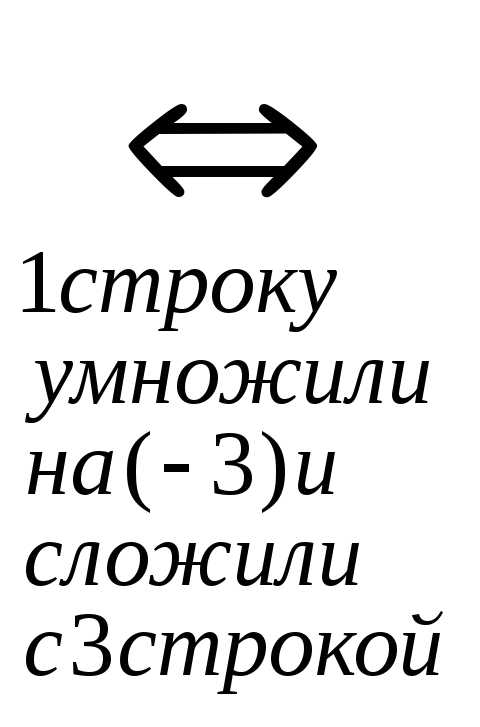

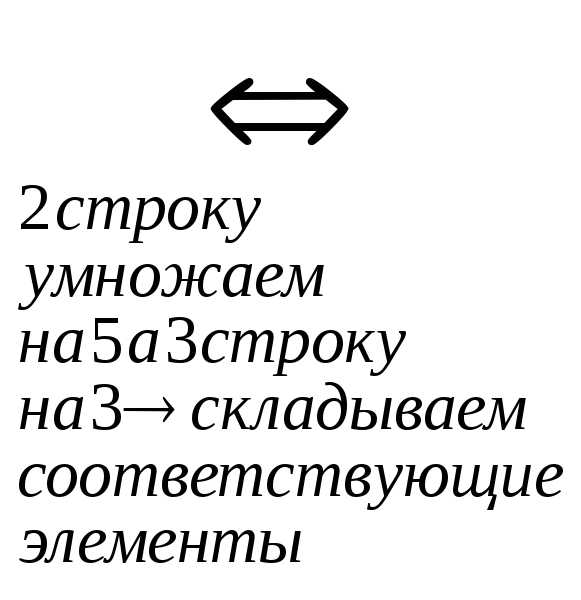
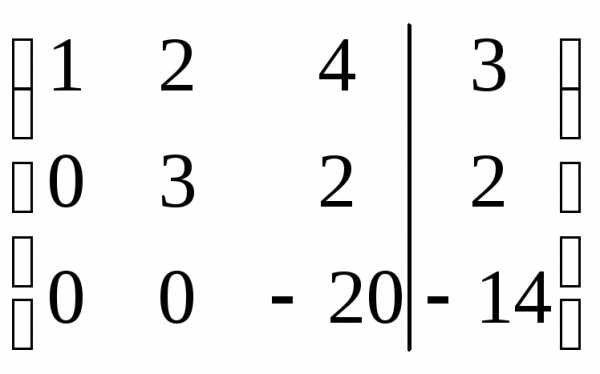
r(A)=r(АВ)=n система совместна и определена.
система совместна и определена.
Отсюда, запишем эквивалентную систему
уравнений, имеем: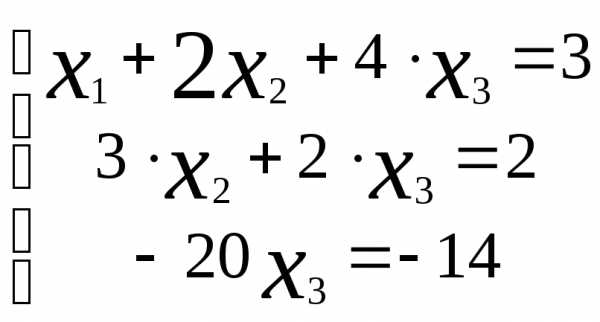
Решая её, получаем: 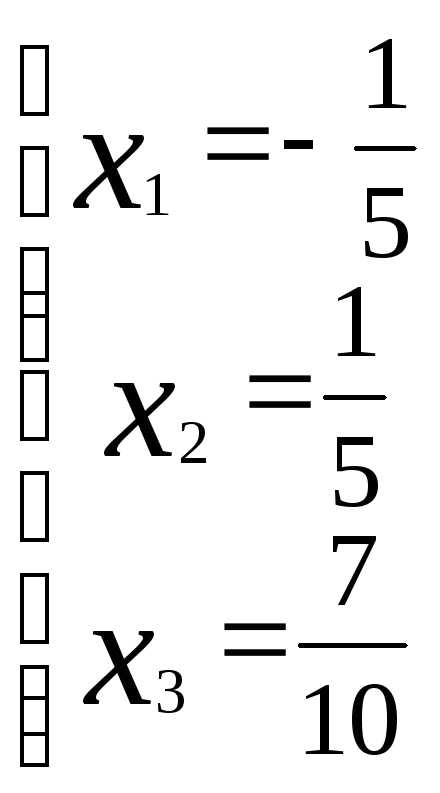
Ответ: 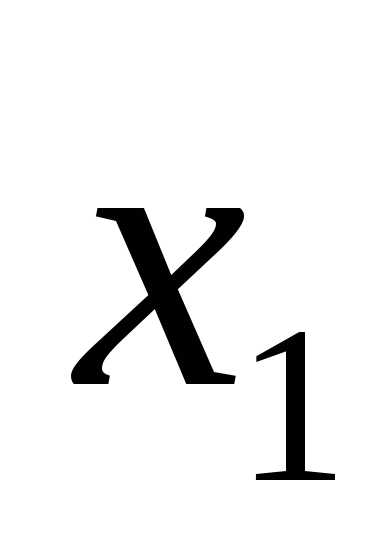 =
=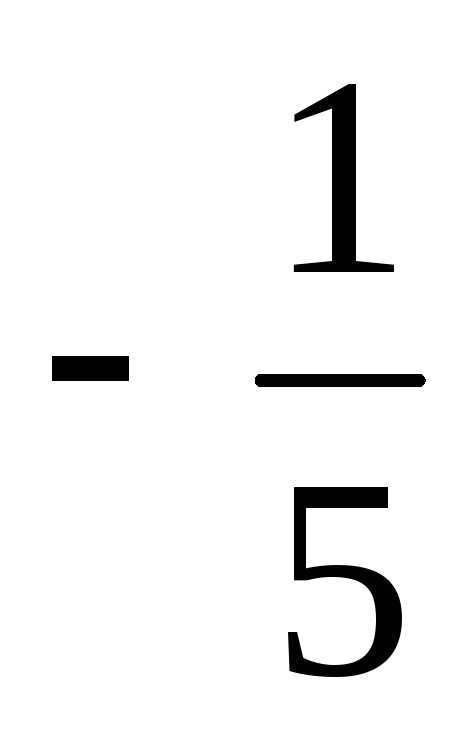 ,
, 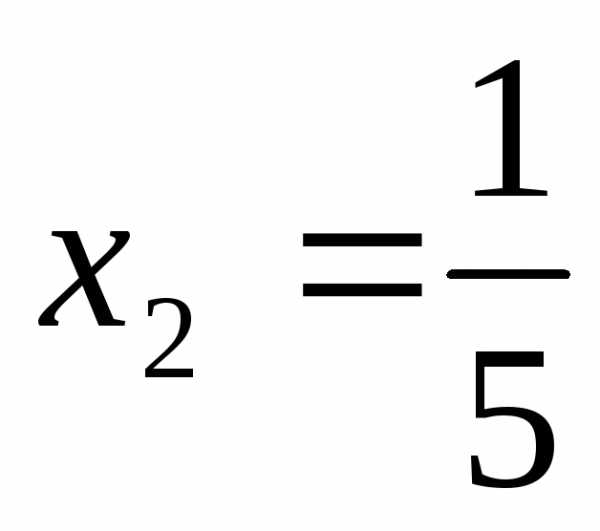 ,
,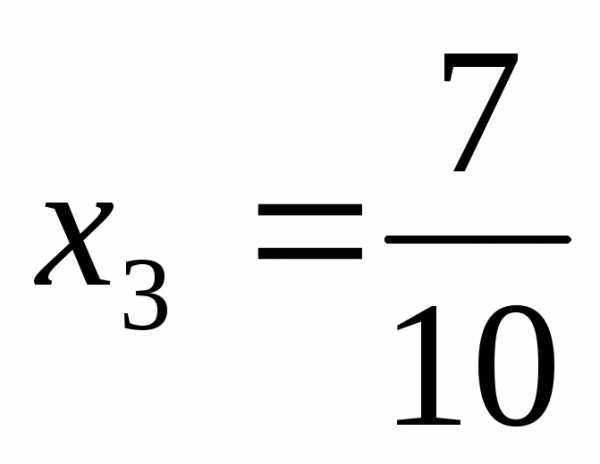 .
.
Пример 4.3
Найти общее решение системы: 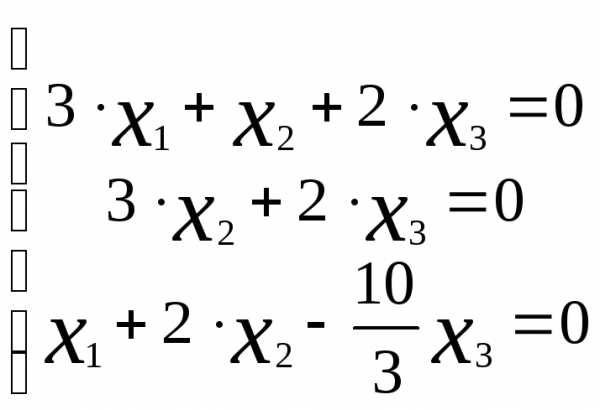 .
.
Решение.
Составим матрицу системы: А=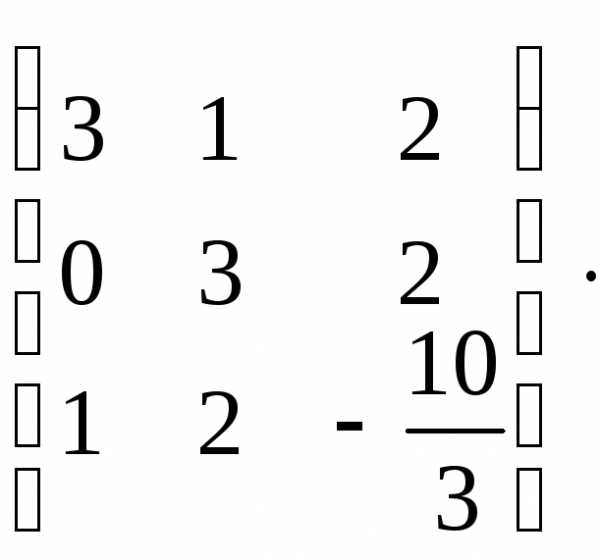
Приведем её к треугольному виду:
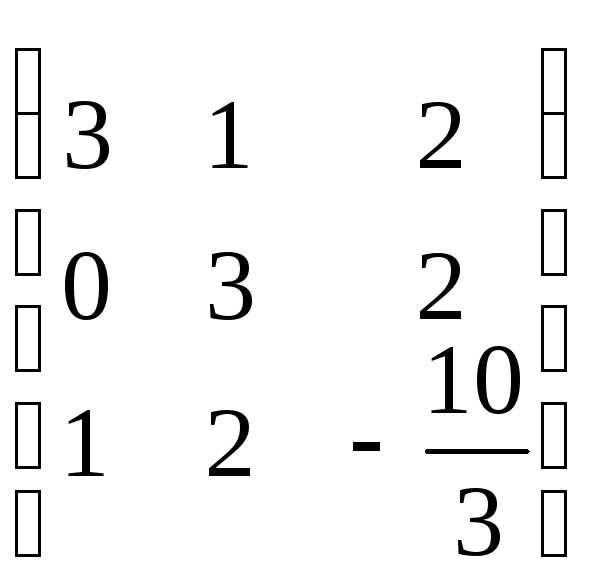

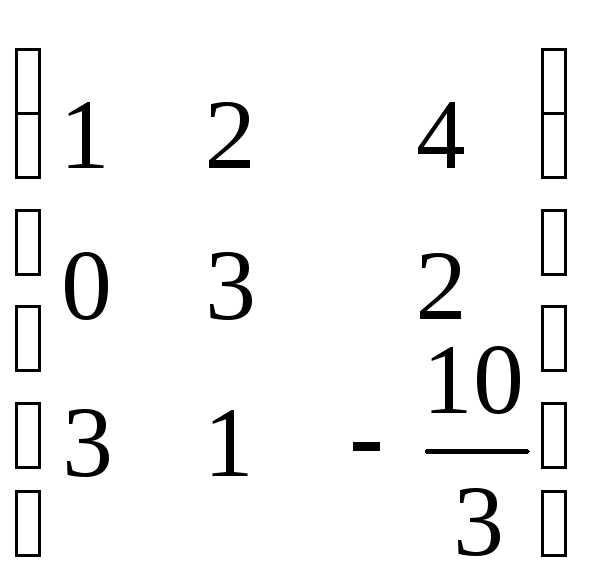
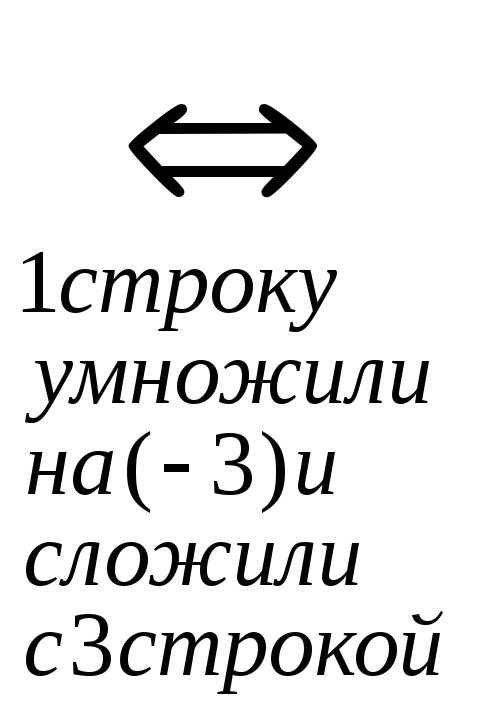
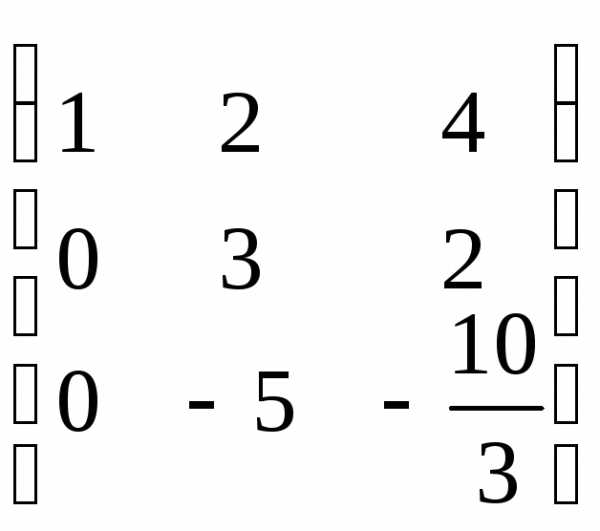
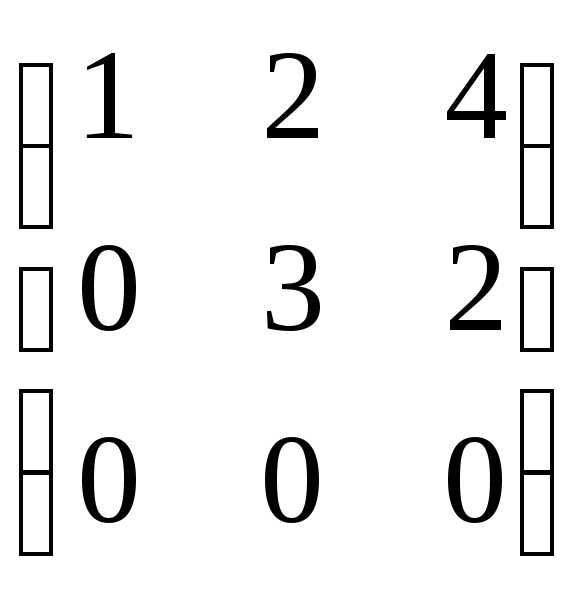
r(A)=2. Запишем
эквивалентную систему уравнений:
Примем за базисные переменные 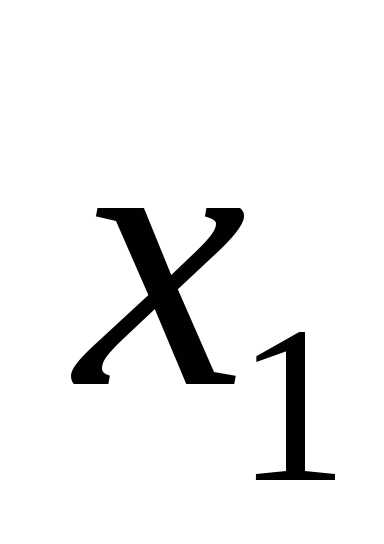 и
и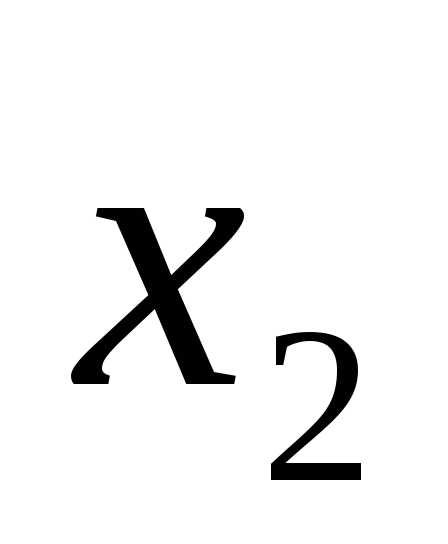 ,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это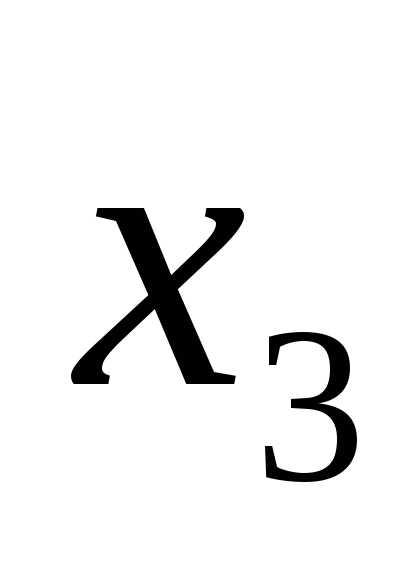 .
.
Выразим базисные переменные через
свободные: 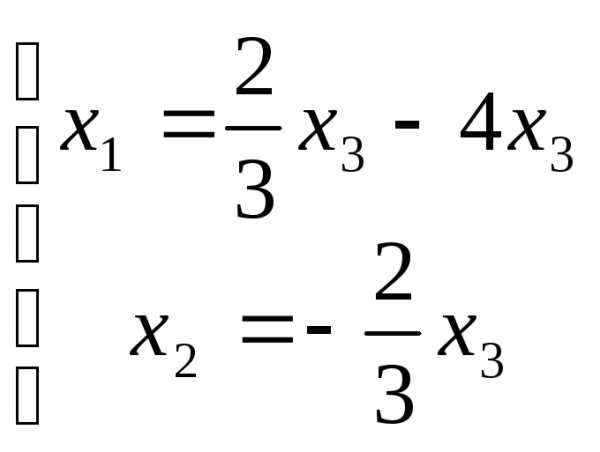

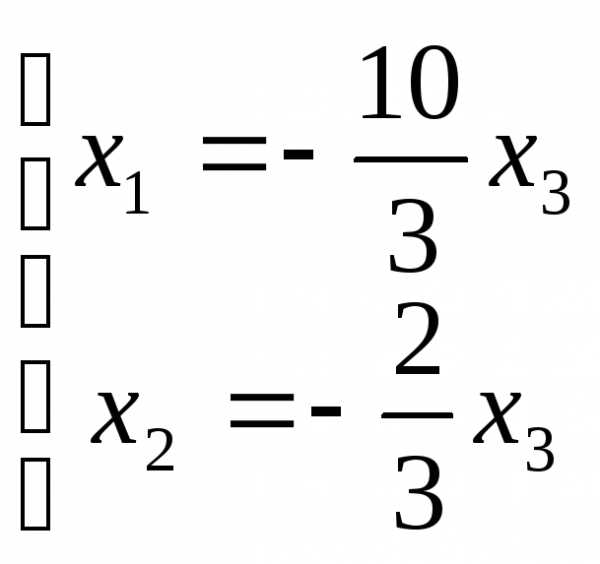 .
Обозначая свободную переменную:
.
Обозначая свободную переменную: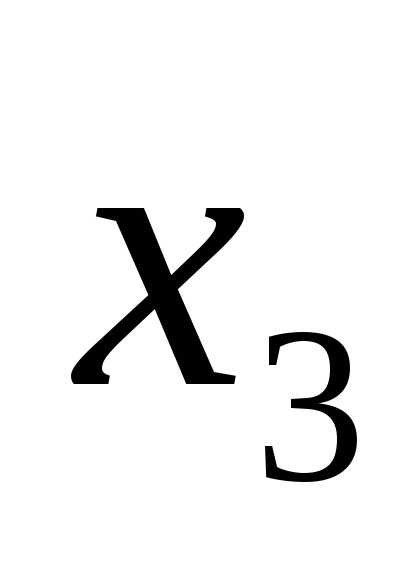 =
=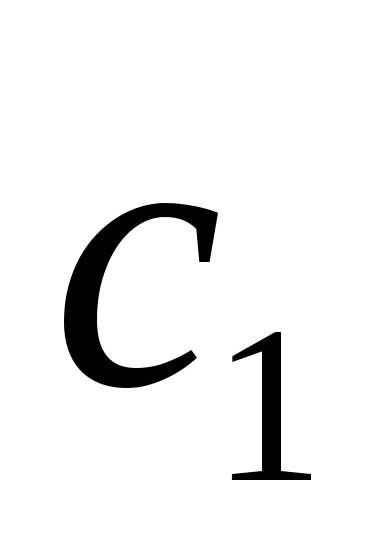 ,
получаем общее решение в виде:
,
получаем общее решение в виде: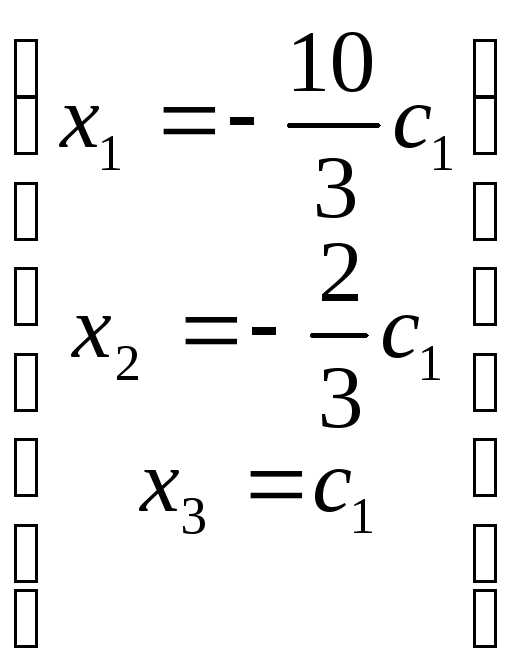
Пример 4.4
Найти общее решение системы: 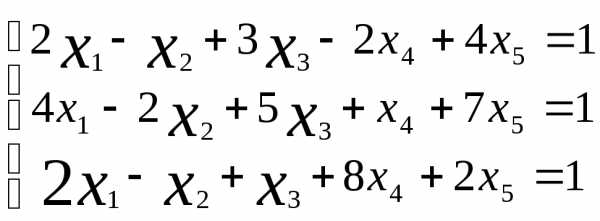
Решение.
Приведем расширенную матрицу системы к ступенчатому виду:
АВ= 


r(A)=r(AВ)=2<n, гдеn-число неизвестных, то система совместная и неопределенная. Запишем эквивалентную систему уравнений:
Примем за базисные переменные 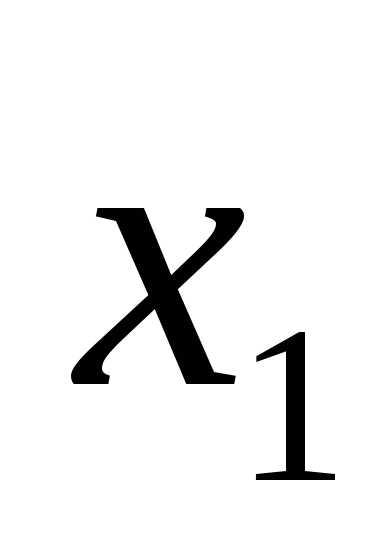 и
и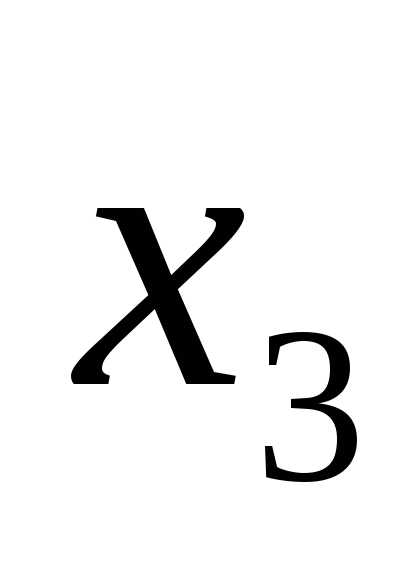 ,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит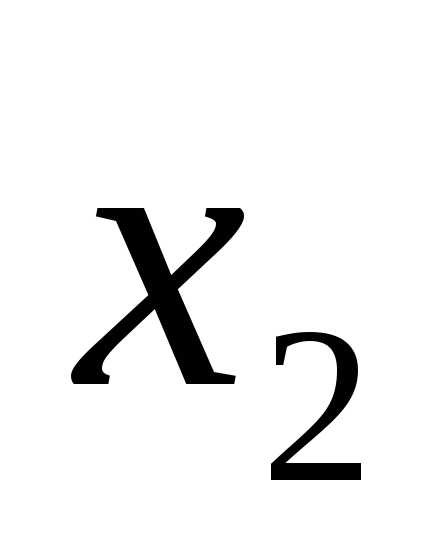 ,
, -свободные
переменные.
-свободные
переменные.
Выразим базисные переменные через
свободные: 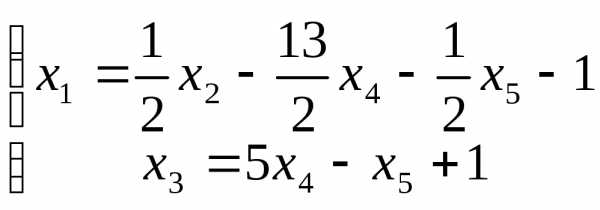 Обозначая свободную переменную:
Обозначая свободную переменную: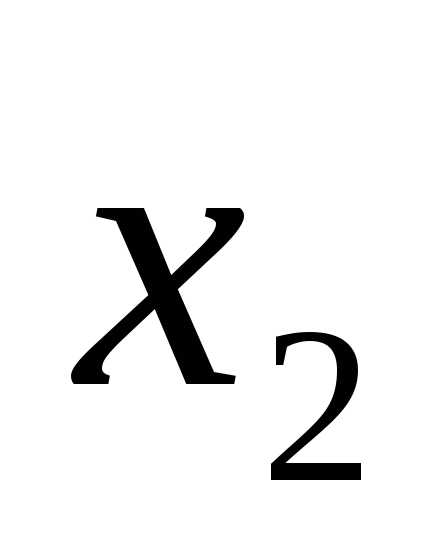 =
=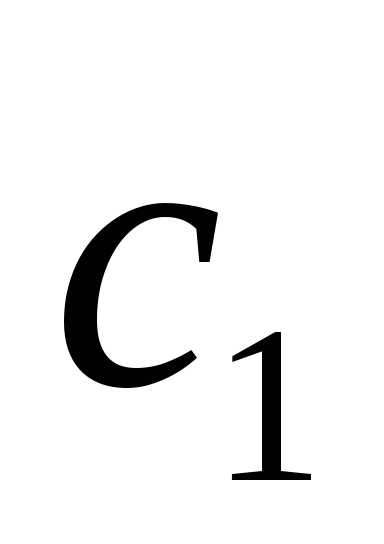 ,
,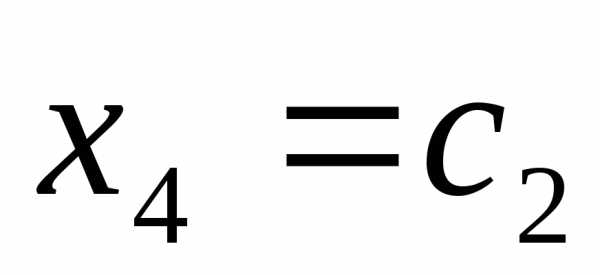 ,
,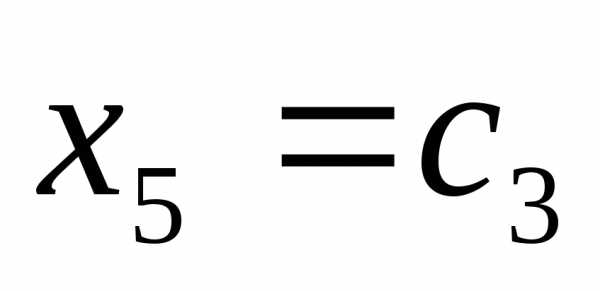 получаем
общее решение в виде:
получаем
общее решение в виде: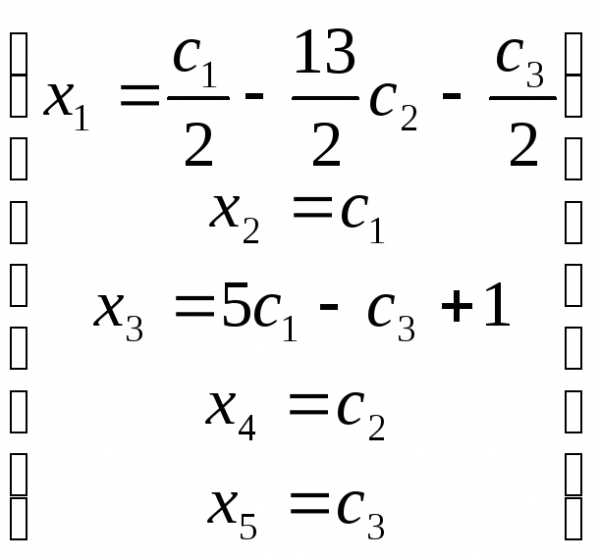 .
.
studfiles.net
Лекция 7 — Обратная матрица и ее построение. Свойства обратных матриц. Решение матричных уравнений.
Страница 1 из 3
Обратная матрица.
Определим операцию деления матриц как операцию, обратную умножению.
Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е — единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E Þ , i=(1,n), j=(1,n),
eij = 0, i ¹ j,
eij = 1, i = j .
Таким образом, получаем систему уравнений:
,
Решив эту систему, находим элементы матрицы Х.
Пример. Дана матрица А = , найти А-1.
Таким образом, А-1=.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
,
где Мji— дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = , найти А-1.
det A = 4 — 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, А-1=.
grishko.esy.es

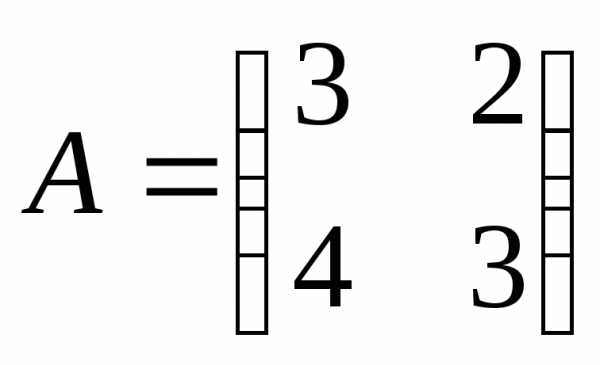 ;
2)
;
2)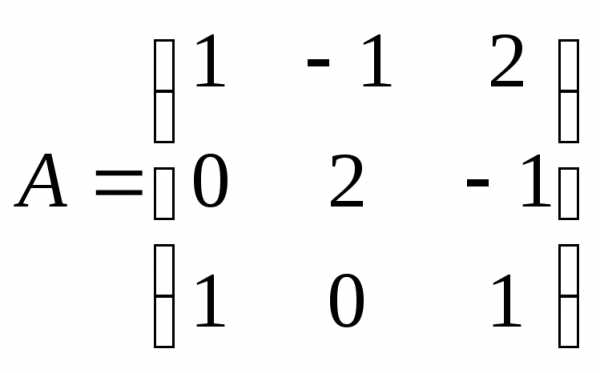 ;
3)
;
3)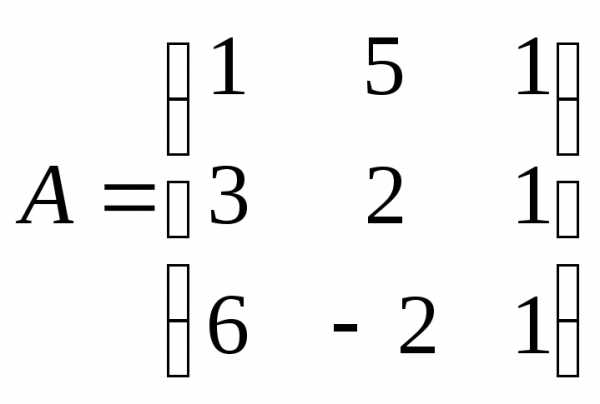 ;
4)
;
4) .
.