Формулы в статистике – формулы по статистике

Формулы по статистике

~ 7 ~

Формулы по статистике

Тема 1: Группировка статистических данных

Определение числа групп (если группи-ка по непрер. приз-ку или дискрет. со многими знач-ями)

Определение величины равного интервала:

Тема 2: Абсолютные и относительные величины

Относительные величины:

1) относит. вел-на структуры:

2) относит. вел-на планового задания:

3) относит. вел-на выполнения плана:

4) относит. вел-на динамики или темп роста:

5) относит. вел-на сравнения

6) относит. вел-на интенсивности (пример: фондоотдача = объем/стоимость (один год))

Тема 3: Средние величины и показатели вариации

Средняя арифметическая

простая:

взвешенная:

Средняя гармоническая

простая:

взвешенная: , сумма значений признака по группе

Свойства средн. арифметической:

1. если каждую вари-ту х умен-ть или увел-ть на одно и то же число, то ср. вел-на умен-ется или увел-ется на это же число;

2. если каждую вари-ту х умен-ть или увел-ть в одно и то же число раз, то ср. вел-на умен-ется или увел-ется в одно и то же число раз;

3. если каждую частоту f умен-ть или увел-ть в одно и то же число раз, то ср. вел-на не изменится.

Ср. вел-на зависит от вар-ты х и структуры совок-сти, кот. харак-ется долями d.

Ряд распределения имеет 3 центра:

1) ср. аримет-кое;

2) мода – наиболее часто встречающаяся вар-та [M₀];

3) медиана – вар-та, стоящая в середине ряда распре-ния. Сначала находят N медианы, кот. равен n/2, если число еди-ц совок-сти n – чётное, или , если число еди-ц совок-сти нечетное [M_e].

Осн. пока-ли вариации:

1) размах вариации:

2) ср. линейное отклонение (ср. арифм-кая из абсолют. откл-ний отдел. значений)

Для несгруппир. данных:

Для сгруппир. данных:

3) ср. квадратическое отклонение (хар-ет ср. абсол. откл-ние вар-ты от ср. вел-ны)

Для несгруппир. данных:

Для сгруппир. данных:

4) Дисперсия – квадрат среднеквадр-ного откл-ния

Для несгруппир. данных:

Для сгруппир. данных:

Общая дисперсия:

(для сгрупп.) (для несгрупп.)

– ср. вел-на резул. приз-ка в сово-сти, — частота (в совокупности!)

Внутригрупповая дисперсия: — кол-во вариант в группе i

Междугрупповая дисперсия: — кол-во вариант в группе i

Правило сложения дисперсий:

Не имеет еди-ц измерения.

5) Коэффициент вариации хар-ет ср. относит. откл-ние вар-ты от ср. вел-ны.

Способ моментов

Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом.

В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.

Способ моментов предполагает следующие действия:

1) Выбирается начало отсчета (из х) – условный нуль (A). Обычно как можно ближе к середине распре-ния.

2) Находятся отклонения вариантов от условного нуля ().

4) Если эти отклонения содержат общий множитель (k), то рассчитанные

отклонения делятся на этот множитель.

Способ моментов:

Средняя:

Дисперсия:

Тема 4: Выборочное наблюдение

Обозначения в теории выборки:

N – числи-ль генер. выборки	n – числи-ль генер. выборки
генер. средняя (оценивают)	– выбор. средняя (рассчитывают)
p – генер. доля (оценивают)	w – выбор. доля (рассчитывают)
P(t) – задаваемый уровень веро-сти

Генер. средняя: с задан. уровнем вероя-сти P(t)

– ошибка выборки для ср. вел-ны

, t – критерий надеж-сти, его вел-на зав-т от уровня задан. вероя-сти P(t)

Если 1) P(t) = 0,683, то t=1; 2) P(t) = 0,954, то t=2 ; 3) P(t) = 0,997, то t=3

– среднеквадр. ошибка выборки

– верна для повторного отбора в выборке.

— для бесповторного отбора

Доказано: с задан. уровнем вероя-сти P(t)

– ошибка выборки для доли

, – среднеквадр. ошибка выборки для доли

–для повторного отбора

— для бесповторного отбора

Тема 5: Ряды динамики

Аналит. пока-ли:

1)

Абсолют. прирост (разница уровней)

(цепной) ; (базисный)

2) Темп роста (отношение уровней)

(цепной) ; (базисный)

3) Темп прироста

(цепной) ; (базисный)

4) Абсолютное значение 1% прироста

(цепной) ; (базисный)

Средние показатели:

1) ср. уровни динам. ряда;

2) ср. аналитич. показ-ли динам. ряда.

Расчет ср. уровня зав-т от вида РД:

а) для интерв. РД с равн. периодами вре-ни – ср. арифмет. простая

б) для интерв. РД с неравн. периодами вре-ни – ср. арифмет. взвешенная

в) для моментных РД с равноотстоящими датами – ср. хронологическая

г) для моментных РД с неравноотстоящими датами

– ср. арифмет. взвешенная

Расчет ср. аналит. показ-лей:

а) ср. абсолют. прирост

б) ср. темп роста

в) ср. темп прироста

Смыкание РД

Для проведения смыкания РД в смыкаемых рядах находится временной момент (дата, период), когда им-ся сведения об изучаемом признаке как в прежних, так и в новых условиях. Рассчитывается коэфф-т, дальнейш. расчеты – по сомкнутом. ряду.

В ходе обработки РД важн. задачей яв-ся выявление основ. тенденции раз-тия явления (тренда) и сглаживание случ. колебаний. Для решения этой задачи сущ-ют особые способы, кот. наз-ют методами выравнивания.

3 основн. способа обработки динамического ряда:

а) укрупнение интервалов РД и расчет средних для кажд. укрупненного интервала;

(переход от менее продолжит.инт-лов к более продолжит. Средняя, рассчитанная по укрупненным инт-лам, позволяет выявить направление и характер (ускорение или замедление) основ. тенденции развития. Средняя рассчитывается по формулам простой средней арифметической.

б) метод скользящей средней;

(вычисл-ся ср. уровень из опред. числа, обычно нечетного, первых по счету уровней ряда. Затем — из такого же числа уровней, но начиная со второго по счету, далее — начиная с третьего и т. д. Т/о, средняя как бы «скользит» по временному ряду от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.

в) аналитическое выравнивание.

Сезонные колебания и волны

Индексами сезонности яв-ся процентные отношения фактических внутригодовых уровней к постоянной или переменной средней. Совокупность этих показателей отражает сезонную волну.

Для выявления сезон. колебаний обычно испо-ют данные за несколько лет, распределенные по месяцам. Для каждого месяца рассчитывается средняя величина уровня, например за 3 года (

), затем из них вычисляется средний уровень для всего ряда (), далее определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда:

где — средний уровень для каждого месяца;

— среднемесячный уровень для всего ряда.

Для наглядного представления сезонной волны индексы сезонности изображают в виде графиков.

Тема 6: Индексы

Индивидуальные индексы:

объема	цен	себестоимости	стоимости	денежных затрат	затрат труда
iq	ip	iz	ipq	iqz	iqt

Общие индексы:

Общий индекс физического объема (как в среднем изм-лось кол-во товаров на рынке)
Абсолютное изм-ние стои-сти за счет изм-ния кол-ва товаров
Общий индекс цен (агрегатный) (как в среднем изм-лись цены на рынке)
Абсолютное изм-ние стои-сти за счет изм-ния цен
Общий индекс товарооборота (стоимости) общ. относит. изме-ния стои-сти товаров на рынке
Общ. абсолют. изм-ние стои-сти товаров на рынке
Взаимосвязь индексов	Ipq = Ip Iq
Общий индекс себестоимости
Общий индекс физич. объема (по себестоимости)
Взаимосвязь между индексами
Общий индекс затрат на производство
Абсолют. сумма экономии, получен. от снижения себестои-сти

Индексы ср. вел-н

К индексам средних величин относятся: индексы переменного состава, постоянного состава и структурных сдвигов.

Индекс постоянного (фиксированного) состава:

Индекс ФС — это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины

Пример:

Индекс переменного состава:

Индекс ПС – индекс, выражающий соотношение ср. уровней изучаемого яв-ния, относящихся к разным периодам времени.

Пример:

Индекс структурных сдвигов:

Индекс СТР – индекс, харак-щий влияние изменения только структуры изучаемого яв-ния на динамику ср. уровня этого яв-ния.

Пример:

Взаимосвязь индексов:

Тема 7: Статистическое изучение связей между признаками

Уравнение регрессии выражает ср. вел-ну рез. признака как ф-цию факт. признака.

Уравнение регрессии в общем виде:

Уравнение регрессии – линия, вокруг кот. группируются точки корр. поля.

Прежде чем определить уравнение регрессии нужно определить его форму (линейная, парабола, гипербола, логарифм). Чаще всего используется линейная форма связи (для парной корреляции (1 рез. и 1 факт)):

– теор. зна-ние рез. приз-ка; – факт. признак; – параметры ур. регрессии.

Чаще эти параметры ищут испо-зуя метод наименьших квадратов:

Для линейн. формы:

Далее получаем следующую систему

Проверка правильности расчета. Для этого в ур. подставляют вместо , вместо (средняя).

Если получается тождество, то уравнение рассчи-но верно.

Основные показатели тесноты связи между признаками:

1) линейный коэффициент корреляции – среднее из произведений

среднеквадратичное отклонение факт. признаков

Чем ближе к 1 или -1, тем теснее связь между признаками.

2) эмпирическое коррел. отношение (см.тему ср. величины)

(коэф. детерминации) , – межгруппов. дисперсия, — общая дисперсия

Чем ближе к 1 или -1, тем теснее связь между признаками.

3) коэффициент рангов Спирмена

Каждой единице совокупности в порядке возраст. значений присваивают номер, кот. наз-ют рангом.

f – разность. рез. и факт. признаков (вариант и частот)

studfiles.net

5.Основные формулы социально-экономической статистики статистика населения

Средняя численность населения (для моментного ряда с равноотстоящими уровнями):

Если есть данные за два момента времени, то

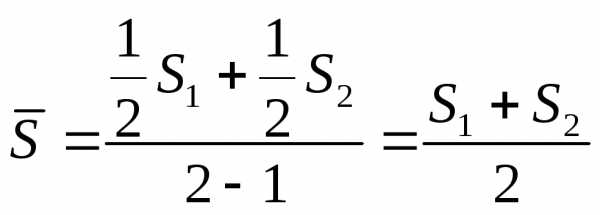
Для моментного ряда с неравными интервалами:

где S — полусумма двух соседних уровней; t — расстояние между уровнями.

Коэффициент рождаемости

Коэффициент смертности

Коэффициент естественного прироста

Коэффициент жизнеспособности (коэффициент Покровского):

.

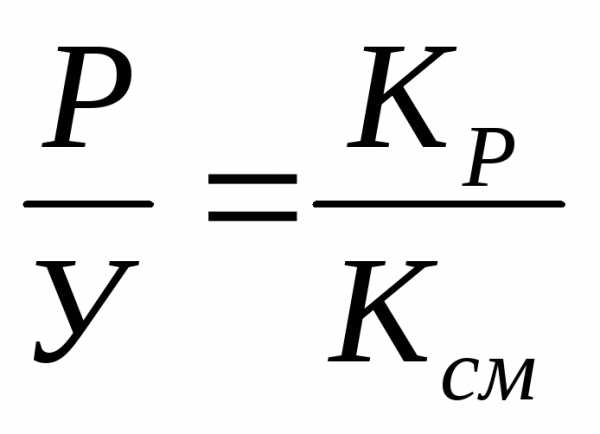Специальный коэффициент рождаемости (коэффи­циент плодовитости, фертильности):

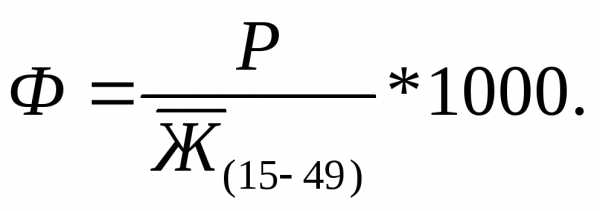
Взаимосвязь между общим и специальным коэффи­циентами рождаемости:

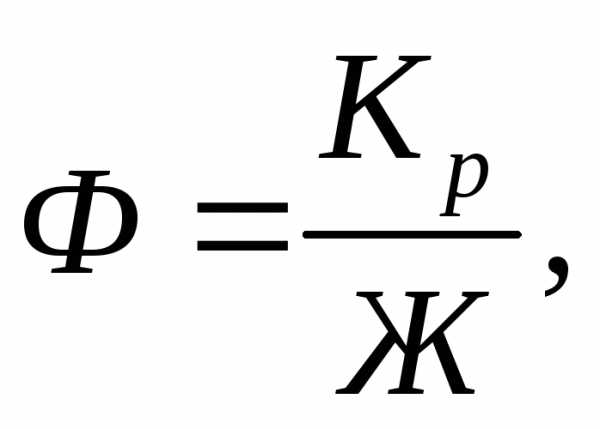
или

К_р= Ф * Ж.

Коэффициент детской смертности (до 1 года):

Коэффициент детской смертности:

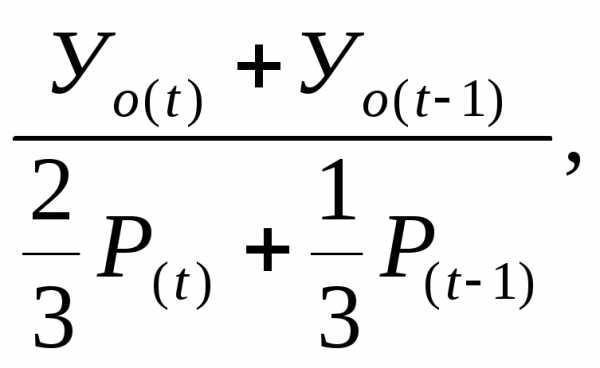
где 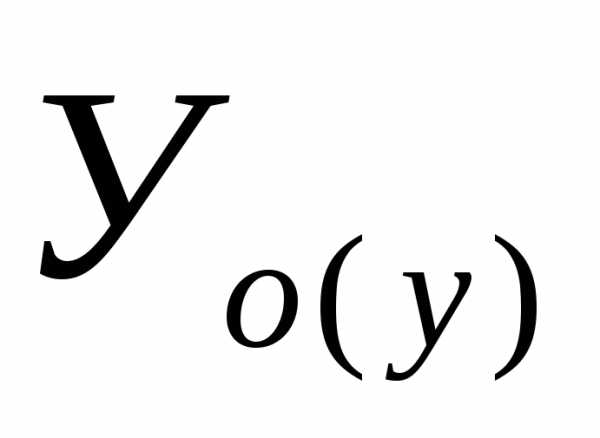— число детей, умерших в возрасте до 1 года из родившихся в данном году;

— число детей, умерших в возрасте до 1 года из родившихся в прошлом году;

— число родившихся в данном году;

— число родившихся в прошлом году.

Коэффициент брачности:

.

Коэффициент разводимости:

Средняя продолжительность предстоящей жизни:

Число умирающих в возрасте X лет:

.

Вероятность умереть в течение года:

.

Вероятность дожить от X лет до (Х+1) года:

.

Число живущих в возрасте X лет:

/

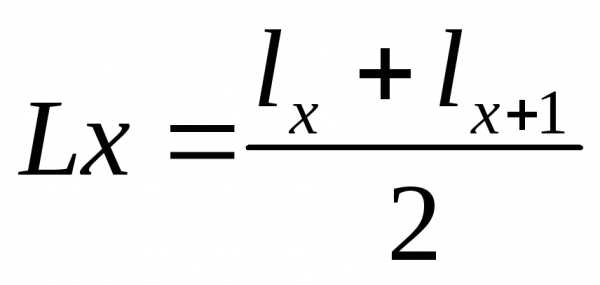Число чел.-лет жизни в возрасте от X лет и старше:

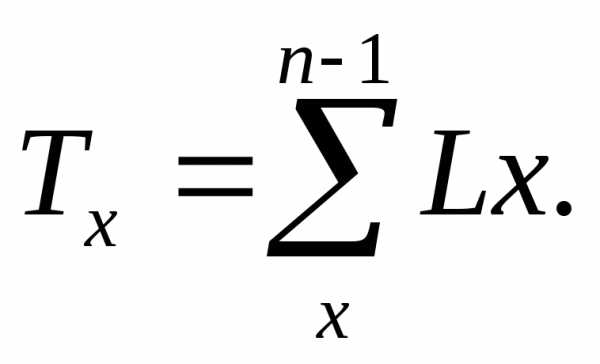
Абсолютный механический прирост:

Коэффициент прибытия:

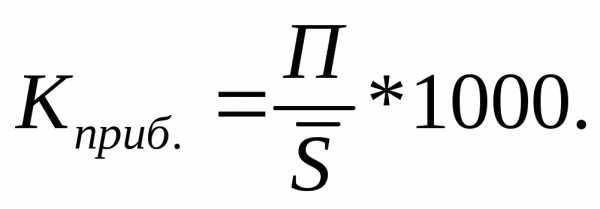
Коэффициент выбытия:

Коэффициент механического прироста:

Общий прирост численности населения:

Коэффициент общего прироста численности населения:

Коэффициент роста:

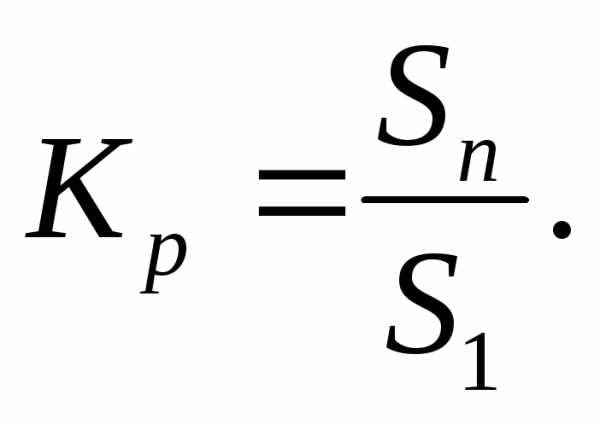
Темп роста:

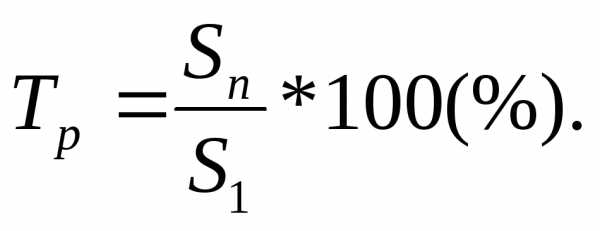
Темп прироста:

Среднегодовой коэффициент роста:

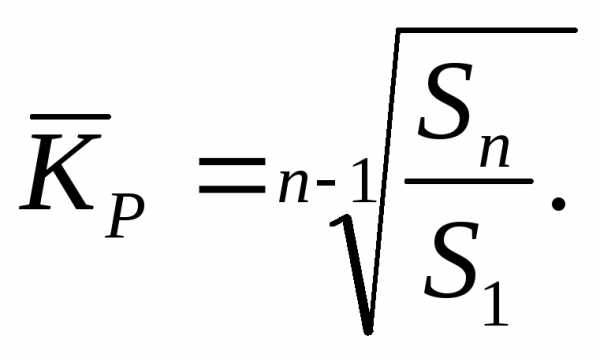
Среднегодовой коэффициент прироста:

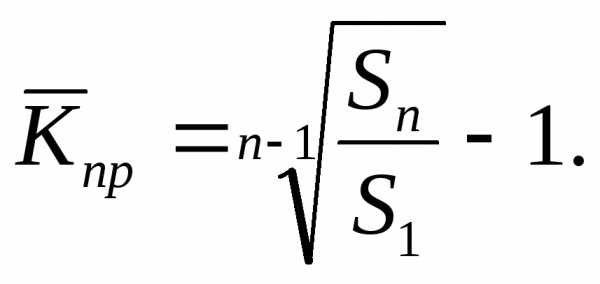
Среднегодовой темп роста:

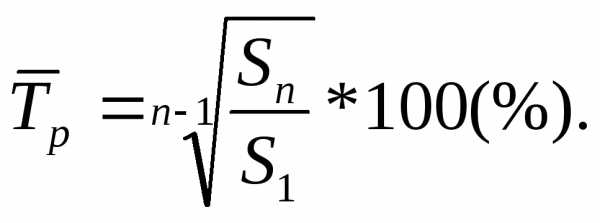
Среднегодовой темп прироста:

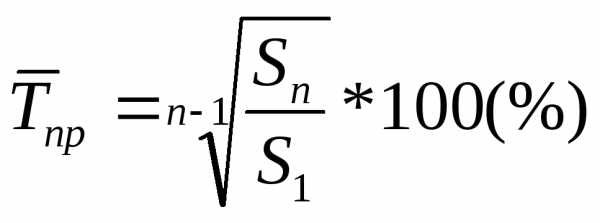
РАСЧЕТ ПЕРСПЕКТИВНОЙ ЧИСЛЕННОСТИ НАСЕЛЕНИЯ

если К в промилле, то

.

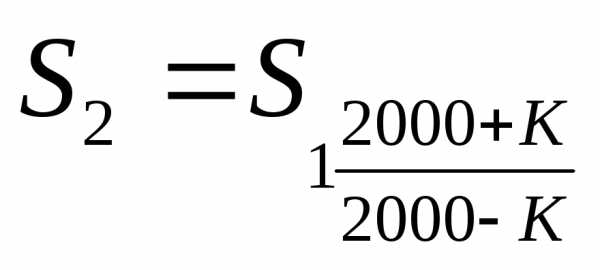Если известна среднегодовая численность населе­ния (или на середину года) и предполагаемый коэффи­циент общего прироста, то

.

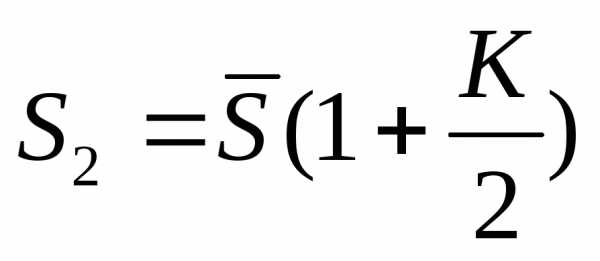Формула Смирнова:

;

где 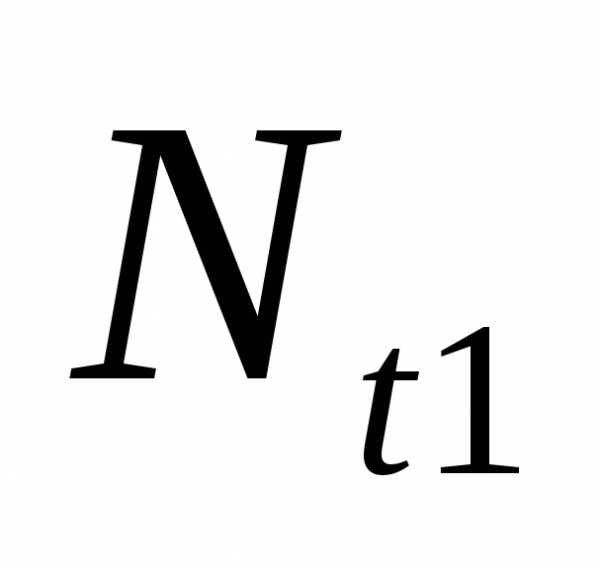— численность населения черезt1лет с начала отсчета;

—численность населения в начале отсчета;

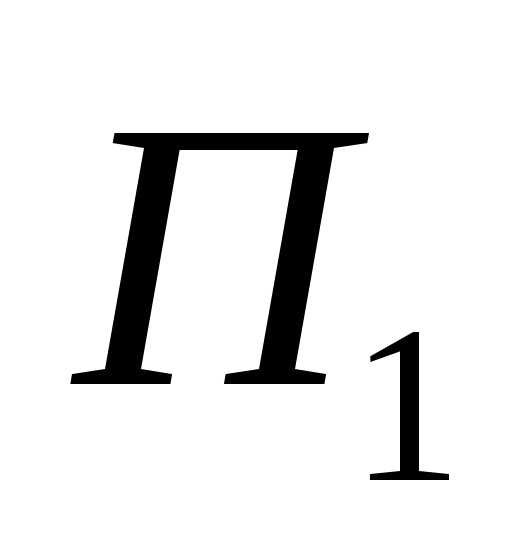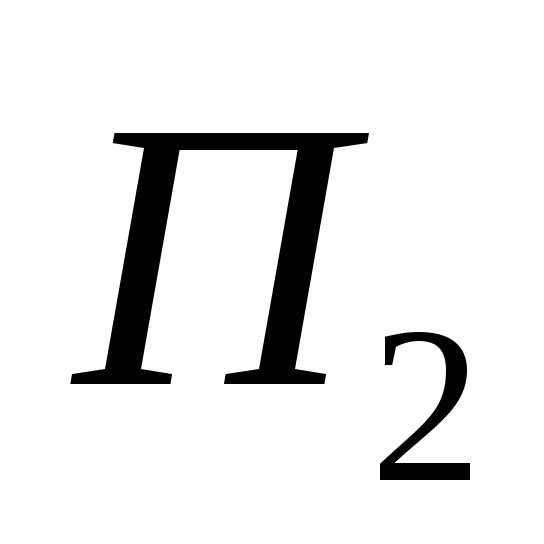—численность населения в конце отсчета;

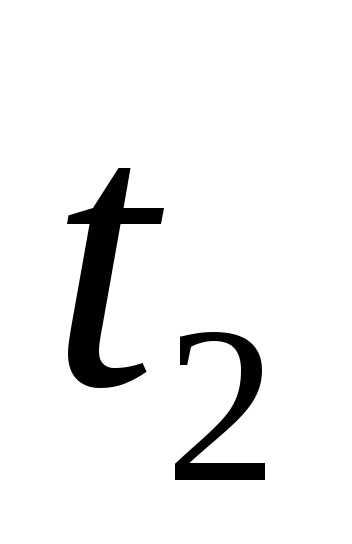—интервал времени в годах между двумя учетами.

Статистика основных фондов

Годовая сумма амортизации:

Годовая норма амортизации:

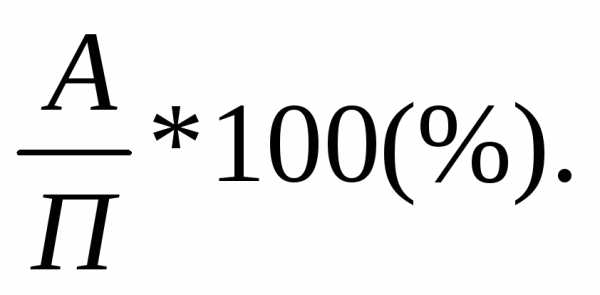
Сумма износа

Полная стоимость — Остаточная стоимость.

Стоимость основных фондов (ОФ) на конец года

ОФ на начало года + Ввод в действие новых ОФ + Капитальный ремонт — Выбытие ОФ — — Амортизация.

Коэффициент обновления:

Коэффициент выбытия:

Коэффициент годности:

Коэффициент износа:

.

Фондоотдача:

Среднегодовая стоимость ОФ:

Фондоемкость:

Фондоемкость:

Фондовооруженность:

Статистика оборотных фондов

Сумма Q авансированных средств (средний остаток оборотных средств):

Коэффициент оборачиваемости:

Коэффициент закрепления оборотных средств:

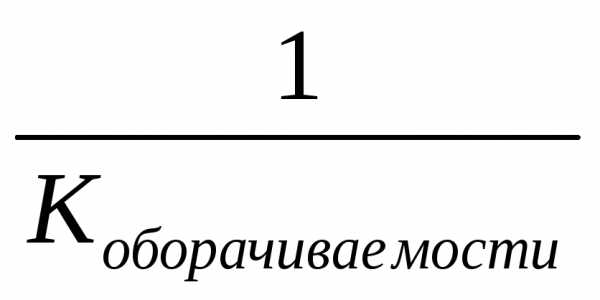
Средняя продолжительность одного оборота :

или

Средние показатели скорости обращения оборотных фондов для нескольких предприятий:

;

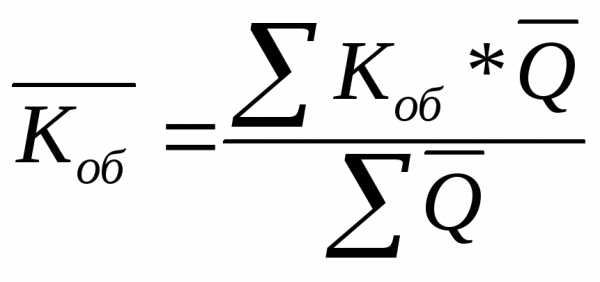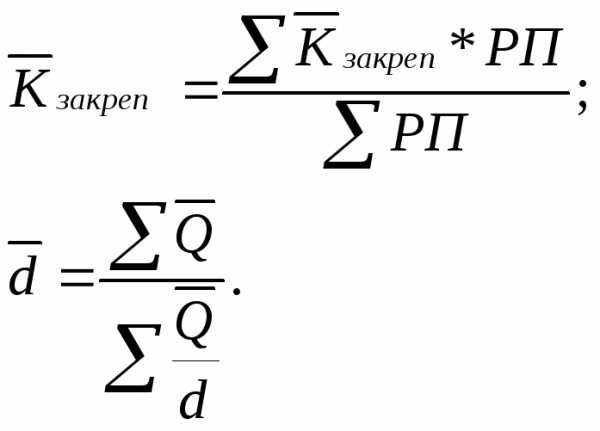
studfiles.net

Формулы по статистике

_1. Количество единиц с одинаковым значением признака обозначается f и называется частота. Очевидно, что суммируя число всех величин с одинаковыми значениями признака, получаем N, то есть

2. Индекс динамики

,

3. темп изменения динамики

.

4. Индекс планового задания

,

5. индекс выполнения плана,

.

6. Индекс структуры (доля)

7.Индекс координации

.

8. Индекс сравнения

,

9. Индекс интенсивности

.

10. Средней арифметической величиной

.

11. взвешенной арифметической средней

12.квадратической средней величиной. Ее формула следующая:

.

13. средней кубической величине, имеющей вид:

.

14. геометрическую среднюю величину, имеющую следующий вид:

.

15. формула средней гармонической взвешенной

16. формула средней гармонической простой Error: Reference source not found:

.

17.степенных средних

=.

18. правилом мажорантности средних:

≤≤≤≤.

19. внешнеторгового оборота

_20. Сальдо внешней торговли

_21. коэффициентом покрытия импорта экспортом, определяемый по формуле Error: Reference source not found:

.

22. Оборот мировой торговли (ОМТ)

23. сальдо мировой торговли (СМТ),

24. доля отдельных стран или групп стран в мировой торговле определяется по формуле Error: Reference source not found:

, или ,

25. доля отдельных стран в экспорте отдельных товаров

26. доля экспорта отдельной страны в валовом национальном продукте (ВНП)

27. коэффициент зависимости национальной экономики от импорта

28. доля экспорта в производстве отдельных видов продукции определяется по формуле Error: Reference source not found: ,

где Q_ij – объем производства i-го товара j-й страны.

29. доля импорта в потреблении отдельных видов продукции показывает зависимость экономики страны от импорта отдельных товаров, определяется по формуле : ,

где И_ij – объем импорта i-го товара j-й страны; P_ij – объем потребления i-го товара j-й страны.

30. коэффициент относительной экспортной специализации:

,

31. коэффициент диверсификации определяется по формуле Error: Reference source not found:

,

32. предельную ошибку выборки

= t,

t – коэффициент доверия

– средняя ошибка выборки

33. повторной выборки по формуле (средняя ошибка выборки)

=

34. бесповторной – по формуле

=

35. доверительный интервал для среднего значения

36. доверительный интервал для доли какого-либо признака

37. формуле Стерждесса

38. длину интервала

где X_мax и X_min — максимальное и минимальное значения в совокупности.

39. нахождения медианы применяется формула:

,

40. точечной модой

где Мо – мода;

Х₀ – нижнее значение модального интервала;

f_Mo – частота в модальном интервале;

f_Mo-1 – частота в предыдущем интервале;

f_Mo+1 – частота в следующем интервале за модальным;

h – величина интервала.

41. размах вариации

42. среднее линейное отклонение Error: Reference source not found:

.

43. среднее квадратическое отклонение для ранжированного ряда

44. среднее квадратическое отклонение для интервального ряда

45. простая дисперсия(для не сгруппированных данных)

46. сгруппированных (взвешенная дисперсия):

47. среднее квартильное расстояние (отклонение),

48. относительный размах вариации

: ;

49. линейный коэффициент вариации:

50. квадратический коэффициент вариации:

51. относительное квартильное расстояние:

52. коэффициент асимметрии

53. К.Пирсон

54. эксцесс

56. находят нормированное (выраженное в σ) отклонение каждого эмпирического значения от средней арифметической:

;

57. вычисляют теоретические частоты m по формуле:

,

58. Число степеней свободы ν определяется по формуле:

ν = k – z – 1

59. Критерий Романовского

60. Критерий Колмогорова

61. Дисперсия доли по формуле

62.формула Пуассона

63. Абсолютное изменение для базисного способа сравнения

_64. Абсолютное изменение для цепного

_65. сумма цепных абсолютных изменений равна последнему базисному изменению, т.е.

.

66. Относительное изменение для базисного способа сравнения

_67. Относительное изменение для цепного

_68. произведение цепных относительных изменений равно последнему базисному изменению, то есть

.

69. Темп изменения(темп прироста)

_70. Базисное среднее абсолютное изменение

^Б =

71. цепное среднее абсолютное изменение

^Ц =

72. аналитическое выравнивание сумма двух

составляющих

_73. Прямая линия

_74. Гипербола

75. Показательная

_76. Степенная

77. сопоставление суммы квадратов отклонений эмпирических уровней от теоретической (остатки)

_78. метод наименьших квадратов (МНК)

_79. критерий Фишера

80. ошибка аппроксимации

81. Коэффициент корреляции знаков (Фехнера)

84. коэффициентом ковариации

85.Линейный коэффициент корреляции

86. критерия Стьюдента

87. Коэффициент эластичности

88. коэффициента автокорреляции:

89. формула Пааше

90. индекс стоимости экспорта (импорта):

;

91. формула Ласпейреса:

,

92. Особенностью расчета индексов средних цен

93. индекс условий торговли

94. Среднее время декларирования товаров

95. сумма модулей абсолютных изменений долей

96. ( индекс Лузмора-Хэнби)

97. ( коэффициент Герфиндаля)

98. Обратная индексу Герфиндаля величина – это эффективное число групп

E = 1/H.

99. индекс Грофмана

100. индекс Липхарта

101. Квадратический индекс структурных сдвигов Казинца

102. индекс Галлахера

103. индекс Монро

104. Интегральный коэффициент структурных сдвигов Гатева

105. Индекс Рябцева

106. Индекс структурных различий Салаи

107. Линейный коэффициент изменения (различия) рангов долей Для четного

для нечетного

studfiles.net

просто о сложных формулах / Stepik.org corporate blog / Habr

Статистика вокруг нас

Статистика и анализ данных пронизывают практически любую современную область знаний. Все сложнее становится провести границу между современной биологией, математикой и информатикой. Экономические исследования и регрессионный анализ уже практически неотделимы друг от друга. Один из известных методов проверки распределения на нормальность — критерий Колмогорова-Смирнова. А вы знали, что именно Колмогоров внес огромный вклад в развитие математической лингвистики?

Еще будучи студентом психологического факультета СПбГУ, я заинтересовался когнитивной психологией. Кстати, Иммануил Кант не считал психологию наукой, так как не видел возможности применять в ней математические методы. Мои текущие исследования посвящены моделированию психических процессов, и я надеюсь, что такие направления в современной когнитивной психологии, как вычислительные и коннективисткие модели, смягчили бы его отношение!

Конечно, статистика применяется далеко за пределами научных лабораторий: в рекламе, маркетинге, бизнесе, медицине, образовании и т.д. Но, что самое интересное, базовые знания анализа данных крайне полезны и в повседневной жизни. Например, думаю, все вы знакомы с понятием среднего арифметического. Среднее значение очень часто используется в СМИ при обсуждении различных социально-экономических показателей — доходов, уровня безработицы и т.д. В 2005 году британские СМИ писали о том, что средний уровень дохода населения не только не возрос, но снизился на 0,2 % по сравнению с предыдущим годом. Мелькали заголовки «Доходы населения снизились впервые с 1990 года». Некоторые политики даже использовали этот факт, критикуя действующее правительство. Однако, важно понимать, что среднее арифметическое — хороший показатель, когда наш признак имеет симметричное распределение (богатых столько же, сколько бедных). Реальное же распределение доходов имеет скорее следующий вид:

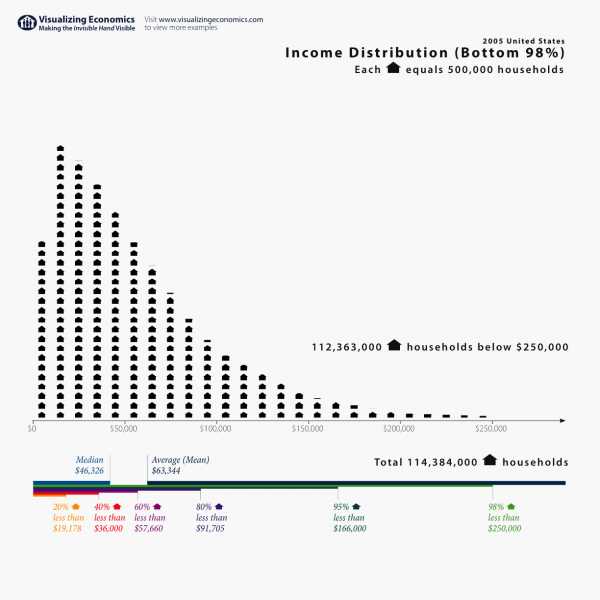
Распределение имеет явно выраженную асимметрию: очень состоятельных людей заметно меньше, чем представителей среднего класса. Это приводит к тому, что в данном случае банкротство одного из миллионеров может значительно повлиять на этот показатель. Гораздо информативнее использовать значение медианы для описания таких данных. Медиана — это значение зарплаты, которое находится в самой середине распределения доходов (50% всех наблюдений меньше медианы, 50% — больше). И, как ни удивительно, медиана дохода в 2005 году в Великобритании, в отличие от среднего значения, продолжила свой рост. Таким образом, если вы знаете о различных типах распределения и различных мерах центральной тенденции (среднее и медиана), то вас не так просто ввести в заблуждение в таких случаях, как описаны в примере.

Черный ящик статистического анализа

Как мы уже выяснили, чем бы вы ни планировали заниматься, вероятность столкнуться с курсом «математическая статистика в вашей области» постепенно приближается к единице. Однако, часто занятия по введению в статистику не вызывают восторга у студентов нетехнических факультетов. Через несколько занятий выясняется, что такие базовые понятия, как, например, корреляция представляют собой нечто следующее:

И, отчаявшись досконально разобраться с происхождением этих сумм и квадратных корней, студент может начать воспринимать статистику следующим образом: «если r > 0, то положительная связь, а если меньше 0, то отрицательная»; «если p уровень значимости меньше 0.05 — то хорошо, если от 0.05 до 0.1 — то не очень хорошо, а если больше 0.1 — то плохо». Помогая студентам готовиться к экзамену, не раз сталкивался с такими заклинаниями! Также, разумеется, никто не рассчитывает все эти показатели вручную, и используя, например, SPSS, можно за секунду загуглить пошаговую инструкцию «как сравнить два средних».

1. Жмем сюда
2. Снимаем/ставим галочки тут
3. p < 0.05 —> profit

Статистический анализ начинает напоминать черный ящик: на вход подаются данные, на выход — таблица основных результатов и значение p-уровня значимости (p-value), который и расставит все точки над i.

О чем нам, собственно, говорит p-value?

Предположим, мы решили выяснить, существует ли взаимосвязь между пристрастием к кровавым компьютерным играм и агрессивностью в реальной жизни. Для этого были случайным образом сформированы две группы школьников по 100 человек в каждой (1 группа — фанаты стрелялок, вторая группа — не играющие в компьютерные игры). В качестве показателя агрессивности выступает, например, число драк со сверстниками. В нашем воображаемом исследовании оказалось, что группа школьников-игроманов действительно заметно чаще конфликтует с товарищами. Но как нам выяснить, насколько статистически достоверны полученные различия? Может быть, мы получили наблюдаемую разницу совершенно случайно? Для ответа на эти вопросы и используется значение p-уровня значимости (p-value) — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет. Иными словами, это вероятность получить такие или еще более сильные различия между нашими группами, при условии, что, на самом деле, компьютерные игры никак не влияют на агрессивность. Звучит не так уж и сложно. Однако, именно этот статистический показатель очень часто интерпретируется неправильно.

А теперь несколько примеров про p-value

Итак, мы сравнили две группы школьников между собой по уровню агрессивности при помощи стандартного t-теста (или непараметрического критерия Хи — квадрат более уместного в данной ситуации) и получили, что заветный p-уровень значимости меньше 0.05 (например 0.04). Но о чем в действительности говорит нам полученное значение p-уровня значимости? Итак, если p-value — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет, то какое, на ваш взгляд, верноеутверждение:

1. Компьютерные игры — причина агрессивного поведения с вероятностью 96%.
2. Вероятность того, что агрессивность и компьютерные игры не связаны, равна 0.04.
3. Если бы мы получили p-уровень значимости больше, чем 0.05, это означало бы, что агрессивность и компьютерные игры никак не связаны между собой.
4. Вероятность случайно получить такие различия равняется 0.04.
5. Все утверждения неверны.

Если вы выбрали пятый вариант, то абсолютно правы! Но, как показывают многочисленные исследования, даже люди со значительным опытом в анализе данных часто некорректно интерпретируют значение p-value (например, можно посмотреть эту интересную статью).

Давайте разберем все ответы по порядку:

1. Первое утверждение — пример ошибки корреляции: факт значимой взаимосвязи двух переменных ничего не говорит нам о причинах и следствиях. Может быть, это более агрессивные люди предпочитают проводить время за компьютерными играми, а вовсе не компьютерные игры делают людей агрессивнее.
2. Это уже более интересное утверждение. Все дело в том, что мы изначально принимаем за данное, что никаких различий на самом деле нет. И, держа это в уме как факт, рассчитываем значение p-value. Поэтому правильная интерпретация: «Если предположить, что агрессивность и компьютерные игры никак не связаны, то вероятность получить такие или еще более выраженные различия составила 0.04».
3. А что делать, если мы получили незначимые различия? Значит ли это, что никакой связи между исследуемыми переменными нет? Нет, это означает лишь то, что различия, может быть, и есть, но наши результаты не позволили их обнаружить.
4. Это напрямую связано с самим определением p-value. 0.04 — это вероятность получить такие или еще более экстремальные различия. Оценить вероятность получить именно такие различия, как в нашем эксперименте, в принципе невозможно!

Вот такие подводные камни могут скрываться в интерпретации такого показателя, как p-value. Поэтому очень важно понимать механизмы, заложенные в основании методов анализа и расчета основных статистических показателей.

Онлайн-курс по основам статистики: сложные формулы несложным языком

Сейчас я пишу диссертацию на факультете психологии СПбГУ и преподаю статистику биологам в Институте биоинформатики. Основываясь на курсе читаемых лекций и собственного исследовательского опыта, возникла идея создать онлайн-курс по введению в статистику на русском языке для всех желающих, необязательно биоинформатиков или биологов.

Существует много хороших онлайн-курсов по анализу данных и статистике (например, такой, такой, или такой), но практически все они на английском языке. Надеюсь, что курс будет полезен для тех, кто только знакомится с основами статистики. В нем я стараюсь в максимально доступной форме разобрать основные идеи и методы анализа данных, уделяя особое внимание самой идее статистической проверки гипотез и интерпретации получаемых результатов. В качестве примеров будут задачи из различных областей: от биоинформатики до социологии. Курс бесплатный и все его материалы останутся открытыми после окончания, начинается 15 февраля.

Полезные материалы

Если вы знаете какие-либо полезные курсы или материалы по введению в статистику — делитесь в комментариях!

habr.com

Формулы по статистике — n1.doc

Средние величины: 3

Простая формула: 3

Средняя гармоническая: 3

Средняя арифметическая 3

Средняя геометрическая 3

Среднее квадратическое 3

Средняя арифметическая взвешенная: 3

Средняя гармоническая взвешенная: 3

Показатели вариации 3

Среднее линейное отклонение: 3

Простая: 3

взвешенная: 3

Дисперсия 3

Среднее квадратическое отклонение: 3

Коэф. осцилляции 3

Относительное линейное отклонение. 3

Коэф. вариации. 4

Дисперсия: 4

Способ моментов: 4

Межгрупповая дисперсия: 4

Внутригрупповая дисперсия: 4

Коэффициент детерминации: 4

Эмпирическое кореляц. отн-е. 4

Ряды динамики 4

Моментные РД – вычисление средней. 4

Абсолютный прирост 4

Темп роста базовый. 4

Темп роста цепной: 4

Темп прироста цепной: 5

Темп прироста базовый: 5

Абсолютное значение 1% прироста. 5

Ср. абсолютный прирост: 5

Ср. темп роста. 5

Ср. темп прироста. 5

Ср. значение 1% прироста. 5

Ур-е прямой: 5

Ошибка аппроксимации: 5

Индексы. 5

P — цен 5

Z – себест-ть ед. прод., т. е. затраты на пр-во ед. прод. 5

W – уровень производит. труда (ср. выработка на 1 раб) 5

t – трудоёмкость 5

Индекс физич. объёма. 6

Общий индекс товарооборота: 6

Индекс товарооборота: 6

Общий индекс физического объёма товарооборота: 6

Общая формула для вычисления всех Интегральных показателей: 6

Индекс Цен по Пааше. 6

Индекс Цен По Ласпейресу: 6

Индекс Цен По Фишеру: 6

Индекс переменного состава: 6

Индекс постоянного состава: 7

Индекс структурных сдвигов: 7

Выборочное наблюдение. 7

Предельная ошибка выборки: 7

Средний размер ошибки признака: 7

Средняя ошибка доли признака: 7

Средний размер ошибки признака: 7

Средняя ошибки доли признака: 7

Взаимосвязи м/у явлениями: 8

Лин. коэф корелляции: 8

Коэф. эластичности 8

Ошибка апроксимации: 8

Расчёт дисперсии: 8

C видов экономической деят-ти. 8

Коэф. роста выпуска товаров: 8

Темп роста выпуска: 8

Темп прироста выпуска товаров: 8

Среднегодовой коэффициент роста выпуска товаров: 8

Среднегодовой темп роста выпуска товаров: 8

Среднегодовой темп прироста выпуска товаров: 8

С рынка товаров и услуг. 9

Коэф неравномерности поставки продукции 9

Дисперсия: 9

Абсолютный размер отклонения (выполнения контракта) 9

Сумма переплаты населения: 9

Территориальный индекс цен: 9

Эмпирический коэф. эластичности: 9

Эмпирический коэф. эластичности динамики: 9

Средний коэф. эластичности: 9

Теоретический коэф. эластичности. 9

По уравнению параболы: 9

С оборота торговли и товарных запасов: 9

Валовый оборот торговли: 9

Удельный вес продажи товара в объёме оборота торговли: 10

Виды Относительных Величин 10

xi – значение признака.

ИСС = суммарное значение или объём осредняемого признака/число единиц.

P = Оборот торговли/кол-во прод. товаров.

Z = Себестоимость прод., всего – затраты по отгр. прод. / кол-во прод.

W = V произвед. прод. (WT) / число раб. (Т).

t – коэффициент кратности ошибки.

Т – численность ген. сов-ти,

— доля данного признака в выборке.

начальный уровень ряда.

Q_n – конечный уровень ряда.

— средняя величина поставки.

— взвешенная.

p_b – цены на товары по сравнимому объекту В.

q – количество проданных товаров.

а₁ – первая производная соотв. ф-ии.

х_i – значение I – фактора.

— теоретическое значение результативного признака.

Оборот торговли в сопост. ценах = оборот в факт. ценах/Индекс цен.

— общий объём оборота торговли.

Время обращения товаров в днях = Ср. сумма запасов за период/Однодневный оборот торговли.

Скорость обращения товаров = Оборот торговли за период/ср. сумма запасов за период.

С – скорость обращения в числе оборотов за период.

— средняя сумма запасов за период.

ОВ выполнения плана = факт отчётного периода/Плановое задание (на отчётный период).

ОВ план. задания = план на тек. период/факт за баз. период.

ОВ динамики = Факт отчётного/факт базисного периода

ОВ план. задания*ОВ выполнения плана = ОВ динамики, всего.

ОВ структуры = 1 часть/вся сов-ть.

Фондоотдача основных средств (Н) = товарооборот/среднегодовая стоимость основных средств.

nashaucheba.ru

Формулы по статистике — matematiku5.ru

ОВПЗ=план текущего/факт прошлого*100%

ОВВП=факт текущего/план текущего*100%

ОВД=факт текущего/факт прошлого*100%=ОВПЗ*ОВВП

ОВС(уд. вес)=i/åi

среднее арифм пр: Х=(х1+х2+…+хn)/n=åx/n

среднее арифм взв: x=åxf/åf

средняя гармонич пр: x=n/å

средняя гармонич взв: x=åW/å, W=xf

средняя хронолог пр: x=(½x1+x2+…+xn-1+½xn)/(n-1)

средняя хронолог взв: x=åxt/åt, t-период времени

средняя геометрич: x=nÖx1*x2*…*xn

средняя квадрат пр: x=Öåx2/n

средняя квадрат взв: x=Öåx2f/åf

с равными интервалами: Mo=Xн+i*

Me=Xн+i*

Абсолютные показатели вариации:

размах: R=Xmax—Xmin

ср. линейное отклонение: d=å|x—x|/n d=å|x—x|f/åf

дисперсия: d2=å(x—x)2/n d2=å(x—x)2f/åf

ср. квадр. отклонение: d=Öå(x—x)2/n d=Öå(x—x)2f/åf

x альтер. признака = p

d2альт. пр=qp

dальт. пр=Öqp

Относительные показатели вариации:

коэф. остилляции: Vo=R/x*100

относ. линейное откл.: Vd=d/x*100

коэф. вариации: V=d/x*100

Момент: Mk=

ассиметрия: AS=x-Mo AS=x-Me

относит. ассиметрия: AS=(x-Mo)/d AS=(x-Me)/d

средняя ошибка: повт. признак: µ=Ö

повт. доля: µ=Ö бесповт. признак: µ=Ö

бесповт. доля: µ=Ö

предельная ошибка: ∆=t*µ (t=1, p=0,683; t=2, p=0,954;

t=3 p=0,997)

доверительный интервал: x-∆≤x≤x+∆ p-∆≤p≤p+∆

относит. ошибка выборки: ∆%=∆/х*100

численность выборки: повт. признак: n=d2t2/∆2

повт. доля: n=p(1-p)t2/∆2

бесповт. признак: n=d2t2N/(∆2N+d2t2)

бесповт. доля: n=p(1-p)t2N/(∆2N+p(1-p)t2)

Абсолют. прирост: А=yn—yn-1 (пер) A=yn—yбаз (пост)

Коэф. роста: Kp=yn/yбаз (пост базой) Kp=yn/yn-1 (перем)

Темп роста: Tp= yn/yбаз*100% Tp= yn/yn-1*100%

Темп прироста: Тпр=Тр-100

Интервальный ряд: y=åy/n

Моментный с равными: y=(½y1+y2+…+yn-1+½yn)/(n-1)

Моментный с неравными: y=åyf/åf

Ср. абсолют. прирост: A=åA/(n-1) A=(yn—y1)/(n-1)

Ср. коэфф. роста: Kp=n-1ÖKp1*Kp2*…*Kpn

Ср. темп роста: Kp*100

Ср. темп прироста: Tp-100

Индивид. индекс физ. объема: iq=q1/q0

Индивид. индекс цены: ip=p1/p0

Индивид. индекс стоимости: ipq=p1q1/p0q0

Общ. индекс себестоимости: Iz=åz1q1/åz0q1

Общ. индекс физ. объема: Iq=åq1p0/åq0p0

Индекс цен Пааше: Ip=åp1q1/åp0q1

Индекс цен Ласпейерса: Ip=åp1q1/åp0q0

Общ. индекс стоимости: Ipq=åp1q1/åp0q0=Ip*Iq

Iр перем.сост. =(∑р1g1/ ∑g1): (∑p0g0/ ∑g0)=p1/p0

Iр пост.сост. =(∑р1g1/ ∑g1): (∑p0g1/ ∑g1)

Iр структ.сдвигов=(∑р0 g1/ ∑g1): (∑p0g0/ ∑g0)=Iр перем/Iр пост.

Коэфф. Фехнера: Кф=(na-nв)/(na+nв) na-(+) nв-(–)

Кф=1, прямая связь

Кф=0, связь отсутствует

Кф=-1, связь обратная

Кофф. корреляции Спирмена: ρ=1-

ВВП произв методом = валовый выпуск товаров и услуг+чистые налоги на продукты и импорт-промежуточное потребление

Чистые налоги на продукты и импорт=налоги на продукты и импорт-величина субсидий на продукты и импорт

Чистый внутренний продукт=ВВП-потребление основного капитала

Вид использования		Выпуск
Промежуточное потребление	4308,7	ВВТУ	6933,5
ВВП	3026	ЧНПиТ	401,2
Итого:	7334,7	Итого:	7334.7

ВВП тремя способами:

ВВП произв. методом=валовый выпуск+ЧНПиИ-промежут. потребление

ВВП распред. методом=оплата труда работников+ЧНПиИ+другие чистые налоги на пр-во и импорт+валовая прибыль

ВВП методом конечного использов.=расходы на конечное потребление+валовые накопления осн. капитала+изменения запасамат. оборотных средств+чистый экспотр

Индекс развития челов. потенциала: ИРЧП=

Ix=(Iфакт-Imin)/(Xmax—Xmin)

Ix1: Xmin=25 лет, Xmin=85 лет

Ix2: Xmin=0, Xmin=100%

Ix3: Xmin=100$, Xmin=5500$

ИПЦ=åip*p0*qn/åp0*qn

matematiku5.ru

Формулы по статистике с описанием [XLS]

Формулы по статистике с описанием [XLS] — Все для студента

• Добавлен пользователем firsovsp, дата добавления неизвестна
• Отредактирован 28.05.2009 21:59

Формулы разбиты по темам на отдельных листах Excel.
Средние.
Средняя арифметическая.
Среднегодовой уровень убыточности.
Средний уровень ряда по формуле средней простой.
Средняя хронологическая.
Средняя арифметическая взвешенная.
Средняя гармоническая взвешенная.
Индексы.
Индексы структуры.
Индекс цен переменного состава.
Индекс цен постоянного состава.
Индекс структуры.
Взаимосвязь между индексами.
Индивидуальные и общие индексы.
Индивидуальный индекс цен.
Индивидуальный индекс физического объема.
Общий индекс цен.
Общий индекс физического объема.
Общий индекс товарооборота.
Разложение абсолютного прироста по факторам.
Общий индекс товарооборота.
Структурные индексы, характеризующие заработную плату.
Индекс средней заработной платы (индекс переменного состава).
Среднее изменение заработной платы (индекс постоянного состава).
Влияние на динамику средней заработной платы изменения структуры.
численности работников (индекс структуры).
Взаимосвязь между индексами.
Индекс покупательной способности рубля.
Индекс реальной зарплаты где l0 и l1 — номинальная заработная плата в.
отчетном и базисном периодах; Ip — индекс потребительских цен.
Индекс сезонности.
Интегральный коэф-т Салаи.
Индексы, характеризующие себестоимость продукции.
Индивидуальный индекс себестоимости.
Сводный индекс затрат на производство.
Сводный (общий) индекс себестоимости.
Индекс физического объема продукции, взвешенный по себестоимости.
Взаимосвязь между индексами.
Индекс структурных сдвигов.
Индекс переменного состава.
Индекс себестоимости фиксированного состава.
Взаимосвязь индексов.
Абсолютная сумма экономии, полученная от снижения себестоимости.
Индексы уровней рентабельности.
Индекс переменного состава.
Индекс постоянного состава.
Индекс структурных сдвигов.
Индексы производительности труда.
Индекс переменного состава.
Индекс постоянного состава.
Индекс структурных сдвигов.
Ряды динамики.
Величина интервала.
Формула Стерджесса.
Абсолютный прирост.
базисный.
цепной.
Темп роста, %.
базисный.
цепной.
Темпы прироста, %.
базисный.
цепной.
Средний годовой темп роста.
Средний годовой темп прироста.
Средний абсолютный прирост.
Коэффициенты роста.
Абсолютное значение 1 % прироста.
Ожидаемый уровень ряда.
Коэффициент детерминации.
Эмпирическое корреляционное отношение.
Соотношения Чеддока.
Коэффициенты для нахождения линейной связи между рядами y и t.
Вариация.
Размах вариации.
Среднее значение признака в каждой группе.
Дисперсия.
Среднее квадратическое отклонение.
Групповая дисперсия.
Межгрупповая дисперсия.
Средняя из групповых дисперсий (выборочная дисперсия).
Правило сложения дисперсий.
Мода.
Медиана.
Квартиль первого порядка.
Квартиль третьего порядка.
Коэффициент вариации.
Линейный коэффициент вариации.
Среднее линейное отклонение (взвешенное).
Критерий Стьюдента для оценки линейного коэффициента корреляции.
Фактические значения t-критерия.
для параметра а.
для параметра а.
Коэффициент Фехнера.
Средние показатели при вариации вокруг средней доли.
Коэффициент корреляции.
Коэффициент эластичности.
Выборочное наблюдение.
Предельная ошибка выборочной доли.
Предельная ошибка выборки (при бесповторном случайном отборе).
Средняя ошибка выборки.
Численность выборки.
Границы генеральной доли.
Дисперсия выборочной доли.
Статистика доходов населения. Социальная статистика.
Децильный коэффициент дифференциации доходов.
Квинтильный коэффициент дифференциации доходов населения Квартильный коэффициент дифференциации доходов населения.
Коэффициент концентрации доходов Лоренца.
Коэффициент жизненности В. И. Покровского.
Общий коэффициент брачности.
Общий коэффициент разводов.
Коэффициент соотношения браков и разводов.
Специальный коэффициент рождаемости или показатель фертильности.
Коэффициент младенческой смертности.
Коэффициент механического прироста.
Коэффициент экономической активности населения.
Коэффициент занятости населения.
Коэффициент безработицы.
Общий коэффициент рождаемости.
Коэффициент смертности.
Коэффициент естественного прироста.
Коэффициент прибытия.
Общий коэффициент выбытия.

• Чтобы скачать этот файл зарегистрируйтесь и/или войдите на сайт используя форму сверху.
• Регистрация

www.twirpx.com