Постройте график функции y = x^2
Задание.
Постройте график функции y = x^2.
Ответ
Для построения функции нужно проанализировать ее уравнение.
Очевидно, что функция содержит квадрат аргумента, следовательно, такая функция является квадратной. Графиком же квадратной функции будет парабола.
Узнаем, как будут направлены ветви параболы. Для этого обратим внимание на знак перед х в квадрате. Условно перед ним стоит знак «плюс», а это значит, что ветви параболы будут смотреть вверх.
Также парабола существует для любых значений аргумента х.
Найдем координаты точки, которая является вершиной параболы. Для этого используем известные формулы:
Получили вершину данной параболы в начале координат.
В принципе, выше приведенных вычислений можно было и не выполнять, так как мы имеем простейшее уравнение параболы, для которой известно, что она симметрична координатной оси Оу и ее вершина совпадает с точкой (0; 0).
Также необходимо вычислить некоторые точки, которые помогут построить данную параболу.
х = 1: — точка (1; 1).
х = 2: —точка (2; 4).
х = —1: —точка с координатами (—1; 1).
х = —2: —точка с координатами (—2; 4).
Покажем все пять точек на координатной плоскости и соединим их.
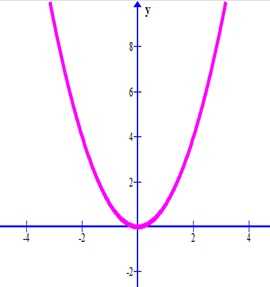
ru.solverbook.com
Постройте график функции y = 2x – 2
Задание.
Постройте график функции y = 2x — 2
Решение.
Функция представлена в виде , следовательно, она линейная.
Начнем с вычисления области определения функции. Поскольку функция является линейной, то она имеет область определения всю числовую прямую.
Такой же вывод можно сделать и об области значений функции.
В таком случае для графика никаких ограничений не будет.
В результате получили, что данная функция является ни четной, ни нечетной.
Как упоминалось выше, функция — линейная. Тогда будет достаточно двух точек, чтобы построить ее график. С этой целью вычислим точки пересечения с координатными осями:
При пересечении оси Ох переменная х = 0. Подставим это значение в функцию:
При пересечении оси Оу переменная у = 0. Решим уравнение:
Итак, получили две точки пересечения с координатами:
(0; —2) и (1; 0).
Поскольку для линейной функции не существует точек минимума или максимума, то производную находить не будет.
Как уже упоминалось, достаточно двух точек, чтобы построить линейную функцию.
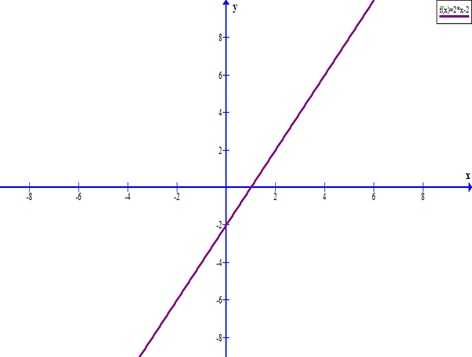
ru.solverbook.com
Постройте график функции y = -2x^2 + 8
Задание.
Постройте график функции y = —2x^2 + 8.
Решение.
Любое построение начинается с рассмотрения самой функции.
Например, из заданной функции становится понятным, что ее графиком будет парабола, та как в ее записи есть квадрат переменной х.
Коэффициент перед квадратом х указывает на то, что ветви параболы будут направлены вниз, так как коэффициент содержит знак «минус».
Для построения параболы важно понимать, будет ли она симметрична одной из координатных осей, найти координаты точки ее вершины и несколько точек, через которые она пройдет. Среди этих точек могут быть точки пересечения с осями координат.
Определим симметричность осям координат:
Получаем, что значения функции для положительных и отрицательных значений аргумента х будут равными. Значит, функция является четной, то есть симметричной оси Оу.
Для вычисления координат вершины параболы есть специальная формула, но так как мы выяснили, что график будет симметричен Оу, значит вершина параболы будет лежать на этой оси, следовательно первой координатой вершины будет х = 0. Найдем у:
Вершина параболы — точка (0; 8).
Найдем точки, в которых парабола пересечет ось Ох. Одной из координат этих точек будет у = 0. Решим уравнение:
и
Две точки пересечения — точки (—2; 0) и (2; 0).
В принципе этих точек достаточно для построения параболы. Проведем через них плавную кривую.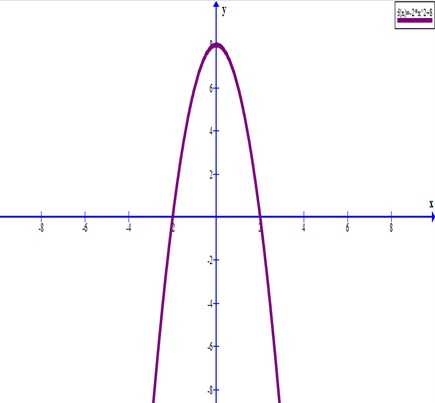
ru.solverbook.com
Постройте график функции y = –2x + 2
Задание.
Построить график функции y = —2x + 2
Решение.
Функции подобного вида строятся очень просто, так как они являются линейными. А как известно линию можно провести всего через две точки. Поэтому все решение сводится к тому, что нужно определить две точки, которые принадлежат этой функции, нанести их на координатную плоскость и провести через них линию. Это и будет графиком заданной функции.
Проведем небольшой анализ данной функции.
Поскольку функция представлена в виде , то, как уже упоминалось выше, она называется линейной. Как известно, линия бесконечна, поэтому и область определения функции, и область ее значений будет вся числовая прямая.
Функция может быть четной, нечетной или ни той, ни другой. Определим это с помощью несложных вычислений:
Получили, что функция является ни той, ни другой.
Для получения точек линейной прямой, через которые можно будет построить график заданной функции, найдем точки пересечения этой прямой с координатными осями.
Сначала найдем точку пересечения с координатной осью Оу. Для этого подставим значение х = 0 в функцию:
Точка пересечения с осью Оу будет иметь координаты (0; 2).
Теперь найдем точку пересечения с координатной осью Ох. Для этого подставим значение у = 0 в функцию и решим полученное простое уравнение:
Точка пересечения с осью Оx будет иметь координаты (1; 0).
Отметим на координатной плоскости полученные точки и проведем через них прямую.
Заданная функция построена.
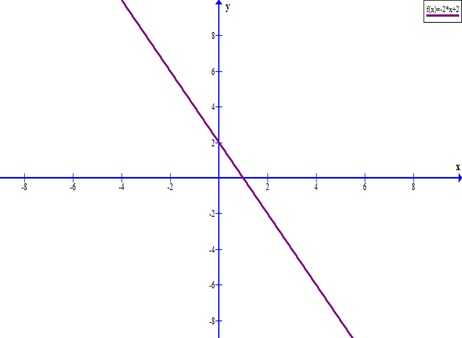
ru.solverbook.com
постройте график функции y=-x^2+2x. у самой вообще не получается!!!
Нарисуй ось ху. И подставляй вместо х цифры, например х=0, то у=0, если х=1.. то у=3, и отмечай их на графике на оси, потом уже соедини точки…
правила почитай<img src=»//otvet.imgsmail.ru/download/d7dd4feb63d905b3796cb35ba165ec9a_i-21.jpg» >
touch.otvet.mail.ru
