Таблица котангенсов, прочитать полную таблицу котангенсов
Содержание:
Котангенс — равен отношению косинуса к синусу (ctg(x) = Cos(x)/Sin(x)), тоесть таблицу котангенсов можно получить просто поделив значения из таблицы косинусов на значения из таблицы синусов. Тангенс и котангенс находятся в прямой зависимости, так как tg(x) = Sin(x)/Cos(x), а ctg(x) = Cos(x)/Sin(x), то ctg(x) = 1/tg(x). Таким образом таблицу котангенсов можно получить из таблицы тангенсов (Надо только подставить нужное Вам значение в предыдущую формулу). Пользуйтесь таблицей котангенсов на здоровье.
Таблица котангенсов 0° — 180°
|
|
|
Таблица котангенсов 180° — 360°
|
|
|
Слишком сложно?
Таблица котангенсов, таблица значений котангенсов не по зубам? Тебе ответит эксперт через 10 минут!
Таблица котангенсов (углы, значения)
В таблице значения котангенсов от 0° до 360°. Таблица котангенсов нужна, когда у вас под рукой нет калькулятора, чтобы узнать, чему равен котангенс угла. Короткая версия таблицы:
Котангенс равен отношению косинуса к синусу: ctg(x)=cos(x)/sin(x).https://uchim.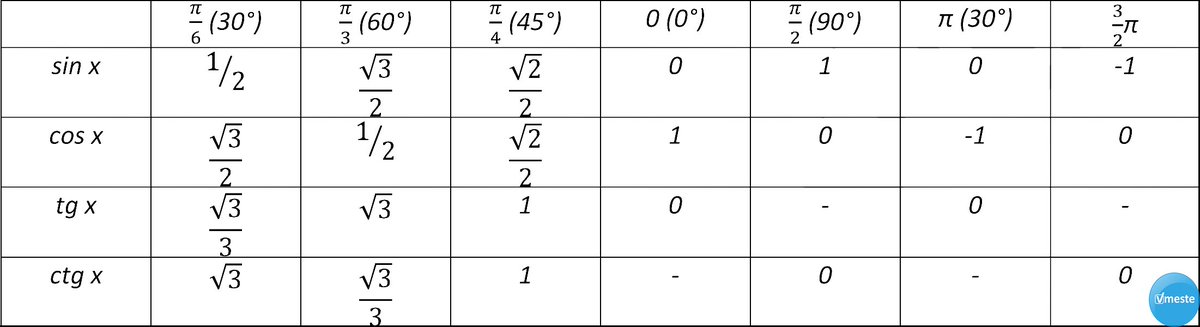 org/matematika/tablica-kotangensov — uchim.org
org/matematika/tablica-kotangensov — uchim.org
Таблица котангенсов для 0°-180°
|
|
|
Таблица котангенсов для 180°-360°
|
|
|
Посмотрите следующие таблицы тригонометрических функций: таблица синусов, таблица косинусов и таблица тангенсов.
Всё для учебы » Математика в школе » Таблица котангенсов (углы, значения)
Таблица котангенсов | Главный механик
Таблица котангенсов Брадиса – тесно связана с таблицей тангенсов. Это естественно, так как приставка “ко” прямо указывает нам на то, что он является обратным значением от тангенса. Это выражается и в тригонометрической формуле нахождения котангенса:
Котангенсы и тригонометрические функции, знакомство
В геометрии важную роль играют тригонометрические функции, которые объясняют, как относятся между собой углы и стороны треугольника с прямым углом. Наука не стоит на месте и развивается, так же как и тригонометрия.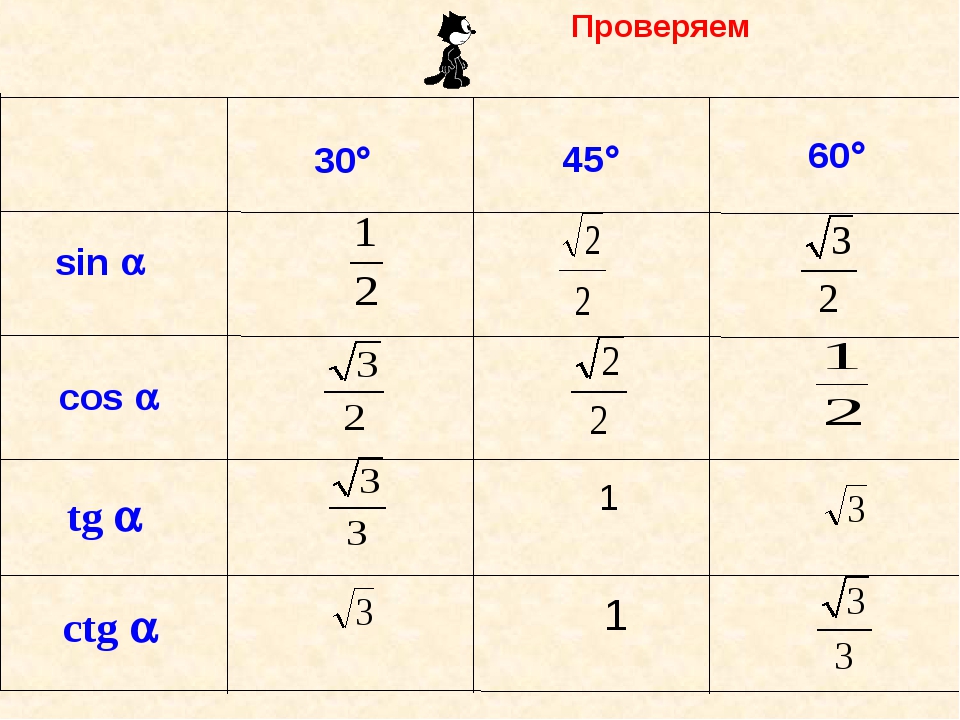 Есть новые решения дифференцированных уравнений, которые выражают тригонометрические функции и о которых Евклид не мог знать.
Есть новые решения дифференцированных уравнений, которые выражают тригонометрические функции и о которых Евклид не мог знать.
В основном, используются для вычислений значений тригонометрических функций, причем только первые из двух могут определяться только с помощью геометрии.
Синус (sin):
Косинус (cos):
Котангенс (ctg):
Тангенс (tg):
Секанс (sec):
Косеканс (cosec):
.Рассматривая прямоугольный треугольник, нужно учесть, что все справочные материалы дают одинаковое обозначение всех его параметров, таких как углы и стороны.
Три угла в нем обозначаются α, β, γ, причем угол 90° всегда обозначается γ. Сторона, лежащая напротив прямого угла, называется гипотенуза и обозначается всегда с. Альфа это первая буква греческого алфавита и угол, с которого начинаются все расчёты, также называется α. Сторона, или катет, лежащая напротив этого угла, называется противолежащей и называется а или ВС от названия вершин. Сторона, которая лежит рядом с углом или катет, называется прилежащей и обозначается b или АС.
Сторона, или катет, лежащая напротив этого угла, называется противолежащей и называется а или ВС от названия вершин. Сторона, которая лежит рядом с углом или катет, называется прилежащей и обозначается b или АС.
По теории Евклида, который довел её раз и навсегда, сумма всех углов этого треугольника, который лежит в одной плоскости, равна 180°или числу π. И значения каждого угла будут находиться в промежутке между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
Синус α можно выразить через отношение катета, который противолежит углу α к гипотенузе нашего треугольника, то есть через формулу sin α = а: с.
Косинус α выражаем, соответственно, выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть через формулу sin α = а: с. Также нужно помнить, что sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α, что помогает при решении задач.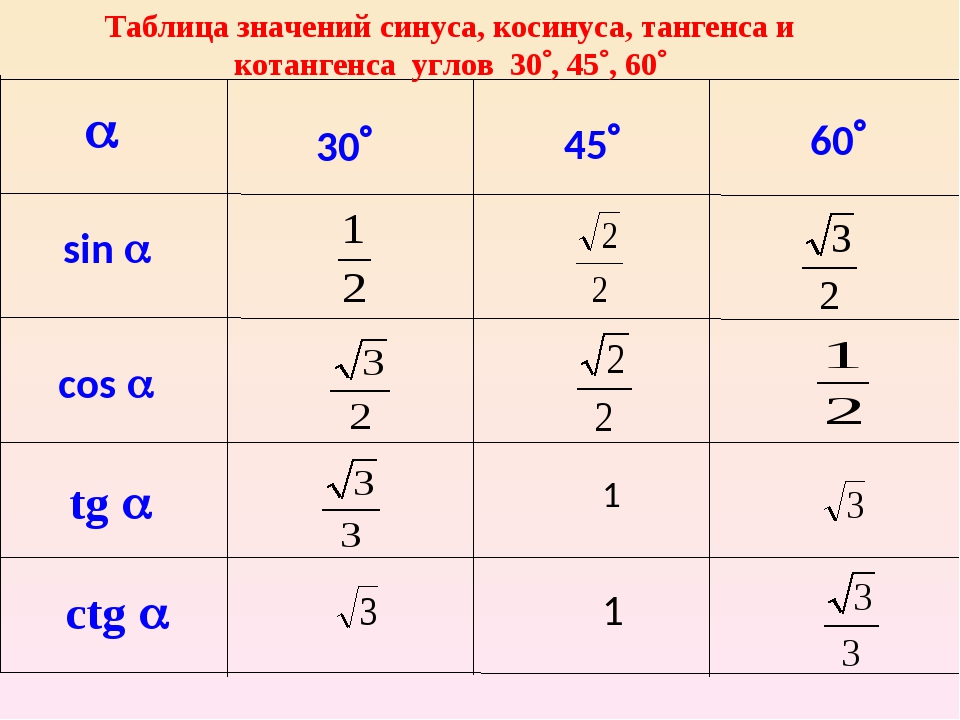
Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
Соответственно, котангенс мы выражаем аналогичным способом ctg α = b : а.
Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b, а косеканс по угла α той же теории как отношение гипотенузы треугольника к катету, который противостоит углу, cosec α = с : a.
Если задать систему координат с центром в точке О, а точка А, которая будет двигаться по окружности, образует радиус ОА. Это наглядно видно на чертеже.
Угол поворота можно считать произвольным и, согласно принятым обозначениям, называется θ. Через эту окружность можно выражать вышеназванные функции.
Например, тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Тогда если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.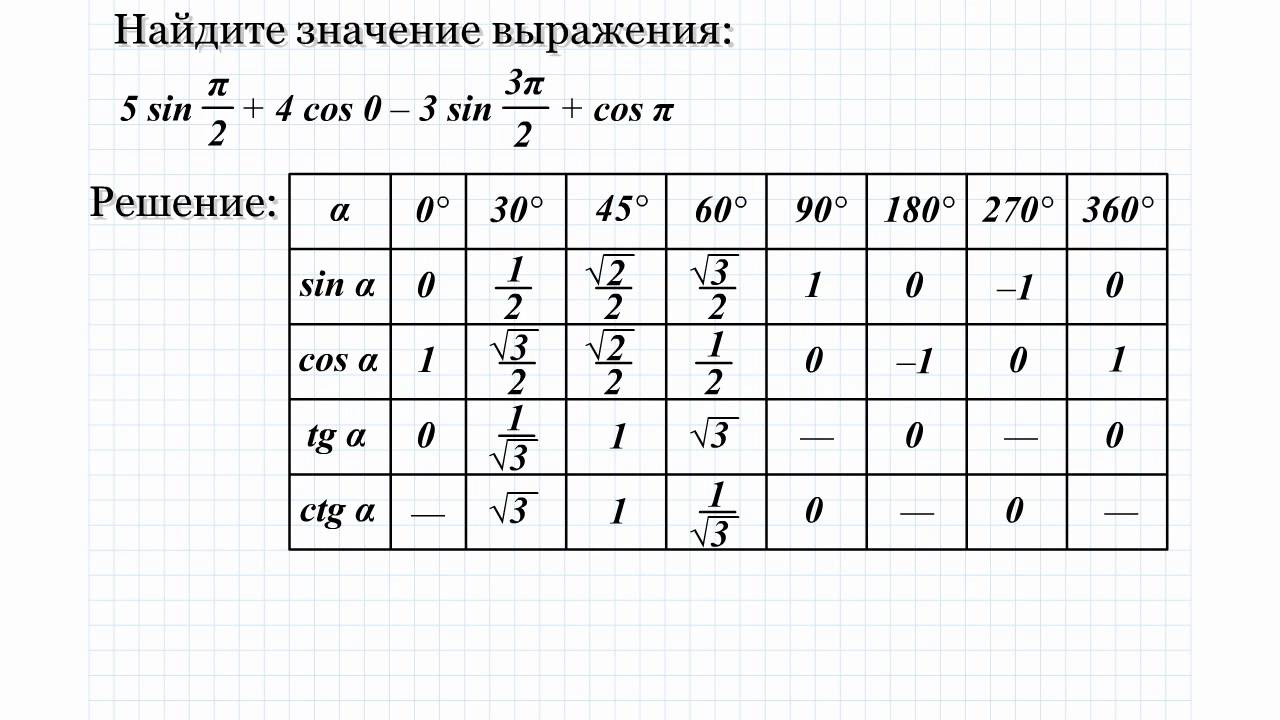
Калькулятор расчета котангенса угла
Применение функции котангенса для решения задач по тригонометрии
Для понимания того, как пользоваться тригонометрическими функциями, нужно практически решить задачу с применением этих функций.
Пример: прямоугольный треугольник АВС, катет ВС = а = 8 см, катет АС = b = 13 см. Нужно найти все недостающие размеры в треугольнике.
Первая формула, которую мы применяем, это ctg α = b : а. Тогда ctg α = 13 : 8=1, 625. Затем по таблице Брадиса для функций тангенсов и котангенсов ищем наше значение котангенса. Котангенсы углов смотрим, начиная с правой стороны таблицы. Находим значение 1,6255, которое равно 30 ° 30′, но оно больше нашего на 0,0005. Можем принять его таким, а можем отнять от найденного значения поправку в 1′. Тогда угол α = 30 ° 29′. Угол β, согласно Эвклиду, будет равен: β = 90° – 30 ° 29′ = 59° 21′.
Затем ищем гипотенузу с. Гипотенузу лучше искать через функцию синуса, то есть через sin α, который равен а: с, тогда с = а : sin α.
Обращаемся к таблице Брадиса, но уже не к значению тангенсов и котангенсов, а там, где указаны значения синуса и косинуса угла.
Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 8 : 0,5068, с = 15,8 см. Задачу мы успешно решили.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как котангенс 30 градусов, котангенс 0 градусов, котангенс 60 градусов, котангенс 90 градусов, котангенс 45 градусов, котангенс 15 градусов, котангенс 75 градусов можно рассматривать намного проще. Нужно знать, что котангенс 0 градусов не существует, а котангенс 90 градусов равен 0.
Можно найти котангенс угла 5 градусов, который равен 11,83 и находится в таблице Брадиса котангенсов для малых углов и добавлять или отнимать от наиболее часто встречающихся углов. Например, угол 45 градусов, его котангенс равен 1, тогда котангенс угла 50 градусов будет равен 1+11,83 = 12,83.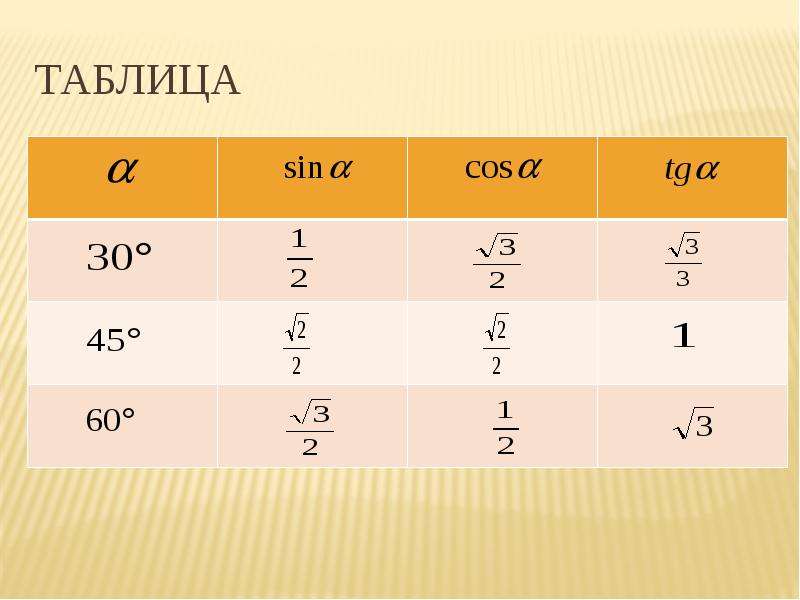 Котангенс 35 градусов можно рассчитать путем добавления к котангенсу 30 градусов угол 5 градусов.
Котангенс 35 градусов можно рассчитать путем добавления к котангенсу 30 градусов угол 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π, которое уже рассчитано. Ниже показана таблица котангенсов и тангенсов основных углов.
| Значение угла α (градусов) | Значение угла α в радианах | ctg (Котангенс) |
|---|---|---|
| Котангенс 0 | 0 | — |
| Котангенс 15 | π/12 | 3.7321 |
| Котангенс 30 | π/6 | 1.7321 |
| Котангенс 45 | π/4 | 1 |
| Котангенс 50 | 5π/18 | 0.8391 |
| Котангенс 60 | π/3 | 0.5774 |
| Котангенс 65 | 13π/36 | 0.4663 |
| Котангенс 70 | 7π/18 | 0.364 |
| Котангенс 75 | 5π/12 | 0.2679 |
| Котангенс 90 | π/2 | 0 |
| Котангенс 105 | 5π/12 | -0. 2679 2679 |
| Котангенс 120 | 2π/3 | -0.5774 |
| Котангенс 135 | 3π/4 | -1 |
| Котангенс 140 | 7π/9 | -1.1918 |
| Котангенс 150 | 5π/6 | -1.7321 |
| Котангенс 180 | π | — |
| Котангенс 270 | 3π/2 | 0 |
| Котангенс 360 | 2π |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты.
Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса. Но можно, если это не экзамен по математике, рассчитать функцию котангенса и онлайн на сайте.
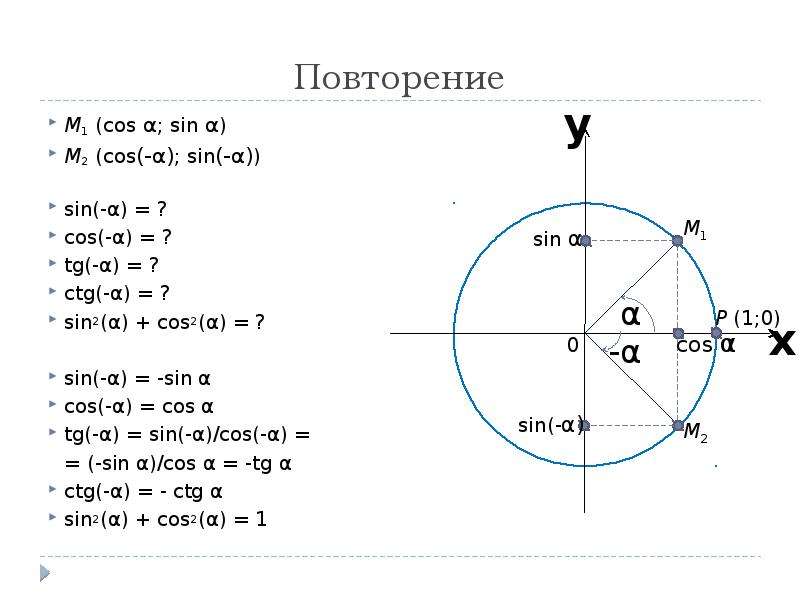
Таблица котангенсов Брадиса для углов до 75 градусов
| ctg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ctg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | 1′ | 2′ | 3′ |
| 0 | 90° | |||||||||||||
| 89° | 0 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 |
| 88° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 |
| 87° | 349 | 367 | 384 | 402 | 419 | 437 | 454 | 472 | 489 | 507 | 524 | 3 | 6 | 9 |
| 86° | 524 | 542 | 559 | 577 | 594 | 612 | 629 | 647 | 664 | 682 | 699 | 3 | 6 | 9 |
| 85° | 699 | 717 | 734 | 752 | 769 | 787 | 805 | 822 | 840 | 857 | 0. 0875 0875 | 3 | 6 | 9 |
| 84° | 0.0875 | 892 | 910 | 928 | 945 | 963 | 981 | 998 | 1016 | 1033 | 1051 | 3 | 6 | 9 |
| 83° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 3 | 6 | 9 |
| 82° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 3 | 6 | 9 |
| 81° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 3 | 6 | 9 |
| 80° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0.1763 | 3 | 6 | 9 |
| 79° | 0. 1763 1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 3 | 6 | 9 |
| 78° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 3 | 6 | 9 |
| 77° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 3 | 6 | 9 |
| 76° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 3 | 6 | 9 |
| 75° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0.2679 | 3 | 6 | 9 |
| 74° | 0.2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 3 | 6 | 9 |
| 73° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 3 | 6 | 9 |
| 72° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 3 | 6 | 10 |
| 71° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 3 | 6 | 10 |
| 70° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0.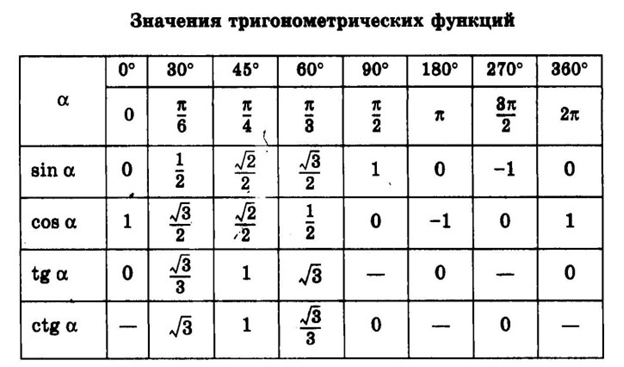 364 364 | 3 | 7 | 10 |
| 69° | 0.364 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 3 | 7 | 10 |
| 68° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 3 | 7 | 10 |
| 67° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 3 | 7 | 10 |
| 66° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 3 | 7 | 10 |
| 65° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0.4663 | 4 | 7 | 11 |
| 64° | 0. 4663 4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 4 | 7 | 11 |
| 63° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 4 | 7 | 11 |
| 62° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 4 | 7 | 11 |
| 61° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 4 | 8 | 11 |
| 60° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0.5774 | 4 | 8 | 12 |
| 59° | 0.5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 4 | 8 | 12 |
| 58° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 4 | 8 | 12 |
| 57° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 4 | 8 | 12 |
| 56° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 4 | 8 | 13 |
| 55° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0. 7002 7002 | 4 | 9 | 13 |
| 54° | 0.7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 4 | 8 | 13 |
| 53° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 5 | 9 | 14° |
| 52° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 5 | 9 | 14 |
| 51° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 5 | 9 | 14 |
| 50° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0.8391 | 5 | 10 | 15 |
| 49° | 0. 8391 8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0.8693 | 5 | 10 | 15 |
| 48° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 5 | 10 | 16 |
| 47° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 6 | 11 | 16 |
| 46° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0.9657 | 6 | 11 | 17 |
| 45° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1 | 6 | 11 | 17 |
| 44° | 1 | 35 | 70 | 105 | 141 | 176 | 212 | 247 | 283 | 319 | 355 | 6 | 12 | 18 |
| 43° | 355 | 392 | 428 | 464 | 501 | 538 | 575 | 612 | 649 | 686 | 724 | 6 | 12 | 18 |
| 42° | 724 | 761 | 799 | 837 | 875 | 913 | 951 | 990 | 1028 | 1067 | 1106 | 6 | 13 | 19 |
| 41° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 7 | 13 | 20 |
| 40° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1. 1918 1918 | 7 | 14 | 21 |
| 39° | 1.1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 7 | 14 | 22 |
| 38° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 8 | 15 | 23 |
| 37° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 8 | 16 | 24 |
| 36° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 8 | 16 | 25 |
| 35° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1.4281 | 9 | 17 | 26 |
| 34° | 1. 4281 4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 9 | 18 | 27 |
| 33° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 10 | 19 | 29 |
| 32° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 10 | 20 | 30 |
| 31° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 11 | 21 | 32 |
| 30° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1.7321 | 11 | 23 | 34 |
| 29° | 1.732 | 1.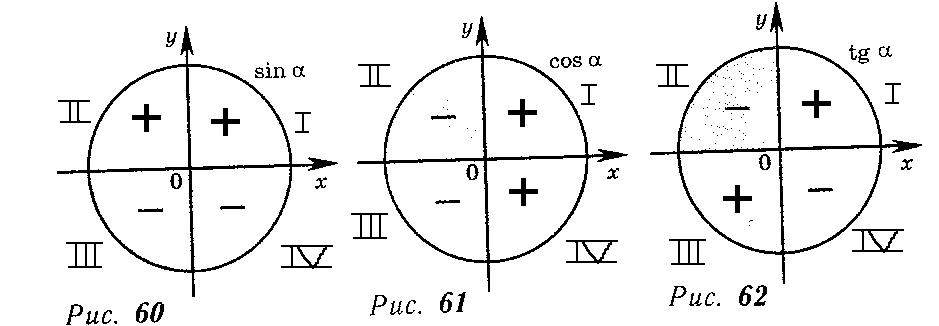 739 739 | 1.746 | 1.753 | 1.76 | 1.767 | 1.775 | 1.782 | 1.789 | 1.797 | 1.804 | 1 | 2 | 4 |
| 28° | 1.804 | 1.811 | 1.819 | 1.827 | 1.834 | 1.842 | 1.849 | 1.857 | 1.865 | 1.873 | 1.881 | 1 | 3 | 4 |
| 27° | 1.881 | 1.889 | 1.897 | 1.905 | 1.913 | 1.921 | 1.929 | 1.937 | 1.946 | 1.954 | 1.963 | 1 | 3 | 4 |
| 26° | 1.963 | 1.971 | 1.98 | 1.988 | 1.997 | 2.006 | 2.014 | 2.023 | 2.032 | 2.041 | 2.05 | 1 | 3 | 4 |
| 25° | 2.05 | 2.059 | 2.069 | 2.078 | 2.087 | 2.097 | 2.106 | 2.116 | 2.125 | 2.135 | 2.145 | 2 | 3 | 5 |
| 24° | 2. 145 145 | 2.154 | 2.164 | 2.174 | 2.184 | 2.194 | 2.204 | 2.215 | 2.225 | 2.236 | 2.246 | 2 | 3 | 5 |
| 23° | 2.246 | 2.257 | 2.267 | 2.278 | 2.289 | 2.3 | 2.311 | 2.322 | 2.333 | 2.344 | 2.356 | 2 | 4 | 5 |
| 22° | 2.356 | 2.367 | 2.379 | 2.391 | 2.402 | 2.414 | 2.426 | 2.438 | 2.45 | 2.463 | 2.475 | 2 | 4 | 6 |
| 21° | 2.475 | 2.488 | 2.5 | 2.513 | 2.526 | 2.539 | 2.552 | 2.565 | 2.578 | 2.592 | 2.605 | 2 | 4 | 6 |
| 20° | 2.605 | 2.619 | 2.633 | 2.646 | 2.66 | 2.675 | 2.689 | 2.703 | 2.718 | 2.733 | 2.747 | 2 | 5 | 7 |
| 19° | 2. 747 747 | 2.762 | 2.778 | 2.793 | 2.808 | 2.824 | 2.84 | 2.856 | 2.872 | 2.888 | 2.904 | 3 | 5 | 8 |
| 18° | 2.904 | 2.921 | 2.937 | 2.954 | 2.971 | 2.989 | 3.006 | 3.024 | 3.042 | 3.06 | 3.078 | 3 | 6 | 9 |
| 17° | 3.078 | 3.096 | 3.115 | 3.133 | 3.152 | 3.172 | 3.191 | 3.211 | 3.23 | 3.251 | 3.271 | 3 | 6 | 10 |
| 16° | 3.271 | 3.291 | 3.312 | 3.333 | 3.354 | 3.376 | 3 | 7 | 10 | |||||
| 3.398 | 3.42 | 3.442 | 3.465 | 3.487 | 4 | 7 | 11 | |||||||
| 15° | 3.487 | 3.511 | 3.534 | 3.558 | 3.582 | 3.606 | 4 | 8 | 12 | |||||
3. 63 63 | 3.655 | 3.681 | 3.706 | 3.732 | 4 | 8 | 13 | |||||||
| 14° | 3.732 | 3.758 | 3.785 | 3.812 | 3.839 | 3.867 | 4 | 9 | 13 | |||||
| 3.895 | 3.923 | 3.952 | 3.981 | 4.011 | 5 | 10 | 14 |
Таблица котангенсов Брадиса для углов, близких к 90 градусам
| ctg | 0′ | 1′ | 2′ | 3′ | 4′ | 5′ | 6′ | 7′ | 8′ | 9′ | 10′ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ctg | 10′ | 9′ | 8′ | 7′ | 6′ | 5′ | 4′ | 3′ | 2′ | 1′ | 0′ |
| 50′ | 4.011 | 4.016 | 4.021 | 4.026 | 4.031 | 4.036 | 4.041 | 4.046 | 4.051 | 4.056 | 4.061 |
| 40′ | 4.061 | 4.066 | 4.071 | 4.076 | 4.082 | 4.087 | 4.092 | 4.097 | 4.102 | 4.107 | 4.113 |
| 30′ | 4.113 | 4.118 | 4.123 | 4.128 | 4.134 | 4.139 | 4.144 | 4.149 | 4.155 | 4.16 | 4.165 |
| 20′ | 4.165 | 4.171 | 4.176 | 4.181 | 4.187 | 4.192 | 4.198 | 4.203 | 4.208 | 4.214 | 4.219 |
| 10′ | 4.219 | 4.225 | 4.23 | 4.236 | 4.241 | 4.247 | 4.252 | 4.258 | 4.264 | 4.269 | 4.275 |
| 13°00′ | 4.275 | 4.28 | 4.286 | 4.292 | 4.297 | 4.303 | 4.309 | 4.314 | 4.32 | 4.326 | 4.331 |
| 50′ | 4.331 | 4.337 | 4.343 | 4.349 | 4.355 | 4.36 | 4.366 | 4.372 | 4.378 | 4.384 | 4.39 |
| 40′ | 4.39 | 4.396 | 4.402 | 4.407 | 4.413 | 4.419 | 4.425 | 4.431 | 4.437 | 4.443 | 4.449 |
| 30′ | 4.449 | 4.455 | 4.462 | 4.468 | 4.474 | 4.48 | 4.486 | 4.492 | 4.498 | 4.505 | 4.511 |
| 20′ | 4.511 | 4.517 | 4.523 | 4.529 | 4.536 | 4.542 | 4.548 | 4.555 | 4.561 | 4.567 | 4.574 |
| 10′ | 4.574 | 4.58 | 4.586 | 4.593 | 4.599 | 4.606 | 4.612 | 4.619 | 4.625 | 4.632 | 4.638 |
| 12°00′ | 4.638 | 4.645 | 4.651 | 4.658 | 4.665 | 4.671 | 4.678 | 4.685 | 4.691 | 4.698 | 4.705 |
| 50′ | 4.705 | 4.711 | 4.718 | 4.725 | 4.732 | 4.739 | 4.745 | 4.752 | 4.759 | 4.766 | 4.773 |
| 40′ | 4.773 | 4.78 | 4.787 | 4.794 | 4.801 | 4.808 | 4.815 | 4.822 | 4.829 | 4.836 | 4.843 |
| 30′ | 4.843 | 4.85 | 4.857 | 4.864 | 4.872 | 4.879 | 4.886 | 4.893 | 4.901 | 4.908 | 4.915 |
| 20′ | 4.915 | 4.922 | 4.93 | 4.937 | 4.945 | 4.952 | 4.959 | 4.967 | 4.974 | 4.982 | 4.989 |
| 10′ | 4.989 | 4.997 | 5.005 | 5.012 | 5.02 | 5.027 | 5.035 | 5.043 | 5.05 | 5.058 | 5.066 |
| 11°00′ | 5.066 | 5.074 | 5.081 | 5.089 | 5.097 | 5.105 | 5.113 | 5.121 | 5.129 | 5.137 | 5.145 |
| 50′ | 5.145 | 5.153 | 5.161 | 5.169 | 5.177 | 5.185 | 5.193 | 5.201 | 5.209 | 5.217 | 5.226 |
| 40′ | 5.226 | 5.234 | 5.242 | 5.25 | 5.259 | 5.267 | 5.276 | 5.284 | 5.292 | 5.301 | 5.309 |
| 30′ | 5.309 | 5.318 | 5.326 | 5.335 | 5.343 | 5.352 | 5.361 | 5.369 | 5.378 | 5.387 | 5.396 |
| 20′ | 5.396 | 5.404 | 5.413 | 5.422 | 5.431 | 5.44 | 5.449 | 5.458 | 5.466 | 5.475 | 5.485 |
| 10′ | 5.485 | 5.494 | 5.503 | 5.512 | 5.521 | 5.53 | 5.539 | 5.549 | 5.558 | 5.567 | 5.576 |
| 10°00′ | 5.576 | 5.586 | 5.595 | 5.605 | 5.614 | 5.623 | 5.633 | 5.642 | 5.652 | 5.662 | 5.671 |
| 50′ | 5.671 | 5.681 | 5.691 | 5.7 | 5.71 | 5.72 | 5.73 | 5.74 | 5.749 | 5.759 | 5.769 |
| 40′ | 5.769 | 5.779 | 5.789 | 5.799 | 5.81 | 5.82 | 5.83 | 5.84 | 5.85 | 5.861 | 5.871 |
| 30′ | 5.871 | 5.881 | 5.892 | 5.902 | 5.912 | 5.923 | 5.933 | 5.944 | 5.954 | 5.965 | 5.976 |
| 20′ | 5.976 | 5.986 | 5.997 | 6.008 | 6.019 | 6.03 | 6.041 | 6.051 | 6.062 | 6.073 | 6.084 |
| 10′ | 6.084 | 6.096 | 6.107 | 6.118 | 6.129 | 6.14 | 6.152 | 6.163 | 6.174 | 6.186 | 6.197 |
| 9°00′ | 6.197 | 6.209 | 6.22 | 6.232 | 6.243 | 6.255 | 6.267 | 6.278 | 6.29 | 6.302 | 6.314 |
| 50′ | 6.314 | 6.326 | 6.338 | 6.35 | 6.362 | 6.374 | 6.386 | 6.398 | 6.41 | 6.423 | 6.435 |
| 40′ | 6.435 | 6.447 | 6.46 | 6.472 | 6.485 | 6.497 | 6.51 | 6.522 | 6.535 | 6.548 | 6.561 |
| 30′ | 6.561 | 6.573 | 6.586 | 6.599 | 6.612 | 6.625 | 6.638 | 6.651 | 6.665 | 6.678 | 6.691 |
| 20′ | 6.691 | 6.704 | 6.718 | 6.731 | 6.745 | 6.758 | 6.772 | 6.786 | 6.799 | 6.813 | 6.827 |
| 10′ | 6.827 | 6.841 | 6.855 | 6.869 | 6.883 | 6.897 | 6.911 | 6.925 | 6.94 | 6.954 | 6.968 |
| 8°00′ | 6.968 | 6.983 | 6.997 | 7.012 | 7.026 | 7.041 | 7.056 | 7.071 | 7.085 | 7.1 | 7.115 |
| 50′ | 7.115 | 7.13 | 7.146 | 7.161 | 7.176 | 7.191 | 7.207 | 7.222 | 7.238 | 7.253 | 7.269 |
| 40′ | 7.269 | 7.284 | 7.3 | 7.316 | 7.332 | 7.348 | 7.363 | 7.38 | 7.396 | 7.412 | 7.429 |
| 30′ | 7.429 | 7.445 | 7.462 | 7.478 | 7.495 | 7.511 | 7.528 | 7.545 | 7.562 | 7.579 | 7.596 |
| 20′ | 7.596 | 7.613 | 7.63 | 7.647 | 7.665 | 7.682 | 7.7 | 7.717 | 7.735 | 7.753 | 7.77 |
| 10′ | 7.77 | 7.788 | 7.806 | 7.824 | 7.842 | 7.861 | 7.879 | 7.897 | 7.916 | 7.934 | 7.953 |
| 7°00′ | 7.953 | 7.972 | 7.991 | 8.009 | 8.028 | 8.048 | 8.067 | 8.086 | 8.105 | 8.125 | 8.144 |
| 50′ | 8.144 | 8.164 | 8.184 | 8.204 | 8.223 | 8.243 | 8.264 | 8.284 | 8.304 | 8.324 | 8.345 |
| 40′ | 8.345 | 8.366 | 8.386 | 8.407 | 8.428 | 8.449 | 8.47 | 8.491 | 8.513 | 8.534 | 8.556 |
| 30′ | 8.556 | 8.577 | 8.599 | 8.621 | 8.643 | 8.665 | 8.687 | 8.709 | 8.732 | 8.754 | 8.777 |
| 20′ | 8.777 | 8.8 | 8.823 | 8.846 | 8.869 | 8.892 | 8.915 | 8.939 | 8.962 | 8.986 | 9.01 |
| 10′ | 9.01 | 9.034 | 9.058 | 9.082 | 9.106 | 9.131 | 9.156 | 9.18 | 9.205 | 9.23 | 9.255 |
| 6°00′ | 9.255 | 9.281 | 9.306 | 9.332 | 9.357 | 9.383 | 9.409 | 9.435 | 9.461 | 9.488 | 9.514 |
| 50′ | 9.514 | 9.541 | 9.568 | 9.595 | 9.622 | 9.649 | 9.677 | 9.704 | 9.732 | 9.76 | 9.788 |
| 40′ | 9.788 | 9.816 | 9.845 | 9.873 | 9.902 | 9.931 | 9.96 | 9.989 | 10.02 | 10.05 | 10.08 |
| 30′ | 10.08 | 10.11 | 10.14 | 10.17 | 10.2 | 10.23 | 10.26 | 10.29 | 10.32 | 10.35 | 10.39 |
| 20′ | 10.39 | 10.42 | 10.45 | 10.48 | 10.51 | 10.55 | 10.58 | 10.61 | 10.64 | 10.68 | 10.71 |
| 10′ | 10.71 | 10.75 | 10.78 | 10.81 | 10.85 | 10.88 | 10.92 | 10.95 | 10.99 | 11.02 | 11.06 |
| 5°00′ | 11.06 | 11.1 | 11.13 | 11.17 | 11.2 | 11.24 | 11.28 | 11.32 | 11.35 | 11.39 | 11.43 |
| 50′ | 11.43 | 11.47 | 11.51 | 11.55 | 11.59 | 11.62 | 11.66 | 11.7 | 11.74 | 11.79 | 11.83 |
| 40′ | 11.83 | 11.87 | 11.91 | 11.95 | 11.99 | 12.03 | 12.08 | 12.12 | 12.16 | 12.21 | 12.25 |
| 30′ | 12.25 | 12.29 | 12.34 | 12.38 | 12.43 | 12.47 | 12.52 | 12.57 | 12.61 | 12.66 | 12.71 |
| 20′ | 12.71 | 12.75 | 12.8 | 12.85 | 12.9 | 12.95 | 13 | 13.05 | 13.1 | 13.15 | 13.2 |
| 10′ | 13.2 | 13.25 | 13.3 | 13.35 | 13.4 | 13.46 | 13.51 | 13.56 | 13.62 | 13.67 | 13.73 |
| 4°00′ | 13.73 | 13.78 | 13.84 | 13.89 | 13.95 | 14.01 | 14.07 | 14.12 | 14.18 | 14.24 | 14.3 |
| 50′ | 14.3 | 14.36 | 14.42 | 14.48 | 14.54 | 14.61 | 14.67 | 14.73 | 14.8 | 14.86 | 14.92 |
| 40′ | 14.92 | 14.99 | 15.06 | 15.12 | 15.19 | 15.26 | 15.33 | 15.39 | 15.46 | 15.53 | 15.6 |
| 30′ | 15.6 | 15.68 | 15.75 | 15.82 | 15.89 | 15.97 | 16.04 | 16.12 | 16.2 | 16.27 | 16.35 |
| 20′ | 16.35 | 16.43 | 16.51 | 16.59 | 16.67 | 16.75 | 16.83 | 16.92 | 17 | 17.08 | 17.17 |
| 10′ | 17.17 | 17.26 | 17.34 | 17.43 | 17.52 | 17.61 | 17.7 | 17.79 | 17.89 | 17.98 | 18.07 |
| 3°00′ | 18.07 | 18.17 | 18.27 | 18.37 | 18.46 | 18.56 | 18.67 | 18.77 | 18.87 | 18.98 | 19.08 |
| 50′ | 19.08 | 19.19 | 19.3 | 19.41 | 19.52 | 19.63 | 19.74 | 19.85 | 19.97 | 20.09 | 20.21 |
| 40′ | 20.21 | 20.33 | 20.45 | 20.57 | 20.69 | 20.82 | 20.95 | 21.07 | 21.2 | 21.34 | 21.47 |
| 30′ | 21.47 | 21.61 | 21.74 | 21.88 | 22.02 | 22.16 | 22.31 | 22.45 | 22.6 | 22.75 | 22.9 |
| 20′ | 22.9 | 23.06 | 23.21 | 23.37 | 23.53 | 23.69 | 23.86 | 24.03 | 24.2 | 24.37 | 24.54 |
| 10′ | 24.54 | 24.72 | 24.9 | 25.08 | 25.26 | 25.45 | 25.64 | 25.83 | 26.03 | 26.23 | 26.43 |
| 2°00′ | 26.43 | 26.64 | 26.84 | 27.06 | 27.27 | 27.49 | 27.71 | 27.94 | 28.17 | 28.4 | 28.64 |
| 50′ | 28.64 | 28.88 | 29.12 | 29.37 | 29.62 | 29.88 | 30.14 | 30.41 | 30.68 | 30.96 | 31.24 |
| 40′ | 31.24 | 31.53 | 31.82 | 32.12 | 32.42 | 32.73 | 33.05 | 33.37 | 33.69 | 34.03 | 34.37 |
| 30′ | 34.37 | 34.72 | 35.07 | 35.43 | 35.8 | 36.18 | 36.56 | 36.96 | 37.36 | 37.77 | 38.19 |
| 20′ | 38.19 | 38.62 | 39.06 | 39.51 | 39.97 | 40.44 | 40.92 | 41.41 | 41.92 | 42.43 | 42.96 |
| 10′ | 42.96 | 43.51 | 44.07 | 44.64 | 45.23 | 45.83 | 46.45 | 47.09 | 47.74 | 48.41 | 49.1 |
| 1°00′ | 49.1 | 49.82 | 50.55 | 51.3 | 52.08 | 52.88 | 53.71 | 54.56 | 55.44 | 56.35 | 57.29 |
| 50′ | 57.29 | 58.26 | 59.27 | 60.31 | 61.38 | 62.5 | 63.66 | 64.86 | 66.11 | 67.4 | 68.75 |
| 40′ | 68.75 | 70.15 | 71.62 | 73.14 | 74.73 | 76.39 | 78.13 | 79.94 | 81.85 | 83.84 | 85.94 |
| 30′ | 85.94 | 88.14 | 90.46 | 92.91 | 95.49 | 98.22 | 101.1 | 104.2 | 107.4 | 110.9 | 114.6 |
| 20′ | 114.6 | 118.5 | 122.8 | 127.3 | 132.2 | 137.5 | 143.2 | 149.5 | 156.3 | 163.7 | 171.9 |
| 10′ | 171.9 | 180.9 | 191 | 202.2 | 214.9 | 229.2 | 245.6 | 264.4 | 286.5 | 312.5 | 343.8 |
| 0°00′ | 343.8 | 382 | 429.7 | 491.1 | 573 | 687.5 | 859.4 | 1146 | 1719 | 3438 |
Котангенс — равен отношению косинуса к синусу (ctg(x) = Cos(x)/Sin(x)), то есть таблицу котангенсов можно получить просто поделив значения из таблицы косинусов на значения из таблицы синусов. Тангенс и котангенс находятся в прямой зависимости, так как tg(x) = Sin(x)/Cos(x), а ctg(x) = Cos(x)/Sin(x), то ctg(x) = 1/tg(x). Таким образом таблицу котангенсов можно получить из таблицы тангенсов (Надо только подставить нужное Вам значение в предыдущую формулу). Пользуйтесь таблицей котангенсов на здоровье.
Таблица котангенсов 0° — 180°
|
|
|
Таблица котангенсов 180° — 360°
|
|
|
Таблица значений в градусах и радианах
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z . 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
tg угла начиная с 0 0 заканчивая 76 0 , ctg угла начиная с 14 0 заканчивая 90 0 .
tg до 90 0 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
а ctg 20 0 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π | |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 1/2 | √ 2/2 | √3 /2 | 1 | -1 |
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° |
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° |
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Для того, чтобы узнать значения тригонометрических функций для некоторых углов, используется тригонометрическая таблица.
В таблице показаны значения синусов, косинусов, тангенсов и катангенсов для углов 0°, 30°, 45°, 60°, 90°, 180°, 270° и 360°, а также значения этих углов в радианах.
Может быть полезно:
значение угла α (градусов) 0 15 30 45 60 75 90 135 180 270 360
значение угла α в радианах 0 π/12 π/6 π/4 π/3 5π/12 π/2 3π/4 π 3π/2 2π
sin (синус) 0 1/2 √2/2 √3/2 1 √2/2 0 -1 0
cos (косинус) 1 √3/2 √2/2 1/2 0 -√2/2 -1 0 1
tg (тангенс) 0 2 – √3 1/√3 1 √3 2 + √3 – -1 0 – 0
ctg (котангенс) – 2 + √3 √3 1 1/√3 2 – √3 0 -1 – 0 –
sec (секанс) 1 2/√3 √2 2 – -√2 -1 – 1
cosec (косеканс) – 2 √2 2/√3 1 √2 – -1 –
В таблице tg30°=√3/3 и соответственно cos30°=√3/3
.А(1;1),В(-2;3),C(-1;2)нүктелері-ABC үшбұрышының төбелері.В бұрышын есептеңдер!
Таблица Брадиса для синусов, косинусов, тангенсов
Представлена таблица Брадиса синусов и косинусов в удобном виде
Полная таблица Брадиса
Чтобы распечатать таблицу Брадиса,
скачайте ее в полном виде в форматеpdf
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | ± 1′ | ± 2′ | ± 3′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,0000 | 90° | ||||||||||||||
| 0° | 0,0000 | 0017 | 0035 | 0052 | 007 | 0087 | 0105 | 0122 | 014 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 061 | 0628 | 0645 | 0663 | 068 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 075 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0872 | 85° | 3 | 6 | 9 |
| 5° | 0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 108 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 134 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 153 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 165 | 1668 | 1685 | 1702 | 1719 | 1736 | 80° | 3 | 6 | 9 |
| 10° | 1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 184 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 213 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 225 | 77° | 3 | 6 | 9 |
| 13° | 225 | 2267 | 2284 | 23 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 247 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 2588 | 75° | 3 | 6 | 8 |
| 15° | 2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 274 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 279 | 2807 | 2823 | 284 | 2857 | 2874 | 289 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 294 | 2957 | 2974 | 299 | 3007 | 3024 | 304 | 3057 | 3074 | 309 | 72° | 3 | 6 | 8 |
| 18° | 309 | 3107 | 3123 | 314 | 3156 | 3173 | 319 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 342 | 70° | 3 | 5 | 8 |
| 20° | 342 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 36 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 373 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 421 | 4226 | 65° | 3 | 5 | 8 |
| 25° | 4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 454 | 63° | 3 | 5 | 8 |
| 27° | 454 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 471 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 497 | 4985 | 5 | 60° | 3 | 5 | 8 |
| 30° | 5 | 5015 | 503 | 5045 | 506 | 5075 | 509 | 5105 | 512 | 5135 | 515 | 59° | 3 | 5 | 8 |
| 31° | 515 | 5165 | 518 | 5195 | 521 | 5225 | 524 | 5255 | 527 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 549 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 565 | 5664 | 5678 | 5693 | 5707 | 5721 | 5736 | 55° | 2 | 5 | 7 |
| 35° | 5736 | 575 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 585 | 5864 | 5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 592 | 5934 | 5948 | 5962 | 5976 | 599 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 606 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 617 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 628 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 632 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 6428 | 50° | 2 | 4 | 7 |
| 40° | 6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 66 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 673 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 682 | 47° | 2 | 4 | 6 |
| 43° | 682 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 6909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 7071 | 45° | 2 | 4 | 6 |
| 45° | 7071 | 7083 | 7096 | 7108 | 712 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 723 | 7242 | 7254 | 7266 | 7278 | 729 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 742 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 749 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 757 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 766 | 40° | 2 | 4 | 6 |
| 50° | 766 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 776 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 788 | 38° | 2 | 4 | 5 |
| 52° | 788 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 807 | 808 | 809 | 36° | 2 | 3 | 5 |
| 54° | 809 | 81 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 8192 | 35° | 2 | 3 | 5 |
| 55° | 8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 829 | 34° | 2 | 3 | 5 |
| 56° | 829 | 83 | 831 | 832 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 848 | 32° | 2 | 3 | 5 |
| 58° | 848 | 849 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 859 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 866 | 30° | 1 | 3 | 4 |
| 60° | 866 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 878 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 887 | 8878 | 8886 | 8894 | 8902 | 891 | 27° | 1 | 3 | 4 |
| 63° | 891 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 898 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 9063 | 25° | 1 | 3 | 4 |
| 65° | 9063 | 907 | 9078 | 9085 | 9092 | 91 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 915 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9265 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 933 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9385 | 9391 | 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 95 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 965 | 9655 | 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 969 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 972 | 9724 | 9728 | 9732 | 9736 | 974 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 977 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 981 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 982 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 9848 | 10° | 1 | 1 | 2 |
| 80° | 9848 | 9851 | 9854 | 9857 | 986 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 988 | 9882 | 9885 | 9888 | 989 | 9893 | 9895 | 9898 | 99 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 991 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 993 | 9932 | 9934 | 9936 | 9938 | 994 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 996 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 998 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 999 | 999 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0° | 0 | 0 | 0 |
| 90° | 0,0000 |
Как пользоваться таблицей Брадиса косинусов или синусов
Таблица Брадиса для синусов и косинусов даёт значение синуса любого острого угла, содержащего целое число градусов
и десятых долей градуса, на пересечении строки, имеющей в заголовке (слева) соответствующее число минут. Так, sin 70° 30`=0.9426.
Для получения синусов прочих углов нужна интерполяция, вводящая поправку на равность между
данным углом и ближайшим табличным. Эта поправка берется из соответствующего столбца поправок справа (курсив).
Она прибавляется к ближайшему меньшему значению синуса, если данный угол превосходит ближайший
меньший табличный на 1,2,3 минуты, и отнимается от ближайшего большего табличного синуса в остальных случаях.
Например, sin 70° 32`=0,9428, так как 9426+2=9428, и sin 70° 34`= 0,9430, так как 9432-2=9430.
Та же таблица синусов и косинусов служит для
разыскания косинусов, при чем надо пользоваться нумерацией градусов справа, нумерацией минут снизу и не забывать,
что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, звменяя их синусами
дополнительных углов.
Значение тангенса любого острого угла, содержащего целое число градусов и минут определяется по табл. если угол заключен между
0° и 76°, и по таблице тангенсов если между 76° и 90. Работа по таблице тангенсов и котангенсов требует применения интерполяции,
облегчаемой поправками, помещенными в столбцах справа (курсив) и ничем не отличается от работы таблицы sin и cos.
Тангенсы углов, которые больше 76 градусов,
содержащих целое число градусов и минут, табл. дает непосредственно (без интерполяции).
Таблицы Брадиса по синусам, косинусам, тангенсам и котангенсам позволяют решать и обратный вопрос, то есть
находить острый угол по данному значению его синуса или тангенса.
Таблица Брадиса для тангенсов tg и котангенсов ctg
Представлена таблица Брадиса для тангенсов и котангенсов в удобном виде
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | ± 1′ | ± 2′ | ± 3′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,0000 | 90° | ||||||||||||||
| 0° | 0 | 0017 | 0035 | 0052 | 007 | 0087 | 0105 | 0122 | 014 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 084 | 0857 | 0875 | 85° | 3 | 6 | 9 |
| 5° | 0875 | 0892 | 091 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 121 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 137 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 153 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 162 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 1763 | 80° | 3 | 6 | 9 |
| 10° | 1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 189 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 198 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 218 | 2199 | 2217 | 2235 | 2254 | 2272 | 229 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 253 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 2679 | 75° | 3 | 6 | 9 |
| 15° | 2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 283 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 323 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 36 | 362 | 364 | 70° | 3 | 7 | 10 |
| 20° | 364 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4 | 402 | 404 | 68° | 3 | 7 | 10 |
| 22° | 404 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 439 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 4663 | 65° | 4 | 7 | 11 |
| 25° | 4663 | 4684 | 4706 | 4727 | 4748 | 477 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 525 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 534 | 5362 | 5384 | 5407 | 543 | 5452 | 5475 | 5498 | 552 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 575 | 5774 | 60° | 4 | 8 | 12 |
| 30° | 5774 | 5797 | 582 | 5844 | 5867 | 589 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 608 | 6104 | 6128 | 6152 | 6176 | 62 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 642 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 672 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 695 | 6976 | 7002 | 55° | 4 | 9 | 13 |
| 35° | 7002 | 7028 | 7054 | 708 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 9 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 74 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14 |
| 37° | 7536 | 7563 | 759 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 804 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 8391 | 50° | 5 | 10 | 15 |
| 40° | 8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 891 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 926 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 949 | 9523 | 9556 | 959 | 9623 | 9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 993 | 9965 | 1.0 | 45° | 6 | 11 | 17 |
| 45° | 1.0 | 1.0035 | 1.007 | 1.0105 | 1.0141 | 1.0176 | 1.0212 | 1.0247 | 1.0283 | 1.0319 | 1.0355 | 44° | 6 | 12 | 18 |
| 46° | 1.0355 | 1.0392 | 1.0428 | 1.0464 | 1.0501 | 1.0538 | 1.0575 | 1.0612 | 1.0649 | 1.0686 | 1.0724 | 43° | 6 | 12 | 18 |
| 47° | 1.0724 | 1.0761 | 1.0799 | 1.0837 | 1.0875 | 1.0913 | 1.0951 | 1.099 | 1.1028 | 1.1067 | 1.1106 | 42° | 6 | 13 | 19 |
| 48° | 1.1106 | 1.1145 | 1.1184 | 1.1224 | 1.1263 | 1.1303 | 1.1343 | 1.1383 | 1.1423 | 1.1463 | 1.1504 | 41° | 7 | 13 | 20 |
| 49° | 1.1504 | 1.1544 | 1.1585 | 1.1626 | 1.1667 | 1.1708 | 1.175 | 1.1792 | 1.1833 | 1.1875 | 1.1918 | 40° | 7 | 14 | 21 |
| 50° | 1.1918 | 1.196 | 1.2002 | 1.2045 | 1.2088 | 1.2131 | 1.2174 | 1.2218 | 1.2261 | 1.2305 | 1.2349 | 39° | 7 | 14 | 22 |
| 51° | 1.2349 | 1.2393 | 1.2437 | 1.2482 | 1.2527 | 1.2572 | 1.2617 | 1.2662 | 1.2708 | 1.2753 | 1.2799 | 38° | 8 | 15 | 23 |
| 52° | 1.2799 | 1.2846 | 1.2892 | 1.2938 | 1.2985 | 1.3032 | 1.3079 | 1.3127 | 1.3175 | 1.3222 | 1.327 | 37° | 8 | 16 | 24 |
| 53° | 1.327 | 1.3319 | 1.3367 | 1.3416 | 1.3465 | 1.3514 | 1.3564 | 1.3613 | 1.3663 | 1.3713 | 1.3764 | 36° | 8 | 16 | 25 |
| 54° | 1.3764 | 1.3814 | 1.3865 | 1.3916 | 1.3968 | 1.4019 | 1.4071 | 1.4124 | 1.4176 | 1.4229 | 1.4281 | 35° | 9 | 17 | 26 |
| 55° | 1.4281 | 1.4335 | 1.4388 | 1.4442 | 1.4496 | 1.455 | 1.4605 | 1.4659 | 1.4715 | 1.477 | 1.4826 | 34° | 9 | 18 | 27 |
| 56° | 1.4826 | 1.4882 | 1.4938 | 1.4994 | 1.5051 | 1.5108 | 1.5166 | 1.5224 | 1.5282 | 1.534 | 1.5399 | 33° | 10 | 19 | 29 |
| 57° | 1.5399 | 1.5458 | 1.5517 | 1.5577 | 1.5637 | 1.5697 | 1.5757 | 1.5818 | 1.588 | 1.5941 | 1.6003 | 32° | 10 | 20 | 30 |
| 58° | 1.6003 | 1.6066 | 1.6128 | 1.6191 | 1.6255 | 1.6319 | 1.6383 | 1.6447 | 1.6512 | 1.6577 | 1.6643 | 31° | 11 | 21 | 32 |
| 59° | 1.6643 | 1.6709 | 1.6775 | 1.6842 | 1.6909 | 1.6977 | 1.7045 | 1.7113 | 1.7182 | 1.7251 | 1.7321 | 30° | 11 | 23 | 34 |
| 60° | 1.7321 | 1.7391 | 1.7461 | 1.7532 | 1.7603 | 1.7675 | 1.7747 | 1.782 | 1.7893 | 1.7966 | 1.804 | 29° | 1 | 2 | 4 |
| 61° | 1.804 | 1.8115 | 1.819 | 1.8265 | 1.8341 | 1.8418 | 1.8495 | 1.8572 | 1.865 | 1.8728 | 1.8807 | 28° | 1 | 3 | 4 |
| 62° | 1.8807 | 1.8887 | 1.8967 | 1.9047 | 1.9128 | 1.921 | 1.9292 | 1.9375 | 1.9458 | 1.9542 | 1.9626 | 27° | 1 | 3 | 4 |
| 63° | 1.9626 | 1.9711 | 1.9797 | 1.9883 | 1.997 | 2.0057 | 2.0145 | 2.0233 | 2.0323 | 2.0413 | 2.0503 | 26° | 1 | 3 | 4 |
| 64° | 2.0503 | 2.0594 | 2.0686 | 2.0778 | 2.0872 | 2.0965 | 2.106 | 2.1155 | 2.1251 | 2.1348 | 2.1445 | 25° | 2 | 3 | 5 |
| 65° | 2.1445 | 2.1543 | 2.1642 | 2.1742 | 2.1842 | 2.1943 | 2.2045 | 2.2148 | 2.2251 | 2.2355 | 2.246 | 24° | 2 | 3 | 5 |
| 66° | 2.246 | 2.2566 | 2.2673 | 2.2781 | 2.2889 | 2.2998 | 2.3109 | 2.322 | 2.3332 | 2.3445 | 2.3559 | 23° | 2 | 4 | 5 |
| 67° | 2.3559 | 2.3673 | 2.3789 | 2.3906 | 2.4023 | 2.4142 | 2.4262 | 2.4383 | 2.4504 | 2.4627 | 2.4751 | 22° | 2 | 4 | 6 |
| 68° | 2.4751 | 2.4876 | 2.5002 | 2.5129 | 2.5257 | 2.5386 | 2.5517 | 2.5649 | 2.5782 | 2.5916 | 2.6051 | 21° | 2 | 4 | 6 |
| 69° | 2.6051 | 2.6187 | 2.6325 | 2.6464 | 2.6605 | 2.6746 | 2.6889 | 2.7034 | 2.7179 | 2.7326 | 2.7475 | 20° | 2 | 5 | 7 |
| 70° | 2.7475 | 2.7625 | 2.7776 | 2.7929 | 2.8083 | 2.8239 | 2.8397 | 2.8556 | 2.8716 | 2.8878 | 2.9042 | 19° | 3 | 5 | 8 |
| 71° | 2.9042 | 2.9208 | 2.9375 | 2.9544 | 2.9714 | 2.9887 | 3.0061 | 3.0237 | 3.0415 | 3.0595 | 3.0777 | 18° | 3 | 6 | 9 |
| 72° | 3.0777 | 3.0961 | 3.1146 | 3.1334 | 3.1524 | 3.1716 | 3.191 | 3.2106 | 3.2305 | 3.2506 | 3.2709 | 17° | 3 | 6 | 10 |
| 73° | 3.2709 | 3.2914 | 3.3122 | 3.3332 | 3.3544 | 3.3759 | 3.3977 | 3.4197 | 3.442 | 3.4646 | 3.4874 | 16° | 3 | 7 | 10 |
| 74° | 3.4874 | 3.5105 | 3.5339 | 3.5576 | 3.5816 | 3.6059 | 3.6305 | 3.6554 | 3.6806 | 3.7062 | 3.7321 | 15° | 4 | 8 | 13 |
| 75° | 3.7321 | 3.7583 | 3.7848 | 3.8118 | 3.8391 | 3.8667 | 3.8947 | 3.9232 | 3.952 | 3.9812 | 4.0108 | 14° | 4 | 10 | 14 |
| 76° | 4.0108 | 4.0408 | 4.0713 | 4.1022 | 4.1335 | 4.1653 | 4.1976 | 4.2303 | 4.2635 | 4.2972 | 4.3315 | 13° | |||
| 77° | 4.3315 | 4.3662 | 4.4015 | 4.4373 | 4.4737 | 4.5107 | 4.5483 | 4.5864 | 4.6252 | 4.6646 | 4.7046 | 12° | |||
| 78° | 4.7046 | 4.7453 | 4.7867 | 4.8288 | 4.8716 | 4.9152 | 4.9594 | 5.0045 | 5.0504 | 5.097 | 5.1446 | 11° | |||
| 79° | 5.1446 | 5.1929 | 5.2422 | 5.2924 | 5.3435 | 5.3955 | 5.4486 | 5.5026 | 5.5578 | 5.614 | 5.6713 | 10° | |||
| 80° | 5.6713 | 5.7297 | 5.7894 | 5.8502 | 5.9124 | 5.9758 | 6.0405 | 6.1066 | 6.1742 | 6.2432 | 6.3138 | 9° | |||
| 81° | 6.3138 | 6.3859 | 6.4596 | 6.535 | 6.6122 | 6.6912 | 6.772 | 6.8548 | 6.9395 | 7.0264 | 7.1154 | 8° | |||
| 82° | 7.1154 | 7.2066 | 7.3002 | 7.3962 | 7.4947 | 7.5958 | 7.6996 | 7.8062 | 7.9158 | 8.0285 | 8.1443 | 7° | |||
| 83° | 8.1443 | 8.2636 | 8.3863 | 8.5126 | 8.6427 | 8.7769 | 8.9152 | 9.0579 | 9.2052 | 9.3572 | 9.5144 | 6° | |||
| 84° | 9.5144 | 9.6768 | 9.8448 | 10187 | 11988 | 13854 | 15789 | 17797 | 19882 | 11.2048 | 11.4301 | 5° | |||
| 85° | 11.4301 | 11.6645 | 11.9087 | 12.1632 | 12.4288 | 12.7062 | 12.9962 | 13.2996 | 13.6174 | 13.9507 | 14.3007 | 4° | |||
| 86° | 14.3007 | 14.6685 | 15.0557 | 15.4638 | 15.8945 | 16.3499 | 16.8319 | 17.3432 | 17.8863 | 18.4645 | 19.0811 | 3° | |||
| 87° | 19.0811 | 19.7403 | 24465 | 21.2049 | 22.0217 | 22.9038 | 23.8593 | 24.8978 | 26.0307 | 27.2715 | 28.6363 | 2° | |||
| 88° | 28.6363 | 31446 | 31.8205 | 33.6935 | 35.8006 | 38.1885 | 49174 | 44.0661 | 47.7395 | 52.0807 | 57.29 | 1° | |||
| 89° | 57.29 | 63.6567 | 71.6151 | 81.847 | 95.4895 | 114.5887 | 143.2371 | 199842 | 286.4777 | 572.9572 | 0° |
Тангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)
Как пользоваться таблицей Брадиса.
На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.
sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.
Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.
Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо
cos 80°27′=80°30′−3′=0.1650−(-0.0009)=0.1659
Решение уравнения tg x = a
| Обычная форма записи решения: | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
Рис. 3
Частные случаи решения уравнений tg x = a
Уравнение: Решение: |
Уравнение: tg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 0 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 1 Решение: |
Уравнение: Решение: |
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тригонометрические функции и их значение в изучении геометрии
В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.
В данный момент используются шесть обозначений для основных тригонометрических функций, причем четыре функции из шести, они стоят в ряду последними, можно определять не только с помощью геометрии.
Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Котангенс (ctg/cot)
Секанс (sec)
Косеканс (cosec/csc)
.Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.
В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.
По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
- Синус α выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть sin α = а: с.
- Косинус α выражается через отношение катета, который прилежит к углу α, и гипотенузы с, cos α = b: с. Кстати, sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α.
- Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
- Котангенс угла α в соответствии равен ctg α = b : а.
- Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b.
- Косеканс угла α составляет отношение гипотенузы треугольника к катету, который противостоит углу, cosecα = с : a.
Эти функции можно выразить и через окружность путем задания системы координат. Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Тангенс — это отношение…
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Приняты обозначения:
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Применение функции тангенса для решения задач
Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.
Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.
Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.
Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.
Нам осталось найти гипотенузу с.
Можем найти её через sin α, который равен а: с, тогда с = а : sin α.
Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π.
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | – |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | – |
| Тангенс 360 | 2π | 0 |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.
Найти тангенс угла tg(α), в прямоугольном треугольнике
Противолежащий катет a
Прилежащий катет b
График тангенса
Функция тангенса пишется как y = tg (x). График в общем виде выглядит следующим образом:
Определение
Геометрический смысл понятия таков: в контексте прямоугольного треугольника тангенс угла – это отношение катета противолежащего к катету прилежащему. Рассмотрим это отношение на конкретной фигуре для удобства понимания.
В данном треугольнике тангенс угла альфа – это отношение С к А. Теперь рассмотрим другой острый угол – β (бета). Для бета тангенс угла – это отношение А к С.
Теперь перейдем к определению тангенса, которое несет алгебраический смысл, для этого нам понадобится единичная окружность.
Для того чтобы отметить в декартовой системе координат численное значение тангенса необходимо для начала провести прямую х = 1, которая будет перпендикулярна оси абсцисс и параллельна оси ординат. После чего отложим от оси абсцисс угол альфа и продлим его сторону до пересечения с прямой х = 1. Ордината точки пересечения в конкретной ситуации будет являться численным значением тангенса отложенного угла.
С точки зрения алгебры, определение тангенса имеет следующий вид: тангенс угла – это отношение синуса данного угла к его косинусу.
Таблица Брадиса tg, ctg
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
Свойства
Тангенс угла tg(α) — есть отношение противолежащего катета a к прилежащему катету b.
Решение уравнения ctg x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
Рис. 4
Частные случаи решения уравнений ctg x = a
Уравнение: Решение: |
Уравнение: ctg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: ctg x = 0 Решение: |
Решение: |
Уравнение: ctg x = 1 Решение: |
Уравнение: Решение: |
Таблица Брадиса – синусы и косинусы.
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Получается, что
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
В частности,
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Обратная к тангенсу функция
Арктангенс x – это обратная функция к тангенсу x, где x – любое число (x∈ℝ).
Если тангенс угла у равняется х (tg y = x), значит арктангенс x равен у:
arctg x = tg-1 x = y
Например:
arctg 1 = tg-1 1 = 45° = π/4 рад
Как связаны тангенс с котангенсом?
Тангенс является обратной функцией от котангенса, а это значит что: tg = 1/ctg. Таким образом, отношение тангенса к котангенсу является равным единице: tg/ctg = 1.
Источники
- https://www.calc.ru/Tablitsa-Bradisa-Tangensy-I-Kotangensy.html
- https://www.resolventa.ru/spr/trig/equation.htm
- https://KtoNaNovenkogo.ru/voprosy-i-otvety/tangens-chto-ehto-takoe-otnoshenie-najti-formulam-kletochkam.html
- https://themechanic.ru/bradis/tablica-tangensov
- https://geleot.ru/education/math/geometry/angle/tangent
- https://MicroExcel.ru/tangens/
- https://1Ku.ru/obrazovanie/56899-tangens-ugla-jeto-otnoshenie-chego-osnovy-trigonometrii/
- https://www.mozgan.ru/Table/TableBradis
PI = 3,141592 … (приблизительно 22/7 = 3,1428)
|
| GAPDH-F | 5 ′ AAA TGG TGA AGG TCG GTG TG |
| GAPDH-R | 5 ′ AGG TCA ATG AAG GGG TCG TT |
| Caspase3-F | 5 ′ TCG CAG CAT TTC TCC TAA G |
| Caspase3-R | 5 ′ CAA CAA AGC CAG TCT AAA CA |
| ИЛ-1бета-F | 5 ′ GTA CAA GGA GAA CCA AGC AA |
| ИЛ-1бета-Р | 5 ′ CCG TCT TTC ATT ACA CAG GA |
| Ил-6-Ф | 5 ′ CAA ATG CTC TCC TAA CAG AT |
| Ил-6-Р | 5 ′ TGT CCA CAA ACT GAT ATG CT |
| TNF-a-F | 5 ′ ACT CTG ACC CCT TTA CTC TG |
| TNF-a-R | 5 ′ GAG CCA TAA TCC CCT TTC TA |
| Bcl2-F | 5 ′ CGT GTA ACT TGT AGC GGA TA |
| Bcl2-R | 5 ′ ATG CTG AAA GGT GAA GAG G |
| Bax-F | 5 ′ GGA GAT GAA CTG GAC AGC AA |
| Bax-R | 5 ′ CAA AGT AGA AGA GGG CAA CC |
| TBP | NM_003194 | Нападающий: TGC ACA GGA GCC AAG AGT GAA |
| Реверс: CAC ATC ACA GCT CCC CAC CA | ||
| YWHAZ | NM_003406 | Нападающий: ACT TTT GGT ACA TTG TGG CTT CAA |
| Реверс: CCG CCA GGA CAA ACC AGT AT | ||
| SDHA | NM_004168 | Нападающий: TGG GAA CAA GAG GGC ATC TG |
| Реверс: CCA CCA CTG CAT CAA ATT CAT G | ||
| PECAM1 | NM_000442 | Нападающий: TCC ACC AGC GTC ATT GGC GT |
| Реверс: TGC CCT TGC GGT GTT AGG CA | ||
| ICAM1 | NM_000201 | Нападающий: GAC CGC AGA GGA CGA GGG CA |
| Реверс: TTG GGC GCC GGA AAG CTG TAG | ||
| SELE | NM_000450 | Вперед: TCT GCT GCT GGA CTC TCC CTC C |
| Реверс: GCA GCT CTG GCA GGA ACA AA | ||
| VCAM1 | NM_001078 | Нападающий: TCC AGG TGG AGC TCT ACT CAT TCC |
| Реверс: CGG TCA AGG GGG TAC ACG CT |
| Целевые белки | Праймер вперед (5′-3 ′) | Праймер обратный (5′-3 ′) | Ожидаемый размер полосы (п.о.) | Ссылка | |||
| Cna Коллагеновый белок | AAA GCG TTG CCT AGT GGA GA | AGT GCC TTC CCA AAC 9 CTT5 | AGT GCC TTC CCA AAC 9 CTT4 | 192 | [1] | ||
| ClfA Коэффициент сцепления A | CGC CGG TAA CTG GTG AAG CT | TGC TCT CAT TCT AGG CGC ACT T | 55 ° C | 314 | 314 | 314 | |
| ClfB Коэффициент сцепления B | ATG ATC TTG CTT GCG TT | CCG ATT CAA GAG TTA CAC C | 47 ° C | 215 | [27] | ||
| Spa Белок A | TCA AGC ACC AAA AGA GGA AGA | GTT TAA CGA CAT GTA CTC CGT TG | 51 ° C | Переменная | [28] | ||
| FnBPA Связывание белка Fibronectin FnBPA 9GCA 9GC4AG GAC AA | CCA TCT ATA GCT GTG TGG | 48 ° C | 1279 | [29] | |||
| FnBPB Связывающий фибронектин белок B | GGA GAA GGA ATT 9000 GCC4 GCC4 GTC GTC | GGA | 56 ° C | 820 | [29] | ||
| Bbp Костный сиалопротеин-связывающий белок | AAC TAC ATC TAG TAC TCA ACA ACA G | ATG TGC TTG AAT AAC ACC 4 9000 ATC 5 | 575 | [30] | |||
| IsdA Определитель поверхности с регулируемым содержанием железа A | CTG CGT CAG CTA ATG TAG GA | TGG CTC TTC AGA GAA GTC AC | 52 ° C | 3325 [250004]||||
| IsdB Железо-регулируемый детерминант поверхности B | ACG AGA GTT TGG TGC GCT AT | GTT GAG GCC CCT ACT TCT GA | 55 ° C | 192 | Это исследование | ||
| SdrD гена | SdrD Serine aspartate CGG AGC TGG TCA AGA AGT AT | TGC CAT CTG CGT CTG TTG TA | 52.3 ° C | 500 | [25] | ||
| SdrE Повторяющийся ген серинового аспартата E | AGA AAG TAT ACT GTA GGA ACT G | GAT GGT TTT GTA GTT ACA TCG T | 50 ° C 433 | 50 ° C | [31] | ||
| TSST-1 Токсин синдрома токсического шока | ACC CCT GTT CCC TTA TCA TC | TTT TCA GTA TTT GTA ACG CC | 53 ° C | 326 | |||
| ETA Эксфолиативный токсин A | GCA GGT GTT GAT TTA GCA TT | AGA TGT CCC TAT TTT TGC TG | 58 ° C | 93 | [33] | в Exfoliative ET | B AGC AAA AGA ATA CAG CG | GTT TTT GGC TGC TTC TCT TG | 58 ° C | 226 | [33] |
| Hla Альфа-токсин | GTA CTA CAG GTA4 TTG GAA TAT TTG AGC TAC | 47 ° C | 274 9000 4 | [34] | |||
| Hlb Бета-токсин | GCC AAA GCC GAA TCT AAG | CGC ATA TAC ATC CCA TGG C | 51 ° C | 840 | 14 [9000] 9000 Stap | 14 | |
| TTG GAA ACG GTT AAA ACG AA | GAA CCT TCC CAT CAA AAA CA | 50 ° C | 120 | [35] | |||
| SEB Стафилококковый энтеротоксин AC 9GAC CA | CGGCA GGT ACT CTA TAA GTG CC | 50 ° C | 478 | [35] | |||
| SEC Стафилококковый энтеротоксин C | GAC ATA AAA GCT AGG AAT TT CAT | TCC50 ° C | 257 | [35] | |||
| SED Стафилококковый энтеротоксин D | CTA GTT TGG TAA TAT CTC CT | TAA TGC TAT ATC TTA 9000 9000 GG | [35] | ||||
| SEE Стафилококковый энтеротоксин E | AGG TTT TTT CAC AGG TCA TCC | CTT TTT TTT CTT CGG TCA ATC | 50 ° C | 209 | [35] | 209 | [35000 | AGA ACC ATC AAA CTC GTA TAG C | 55 ° C | 287 | [35] |
| SEH Стафилококковый энтеротоксин H | GTA CAC TAGC TAGCGAC CTT TAC TTA TTT CGC TGT C | 48.4 ° C | 213 | [35] | |||
| SEI Стафилококковый энтеротоксин I | GGT GAT ATT GGT GTA GGT AAC | ATC CAT ATT CTT TGC CTT TAC CAG | 459 | 35] | |||
| SEJ Стафилококковый энтеротоксин J | CAT CAG AAC TGT TGT TCC GCT AG | TGA ATT TTA CCA TCA AAG GTA C | 50 ° C | 1426464 | |||
| Обеспечить регресс | Универсальный оборот | 5 ’- GAG GTA TTC GCA CTG GAT AC — 3’ |
| RT | РНУ-48 | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACG GTC AG — 3’ |
| Вперед | РНУ-48 | 5 ’- CCA TGA GTG TGT CGC TGA TG — 3’ |
| RT | РНУ-49 | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACA ATC AG — 3’ |
| Вперед | РНУ-49 | 5 ’- AAG CGA TAA CTG ACG AAG ACT AC — 3’ |
| RT | лет-7а | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACA ACT AT — 3’ |
| Вперед | летать-7а | 5’- CGG TGA GGT AGT AGG TTG TAT — 3 ’ |
| RT | miR-16b | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACC GCC AA — 3’ |
| Вперед | miR-16b | 5’- CCT AGC AGC ACG TAA ATA TTG G — 3 ’ |
| RT | miR-17 | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACC TAC CT — 3’ |
| Вперед | miR-17 | 5 ’- GCG GCA AAG TGC TTA CAG TG — 3’ |
| RT | miR-21 | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACT CAA CA — 3’ |
| Вперед | miR-21 | 5 ’- GCC CGC TAG CTT ATC AGA CTG ATG — 3’ |
| RT | miR-31 | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACA GCT AT — 3’ |
| Вперед | miR-31 | 5’- CAG GCA AGA TGC TGG CAT AG — 3 ’ |
| RT | miR-34a | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACA CAA CC — 3’ |
| Вперед | miR-34a | 5 ’- TGG CAG TGT CTT AGC TGG TTG — 3’ |
| RT | miR-92a | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACA CAG GC — 3’ |
| Вперед | miR-92a | 5 ’- CCC TAT TGC ACT TGT CCC G — 3’ |
| RT | miR-125a | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACT CAC AG — 3’ |
| Вперед | miR-125a | 5 ’- TCC CTG AGA CCC TTT AAC C — 3’ |
| RT | miR-125b | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACT CAC AA — 3’ |
| Вперед | miR-125b | 5’- CTC CCT GAG ACC CTA ACT TG — 3 ’ |
| RT | miR-195-5b | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACG CCA AT — 3’ |
| Вперед | miR-195-5b | 5’- GGT AGC AGC ACA GAA ATA TTG G — 3 ’ |
| RT | miR-203a | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACC TAG TG — 3’ |
| Вперед | miR-203a | 5’- CCG TGA AAT GTT TAG GAC CAC — 3 ’ |
| RT | miR-223 | 5 ’- GTC GTA TCC AGT GCA GGG TCC GAG GTA TTC GCA CTG GAT ACG ACT GGG GT — 3’ |
| Вперед | miR-223 | 5’- CCC TGT CAG TTT GTC AAA TAC C- 3 ’ |
Онлайн-калькулятор: Тригонометрические функции
Элементарные функцииТригонометрические функции — это набор элементарных функций, которые связывают углы треугольника с длинами сторон треугольника.Их также называют круговыми функциями. Смотрите картинку.
Тригонометрические функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
косек — косеканс
30 — версия — косеканс
30 — версия синус)
vercos — веркосинус (стихийный косинус)
haversin — haversed sine
exsec — exsecant
excsc — excosecant
Чтобы вычислить эти функции, введите значение угла в поле Угол и получите таблицу результатов.Угол может быть введен в градусах, радианах, градусах, минутах или секундах.
Тригонометрические функции
Точность вычисленияЦифры после десятичной точки: 10
Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера.
Скачать закрыть
content_copy Ссылка сохранить Сохранить расширение Виджет
Ну, немного теории школьного уровня.
Синус угла (sin) — это отношение длины противоположной стороны к длине гипотенузы.
Косинус угла (cos) — это отношение длины соседней стороны к длине гипотенузы.
Все остальные функции выражаются через синус и косинус следующим образом:
Касательная:
(отношение длины противоположной стороны к длине соседней стороны)
Котангенс:
(отношение длины соседней стороны к длине противоположной стороны)
Секущая:
( отношение длины гипотенузы к длине прилегающей стороны)
Косеканс:
(отношение длины гипотенузы к длине противоположной стороны)
Другие тригонометрические функции:
Проверенный синус:
Крытый синус:
Собственный синус:
Exsecant:
Excosecant:
Таблица 1 — Неэруптивная лихорадка, связанная с Rickettsia felis, Сенегал — Том 16, номер 7 — июль 2010 г. — Журнал Emerging Infectious Diseases
Кристина Соколовски, Олег Медианников, Шейх Сохна, Адама Толл, Жорж Диатта, Юбер Бассен, Жан-Франсуа Трапе и Дидье РаульПринадлежность к авторам: Unité de Recherche sur les Maladies Infectieuses et Tropicales Emergentes, Марсель, Франция (C.Соколовский, О. Медианников, Д. Рауль); Unité de Recherche sur les Maladies Infectieuses et Tropicales Emergentes, Дакар, Сенегал (О. Медианников, К. Сохна, Дж. Диатта, Х. Бассен, Ж.-Ф. Трапе); Institut Pasteur de Dakar, Дакар (А. Талль)
Целевые последовательности, праймеры и зонды, использованные в исследовании Rickettsia felis , сельский Сенегал, ноябрь 2008 г. — июль 2009 г.
| Количественное обозначение и специфичность ПЦР в реальном времени | Целевой ген | Прямой праймер (5 ‘→ 3’) | Обратный праймер (5 ‘→ 3’) | Зонд |
|---|---|---|---|---|
| Система RKND03; Rickettsia родоспецифичный | glt A | GTG-AAT-GAA-AGA-TTA-CAC-TAT-TTA-T | GTA-TCT-TAG-CAA-TCA-TTC-TAA-TAG-C | 6-FAM-CTA-TTA-TGC-TTG-CGG-CTG-TCG-GTT-C-TAMRA |
| 1029 система; Rickettsia родоспецифичный | Гипотетический белок (ген RC0338) | GAM-AAA-TGA-ATT-ATA-TAC-GCC-GCA-AA | ATT-ATT-KCC-AAA-TAT-TCG-TCC-TGT-AC | 6-FAM-CTC-AAG-ATA-AGT-ATG-AGT-TAA-ATG-TAA-A-TAMRA |
| Система Rpr 331; специфично для тифа группы риккетсий | Гликозилтрансфераза | TGC-TTC-ATG-GGC-AAT-GTC-TG | TTG-AGC-ATA-AAA-CTG-CCC-TGC-T | 6-FAM-CGC-TGG-ATT-ATC-AAA-AGA-ATT-AGC-ACG-TAMRA |
| Специально для R. |


 6643
6643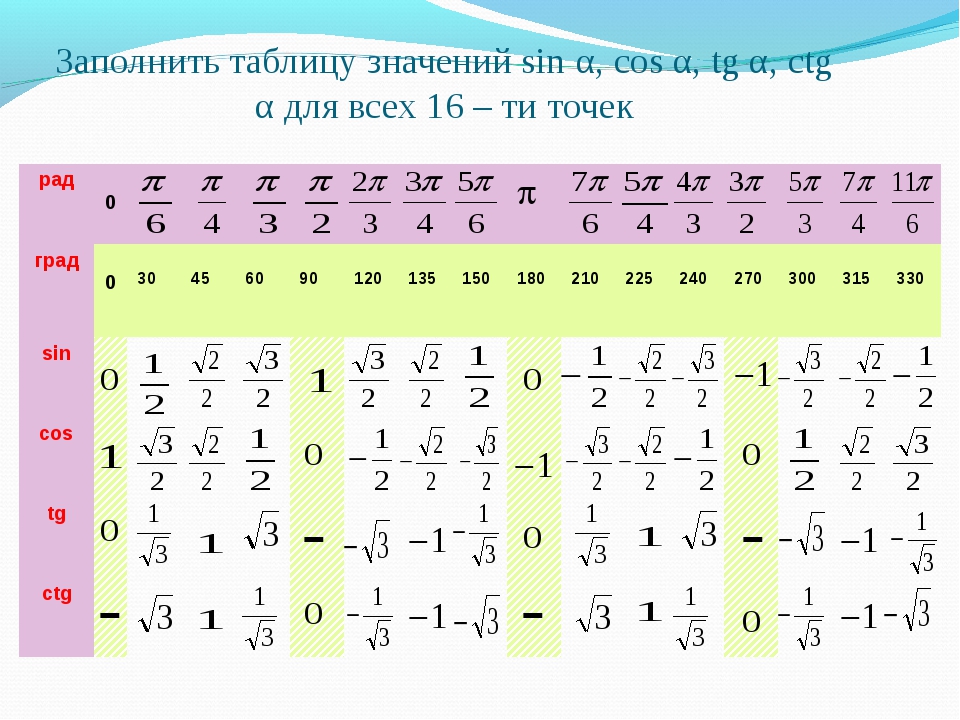 7002
7002 2126
2126 2126
2126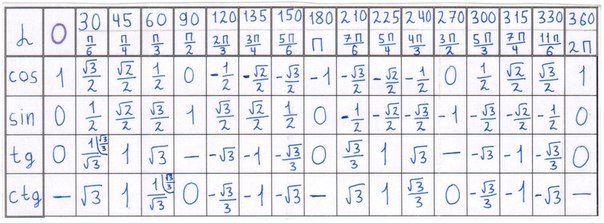 6745
6745 5399
5399 6713
6713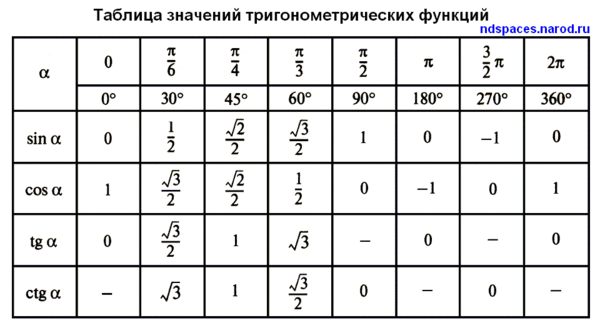 6713
6713
 6745
6745 2126
2126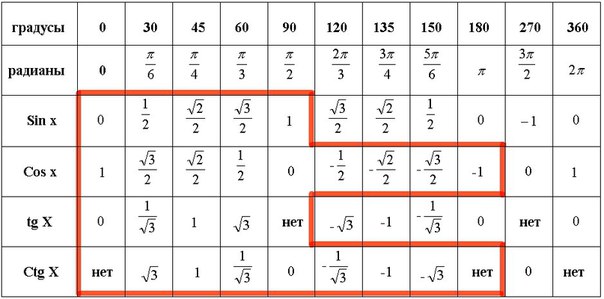 1944
1944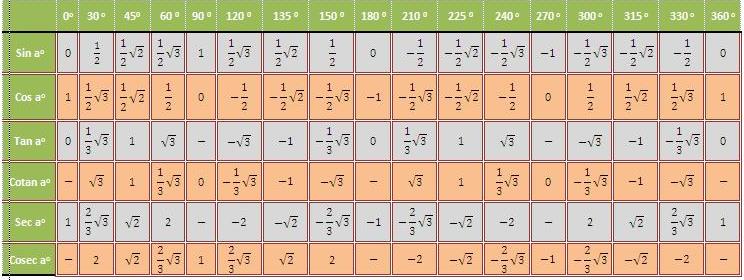 6494
6494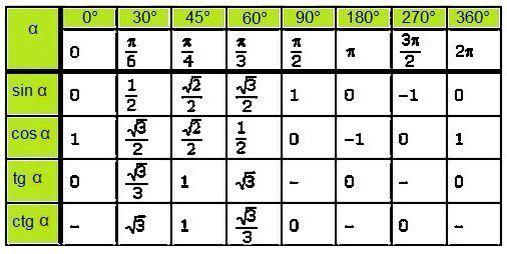 4826
4826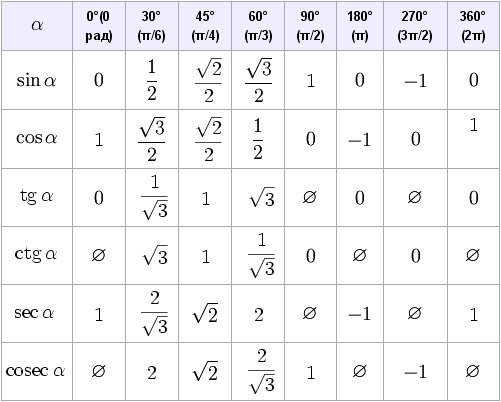 1446
1446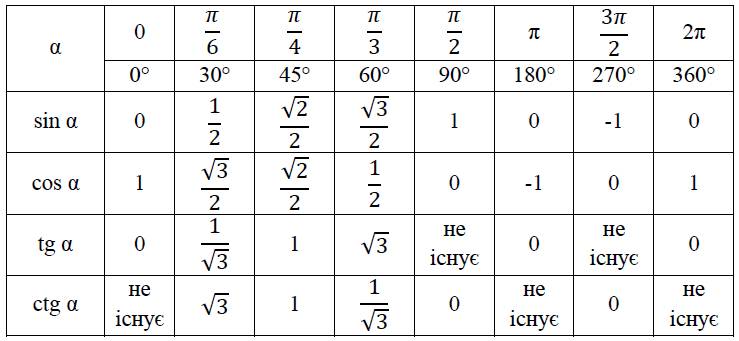 4751
4751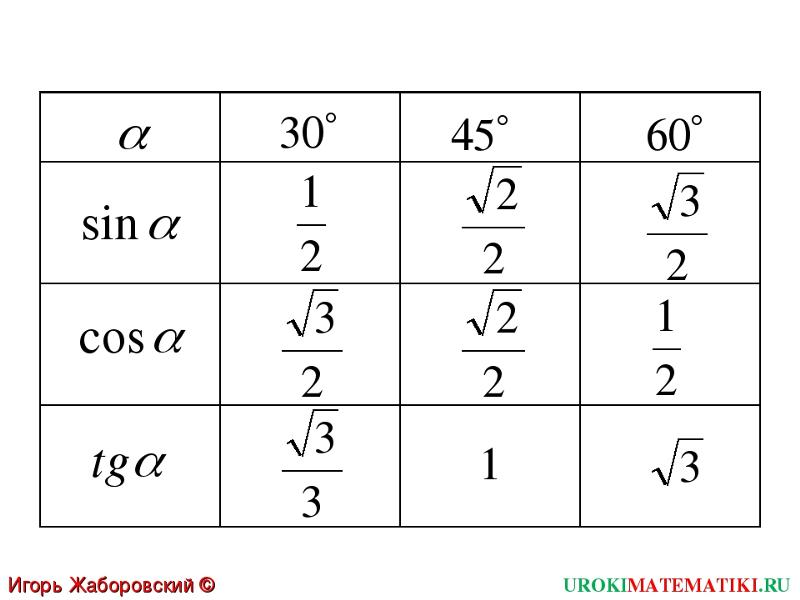 9325
9325 3443
3443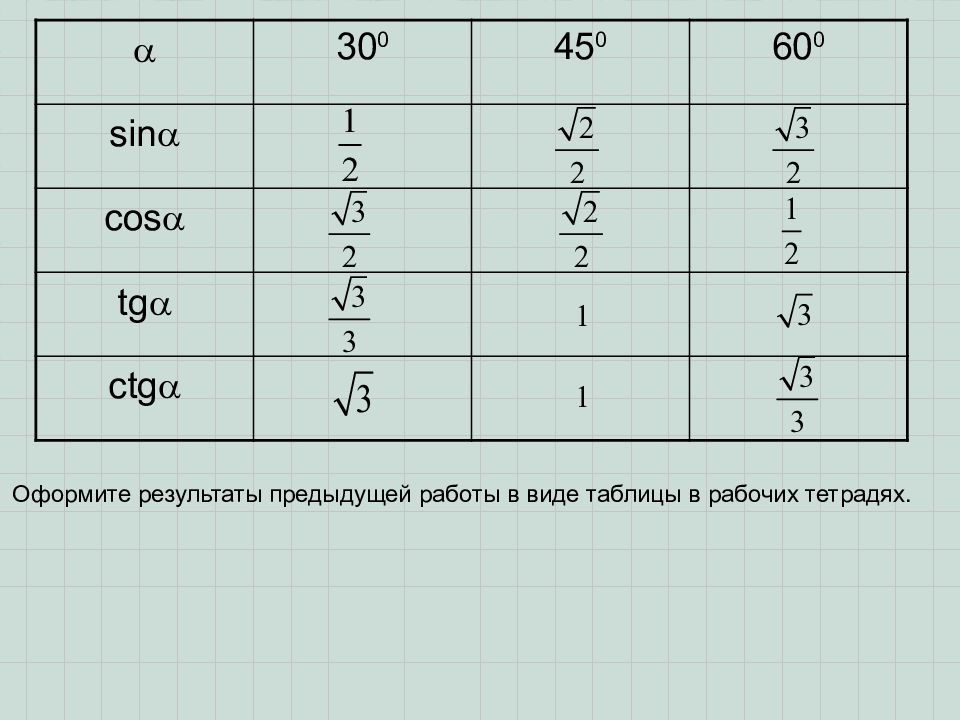 1051
1051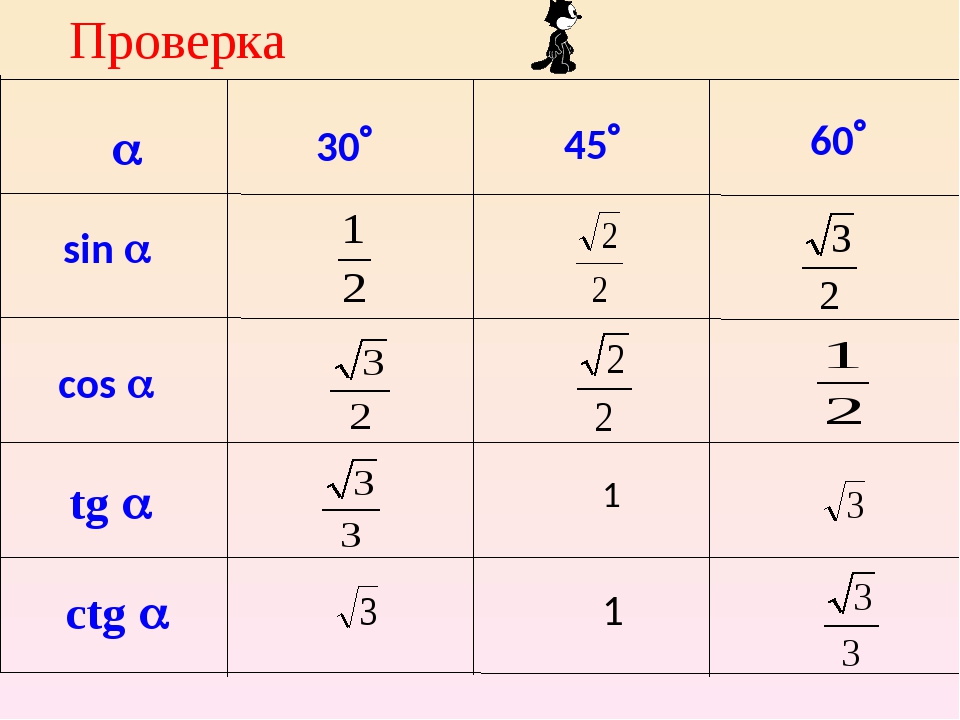 5774
5774 327
327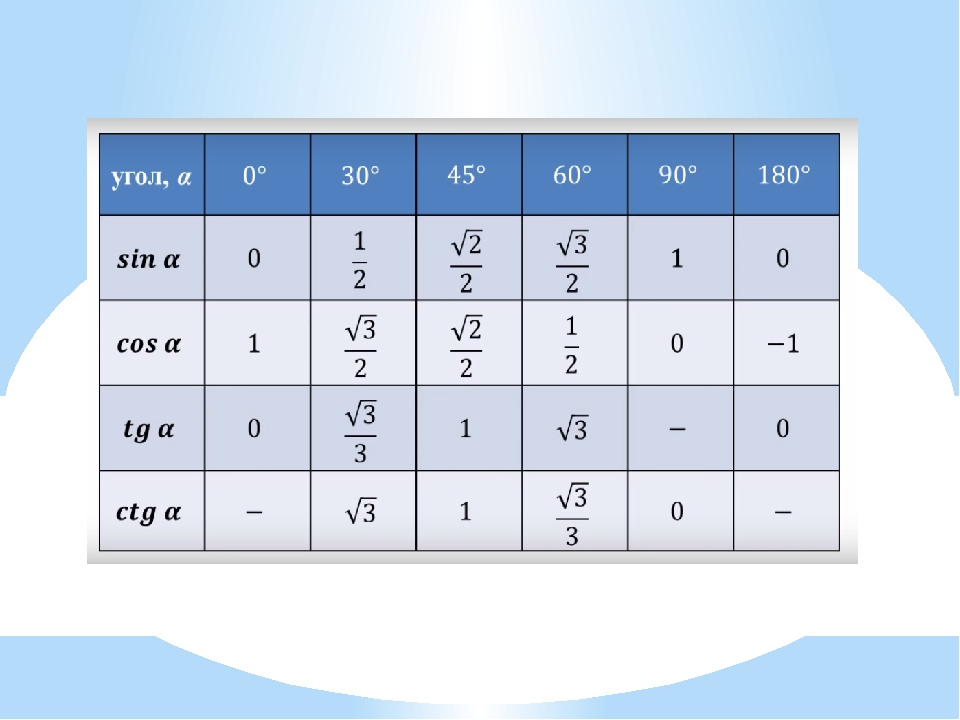 3315
3315 3138
3138 5399
5399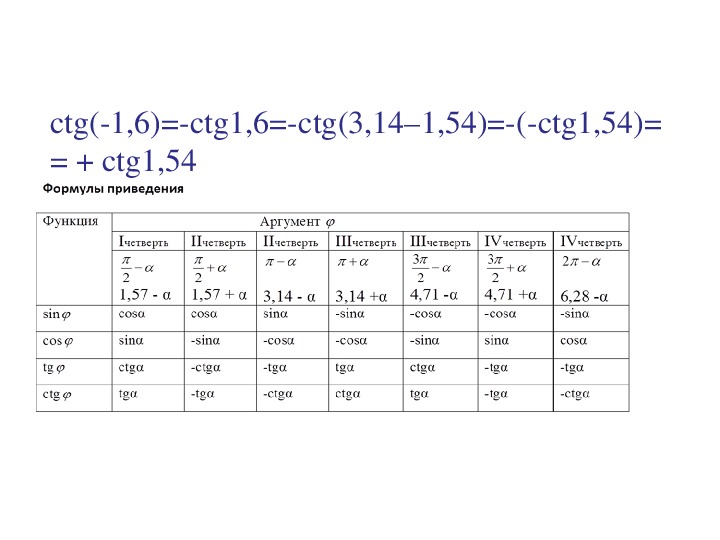 6494
6494 1584
1584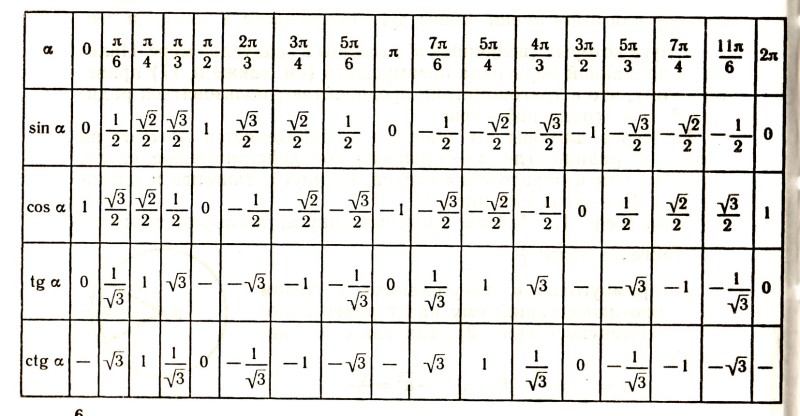 2679
2679 7813
7813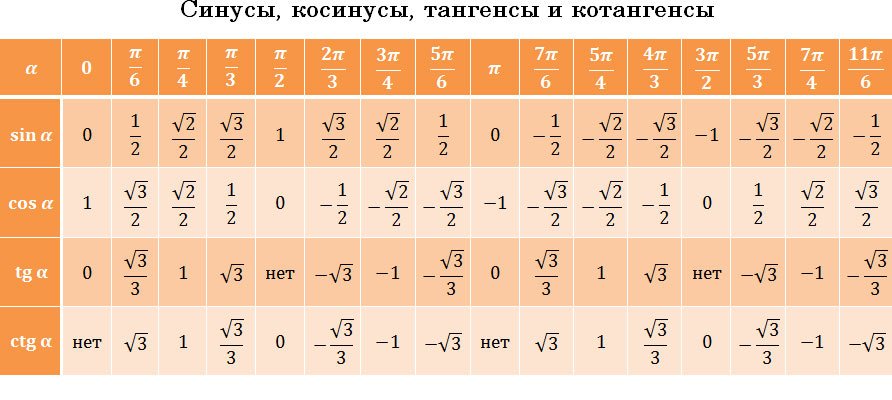 8807
8807 3007
3007