Функция лапласа локальная таблица – Таблица значений локальной функции Лапласа

Таблица значений локальной функции Лапласа

Значения плотности стандартного нормального распределения

   

	0	1	2	3	4	5	6	7	8	9
0,0	0,398942	0,398922	0,398862	0,398763	0,398623	0,398444	0,398225	0,397966	0,397668	0,397330
0,1	0,396953	0,396536	0,396080	0,395585	0,395052	0,394479	0,393868	0,393219	0,392531	0,391806
0,2	0,391043	0,390242	0,389404	0,388529	0,387617	0,386668	0,385683	0,384663	0,383606	0,382515
0,3	0,381388	0,380226	0,379031	0,377801	0,376537	0,375240	0,373911	0,372548	0,371154	0,369728
0,4	0,368270	0,366782	0,365263	0,363714	0,362135	0,360527	0,358890	0,357225	0,355533	0,353812
0,5	0,352065	0,350292	0,348493	0,346668	0,344818	0,342944	0,341046	0,339124	0,337180	0,335213
0,6	0,333225	0,331215	0,329184	0,327133	0,325062	0,322972	0,320864	0,318737	0,316593	0,314432
0,7	0,312254	0,310060	0,307851	0,305627	0,303389	0,301137	0,298872	0,296595	0,294305	0,292004
0,8	0,289692	0,287369	0,285036	0,282694	0,280344	0,277985	0,275618	0,273244	0,270864	0,268477
0,9	0,266085	0,263688	0,261286	0,258881	0,256471	0,254059	0,251644	0,249228	0,246809	0,244390
1,0	0,241971	0,239551	0,237132	0,234714	0,232297	0,229882	0,227470	0,225060	0,222653	0,220251
1,1	0,217852	0,215458	0,213069	0,210686	0,208308	0,205936	0,203571	0,201214	0,198863	0,196520
1,2	0,194186	0,191860	0,189543	0,187235	0,184937	0,182649	0,180371	0,178104	0,175847	0,173602
1,3	0,171369	0,169147	0,166937	0,164740	0,162555	0,160383	0,158225	0,156080	0,153948	0,151831
1,4	0,149727	0,147639	0,145564	0,143505	0,141460	0,139431	0,137417	0,135418	0,133435	0,131468
1,5	0,129518	0,127583	0,125665	0,123763	0,121878	0,120009	0,118157	0,116323	0,114505	0,112704
1,6	0,110921	0,109155	0,107406	0,105675	0,103961	0,102265	0,100586	0,098925	0,097282	0,095657
1,7	0,094049	0,092459	0,090887	0,089333	0,087796	0,086277	0,084776	0,083293	0,081828	0,080380
1,8	0,078950	0,077538	0,076143	0,074766	0,073407	0,072065	0,070740	0,069433	0,068144	0,066871
1,9	0,065616	0,064378	0,063157	0,061952	0,060765	0,059595	0,058441	0,057304	0,056183	0,055079
2,0	0,053991	0,052919	0,051864	0,050824	0,049800	0,048792	0,047800	0,046823	0,045861	0,044915
2,1	0,043984	0,043067	0,042166	0,041280	0,040408	0,039550	0,038707	0,037878	0,037063	0,036262
2,2	0,035475	0,034701	0,033941	0,033194	0,032460	0,031740	0,031032	0,030337	0,029655	0,028985
2,3	0,028327	0,027682	0,027048	0,026426	0,025817	0,025218	0,024631	0,024056	0,023491	0,022937
2,4	0,022395	0,021862	0,021341	0,020829	0,020328	0,019837	0,019356	0,018885	0,018423	0,017971
2,5	0,017528	0,017095	0,016670	0,016254	0,015848	0,015449	0,015060	0,014678	0,014305	0,013940
2,6	0,013583	0,013234	0,012892	0,012558	0,012232	0,011912	0,011600	0,011295	0,010997	0,010706
2,7	0,010421	0,010143	0,009871	0,009606	0,009347	0,009094	0,008846	0,008605	0,00837	0,008140
2,8	0,007915	0,007697	0,007483	0,007274	0,007071	0,006873	0,006679	0,006491	0,006307	0,006127
2,9	0,005953	0,005782	0,005616	0,005454	0,005296	0,005143	0,004993	0,004847	0,004705	0,004567
3,0	0,004432	0,004301	0,004173	0,004049	0,003928	0,003810	0,003695	0,003584	0,003475	0,003370
3,1	0,003267	0,003167	0,00307	0,002975	0,002884	0,002794	0,002707	0,002623	0,002541	0,002461
3,2	0,002384	0,002309	0,002236	0,002165	0,002096	0,002029	0,001964	0,001901	0,001840	0,001780
3,3	0,001723	0,001667	0,001612	0,001560	0,001508	0,001459	0,001411	0,001364	0,001319	0,001275
3,4	0,001232	0,001191	0,001151	0,001112	0,001075	0,001038	0,001003	0,000969	0,000936	0,000904
3,5	0,000873	0,000843	0,000814	0,000785	0,000758	0,000732	0,000706	0,000681	0,000657	0,000634
3,6	0,000612	0,00059	0,000569	0,000549	0,000529	0,000510	0,000492	0,000474	0,000457	0,000441
3,7	0,000425	0,000409	0,000394	0,000380	0,000366	0,000353	0,000340	0,000327	0,000315	0,000303
3,8	0,000292	0,000281	0,000271	0,000260	0,000251	0,000241	0,000232	0,000223	0,000215	0,000207
3,9	0,000199	0,000191	0,000184	0,000177	0,000170	0,000163	0,000157	0,000151	0,000145	0,000139
4,0	0,000134	0,000129	0,000124	0,000119	0,000114	0,000109	0,000105	0,000101	0,000097	0.000093

Вернуться Статистические таблицы

helpstat.ru

3.2. Формула Лапласа — Мои статьи — Каталог статей

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит ровно k раз (последовательность не важна), приближенно равна (при этом чем больше n, тем точнее вероятность):

 

 

Значения функции находятся в таблице для функции  ф (х). 

Важно помнить, что функция  ф (х)  — четная

=>  ф (-х)  =  ф (х). 

 

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна:

 

 

 

Для нахождения значений используют таблицу функции Лапласа для х:

0 , если же х>5, то автоматически Ф(х) = 0,5.

Функции Лапласа нечетная, т.е. Ф (-х) = — Ф(х).

Задача 1. Найдите вероятность того, что число зачисленных абитуриентов в институт психологии равно 86 из 250, подавших заявления. если вероятность зачисления для каждого абитуриента равна 0,35.

Решение

По условию задачи: р = 0.35; q = 0,65; n = 250;k = 86. В связи с тем, что n = 250 достаточно большое число, то целесообразней воспользоваться локальной теоремой Лапласа: 

 

 

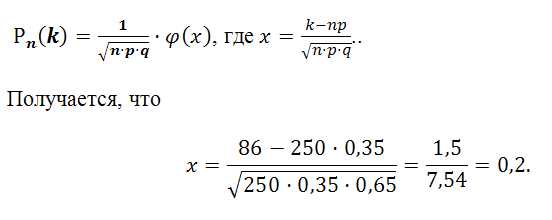
По таблице № 1 значений функции Лапласа найдем значение при х = 0,2, т.е. ф (х) = 0,391.

Тогда вероятность зачисления 86 абитуриентов в институт психологии равна

 

Ответ: 0,052.

 

 

Задача 2. Известно, что вероятность появления в семье мальчика равна 40 %.  Сколько семей необходимо опросить, чтобы с вероятностью 0,75 утверждать, что в этих семьях родились мальчики, если всего в опросе участвовало 150 детей?

Решение

По условию задачи: n = 150; р = 0,4; q = 0,6.

Тогда, пусть было опрошено а– семей. Чтобы найти неизвестное а, при условии, что n p q > 10, воспользуемся интегральной теоремой Лапласа:

 

 

 

В результате, получаем неравенство: 

 

Из таблицы № 2 для функции Лапласа получаем соответствующие значения, при Ф(х) > 0,25, то х > 0,67. Тогда неравенство принимает вид:  

 

Следовательно, необходимо будет опросить 62 семьи, чтобы с вероятностью 0,75 утверждать, что в каждой из них ребенок – мальчик.

Ответ: 62.

Задача 3. Вероятность встретить на улице в солнечный день человека с зонтом равна 0,01. Чему равна вероятность того, что из 1 000 встречных мимо вас пройдет не более 4 человек с зонтами.

Решение

Пусть событие А – {мимо вас пройдет не более 4 человек с зонтами в солнечный день}; тогда событие А₀ – {мимо вас не пройдет ни один человек с зонтом в солнечный день}; событие А₁ – {мимо вас пройдет 1 человек с зонтом в солнечный день};событие А₂ – {мимо вас пройдет 2 человека с зонтами в солнечный день};событие А₃ – {мимо вас пройдет 3 человека с зонтами в солнечный день}; событие А₄ – {мимо вас пройдет 4 человека с зонтами в солнечный день}.

Получается, что событие А есть сумма событий А₀; А₁;А₂;А₃;А₄:

А = А₀+А₁+А₂+А₃+А₄.

Так как события А₀; А₁;А₂;А₃;А₄ несовместны, то соответственно вероятность события. А есть:

Р(А) = Р(А₀) + Р(А₁) +Р(А₂) + Р(А₃) +Р(А₄).

 

Ответ: 0,777.

Пользоваться таблицей несложно: вначале смотрим на столбец, а потом на строку, например, Ф(0,22) = 0,3894; Ф(2,99) = 0,0046.

Таблица значений локальной функции Лапласа (таб. № 1)

 

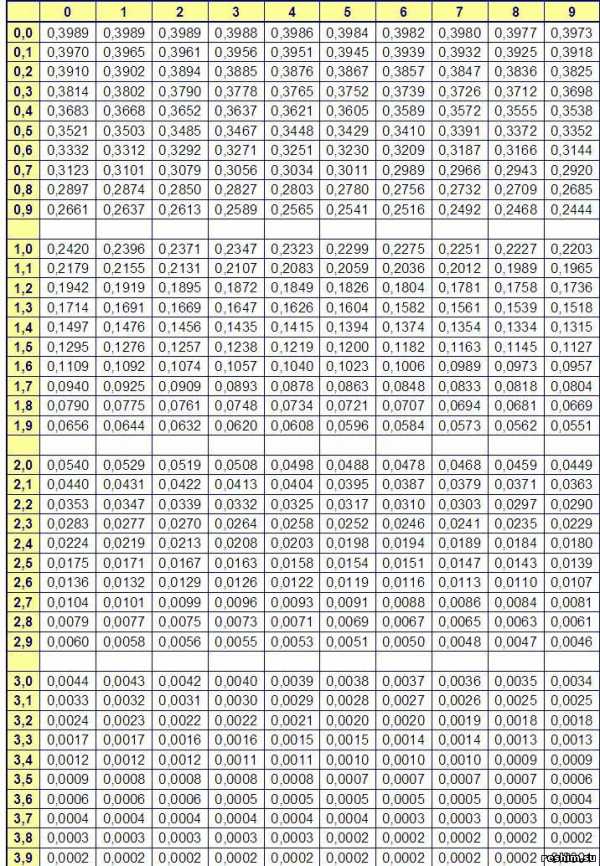
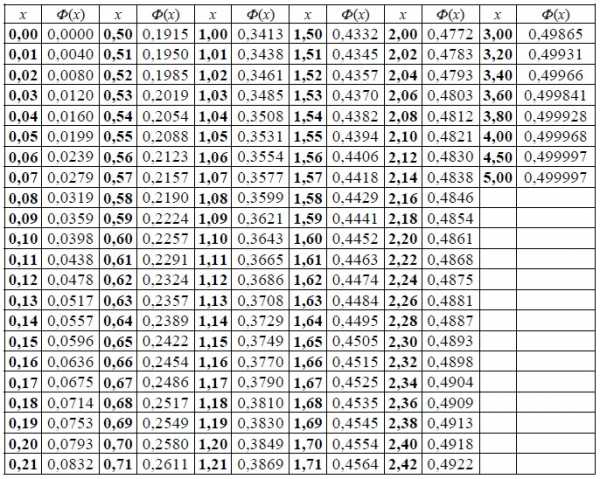
Таблица значений интегральной функции Лапласа (таб. № 2)

stochastic5.ucoz.net

Таблица значений локальной функции Лапласа

Таблица значений локальной функции Лапласа 

 01234567890,00,39890,39890,39890,39880,39860,39840,39820,39800,39770,39730,10,39700,39650,39610,39560,39510,39450,39390,39320,39250,39180,20,39100,39020,38940,38850,38760,38670,38570,38470,38360,38250,30,38140,38020,37900,37780,37650,37520,37390,37260,37120,36980,40,36830,36680,36520,36370,36210,36050,35890,35720,35550,35380,50,35210,35030,34850,34670,34480,34290,34100,33910,33720,33520,60,33320,33120,32920,32710,32510,32300,32090,31870,31660,31440,70,31230,31010,30790,30560,30340,30110,29890,29660,29430,29200,80,28970,28740,28500,28270,28030,27800,27560,27320,27090,26850,90,26610,26370,26130,25890,25650,25410,25160,24920,24680,2444           1,00,24200,23960,23710,23470,23230,22990,22750,22510,22270,22031,10,21790,21550,21310,21070,20830,20590,20360,20120,19890,19651,20,19420,19190,18950,18720,18490,18260,18040,17810,17580,17361,30,17140,16910,16690,16470,16260,16040,15820,15610,15390,15181,40,14970,14760,14560,14350,14150,13940,13740,13540,13340,13151,50,12950,12760,12570,12380,12190,12000,11820,11630,11450,11271,60,11090,10920,10740,10570,10400,10230,10060,09890,09730,09571,70,09400,09250,09090,08930,08780,08630,08480,08330,08180,08041,80,07900,07750,07610,07480,07340,07210,07070,06940,06810,06691,90,06560,06440,06320,06200,06080,05960,05840,05730,05620,0551           2,00,05400,05290,05190,05080,04980,04880,04780,04680,04590,04492,10,04400,04310,04220,04130,04040,03950,03870,03790,03710,03632,20,03530,03470,03390,03320,03250,03170,03100,03030,02970,02902,30,02830,02770,02700,02640,02580,02520,02460,02410,02350,02292,40,02240,02190,02130,02080,02030,01980,01940,01890,01840,01802,50,01750,01710,01670,01630,01580,01540,01510,01470,01430,01392,60,01360,01320,01290,01260,01220,01190,01160,01130,01100,01072,70,01040,01010,00990,00960,00930,00910,00880,00860,00840,00812,80,00790,00770,00750,00730,00710,00690,00670,00650,00630,00612,90,00600,00580,00560,00550,00530,00510,00500,00480,00470,0046           3,00,00440,00430,00420,00400,00390,00380,00370,00360,00350,00343,10,00330,00320,00310,00300,00290,00280,00270,00260,00250,00253,20,00240,00230,00220,00220,00210,00200,00200,00190,00180,00183,30,00170,00170,00160,00160,00150,00150,00140,00140,00130,00133,40,00120,00120,00120,00110,00110,00100,00100,00100,00090,00093,50,00090,00080,00080,00080,00080,00070,00070,00070,00070,00063,60,00060,00060,00060,00050,00050,00050,00050,00050,00050,00043,70,00040,00040,00040,00040,00040,00040,00030,00030,00030,00033,80,00030,00030,00030,00030,00030,00020,00020,00020,00020,00023,90,00020,00020,00020,00020,00020,00020,00020,00020,00020,0001 

studfiles.net

Функция Лапласа в Excel

Одной из самых известных неэлементарных функций, которая применяется в математике, в теории дифференциальных уравнений, в статистике и в теории вероятностей является функция Лапласа. Решение задач с ней требует существенной подготовки. Давайте выясним, как можно с помощью инструментов Excel произвести вычисление данного показателя.

Функция Лапласа

Функция Лапласа имеет широкое прикладное и теоретическое применение. Например, она довольно часто используется для решения дифференциальных уравнений. У этого термина существует ещё одно равнозначное название – интеграл вероятности. В некоторых случаях основой для решения является построение таблицы значений.

Оператор НОРМ.СТ.РАСП

В Экселе указанная задача решается с помощью оператора НОРМ.СТ.РАСП. Его название является сокращением от термина «нормальное стандартное распределение». Так как его главной задачей является возврат в выделенную ячейку стандартного нормального интегрального распределения. Данный оператор относится к статистической категории стандартных функций Excel.

В Excel 2007 и в более ранних версиях программы этот оператор назывался НОРМСТРАСП. Он в целях совместимости оставлен и в современных версиях приложений. Но все-таки в них рекомендуется использование более продвинутого аналога – НОРМ.СТ.РАСП.

Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:

=НОРМ.СТ.РАСП(z;интегральная)

Устаревший оператор НОРМСТРАСП записывается так:

=НОРМСТРАСП(z)

Как видим, в новом варианте к существующему аргументу «Z» добавлен аргумент «Интегральная». Нужно заметить, что каждый аргумент является обязательным.

Аргумент «Z» указывает числовое значение, для которого производится построение распределения.

Аргумент «Интегральная» представляет собой логическое значение, которое может иметь представление «ИСТИНА» («1») или «ЛОЖЬ» («0»). В первом случае в указанную ячейку возвращается интегральная функция распределения, а во втором – весовая функция распределения.

Решение задачи

Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:

=НОРМ.СТ.РАСП(z;интегральная(1))-0,5

Теперь давайте на конкретном примере рассмотрим использование оператора НОРМ.СТ.РАСП для решения конкретной задачи.

1. Выделяем ячейку, куда будет выводиться готовый результат и щелкаем по значку «Вставить функцию», расположенному около строки формул.



2. После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».



3. Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».



4. После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.



5. Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.



6. Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.

Как видим, вычислить функцию Лапласа для конкретного заданного числового значения в программе Excel не составляет особенного труда. Для этих целей применяется стандартный оператор НОРМ.СТ.РАСП.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Локальная теорема Муавра — Лапласа

27 октября 2011

Рассмотрим последовательность из $n$ независимых опытов, в каждом из которых событие $A$ может произойти с вероятностью $p$, либо не произойти — с вероятностью $q=1-p$. Обозначим через P _n (k) вероятность того, что событие $A$ произойдет ровно $k$ раз из $n$ возможных.

В таком случае величину P _n (k) можно найти по теореме Бернулли (см. урок «Схема Бернулли. Примеры решения задач»):

Эта теорема прекрасно работает, однако у нее есть недостаток. Если $n$ будет достаточно большим, то найти значение P _n (k) становится нереально из-за огромного объема вычислений. В этом случае работает Локальная теорема Муавра — Лапласа, которая позволяют найти приближенное значение вероятности:

Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число $n$ велико, а число $p$ отлично от 0 и 1, тогда:

Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоваться даже на контрольных работах и экзаменах.

Функция Гаусса обладает двумя свойствами, которые следует учитывать при работе с таблицей значений:

1. φ(−x) = φ(x) — функция Гаусса — четная;
2. При больших значениях x имеем: φ(x) ≈ 0.

Локальная теорема Муавра — Лапласа дает отличное приближение формулы Бернулли, если число испытаний n достаточно велико. Разумеется, формулировка «число испытаний достаточно велико» весьма условна, и в разных источниках называются разные цифры. Например:

1. Часто встречается требование: n · p · q > 10. Пожалуй, это минимальная граница;
2. Другие предлагают работать по этой формуле только для $n > 100$ и n · p · q > 20.

На мой взгляд, достаточно просто взглянуть на условие задачи. Если видно, что стандартная теорема Бернулли не работает из-за большого объема вычислений (например, никто не будет считать число 58! или 45!), смело применяйте Локальную теорему Муавра — Лапласа.

К тому же, чем ближе значения вероятностей $q$ и $p$ к 0,5, тем точнее формула. И, наоборот, при пограничных значениях (когда $p$ близко к 0 или 1) Локальная теорема Муавра — Лапласа дает большую погрешность, значительно отличаясь от настоящей теоремы Бернулли.

Однако будьте внимательны! Многие репетиторы по высшей математике сами ошибаются в подобных расчетах. Дело в том, что в функцию Гаусса подставляется довольно сложное число, содержащее арифметический квадратный корень и дробь. Это число обязательно надо найти еще до подстановки в функцию. Рассмотрим все на конкретных задачах:

Задача. Вероятность рождения мальчика равна 0,512. Найдите вероятность того, что среди 100 новорожденных будет ровно 51 мальчик.

Итак, всего испытаний по схеме Бернулли n = 100. Кроме того, p = 0,512, q = 1 − p = 0,488.

Поскольку n = 100 — это достаточно большое число, будем работать по Локальной теореме Муавра — Лапласа. Заметим, что n · p · q = 100 · 0,512 · 0,488 ≈ 25 > 20. Имеем:

Поскольку мы округляли значение n · p · q до целого числа, ответ тоже можно округлить: 0,07972 ≈ 0,08. Учитывать остальные цифры просто нет смысла.

Задача. Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течение одного часа он позвонит на станцию, равна 0,02. Найти вероятность того, что в течение часа позвонят ровно 5 абонентов.

По схеме Бернулли, n = 200, p = 0,02, q = 1 − p = 0,98. Заметим, что n = 200 — это неслабое число, поэтому используем Локальную теорему Муавра — Лапласа. Для начала найдем n · p · q = 200 · 0,02 · 0,98 ≈ 4. Конечно, 4 — это слишком мало, поэтому результаты будут неточными. Тем не менее, имеем:

Округлим ответ до второго знака после запятой: 0,17605 ≈ 0,18. Учитывать больше знаков все равно не имеет смысла, поскольку мы округляли n · p · q = 3,92 ≈ 4 (до точного квадрата).

Задача. Магазин получил 1000 бутылок водки. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Найти вероятность того, что магазин получит ровно две разбитых бутылки.

По схеме Бернулли имеем: n = 1000, p = 0,003, q = 0,997. Отсюда n · p · q = 2,991 ≈ 1,73² (подобрали ближайший точный квадрат). Поскольку число n = 1000 достаточно велико, подставляем все числа в формулу Локальной теоремы Муавра — Лапласа:

Мы сознательно оставляем лишь один знак после запятой (на самом деле там получится 0,1949…), поскольку изначально использовали довольно грубые оценки. В частности: 2,991 ≈ 1,73². Тройка в числителе внутри функции Гаусса возникла из выражения n · p = 1000 · 0,003 = 3.

Смотрите также:

1. Зачем нужна интегральная теорема Муавра-Лапласа и как её правильно применять?
2. Схема Бернулли. Примеры решения задач
3. Площадь круга
4. Уравнение касательной к графику функции
5. Специфика работы с логарифмами в задаче B15
6. Задача B5: площадь фигуры без клеток

www.berdov.com

таблица значений функции Лапласа

Сайт www.MatBuro.ru

©МатБюро — Решение задач по высшей математике, теории вероятностей

		Функция Лапласа			y =Φ(x)=			1	∫x	e−t2 / 2dt
								2π
									0
x	Φ(x)	x	Φ(x)	x		Φ(x)		x			Φ(x)
0	0
0,01	0,004	0,13	0,0517	0,25		0,0987		0,37			0,1443
0,02	0,008	0,14	0,0557	0,26		0,1026		0,38			0,148
0,03	0,012	0,15	0,0596	0,27		0,1064		0,39			0,1517
0,04	0,016	0,16	0,0636	0,28		0,1103		0,4			0,1554
0,05	0,0199	0,17	0,0675	0,29		0,1141		0,41			0,1591
0,06	0,0239	0,18	0,0714	0,3		0,1179		0,42			0,1628
0,07	0,0279	0,19	0,0753	0,31		0,1217		0,43			0,1664
0,08	0,0319	0,2	0,0793	0,32		0,1255		0,44			0,17
0,09	0,0359	0,21	0,0832	0,33		0,1293		0,45			0,1736
0,1	0,0398	0,22	0,0871	0,34		0,1331		0,46			0,1772
0,11	0,0438	0,23	0,091	0,35		0,1368		0,47			0,1808
0,12	0,0478	0,24	0,0948	0,36		0,1406		0,48			0,1844
0,49	0,1879	1,02	0,3461	1,55		0,4394		2,16			0,4846
0,5	0,1915	1,03	0,3485	1,56		0,4406		2,18			4854
0,51	0,195	1,04	0,3508	1,57		0,4418		2,2			0,4861
0,52	0,1985	1,05	0,3531	1,58		0,4429		2,22			0,4868
0,53	0,2019	1,06	0,3554	1,59		0,4441		2,24			0,4875
0,54	0,2054	1,07	0,3577	1,6		0,4452		2,26			0,4881
0,55	0,2088	1,08	0,3599	1,61		0,4463		2,28			0,4887
0,56	0,2123	1,09	0,3621	1,62		0,4474		2,3			0,4893
0,57	0,2157	1,1	0,3643	1,63		0,4484		2,32			0,4898
0,58	0,219	1,11	0,3665	1,64		0,4495		2,34			0,4904
0,59	0,2224	1,12	0,3686	1,65		0,4505		2,36			0,4908
0,6	0,2257	1,13	0,3708	1,66		0,4515		2,38			0,4913
0,61	0,2291	1,14	0,3729	1,67		0,4525		2,4			0,4918
0,62	0,2324	1,15	0,3749	1,68		0,4535		2,42			0,4922
0,63	0,2357	1,16	0,377	1,69		0,4545		2,44			0,4927
0,64	0,2389	1,17	0,379	1,7		0,4554		2,46			0,4931
0,65	0,2422	1,18	0,381	1,71		0,4564		2,48			0,4934
0,66	0,2454	1,19	0,383	1,72		0,4573		2,5			0,4938
0,67	0,2486	1,2	0,3849	1,73		0,4582		2,52			0,4941
0,68	0,2517	1,21	0,3869	1,74		0,4591		2,54			0,4945
0,69	0,2549	1,22	0,3888	1,75		0,4599		2,56			0,4948
0,7	0,258	1,23	0,3907	1,76		0,4608		2,58			0,4951
0,71	0,2611	1,24	0,3925	1,77		0,4616		2,6			0,4953
0,72	0,2642	1,25	0,3914	1,78		0,4625		2,62			0,4956
0,73	0,2673	1,26	0,3962	1,79		0,4633		2,64			0,4959
0,74	0.2703	1,27	0,398	1,8		0,4641		2,66			0,4961
0,75	0,2734	1,28	0,3997	1,81		0,4649		2,68			0,4963
0,76	0,2764	1,29	0,4015	1,82		0,4656		2,7			0,4965
0,77	0,2794	1,3	0,4032	1,83		0,4664		2,72			0,4967
0,78	0,2823	1,31	0,4049	1,84		0,4671		2,74			0,4969

Сайт www.MatBuro.ru

©МатБюро — Решение задач по высшей математике, теории вероятностей

x	Φ(x)	x	Φ(x)	x	Φ(x)	x	Φ(x)
0,79	0,2852	1,32	0,4066	1,85	0,4678	2,76	0,4971
0,8	0,2881	1,33	0,4082	1,86	0,4686	2,78	0,4973
0,81	0,291	1,34	0,4099	1,87	0,4693	2,8	0,4974
0,82	0,2939	1,35	0,4115	1,88	0,4699	2,82	0,4976
0,83	0,2967	1,36	0,4131	1,89	0,4706	2,84	0,4977
0.84	0,2995	1,37	0,4147	1,9	0,4713	2,86	0,4979
0,85	0,3023	1,38	0,4162	1,91	0,4719	2,88	0,498
0,86	0,3051	1,39	0,4177	1,92	0,4726	2,9	0,4981
0,87	0,3078	1,4	0,4192	1,93	0,4732	2,92	0,4982
0,88	0,3106	1,41	0,4207	1,94	0,4738	2,94	0,4984
0,89	0,3133	1,42	0,4222	1,95	0,4744	2,96	0,4985
0,9	0,3159	1,43	0,4236	1,96	0,475	2,98	0,4986
0,91	0,3186	1,44	0,4251	1,97	0,4756	3	0,49865
0,92	0,3112	1,45	0,4265	1,98	0,4761	3,2	0,49931
0,93	0,3238	1,46	0,4279	1,99	0,4767	3,4	0,49966
0,94	0,3264	1,47	0,4292	2	0,4772	3,6	0,499841
0,95	0,3289	1,48	0,4306	2,02	0,4783	3,8	0,499928
0,96	0,3315	1,49	0,4319	2,04	0,4793	4	0,499968
0,97	0,334	1,5	0,4332	2,06	0,4803	4,5	0,499997
0,98	0,3365	1,51	0,4345	2,08	0,4812	5	0,5
0,99	0,3389	1,52	0,4357	2,1	0,4821
1	0,3413	1,53	0,437	2,12	0,483
1,01	0,3438	1,54	0,4382	2,14	0,4838

studfiles.net

Интегральная теорема Муавра-Лапласа

17 сентября 2015

Данная теорема является дальнейшим развитием схемы Бернулли и позволяет работать с диапазонами: какова вероятность, что число успехов будет лежать в пределах указанного отрезка.

Интегральная теорема Муавра-Лапласа. Пусть число испытаний $n$ достаточно велико, а вероятность успеха $0<\,p\,<1$. Пусть также$q=1-p$ — вероятность неудачного испытания. Тогда вероятность того, что число успехов будет лежать в пределах от ${{k}_{1}}$ до ${{k}_{2}}$, можно примерно посчитать по формуле:

\[{{P}_{n}}\left( {{k}_{1}};{{k}_{2}} \right)\approx \Phi \left( \frac{{{k}_{2}}-np}{\sqrt{npq}} \right)-\Phi \left( \frac{{{k}_{1}}-np}{\sqrt{npq}} \right)\]

где

\[\Phi \left( x \right)=\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}\int\limits_{0}^{x}{{{e}^{-\frac{{{t}^{2}}}{2}}}dt}\]

Функция $\Phi \left( x \right)$ называется функцией Лапласа и содержит в себе интеграл, который не считается напрямую. Как следствие, значения этой функции сведены в таблицу, которую можно загрузить прямо на этой странице.

Разумеется, в таблице приведены не все возможные значения. Для больших значений $x$ (скажем, для $x>6$ ) считают, что $\Phi \left( x \right)\approx 0,5$. Кроме того, функция Лапласа является нечётной, поэтому из неё можно выносить знак «минус»:

\[\Phi \left( -x \right)=-\Phi \left( x \right)\]

Это прямо следует из определения, в котором присутствует определённый интеграл.

Что такое «интегральная теорема Муавра-Лапласса»?

Сегодня мы разберем интегральную теорему Муавра-Лапласа. Это «старшая сестра» второй версии теоремы Муавра-Лапласа, разобранной в прошлом уроке. Во-первых, разберемся, зачем вообще нужна еще одна теорема — интегральная.

Допустим, у нас есть 1000 изделий, о которых известно, что там в среднем есть 10% брака. Однако это не означает, что в партии из 1000 изделий будет ровно 100 бракованных изделий, скорее всего, их будет 101-102 или 98, но не 100. Вероятность того, что будет ровно 100, легко считается при помощи более легкой теоремы Муавра-Лапласа, и вы можете сами убедиться, что она будет велика. В этом случае возникает вопрос: «Какова тогда вероятность, что деталей будет от 95 до 105, либо от 50 до 150?». Считать такую конструкцию при помощи первой версии теоремы Муавра-Лапласса крайне сложно, потому что нам придется отдельно посчитать, какова возможность того, что бракованных изделий будет 50, 51, 51 и так до 150, т.е. сто отдельных однотипных вычислений. Это очень трудоемко и бессмысленно. Вот именно в таких примерах нам на помощь приходит интегральная теорема Муавра-Лапласа. С назначением самой интегральной теоремы все ясно, теперь давайте разберемся с ее формулой.

Вероятность того, что при $n$-испытаниях количество успешных испытаний будет в пределах от ${{K}_{1}}$ до ${{K}_{2}}$ выражается следующей формулой:

\[{{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\]

Сама же функция $F$ называется функцией Муавра-Лапласа, и выглядит она следующим образом:

\[F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\]

Сразу же скажу, что данный интеграл «красиво» не считается, поэтому вместо красивого интегрирования у вас всегда будет в распоряжении таблица значений функции Лапласа, и с помощью этой таблицы, а также некоторых способов, которые мы разберем чуть позже в этом уроке, мы и будем решать все примеры на данную интегральную теорему.

Разумеется, возникает вопрос «А что это за буквы такие — $n$, $q$, $p$?».

С $n$, я думаю, все понятно — это число испытаний.

$p$ — это вероятность успеха в каждом конкретном испытании.

$q$ — по аналогии с формулой Бернули это вероятность провала, т.е. неуспеха в каждом конкретносм испытании. Считатеся она по очень простой формуле:

\[q=1-p\]

Надеюсь, с буквами теперь понятно, поэтому перейдем к решению конкретных примеров.

Задача № 1

Начнем мы с довольно простой задачи, однако уже на ее примеры мы познакомимся с особенностями применения интегральной теоремы Муавра-Лапласса.

Известно, что в среднем 5% студентов носят очки. Какова вероятность того, что из 200 студентов, находящихся в аудитории, окажется не менее 10%, носящих очки?

В первую очередь, давайте запишем саму интегральную теорему Муавра-Лапласса:

\[{{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\]

При этом полезно помнить еще одну формулу:

\[F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\]

Собственно, из-за этого интеграла, присутствуещего в функции Муавра-Лапласса, сама теорема и называется интегральной.

При первом взгляде на эту интегральную теорему многие ученики приходят в шок — уж больно много здесь разных конструкций, корней, вычислений и т.д. На самом деле, все очень просто, и сейчас вы сами в этом убедитесь.

Для начала давайте выпишем все значения. Итак, нам известно следующее:

• Всего студентов 200 — $n=200$;
• Вероятность попадания студента, который носит очки — $p=0,05$;
• Вероятность того, что студенты не носят очки будет равна $1-0,05=0,95$.

Далее мы можем найти $\sqrt{npq}$:

\[\sqrt{npq}=\sqrt{200\cdot 0,05\cdot 0,95}=\sqrt{9,5}\approx 3,08\]

Разумеется, такие вычисления выполняются на калькуляторе.

Кроме того, в нашей формуле, в интегральной теореме Муавра-Лапласса, мы наблюдаем выражение $np$ — произведение количества испытаний на вероятность успеха:

\[np=200\cdot 0,05=10\]

Давайте перепишем формулу с учетом всех фактов:

\[{{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{200-10}{3,08} \right)-F\left( \frac{20-10}{3,08} \right)=\]

\[=F\left( 61,7 \right)-F\left( 3,25 \right)\]

И вот здесь нас поджидает первая проблема: если мы посмотрим на таблицу значений, то значение $3,25$ здесь еще присутствует, но вот числа от $60$ и более здесь вообще не представлены. Для решения этого вопроса предлагаю взглянуть на исходную формулу Муавра-Лапласса:

\[F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\]

При больших «иксах» ${{e}^{-\frac{{{t}^{2}}}{2}}}$ будет очень маленьким числом, т.е. возрастание $x$ дает очень маленькую, стремящуюся к «нулю» добавку к вероятности. Поэтому для всех «иксов», начиная от шести и более примерно считается, что значение функции Лапласса равно $0,5$. $$ $$

Итак, продолжим наше решение:

\[{{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx 0,5-0,49942=0,00058=5,8\cdot {{10}^{-4}}\]

Нюансы решения

Как видите, ничего сверхъестественного. Все применение интегральной теоремы Муавра-Лапласса сводится к следующему:

1. Аккуратно выписать все значения: число испытаний, вероятность и «единицу» «минус» вероятность.
2. Посчитать корни и величины.
3. Пробежаться глазами по таблице и найти значение функции в тех точках, которые мы получили.

Однако, как вы понимаете, это была самая простая задача — существуют гораздо более сложные и навороченные. И один из самых «противных» типов заданий на применение интегральной теоремы Муавра-Лапласса состоит в том, что общая вероятность, которую мы обычно рассчитываем по формуле, нам известна, а необходимо найти либо ${{K}_{1}}$, либо ${{K}_{2}}$. Вот именно сейчас такую задачу мы и решим. 

Самое обидное, что именно такие чаще всего и попадаются на всяких контрольных, зачетах и экзаменах. Они будут вам встречаться на исследованиях, где необходимо определить какую-нибудь статистическую величину. Поэтому именно сейчас мы попытаемся решить такую задачу.

Задача № 2

Театр, вмещающий 1000 человек, имеет два разных входа, каждым из которых любой зритель может воспользоваться с равной вероятностью. Около каждого входа имеется свой гардероб. Сколько мест должно быть в каждом гардеробе, чтобы с вероятностью в 0,99 любой зритель смог раздеться в том гардеробе, в который он обратился сразу после входа в театр.

Я думаю, очевидно, что в данной задаче общее количество испытаний, т.е. человек, которые придут в театр, не более 1000 — $n=1000$.

Всего входов два, при этом в каждый с одинаковой вероятностью входит один и тот же человек — $p=\frac{1}{2}$.

Следовательно, $q=1-\frac{1}{2}=\frac{1}{2}$.

Кроме того, общая возможность того, что при 1000 испытаний количество успеха попадет в искомый нами диапазон, равно 0,99 — ${{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)=0,99$. Остается разобраться с числами ${{K}_{1}}$ и ${{K}_{2}}$, т.е. границами диапазона. ${{K}_{1}}$ — наименьшее количество людей, которые могут обратиться в данный гардероб. Очевидно, будет «ноль», потому что меньше нуля прийти не может — ${{K}_{1}}=0$. Остается вопрос: «Чему равно ${{K}_{2}}$?». Именно это нам и нужно найти по условию.

Опять запишем интегральную теорему Муавра-Лапласса:

\[{{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\]

Посмотрим:

\[np=1000\cdot \frac{1}{2}=500\]

\[\sqrt{npq}=\sqrt{1000\cdot \frac{1}{2}\cdot \frac{1}{2}}=\sqrt{250}=5\sqrt{10}=15,8\]

Подставим все полученные числа в формулу, с учетом того, что ${{K}_{1}}=0$:

\[{{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-500}{15,8} \right)-F\left( \frac{0-500}{15,8} \right)=0,99\]

Теперь внимательно посмотрим на эту формулу. Отдельно посчитаем значение функции Муавра-Лапласса в следующей точке:

\[F\left( \frac{-500}{15,8} \right)=-F\left( 31,6 \right)=0,5\]

Итого переписывая, мы получаем: 

\[F\left( \frac{{{K}_{2}}-500}{15,8} \right)+0,5=0,99\]

\[F\left( \frac{{{K}_{2}}-500}{15,8} \right)=+0,49\]

Единственный способ, при помощи которого можно решить этот пример — это взять таблицу значений функции Муавра-Лапласса и посмотреть, когда она равна $0,49$, при каком $x$. Проблема состоит в том, что точного значения мы не найдем. Однако есть значение функции Муавра-Лапласса в точках $2,32$ и $2,34$ :

\[F\left( 2,32 \right)=0,48983\]

\[F\left( 2,34 \right)=0,49036\]

Где-то между ними лежит наша искомая величина $0,49$. А между числами $2,32$ и $2,34$ лежит величина $2,33$. Так и запишем:

\[\frac{{{K}_{2}}-500}{15,8}=2,33\]

Теперь нам осталось решить простейшее уравнение:

\[{{K}_{2}}-500=2,33\cdot 15,8\]

\[{{K}_{2}}-500=36,8\]

\[{{K}_{2}}\approx 536,8=537\]

Ответ: 537.

Каверзные вопросы

Подождите, есть несколько вопросов. Во-первых, почему мы так легко вынесли «минус» из функции Лапласса наружу, а во-вторых, почему мы постоянно пользуемся калькулятором?

Давайте для начала посмотрим на формулу функции Муавра-Лапласса:

\[F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\]

Это, прежде всего, интеграл от «нуля» до $x$ в прелах четной функции, поэтому если перед $x$ внезапно появится «минус», мы можем поменять местами верхние и нижнее пределы интегрирования, при том перед самим интегралом также появится знак «минус», и больше никаких изменений не будет. Это одно из ключевых свойств определенного интеграла.

Кроме того, в таблице значений все аргументы функций приведены именно в виде десятичных дробей, поэтому считая значение функции, мы просто обязаны перевести то, что стоит у нас внутри скобок, в десятичную дробь, в том числе с помощью калькулятора.

В заключение посмотрим еще одну задачку, в которой мы не только еще раз отработаем использование стандартной формулы, но и вспомним, что такое вторая версия теоремы Муавра-Лапласса, отличная от интегральной, и в каких ситуациях она применяется.

Задача № 3

Радиотелеграфная станция передает цифровой текст. В силу наличия помех каждая цифра независимо от других может быть неправильно принята с вероятностью 0,01. Найдите вероятность того, что в принятом тексте, содержащем 1100 цифр, будет:

а) 15 ошибок;

б) менее 20 ошибок.

Решение пункта б)

Что касается б), то тут все вполне очевидно — это чистейшая теорема Муавра-Лапласса, причем интегральная. Так и запишем:

\[n=1100\]

\[p=0,01\]

\[q=0,99\]

\[{{K}_{1}}=0\]

\[{{K}_{2}}=19\]

Теперь запишем интегральную формулу Муавра-Лапласса:

\[{{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\]

Посчитаем:

\[np=1100\cdot 0,01=11\]

\[\sqrt{npq}=\sqrt{11\cdot 0,99}=\sqrt{\frac{11\cdot 11\cdot 9}{100}}=\sqrt{\frac{{{11}^{2}}\cdot {{3}^{2}}}{{{10}^{2}}}}=\frac{11\cdot 3}{10}=3,3\]

Осталось подставить числа в формулу:

\[{{P}_{1100}}\left( 0;19 \right)\approx F\left( \frac{19-11}{3,3} \right)-F\left( \frac{0-11}{3,3} \right)=\]

\[=F\left( 2,42 \right)+F\left( 3,33 \right)=\]

\[=0,49224+0,49960=0,99184\approx 0,99\]

Ответ: 0,99

Решение пункта а)

А теперь давайте разберемся с пунктом а). В нем от нас требуется, чтобы при тех же исходных данных, вычислить, что в итоге появится ровно 15 ошибок.

Очевидно, что это идеальная задача для применения второй версии теоремы Муавра-Лапласса — не интегральной. Давайте я ее запишу:\[\]

\[{{P}_{n}}\left( K \right)\approx \frac{1}{\sqrt{npq}}\cdot \varphi \left( \frac{K-np}{\sqrt{npq}} \right)\]

Выпишем известные данные:

\[n=1100\]

\[p=0,01\]

\[q=0,99\]

Решим:

\[{{P}_{1100}}\left( 15 \right)\approx \frac{1}{3,3}\cdot \varphi \left( \frac{15-11}{3,3} \right)\approx 0,303\cdot \varphi \left( 1,212 \right)\approx \]

\[\approx 0,303\cdot 0,1919\approx 0,058\]

Ответ: 0,058.

Ключевые моменты

Вот и все, что я хотел вам рассказать об интегральной теореме Муавра-Лапласса, такой, на первый взгляд сложной, но очень простой на практике. Все, что вам необходимо — это

1. Знать сами формулы для обеих теорем Муавра-Лапласса, в том числе, интегральной.
2. Грамотно считать корни и элементы $np$, которые являются матожиданием.

В ближайшее время я размещу на своем сайте целый комплект задач, посвященный теоремам Муавра-Лапласса, в том числе, интегральной. Поэтому присоединяйтесь к нам на YouTube, ставьте лайки и пишите комментарии. До новых встреч!   

Смотрите также:

1. Локальная теорема Муавра — Лапласа
2. Схема Бернулли. Примеры решения задач
3. Тест по теории вероятностей (1 вариант)
4. Задача 7 — геометрический смысл производной
5. Периодические десятичные дроби
6. Задача B5: площадь фигур с вершиной в начале координат

www.berdov.com