Деление дробей | Математика
Деление дробей — тема, которая включает в себя действия с обыкновенными дробями, смешанными числами и десятичными дробями.
Запишем на одной странице все правила, касающиеся деления обыкновенных дробей, смешанных чисел и натуральных чисел.
1. Деление обыкновенных дробей.
Чтобы разделить дробь на дробь, надо делимое умножить на число, обратное делителю.
(то есть первую дробь нужно переписать без изменений и умножить её на «перевёрнутую» вторую дробь).
При умножении дробей проще сокращать множители, чем результат.
Если в результате получается неправильная дробь, нужно выделить из неё целую часть.
Примеры деления обыкновенных дробей:
2. Деление обыкновенной дроби на натуральное число.
Применив правило деления обыкновенных дробей
приходим к выводу:
Чтобы разделить дробь на натуральное число, надо знаменатель умножить на это число, а числитель оставить без изменения
Примеры деления обыкновенной дроби на число:
Заметим, что если числитель дроби делится на число без остатка, при делении можно числитель разделить на число, а знаменатель оставить тем же:
Стоит ли запоминать ещё одно правило или использовать одно правило для всех случаев — решать вам.
3. Деление натурального числа на дробь.
Применив правило деления обыкновенных дробей
приходим к выводу:
чтобы разделить натуральное число на дробь, надо в числитель записать произведения этого числа и знаменателя, а в знаменатель записать числитель.
Можно запомнить это правило и применять его в дальнейшем. А можно делить число на дробь, применяя для всех случаев деления дробей одно правило. Выбирайте, что для вас удобнее.
Примеры деления натурального числа на дробь:
Здесь можно сделать ещё один вывод:
4. Деление смешанных чисел.
Чтобы разделить смешанные числа (смешанные дроби), надо превратить их в неправильные дроби и разделить по правилу деления обыкновенных дробей:
(эту формулу запоминать не надо. Достаточно знать, как переводить смешанные дроби в неправильные и делить обыкновенные дроби).
Примеры деления смешанных дробей:
Примеры деления смешанного числа и обыкновенной дроби:
В следующий раз рассмотрим все правила, касающиеся деления десятичных дробей.
www.for6cl.uznateshe.ru
Деление дробей
Деление обыкновенных дробей
Чтобы разделить две дроби нужно выполнить следующие шаги:
- 1 Перевернуть вторую дробь(поменять числитель и знаменатель местами) и умножить полученные дроби . Следующие шаги, 2—4, в точности повторяют процесс умножения дробей.
- 2 Перемножить числители дробей между собой 5 × 4 = 20.
- 3 Перемножить знаменатели дробей между собой 8 × 3 = 24.
- 4 Сократим полученную дробь , в результате получим .
Деление обыкновенных дробей можно записать в виде:
При деление дробей не имеет значения, имеют ли они одинаковый знаменатель или разный.
Пример Выполните деление дробей
.
Чтобы проверить результат деления дробей, можно воспользоваться калькулятором дробей.
Пример Разделить дроби .
.
Деление дроби на число
Чтобы разделить дробь на число, нужно умножить знаменатель на числитель, а числитель оставить без изменения, затем сократить дробь.
Пример Разделим дробь на число
.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
calcs.su
Умножение дробей, деление дробей
Умножение обыкновенных дробей
Определение 1
Умножение дробей рассматривается как действие нахождения дроби от дроби.
Рассмотрим пример.
Пусть на тарелке лежит $\frac{1}{3}$ часть яблока. Нужно найти $\frac{1}{2}$ часть от нее. Необходимая часть является результатом умножения дробей $\frac{1}{3}$ и $\frac{1}{2}$. Результат умножения двух обыкновенных дробей — это обыкновенная дробь.
Умножение двух обыкновенных дробей
Правило умножения обыкновенных дробей:
Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:
Пример 1
Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.
Решение.
Воспользуемся правилом умножения обыкновенных дробей:
\[\frac{3}{7}\cdot \frac{5}{11}=\frac{3\cdot 5}{7\cdot 11}=\frac{15}{77}\]Ответ: $\frac{15}{77}$
Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.
Пример 2
Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.
Решение.
Используем правило умножения обыкновенных дробей:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}\]В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:
Краткое решение:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}=\frac{1}{24}\]Ответ: $\frac{1}{24}.$
При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.
Пример 3
Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.
Решение.
Воспользуемся формулой умножения обыкновенных дробей:
\[\frac{6}{75}\cdot \frac{15}{24}=\frac{6\cdot 15}{75\cdot 24}\]Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$. Разложим числитель и знаменатель на простые множители и произведем сокращение:
\[\frac{6\cdot 15}{75\cdot 24}=\frac{2\cdot 3\cdot 3\cdot 5}{3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3}=\frac{1}{5\cdot 2\cdot 2}=\frac{1}{20}\] Ответ: $\frac{1}{20}.$При умножении дробей можно применять переместительный закон:
Умножение обыкновенной дроби на натуральное число
Правило умножения обыкновенной дроби на натуральное число:
Результатом умножения дроби на натуральное число является дробь, у которой числитель равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби:
где $\frac{a}{b}$ — обыкновенная дробь, $n$ — натуральное число.
Пример 4
Выполнить умножение дроби $\frac{3}{17}$ на $4$.
Решение.
Воспользуемся правилом умножения обыкновенной дроби на натуральное число:
\[\frac{3}{17}\cdot 4=\frac{3\cdot 4}{17}=\frac{12}{17}\]Ответ: $\frac{12}{17}.$
Не стоит забывать о проверке результата умножения на сократимость дроби или на неправильную дробь.
Пример 5
Умножить дробь $\frac{7}{15}$ на число $3$.
Решение.
Воспользуемся формулой умножения дроби на натуральное число:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}\]По признаку деления на число $3$} можно определить, что полученную дробь можно сократить:
\[\frac{21}{15}=\frac{21:3}{15:3}=\frac{7}{5}\]В результате получили неправильную дробь. Выделим целую часть:
\[\frac{7}{5}=1\frac{2}{5}\]Краткое решение:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}=\frac{7}{5}=1\frac{2}{5}\]Сократить дроби также можно было заменой чисел в числителе и знаменателе на их разложения на простые множители. В таком случае решение можно было записать так:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{7\cdot 3}{3\cdot 5}=\frac{7}{5}=1\frac{2}{5}\]Ответ: $1\frac{2}{5}.$
При умножении дроби на натуральное число можно использовать переместительный закон:
Деление обыкновенных дробей
Операция деления является обратной к умножению и результатом ее является дробь, на которую нужно умножить известную дробь чтобы получить известное произведение двух дробей.
Деление двух обыкновенных дробей
Правило деления обыкновенных дробей:
При делении обыкновенной дроби $\frac{a}{b}$ на дробь $\frac{c}{d}$ необходимо делимое умножить на число, которое является обратным делителю:
Пример 6
Выполнить деление дробей $\frac{7}{4}$ и $\frac{3}{5}$.
Решение.
Числом, обратным делителю $\frac{3}{5}$, является дробь $\frac{5}{3}$. Воспользуемся правилом деления обыкновенных дробей:
\[\frac{7}{4}:\frac{3}{5}=\frac{7}{4}\cdot \frac{5}{3}=\frac{7\cdot 5}{4\cdot 3}=\frac{35}{12}\]Ответ: $\frac{35}{12}.$
Результат деления дробей необходимо проверять на сократимость дроби и на возможность выделения целой части из неправильной дроби.
Пример 7
Выполнить деление дробей $\frac{8}{15}:\frac{12}{35}$.
Решение.
Применим правило деления дробей:
\[\frac{8}{15}:\frac{12}{35}=\frac{8}{15}\cdot \frac{35}{12}=\frac{8\cdot 35}{15\cdot 12}\]Очевидно, что числитель и знаменатель полученной дроби можно разложить на простые множители и произвести сокращение:
В результате получили неправильную дробь, из которой выделим целую часть:
\[\frac{14}{9}=1\frac{5}{9}\]Ответ: $1\frac{5}{9}.$
spravochnick.ru
Умножение и деление обыкновенных дробей
Правило 1.
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения.
Правило 2.
Чтобы умножить дробь на дробь, надо:
1. найти произведение числителей и произведение знаменателей этих дробей
2. первое произведение записать числителе, а второе — знаменателем.
Правило 3.
Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Правило 4.
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
Пример 1.
Вычислите
Пример 2.
Вычислите
Пример 3.
Вычислите
Пример 4.
Вычислите
ya-znau.ru
Умножение и деление алгебраических дробей
Мы умеем выполнять умножение и деление арифметических дробей, например:
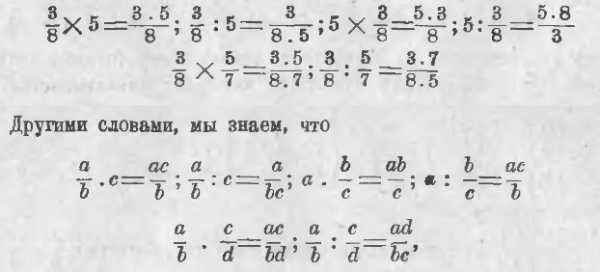
если буквы a, b, c и d обозначают арифметические целые числа.
Возникает вопрос, не остаются ли в силе эти равенства, если a, b, c и d будут обозначать: 1) какие-нибудь арифметические числа и 2) любые относительные числа.
Прежде всего придется рассмотреть сложные дроби, например:


Этих примеров уже достаточно, чтобы убедиться в справедливости равенств, относящихся к умножению и делению дробей, когда числа a, b, c и d какие угодно (целые или дробные) арифметические. Заметим, что основных равенств лишь 2, а именно:
Остается теперь рассмотреть, останутся ли справедливыми эти равенства, если некоторые из чисел a, b, c и d предположить отрицательными: если, например, a отрицательное число, b, c и d – положительные, то дробь отрицательна, а дробь положительна; поэтому, например, от деления на должно получиться отрицательное число, но мы видим, что, согласно нашему предположению, и выражение должно выразить отрицательное число, т. е. равенство оправдывается и в этом случае. Легко также рассмотреть и другие предположения для знаков числе a, b, c и d. Результатом этого рассмотрения является убеждение в справедливости равенств
и для случая, когда a, b, c и d выражают любые относительные числа, т. е. для умножения и деления алгебраических дробей остаются в силе те же правила, как и для арифметических.
Теперь мы можем выполнять умножение и деление алгебраических дробей. Наибольшие затруднения представляет здесь вопрос о сокращении дробей, получаемых после умножения или деления. Если алгебраические дроби одночленные, то сокращение полученного результата не представит затруднений, а если дроби алгебраические, то является необходимым предварительно числителя и знаменателя каждой из данных дробей разлагать на множители.
Примеры:
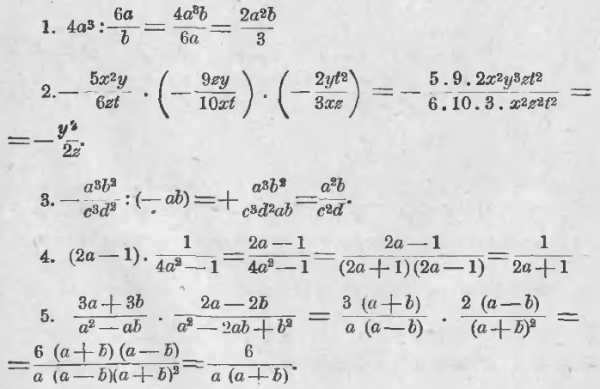
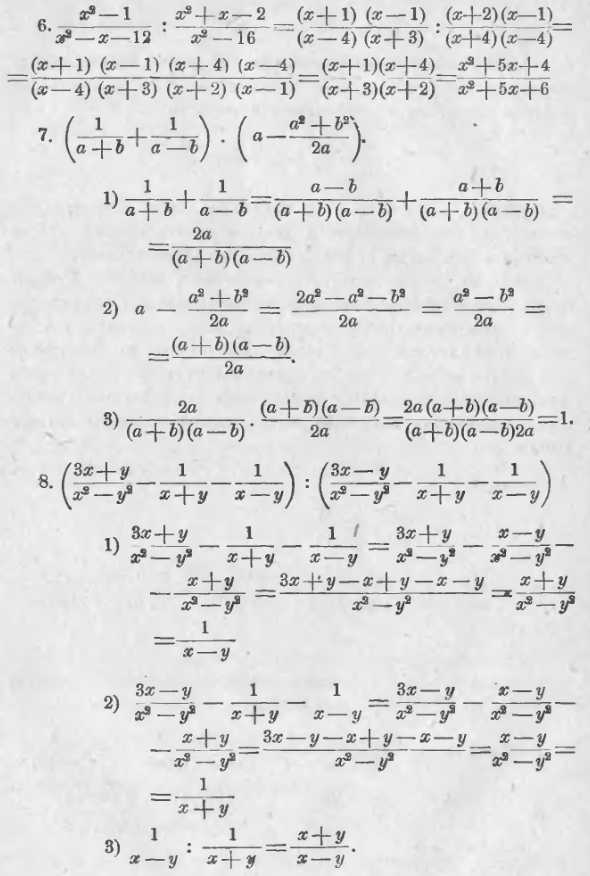
maths-public.ru
Деление обыкновенных дробей. Видеоурок. Математика 6 Класс
Как выполнить деление обыкновенных дробей? Как разделить смешанные числа? Как найти частное от деления обыкновенной дроби на натуральное число? Данный урок посвящен развернутому ответу на эти вопросы. Новое правило иллюстрируется примерами.
Вторая часть урока посвящена задачам на составление уравнений. Представленные рассуждения позволяют продолжить формирование навыка решения задач данного типа.
Тема: Умножение и деление обыкновенных дробей
Урок: Деление обыкновенных дробей
Площадь прямоугольника м2. Длина одной стороны . Найдите длину другой стороны.
Решение.
Обозначим за (м) длину неизвестной стороны.
Найдем площадь прямоугольника: (м2)
С другой стороны, по условию (м2). Составим уравнение:
Умножим обе части равенства на , т.е. на число обратное числу .
Произведение равно единице, поэтому
.
Ответ: длина другой стороны прямоугольника м.
В ходе решения мы искали неизвестный множитель. Вообще, чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. Таким образом, . С другой стороны. Значит, Деление можно заменить умножением на число обратное делителю.
Разделить на .
Решение.
;
Представим смешанные числа в виде неправильных дробей. Затем заменим деление умножением на число обратное делителю. (т.е. поменяем в делителе числитель и знаменатель местами, а деление заменим умножением.
=
Разделить на .
Решение.
Представим смешанное число в виде неправильной дроби. Затем заменим деление умножением на число обратное делителю.
С какой скоростью должен двигаться трактор, чтобы пройти 15 км за часа?
Решение
Чтобы найти пройденный путь нужно скорость умножить на время:
Значит, чтобы найти скорость нужно путь разделить на время: .
Чтобы выполнить деление на обыкновенную дробь , мы делимое 15 умножили на число обратное делителю, т.е. на дробь .
Ответ: 18км/ч.
Сумма двух чисел равна . Одно из них в раза больше другого. Найдите эти числа.
Решение.
Обозначим за первое число. Тогда второе число равно
Сумма первого и второго числа: , а по условию это .
Составим уравнение: = .
= .
.
Упростим левую часть, вынесем общий множитель за скобки. Первое слагаемое – это просто «x», поэтому в скобках от первого слагаемого остается единица.
Чтобы найти неизвестный множитель нужно произведение разделить на известный.
;
Представим смешанные числа в виде неправильных дробей и выполним деление
первое число. Тогда второе число:
Ответ: первое число, второе число .
Два пешехода вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 5 км. Скорость первого пешехода составляла скорости второго. Найдите скорость каждого пешехода, если они встретились через полчаса.
Решение.
Обозначим за (км/ч) скорость второго пешехода.
Тогда скорость первого равна (км/ч)
За полчаса, т.е. за , первый прошел (км), а второй (км)
Значит, вместе они прошили , а по условию это км.
Составим уравнение: .
5 |
Упростим левую часть, вынесем общий множитель за скобки. Второе слагаемое – это «x», поэтому в скобках от первого слагаемого остается единица.
;
Умножили левую и правую часть на 2.
Чтобы найти неизвестный множитель нужно произведение разделить на известный.
Представим смешанное число в виде неправильной дроби и выполним деление.
Решив уравнение, мы нашли значение переменной . Значит, скорость второго пешехода равна 6 (км/ч). Тогда скорость первого пешехода (км/ч).
Ответ: (км/ч) и 6 (км/ч).
Список рекомендованной литературы
- Математика 6. Виленкин Н.Я. Жохов В.И.Чесноков А.С. Шварцбурд С.И, Мнемозина. М.2012.
- Математика 6 класс. Мерзляк А.Г., Полонский В.В., Якир М.С. Гимназия. 2006
interneturok.ru
Как делить дроби | Математика
Чтобы понять, как делить дроби, изучим правило и на примерах рассмотрим, как его применять.
Правило деления обыкновенных дробей
Чтобы разделить две дроби, надо первое число умножить на число, обратное ко второму (то есть первую дробь умножаем на перевернутую вторую).
Примеры деления обыкновенных дробей:
Чтобы разделить эти дроби, первую дробь переписываем и умножаем на дробь, обратную ко второй (делимое умножаем на число, обратное делителю). Сократить здесь ничего нельзя.
Чтобы разделить данные дроби, первое число переписываем без изменений и умножаем на число, обратное ко второму. Сокращаем 6 и 9 на 3, 20 и 25 — на 5. Полученная в результате дробь 8/15 — правильная и несократимая. Значит, это — окончательный ответ.
Первую дробь оставляем без изменений и умножаем на число, обратное ко второй дроби. Сокращаем 45 и 36 на 9, 65 и 52 — на 13. В результате получили неправильную дробь, из которой выделяем целую часть.
При деление двух равных чисел получаем единицу, поэтому сразу можем записать ответ.
Чтобы разделить дроби, первую умножаем на число, обратное ко второму. Сокращаем 23 и 23 на 23, 14 и 7 — на 7. Поскольку в знаменателе стоит единица, ответ — целое число.
В следующий раз рассмотрим, как разделить целое число на дробь.
www.for6cl.uznateshe.ru
