Окружность и круг — геометрия и искусство
В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.
В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет.
На рис. 2 изображены две окружности и цепочка окружностей, каждая из которых касается этих двух окружностей и двух соседей по цепочке. Швейцарский геометр Якоб Штейнер около 150 лет назад доказал следующее утверждение: если при некотором выборе третьей окружности цепочка замкнется, то она замкнется и при любом другом выборе третьей окружности. Отсюда следует, что если однажды цепочка не замкнулась, то она не замкнется при любом выборе третьей окружности. Художнику, рисовавшему изображенную цепочку, пришлось бы немало потрудиться, чтобы она получилась, или обратиться к математику для расчета расположения двух первых окружностей, при котором цепочка замыкается.
Вначале мы упомянули о колесе, но еще до колеса люди использовали круглые бревна — катки для перевозки тяжестей.
А можно ли использовать катки не круглой, а какой-нибудь другой формы? Немецкий инженер Франц Рело обнаружил, что таким же свойством обладают катки, форма которых изображена на рис. 3. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.
Энц. «Я познаю мир. Математика», 2006
geometry-and-art.ru
Тригонометрический круг — это… Что такое Тригонометрический круг?
Тригонометрический круг — построенная на плоскости с прямоугольными декартовыми координатами окружность, имеющая центр в точке начала координат и единичный радиус, т.е. единичная окружность, которая используется для геометрического определения тригонометрических функций. Название «тригонометрический круг» не совсем удачно, поскольку речь идёт об окружности, а не о круге; тем не менее, часто используется именно это название.
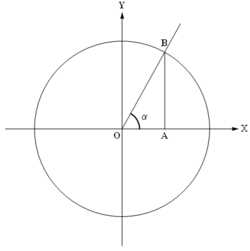Единичная окружность и угол , отложенный от оси абсцисс в верхнюю полуплоскостьОпределение тригонометрических функций произвольного угла строится с помощью тригонометрического круга следующим образом. Угол (назовём его ) откладывается от положительной полупрямой оси абсцисс в верхнюю полуплоскость («против часовой стрелки») и рассматривается точка пересечения полученного луча (составляющего угол с положительной полупрямой оси абсцисс) с единичной окружностью. Абсцисса этой точки принимается за , ордината — за . Для введения других тригонометрических функций используются дополнительные построения, такие, например, как линия тангенсов (прямая ) и линия котангенсов (прямая ).
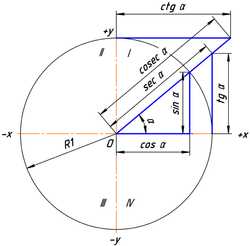Численные значения тригонометрических функций угла на тригонометрическом круге (радиус равен единице)dic.academic.ru
Круг (геометрия) — Циклопедия
Круг Окружность и круг // Мрия Урок [12:19]Круг — плоская геометрическая фигура, ограниченная окружностью. Иными словами, круг — это множество, состоящее из всех точек плоскости, расстояние от которых до данной точки (центр круга) не превышает заданного расстояния (радиуса). Окружность является границей круга.
Круг называется замкнутым или открытым в зависимости от того содержит ли он окружность, его ограничивающую. В декартовых координатах, открытый круг с центром [math](a, b)[/math] и радиусом R задаётся формулой:
- [math]D=\{(x, y)\in {\mathbb R^2}: (x-a)^2+(y-b)^2 \lt R^2\}[/math]
Закрытый круг задается нестрогим неравенством
- [math]\overline{ D }=\{(x, y)\in {\mathbb R^2}: (x-a)^2+(y-b)^2 \leqslant R^2\}.[/math]
Окружность является обобщением понятия круга на метрическом пространстве.
Иногда вместо термина круг используют термин диск.
Центр, радиус, хорда и диаметр круга являются центром, радиусом, хордой и диаметром соответствующего круга.
Площадью круга называется площадь плоской фигуры, ограниченной окружностью. Площадь круга вычисляется по формуле:
- [math]S=\pi r^2 \ [/math], де [math] \pi \approx 3{,}141592654[/math] — число пи (математическая константа).
Периметром круга называют длину окружности, его ограничивающей:
- [math]L=2\pi r .[/math]
cyclowiki.org
Круг — это… Круг — геометрическая фигура
Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас – атомы и молекулы – имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды – основы всего живого – тоже имеют круглую форму. Даже природа создает свою жизнь в кругах. Например, можно вспомнить про птичье гнездо – птицы вьют его также в этой форме.
Данная фигура в древних помыслах культур
Круг – это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.
Издавна круг – это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в этой фигуре эквивалентны, линия круга не имеет ни начала, ни конца.
А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг – конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.
Эта фигура имеет глубокий магический и мистический состав, которым его наделили многие поколения людей из разных культур. Но что собой представляет круг как фигура в геометрии?Что такое окружность
Часто понятие круга путают с понятием окружности. Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.
По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.
Что необходимо знать и чем уметь пользоваться, чтобы построить окружность
Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей. С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.
Какими величинами характеризуется окружность
Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим радиус окружности. Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.
Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.
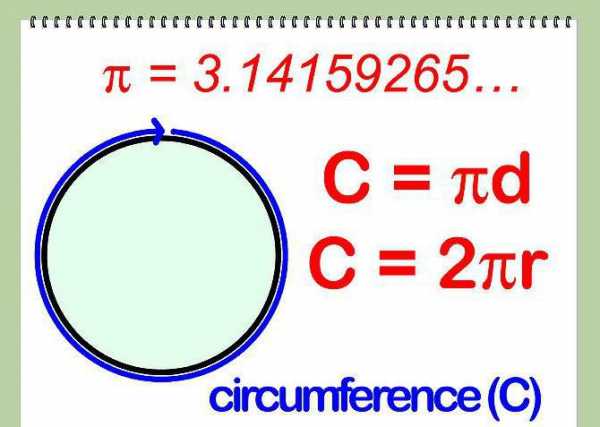
В этой формуле С – длина окружности, r – радиус окружности, d – диаметр, а число Пи – константа со значением 3,14.
Кстати, константа Пи была вычислена как раз из окружности.
Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.
В чем же главное отличие круга от окружности
По сути, окружность – это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее – это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.
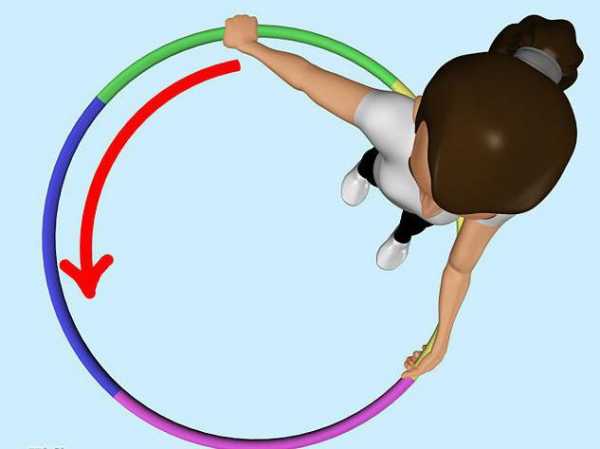
Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг – это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.
Перейдем непосредственно к понятию круга
Круг – геометрическая фигура, которая является частью плоскости, ограниченной окружностью. Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.
Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).
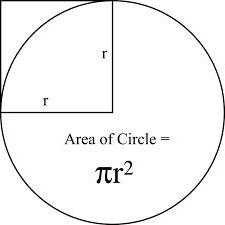
В данной формуле S – площадь, r – радиус круга. Число Пи – снова та же константа, равная 3,14.
Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.
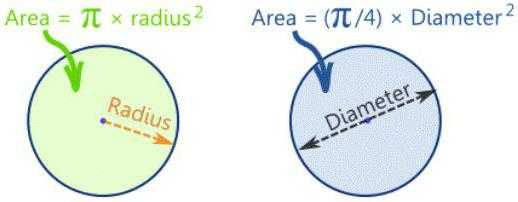
Одна четвертая появляется из того, что радиус – это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:
r*r = 1/2*d*1/2*d;
r*r = 1/4*d*d.
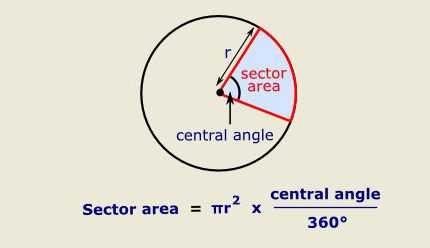
Круг – это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.
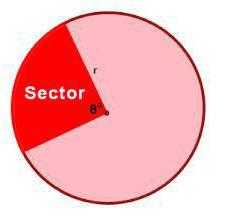
Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.
Использование фигуры в задачах с многоугольниками
Также круг – геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.
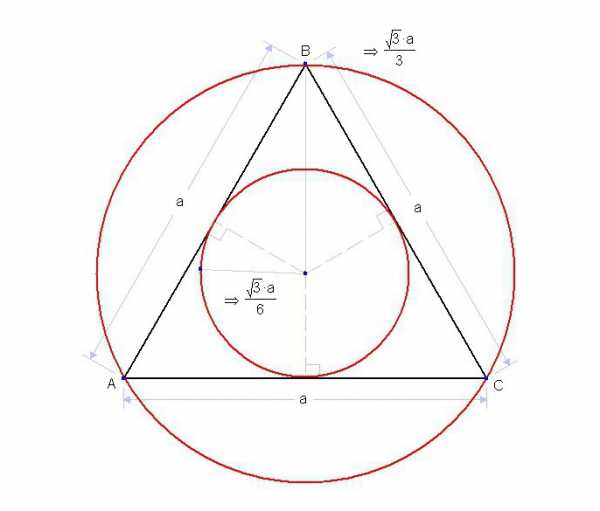
Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.
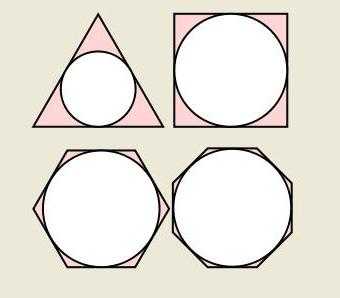
Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.
Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).
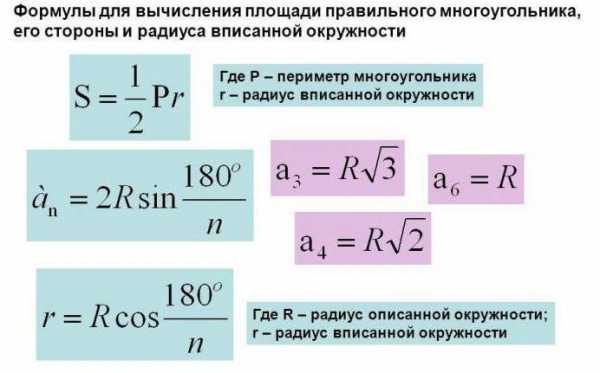
Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью
Перед нами канализационный люк. Если он открыт, то железная каемка люка – это окружность. Если он закрыт, то крышка выступает в роли круга.
Окружностью также можно назвать любое кольцо – золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, – тоже окружность.
А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, –это круг.
Горлышко бутылки или банки при виде сверху – это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.
Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.
fb.ru
Геометрические фигуры для детей. Круг.
Сегодня мы будем делать цыплёнка. Каким цветом цыпленок? Правильно, жёлтый. Из всех кругов выбери только желтые круги. Потом отложи отдельно голубые круги и зеленые.
Сначала просто выкладываем цыплёнка на бумаге без клея, чтобы у малыша было понимание того, что мы делаем, это также поможет избежать ошибок при работе с клеем.
Большой жёлтый круг будет туловищем цыпленка. Куда мы его положим? (предлагаем ребенку самому выбрать место на листе бумаги).
Кружок поменьше будет головой. Где у нашего цыплёнка будет голова? (ребёнок пусть снова сам выберет место, в какую сторону будет смотреть цыплёнок: вверх на небо и солнце или вниз на травку, может он будет клевать зернышки. Помогайте малышу фантазировать, предлагайте варианты. Маленьким можно подсказать, посоветовать, но не настаивайте, пусть он сам сделает выбор)
Где маленький чёрный кружок? Это будет глаз. Маленький треугольник — клюв, два одинаковых треугольника — лапки. Разложи фигуры на свои места.
Чего не хватает нашему цыпленку? Правильно, крыльев! У нас есть ещё 2 жёлтых круга, один мы отложим — это будет солнце, а из второго сделаем крылья. Как ты думаешь, как из одного круга сделать два крыла? (с этим справятся дети от трёх лет. Пусть ребёнок подержит круг в руках, повертит, приложит к бумаге, возможно, у него появится ответ).
Мы разрежем круг напополам. Для этого давай найдем центр круга. Где центр (середина) у круга? (можно дать ребенку карандаш и предложить самому найти и отметить центр с тыльной (не цветной!) стороны листа. Даже если точка не в центре, а где-то рядом, ничего страшного, похвалите кроху! Если ребёнок мал, сделайте все сами, объясняя каждое действие).
Через центр теперь проведем прямую линию, которая разделит круг напополам. По этой линии мы разрежем наш круг на две части. Получилось два крыла (обязательно разрезайте через точку (центр), указанную ребёнком, во-первых, ребёнок будет чувствовать, что его мнение важно для вас и вы прислушиваетесь к нему, а во-вторых — аппликация будет более художественной)
В ходе занятия для детей постарше можно объяснить, что такое полукруг (или вспомнить эту фигуру)
Посмотри, какие фигуры у нас получились. Это фигура называется полукруг. Пол круга — полукруг (повторяем несколько раз и предлагаем повторить название)
Где будут крылышки у нашего цыплёнка?
Цыплёнка выложили на бумаге, теперь можно приклеить его.
Цыплёнок готов.
Давай возьмём большие зелёные круги (или 1 круг) — это будет наша травка. Как ты думаешь, как из круга сделать травку? Правильно, снова разрезать напополам (повторяем шаги, как с крылышками: даём ребёнку отметить центр, разрезаем и приклеиваем снизу). Чтобы травка была натуральнее, можно сделать небольшие надрезы по округлой стороне.
На небо приклеиваем солнышко.
Облака можно сделать разными способами:
1. Наклеить кружки внахлёст, формируя облако. Разный размер кружков сделает форму облака более натуральной.
2. Разрезать круги напополам и также наклеивать внахлёст.
У нас получилось по-другому: Поля захотела сложить круги напополам и приклеить только одну половину круга. Таким образом мы уже делали другие поделки и этот вариант ей понравился.
Когда бумага окончательно высохнет, можно дорисовать солнечные лучи и цветы на травке карандашом. Можно сделать это пластилином. Пусть малыш выбирает сам.
novye-deti.ru
Круг (фигура) — это… Что такое Круг (фигура)?
ФИГУРА — (лат. figura, от fingere лепить, ваять). 1) наружный вид предмета, внешнее очертание. 2) в геометрии: очерк плоскости, чертеж. 3) в картах: туз, король, дама, валет. 4) в риторике: украшение речи, оборот, употребляемый для красоты слога. 5) в… … Словарь иностранных слов русского языка
КРУГ — один из наиболее распространённых элементов мифопоэтической символики гетерогенного происхождения и значения, но чаще всего выражающий идею единства, бесконечности и законченности, высшего совершенства. К. как фигура, образуемая правильной кривой … Энциклопедия мифологии
Фигура (в геометрии) — Фигура термин, формально применимый к произвольному множеству точек; тем не менее обычно фигурой называют множества на плоскости, которые ограничены конечным числом линий. Например: квадрат, круг, угол … Википедия
КРУГ — КРУГ, плоская геометрическая фигура, являющаяся местом точек, расположенных на одинаковом расстоянии от некоторой точки (центра). Это расстояние называется радиусом круга (r). Площадь круга вычисляется по формуле pr2, а длина окружности равна 2pr … Научно-технический энциклопедический словарь
Круг (значения) — В Викисловаре есть статья «круг» … Википедия
КРУГ — первичный символ единства и бесконечности, знак абсолюта и совершенства. Как бесконечная линия, круг символизирует время в вечности, а как макро космический знак образует круг Зодиака. Он является древнейшим мистическим символом, традиционно… … Символы, знаки, эмблемы. Энциклопедия
Фигура постоянной ширины — Треугольник Рело. Кривая постоянной ширины a плоская выпуклая кривая, длинa ортогональной проекции которой на любую прямую равна a. Иными словами, кривой постоянной ширины называется плоская выпуклая кривая, расстояние между любыми двумя… … Википедия
круг — ▲ плоская фигура ↑ внутри, окружность круг область (плоская фигура), ограниченная окружностью. в радиусе каком … Идеографический словарь русского языка
Фигура (геометрия) — У этого термина существуют и другие значения, см. Фигура. Фигура термин, формально применимый к произвольному множеству точек; тем не менее, обычно фигурой называют множества на плоскости, которые ограничены конечным числом линий. Примеры Квадрат … Википедия
Фигура — (от лат. figura внешние очертания, образ, изображение, способ, характер, свойство). 1) Характерная группа звуков (мелодич. Ф.) или ритмич. долей, длительностей (ритмич. Ф.), обычно неоднократно повторяющаяся. 2) Элемент… … Музыкальная энциклопедия
dic.academic.ru
ОСНОВЫ КОМПОЗИЦИИ: Геометрия в фотографии
09 Февраля 2016
Фотография — это то, чем становятся живопись, композиция, пластический ритм, геометрия, размещенные в считанных долях секунды (Анри Картье-Брессон).
Фото: Ronald Koster
Когда мы думаем о композиции в фотографии, первое, что приходит в голову — это золотое сечение, правило третей, формат кадра, контраст, точка съемки…
Но есть еще один важный элемент в композиции – геометрия. Геометрия в фотографии — это простые формы, такие как квадрат, треугольник, круг, прямые и кривые линии.
Геометрические объекты обычно вспомогательные, они усиливают восприятие и могут объединять отдельные элементы фотографии в единое целое. Выбирая ту или иную геометрическую форму в фотографии, автор может заранее акцентировать внимание будущего зрителя на его определенных зонах. Установлено, например, что углы квадрата оказываются очень активными зонами, а для круга или овала – это центр. Не случайно, с давних времен сложилась традиция портретов в овале. Углы не отвлекали внимание от главного — изображения лица. Наиболее распространенный и наиболее разносторонний геометрический инструмент – это линии. Более подробно о них читайте в нашей отдельной статье.
Фактически, любой объект окружающей среды можно сравнить с какой-либо геометрической фигурой, но все они пробуждают у зрителя разные эмоции и чувства. Простые геометрические формы, такие как круг и квадрат, намного быстрее фиксируются нашим глазом и воспринимаются мозгом, а следовательно и лучше запоминаются, нежели сложные и неправильные. Вообще выделяют три базовых фигуры. Это прямоугольник, треугольник и круг. Всё остальное – овал, квадрат, трапеция, эллипс, ромб всего лишь их вариации. Все они отличаются как графически, так и (не удивляйтесь) эмоционально.
КВАДРАТ В КОМПОЗИЦИИ
Квадрат — это самая устойчивая, законченная форма, готовая вызывать утверждающие образы. Он ассоциируется с такими понятиями, как порядок, стабильность, надежность, прочность. В то же время, квадрат воспринимается несколько приземленно и тяжеловесно.
Фото: Robertino Nikolic. “Свет играет с геометрией или геометрия со светом?”. Победитель конкурса Black & White Spider Awards, 2007.
Фото: Alma (источник — 1510.deviantart.com)
Фото: G. Diaz Deleon
ПРЯМОУГОЛЬНИК В КОМПОЗИЦИИ
Прямоугольник, расположенный̆ большей̆ стороной̆ по горизонтали вызывает ощущение стабильности, покоя, основательности.
Фото: Guerel Sahin
Фото: Guerel Sahin
Особенно гармонично смотрится, если он выполнен в пропорциях «золотого сечения». Прямоугольник, расположенный̆ большей̆ стороной̆ вдоль вертикали, создаёт ощущение лёгкости, воздушности.
Фото: Joe McNally
ТРЕУГОЛЬНИК В КОМПОЗИЦИИ
Треугольник — наиболее часто встречающаяся в природе форма. Треугольник — самая динамичная, неустойчивая форма, которая ассоциируется с движением, развитием, скоростью. В положении «вершиной вверх» вызывает образы устойчивости, стабильности (пирамида). Несколько треугольников — позитивное динамическое движение. В положении «вершиной вниз» – шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.
Фото: Josh Johnson
КРУГ В КОМПОЗИЦИИ
В форме круга более чем, в какой̆ — либо, выражена идея природы, земли, мироздания. Круги изобилуют как в природе, так и в мире рукотворных предметов. Поэтому такие понятия как «добро», «жизнь», «счастье», «процветание» ассоциируются у человека именно с этой̆ формой̆. Данная форма направляет взгляд внутрь кадра. Круг ассоциируется с чем-то легким, воздушным и при этом – уравновешенным. Но, в отличие от квадрата, это равновесие ближе к физическому понятию «неустойчивое равновесие». Круги — самые приятные глазу фигуры, которые можно смело использовать в кадре. Они сразу приковывают внимание зрителя и, благодаря своей идеальной симметричности, привносят в изображение гармонию. Поскольку у круга нет углов, он прекрасно контрастирует с прямоугольным обрезом кадра.
Фото: Steve McCurry
Фото: Georgios Karamanis
Фото: Elia Locardi
Как и треугольник, круг — очень эффектная геометрическая фигура, которую можно с пользой применить в композиции кадра, хотя и с другим смыслом. В отличие от диагоналей, заряжающих кадр динамикой и напряжением, кривые линии создают гармонию. Таким образом, можно создавать выразительные и информативные композиции, основанные на простых геометрических фигурах.
Фото: William Morris Kahn
Фото: Joe McNally
Фото: Joe McNally
Геометрические объекты можно условно разделить на три группы по их функциям: направляющие линии, разделители пространства и обрамление. Разделители пространства делят снимок на отдельные зоны, несущие свою смысловую нагрузку, но работающие вместе для создания единой композиции. Примером, простейшего разделителя пространства может послужить линия горизонта, отделяющая небо от поверхности моря. Очень хорошо смотрятся в качестве разделителя пространства треугольники, но и такие элементы, как диагонали и незамкнутые линии, тоже уверенно можно использовать.
Фото: Вадим Докторов
Обрамления носят функцию притяжения взгляда зрителя и его фокусировку на основном объекте. В качестве обрамляющих элементов отлично работают дверные проемы, арки, окна. Кроме того, великолепно с этой функцией справляются и естественные элементы, например, ветви деревьев. Важно чтобы обрамление присутствовало, как минимум, с двух сторон снимка и было выполнено в спокойной тональности, желательно более темной, чем главный объект, чтобы не отвлекать зрителя. Обрамляющий элемент должен иметь интересный цвет, форму, текстуру или иные примечательные характеристики, но стоит помнить, что обрамляющие элементы должны направлять, а не отвлекать. Особенно хорошо в этом плане работают треугольники или арки. Арка способна создать интересную динамичную композицию.
Фото: Guerel Sahin
Фото: Ian Plant
Фото: Tom La
Пробуйте, экспериментируйте и не забывайте, что в одном снимке вы можете использовать сразу несколько геометричских фигур для построения композиции.
Другие статьи о композиции в фотографии:
Золотое сечение в фотографии
Сила линий в фотографии
Формат кадра в фотографии
Контраст в фотографии (Часть 1)
Контраст в фотографии (Часть 2)
Точка съемки и выбор плана
Ракурс
Равновесие в композиции
photodzen.com