Четные и нечетные функции: графики и свойства
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. Для обозначения используют запись y=f(x). У каждой функции существует ряд основных свойств, таких как монотонность, четность, периодичность и другие.
Рассмотри подробнее свойство четности.
Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:
1. Область определения данной функции должна быть симметрична относительно точки О. То есть если некоторая точка a принадлежит области определения функции, то соответствующая точка -a тоже должна принадлежать области определения заданной функции.
2. Значение функции в точке х, принадлежащей области определения функции должно равняться значению функции в точке -х. То есть для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = f(-x).
График четной функции
Если построить график четной функции он будет симметричен относительно оси Оу.
Например, функция y=x^2 является четной. Проверим это. Область определения вся числовая ось, а значит, она симметрична относительно точки О.
Возьмем произвольное х=3. f(x)=3^2=9.
f(-x)=(-3)^2=9. Следовательно, f(x) = f(-x). Таким образом, у нас выполняются оба условия, значит функция четная. Ниже представлен график функции y=x^2.
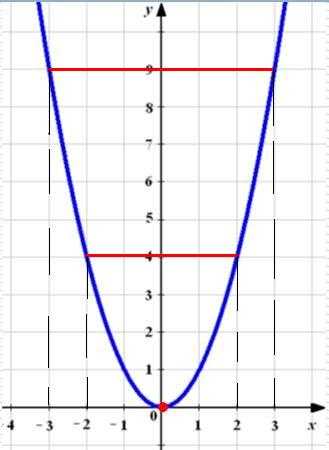
На рисунке видно, что график симметричен относительно оси Оу.
График нечетной функции
Функция y=f(x) называется нечетной, если она удовлетворяет следующим двум условиям:
1. Область определения данной функции должна быть симметрична относительно точки О. То есть если некоторая точка a принадлежит области определения функции, то соответствующая точка -a тоже должна принадлежать области определения заданной функции.
2. Для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = -f(x).
График нечетной функции симметричен относительно точки О – начала координат. Например, функция y=x^3 является нечетной. Проверим это. Область определения вся числовая ось, а значит, она симметрична относительно точки О.
Возьмем произвольное х=2. f(x)=2^3=8.
f(-x)=(-2)^3=-8. Следовательно, f(x) = -f(x). Таким образом, у нас выполняются оба условия, значит функция нечетная. Ниже представлен график функции y=x^3.
На рисунке наглядно представлено, что нечетная функция y=x^3 симметрична относительно начала координат.
Нужна помощь в учебе?
Предыдущая тема: Сумма бесконечной геометрической прогрессии при |q|
Следующая тема:   Функция y=x^n: линейная функция, квадратичная, кубическая и y=1/x
Все неприличные комментарии будут удаляться.
www.nado5.ru
Определения и свойства четных и нечетных функций. Видеоурок. Алгебра 9 Класс
В этом уроке будут даны строгие определения четных и нечетных функций, рассмотрены их свойства, решены некоторые задачи.
Определение 1: Функция называется четной, если для любого значения x из множества X выполняется равенство:
Определение 2: Функция называется нечетной, если для любого значения x из множества X выполняется равенство:
Примеры:
1. четная, т.к.
2. нечетная, т.к.
3. четная,
4. нечетная, .
Дадим развернутое определение четной функции.
Определение 3: Функцию называют четной, если выполнены два условия для всех
1. Область определения симметрична относительно нуля, т.е.
2.
Из определения вытекает важное свойство четной функции:
График четной функции симметричен относительно оси y (Рис. 1).
Дадим развернутое определение нечетной функции.
Определение 4: Функцию называют нечетной, если выполнены два условия для всех
1. Область определения симметрична относительно нуля, т.е.
interneturok.ru
Чётные и нечётные функции. Видеоурок. Алгебра 9 Класс
Данный видеоурок посвящен теме «Чётные и нечётные функции». Рассматривается определение и условия существования четной и нечетной функции. Строятся графики этих функций и описываются их свойства. Объясняется отличие четной функции от нечетной, а также ее отличие от функции общего вида.
Алгебра_ 9 класс
Итоговое повторение курса алгебры 9-го класса
Четные и нечетные функции
1.1.
Конспект.Какую функцию называют четной? А какую нечетной? Что такое функция общего вида? Как определить вид функции? Развернутый ответ на эти вопросы иллюстрируется исследованием на четность (нечетность) различных функций. Особое внимание уделено степенной функции
1. Какую функцию называют четной? Определение и свойство графика четной функции.
Функцию называют четной, если выполнены два условия:
1) Область определения симметрична относительно .
2) Для любого справедливо .
Разберем данное определение.
1) Первое условие означает: если отрезок то и отрезок .
Заметим, что если не симметрична, то функция является функцией общего вида.
2) Второе условие означает: если точка с координатами принадлежит графику функции, то и точка с координатами
Заметим, что точки симметричны относительно оси Оу.
Следствие: График четной функции симметричен относительно оси Оу.
Обратно: Если график функции не симметричен относительно оси Оу, то это график функции, которая не обладает свойством четности.
2. Какую функцию называют нечетной? Определение и свойство графика нечетной функции.
Функцию называют нечетной, если выполнены два условия:
1) Область определения симметрична относительно .
2) Для любого
interneturok.ru
Четные и нечетные функции
Определение. Функция 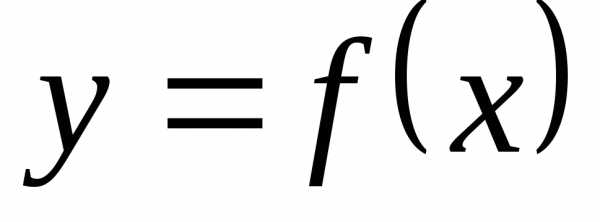 называетсячетной, если она не
изменяет своего значения при изменении
знака аргумента, т.е..
называетсячетной, если она не
изменяет своего значения при изменении
знака аргумента, т.е..
Например,
;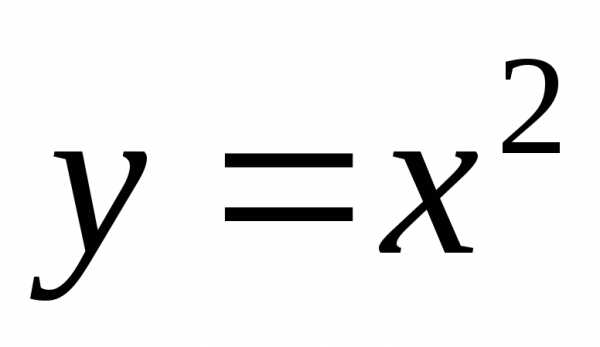 ;
;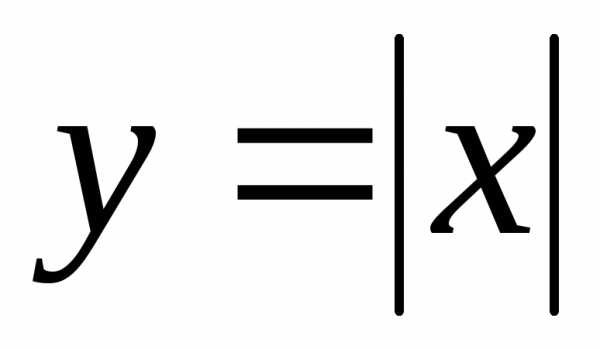 – четные функции.
– четные функции.
График четной
функции расположен симметрично
относительно оси 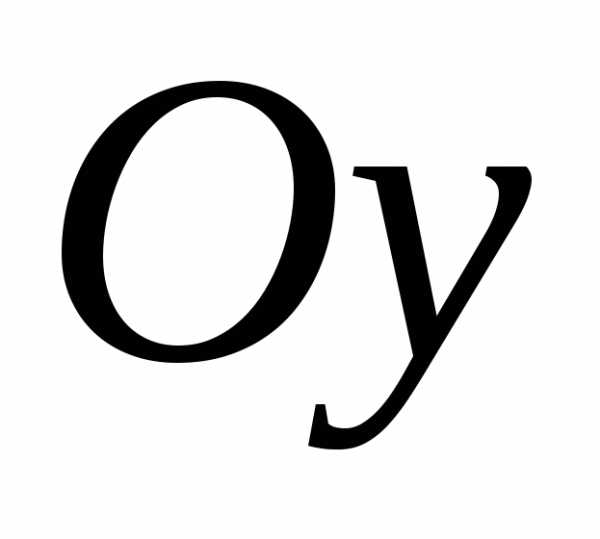 (рис.1.4).
(рис.1.4).
Рис. 1.4
Определение.
Функция называетсянечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е..
Например,
;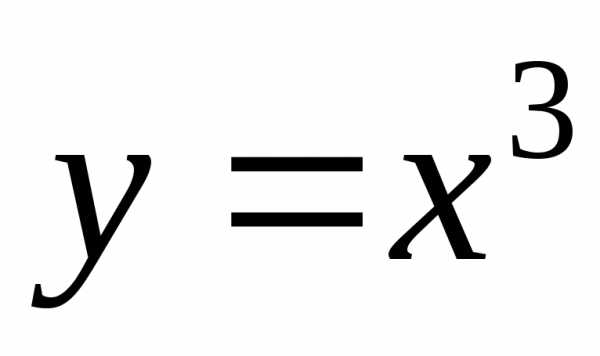 – нечетные функции.
– нечетные функции.
Рис. 1.5
Функция может быть ни четной. ни нечетной, и в этом случае её называют функцией общего вида.
Например, 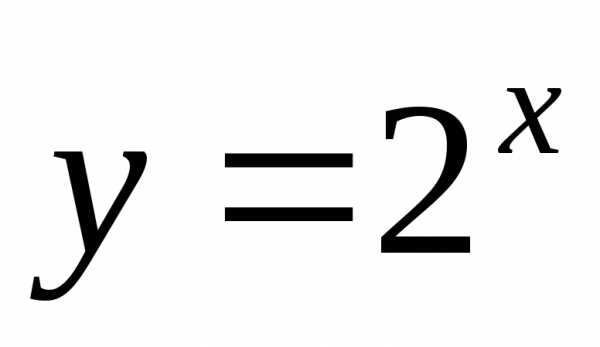 ;
;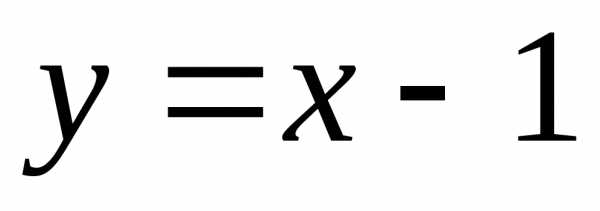 ;
;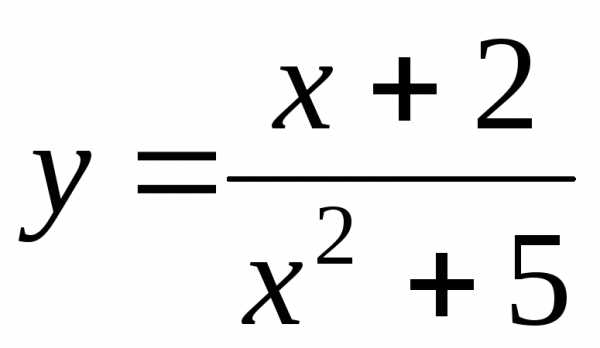 .
.
Графики таких
функций не симметричны ни относительно
оси 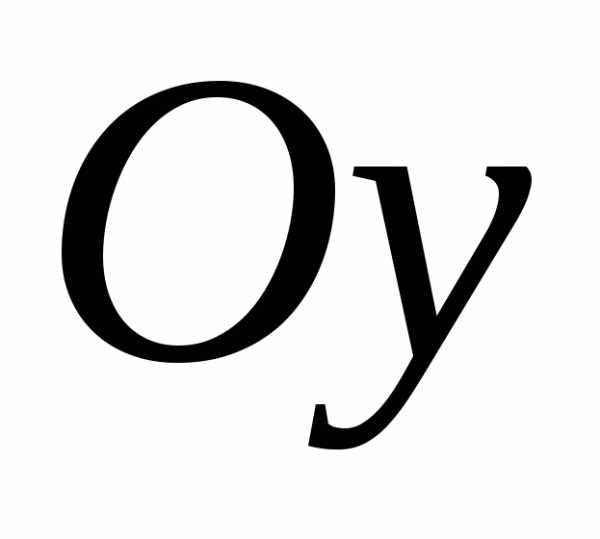 ,
ни относительно начала координат.
,
ни относительно начала координат.
Периодические функции
Определение.
Функция 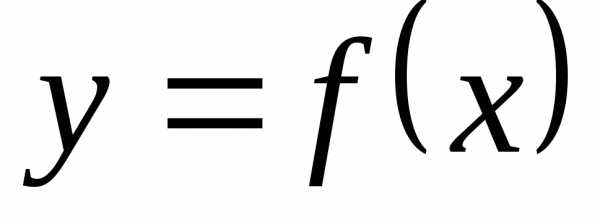 называется периодической, если существует
такое положительное число
называется периодической, если существует
такое положительное число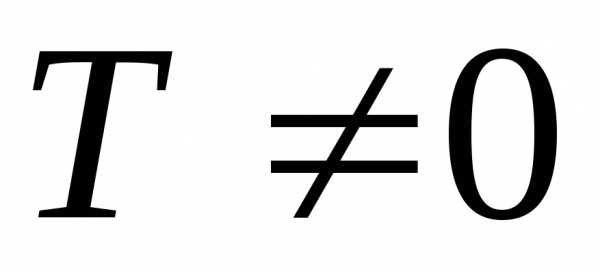 ,
чтов
области определения функции.
,
чтов
области определения функции.
Наименьшее из
положительных чисел Т, удовлетворяющих
условию определения, называетсяпериодомфункции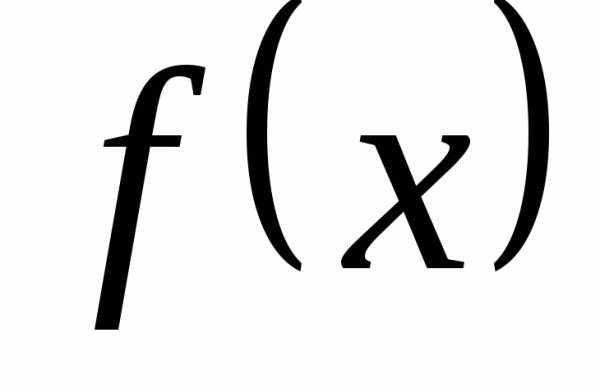 .
.
Например, функции
,являются периодическими с периодом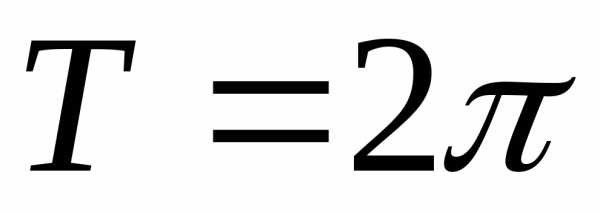 .
.
Нули функции
Определение.
Значение аргумента,
при котором функция обращается в нуль, 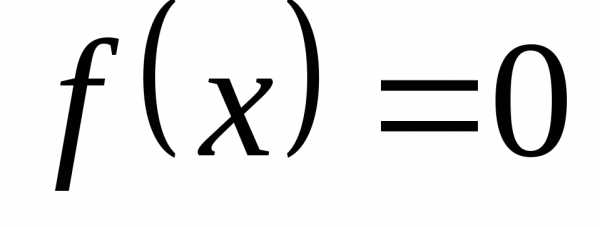 ,
называетсянулем функции.
,
называетсянулем функции.
Например, нулями
функции 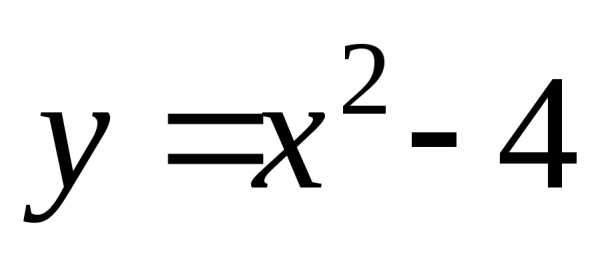 являются значения
являются значения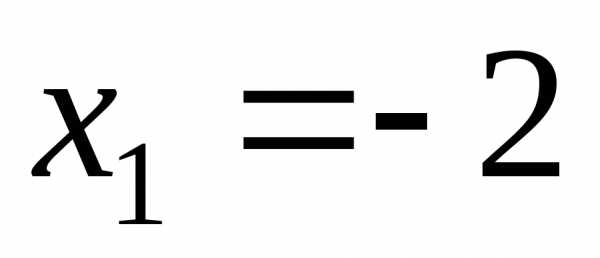 и
и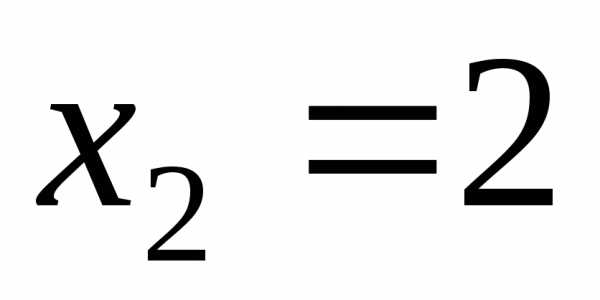 .
.
Монотонные функции
Определение.
Функция называется
Рис. 1.6 Рис. 1.7
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
Ограниченные функции
Определение.
Функция 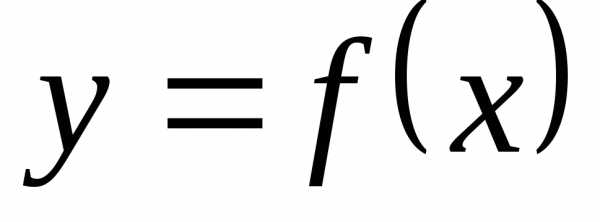 называетсяограниченнойна множествеХ, если существует такое число
называетсяограниченнойна множествеХ, если существует такое число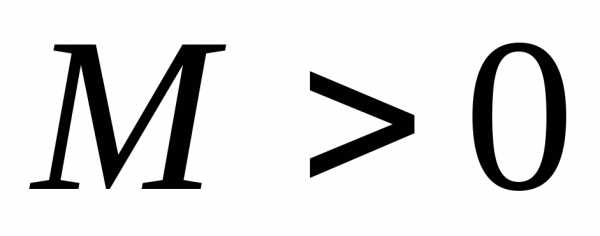 ,
что для всех
,
что для всех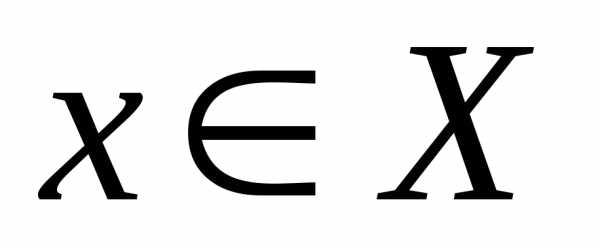 выполняется неравенство
выполняется неравенство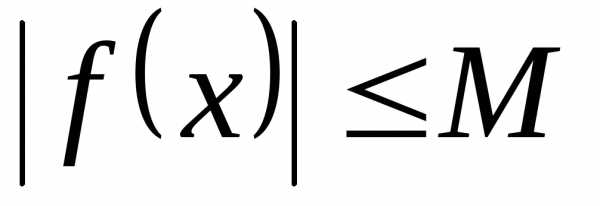 .
.
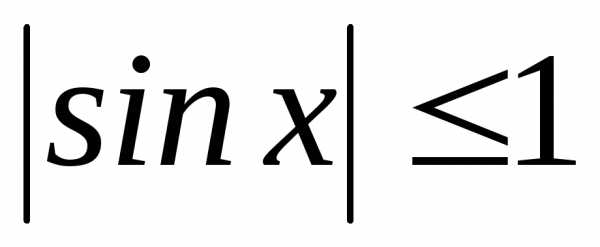 и
и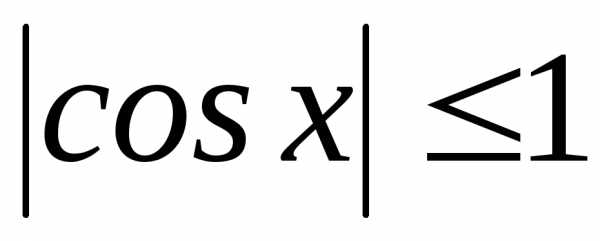 для.
для. График ограниченной
функции лежит между прямыми 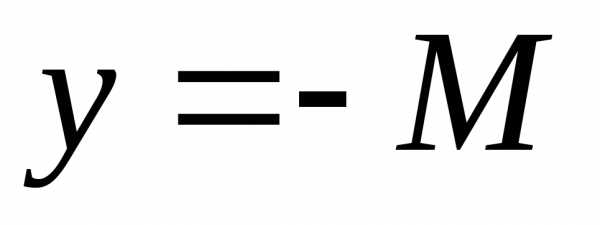 и
и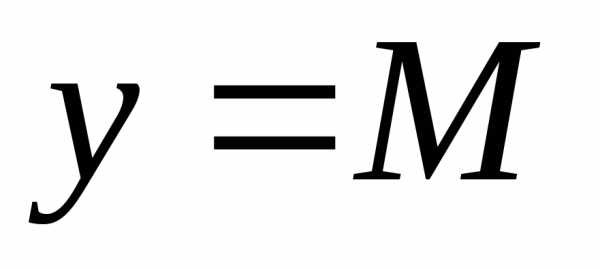 (рис.1.8).
(рис.1.8).
Рис. 1.8
УПРАЖНЕНИЯ
Найти область определения следующих функций:
1)
; Ответ: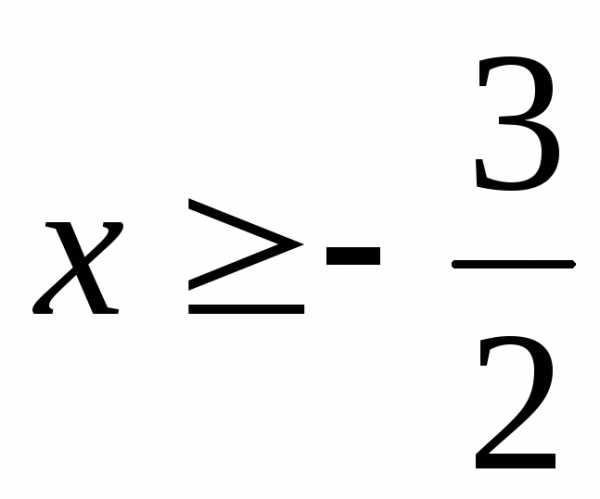 ;
;
2) 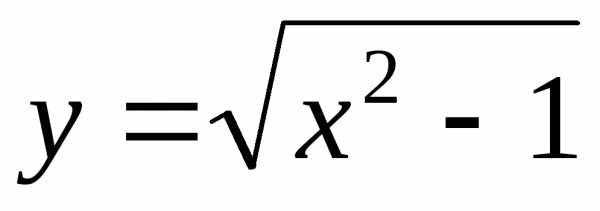 ; Ответ:
; Ответ: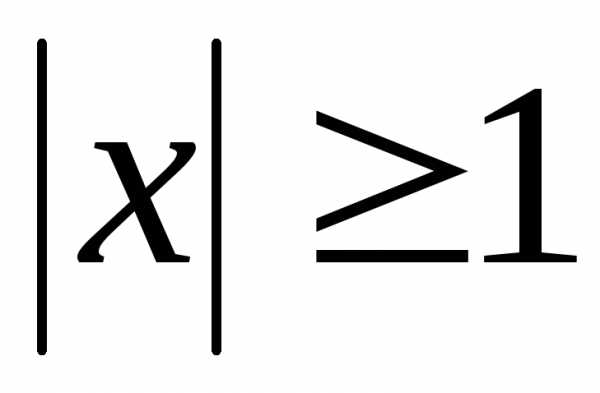 ;
;
3) 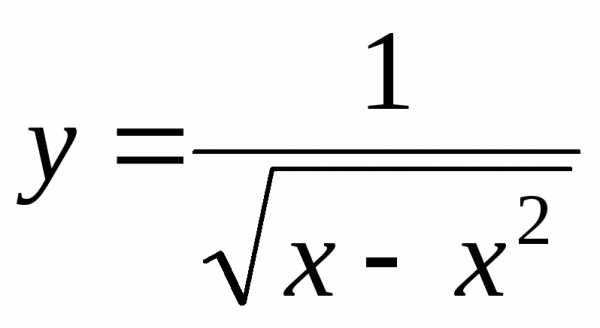 ; Ответ:;
; Ответ:;
4)
; Ответ: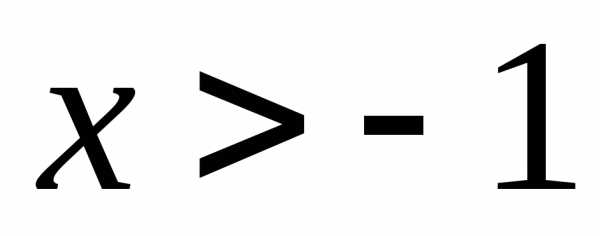
Найти множество значений функции:
1) ; Ответ:;
2) ; Ответ:;
3) ; Ответ:.
Найти
 ,
, ,
, ,
, ,
если.
,
если.
Ответ: 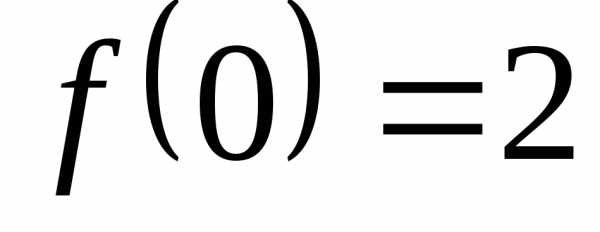 ;
; ;;.
;;.
Пусть
и и
и .
Найти
.
Найти
 .
.
Ответ: ;.
Установить чётность или нечётность функции:
1) ; Ответ: чётная;
2) ; Ответ: чётная;
3) 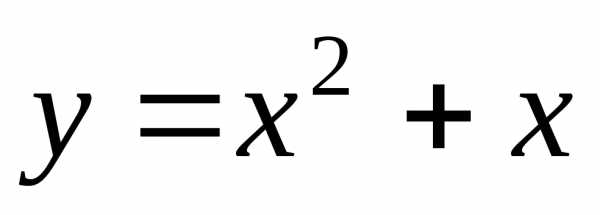 ; Ответ:
общего вида;
; Ответ:
общего вида;
4) ; Ответ: нечётная.
Найти основные периоды функций:
1)
; Ответ: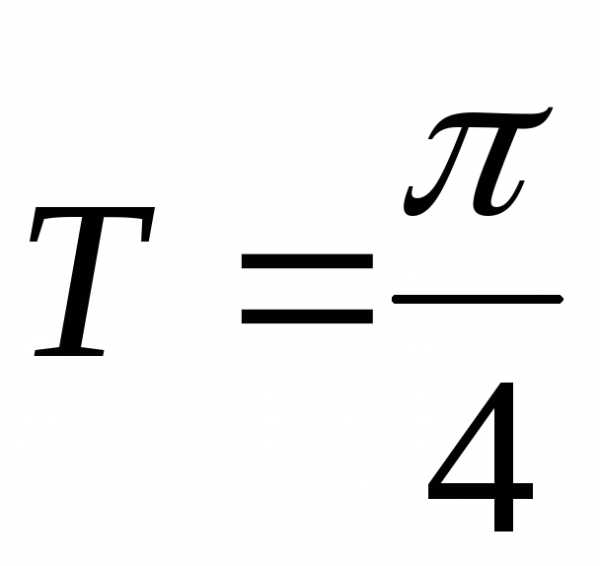 ;
;
2)
; Ответ: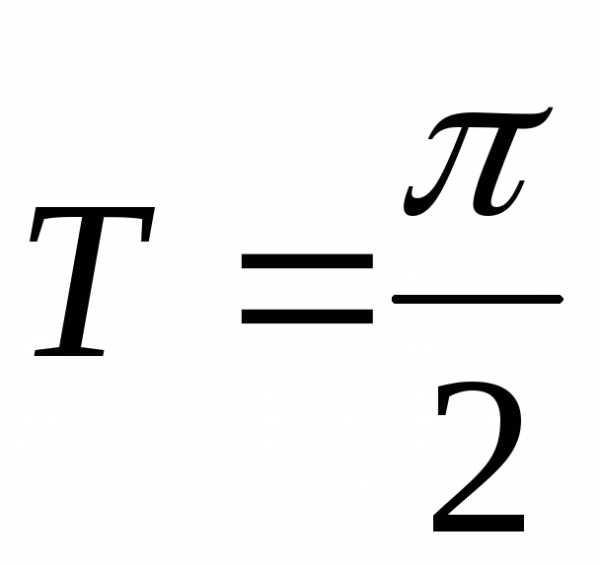 ;
;
3)
; Ответ: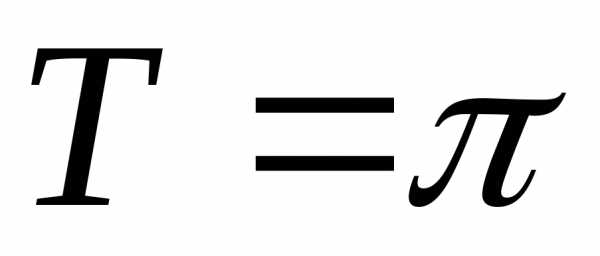 .
.
Введя промежуточные аргументы, представить данную функцию, как суперпозицию других функций:
1)
; Ответ: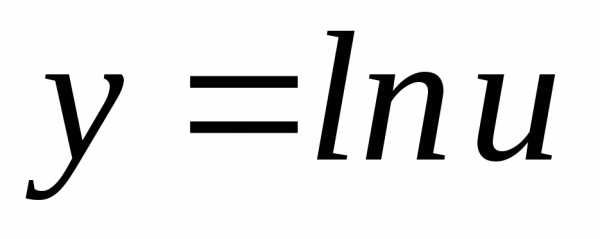 ;
;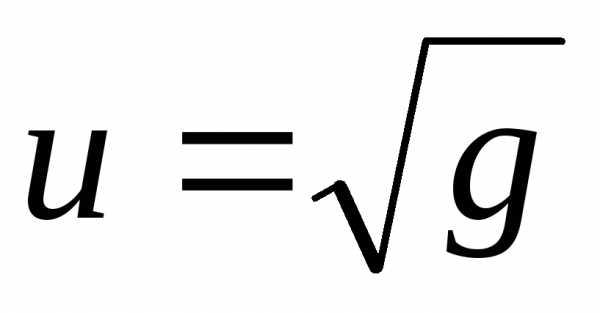 ;;
;;
2)
;
Ответ: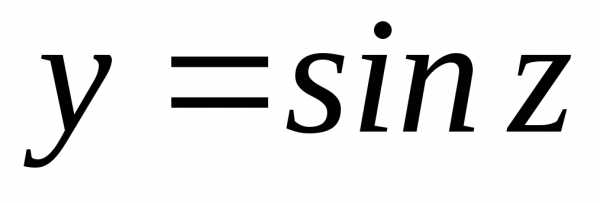 ;
;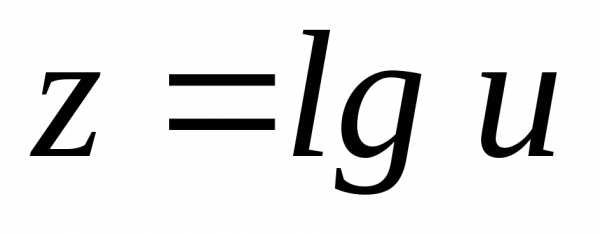 ;;
;;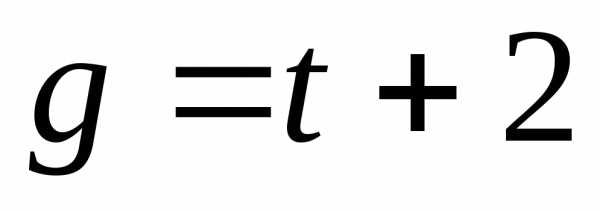 ;
;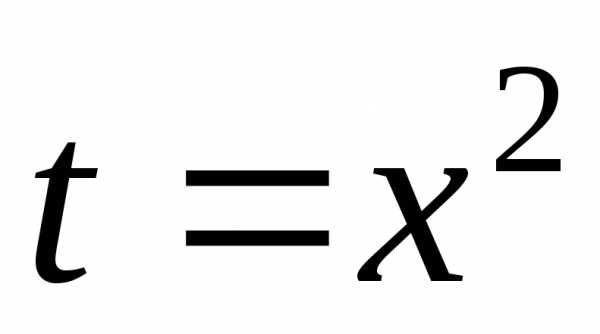 .
.
Для данных функций найти явные обратные:
1)
; Ответ: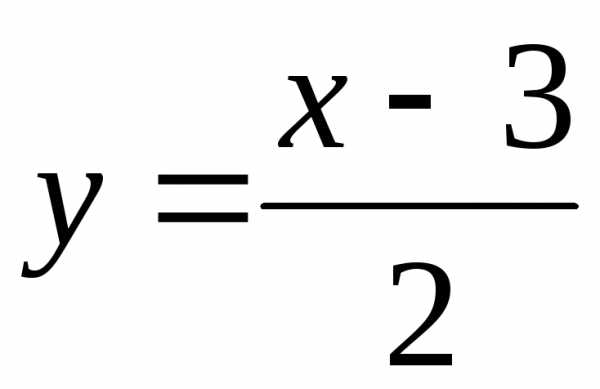 ;
;
2) 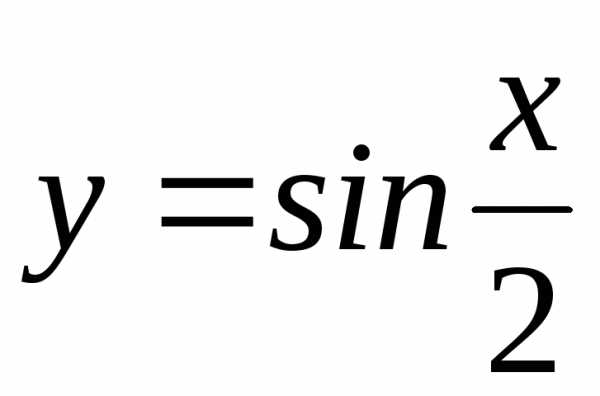 ; Ответ:;
; Ответ:;
3) 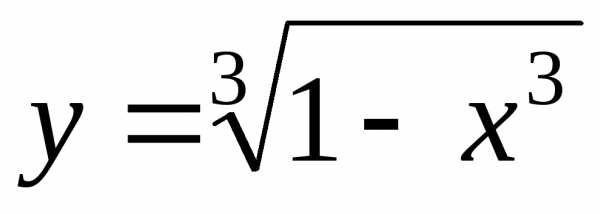 ; Ответ:
; Ответ: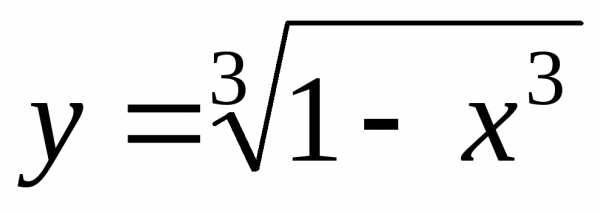 .
.
studfiles.net
Четные и нечетные функции
Четные функции
Определение 1
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться
\[f\left(x\right)=f(-x)\]Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
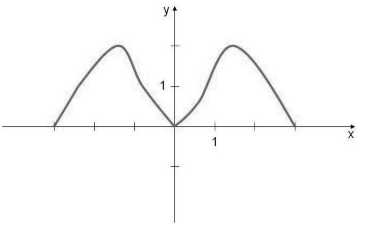
Рисунок 1.
Для исследования функции на четность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 1.
Нечетные функции
Определение 2
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться
\[f\left(-x\right)=-f(x)\]Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
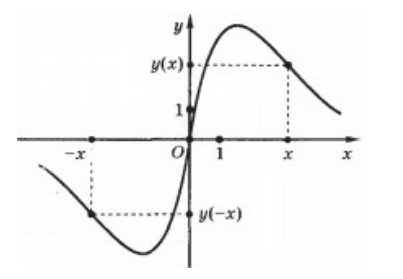
Рисунок 2.
Для исследования функции на нечетность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 2.
Функция общего вида
Определение 3
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть функцией общего вида, если она не будет ни четной, ни нечетной.
Для того чтобы понять, что данная функция является функцией общего вида, необходимо в его аналитической записи заменить переменную $x$ на переменную $—x$, произвести, при необходимости элементарные преобразования, и проверить невыполнение условий определений 1 и 2.
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
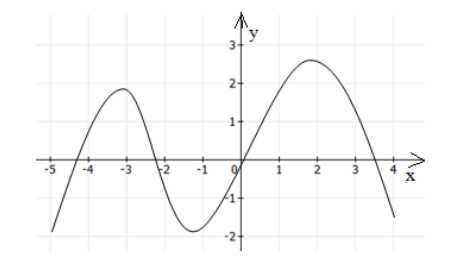
Рисунок 3.
Пример задачи
Пример 1
Исследовать функцию на четность и нечетность и построить их графики.
а) $f(x)=x^2+3$
б) $f(x)=\frac{x^2+4}{x}$
в) $f\left(x\right)=sinx+cosx$
Решение.
а) $f(x)=x^2+3$
$f\left(-x\right)={(-x)}^2+3=x^2+3=f(x)$\textit{ }следовательно, $f(x)$ — четная функция.
Изобразим её на графике:
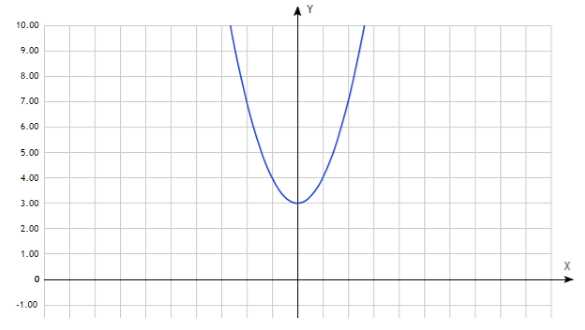
Рисунок 4.
б) $f(x)=\frac{x^2+4}{x}$
$f\left(-x\right)=\frac{{\left(-x\right)}^2+4}{-x}=-\frac{x^2+4}{x}$ следовательно, $f(x)$ — нечетная функция.
Изобразим её на графике:
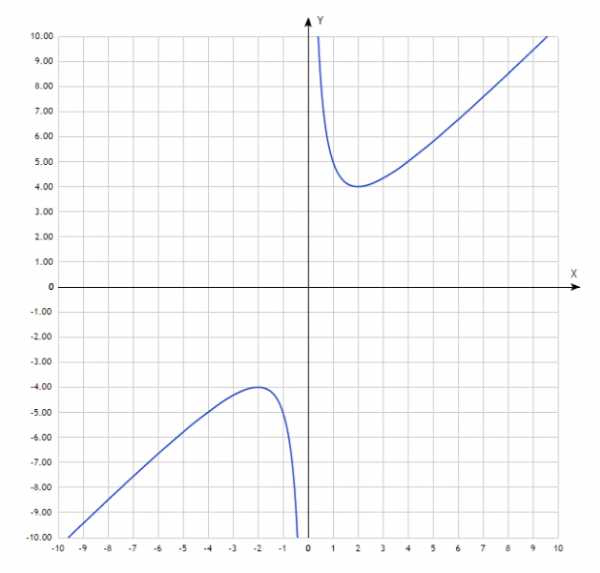
Рисунок 5.
в) $f\left(x\right)=sinx+cosx$
$f\left(-x\right)={\sin \left(-x\right)\ }+{\cos \left(-x\right)\ }=cosx-sinx$ следовательно, $f\left(x\right)$ — функция общего вида.
Изобразим её на графике:
Рисунок 6.
spravochnick.ru
2.3.Построение графиков чётной и нечётной функций
Как уже отмечалось, для чётной функции y=f(x) во всей области изменения её аргумента справедливо соотношение f(x)=f(- x). Следовательно, функция такого рода принимает одинаковые значения при всех значениях аргумента, равных по абсолютной величине, но противоположных по знаку. График чётной функции симметричен относительно оси ординат.
Для
построения графика чётной функции
y=f(x)
следует построить ветвь графика этой
функции только в области положительных
значений аргумента x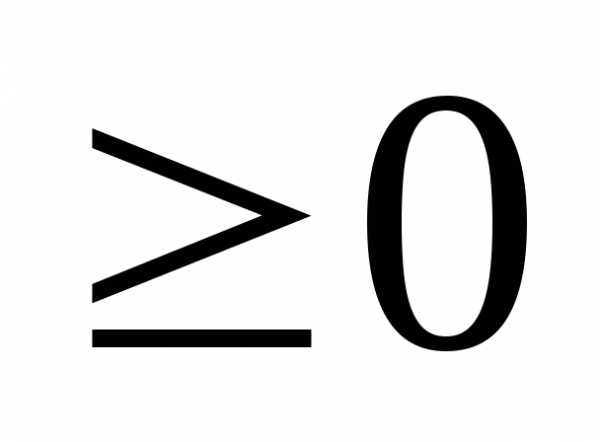 .
График функции y=f(x)
в области отрицательных значений
аргумента симметричен построенной
ветви относительно оси ординат и
получается отражением её относительно
этой оси.
.
График функции y=f(x)
в области отрицательных значений
аргумента симметричен построенной
ветви относительно оси ординат и
получается отражением её относительно
этой оси.
Пример
8. Построить
график функции y=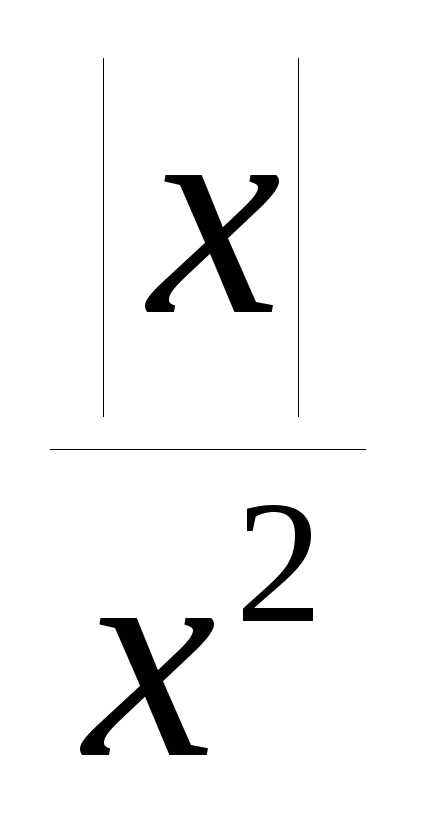 .
.
Р
е ш е н и е: Данная функция – чётная,
поэтому достаточно построить её график
лишь в области положительных значений
x
(точка x=0
не входит в область определения функции).
При x>0
исходная функция имеет вид y= .
График функцииy=
.
График функцииy=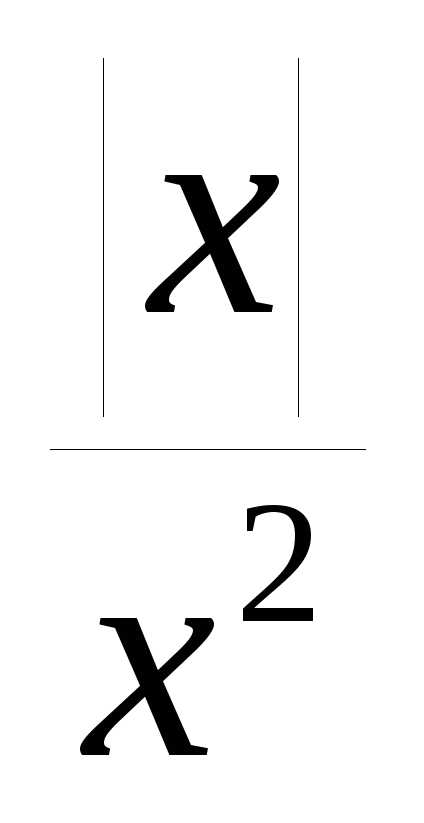 в области отрицательных значенийx
получаем отражением относительно оси
ординат (рис.11).
в области отрицательных значенийx
получаем отражением относительно оси
ординат (рис.11).
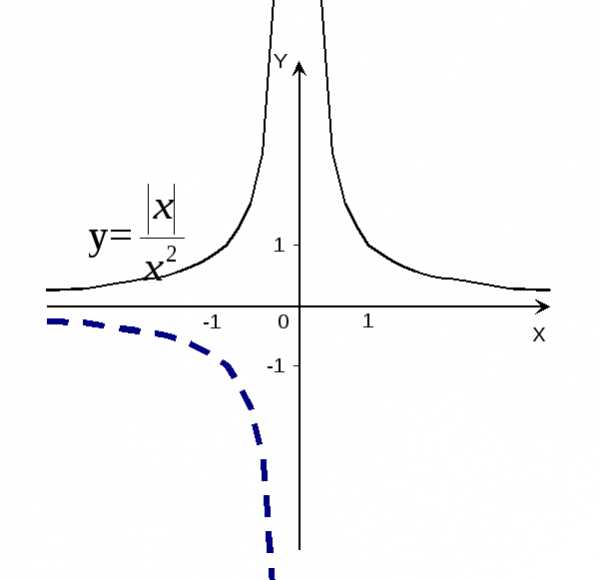
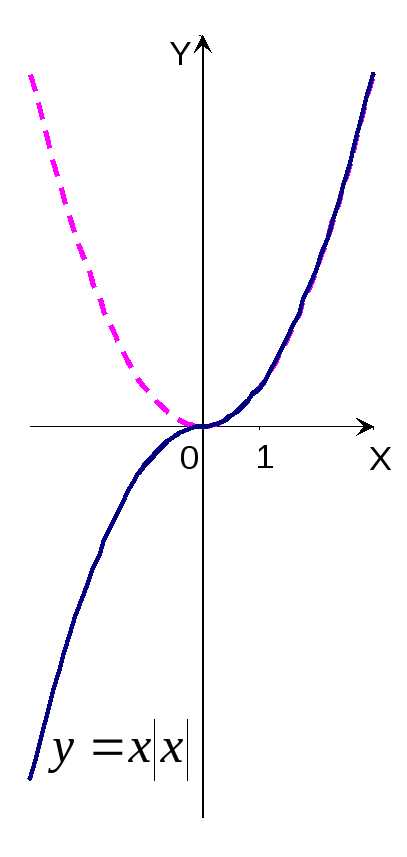
Рис.11
Рис.12
Рис.13.
Для нечётной функции y=f(x) в области всех значений аргумента справедливо равенство f(-x)= -f(x). Таким образом, в области отрицательных значений аргумента ординаты графика нечётной функции равны по величине, но противоположны по знаку ординатам графика той же функции при соответствующих положительных значениях x. График нечётной функции симметричен относительно начала координат.
Для
построения графика нечётной функции
y=f(x)
следует строить ветвь графика этой
функции только в области положительных
значений аргумента (x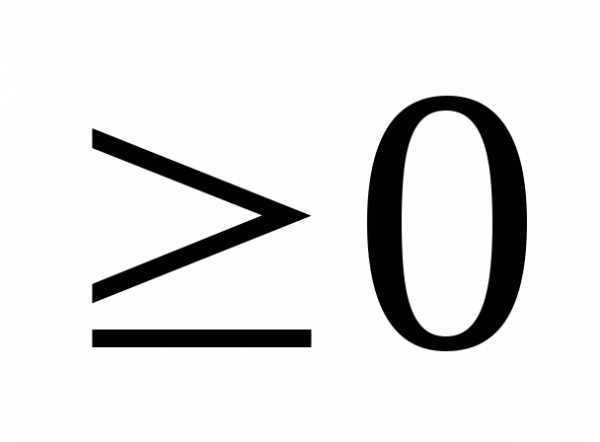 ).
).
График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений x относительно оси абсцисс.
Пример
9. Построить
график функции y=x .
.
Р
е ш е н и е: Исходная функция является
нечётной, поэтому строим её в области
положительных значений аргумента
(x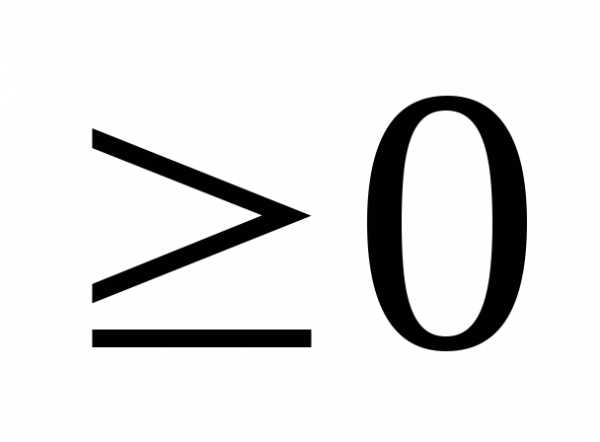 ),
где она имеет вид y=x2.
График функции y=x
),
где она имеет вид y=x2.
График функции y=x в области отрицательных значений
аргумента получаем отражением
построенной ветви относительно начала
координат (рис.12).
в области отрицательных значений
аргумента получаем отражением
построенной ветви относительно начала
координат (рис.12).
Пример
10. Построить
график функции y=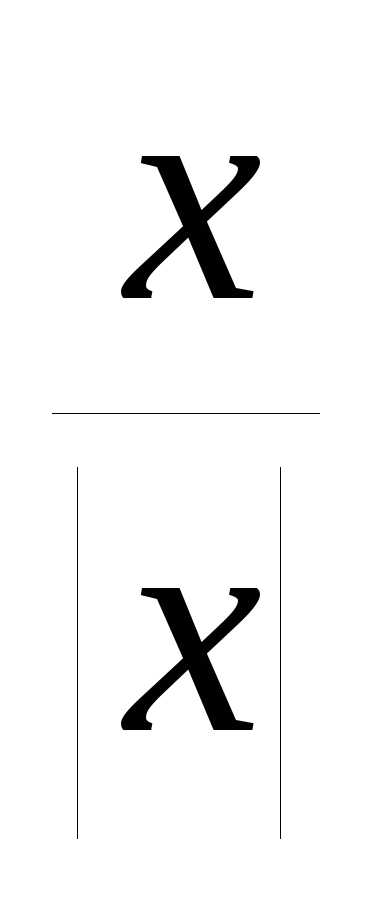 .
.
Р е ш е н и е: Данная функция является нечётной, поэтому строим её график лишь в области x>0 (точка x=0 не входит в область определения функции), где она имеет вид y=1. Ветвь графика данной функции при x<0 получаем отражением относительно начала координат построенной ветви кривой (рис.13). Стрелки означают, что точки (0,1) и (0,-1) не принадлежат графику.
2.4. Построение графика обратной функции
Прямая
и обратная функции выражают одну и ту
же зависимость между переменными x
и y,
с тем только отличием, что в обратной
функции эти переменные поменялись
ролями, что равносильно изменению
обозначений осей координат. Поэтому
график обратной функции симметричен
графику прямой функции относительно
биссектрисы  I
и III
координатных углов, т.е. относительно
прямой y=x.
Таким образом, получаем следующее
правило.
I
и III
координатных углов, т.е. относительно
прямой y=x.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=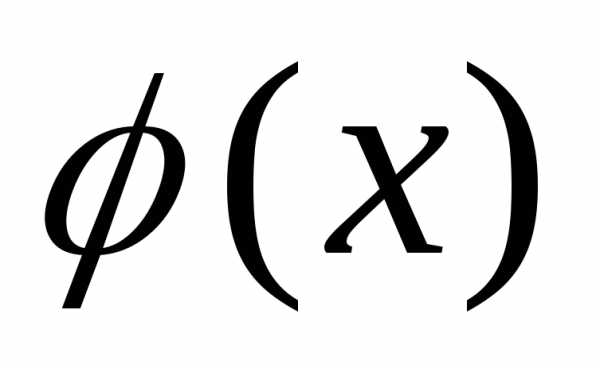 ,
обратной по отношению к функцииy=f(x),
следует построить график y=f(x)
и отразить его относительно прямой y=x.
,
обратной по отношению к функцииy=f(x),
следует построить график y=f(x)
и отразить его относительно прямой y=x.
Пример
11. Построить
график функции y= .
.
Р
е ш е н и е: Ч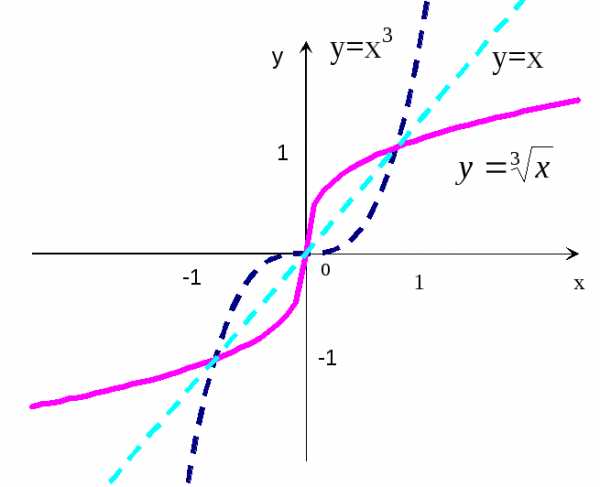 тобы
построить график данной функции,
рассмотрим график параболыy=x2 (рис.14 – пунктирная кривая) и график
обратной к ней функции y=
тобы
построить график данной функции,
рассмотрим график параболыy=x2 (рис.14 – пунктирная кривая) и график
обратной к ней функции y=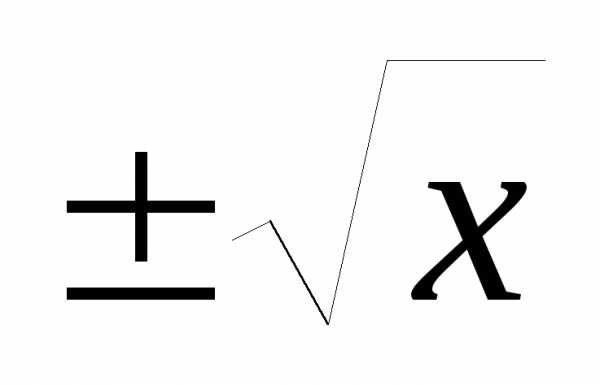 ,
получаемый отражением параболы
относительно прямой y=x.
Обратная функция является двузначной.
В силу того, что исходная функция y=
,
получаемый отражением параболы
относительно прямой y=x.
Обратная функция является двузначной.
В силу того, что исходная функция y= однозначна и область её изменения есть
полуинтервал 0
однозначна и область её изменения есть
полуинтервал 0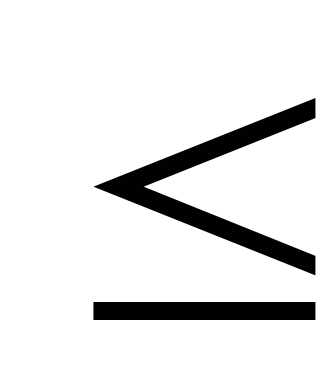 y<
y< ,
графиком функцииy=
,
графиком функцииy= является верхняя ветвь отражённой
параболы (сплошная кривая). Нижняя же
ветвь (штрих-пунктир) представляет
собой график функцииy=
—
является верхняя ветвь отражённой
параболы (сплошная кривая). Нижняя же
ветвь (штрих-пунктир) представляет
собой график функцииy=
— .
.
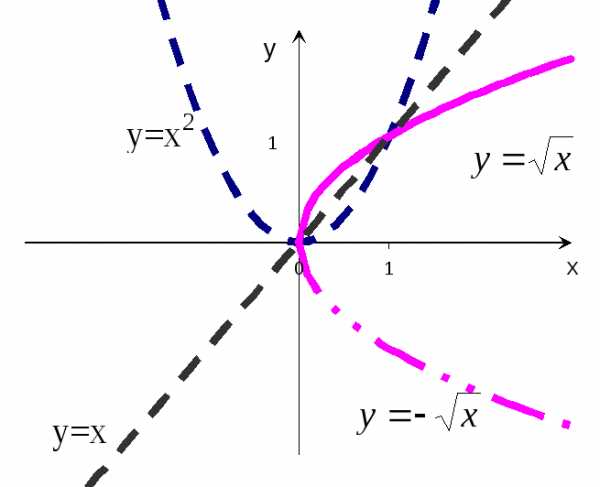
Рис.15
Пример
12. Построить
график функции y= .
.
Р
е ш е н и е: Данная функция является
обратной по отношению к функции y=x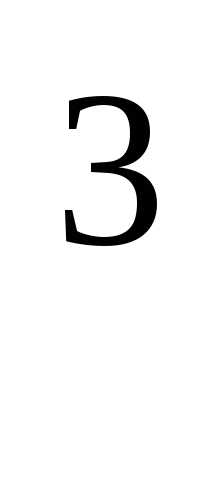 ,
поэтому строим график функции
,
поэтому строим график функции  y=x
y=x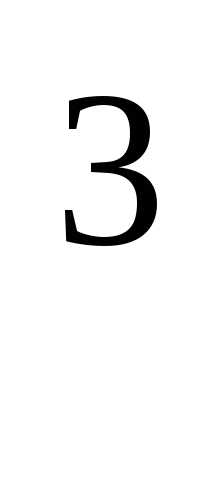 и отражаем его относительно прямой y=x
(рис.15).
и отражаем его относительно прямой y=x
(рис.15).
studfiles.net
Чётная функция — это… Что такое Чётная функция?
- Чётная функция
f(x) = x — пример нечётной функции.
f(x) = x2 — пример чётной функции.
f(x) = x3, нечётная
f(x) = x3 + 1 ни чётная, ни нечётная
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Или по-другому
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Определения
- Функция называется нечётной, если справедливо равенство
- Функция f называется чётной, если справедливо равенство
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства
- График нечётной функции симметричен относительно начала координат O.
- График чётной функции симметричен относительно оси ординат Oy.
- Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:
- f(x) = g(x) + h(x),
где
- Функция — единственная функция, одновременно являющаяся нечётной и чётной.
- Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка сохраняет чётность.
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
Wikimedia Foundation. 2010.
- Чётное число
- Чётность (математика)
Смотреть что такое «Чётная функция» в других словарях:
Нечётная функция — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
чётная функция — lyginė funkcija statusas T sritis fizika atitikmenys: angl. even function vok. gerade Funktion, f rus. чётная функция, f pranc. fonction paire, f … Fizikos terminų žodynas
нечётная функция — nelyginė funkcija statusas T sritis fizika atitikmenys: angl. odd function vok. ungerade Funktion, f rus. нечётная функция, f pranc. fonction impaire, f … Fizikos terminų žodynas
нечётная функция — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN odd function … Справочник технического переводчика
Нечётная функция — функция, удовлетворяющая равенству f ( x) = f (x). См. Чётные и нечётные функции … Большая советская энциклопедия
НЕЧЁТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех х … Естествознание. Энциклопедический словарь
нечётная функция — функция, удовлетворяющая равенству f(–х) = f(х) при всех х. * * * НЕЧЕТНАЯ ФУНКЦИЯ НЕЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех х … Энциклопедический словарь
чётная функция — функция, удовлетворяющая равенству f( х) = f(х) при всех х. * * * ЧЕТНАЯ ФУНКЦИЯ ЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех x … Энциклопедический словарь
Функция Доусона — вблизи начала координат … Википедия
Функция Хевисайда — Единичная функция Хевисайда Функция Хевисайда (единичная ступенчатая функция, функция единичного скачка, включенная единица) кусочно постоянная функция, равная нулю для отрицательных значений аргумента и единице для пол … Википедия
dic.academic.ru

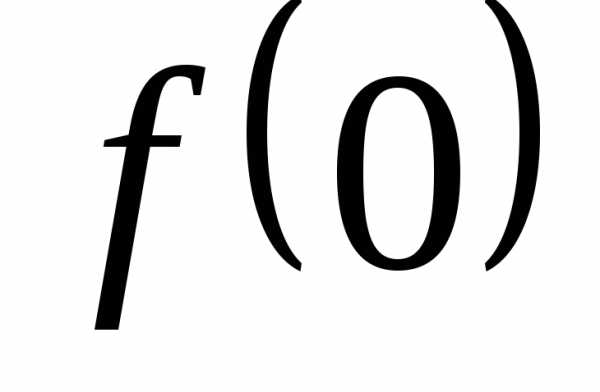 ,
,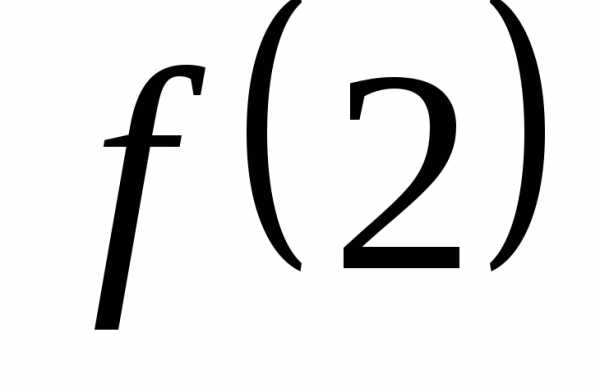 ,
,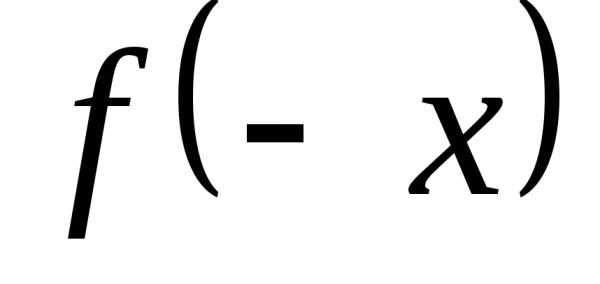 ,
,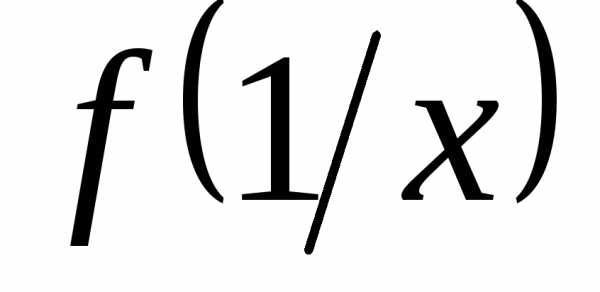 ,
если.
,
если.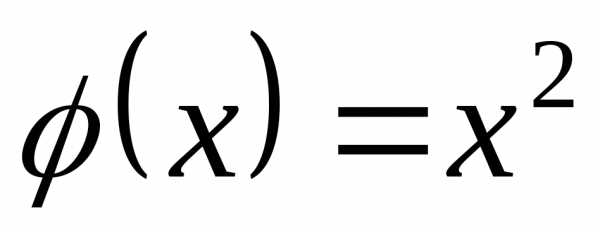 и
и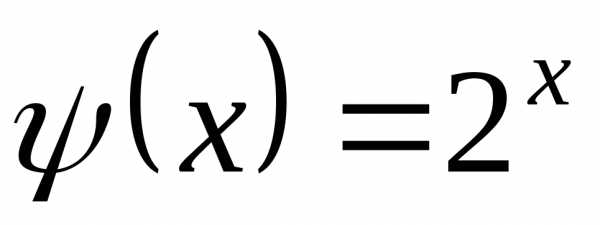 .
Найти
.
Найти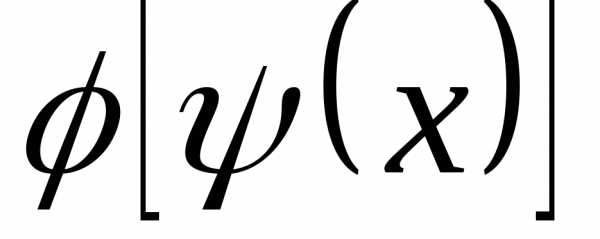
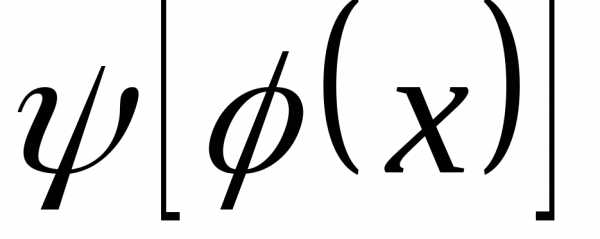 .
.