График функции y=f(x)+b | Алгебра
График функции y=f(x)+b (b>0) можно получить из графика функции y=f(x) с помощью параллельного переноса (сдвига) вдоль оси Oy на b единиц вверх.
При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; y+b) графика функции y=f(x)+b (то есть абсцисса (координата x) каждой точки остается без изменения, а ордината (координата y ) увеличивается на b.
Один из вариантов преобразования — осуществить параллельный перенос начала отсчёта, точки O(0;0), в точку O1(0;b) и построить график y=f(x) с началом отсчёта от точки O1.
Примеры.
1) График функции y=x²+3 может быть получен из графика функции y=x² с помощью параллельного переноса вдоль оси Oy на 3 единицы вверх.
Строим параболу y=x². Затем переносим каждую из основных точек на 3 единицы вверх.
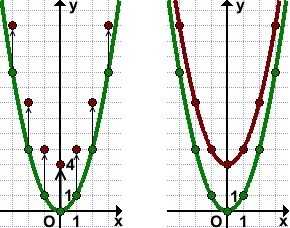
y=x²+3 из y=x²
Можно перенести только вершину параболы, точку (0; 0), на 3 единицы вверх, в точку (0; 3), и от новой вершины строить параболу y=x² (1 единица вправо, 1 — вверх; 1 единица влево, 1 — вверх; 2 единицы вправо, 2 — вверх и т.д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).
1) График функции y=x³+2 может быть получен из графика функции y=x³ с помощью параллельного переноса вдоль оси Oy на 2 единицы вверх.
Можно обойтись без построения начального графика y=x³, достаточно обозначить его основные точки, и выполнить параллельный перенос каждой из них на 2 единицы вверх.
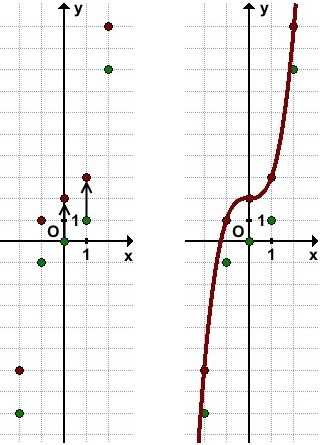
y=x³+2 из y=x³
3) График функции y=√x+4 может быть получен из графика функции y=√x параллельным переносом на 4 единицы вверх вдоль оси Oy.
Строим график функции y=√x по основным точкам. Затем переносим каждую из этих точек вверх на 4 единицы.
Через полученные точки проводим ветвь параболы:
В следующих раз рассмотрим рассмотрим построение графиков вида y=f(x)-b.
Преобразование графиков позволяет на основе графиков элементарных функций получать графики сложных функций. Умение преобразовывать графики в алгебре пригодится не только при изучении функций, но и при решении уравнений и неравенств, в частности, при решении заданий с параметрами.
www.algebraclass.ru
Преобразование графиков
Параллельный перенос.
ПЕРЕНОС ВДОЛЬ ОСИ ОРДИНАТ
f(x) => f(x) — b
Пусть требуется построить график функции у = f(х) — b. Нетрудно заметить, что ординаты этого графика для всех значений x на |b| единиц меньше соответствующих ординат графика функций у = f(х) при b>0 и на |b| единиц больше — при b0 или вверх при bДля построения графика функции y + b = f(x) следует построить график функции y = f(x) и перенести ось абсцисс на |b| единиц вверх при b>0 или на |b| единиц вниз при b
ПЕРЕНОС ВДОЛЬ ОСИ АБСЦИСС
f(x) => f(x + a)
Пусть требуется построить график функции у = f(x + a). Рассмотрим функцию y = f(x), которая в некоторой точке x = x1 принимает значение у1 = f(x1). Очевидно, функция у = f(x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 — a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции. Следовательно, график функции у = f(x + a) может быть получен параллельным перемещением графика функции y = f(x) вдоль оси абсцисс влево на |a| единиц при a > 0 или вправо на |a| единиц при a Для построения графика функции y = f(x + a) следует построить график функции y = f(x) и перенести ось ординат на |a| единиц вправо при a>0 или на |a| единиц влево при a
Примеры:
2.y=f(x)+b
Отражение.
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = F(-X)
f(x) => f(-x)
Очевидно, что функции y = f(-x) и y = f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y = f(-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х. Таким образом, получаем следующее правило.
Для построения графика функции y = f(-x) следует построить график функции y = f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f(-x)
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = — F(X)
f(x) => — f(x)
Ординаты графика функции y = — f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило.
Для построения графика функции y = — f(x) следует построить график функции y = f(x) и отразить его относительно оси абсцисс.
Примеры:
2.y=f(-x)
3.y=-f(-x)
Деформация.
ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ ОРДИНАТ
f(x) => k•f(x)
Рассмотрим функцию вида y = k•f(x), где k > 0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в k раз больше ординат графика функции у = f(x) при k > 1 или 1/k раз меньше ординат графика функции y = f(x) при kДля построения графика функции y = k•f(x) следует построить график функции y = f(x) и увеличить его ординаты в k раз при k > 1(произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/k раз при k
k > 1 — растяжение от оси Ох
0 — сжатие к оси OX
ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ АБСЦИСС
f(x) => f(k•x)
Пусть требуется построить график функции y = f(kx), где k>0. Рассмотрим функцию y = f(x), которая в произвольной точке x = x1 принимает значение y1 = f(x1). Очевидно, что функция y = f(kx) принимает такое же значение в точке x = x2, координата которой определяется равенством x1 = kx2, причем это равенство справедливо для совокупности всех значений х из области определения функции. Следовательно, график функции y = f(kx) оказывается сжатым (при k1) вдоль оси абсцисс относительно графика функции y = f(x). Таким образом, получаем правило.
k > 1 — сжатие к оси Оу
0 — растяжение от оси OY
Работу выполнили Чичканов Александр, Леонов Дмитрий под руководством Ткач Т.В, Вязовова С.М, Островерховой И.В.
©2014
www.tofmal.ru
График функции y=f(x)/k | Алгебра
График функции y=f(x)/k (где k>1) может быть получен из графика функции y=f(x) с помощью сжатия к оси Ox в k раз.
При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; y/k) графика функции y=f(x)/k:
(x; y) → (x; y/k)
(то есть абсцисса (x) каждой точки начального графика остаётся неизменной, а ордината (y) уменьшается в k раз).Точки, лежащие на оси Ox при сжатии к оси абсцисс остаются на месте (так как 0/k=0).
Примеры.
1) График функции y=x²/3 можно получить из графика функции y=x² сжатием к оси Ox в 3 раза.
Строим параболу y=x² (достаточно отметить базовые точки). Координату x каждой точки оставляем без изменения, координату y делим на 3.
(1; 1) → (1; 1/3),
(-1; 1) → (-1; 1/3),
(2; 4) → (2; 4/3),
(-2; 4) → (-2; 4/3),
(3; 9) → (3; 3),
(-3; 9) → (-3; 3).
Таким образом, каждая точка нового графика соответственно располагается под точкой первоначального графика, но в 3 раза ближе к оси абсцисс.
Вершина параболы при сжатии к оси Ox остаётся на месте (0:3=0).
2) График функции y=x³/4 может быть получен из графика функции y=x³ сжатием к оси абсцисс в 4 раза.
Для построения графика абсциссы базовых точек графика кубической функции оставляем неизменными, а каждую ординату делим на 4:
(1; 1) → (1; 1/4),
(-1; -1) → (-1; -1/4),
(2; 8) → (2; 8/3),
(-2; 8) → (-2; -8/3).
Точка (0; 0) при таком преобразовании остаётся на месте.
3) График функции y=(1/2)√x можно получить сжатием к оси Ox графика функции y=√x.
Координату x каждой из базовых точек графика y=√x оставляем без изменений, координату y делим на 2:
(0; 0) → (0; 0),
(1;1) → (1; 1/2),
(4; 2) → (4; 1),
(9; 3) → (9; 9/2) и т. д.
Геометрические преобразования дают возможность на основании графиков элементарных функций строить многие другие графики. Умение строить графики функций востребовано при решений заданий из различных разделов алгебры.
www.algebraclass.ru
График функции y=f(x)-b | Алгебра
График функции y=f(x)-b (b>0) может быть получен из графика функции y=f(x) при помощи параллельного переноса (или сдвига) вдоль оси Oy на b единиц вниз. При таком преобразовании каждая точка (x; y) первоначального графика переходит в точку (x; y-b) нового графика:
(x; y) → (x; y-b)
(то есть абсцисса (x) каждой точки остаётся без изменений, а ордината (y) уменьшается на b).
Другой вариант построения графика — осуществить параллельный перенос на b единиц вниз начала отсчёта, точки O (0; 0), в точку O1 (0; -b), и построить график функции y=f(x) с началом отсчёта в точке O1.
Примеры.
1) График функции y=x²-5 может быть получен из графика функции y=x² с помощью параллельного переноса на 5 единиц вниз.
Отмечаем базовые точки графика y=x² и сдвигаем каждую из них вниз на 5 единиц. Через новые точки проводим параболу.
Другой вариант — выполнить параллельный перенос вершины параболы O (0; 0) в точку O1 (0; -5), и построить график функции y=x² с началом отсчёта в точке O1.
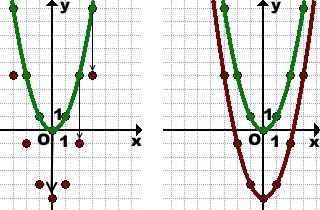
График функции y=x²-5 получен из графика y=x²
2) График функции y=6/x -3 можем получить из графика функции y=6/x, осуществив его параллельный перенос на 3 единицы вниз вдоль оси Oy. При этом асимптота y=0 (ось Ox) графика y=6/x также подвергается параллельному переносу и переходит в новую асимптоту — прямую y= -3:
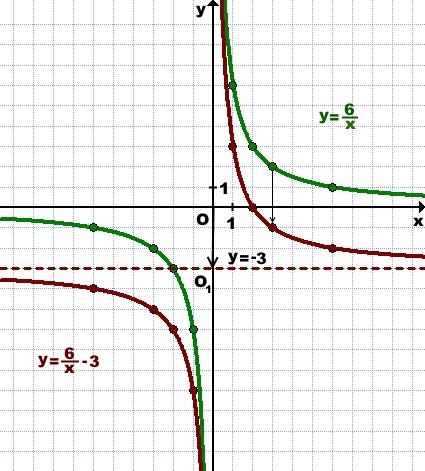
3) График функции y=|х|-4 может быть получен из графика функции y=|х| с помощью параллельного переноса на 4 единицы вниз вдоль оси Oy:
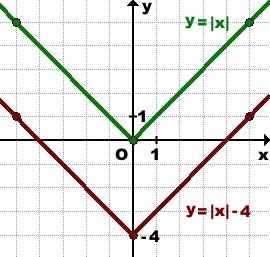
Преобразование графиков в алгебре — одна из наиболее важных тем. Навыки построения графиков с помощью геометрических преобразований, в том числе, параллельного переноса, требуются не только при изучении функций, но также применяются при решений различных заданий из других тем.
www.algebraclass.ru
График функции y=kf(x) | Алгебра
График функции y=kf(x) (k>1) можно получить из графика функции y=f(x) растяжением от оси Ox в k раз. При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; ky) графика функции y=kf(x):
(x; y) → (x; ky)
(то есть абсцисса (x) каждой точки начального графика остаётся без изменений, а ордината (y) увеличивается в k раз).
При растяжении от оси Ox точки графика y=f(x), лежащие на оси абсцисс, остаются на месте, так как k∙0=0.
Примеры.
1) График функции y=3x² получен из графика функции y=x² растяжением в 3 раза от оси Ox.
При растяжении графика от оси абсцисс нужно ординату каждой точки увеличить в 3 раза.
Для построения графика отмечаем базовые точки графика y=x². Для каждой точки координату x оставляем неизменной, значение координаты y умножаем на 3. Таким образом, каждая точка нового графика располагается строго над соответствующей точкой графика y=x², в 3 раза дальше от оси Ox.
Вершина параболы y=x², точка O (0; 0), остаётся на месте (так как 3∙0=0).
График y=3x² из y=x²
(1; 1) → (1; 3),
(-1; 1) → (-1; 3),
(2; 4) → (2; 12),
(-2; 4) → (-2; 12)
и т. д.
2) График функции y=2|х| можно получить из графика функции y=|х| растяжением от оси абсцисс в 2 раза.
Точка O (0; 0) остаётся на месте. В I и II координатных четвертях берём по одной точке графика y=|х|, например, (5; 5) и (-5; 5). Их абсциссы оставляем без изменений, а ординаты удваиваем:
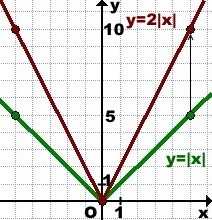
График y=2|х| из y=|х|
(5; 5)→ (5; 10),
(-5; 5)→ (-5; 10).
Через эти точки из точки O проводим лучи.
Получаем график функции y=2|х|
3) График функции y=4√x можно получить из графика функции y=√x растяжением от оси Ox в 4 раза.
Координату x каждой из базовых точек графика y=√x оставляем без изменений, координату y увеличиваем в 4 раза. Точка O (0; 0) при этом остаётся на месте.
Через полученные точки проводим новый график:
График y=4√x из y=√x
(0; 0) → (0; 0),
(1; 1) → (1; 4),
(4; 2) → (4; 8),
(9; 3) → (9; 12),
и т. д.
Преобразование графиков может быть использовано для построения графиков функций в ходе решения примеров из разных разделов алгебры.
www.algebraclass.ru
Графики функций и их модификация
Разделы: Математика
Графиком функции у=f(х), где , называется множество всех точек координатной плоскости хОу вида (х;f(х)) или графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Параллельный перенос (сдвиг) вдоль оси абсцисс
График функции у=f(х+а) получаем с помощью параллельного переноса (сдвига) последнего вдоль оси Ох на |а| единиц масштаба в направлении, имеющем знак, противоположный знаку числа а.
Например, для построения графика функции у=f(х+2) вспомогательную ось ординат графика функции у=f(х) переносим параллельно вдоль оси абсцисс на две единицы масштаба вправо или сам график переносим на две единицы влево.
Параллельный перенос (сдвиг) вдоль оси ординат
График функции у=f(х+b) получаем из графика функции у=f(х) с помощью параллельного переноса (сдвига) последнего вдоль оси Оу на |b| единиц масштаба в направлении, имеющем знак числа b.
Например, для построения графика функции у=f(х)-4 вспомогательную ось абсцисс графика функции у=f(х) поднимаем вдоль оси ординат на четыре единицы или сам график переносим на 4 единицы вниз.
Растяжение или сжатие по оси абсцисс
График функции у=f(kх) получаем из графика функции у=f(х ) с помощью сжатия по оси абсцисс исходного графика пропорционально коэффициенту k при аргументе: если k>1, то график сжимается в k раз, а если 0<k<1, то график растягивается в раз.
Построим графики функций у=f(2х) и
Растяжение или сжатие по оси ординат
График функции у=mf(х) получаем из графика функции у=f(х) с помощью растяжения этого графика по оси ординат пропорционально m при функции (если m>1, то график растягивается в m раз, если 0<m<1, то график сжимается в раз).
Построим графики функций у=3f(х) и у=f(х).
Построение графика функции у=-f(х)
График функции у=-f(х) получаем из графика функции у=f(х) с помощью симметрии относительно оси абсцисс.
Построим график этой функции.
Построение графика функции у=f(-х)
График функции у=f(-х) получаем из графика функции у=f(х) с помощью симметрии относительно оси ординат.
Построим график этой функции.
Построение графика функции у=|f(х)|
Для построения графика функции у=|f(х)|, надо построить график функции у=f(х), далее оставить без изменения все части построенного графика, которые лежат выше оси абсцисс или на оси, а части, расположенные ниже её, отобразить симметрично относительно этой оси.
Строим график этой функции:
Построение графика функции у= f(|х|)
Для построения графика функции у=f(|х|), надо построить график функции у=f(х) для х?0, а затем отобразить построенную часть симметрично относительно оси ординат. Обе части в совокупности дадут график функции у=f(|х|).
Построение графика функции y=-f(-х)
Для построения графика функции y=-f(-х), надо построить график функции у = f(х), затем выполнить симметрию относительно начала координат. В результате получим график заданной функции.
22.07.2010
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
График функции по графику производной
По графику производной y= f ‘ (x) можно не только исследовать поведение функции y=f(x) , но и попытаться построить ее график.
Поскольку для одной функции первообразных существует бесконечное множество, график функции по графику производной можно построить лишь схематично: точки экстремума и промежутки возрастания и убывания функции определить можно, а нули функции и экстремумы — нет.
Дан график производной: y= f ‘ (x):
Построить график функции y=f(x).
Решение:
Точки x=x2, x=x3, x=x4, в которых производная y= f ‘ (x) обращается в нуль — это точки экстремума функции y=f(x).
В точках x=x2 и x=x4 производная меняет знак с «-«на «+», поэтому x2 и x=x4 — точки минимума функции y=f(x).
В точке x=x3 производная меняет знак с «+» на «-«, поэтому x=x3 — точка максимума функции.
На промежутках [x1;x2] и [x3;x4] f ‘ (x)<0, поэтому y=f(x) на этих промежутках убывает.
На промежутках [x2;x3] и [x4;x5] f ‘ (x)>0, поэтому для y=f(x) они являются промежутками возрастания.
Сказать что-то более определенное о нулях и других значениях функции y=f(x) не получится. Данный эскиз графика y=f(x) — один из множества графиков первообразных для функции y= f ‘ (x). Другие могут быть получены из него параллельным переносом вдоль оси oy.
Если график производной y= f ‘ (x) представляет собой прямую, параллельную оси ox (y=b, где b- число),, то функция y=f(x) — линейная. Она является возрастающей, если b>0, убывающей, если b<0, и постоянной, если b=0.
www.uznateshe.ru
