Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.Графики тригонометрических функций. Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах. Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
Из графиков видно что:
Углы произвольной величины На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О — отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке — отрицательным.
Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
Пусть ОА вращается дальше таким образом, что Θ4— любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. слева. График. Положительные и отрицательные значения синусов, косинусов и тангенсов.
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины. Пример 1 Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071 |
dpva.ru
Гармоническое колебание, уравнения, графики движения. Изменение координаты, скорости, ускорения со временем. Примеры, тесты
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
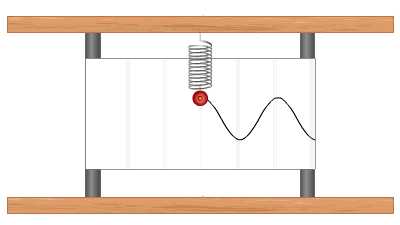
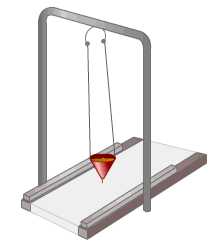
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
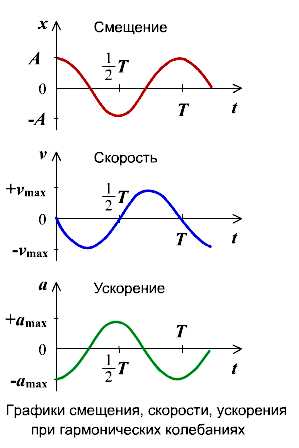
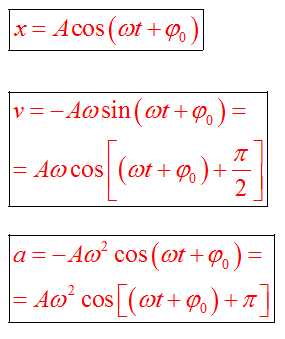
Если колебание описывать по закону синуса

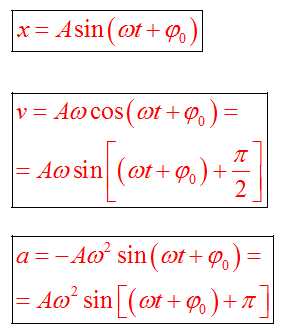
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Находим производную сложной функции.
fizmat.by
график косинуса — с русского на английский
См. также в других словарях:
Интегральный косинус — График интегрального косинуса для 0 < x ≤ 8π. Интегральный косинус специальная функция, определяемая интегралом … Википедия
История тригонометрии — Геодезические измерения (XVII век) … Википедия
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Отрицательная частота — Понятие отрицательной и положительной частоты может быть показано на примере вращающегося в ту или другую сторону вектора. Частота со знаком отражает как скорость, так и направление вращения. Скорость выражена в оборотах (циклах) в секунду… … Википедия
Полярная система координат — Полярная сетка, на которой отложено несколько углов с пометками в градусах. Полярная система координат двумерная система координат, в которой каждая точка на плоскости определяется двумя числами полярным углом и полярны … Википедия
Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение … Википедия
Sh x — Гиперболические функции семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение 2 Свойства … Википедия
Синус-верзус — Определение тригонометрических функций на единичной окружности. Отрезок CD описывает версинус. Синус верзус (sinus versus обращённый синус; другие написания: версинус, синус версус, называется также «стрелка дуги») одна из редко… … Википедия
КОСИНУС — (cosine) В прямоугольном треугольнике отношение катета и гипотенузы, образующих угол. Косинус угла х записывается как cos х. Если начертить окружность радиусом, равным единице, то при измерении величины угла против часовой стрелки, начиная с… … Экономический словарь
Нуль функции — Нули косинуса на интервале [ 2π,2π] (красные точки) Нуль функции в математике элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции … Википедия
translate.academic.ru
график косинуса — это… Что такое график косинуса?
- график косинуса
- cosine curve
Большой англо-русский и русско-английский словарь. 2001.
- график косеканса
- график котангенса
Смотреть что такое «график косинуса» в других словарях:
Интегральный косинус — График интегрального косинуса для 0 < x ≤ 8π. Интегральный косинус специальная функция, определяемая интегралом … Википедия
История тригонометрии — Геодезические измерения (XVII век) … Википедия
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Отрицательная частота — Понятие отрицательной и положительной частоты может быть показано на примере вращающегося в ту или другую сторону вектора. Частота со знаком отражает как скорость, так и направление вращения. Скорость выражена в оборотах (циклах) в секунду… … Википедия
Полярная система координат — Полярная сетка, на которой отложено несколько углов с пометками в градусах. Полярная система координат двумерная система координат, в которой каждая точка на плоскости определяется двумя числами полярным углом и полярны … Википедия
Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение … Википедия
Sh x — Гиперболические функции семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение 2 Свойства … Википедия
Синус-верзус — Определение тригонометрических функций на единичной окружности. Отрезок CD описывает версинус. Синус верзус (sinus versus обращённый синус; другие написания: версинус, синус версус, называется также «стрелка дуги») одна из редко… … Википедия
КОСИНУС — (cosine) В прямоугольном треугольнике отношение катета и гипотенузы, образующих угол. Косинус угла х записывается как cos х. Если начертить окружность радиусом, равным единице, то при измерении величины угла против часовой стрелки, начиная с… … Экономический словарь
Нуль функции — Нули косинуса на интервале [ 2π,2π] (красные точки) Нуль функции в математике элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции … Википедия
dic.academic.ru
