Александра Сергеевна МаловаОсновы эконометрики в среде GRETL. Учебное пособие
[email protected]
Введение
Цель данного пособия – познакомить читателя с основами проведения эконометрических исследований в среде GRETL. Основная аудитория данной книги – студенты бакалавриата, обучающиеся по направлениям «Экономика», «Бизнес-информатика», «Управление персоналом», «Менеджмент», однако она может быть полезна и студентам других направлений, а также представителям бизнес-сообщества, которые по роду своей деятельности столкнулись с необходимостью проведения эконометрических исследований. Данное учебное пособие – это попытка практического изложения основ эконометрики с минимальными теоретическими выкладками, при этом предполагается, что недостаток теоретических знаний должен быть восполнен читателем самостоятельно с помощью учебников по основам эконометрики. Для обеспечения связи практических навыков с теоретическими знаниями в области эконометрики ко всем рассматриваемым темам даются ссылки на литературу. При этом основная задача данного пособия – помочь читателю в освоении эконометрики, изложить некоторые технические аспекты проведения исследований с использованием среды GRETL. Почему именно GRETL? Данный эконометрический пакет является бесплатным программным продуктом, который, с одной стороны, доступен любому пользователю, а с другой – обладает достаточно обширными возможностями для анализа данных и проведения эмпирических исследований. Немаловажным является и то, что в GRETL имеется значительный пул данных из большинства классических зарубежных учебников по основам эконометрики, что позволит достаточно легко переключиться с простейших примеров, рассмотренных в данном пособии, на более сложные содержательные задачи и кейсы из учебников.
В данном пособии весь материал излагается с точки зрения практики – то есть все основные разделы курса эконометрики для бакалавриантов даны в примерах и задачах. Поскольку невозможно приобрести навык проведения эконометрических расчетов, только изучая учебник, предполагается, что читатель должен иметь возможность проделать все излагаемые действия на практике. С этой целью в пособии использовались данные из учебника J. M. Wooldridge «Basic econometrics», которые доступны в GRETL. Все наборы данных при первом обращении к ним в пособии обозначены ссылками и указателями на источник.
Перед тем как начать осваивать основы эконометрики в среде GRETL, необходимо скачать и установить на свой компьютер сам статистический пакет. Он доступен по ссылке http://GRETL.sourceforge.net/. Вся информация о том, как установить GRETL, приводится на сайте, поэтому нет нужды в подробном изложении, стоит лишь сказать, что программа имеет версию как под ОС Windows, так и под Mac OS, а также что библиотеки данных должны быть установлены отдельно, для этого нужно перейти по ссылке http://GRETL.sourceforge.net/GRETL_data.html.
Удачи в проведении интересных, содержательных и полезных эконометрических исследований!
1. Линейная регрессионная модель
Для начала введем некоторые обозначения. Предположим, что некоторая величина Y зависит от величин . Введем понятие регрессионного уравнения – это уравнение вида , где . Через n обозначим число наблюдений, по которым строится регрессия, k – число регрессоров в модели, – случайная величина, которая носит название ошибки регрессии.
Модель такого вида называется классической линейной регрессионной моделью (ЛРМ) в случае, если выполняются следующие предпосылки:
1. , – линейная спецификация модели, где – коэффициенты модели, которые подлежат определению, , – ошибки модели.
2. , – детерминированные величины.
3. – математическое ожидание ошибок равно нулю, , дисперсия ошибок не зависит от номера наблюдения.
4. , – совместное математическое ожидание ошибок разных наблюдений равно нулю.
5. Если выполняется дополнительная предпосылка о нормальном распределении ошибок , то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).
Подробнее о предпосылках линейной регрессионной модели можно прочесть в [2, 3].
2. Оценка линейной регрессионной модели
Рассмотрим множественную линейную регрессию
, ,
где – средний уровень заработной платы в час в долларах, – образование в годах, – общий стаж работы в годах, – опыт работы у текущего работодателя, в годах, – ошибка регрессии, n – число наблюдений [файл с данными wage1.gdt].
Для того чтобы оценить предложенную модель по методу наименьших квадратов (МНК), используем команду меню Модель – Метод наименьших квадратов.
В появившемся диалоговом окне в поле Зависимая переменная помещаем переменную (для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная. Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).
Для дальнейшего удобства можно поставить галочку в окошке Установить по умолчанию. Это делается для того, чтобы при изменении спецификации исследуемой модели зависимая переменная не менялась. В окно Регрессоры
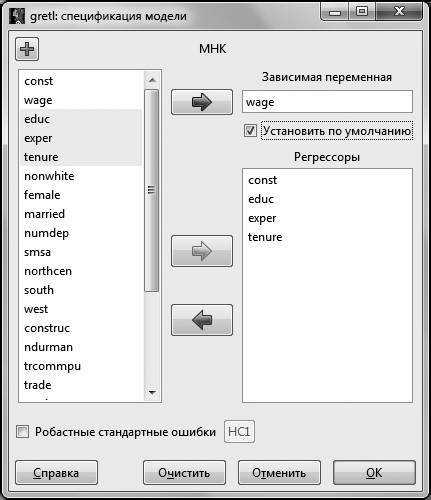
Рис. 2.1
После этого нажимаем ОК. В результате коэффициенты модели были оценены методом наименьших квадратов. Результат оценки представлен на рис. 2.2.
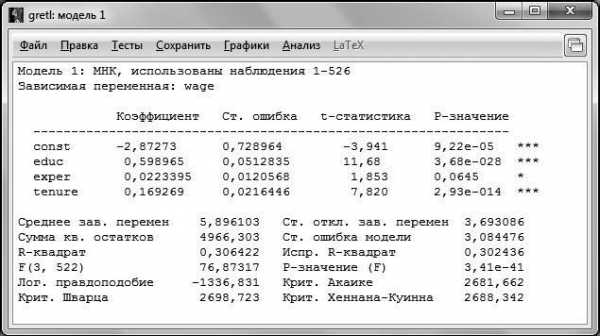
Рис. 2.2
Для того чтобы понимать, какие результаты позволяет получить GRETL, разберем информацию, представленную на распечатке по строкам сверху вниз.
В первой строке указывается метод оценки и количество наблюдений, по которым производилась оценка. Достаточно часто случается, что количество наблюдений, по которым производилась оценка, не совпадает с числом наблюдений в исходной выборке, даже если она не была ограничена. Это может быть связано, например, с наличием пропусков в данных.
Вторая строка напоминает нам о том, какая переменная была выбрана в качестве зависимой.
После двух первых строк следуют подтаблицы непосредственно с результатами оценивания. В первой подтаблице указаны регрессоры, включенные в модель, напротив каждого из них указывается его коэффициент (столбец Коэффициенты), стандартная ошибка оценки коэффициента (столбец Ст. ошибка), значение статистики Стьюдента для коэффициента (столбец t-статистика) и вероятность ошибки I рода (столбец P-значение). Стоит отметить, что константа тоже является регрессором, и для нее также рассчитываются все указанные характеристики.
По распечатке, представленной на рис. 2.2, мы можем выписать получившееся уравнение регрессии:
Аналогично можно получить оцененное уравнение и в GRETL, для этого выбираем в меню регрессии Файл – Просмотреть как уравнение.
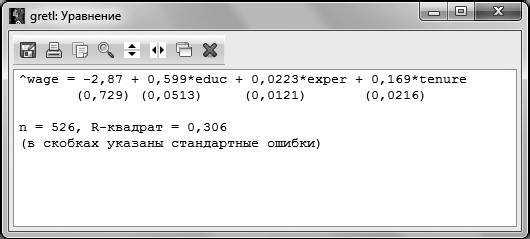
Рис. 2.3
Однако для того, чтобы иметь возможность дать интерпретацию коэффициентам регрессии и строить прогнозы, необходимо проверить, является ли полученная модель адекватной.
Для этого, в свою очередь, необходимо провести ряд эконометрических тестов, а именно проверить значимость регрессии в целом, значимость отдельных коэффициентов регрессии, оценить качество полученного регрессионного уравнения. Вообще говоря, перед проверкой значимости и качества уравнения необходимо провести тесты на выполнение основных предпосылок линейной регрессионной модели (гомоскедастичность, отсутствие автокорреляции). На данном этапе мы будем считать эти тесты проведенными и вернемся к вопросам выполнения предпосылок ЛРМ позднее.
3. Тест Фишера (Fisher test)
Для начала проверим гипотезу о незначимости регрессии в целом. Тест позволит понять, является ли построенная модель адекватной с точки зрения статистики. Для этой цели воспользуемся тестом Фишера [3].

Сформулируем гипотезы для проверки незначимости регрессии в целом в рассматриваемом примере [ файл с данными wage1.gdt] модели , :
как минимум один из коэффициентов отличен от нуля.
Для принятия решения о том, какую гипотезу нужно отвергнуть, построим F-статистику. Для этого нам должны быть известны (помимо уже имеющихся параметров n – объем выборки и k – число регрессоров в модели) величины RSS и ESS. В явном виде в распечатке на рис. 2.2 дано значение ESS – сумма квадратов остатков, которая составляет ESS = 4966,3, а также из распечатки известен коэффициент детерминации (подробнее о коэффициенте детерминации и его интерпретации можно прочесть в § 7).
Если вспомнить, что ,1 а , то можно путем простых алгебраических преобразований найти необходимую нам величину RSS. При этом . Отсюда можно вычислить . Критическое значение F-статистики возьмем на уровне значимости 5 %: (чтобы получить это значение, в основном меню
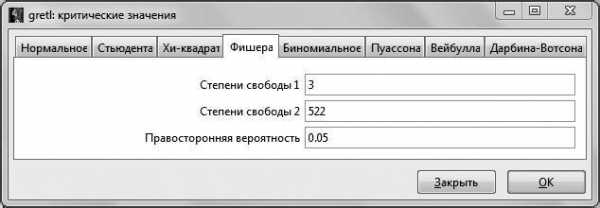
Рис. 3.1
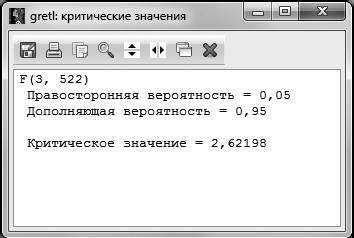
Рис. 3.2
Уровень значимости, на котором принимается решение о том, какую гипотезу не отвергать, остается на усмотрение исследователя. Как правило, если нет представления, какой именно уровень значимости брать, предлагается выбирать 5 %. В случаях работы с маленьким по объему выборками (от 30 до 100 наблюдений) предлагается брать уровень значимости 10 %. Для больших выборок (более 1000 наблюдений) можно взять уровень значимости 1 %. В нашем случае объем выборки средний (526 наблюдений, эта информация дана в первой строке распечатки на рис. 2.2.), поэтому можно было принять .
Сравниваем расчетное значение F-статистики с критическим , то есть 78,2 > 2,6. Следовательно, можно сделать вывод, что гипотеза о незначимости регрессии в целом отвергается.
Тест Фишера можно провести также в полуавтоматическом режиме и в автоматическом режиме. Полуавтоматический режим состоит в том, что нам не нужно вручную вычислять значение расчетной F-статистики, оно дано в распечатке на рис. 2.2. В этом случае нужно лишь выяснить критическое значение F-статистики и сравнить расчетное значение с критическим.
В автоматическом режиме нужно также воспользоваться распечаткой GRETL и посмотреть на р-значение статистики Фишера на рис. 2.2 (в распечатке р-значение (F)). В р-значении содержится вероятность ошибки I рода. Таким образом, р-значение (F) для теста Фишера – это вероятность ошибки I рода при тестировании гипотезы . По существу это вероятность ошибиться, отвергнув гипотезу
Стоит обратить внимание еще на один полезный факт. При расчете F-статистики вручную мы использовали формулу . Используя соотношение , можно переписать расчетную статистику через коэффициент детерминации, не используя квадраты остатков .
4. Тест Стьюдента (t-test)
После того как мы проверили незначимость регрессионного уравнения в целом, рассмотрим, как проверять незначимость коэффициентов при отдельных регрессорах. Для этой цели воспользуемся тестом Стьюдента [3].

Проверим незначимость коэффициента при переменной . Сформулируем гипотезы теста для указанной переменной [файл с данными wage1.gdt]. Они будут выглядеть следующим образом:
Значение оцененного коэффициента при этой переменной находится в столбце «
Рис. 4.1
В открывшемся окне «Критические значения» выберем вкладку, соответствующую распределению Стьюдента, и введем нужные параметры распределения.
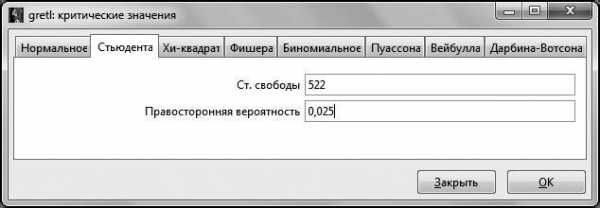
Рис. 4.2
Стоит обратить внимание на то, что в GRETL предполагается для распределения Стьюдента вводить не двустороннюю вероятность, а только правостороннюю вероятность, то есть в нашем случае это 2,5 %. После нажатия клавиши ОК получаем искомое критическое значение .
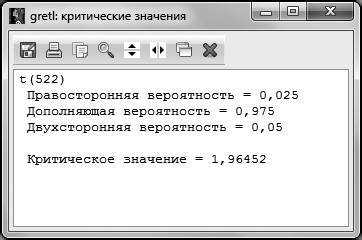
Рис. 4.3
После этого сравниваем расчетное и критическое значение статистик для переменной . В нашем случае (|11,68 | > 1,96), отсюда можно сделать вывод, что гипотеза H0 отвергается, то есть можно говорить о том, что регрессор значим.
Рассмотренный способ проверки гипотезы незначимости коэффициента при отдельном регрессоре позволяет соотнести теоретические знания о проверке незначимости с практикой. Однако ту же самую процедуру можно несколько упростить. Обратим внимание, что в столбце t-статистика для всех переменных уже указаны расчетные значения статистики. Так, например, для переменной указано полученное нами значение . Это несколько сокращает процедуру проверки, однако сравнение расчетного и критического значения t-статистики все же приходится проделывать самостоятельно.
Существует еще более простой и быстрый способ проверки незначимости коэффициента.
В рассматриваемом примере p-значение переменной составляет , то есть практически равно 0. В этом случае, p-значение переменной меньше заданного уровня значимости . Это значит, что можно отвергнуть гипотезу H0, то есть коэффициент при регрессоре значим.
Аналогичную проверку незначимости мы можем провести для коэффициентов остальных регрессоров. На 5 %-ном уровне значимости можно утверждать, что коэффициент при и константа – значимы, коэффициент при на 5 %-ном уровне не значим, однако он является значимым на 10 %-ном уровне значимости.

В программе GRETL предусмотрена визуализация значимости коэффициентов при отдельных регрессорах на разных уровнях значимости. Для этого справа от каждого регрессора расположены звездочки:
• Наличие одной звездочки говорит о том, что коэффициент значим только на 10 %-ном уровне.
• Наличие двух звездочек говорит о значимости коэффициента на 5 %-ном уровне.
• Три звездочки информируют о значимости коэффициента на 1 %-ном уровне.
• Отсутствие звездочек говорит о незначимости коэффициента на 10 %-ном уровне.
Мы проверили незначимость коэффициентов при всех регрессорах, включенных в модель. Если мы хотим ориентироваться на 5 %-ный уровень значимости, то нужно удалить переменную с незначимым коэффициентом. Для того чтобы это сделать в окне с построенной моделью (в нашем случае это окно Модель 1, но, вообще говоря, это может быть Модель № в зависимости от того, сколько вы моделей построили до этого), выбираем пункт меню Правка – Изменить модель.
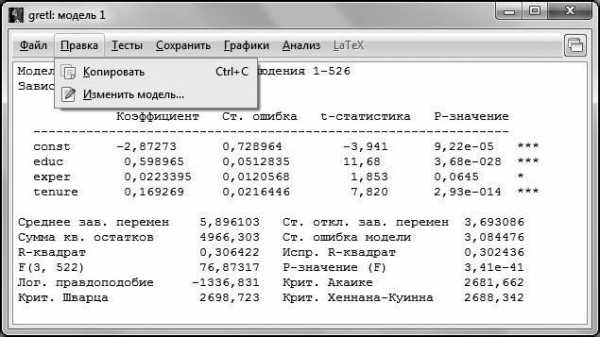
Рис. 4.4
В открывшемся окне выделяем переменную и красной стрелкой удаляем ее из независимых переменных.
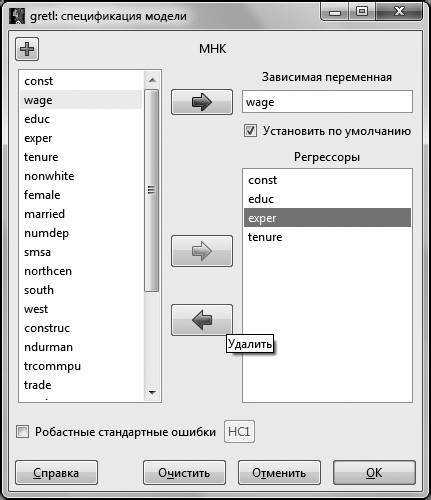
Рис. 4.5
Обновленная модель представлена на рис. 4.6.
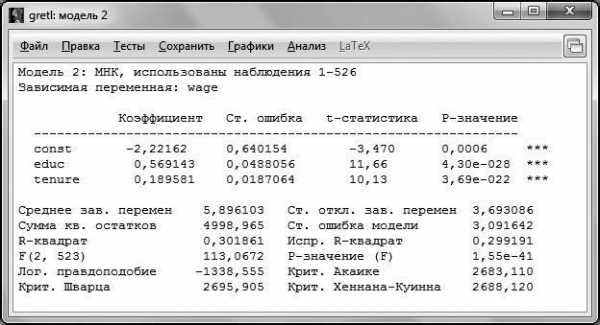
Рис. 4.6
Как видно из распечатки, все коэффициенты регрессии в обновленной модели значимы на 1 %-ном уровне (следовательно, и на 5 %-ном уровне они тоже значимы). Возможности t-теста не ограничиваются только проверкой незначимости коэффициентов при регрессорах. На самом деле проверка незначимости коэффициента является частным случаем проверки равенства коэффициента при регрессоре конкретному значению [2, 3].

Разберем это на примере. Проверим, а можем ли мы округлить коэффициент при переменной до 0,2. Сформулируем гипотезы для проверки этого предположения:
Для проверки такого рода гипотезы уже нельзя воспользоваться рассчитанным в GRETL значением t-статистики, а также р-значением, поэтому вычислим значение t-статистики для переменной самостоятельно: . Значение критической точки Стьюдента составит .
Сравниваем расчетную статистику и критическую и получаем, что , то есть (|–0,56 | < 1,96). В этом случае, мы можем принять нулевую гипотезу и округление коэффициента перед до 0,2 будет статистически корректно. Аналогичные гипотезы мы можем проверять для остальных коэффициентов регрессии.
Проверить, может ли коэффициент при регрессоре равняться заданному значению, позволяет также доверительный интервал [2, 3].

Используя данные из распечатки на рис. 4.6, можно построить доверительные интервалы для всех коэффициентов самостоятельно либо воспользоваться встроенной функцией GRETL для построения доверительного интервала.
Для этого в окне модели вызовем пункт меню Анализ – Доверительные интервалы для коэффициентов.
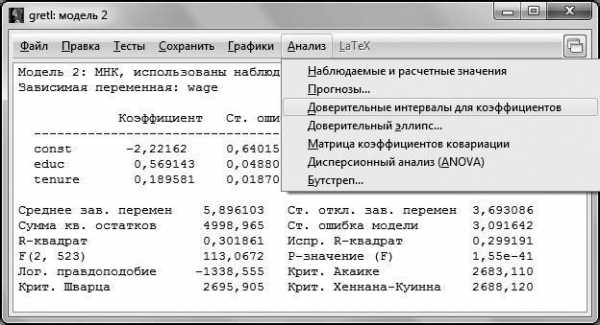
Рис. 4.7
Результатом работы данной функции является следующее окно (рис. 4.8).
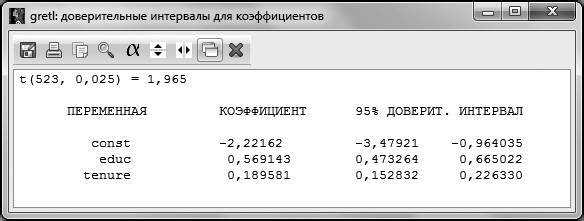
Рис. 4.8
Истинное значение коэффициента при переменной с вероятностью 95 % накрывается интервалом .
Нужно обратить внимание на то, что с помощью доверительного интервала можно проверять незначимость коэффициентов при регрессорах. В случае, если доверительный интервал накрывает 0 (то есть истинное значение коэффициента может принимать нулевое значение), можно сделать вывод о том, что коэффициент не значим.
Еще одна возможность для проверки гипотез с помощью теста Стьюдента – это односторонние гипотезы [2, 3].

Разберем, как проводится односторонний t-тест на примере. Проверим, верно ли, что коэффициент перед переменной можно считать большим 0,2.
Значение расчетной статистики для этого теста будет такое же, как и в предыдущем тесте (проверка равенства коэффициента заданному значению). Критическая точка составит . Сравнивая расчетное значение статистики с критическим, получаем , то есть –0,56 < 1,65. Значит, гипотеза H0 принимается.
По сути, все разновидности t-теста и построение доверительного интервала для коэффициента – это две стороны одной медали. Полезные результаты можно получать и тем и другим способом, выбор способа ответа на вопросы о незначимости коэффициента при регрессоре и соотношения коэффициента регрессора с заданным значением возлагается на исследователя.
fictionbook.ru
Общие сведения о пакете GRETL — Студопедия.Нет
Министерство образования и науки Украины Севастопольский национальный технический университет
РЕАЛИЗАЦИЯ ЭКОНОМЕТРИЧЕСКИХ МЕТОДОВ
ОБРАБОТКИ ФИНАНСОВО-ЭКОНОМИЧЕСКОЙ ИНФОРМАЦИИ В GRETL 1.7.1
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторному практикуму
по дисциплине «Эконометрия»
для студентов специальности
6.050201 — «Менеджмент организаций»
всех форм обучения
Севастополь
2008
УДК 658
«Реализация эконометрических методов обработки финансово-экономической информации в GRETL 1.7.1»
методические указания к выполнению лабораторных работ по дисциплине «Эконометрия» для студентов специальности 8.050201 – «Менеджмент организаций» всех форм обучения / Сост. А.В. Цуканов, Т.А. Кокодей. – Севастополь: Изд-во СевНТУ, 2008г. – 135 с.
Целью методических указаний являетсяполучение практических навыков построения эконометрических моделей при изучении экономических явлений и процессов с использованием системы Gretl 1.7.1.
Методические указания утверждены на заседании кафедры менеджмента и экономико-математических методов, (протокол № 5 от 23.01.2008 г.).
Допущено учебно-методическим центром СевНТУ в качестве методических указаний.
Рецензент:
Фисун С.Н., канд. техн. наук, доцент кафедры «Кибернетика и вычислительная техника».
СОДЕРЖАНИЕ
| Лабораторная работа №1. Введение в пакет программ GRETL 1.7.1………… | 5 |
| 1. Цель работы……………………………………………………………………………… | 5 |
| 2. Теоретический раздел……………………………………………………………… | 5 |
| 2.1. Общие сведения о пакете Gretl………………………………………………….. | 5 |
| 2.2. Стартовый экран Gretl…….……………………………………………………… | 6 |
| 2.3. Построение набора статистических данных………………………………………… | 7 |
| 2.3.1. Ручной ввод информации с клавиатуры……………………………………… | 8 |
| 2.3.2. Импорт данных…………………………………………………………………. | 10 |
| 2.4.Открытие встроенного или ранее созданного набора данных………………… | 11 |
| 2.5 Редактирование набора статистических данных…………………………………….. | 12 |
| 2.6. Экспорт данных………………………………………………………………….. | 15 |
| 3. Порядок выполнения лабораторной работы…………………………………….. | 16 |
| 4. Содержание отчета о выполнении лабораторной работы………………………. | 17 |
| Библиографический список………………………………………………………….. | 18 |
| Лабораторная работа №2. Линейный регрессионный анализ взаимосвязи статистических данных в среде GRETL 1.7.1……………………………………………. | 19 |
| 1. Цель работы………………………………………………………………………… | 19 |
| 2. Теоретические сведения о линейном регрессионном анализе…………………….. | 19 |
| 3. Описание средств системы Gretl для выполнения регрессионного анализа……………………………………………………………….……………….. | 21 |
| 3.1. Оценка параметров линейной регрессионной модели методом 1МНК (OLS) и проверка адекватности модели……………………………………………………. | 21 |
| 3.2. Анализ выполнения предпосылок 1МНК…….………………………………… | 28 |
| 4. Порядок выполнения лабораторной работы ……………………………………….. | 33 |
| 5. Содержание отчёта о выполнении лабораторной работы…………………………. | 33 |
| Библиографический список…..………………………………………………………. | 34 |
| Приложение А. (справочное) Основные описательные статистики………………. | 35 |
| Приложение Б. (справочное) Статистические таблицы в GRETL…………………. | 36 |
| Приложение В. (справочное) Построение графиков………………………………….. | 38 |
| Лабораторная работа №3. Применение GRETL 1.7.1. при построении и анализе регрессионных моделей с гетероскедастичной случайной составляющей………………………………………………………………………… | 40 |
| 1. Цель работы…………………………………………………………………………… | 40 |
| 2. Теоретические сведения …………………………………………..………………. | 40 |
| 3. Описание средств системы Gretl для выполнения регрессионного анализа при наличии гетероскедастичности……………………………………………………… | 43 |
| 3.1. Пример обнаружения гетероскедастичности в Gretl ………………………….. | 43 |
| 3.2. Оценивание гетероскедастичной модели с использованием взвешенного метода наименьших квадратов ВМНК (WLS)……………………………………… | 50 |
| 4. Порядок выполнения лабораторной работы ……….……………………………. | 59 |
| 5. Содержание отчёта о выполнении лабораторной работы………………………….. | 59 |
| Библиографический список………………………………………………………….. | 60 |
| Лабораторная работа №4. Реализация метода главных компонент в среде GRETL 1.7.1………………………………………………………………………….. | 61 |
| 1. Цель работы………………………………………………………………………… | 61 |
| 2. Теоретический раздел ………………………………………………………………………………. | 61 |
| 3. Пример практической реализации метода главных компонент с использованием системы Gretl………………………………………………….…… | 62 |
| 3.1.3.1. Исходная информация……………………………………………………………. | 63 |
| 3.2.Построение главных компонент и интерпретация результатов моделирования………………………………………………………………………… | 68 |
| 4. Порядок выполнения лабораторной работы ……….……………………………. | 74 |
| 5. Содержание отчёта о выполнении лабораторной работы………………………….. | 76 |
| Библиографический список…..……………………………………………………… | 77 |
| Приложение А. (справочное) Основные показатели результатов деятельности компаний Ford Motor Company и General Motors (2002-2006)……………………… | 78 |
| Лабораторная работа №5. Анализ временных рядов в среде Gretl 1.7.1.……. | 82 |
| 1. Цель работы………………………………………………………………………… | 82 |
| 2. Теоретический раздел ………………………………………….……………………. | 82 |
| 2.1. Анализ тренда………………………………………………………………………. | 83 |
| 2.2. Декомпозиция временного ряда..……………………………………………….. | 85 |
| 2.3. Анализ сезонности. Коррелограмма……………………………………………. | 86 |
| 2.4. Метод авторегрессии……………………………………………………………….. | 87 |
| 2.5. Спектральный (Фурье) анализ…………………………………………………. | 87 |
| 3. Описание средств анализа временных рядов системы Gretl……………………. | 88 |
| 3.1. Пример построение полиномиальной модели тренда…………………………. | 88 |
| 3.2. Пример декомпозиции динамики макроэкономических показателей…………… | 95 |
| 3.3. Пример анализа сезонности с применением коррелограммы ………………… | 102 |
| 3.4. Пример применения метода авторегрессии……………………………………. | 104 |
| 3.5. Пример применения метода спектрального (Фурье) анализа………………… | 107 |
| 4. Порядок выполнения лабораторной работы ……………………………………….. | 109 |
| 5. Содержание отчёта о выполнении лабораторной работы……………………….. | 110 |
| Библиографический список…..……………………………………………………… | 111 |
| Приложение А. (справочное) Исходные данные……………………………………………….. | 112 |
| Лабораторная работа №6 Анализ систем одновременных эконометрических уравнений в среде Gretl 1.7.1………………………………… | 115 |
| 1. Цель работы………………………………………………………………………… | 115 |
| 2. Теоретический раздел…………………………………………..……………………. | 115 |
| 3. Описание средств анализа систем одновременных эконометрических уравнений пакета Gretl………………………………………………….………………… | 117 |
| 4. Порядок выполнения лабораторной работы ……………………………………….. | 128 |
| 5. Содержание отчёта о выполнении лабораторной работы………………………….. | 134 |
| Библиографический список…..……………………………………………………… | 135 |
ЛАБОРАТОРНАЯ РАБОТА №1
ВВЕДЕНИЕ В ПАКЕТ ПРОГРАММ GRETL 1.7.1
Цель работы
Целью данной работы является ознакомление с функциональными возможностями программного продукта Gretl 1.7.1.
ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
Общие сведения о пакете GRETL
Пакет программ GRETL (GNU Regression Econometrics and Time Series Library) представляет собой инструментарий для практической реализации сложных вычислительных процедур эконометрического моделирования. В 2002 году его автор проф. Аллен Котрелл (США) включил GRETL в проект www.sourceforget.net, делая его общедоступным, бесплатным продуктом с возможностью дальнейшей доработки открытых кодов (Open Source – свободным программным обеспечением). Таким образом, данный пакет программ, статистические данные для обработки, учебное пособие и исходный код всех выпущенных версий доступны на Интернет-сайтах http://gretl.sourceforge.net или http://www.kufel.torun.pl.
Возможности программы:
1. Основные описательные статистики (среднее арифметическое, медиана, минимальное и максимальное значения, среднеквадратическое отклонение, коэффициент изменчивости (вариации), коэффициент асимметрии, коэффициент эксцесса).
2. Проверка нормальности распределения, распределение частот случайной величины, распределение плотности вероятностей, определение коэффициентов корреляции и т.д.
3. Предусматривает непосредственный доступ к статистическим таблицам. Пакет Gretl содержит встроенные статистические таблицы для следующих распределений: нормального, t-распределения Стьюдента, F-распределения Фишера, хи-квадрат, Пуассона, биномиального и распределения Дарбина-Уотсона. Существует возможность вычисления критических значений, p-value.
4. Анализ временных рядов (набор методов оценивания обобщённым МНК, модели ARMAX и GARCH , система уравнений авторегрессии (VAR), проверка коинтеграции; построение линии тренда, коррелограммы, периодограммы; проверка единичных корней, моделирование типа ARIMA, а также процедуры десезонализации X-12-ARIMA и TRAMO).
5. Регрессионный анализ (одношаговый метод наименьших квадратов (1МНК), взвешенный МНК, двухшаговый МНК — оценка систем одновременных уравнений, методы оценивания логитовых, пробитовых и тобитовых моделей и нелинейных моделей, и т.д.)
6. Метод главных компонент.
7. Экспорт и импорт Gretl- Microsoft Excel и текстовые редакторы (Notepad и т.д).
8. Построение графиков и др.
Запуск программы осуществляется через Пуск-Программы-Gretl-Gretl или двойным щелчком мыши по иконке Gretl на рабочем столе.
Стартовый экран Gretl
Стартовый экран пакета программ GRETL (рисунок 1) подразделяется на три части:
— Меню, из которого реализуется набор функций.Меню функций состоит из следующих разделов: File(файл), Tools (инструменты), Data(данные),View(вид), Add(добавить), Sample(выборка), Variable (переменная), Model(модель), Help(помощь). Каждый раздел содержит группу программных функций.
— Список переменных (процессов), который содержит перечень названий и описаний переменных открытого набора данных.
— Набор иконок (пронумерованный от 1 до 10), обеспечивает быстрый доступ
к выбранным программным функциям. Набор иконок №1-10, рисунок 1. обеспечивает быстрый доступ к некоторым программным функциям:
1. Открывает окно системного калькулятора.
2. Открывает новое окно для скриптов GRETL.
3. Открывает окно инструкций GRETL.
4. Открывает окно иконок.
5. Обращается к сайту пакета программ GRETL.
6. Открывает окно «Руководство» в pdf формате.
7. Открывает окно помощи.
8. Открывает окно определения графика разброса точек.
9. Открывает окно спецификации модели для оценивания с применением МНК.
10. Открывает окно с примерами – базы фактических данных.
|
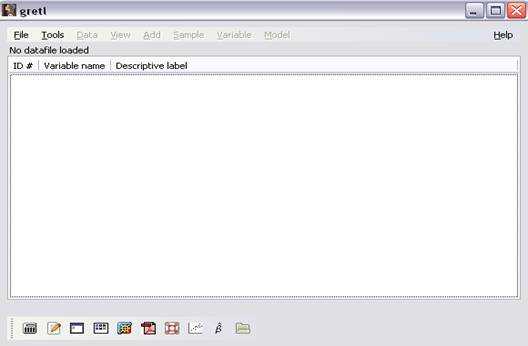
Рисунок 1 — Стартовый экран GRETL
studopedia.net
Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде Gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска
Пивенко Кристина Александровна1, Баженов Руслан Иванович2
1Приамурский государственный университет им.Шолом-Алейхема, студент
2Приамурский государственный университет им.Шолом-Алейхема, к.п.н., доцент, зав.кафедрой информатики и вычислительной техники
Pivenko Kristina Aleksandrovna1, Bazhenov Ruslan Ivanovich2
1Sholom-Aleichem Priamursky State University, student
2Sholom-Aleichem Priamursky State University, Candidate of pedagogical sciences, associate professor, Head of the Department of Computer Science
Библиографическая ссылка на статью:
Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде Gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска // Экономика и менеджмент инновационных технологий. 2015. № 4. Ч. 1 [Электронный ресурс]. URL: http://ekonomika.snauka.ru/2015/04/8362 (дата обращения: 07.02.2019).
В современном мире автомобиль перестал быть роскошью, он стал средством передвижения, доступным многим. Для большинства граждан предпочтительнее купить поддержанный автомобиль, а не новый, только что сошедший с конвейера. Какую сумму правильно будет заплатить за б/у автомобиль? За сколько можно продать свой автомобиль? С этими вопросами сталкиваются многие из нас. Чтобы правильно дать ответ, необходимо учесть определенные параметры: тип кузова, год выпуска, объем двигателя, тип коробки передач, пробег. Используя регрессионную модель в среде Gretl, можем найти зависимость стоимости автомобиля от данных параметров.
Ряд ученых изучает проблемы и методы построения различных регрессионных моделей. Базовые принципы использования метода регрессионного анализа были разработаны С.И. Носковым и М.П. Базилевским [1]. Использовалась множественная регрессия О.В. Гусевым и А.В. Жуковым [2] для идентификации перегрузки сервера. А.А. Жарков и Н.А. Анисимова [3] метод множественной регрессии применили для определения рыночной стоимости квартиры с учетом сроков и условий реализации жилья. Расчет логистических издержек при помощи метода множественной регрессии разработан И.А. Семеновым и А.А. Носковым [4]. С использованием Gretl определяются причины трудового оппортунизма сотрудников Р.З. Мухаметзяновым [5]. Особенности использования среды Gretl в целях построения экономических моделей рассматриваются А.А.Тусковым [6]. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования рассмотрела Ю.Г.Зарезина [7]. Р.И. Баженовым и др. [8-14] изучены проблемы использования регрессионных моделей для анализов различных видов. Изучением регрессионного анализа занимаются также зарубежные ученые [15-16].
По данным сайта www.avito.ru был осуществлен сбор экспериментальных наблюдений. Рассматривались объявления о продаже автомобилей в г.Биробиджан и в г.Хабаровск. Были выбраны следующие критерии: марка, тип кузова, год выпуска, объем двигателя, тип коробки передач, тип привода, пробег, стоимость.
Тип кузова кодируется следующим образом:
1 – седан;
2 – хэтчбэк;
3 – универсал;
4 – кроссовер;
5 – минивэн;
6 – пикап;
7 – внедорожник;
8 – купе.
Тип коробки передач обозначим:
1 – автоматическая;
2 – механическая.
Привод определим:
1 – передний;
2 – задний;
3 – полный.
Создадим таблицу данных в MS Excel. Используя данные 200 объявлений (рис.1).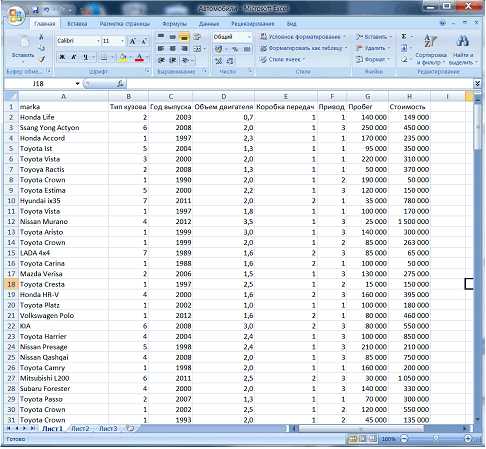
Рисунок 1- Фрагмент данных в Excel
Введем обозначения переменных: тип кузова – х1, год выпуска – х2, объем двигателя – х3, коробка передач – х4, привод – х5, пробег – х6, стоимость – y (рис.2.).
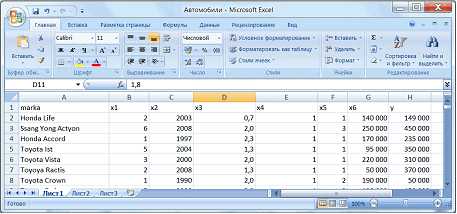
Рисунок 2 – Обозначение переменных
Следующий шаг – открыть данные таблицы Excel в Gretl (рис.3).
Рисунок 3 – Среда Gretl
В окне программы появляются переменные, которые необходимы, чтобы построить регрессионную модель (рис.4).
Рисунок 4 – Рабочее окно программы
Необходимо просмотреть получившуюся таблицу (рис. 5-6).
Рисунок 5 – Контекстное меню выделенных переменных
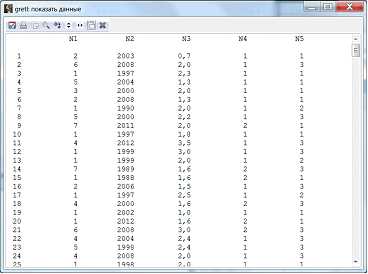
Рисунок 6 – Просмотр таблицы данных
Так как у нас получилось больше шести столбцов данных, то оставшиеся 2 столбца найдем внизу таблицы (рис.7).
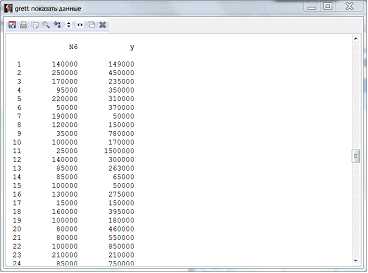
Рисунок 7 – Таблица данных (окончание)
Для решения нашей задачи найдем регрессионную модель, используя метод наименьших квадратов (рис.8).
Рисунок 8 – Меню Модель
Перейдем к построению уравнения модели (рис.9)
Рисунок 9 – Окно спецификации модели
Получившаяся модель и ее описательные статистики показаны на рисунке (рис.10).
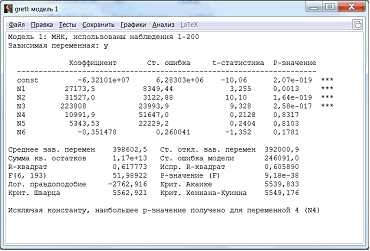
Рисунок 10 – Регрессионная модель
По значению R-квадрата можно судить о доле вариации результативного признака с учетом воздействия изучаемых факторов. В данной модели 61,8% вариации переменной Y зависит от влияния включенных факторов, 38,2% обусловлены другими факторами. Если коэффициент выше 80%, то модель считается достаточно хорошей. А у нас слишком низкий R-квадрат. Использование линейной аналитической формы модели может стать вероятной причиной ее слабости. Поэтому найдем другую модель.
При помощи теста на нелинейность можно проверить обоснованность применения степенной модели (рис.11).
Рисунок 11 – Выбор теста на нелинейность
Проверим модель на нелинейность (логарифмы) (рис. 12).

Рисунок 12 – Тест на нелинейность (логарифмы)
Тест нелинейности для логарифмов (значение p=0,0000001) свидетельствует, что нулевую гипотезу (о линейности аналитической формы) следует отклонить, поскольку значение TR2 = 43,7347 превышает критическое значение х2(1%; 5) = 15,086; по этой причине существуют основания для принятия степенной формы модели (с логарифмированными переменными).
Исследования параметров привели к выводу, что существует логарифмическая зависимость.
Найдем зависимость lny от х1, х2, х3, х4, х5, lnx6 (рис.13).
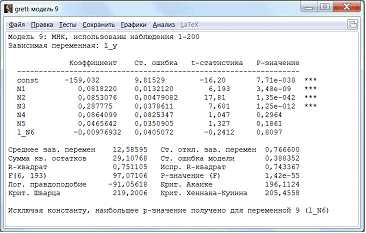
Рисунок 13 – Новая регрессионная модель
В этой модели R-квадрат у нас уже 75,1%. Значит, модель более точная, чем предыдущая.
Перейдем к решению уравнения
Введем в Excel данные const, х1, х2, х3, х4, х5, х6 (рис. 14). Коэффициенты: a – тип кузова, b – год выпуска, с – объем двигателя, d – коробка передач, e – привод, f – пробег.
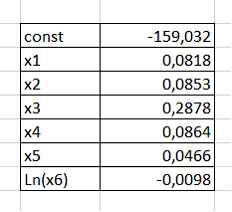
Рисунок 14 – Данные в Excel
В ячейку, окрашенную в оранжевый цвет, вводим формулу расчета (рис.15). В таблицу Excel вводим необходимые параметры того автомобиля, который мы хотим купить или продать, в ячейки, окрашенные в синий цвет.
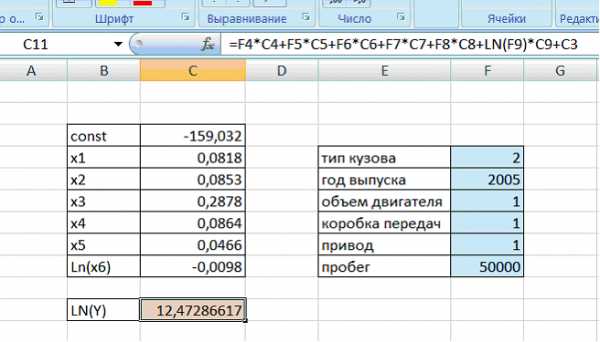
Рисунок 15 – Ввод данных
В ячейку, окрашенную в зеленый цвет, вводим формулу расчета стоимости автомобиля. После этого в ячейке, выделенной зеленым цветом, отобразится стоимость данного автомобиля (рис.16).
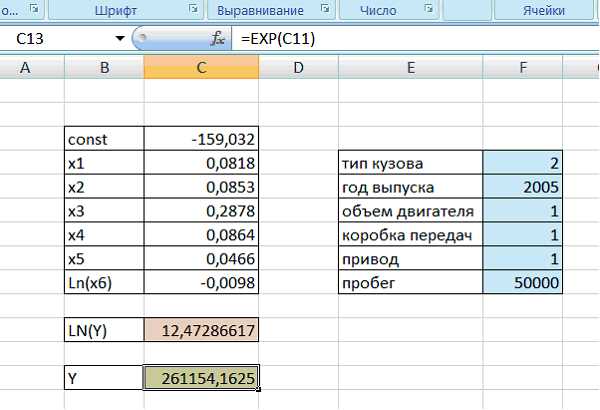
Рисунок 16 – Расчет стоимости автомобиля по заданным параметрам
Если мы хотим узнать стоимость другого автомобиля, то нужно просто в ячейки, окрашенные в синий цвет ввести другие параметры.
Полученную регрессионную модель можно использовать в работе агентств, занимающихся продажей поддержанных автомобилей. Описание принципов построения регрессионной модели может пригодиться в преподавании студентам различных направлений [17-19].
Библиографический список
- Базилевский М.П., Носков С.И. Методические и инструментальные средства построения некоторых типов регрессионных моделей // Системы. Методы. Технологии. 2012. №1. С. 80-87.
- Гусев О.В., Жуков А.В. Способ идентификации перегрузки с использованием множественной регрессии // Информационная среда вуза XXI века. Материалы VII Международной научно-практической конференции. Петрозаводск, 2013. С. 57-61.
- Жарков А.А., Анисимова Н.А. Механизм формирования стоимости квартир на региональном рынке жилья // Регион: системы, экономика, управление. 2009. № 4. С. 47-53.
- Семенов И.А., Носков А.А. Модель расчета общих логистических издержек методом множественной регрессии // Вестник Саратовского государственного технического университета. 2011. Т. 4. № 2с. С. 397-400.
- Мухаметзянов Р.З. Анализ трудового оппортунизма сотрудников // Science time. 2014. №6 (6). С. 132-147.
- Тусков А.А. Применение Gretl для построения многофакторной модели // Модели, системы, сети в экономике, технике, природе и обществе. 2011. №1. С. 154-159.
- Зарезина Ю.Г. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования // Новое слово в науке и практике: гипотезы и апробация результатов исследований. 2015. № 15. С. 223-228.
- Пронина О.Ю., Баженов Р.И. Исследование методов регрессионного анализа программной среды Eviews // Nauka-Rastudent.ru. 2015. № 1 (13). С. 45.
- Лагунова А.А., Баженов Р.И. Разработка в среде Gretl регрессионной модели рынка вторичного жилья г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 40.
- Муллинов Д.О., Баженов Р.И. Разработка в среде Eviews регрессионной модели рынка гаражных помещений г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 43.
- Баженов Р.И. Информационная безопасность и защита информации: практикум. Биробиджан: Изд-во ГОУВПО «ДВГСГА», 2011. 140 с.
- Vexler V.A., Bazhenov R.I., Bazhenova N.G. Entity-relationship model of adult education in regional extended education system // Asian Social Science. 2014. Т. 10. № 20. С. 1-14.
- Векслер В.А., Баженов Р.И. Формирование модели обучения взрослых основам информационных технологий: региональный аспект: монография. -Биробиджан: Издательский центр ФГБОУ ВПО «ПГУ им. Шолом-Алейхема», 2014. 126 с.
- Наумов А.А., Баженов Р.И. О неустойчивости метода нормализации критериев // Современные научные исследования и инновации. 2014. № 11-1 (43). С. 64-68.
- Baiocchi G., Distaso W. GRETL: Econometric software for the GNU generation // Journal of Applied Econometrics. 2003. Т. 18. №. 1. С. 105-110.
- Mixon Jr J. W., Smith R. J. Teaching undergraduate econometrics with GRETL // Journal of Applied Econometrics. 2006. Т. 21. №. 7. С. 1103-1107.
- Баженов Р.И. Об организации научно-исследовательской практики магистрантов направления «Информационные системы и технологии» // Современные научные исследования и инновации. 2014. № 9-2 (41). С. 62-69.
- Баженов Р.И. Проектирование методики обучения дисциплины «Интеллектуальные системы и технологии» // Современные научные исследования и инновации. 2014. № 5-2 (37). С. 48.
- Баженов Р.И. Об организации деловых игр в курсе «Управление проектами информационных систем» // Научный аспект. 2014. Т. 1. № 1. С. 101-102.
Количество просмотров публикации: Please wait
Все статьи автора «Баженов Руслан Иванович»
ekonomika.snauka.ru
Куфель Т. Эконометрика: решение задач с применением пакета программ GRETL [PDF]
Монография, Варшава, 2007, 200 с.Введение в пакет программ gretlЛицензия
Инсталляция
Меню и настройки пакета программ gretl
Рабочие сессии и работа с консолью
Статистические данные
Построение набора данных
Ввод данных — импорт данных
Описание набора данных и сохранение файла данных
Объявление типа данных
Агрегирование временных рядов
Преобразование переменных-процессов
Основные описательные статистики
Распределения переменной
Графики
Интернет-сервер со статистическими данными
Примеры из учебных пособий по эконометрике
Статистические тесты
Статистические таблицы в gretl
Калькулятор статистических тестов
Статистические тесты для переменных в базе gretl
Эконометрические модели для срезов данных
Подбор переменных модели — матрица корреляции
Оценивание параметров модели с применением классического метода Наименьших квадратов (кмнк)
Верификация эконометрической модели
Оценивание значимости структурных Параметров, t-тест Стьюдента и f-тест Снедекера.
Оценивание степени соответствия модели
Оценивание нормальности распределения остатков модели
Оценивание однородности дисперсии
Остатков модели. Проверка гетероскедастичности
Оценивание линейности
Аналитической формы модели
Подведение итогов сессии построения
Эконометрической модели
Характеристики экономических процессов
Функции автокорреляции и частичной автокорреляции
Периодограмма и спектр процессов
Проверка единичных корней
Оценивание дробного значения d
Основные модели экономических процессов
Полиномиальные модели тренда — Выбор степени полинома
Эконометрические модели сезонных колебаний
Авторегрессионные модели ar(p)
Модели arma(£ , q)
Модели arima(f , d, q)
Процедуры исключения сезонности
Метод x-12-arima
Метод tramo/seats
Причинно-следственные эконометрические модели экономических процессов
Спецификация модели согласно концепции Конгруэнтного моделирования
Оценивание параметров модели Методом наименьших квадратов
Верификация модели
Исследование значимости оценок
Параметров — исключение a posteriori
Тест автокорреляции дарвина—уотсона
Тест автокорреляции (тест quenouille)
H-тест автокорреляции дарбина
Тест автокорреляции на основании pacf
Тест автокорреляции бройша—годфри
Тест автокорреляции аджунга—бокса
Выявление эффекта arch в процессе остатков
Проверка стабильности Параметров — тест Чоу
Проверка стабильности
Параметров — тест cusum
Проверка нормальности
Распределения остатков
Проверка значимости пропущенных
И добавленных процессов (omit variables, add variables)
Эконометрическое прогнозирование
Прогнозирование по моделям, учитывающим тренд и сезонность
Прогнозы статического и динамического типа
Обобщенный метод наименьших квадратов (омнк)
Оценивание модели в условиях
Автокорреляции случайной составляющей
Метод Кохрейна—Оркотта
Метод Хилдрета—Лу
Метод Прайса—Уинстена
Обобщенный метод Кохрейна—Оркотта
Оценивание модели в условиях гетероскедастичности
Метод корректировки Гетероскедастичности случайной составляющей
Метод HCCM
Взвешенный метод наименьших
Квадратов (случай гетероскедастичности)
Взвешенный метод наименьших квадратов — модели для одноименных наблюдений Специальные модели
Логитовые и пробитовые модели
Тобитовые модели
Системы эконометрических уравнений
Двухшаговый метод наименьших квадратов
модели var
www.twirpx.com
ЭконометрияЛабораторныеGretl — Стр 2
11
2.4.Открытие встроенного или ранее созданного набора данных
ВGRETL существуют встроенные примеры наборов данных (*.gdt),
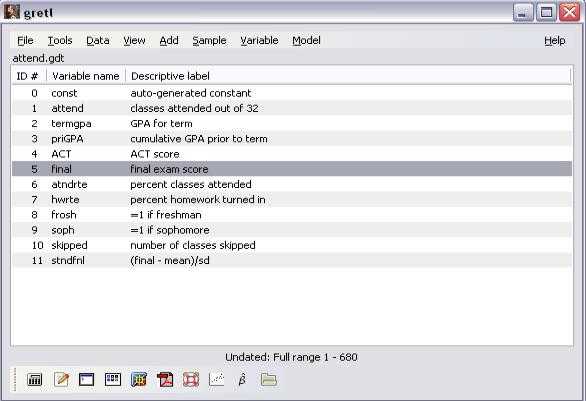
созданные разработчиками и преподавателями. Для их открытия необходимо обратиться к команде File\Open Data\Sample File и выбрать (на соответствующей закладке, например Wooldridge) имя открываемого файла, например, attend.gdt двойным щелчком мыши (рисунок 6).
Для просмотра значений отдельной переменной обратимся к команде: Variable\Display Values (или дважды щёлкнем мышью по названию переменной).
Для просмотра всего набора данных обратимся к команде: View\Icon
View\Data Set
Открытый набор данных, рисунок 6, состоит из 11 переменных, атрибуты которых -номера(ID#), названия (Variable name) и описания\формулы (Descriptive label)- представлены в списке переменных стартового экрана.
Рисунок 6 — Набор данных Class Attendence Rates and Grades (Посещаемость занятий и оценки) с закладки Wooldridge
Аналогичным образом можно открыть созданные ранее (в Примере 1 и Примере 2) на рабочем столе файлы example1.gdt и example2.gdt при помощи File\Open Data\User File, выбрав их в открывшемся окне.
Просмотреть общую информацию о наборе данных можно выбрав
Data\Print Description
12
2.5. Редактирование набора статистических данных
Возможны следующие операции над переменными открытого набора данных:
1.Добавление переменной вручную: Variable\Define new variable или из
Excel файла: File\Append Data\Excel
2.Удаление переменной: нажатие кнопки DEL на клавиатуре.
3.Редактирование значений переменной: Data\Edit Values.
4.Добавление наблюдений: Data\Add Observations.
5.Изменение атрибутов переменной: Variable\Edit Attributes.
6. Просмотр и редактирование всего набора данных:View\Icon View\Data
Set.
7. Удаление наблюдений с пропущенными значениями: Sample\Drop all obs with missing values.
Функция Variable\Define New Variable позволяет добавить ещё одну переменную, а функция Data\Add Observations – добавить определённое число наблюдений к существующему выбранному ряду. Двойной щелчёк мыши по названию переменной позволяет просмотреть ряд её значений, а функция Data\Edit Values – редактировать данные значения. Удаление переменной из списка осуществляется нажатием кнопки del на клавиатуре. Чтобы изменить атрибуты переменной необходимо щелчком мыши выбрать её название в списке и вызвать функцию Variable\Edit Attributes, затем в открывшемся диалоговом окне ввести новое имя переменной (Name of variable) и её формулу или текстовое описание (Description).
Быстрый доступ к данным функциям возможен из контекстного меню, вызванного нажатием правой кнопкой мыши на выбранной переменной в списке стартового экрана.
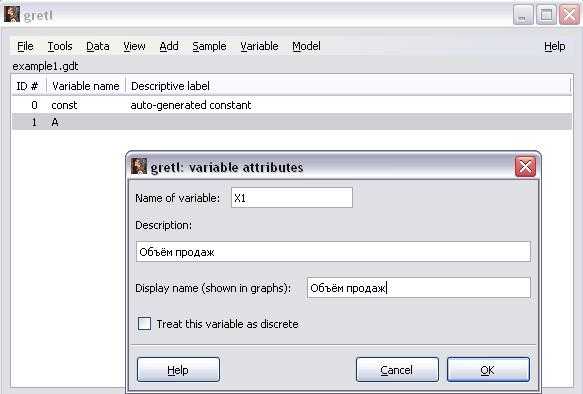
Пример 3. Редактирование набора данных example1.gdt: 1. Откроем ранее созданный (Примере1) набор данных example1.gdt:File\Open Data\User File (рисунок 7)
2. Изменим название переменной на X1 и введём её описание «Объём продаж»: Variable\Edit Attributes (рисунок 7)
13
Рисунок 7 — Изменение атрибутов переменной: ввод названия и описания
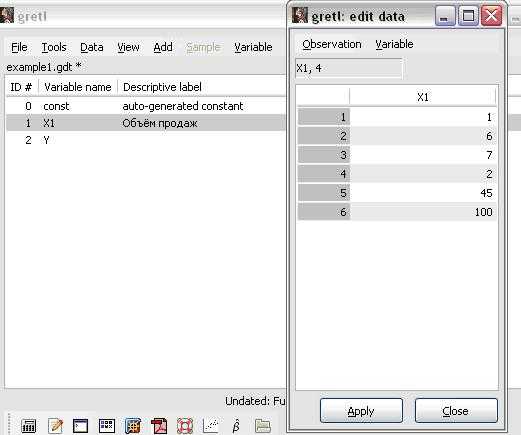
3. Добавим в набор новую переменную Y. Для этого выберем команду Define new variable в менюVariable и в открывшемся окне редактирования введём её значения:
-4,223,8 34,2 748,992 1615 (рисунок 8)
4.Щелчком мыши выберем переменную X1 из списка (рисунок 8) и добавим одно наблюдение “100” к ряду её значений: Data\Add Observations (введём 1) иData\Edit Values (в открывшемся окне “Edit data” введём шестое наблюдение “100”).
5.В этом же окне «Edit data» вручную изменим значение четвёртого наблюдения на 30,7 (рисунок 8), нажмём кнопки «apply» и «close» для завершения редактирования значений переменной X1.
6.Аналогичным образом выберем переменную Y, обратимся к команде Data\Edit Values и введём ещё одно значение ряда 7995.
14
Рисунок 8 — Редактирование значений переменной X1
8.В ранее созданном (в Примере 2.) на рабочем столе файле example2.xls изменим название переменной X1 на X3. Затем добавим к редактируемому в данном примере набору данных example1.gdt переменные из файла example2.xls: File\Append Data\Excel (выбрать название файла). В результате в список переменных стартового экрана будут добавлены переменные X2 и X3.
9.Откроем весь набор данных для редактирования: View\Icon View\Data Set (рисунок 9).
10.Удалим наблюдения №7-9с пропущенными значениями переменных X1 и Y, сократив выборку до шести первых наблюдений:Sample\Drop all obs with missing values. Нажмём кнопки «apply» и «close». Сохраним набор данныхFile\Save Data, ответив «no» на вопрос о восстановлении первоначального размера выборки.
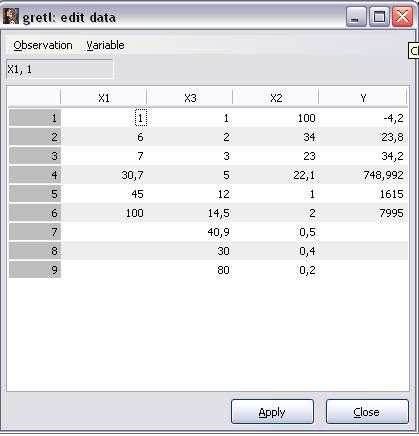
15
Рисунок 9 — Окно редактирования набора данных
2.6. Экспорт данных
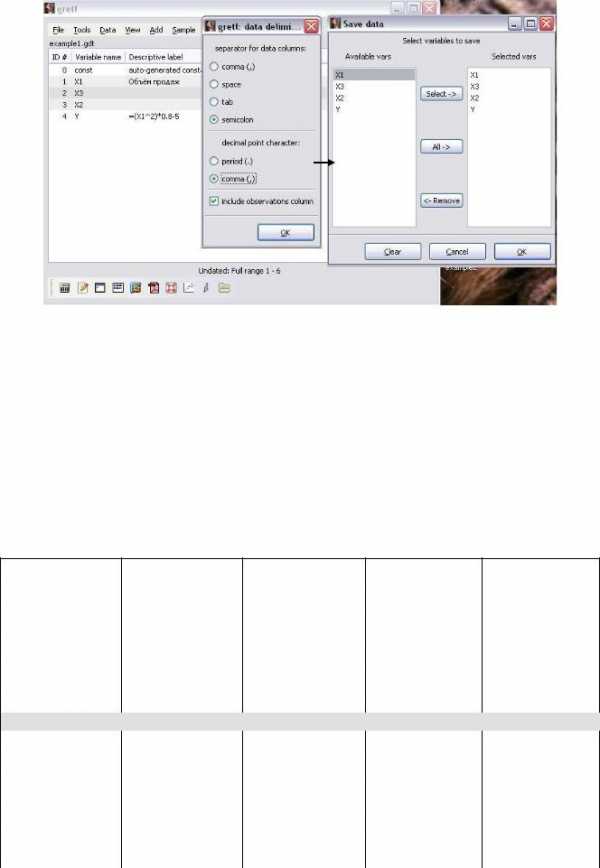
Экспорт данных в Excel осуществляется с использование команды File\Export Data\SCV Экспортируем в Excel полученный в Примере 3 набор данных:
1.Откроем в Gretl файл example1.gdt (File\Open Data\User File).
2.Обратимся к команде File\Export Data\SCV. В открывшемся окне поставим флажки разделителей semicolon и comma (,) для интерпретации информации в Excel как количественных данных в отдельных столбцах, рисунок 10.
3.В открывшемся окне Save Data при помощи кнопки Select перенесём все переменные из списка в левой части окна в правую часть и нажмём кнопку ОК.
4.Введём имя файла example1.csv и нажмём кнопку save. Данный файл появится на рабочем столе.
16
Рисунок 10 — Экспорт данных из среды GRETL в таблицу Excel
3.ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1.Выполнить примеры №1-3данных методических указаний.
2.Выполнить упражнения №1-3согласно варианту.
3.Подготовить отчёт по выполненной работе в электронном виде (MS-Word).Упражнение 1. Создать набор данных из двух переменных X1 и X2(тип
данных – cross-sectional)по исходной информации, представленной в таблице 4 согласно варианту. Сохранить в файл Ex1.gdt на рабочем столе и закрыть созданный набор данных.
Таблица 4 -Значенияпеременной X1 и X2 по вариантам№№1-10
№1 |
| №2 |
| №3 |
| №4 |
| №5 |
|
3 | 1 | 3,5 | 2 | 3,6 | 1 | 10 | 11 | 0 | 10 |
|
|
|
|
|
|
|
|
|
|
5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 6,3 |
|
|
|
|
|
|
|
|
|
|
7 | 7 | 9 | 7,5 | 7,1 | 7 | 7,9 | 41,5 | 7,1 | 7 |
|
|
|
|
|
|
|
|
|
|
10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 |
|
|
|
|
|
|
|
|
|
|
40,2 | 40 | 30,2 | 40,2 | 30,2 | 40,2 | 40,2 | 40,2 | 40,2 | 40,2 |
|
|
|
|
|
|
|
|
|
|
80 | 80 | 80 | 80 | 80 | 81 | 80 | 80 | 80 | 87 |
|
|
|
|
|
|
|
|
|
|
100 | 101 | 200 | 100 | 100 | 101 | 100 | 100 | 100 | 106 |
|
|
|
|
|
|
|
|
|
|
120 | 120 | 130 | 120 | 129 | 121 | 120 | 128 | 120 | 125 |
|
|
|
|
|
|
|
|
|
|
№6 |
| №7 |
| №8 |
| №9 |
| №10 |
|
3 | 1 | 3,5 | 2 | 3,6 | 1 | 10 | 11 | 0 | 10 |
|
|
|
|
|
|
|
|
|
|
5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 5,3 | 6,3 |
|
|
|
|
|
|
|
|
|
|
7 | 7 | 9 | 7,5 | 7,1 | 7 | 7,9 | 41,5 | 7,1 | 7 |
|
|
|
|
|
|
|
|
|
|
10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 | 10,3 |
|
|
|
|
|
|
|
|
|
|
40,2 | 40 | 30,2 | 40,2 | 30,2 | 40,2 | 40,2 | 40,2 | 40,2 | 40,2 |
|
|
|
|
|
|
|
|
|
|
80 | 80 | 80 | 80 | 80 | 81 | 80 | 80 | 80 | 87 |
|
|
|
|
|
|
|
|
|
|
100 | 101 | 200 | 100 | 100 | 101 | 100 | 100 | 100 | 106 |
|
|
|
|
|
|
|
|
|
|
120 | 120 | 130 | 120 | 129 | 121 | 120 | 128 | 120 | 125 |
|
|
|
|
|
|
|
|
|
|
17
Упражнение 2.
Импортировать файл example2.xls (созданный в вышеописанном Примере 2) в среду Gretl как временной ряд с поквартальными данными, начиная с даты X.0X.2008г., где Х – номер варианта.
Упражнение 3.
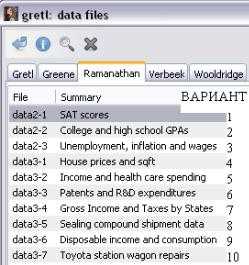
1.Открыть встроенный набор данных File\Open data\Sample File\Ramanathan\файл в зависимости от варианта (рисунок 11).
2.Просмотреть общую текстовую информацию о наборе данных
Data\Print Description.
3.Изменить первые три значения одной из переменных.
4.Сократить выборку на последние пять наблюдений.
5.Экспортировать данные в таблицу Excel.
Рисунок 11 — Варианты заданий для выполнения упражнения 3
4. СОДЕРЖАНИЕ ОТЧЕТА О ВЫПОЛНЕНИИ ЛАБОРАТОРНОЙ РАБОТЫ
1)Название и цель работы.
2)Постановка задачи.
3)Этапы выполнения задачи в Gretl.
4)Выводы.
18
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Куфель Т. Эконометрика. Решение задач с применением пакета программ GRETL / Т. Куфель. — М.: Горячая линия – Телеком, 2007. – 200с.
2.Using gretl for Principles of Econometrics, 3rd Edition Version 1.01 Lee C. Adkins Professor of Economics Oklahoma State University // http://www.learneconometrics.com/gretl.html
3.Уокенбах Дж. Microsoft Office Excel 2007. Библия пользователя / Дж. Уокенбах. — М.: Диалектика, 2008.- 816с.
4.Карлберг К. Бизнес-анализс помощью Microsoft Excel/ К. Карлберг — М.: Вильямс, 2007.- 464с.
5.Джелен Б. Сводные таблицы в Microsoft Excel/ Б. Джелен — М.: Вильямс, 2007.- 320с.
19
ЛАБОРАТОРНАЯ РАБОТА №2 ЛИНЕЙНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ ВЗАИМОСВЯЗИ
СТАТИСТИЧЕСКИХ ДАННЫХ В СРЕДЕ GRETL 1.7.1.
1. ЦЕЛЬ РАБОТЫ
Целью данной работы является получение практических навыков регрессионного анализа в системе Gretl для автоматизированного поиска ранее неизвестных закономерностей в имеющихся в распоряжении менеджера данных с последующим использованием полученной информации для подготовки управленческих решений.
2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ О ЛИНЕЙНОМ РЕГРЕССИОННОМ АНАЛИЗЕ
Целью | регрессионного | анализа является оценка функциональной | |
зависимости | ˆ | …, xn ) | u результативного признака (y) от факторных |
y f (x1, x2, | |||
(x1, x2, …, xn ) . Формулы (1) и (2) представляют собой линейные модели парной и множественной регрессии соответственно.
y f (x) u0 1 x u, | (1) |
y 0 1 x1 n xn u, | (2) |
где y — фактическое значение результативного признака;xi -признак-фактор;
ai – параметр регрессионной модели;
u — случайная ошибка (остаток), характеризующая отклонения реального значения результативного признака от теоретического. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
Оценивание параметров линейной модели основан на обычном или одношаговом методе наименьших квадратов (1МНК или OLS – Ordinary Least Squares).
Этот метод позволяет получить такие оценки параметров, при которых
сумма квадратов отклонений фактических значений результативного признака
~
(y) от расчетных (теоретических)yx минимальна, формула (3).
| ~ |
| 2 | min , |
|
|
| (3) | |
( yiyxi | ) |
|
|
|
| ||||
i |
|
|
|
|
|
|
|
|
|
Статистическое | моделирование | связи | методом | линейного | |||||
регрессионного анализа осуществляется в 3 этапа: |
|
|
| ||||||
a) Оценка | параметров линейной | регрессионной | модели методом | ||||||
1МНК |
|
|
|
|
|
|
|
|
|
Вектор оценок | параметров модели | (2) определяется | выражением (4). | ||||||
1 | X T Y |
|
|
|
| (4) | |||
X T X |
|
|
|
| |||||
b) Проверка | адекватности регрессионной | модели | (проверки | ||||||
значимости индивидуальных оценок коэффициентов модели с помощью t-
20
критерия Стьюдента и оценка значимости уравнения регрессии в целом с помощью F-критерияФишера)
На первом шаге проверки адекватности (качества) модели оценивается существенность влияния каждой объясняющей переменной xi , на зависимую переменную y, для этого необходимо оценить значимость полученных параметров i , используя t- критерий Стьюдента, формула (5). Значимость
параметра определяется путём проверки нулевой гипотезы о равенстве его нулю (для выбранного уровня значимости).
t p |
|
| i |
|
|
| , |
| (5) | |
|
|
|
|
| ||||||
|
|
|
|
|
| |||||
|
|
|
|
|
| |||||
| 2 |
| ||||||||
i |
|
|
|
|
|
|
| |||
|
|
| i |
|
|
| ||||
где i — оценкаi -гокоэффициента модели, COEFFICIENT; | ||||||||||
|
|
|
|
| ||||||
2 | — оценка дисперсии параметра | , | 2 = STDERROR. | |||||||
i |
|
|
|
|
|
| i |
| i | |
На втором шаге проверки адекватности модели оценивается её значимость (пригодность) в целом , используя показатели: F-критерий Фишера, формула (6), коэффициент детерминации R 2 , формула (7), (Unadjusted R2 и Adjusted R2), сумма квадратов остатков RSS Sum of squared residuals),
стандартная ошибка регрессии (Standard error of residuals), информационные критерии (Akaike information criterion, Schwarz Bayesian criterion, Hannan-Quinncriterion).
Значимость регрессии проверяется путём проверки нулевой гипотезы о равенстве нулю всех параметров модели (для выбранного уровня значимости).
Fр |
|
| R2 |
| n k | , | (6) |
| R2 | k 1 | |||||
| 1 |
|
|
| |||
где R 2 — коэффициент детерминации — часть вариации (дисперсии) зависимой переменной y, которая объясняется уравнением регрессии, UNADJUSTED R2.
|
|
|
|
|
|
|
| |
R2 | ˆ Т XТ Y n Y | 2 | , | (7) | ||||
|
|
|
|
| ||||
Y Т Y n Y2 | ||||||||
|
|
| ||||||
n — число наблюдений;
k – число коэффициентов факторов.
При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты:
— Построенная модель на основе ее проверки по F-критериюФишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может
быть использована для принятия решений к осуществлению прогнозов.
— Модель по F-критериюФишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия
некоторых решений, но не для производства прогнозов.
— Модель по F-критериюФишера адекватна, но все коэффициенты регрессии
studfiles.net
Куфель Т. Эконометрика: решение задач с применением пакета программ GRETL — Материалы по Gretl — Специальная литература — Каталог материалов
Рассмотрены методы решения основных эконометрических задач с использованием пакета программ GRETL (GNU Regression Econometrics Time-series Library), предназначенного для практической реализации сложных вычислительных процедур эконометрического моделирования. Пакет программ GRETL и представленные в работе статистические данные доступны на интернет-сайте автора http://www.kufel.torun.pl. Для студентов, аспирантов и преподавателей экономических ВУЗов, а также для научных работников, ведущих экономические исследования.
СОДЕРЖАНИЕ
Предисловие к русскому изданию
Предисловие
1. Введение в пакет программ GRETL
1.1. Лицензия
1.2. Инсталляция
1.3. Меню и настройки пакета программ GRETL
1.4. Рабочие сессии и работа с консолью
2. Статистические данные
2.1. Построение набора данных
2.2. Ввод данных — импорт данных
2.3. Описание набора данных и сохранение файла данных
2.4. Объявление типа данных
2.5. Агрегирование временных рядов
2.6. Преобразование переменных-процессов
2.7. Основные описательные статистики
2.8. Распределения переменной
2.9. Графики
2.10. Интернет-сервер со статистическими данными
2.11. Примеры из учебных пособий по эконометрике
3. Статистические тесты
3.1. Статистические таблицы в GRETL
3.2. Калькулятор статистических тестов
3.3. Статистические тесты для переменных в базе GRETL
4. Эконометрические модели для срезов данных
4.1. Подбор переменных модели — матрица корреляции
4.2. Оценивание параметров модели с применением классического метода наименьших квадратов (КМНК)
4.3. Верификация эконометрической модели
4.3.1. Оценивание значимости структурных Параметров, t-тест Стьюдента и F-тест Снедекера.
4.3.2. Оценивание степени соответствия модели
4.3.3. Оценивание нормальности распределения остатков модели
4.3.4. Оценивание однородности дисперсии остатков модели. Проверка гетероскедастичности
4.3.5. Оценивание линейности аналитической формы модели
4.4. Подведение итогов сессии построения эконометрической модели
5. Характеристики экономических процессов
5.1. Функции автокорреляции и частичной автокорреляции
5.2. Периодограмма и спектр процессов
5.3. Проверка единичных корней
5.4. Оценивание дробного значения d
6. Основные модели экономических процессов
6.1. Полиномиальные модели тренда — Выбор степени полинома
6.2. Эконометрические модели сезонных колебаний
6.3. Авторегрессионные модели AR(p)
6.4. Модели ARMA(£ , q)
6.5. Модели ARIMA(f , d, q)
6.6. Процедуры исключения сезонности
6.6.1. Метод X-12-ARIMA
6.6.2. Метод TRAMO/SEATS
7. Причинно-следственные эконометрические модели экономических процессов
7.1. Спецификация модели согласно концепции Конгруэнтного моделирования
7.2. Оценивание параметров модели Методом наименьших квадратов
7.3. Верификация модели
7.3.1. Исследование значимости оценок параметров — исключение a posteriori
7.3.2. Тест автокорреляции Дарвина—Уотсона
7.3.3. Тест автокорреляции (тест Quenouille)
7.3.4. H-тест автокорреляции Дарбина
7.3.5. Тест автокорреляции на основании PACF
7.3.6. Тест автокорреляции Бройша—Годфри
7.3.7. Тест автокорреляции Аджунга—Бокса
7.3.8. Выявление эффекта ARCH в процессе остатков
7.3.9. Проверка стабильности параметров — тест Чоу
7.3.10. Проверка стабильности параметров — тест CUSUM
7.3.11. Проверка нормальности распределения остатков
7.3.12. Проверка значимости пропущенных и добавленных процессов (omit variables, add variables)
8. Эконометрическое прогнозирование
8.1. Прогнозирование по моделям, учитывающим тренд и сезонность
8.2. Прогнозы статического и динамического типа
9. Обобщенный метод наименьших квадратов (омнк)
9.1. Оценивание модели в условиях автокорреляции случайной составляющей
9.1.1. Метод Кохрейна—Оркотта
9.1.2. Метод Хилдрета—Лу
9.1.3. Метод Прайса—Уинстена
9.1.4. Обобщенный метод Кохрейна—Оркотта
9.2. Оценивание модели в условиях гетероскедастичности
9.2.1. Метод корректировки Гетероскедастичности случайной составляющей
9.2.2. Метод HCCM
9.2.3. Взвешенный метод наименьших квадратов (случай гетероскедастичности)
9.3. Взвешенный метод наименьших квадратов — модели для одноименных наблюдений
10. Специальные модели
10.1. Логитовые и пробитовые модели
10.1.1. Прогнозирование двоичной переменной
10.2. Тобитовые модели
11. Системы эконометрических уравнений
11.1. Двухшаговый метод наименьших квадратов
11.2. Модели VAR
11.2.1. Проверка значимости временного лага порядка p
11.2.2. Функция импульсных откликов в модели VAR
Литература
www.statproject.ru
