Степенные ряды. Интервал сходимости степенного ряда. Разложение функций в степенные ряды.
Степенным рядом называется ряд вида:
,
где называются коэффициентами степенного ряда.
Придавая х различные числовые значения, будем
получать различные
числовые ряды, которые могут оказаться
сходящимися или расходящимися. Множество
тех значений х,
при которых степенной ряд
сходится,
называется областью его сходимости. Это множество всегда
не пусто, так как любой степенной ряд
сходится при 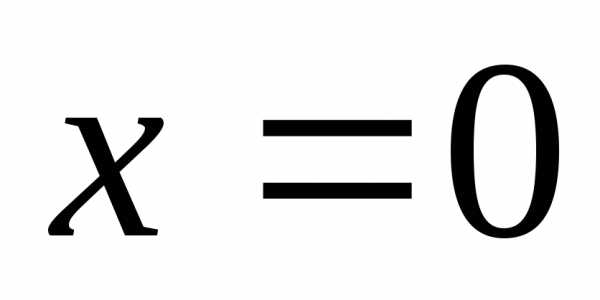 .
.
Очевидно, что частичная сумма степенного ряда
является
функцией переменной х. Поэтому и сумма ряда S
также является некоторой функцией
переменной х, определенной
в области сходимости ряда: 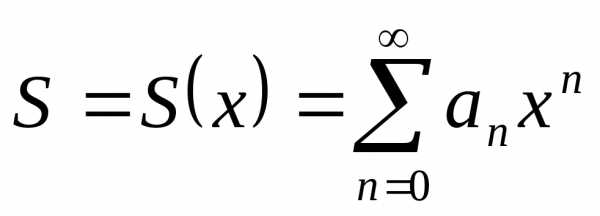
Рассмотрим теорему, имеющую важное значение в теории степенных рядов и касающуюся области сходимости степенного ряда.
Теорема Абеля. (Абель Нильс Хенрик (1802—1829) — норвежский математик).
1) Если степенной
ряд сходится
при , то он сходится,
и притом абсолютно, для всех х,
удовлетворяющих условию 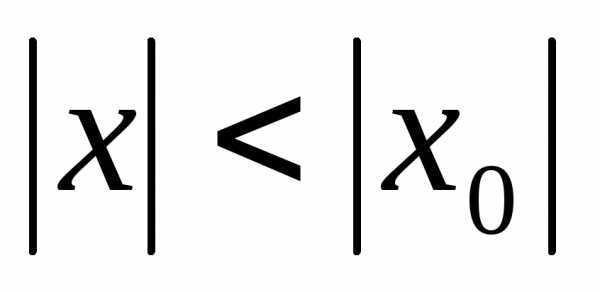 ;
;
2) если степенной
ряд расходится
при 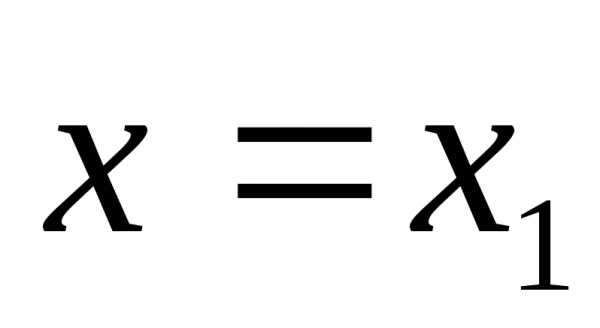 ,
то он расходится для всех х, удовлетворяющих
условию
,
то он расходится для всех х, удовлетворяющих
условию 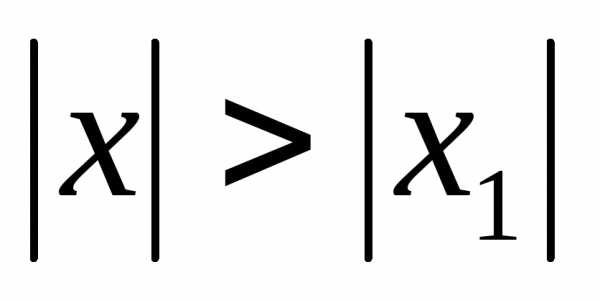 .
.
Теорема
Абеля утверждает, что если 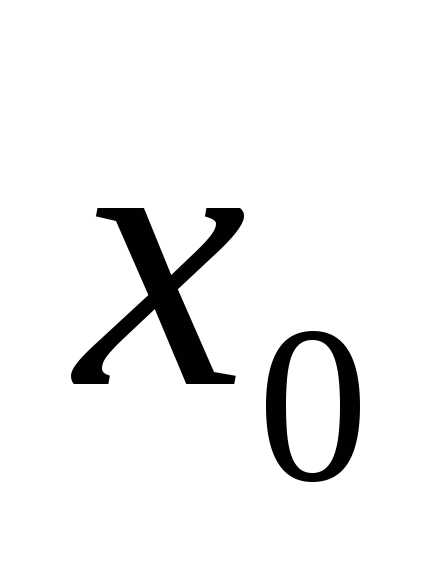 —
точка
сходимости степенного ряда, то во всех
точках, расположенных на интервале (
—
точка
сходимости степенного ряда, то во всех
точках, расположенных на интервале ( 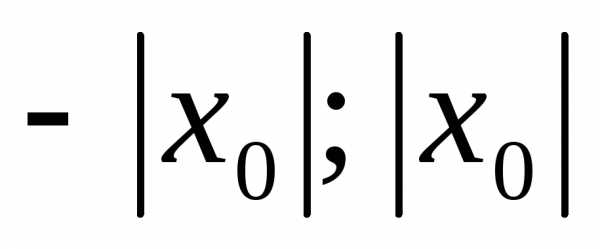 )
этот ряд сходится абсолютно, а
если
)
этот ряд сходится абсолютно, а
если 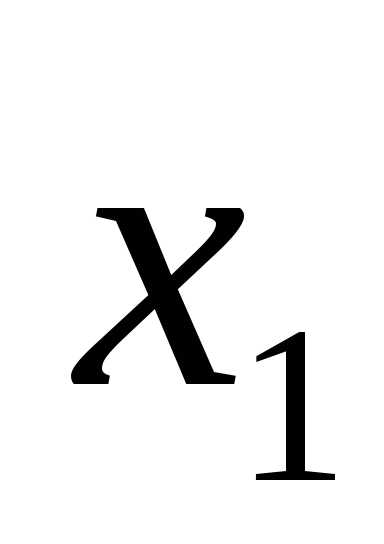 —точка
расходимости степенного ряда, то во
всех точках, расположенных вне интервала
(
—точка
расходимости степенного ряда, то во
всех точках, расположенных вне интервала
(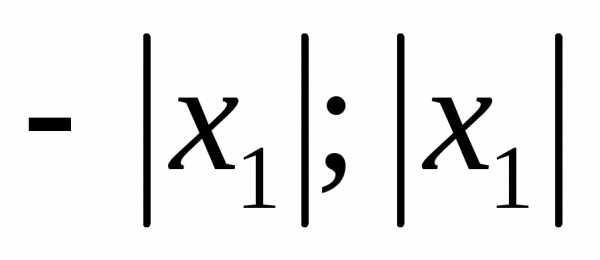 )
ряд расходится.
)
ряд расходится.
Отсюда вытекает следующая теорема:
Если
ряд 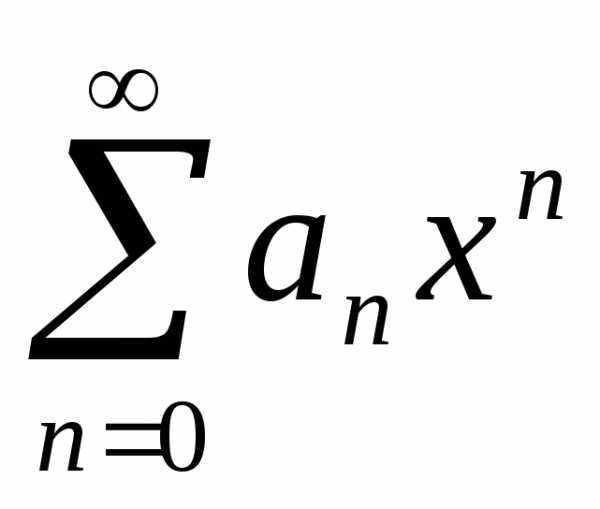 сходится не при всех значениях х и не только при
сходится не при всех значениях х и не только при 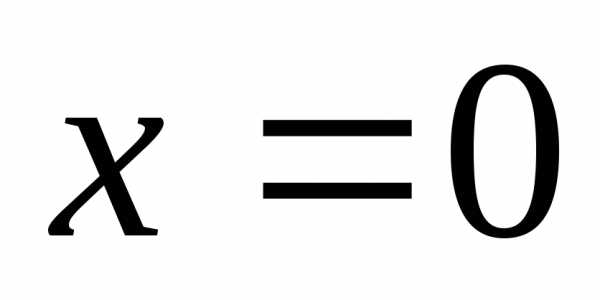 ,
то существует число
,
то существует число такое, что ряд
абсолютно сходится при
такое, что ряд
абсолютно сходится при 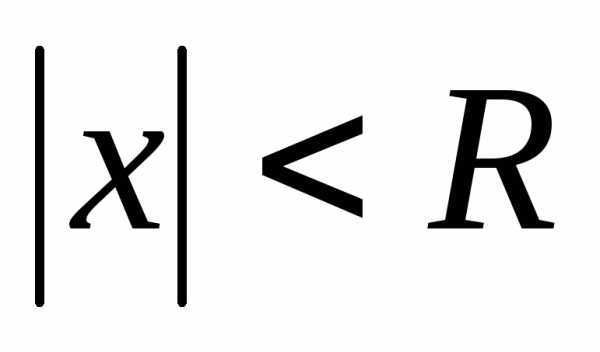
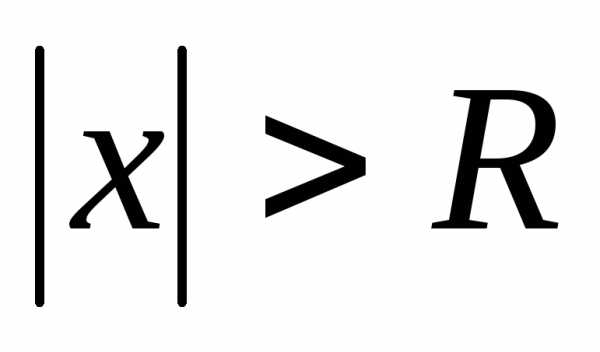 .
. Интервал 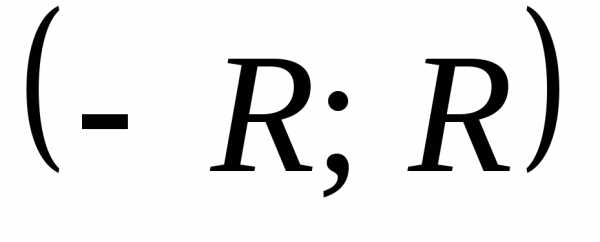 называетсяинтервалом
сходимости степенного ряда.
Число R называется радиусом
сходимости степенного
ряда. Отметим, что интервал сходимости у
некоторых рядов охватывает всю числовую
прямую (в этом случае пишут
называетсяинтервалом
сходимости степенного ряда.
Число R называется радиусом
сходимости степенного
ряда. Отметим, что интервал сходимости у
некоторых рядов охватывает всю числовую
прямую (в этом случае пишут 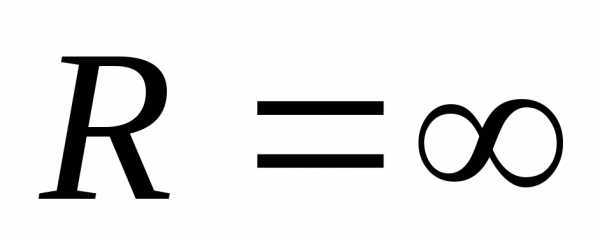 ),
у других вырождается в одну точку (
),
у других вырождается в одну точку (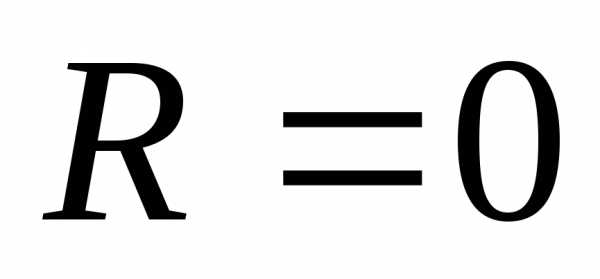 ).
).
Итак,
всякий степенной ряд имеет свой радиус
сходимости R.
При 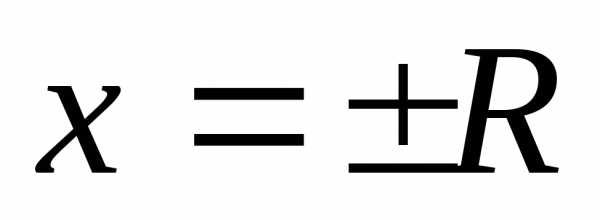 ряд может либо сходиться, либо расходиться.
Этот вопрос решается для каждого
конкретного ряда.
ряд может либо сходиться, либо расходиться.
Этот вопрос решается для каждого
конкретного ряда.
Если
существует предел 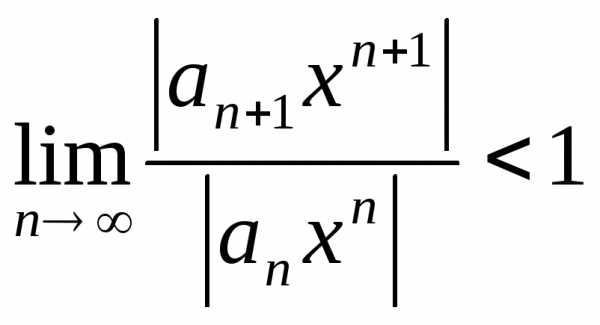 ,то радиус
сходимости ряда
,то радиус
сходимости ряда 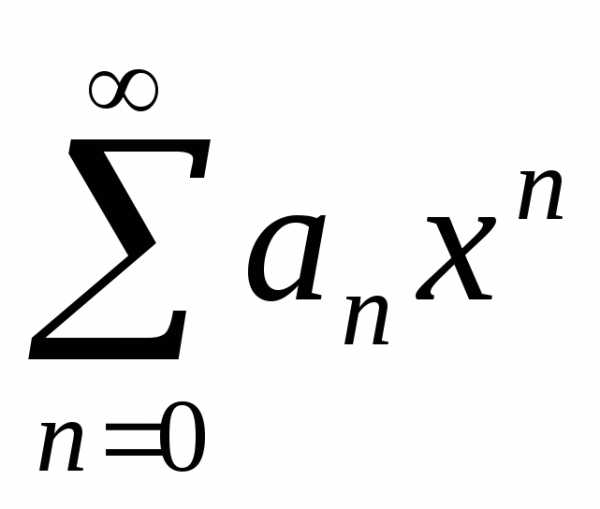 равен
равен 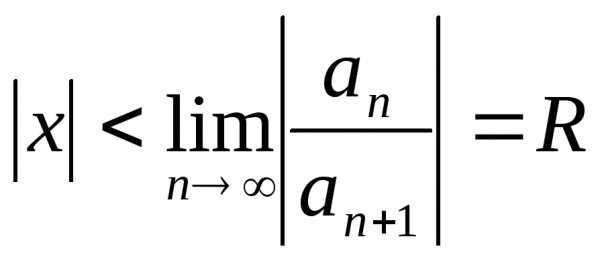 .
.
Свойства степенных рядов.
Пусть
функция 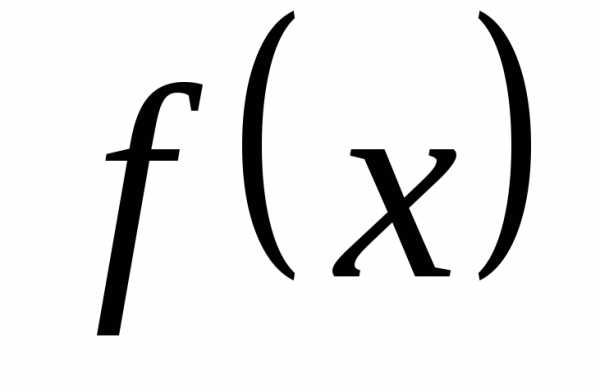 является
суммой
степенного ряда
является
суммой
степенного ряда
,
интервал
сходимости которого 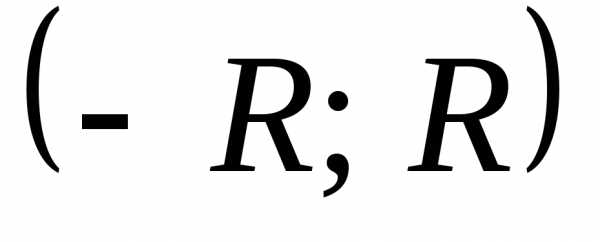 .
.
В
этом случае говорят, что на интервале 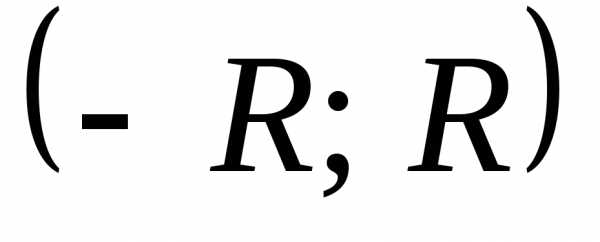 функция
функция разлагается
в степенной ряд (или в ряд по степеням
разлагается
в степенной ряд (или в ряд по степеням
Имеют место две теоремы о свойствах степенных рядов.
Если функция
 на интервале
на интервале  разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная
разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная  может быть найдена почленным
дифференцированием ряда, т.е.:
может быть найдена почленным
дифференцированием ряда, т.е.:
.
Аналогично
могут быть вычислены производные любого
порядка функции 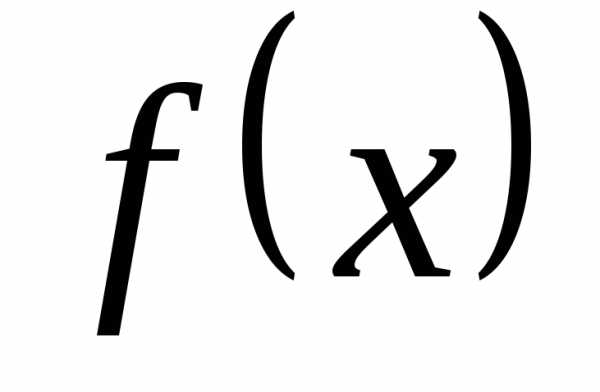 .
При этом соответствующие ряды имеют
тот же
интервал
сходимости, что и степенной ряд.
.
При этом соответствующие ряды имеют
тот же
интервал
сходимости, что и степенной ряд.
Если функция
на интервале
 разлагается
в степенной ряд, то она
интегрируема в интервале
разлагается
в степенной ряд, то она
интегрируема в интервале  и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если ,
то:
и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если ,
то:
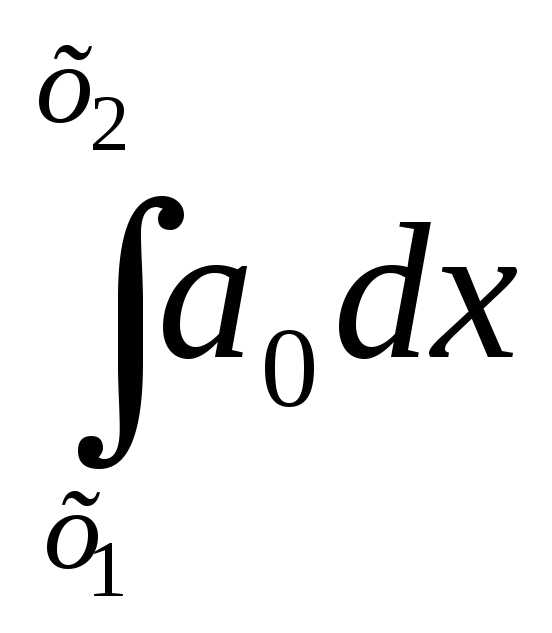 +
+
+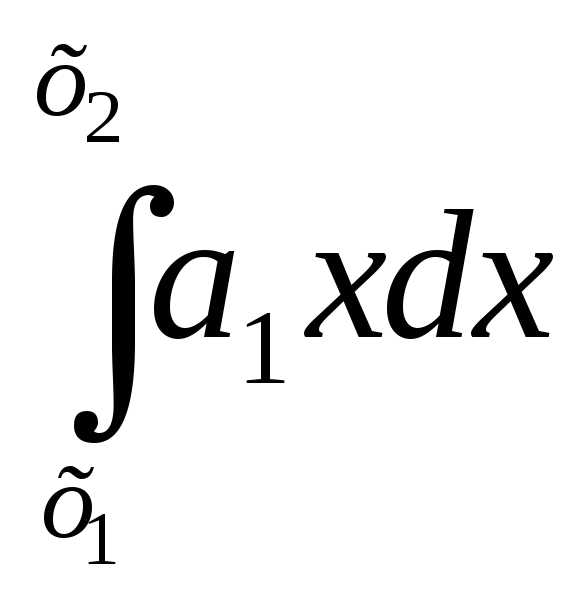 +
+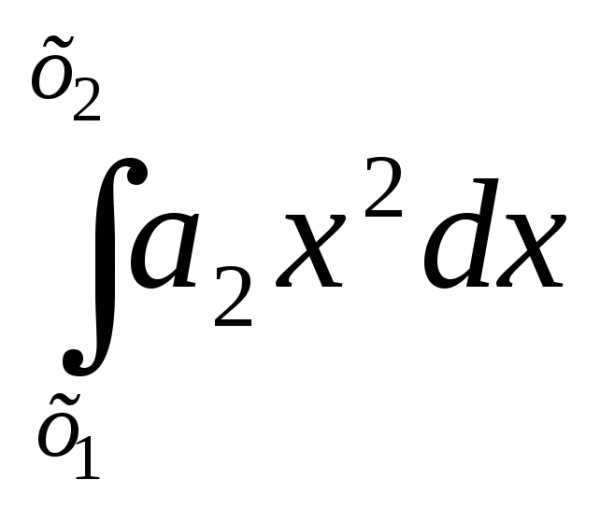 … +
… +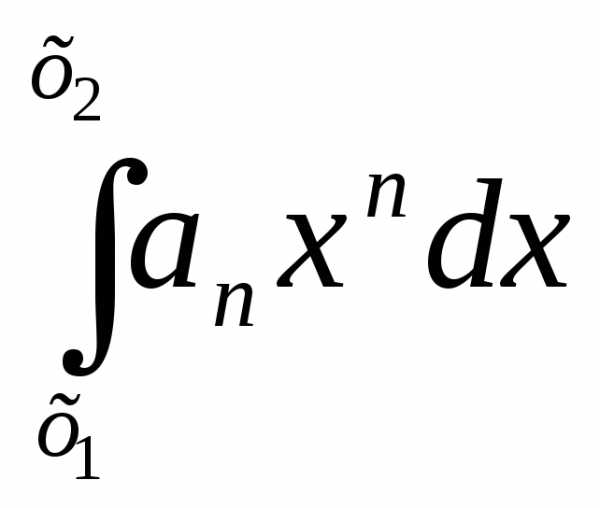 +….
+….
Теорема. Если функция 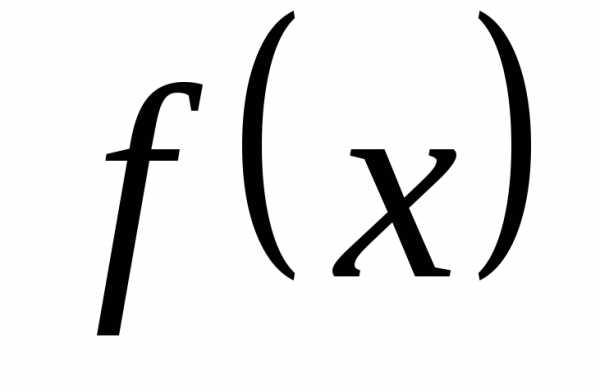 на интервале
на интервале
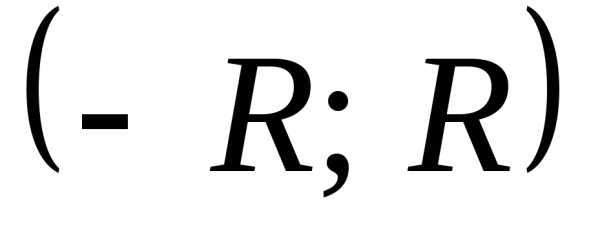 разлагается в степенной ряд:
разлагается в степенной ряд: ,
то это разложение единственно.
Пусть
функция 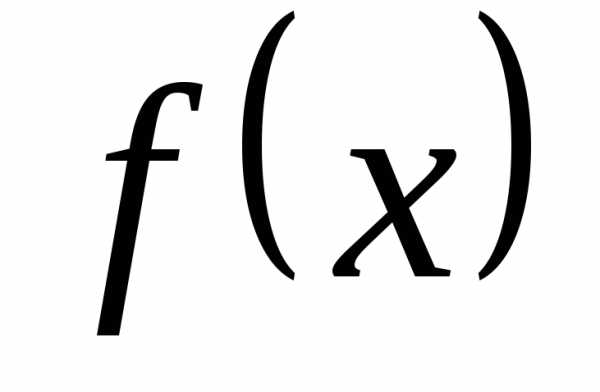 бесконечное число раз дифференцируема
в точке
бесконечное число раз дифференцируема
в точке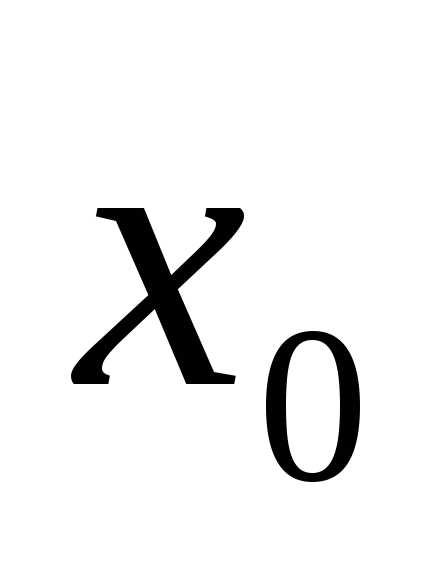 ,
тогда в окрестности этой точки функция
раскладывается в степенной ряд:
,
тогда в окрестности этой точки функция
раскладывается в степенной ряд:
,
называемый рядом Тейлора.
При 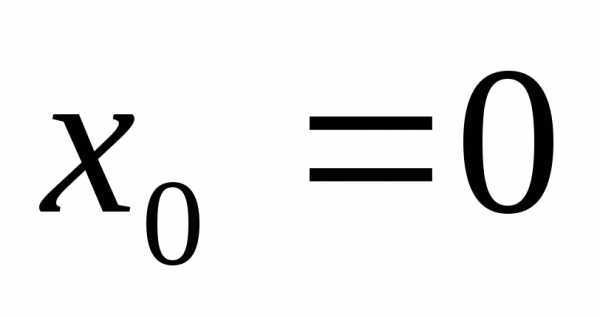 функция
функция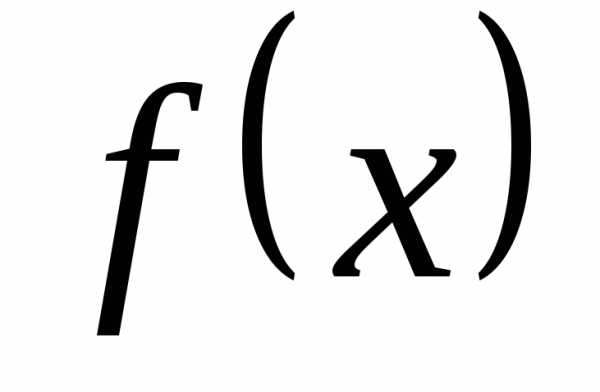 разлагается в степенной ряд:
разлагается в степенной ряд:
,
называемый рядом Маклорена.
Для
того чтобы ряд Маклорена сходился
на 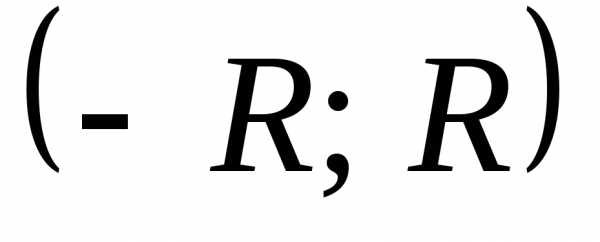 и имел своей
суммой функцию
и имел своей
суммой функцию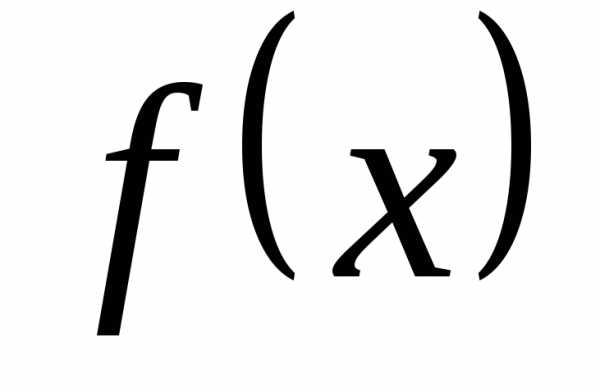 ,
необходимо и достаточно, чтобы на
,
необходимо и достаточно, чтобы на 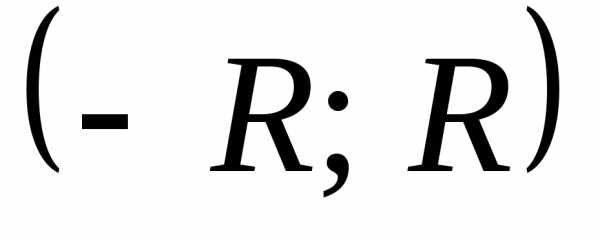 остаточный
член
остаточный
член 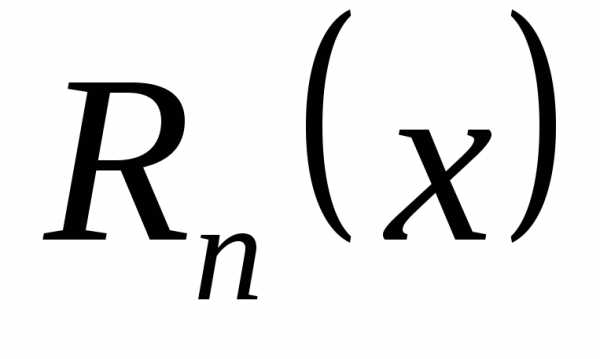 формулы Маклорена стремился к
нулю при ,т.е. для любого .
формулы Маклорена стремился к
нулю при ,т.е. для любого .
Рассмотрим разложения в ряд Маклорена некоторых элементарных функций:
;
;
;
studfiles.net
Степенные ряды. Интервал сходимости | Primer.by
, где — постоянные числа, называемые коэффициентами ряда.
Областью сходимости степенного ряда всегда является некоторый интервал.
Теорема (Абеля):
1) Если степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно сходится при всяком значении х, для которого
;
2) Если ряд расходится при некотором значении , то он расходится при всяком х, для которого
Теорема:
Областью сходимости степенного ряда является интервал с цетром в начале координат.
Определение:
Интервалом сходимости степенного ряда называется интервал от –R до +R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называется радиусом сходимости степенного ряда.
На концах интервала вопрос о сходимости ряда решается индивидуально для каждого конретного ряда.
Отметим , что у некоторых рядов интервал сходимости вырождается в точку (R=0), у других охватывает всю ось ОХ (R=).
Радиус сходимости степенного ряда определяется по формуле
или
Примеры:
Пример1:
Найти область сходимости ряда
Решение.
Радиус сходимости степенного ряда можно найти по формуле: .
Т.к. и , то
.
Итак, радиус сходимости ряда . Т.о. данный степенной ряд расходится, при .
Исследуем сходимость ряда при .
Пусть. Подставим в заданный степенной ряд и получим ряд
, который сходится.
Итак, областью сходимости данного степенного ряда является значение .
Пример2:
Найти область сходимости степенного ряда .
Решение.
Радиус сходимости степенного ряда можно найти по формуле: .
Т.к. и , то
.
Итак, радиус сходимости ряда . Определим интервал сходимости данного степенного ряда:
.
– интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.
Пусть . Подставим в заданный степенной ряд и получим числовой ряд с положительными членами:
Получили расходящийся обобщенный гармонический ряд.
Значит, не принадлежит области сходимости степенного ряда.
Пусть. Подставим в заданный степенной ряд и получим знакочередующийся ряд
.
Для членов полученного ряда:
1)
2) , т.е.
В соответствии с признаком Лейбница данный ряд сходится и принадлежит области сходимости степенного ряда.
Итак, областью сходимости данного степенного ряда является промежуток .
primer.by
2.2. Интервал и радиус сходимости степенного ряда Примеры решения задач
Пример 1. Найти область сходимости степенного ряда:
а) 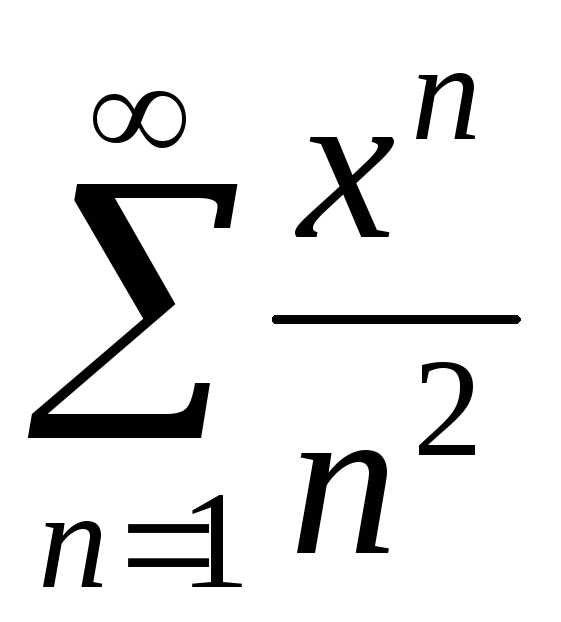 ; б)
; б)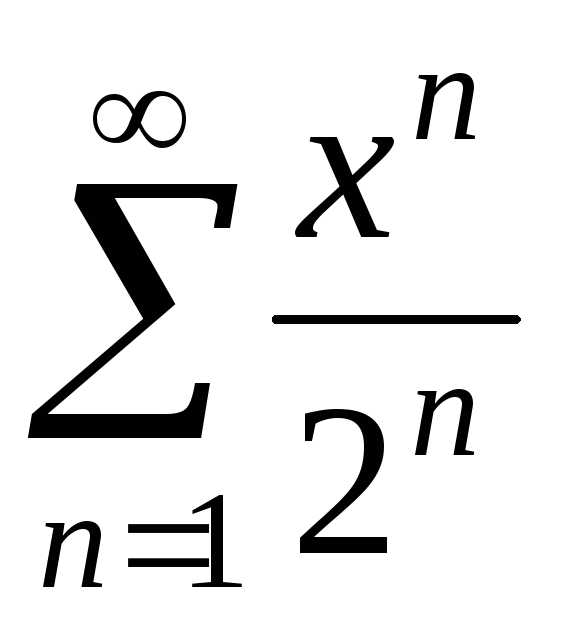 ;
;
в) 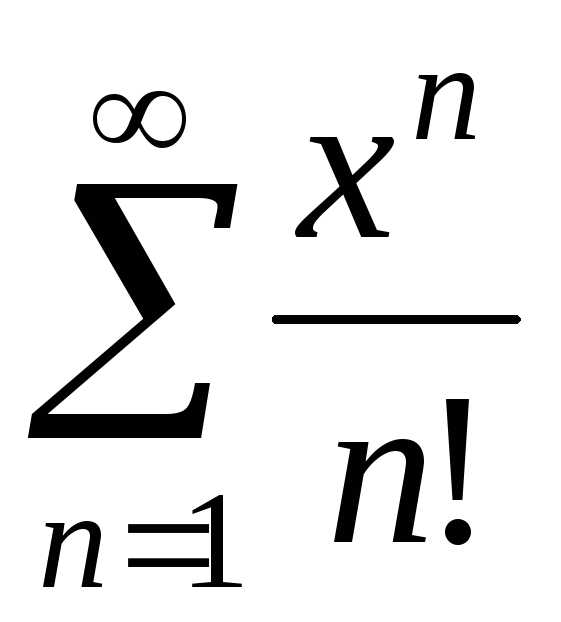 ; г)
; г)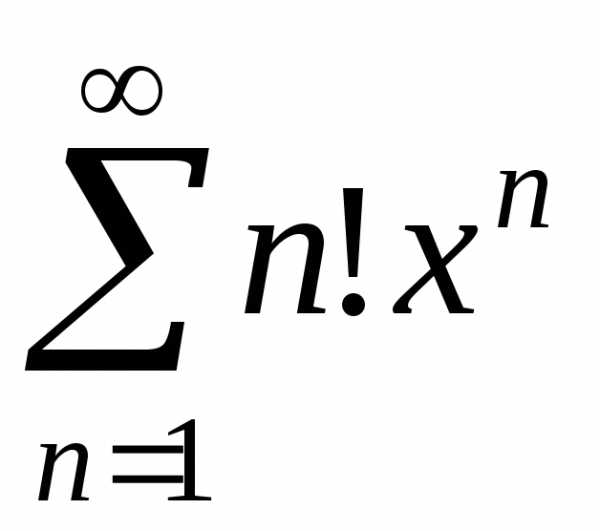 ;
;
д) 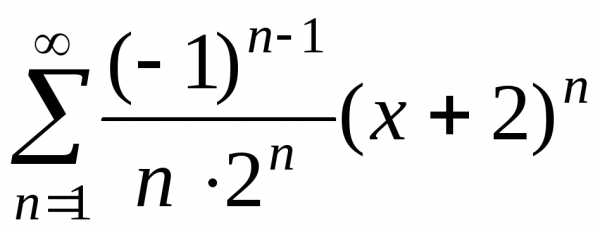 .
.
а) Найдем радиус сходимости R.
Так как 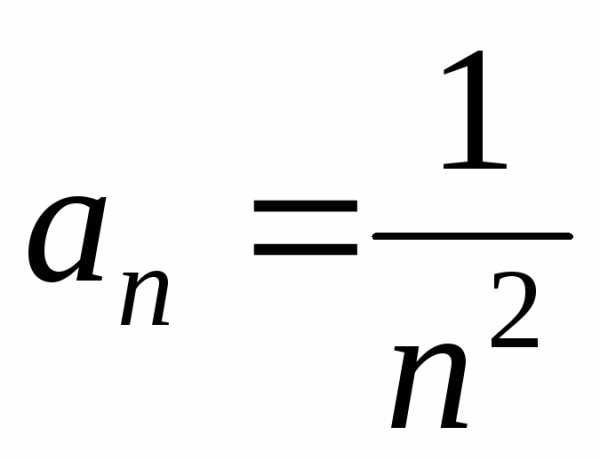 ,
,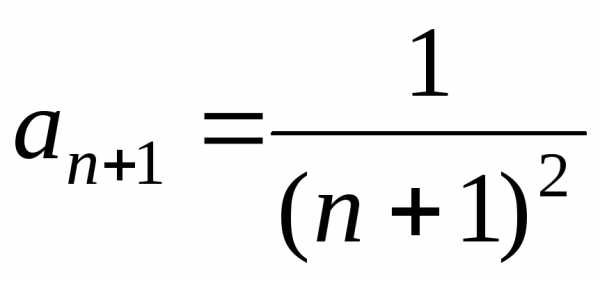 ,
то
,
то
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству 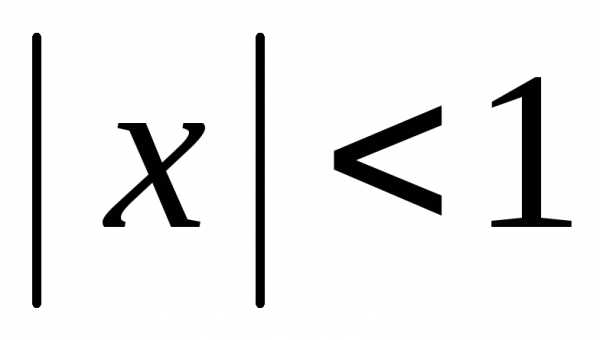 ,
то есть интервал сходимости ряда
,
то есть интервал сходимости ряда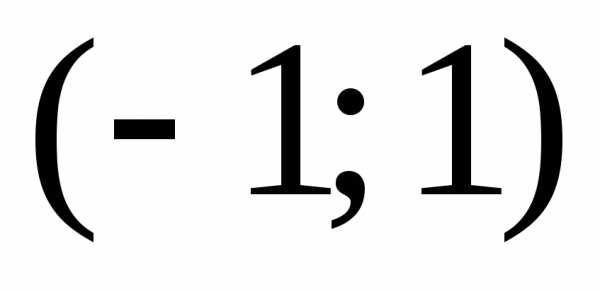 .
.
Исследуем на сходимость данный ряд на концах интервала сходимости.
При 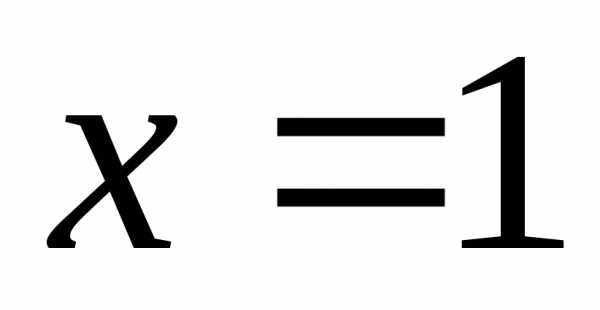 получаем
числовой ряд
получаем
числовой ряд 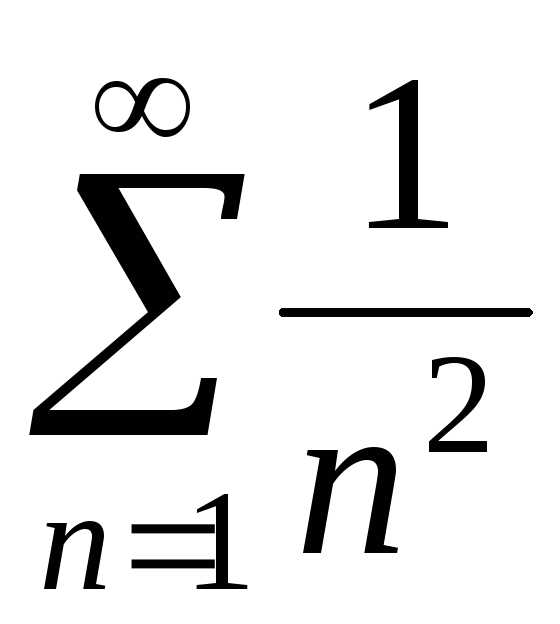 .
Этот ряд сходится, так как является
обобщенным гармоническим рядом
.
Этот ряд сходится, так как является
обобщенным гармоническим рядом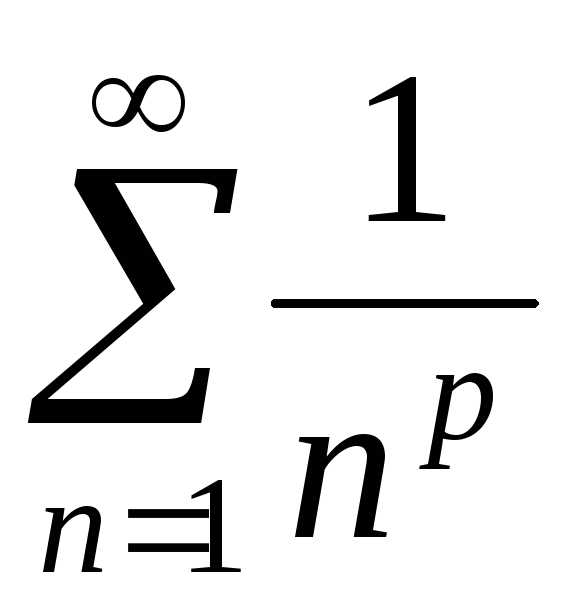 при
при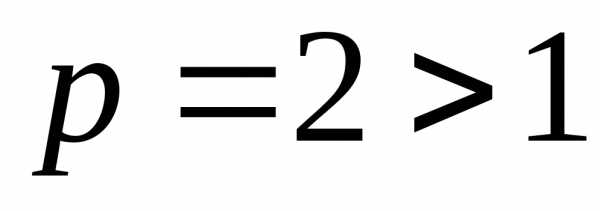 .
.
При 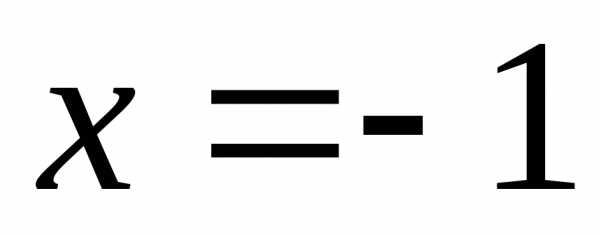 получаем
числовой ряд
получаем
числовой ряд 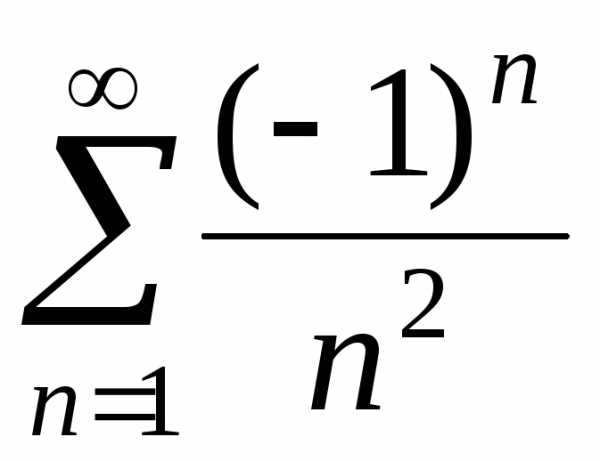 .
Этот ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин
его членов
.
Этот ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин
его членов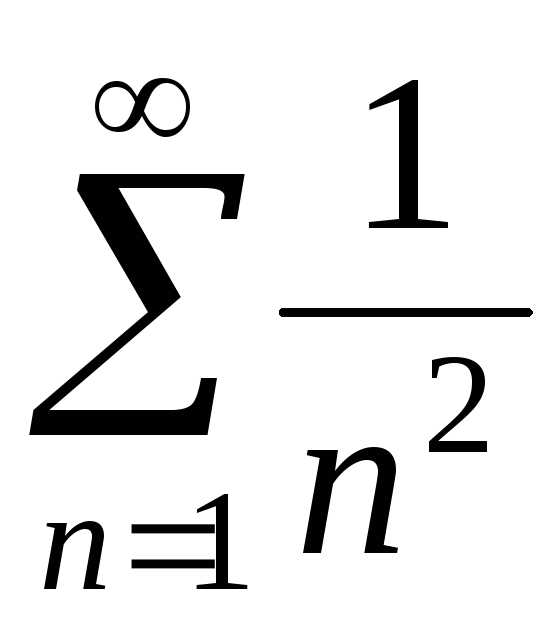 ,
сходящийся.
,
сходящийся.
Итак, область
сходимости данного ряда 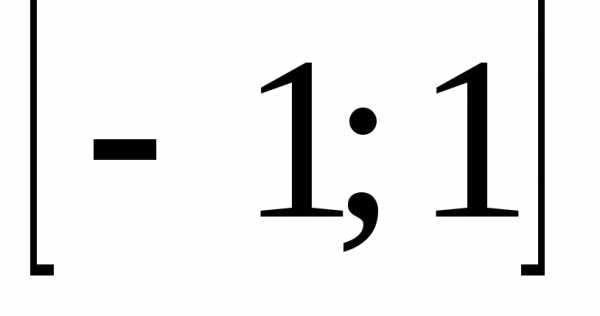 .
.
б) Найдем радиус
сходимости R.
Так как 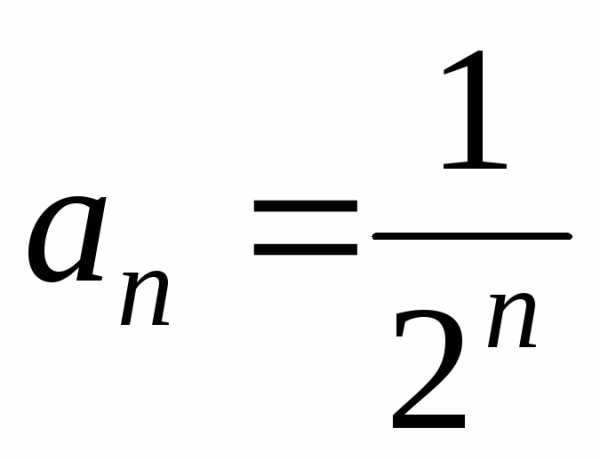 ,
то
,
то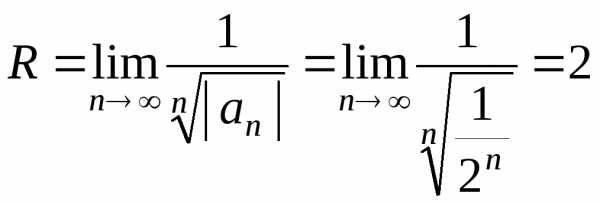 .
.
Итак, интервал
сходимости ряда 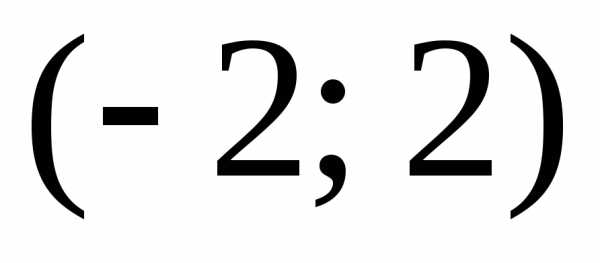 .
.
Исследуем на сходимость данный ряд на концах интервала сходимости.
При 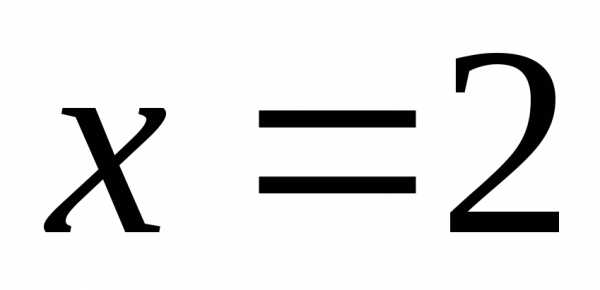 имеем числовой ряд
имеем числовой ряд 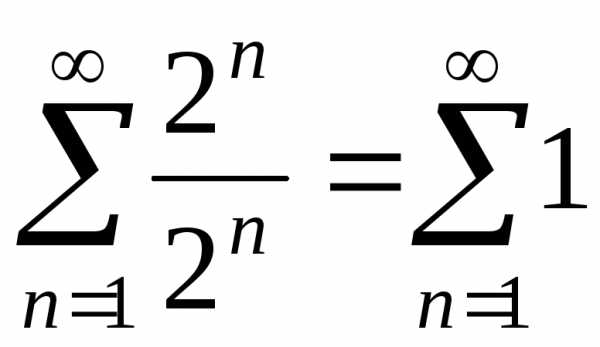 .
Этот ряд расходящийся, так как.
.
Этот ряд расходящийся, так как.
При 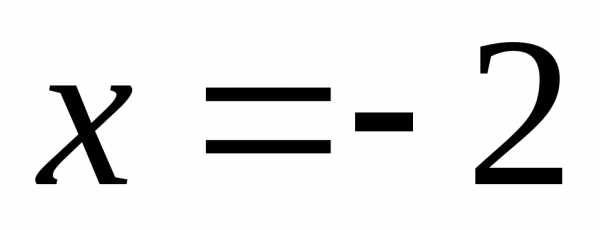 имеем числовой ряд
.
Этот ряд расходящийся, так как
не существует.
имеем числовой ряд
.
Этот ряд расходящийся, так как
не существует.
Итак, область
сходимости данного ряда 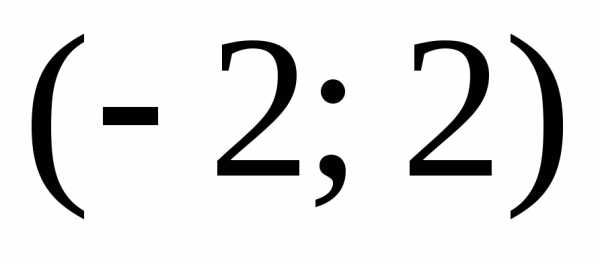 .
.
в) Найдем радиус
сходимости R.
Так как 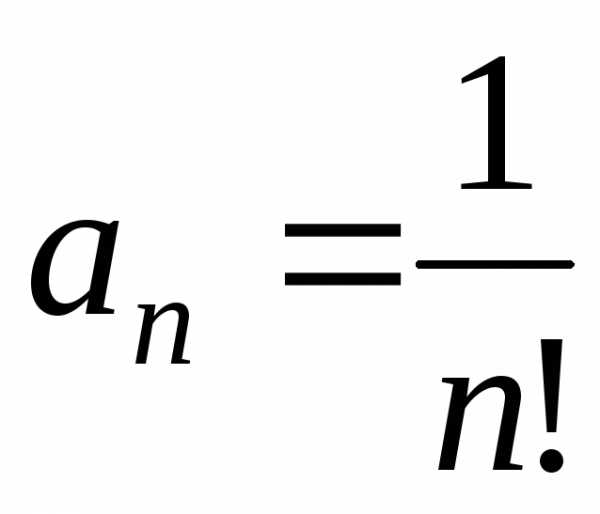 ,
,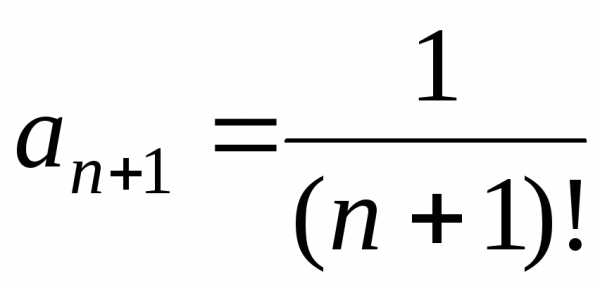 то.
то.
Итак, интервал сходимости . Область сходимости данного ряда совпадает с интервалом сходимости, то есть ряд сходится при любом значении переменнойx.
г) Найдем радиус сходимости R.
Так как 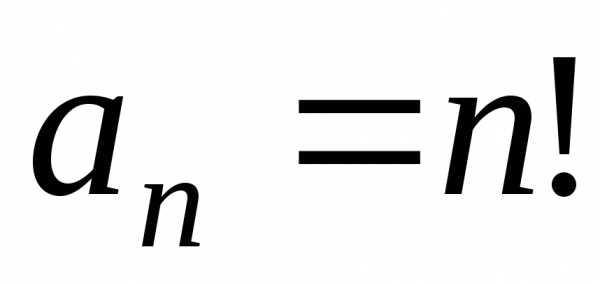 ,то.
,то.
Так как 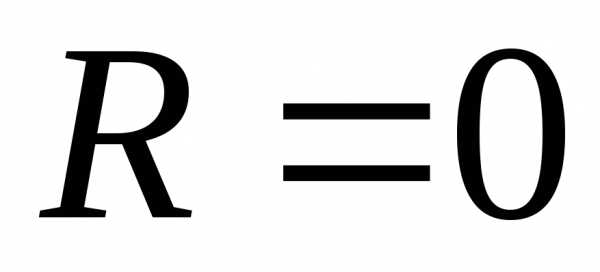 ,
то ряд сходится только в точке
,
то ряд сходится только в точке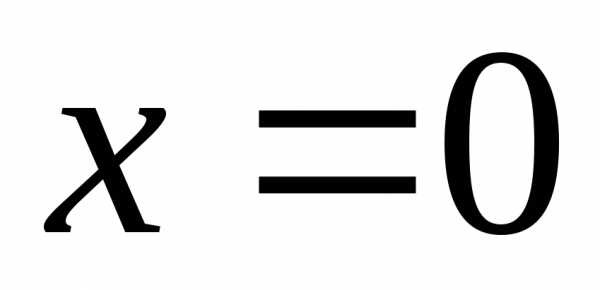 .
Значит, область сходимости данного ряда
представляет собой одну точку
.
Значит, область сходимости данного ряда
представляет собой одну точку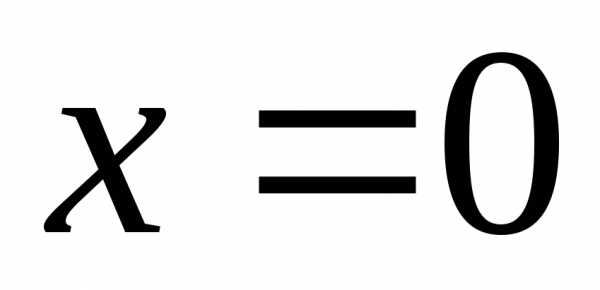 .
.
д) Найдем радиус сходимости R.
Так как 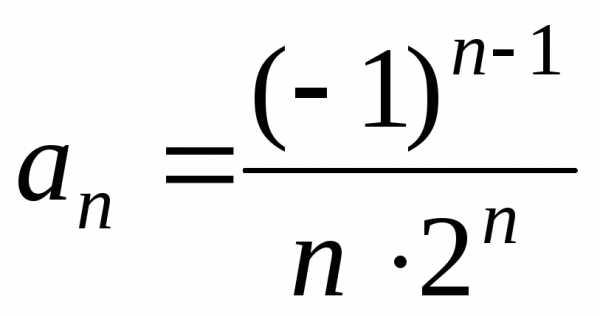 ,
,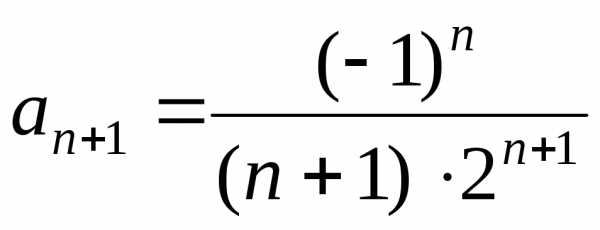 ,
то
,
то
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству 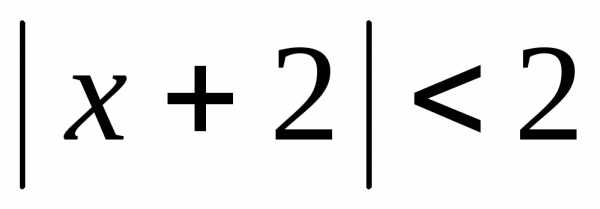 ,
то есть.
,
то есть.
Отсюда
− интервал сходимости,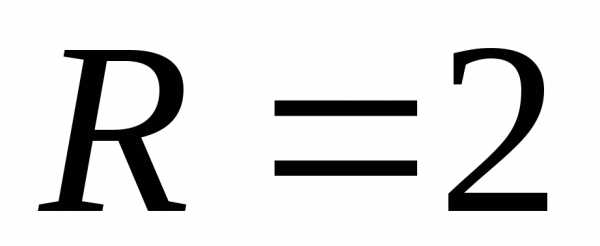 − радиус сходимости.
− радиус сходимости.
Исследуем данный ряд на сходимость на концах интервала сходимости.
При 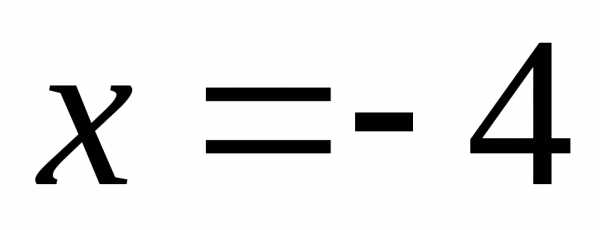 получаем числовой ряд
получаем числовой ряд
,
который расходится (гармонический ряд).
При 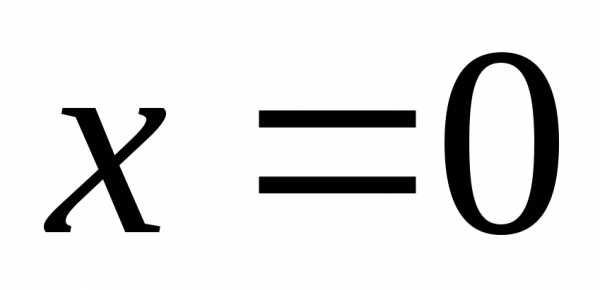 получаем числовой ряд,
который сходится условно (ряд сходится
по признаку Лейбница, а ряд, составленный
их абсолютных величин его членов,
расходится, так как является гармоническим).
получаем числовой ряд,
который сходится условно (ряд сходится
по признаку Лейбница, а ряд, составленный
их абсолютных величин его членов,
расходится, так как является гармоническим).
Итак, область
сходимости ряда  .
.
2.3. Ряды Тейлора и Маклорена.
Разложение функций в степенной ряд.
Приложение степенных рядов к приближенным вычислениям
Примеры решения задач
Пример 1. Разложить в степенной ряд функции:
а) ; б);
в) 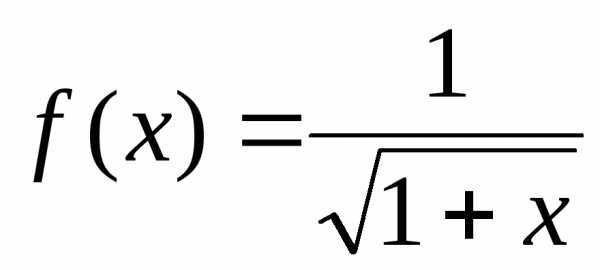 ; г)
; г)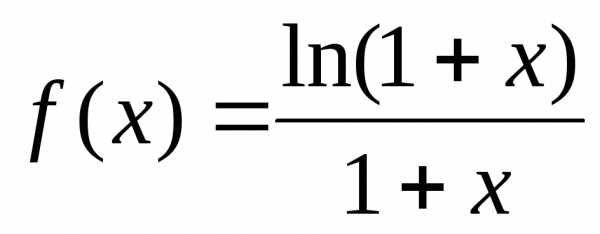 .
.
а) Заменив в формуле x на 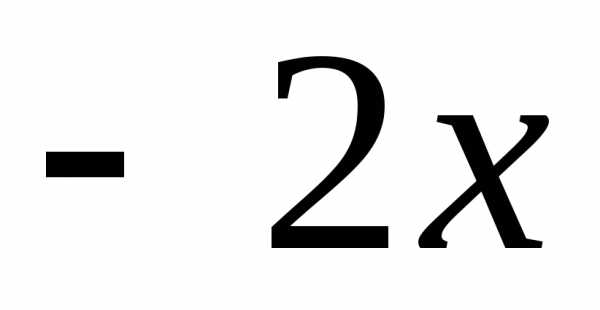 ,
получим искомое разложение:
,
получим искомое разложение:
, где
или
.
б) Заменяя в равенстве
,
где x на 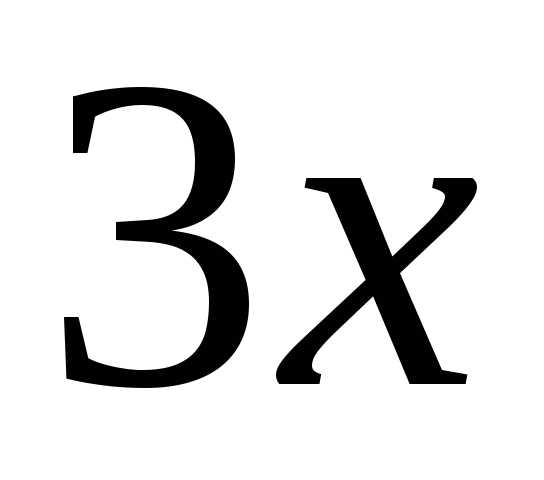 ,
получим искомое разложение:
,
получим искомое разложение:
.
в) Данную функцию можно записать так: 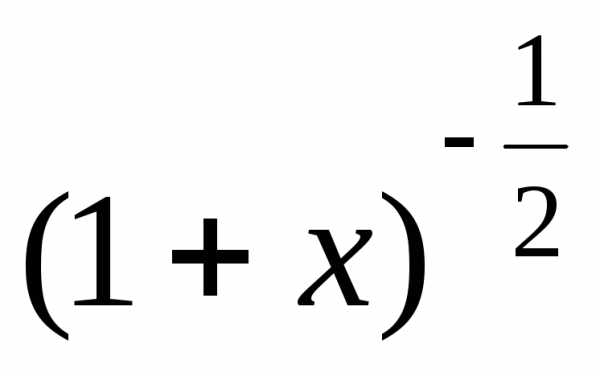 .
Чтобы найти искомый ряд, достаточно в
разложение
.
Чтобы найти искомый ряд, достаточно в
разложение
.,
где
подставить 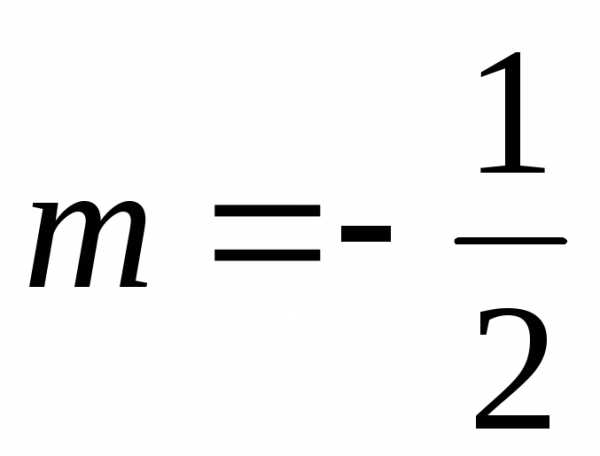 .
Тогда получим:
.
Тогда получим:
или
.
г) Данную функцию можно переписать так: .
Функцию 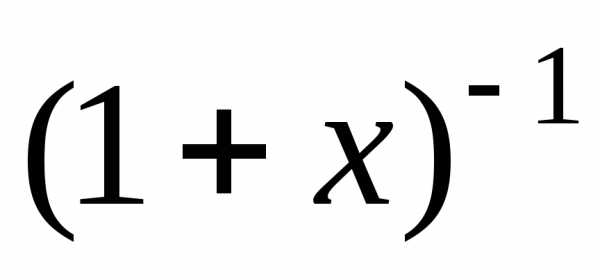 можно разложить в степенной ряд, положив
в биномиальном ряде
можно разложить в степенной ряд, положив
в биномиальном ряде 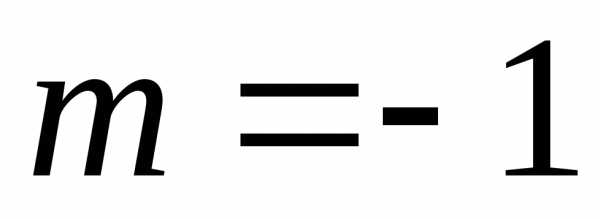 ,
получим .
,
получим .
, где .
Чтобы получить искомое разложение, достаточно перемножить полученные ряды (ввиду абсолютной сходимости этих рядов).
Следовательно,
, где .
Пример 2. Найти приближенные значения данных функций:
а)  с точностью до 0,0001;
с точностью до 0,0001;
б) 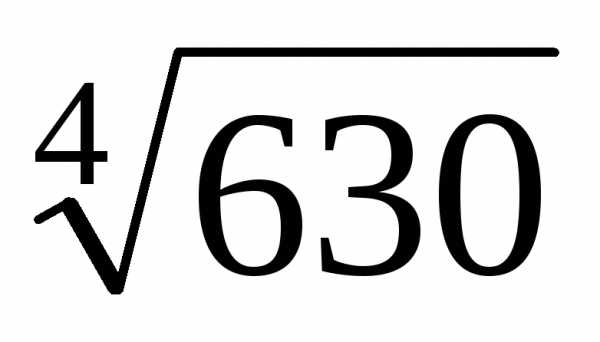 с точностью до 0,00001.
с точностью до 0,00001.
а) Так как 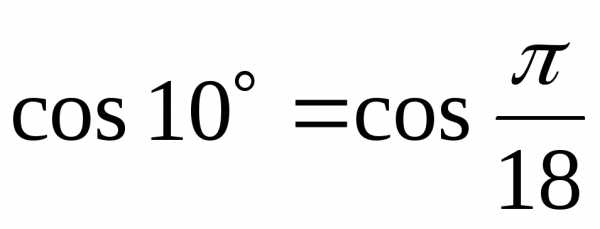 ,
то в разложение функции ,
где подставим :
,
то в разложение функции ,
где подставим :
или
Так как , то требуемая точность будет обеспечена, если ограничиться только первыми двумя членами полученного разложения.
Итак,
.
б) .
Используем биномиальный ряд
., где .
Полагая
и 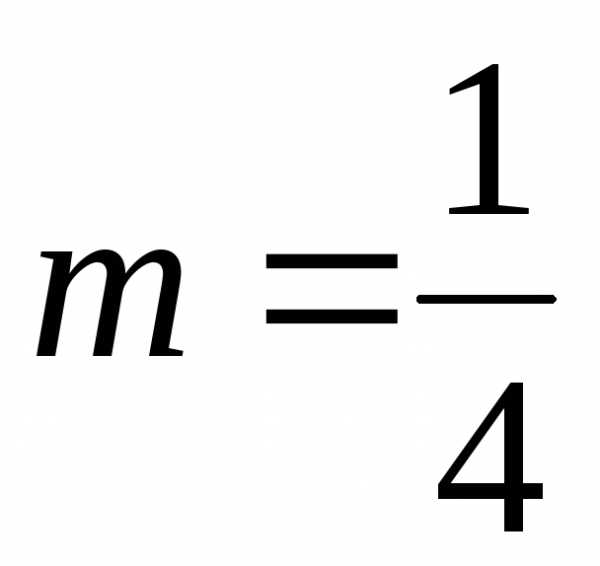 ,
получим следующее разложение:
,
получим следующее разложение:
или
.
Если в последнем
знакочередующемся ряде учитывать только
первые два члена, а остальные отбросить,
то погрешность при вычислении 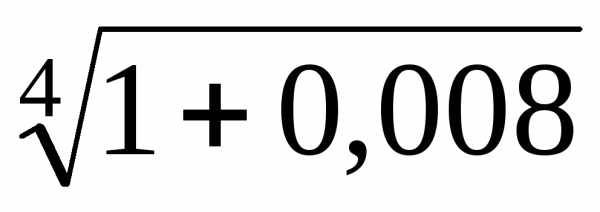 не превысит по абсолютной величине
0,000006. Тогда погрешность при вычислении не превысит числа .
Следовательно,
не превысит по абсолютной величине
0,000006. Тогда погрешность при вычислении не превысит числа .
Следовательно,
.
Пример 3. Вычислить с точностью до 0,001:
а) 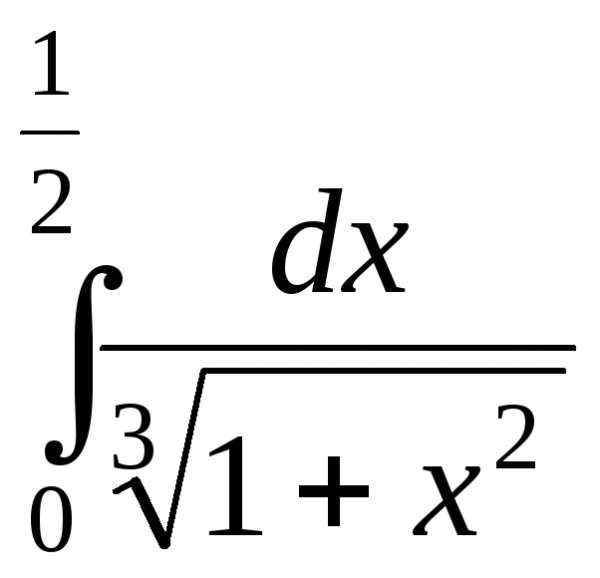 ; б)
; б) 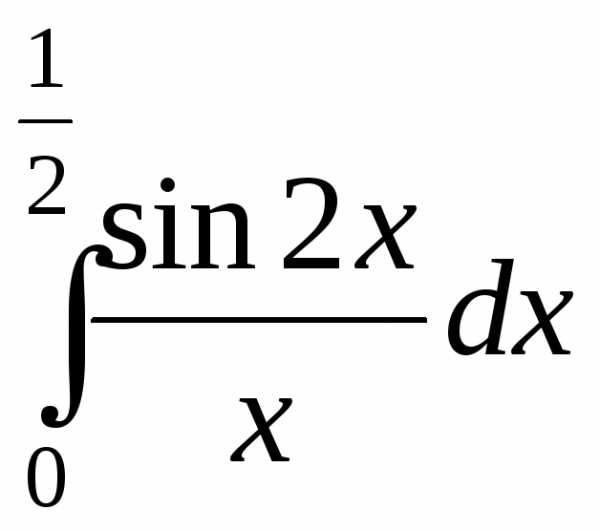 .
.
а) 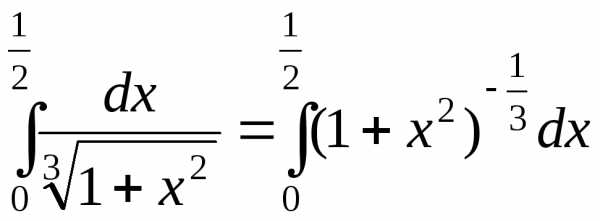 .
.
Разложим
подынтегральную функцию в степенной
ряд. Для этого подставим в биномиальный
ряд 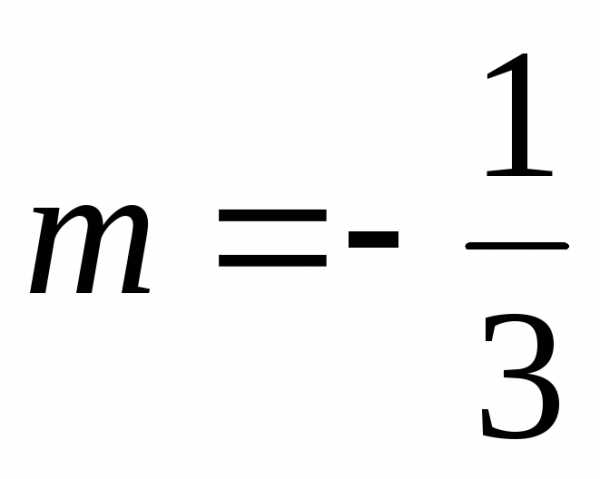 и заменим x на
и заменим x на 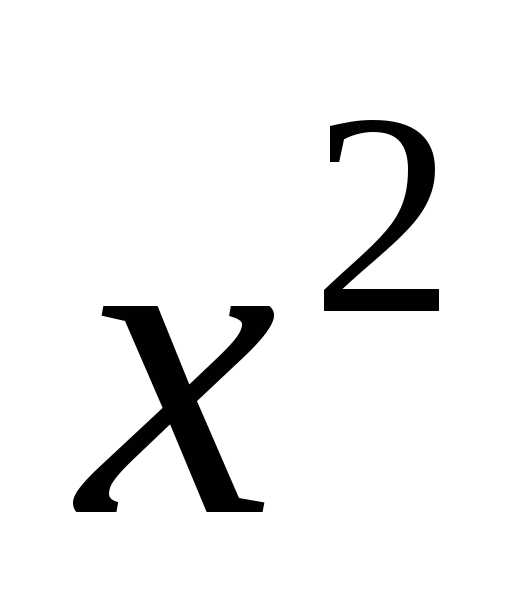 :
:
.
Так как отрезок
интегрирования  принадлежит области сходимости
полученного ряда
принадлежит области сходимости
полученного ряда 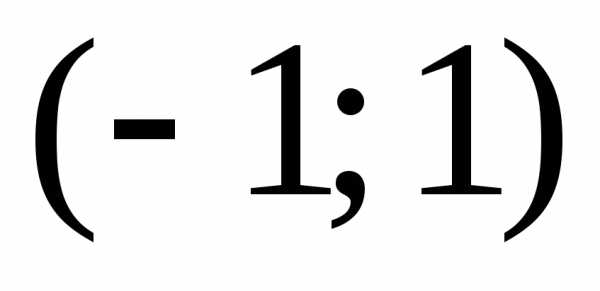 ,
то будем интегрировать почленно в
указанных пределах:
,
то будем интегрировать почленно в
указанных пределах:
.
В полученном знакочередующемся ряде четвертый член по абсолютной величине меньше 0,001. Следовательно, требуемая точность будет обеспечена, если учитывать только первые три члена ряда.
.
Так как первый из отброшенных членов имеет знак минус, то полученное приближенное значение будет с избытком. Поэтому ответ с точностью до 0,001 равен 0,487.
б) Предварительно представим подынтегральную функцию в виде степенного ряда. Заменим в разложении функции
, где
x на 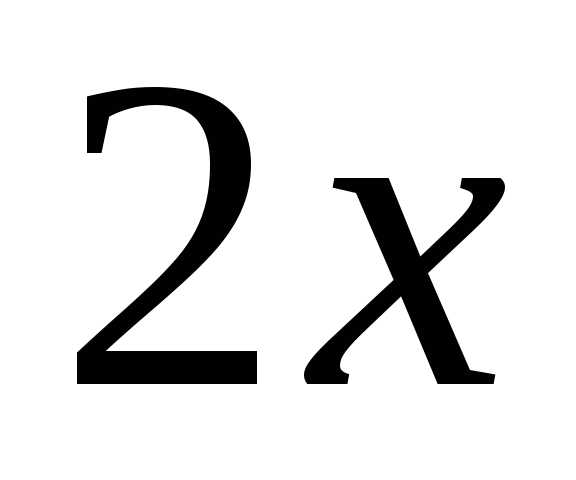 ,
получим:
,
получим:
Тогда .
.
Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Четвертый член ряда по абсолютной величине меньше 0,001. Чтобы обеспечить требуемую точность, достаточно найти сумму первых трех членов.
Следовательно, .
studfiles.net
Степенные ряды
ВЫСШАЯ МАТЕМАТИКА
Степенные ряды
Содержание
1. Определение степенного ряда. Теорема Абеля
2. Свойства степенных рядов
3. Ряды Тейлора, Маклорена для функций
4. Разложение некоторых элементарных функций в ряд Маклорена
5. Приложения степенных рядов
1. Определение степенного ряда. Теорема Абеля
Степенные ряды являются частным случаем функциональных рядов.
Определение 1.1. Степенным рядом называется функциональный ряд вида.(1.1)
Здесь – постоянные вещественные числа, называемые коэффициентами степенного ряда; а – некоторое постоянное число, х – переменная, принимающая значения из множества действительных чисел.
При степенной ряд (1.1) принимает вид
. (1.2)
Степенной ряд (1.1) называют рядом по степеням разности , ряд (1.2) – рядом по степеням х.
Если переменной х придать какое-либо значение, то степенной ряд (1.1) (или (1.2)) превращается в числовой ряд, который может сходиться или расходиться.
Определение 1.2. Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится.
Ряд (1.1) с помощью подстановки приводится к более простому виду (1.2), поэтому вначале будем рассматривать степенные ряды вида (1.2).
Для нахождения области сходимости степенного ряда важную роль играет следующая теорема.
Теорема 1.1 (Теорема Абеля):
если степенной ряд (1.2) сходится при , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству ; если же ряд (1.2) расходится при , то он расходится при всех значениях х, удовлетворяющих неравенству .
Теорема Абеля дает ясное представление о структуре области сходимости степенного ряда.
Теорема 1.2:
область сходимости степенного ряда (1.2) совпадает с одним из следующих интервалов:
1) ; 2) ; 3) ; 4) ,
где R – некоторое неотрицательное действительное число или .
Число R называется радиусом сходимости, интервал – интервалом сходимости степенного ряда (1.2).
Если , то интервал сходимости представляет собой всю числовую ось .
Если , то интервал сходимости вырождается в точку .
Замечание: если – интервал сходимости для степенного ряда (1.2), то – интервал сходимости для степенного ряда (1.1).
Из теоремы 1.2 следует, что для практического нахождения области сходимости степенного ряда (1.2) достаточно найти его радиус сходимости R и выяснить вопрос о сходимости этого ряда на концах интервала сходимости , т. е. при и .
Радиус сходимости R степенного ряда можно найти по одной из следующих формул:
формула Даламбера:
;(1.3)
формула Коши:
.(1.4)
Если в формуле Коши , то полагают , если , то полагают .
Пример 1.1. Найти радиус сходимости, интервал сходимости и область сходимости степенного ряда .
Решение
Найдем радиус сходимости данного ряда по формуле
В нашем случае
, .
Тогда .
Следовательно, интервал сходимости данного ряда имеет вид .
Исследуем сходимость ряда на концах интервала сходимости.
При степенной ряд превращается в числовой ряд
.
который расходится как гармонический ряд.
При степенной ряд превращается в числовой ряд
.
Это – знакочередующийся ряд, члены которого убывают по абсолютной величине и . Следовательно, по признаку Лейбница этот числовой ряд сходится.
Таким образом, промежуток – область сходимости данного степенного ряда.
studfiles.net
Глава 2. Степенные ряды
42
2.1. Область сходимости функционального ряда
Пусть задана последовательность функций
с общей областью
определения 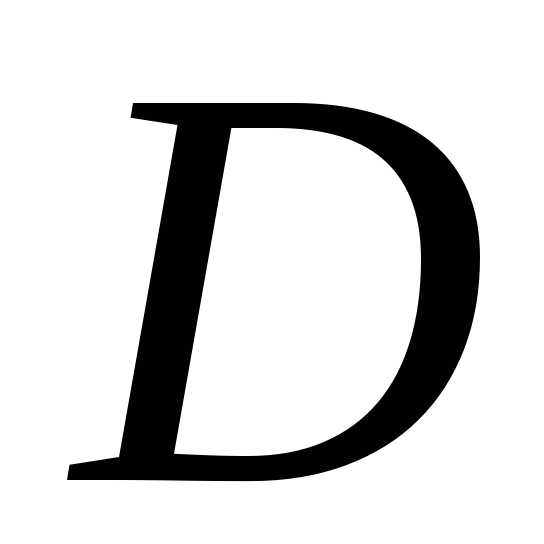 .
.
Определение. Функциональным рядом называется выражение
. (18)
При фиксированном 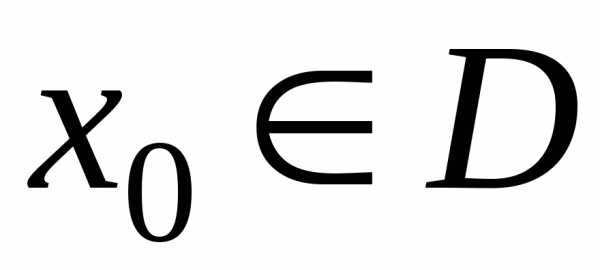 функциональному ряду (18) соответствует
числовой ряд
функциональному ряду (18) соответствует
числовой ряд
. (19)
При одних значениях 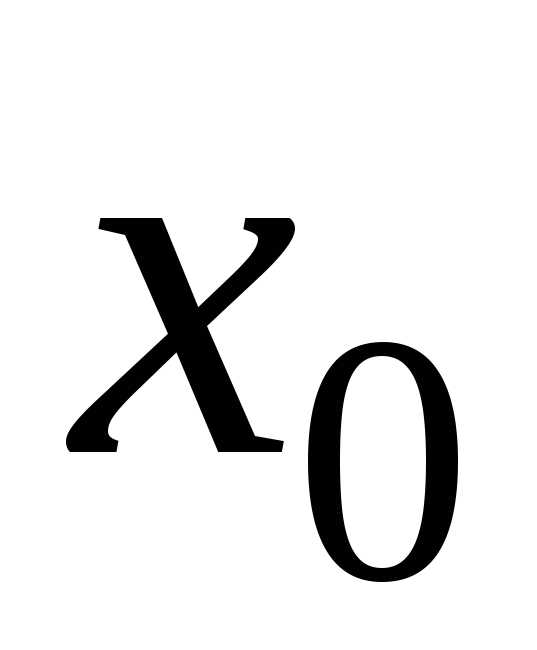 этот числовой ряд может сходиться, при
других — расходиться.
этот числовой ряд может сходиться, при
других — расходиться.
Определение. Совокупность  всех тех значений
всех тех значений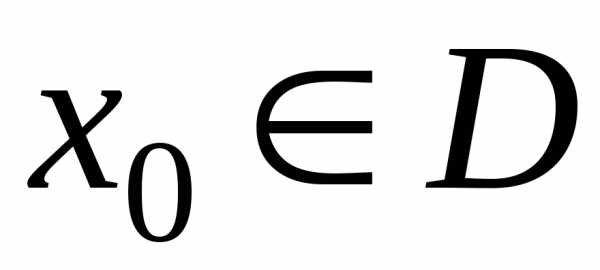 ,
при которых числовой ряд (19) сходится,
называетсяобластью
сходимости функционального ряда (18).
,
при которых числовой ряд (19) сходится,
называетсяобластью
сходимости функционального ряда (18).
При 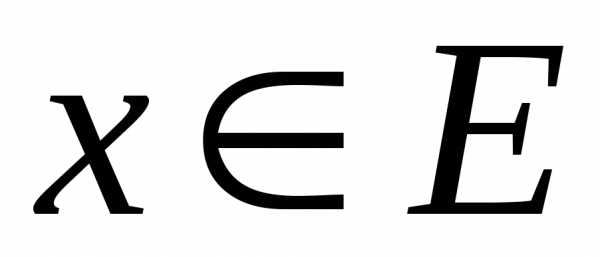 определена функция
определена функция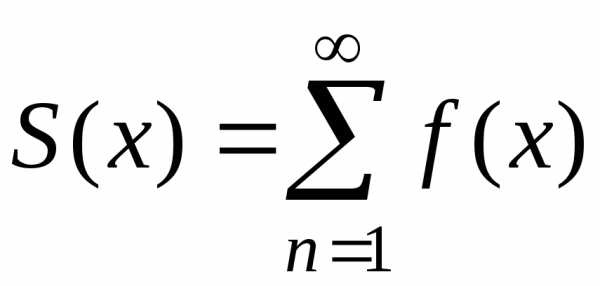 — сумма числового ряда (19) в точке
— сумма числового ряда (19) в точке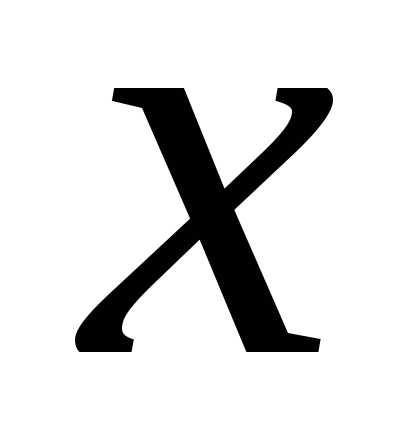 .
.
Примеры. 1. Пусть 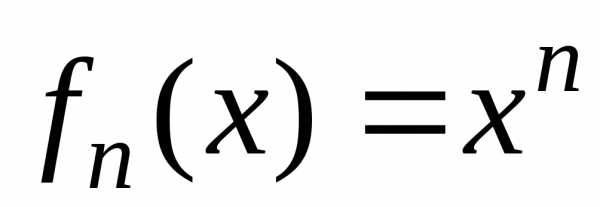 .
Функциональный ряд
.
Функциональный ряд
образован
геометрической прогрессией со знаменателем 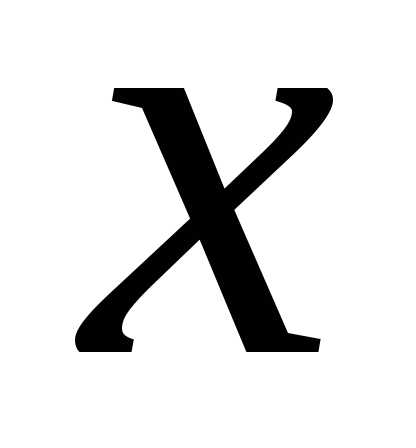 .
Как установлено в п.1.3. ряд сходится при
.
Как установлено в п.1.3. ряд сходится при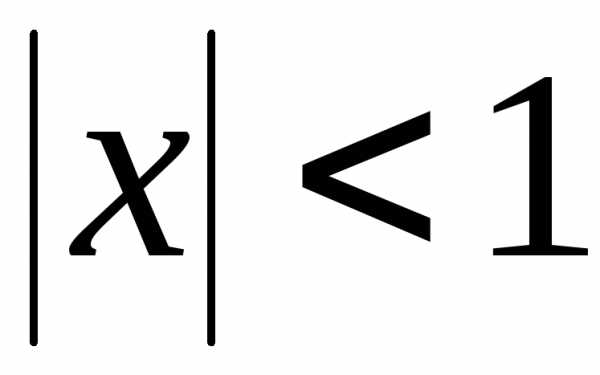 и расходится при
и расходится при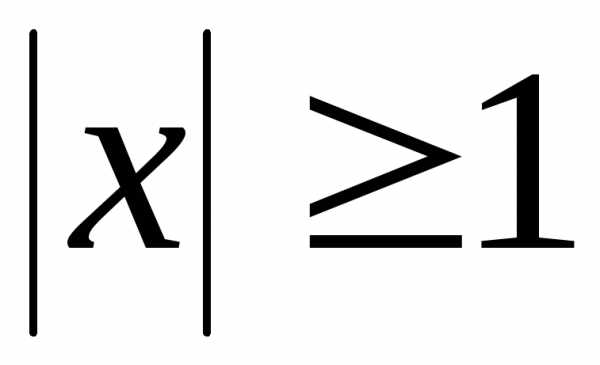 .
Следовательно, область сходимости.
.
Следовательно, область сходимости.
2. Пусть
.
При общий член ряда
общий член ряда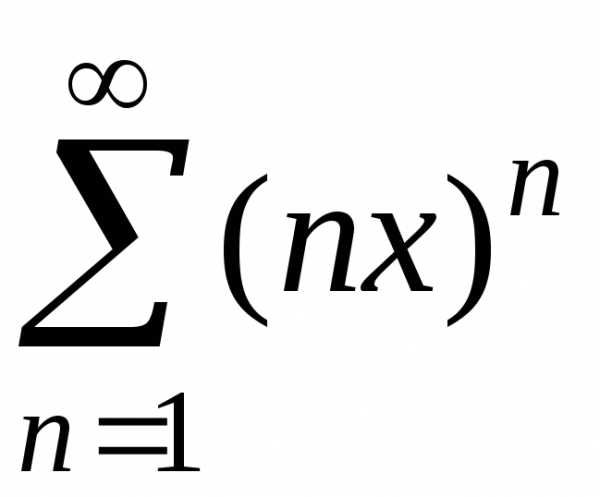 не стремится к нулю; следовательно, ряд
расходится. Область сходимости состоит
из одной точки:
не стремится к нулю; следовательно, ряд
расходится. Область сходимости состоит
из одной точки: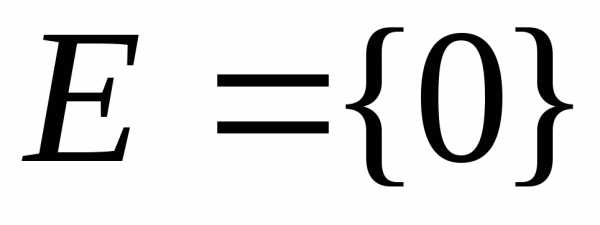 .
.
3. Пусть 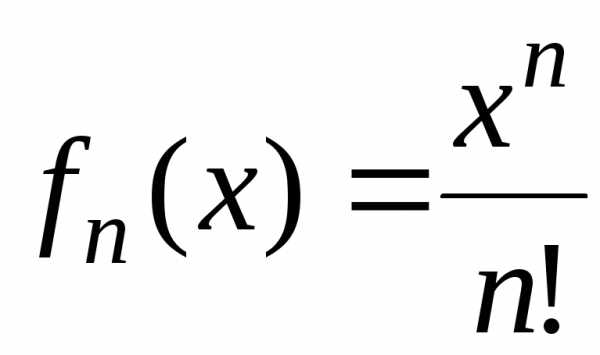 . Ряд
. Ряд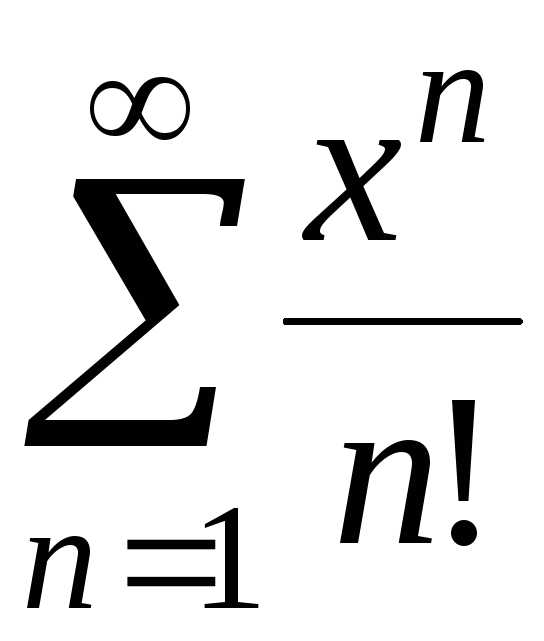 ,
очевидно, сходится при
,
очевидно, сходится при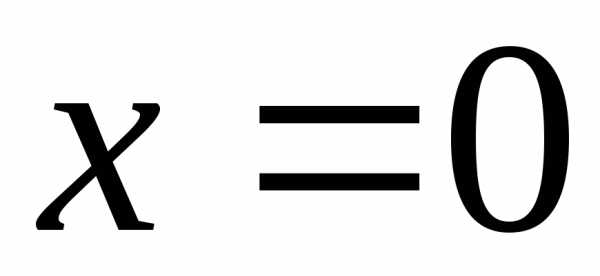 .
При
.
При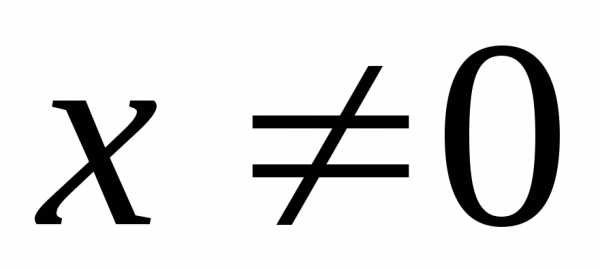 ряд сходится абсолютно на основании
признака Даламбера:
ряд сходится абсолютно на основании
признака Даламбера:
Область сходимости .
2.2. Теорема Абеля для степенных рядов
Определение. Степенным
рядом в окрестности точки 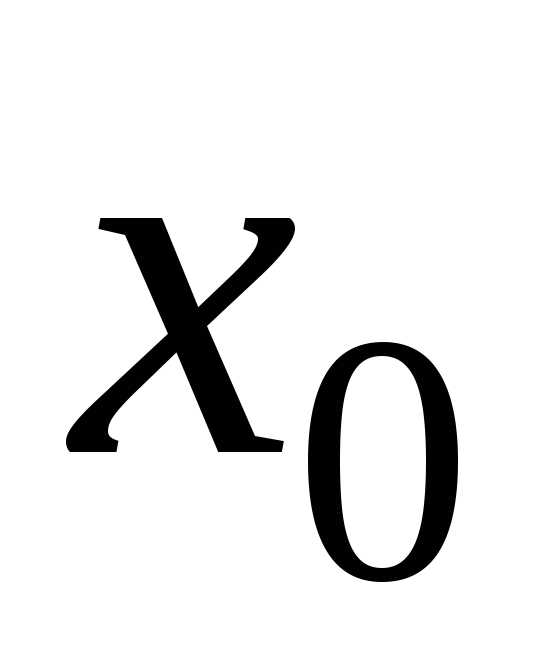 называется функциональный ряд вида
называется функциональный ряд вида
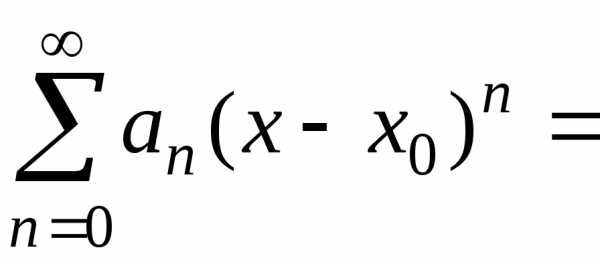
. (20)
Ряд (20) называют
также рядом
по степеням 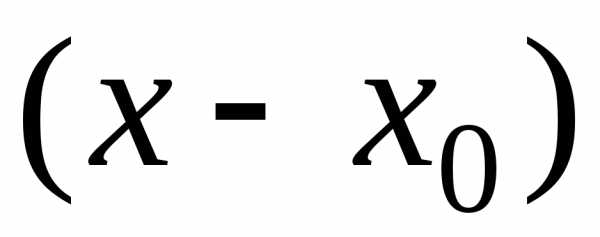 .
Числа
.
Числа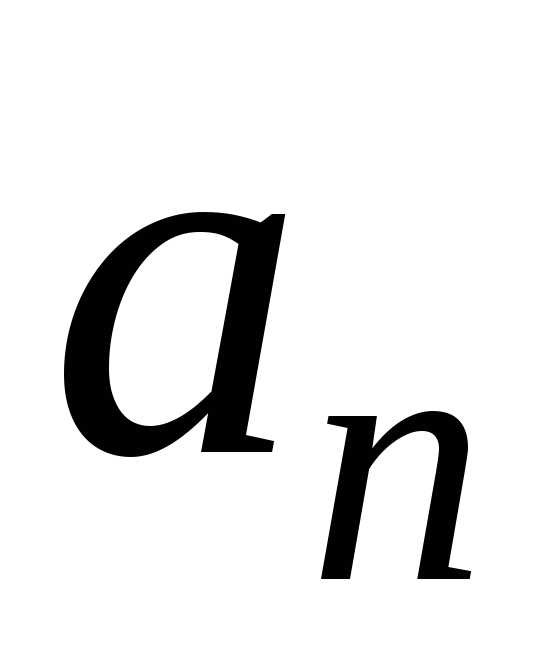 называютсякоэффициентами
степенного ряда.
называютсякоэффициентами
степенного ряда.
Замечание. Степенной ряд (20) заведомо сходится при 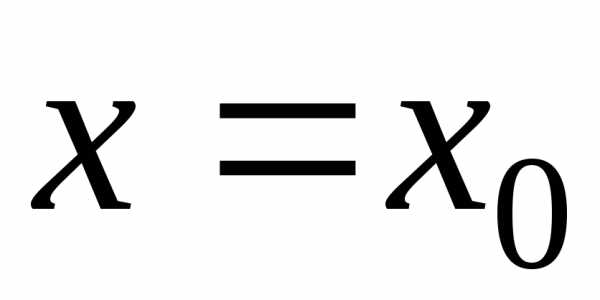 ,
и его сумма равна
,
и его сумма равна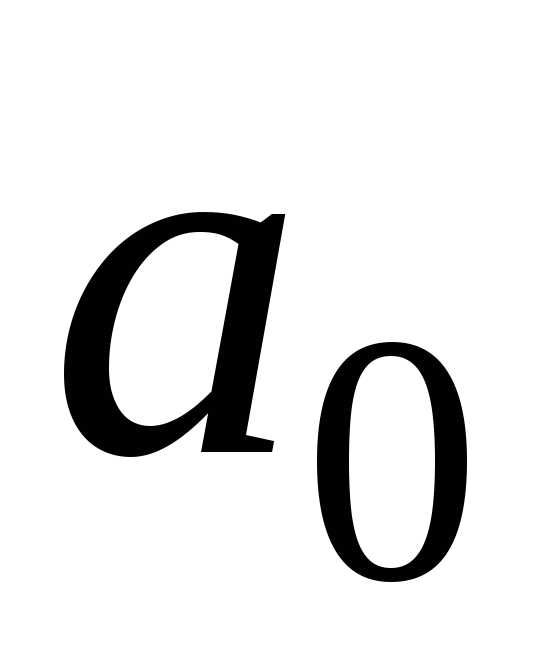 .
.
Рассмотрим
степенной ряд в окрестности нулевой
точки (ряд по степеням 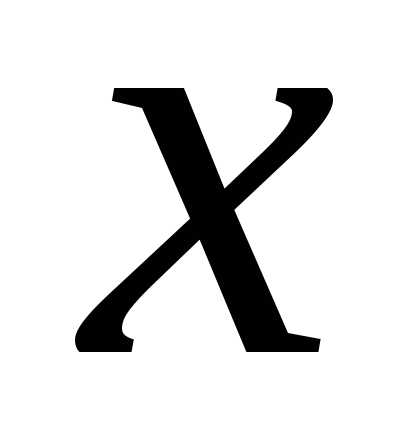 ):
):
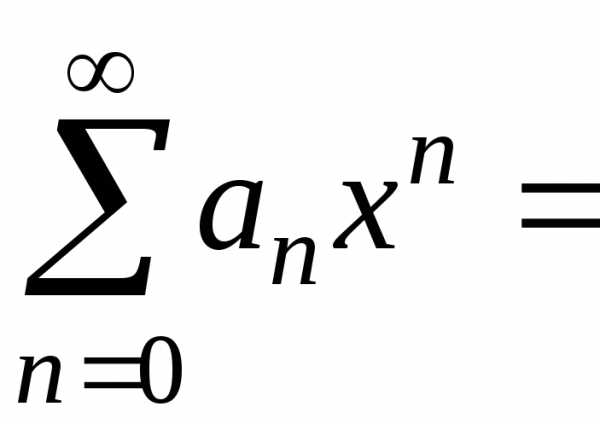 . (21)
. (21)
Он заведомо сходится
в точке 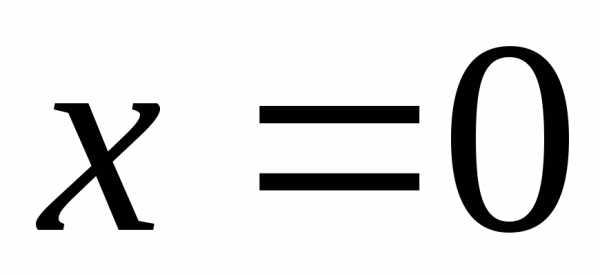 .
.
Теорема
Абеля. 1. Если
степенной ряд (21) сходится в точке 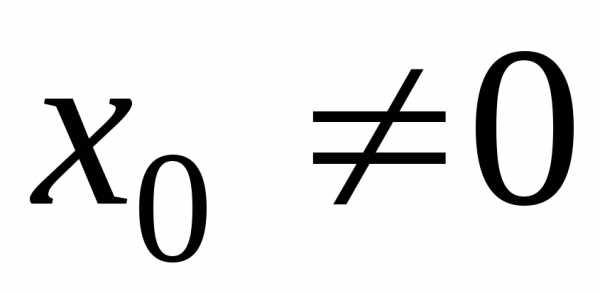 ,
то онабсолютно сходится при всех
,
то онабсолютно сходится при всех 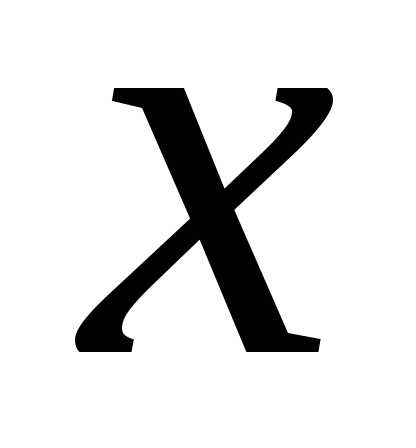 ,
удовлетворяющих условию
,
удовлетворяющих условию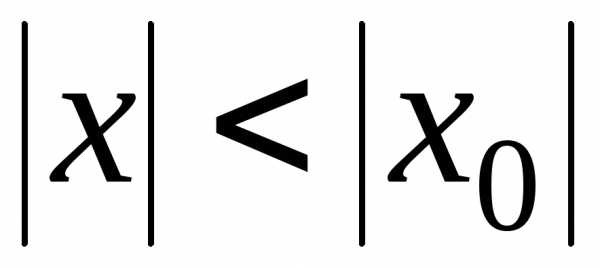 ,
то есть при.
,
то есть при.
2. Если степенной ряд (21) расходится в точке 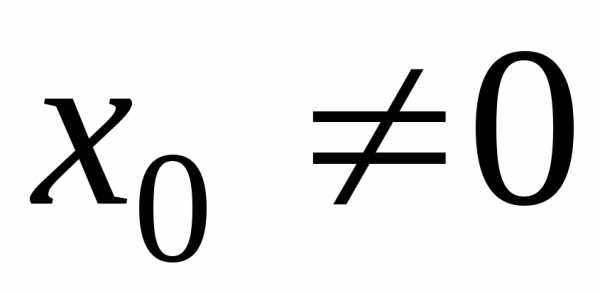 ,
то он расходится при всех
,
то он расходится при всех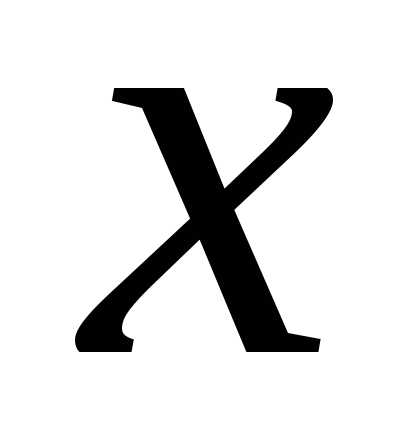 ,
удовлетворяющих условию
,
удовлетворяющих условию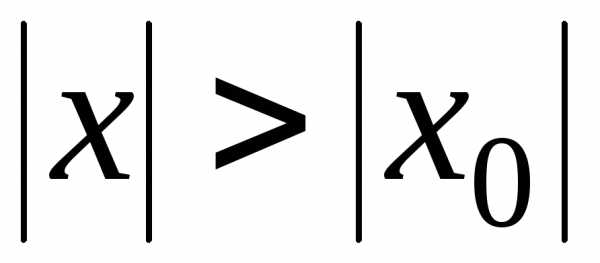 .
.
Доказательство. 1. Пусть числовой ряд 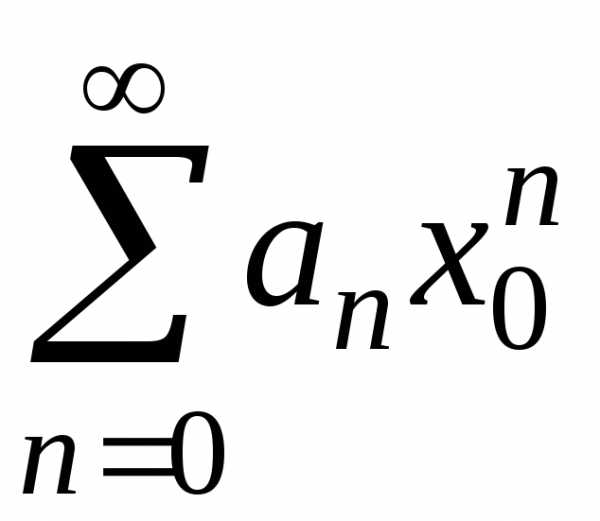 сходится, и
сходится, и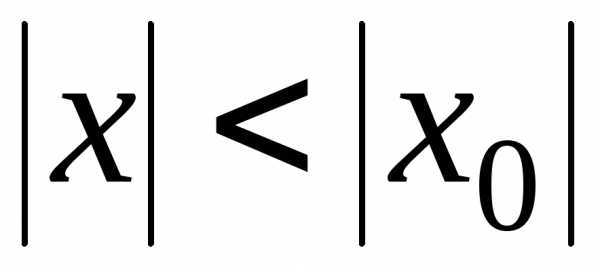 .
По необходимому признаку сходимости
.
По необходимому признаку сходимости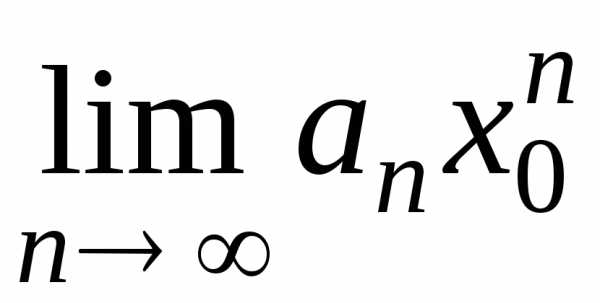 =0.
В силу ограниченности сходящейся
последовательности существует число
=0.
В силу ограниченности сходящейся
последовательности существует число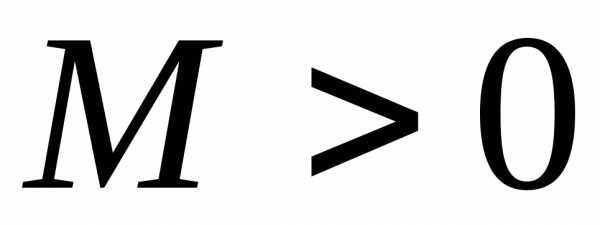 такое, что при всех
такое, что при всех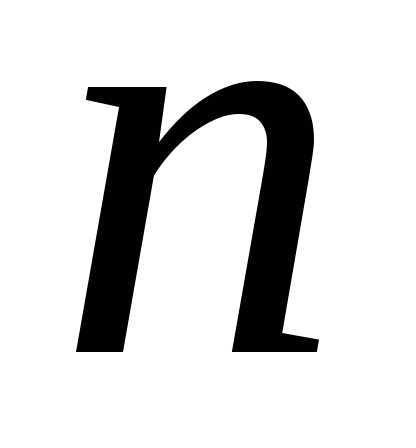 выполняется неравенство:
выполняется неравенство:
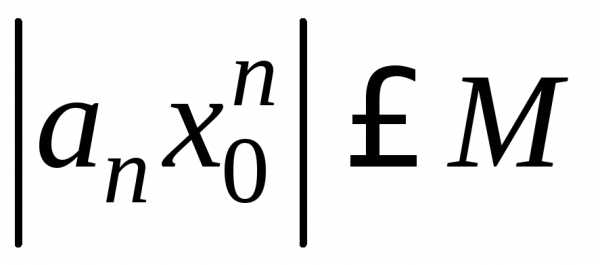 .
(22)
.
(22)
Запишем ряд (21) в виде:
.
Поскольку речь идет об абсолютной сходимости, рассмотрим ряд, составленный из модулей:
. (23)
Каждый член этого
положительного ряда в силу (22) меньше
соответствующего члена сходящегося
ряда 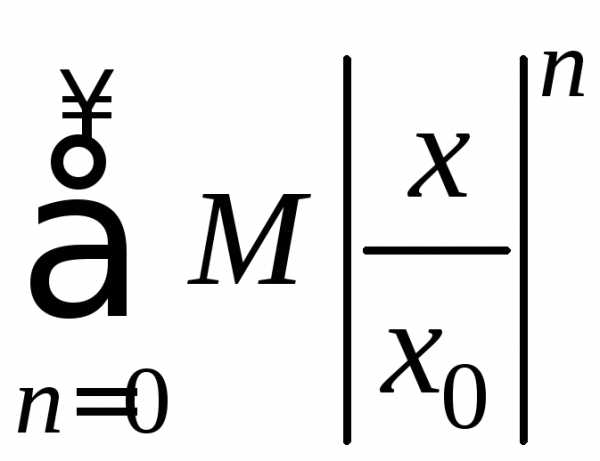 ,
образованного геометрической прогрессией
с начальным членом
,
образованного геометрической прогрессией
с начальным членом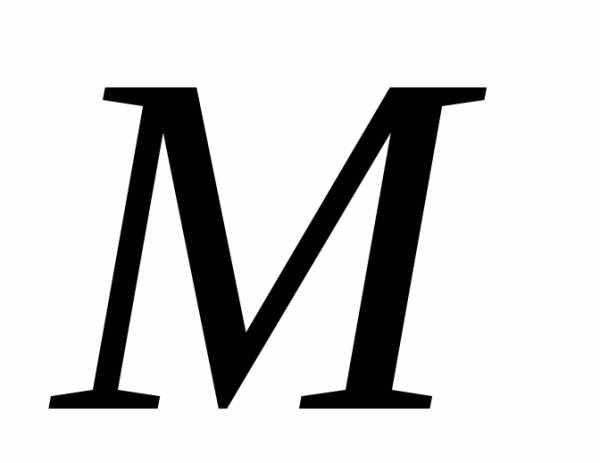 и со знаменателем
и со знаменателем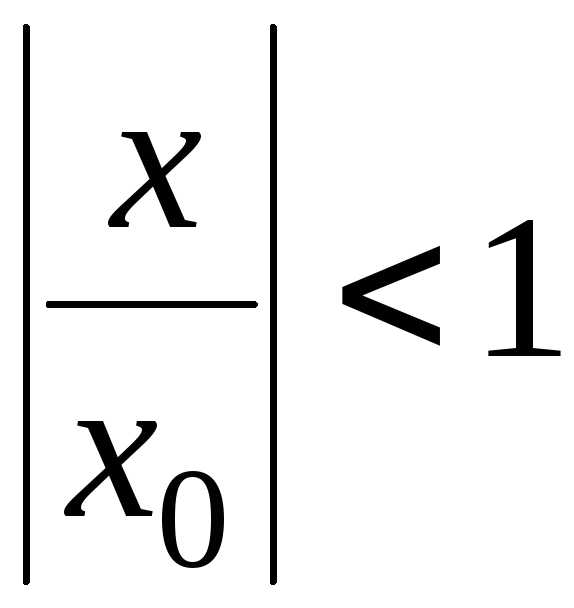 :
:
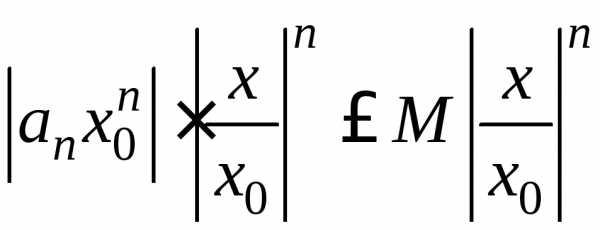 .
.
Поэтому ряд (23) сходится, то есть ряд (21) сходится абсолютно.
2. Пусть числовой ряд вида (21)
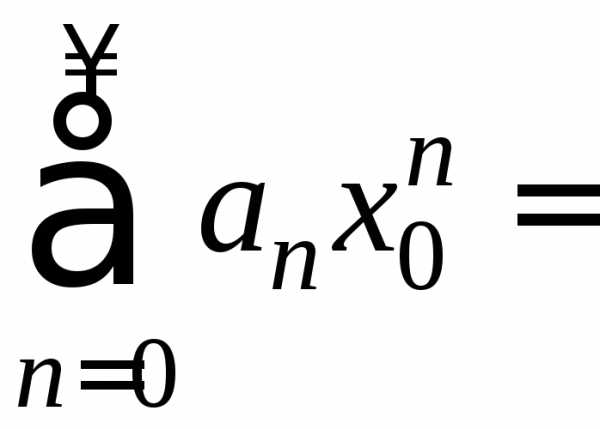 .
.
расходится в
некоторой точке 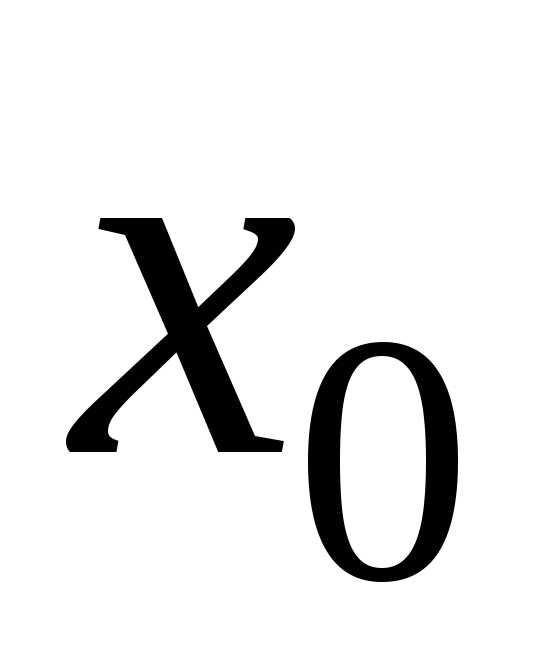 ,
и
,
и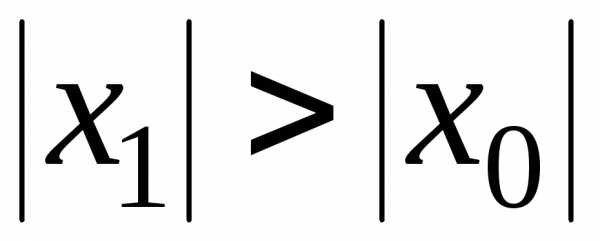 .
Если бы в точке
.
Если бы в точке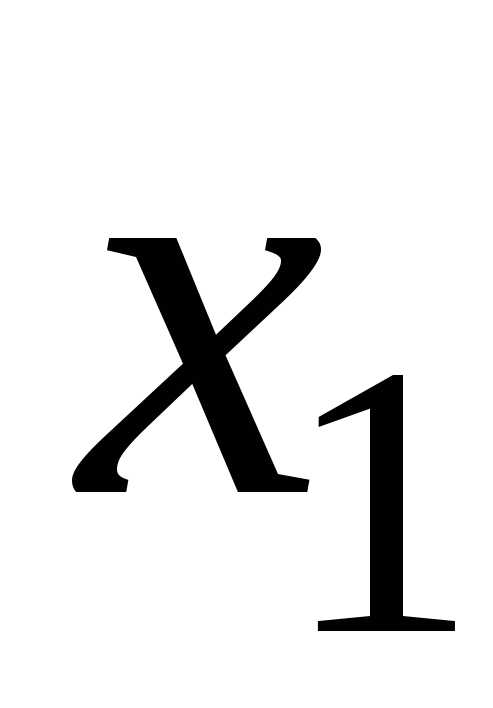 ряд сходился, то по первому утверждению
теоремы он сходился бы в точке
ряд сходился, то по первому утверждению
теоремы он сходился бы в точке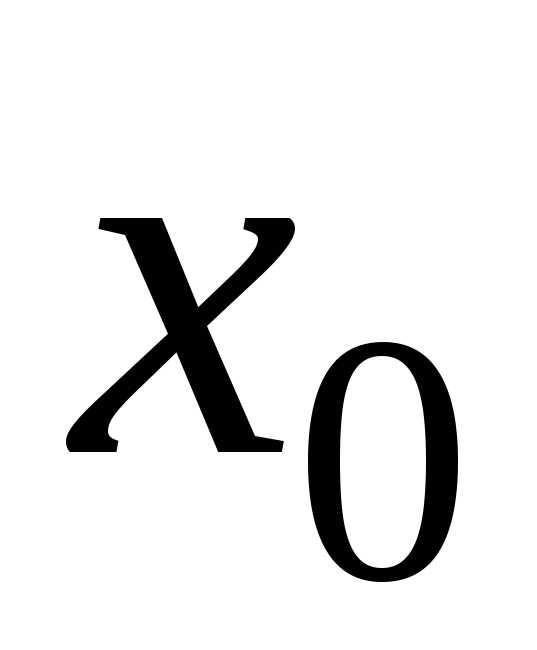 ,
что противоречит предположению. ■
,
что противоречит предположению. ■
2.3. Радиус сходимости степенного ряда
Из теоремы Абеля
следует, что областью
сходимости степенного ряда (21) является
либо единственная точка 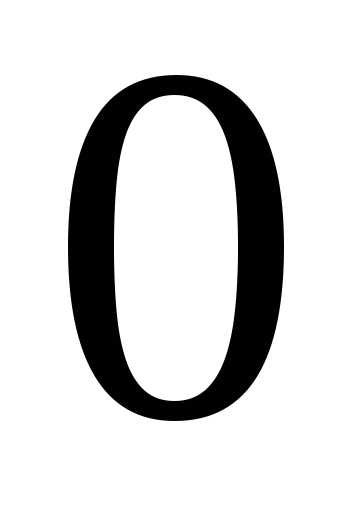 ,
либо промежутокчисловой оси с центром в нулевой точке,
либо вся числовая ось .
Действительно, если
,
либо промежутокчисловой оси с центром в нулевой точке,
либо вся числовая ось .
Действительно, если — точка сходимости, то и интервалвходит в область сходимости; если же
— точка сходимости, то и интервалвходит в область сходимости; если же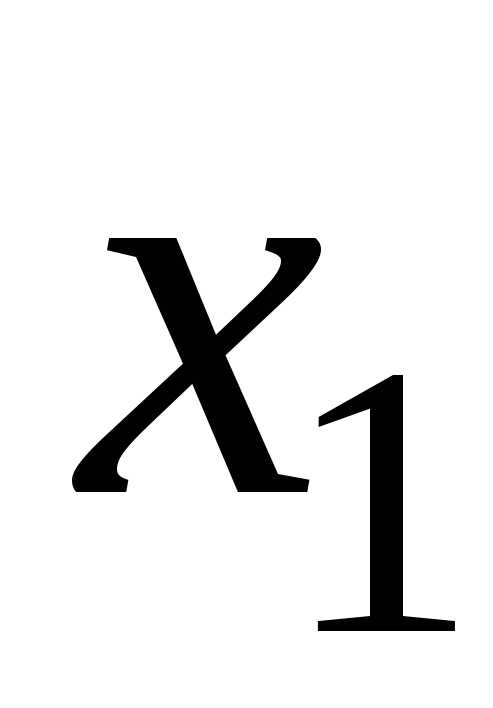 — точка расходимости, то промежутки
— точка расходимости, то промежутки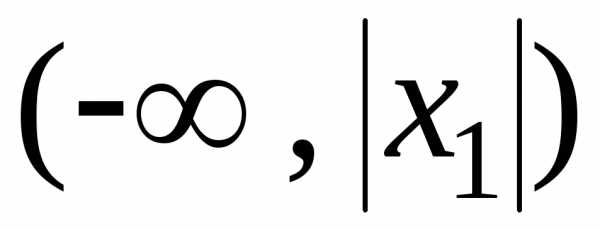 и
и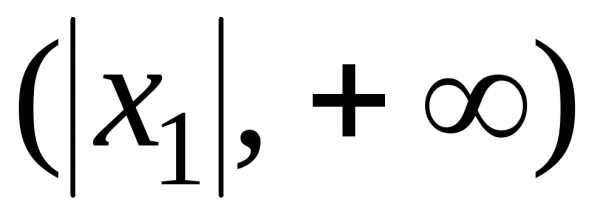 состоят из точек расходимости. (Граничная
точка
состоят из точек расходимости. (Граничная
точка области сходимости является точной
верхней границей [1] тех положительных
чисел
области сходимости является точной
верхней границей [1] тех положительных
чисел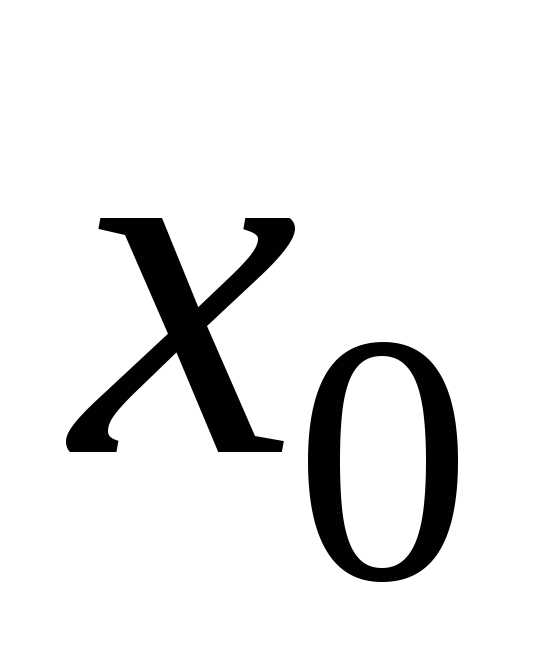 ,
для которых степенной ряд сходится.)
,
для которых степенной ряд сходится.)
Определение. 1. Если областью
сходимости степенного ряда (20) является конечный промежуток, то
интервалом сходимости степенного ряда (20) называется интервал 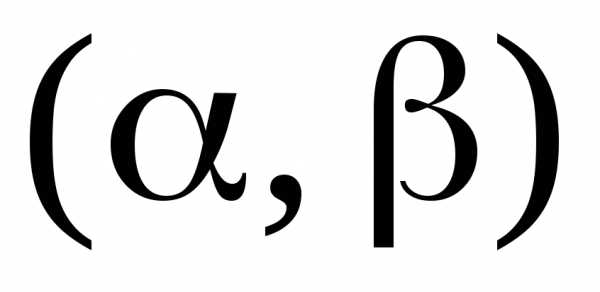 такой, что в точкахряд сходится абсолютно, а в точкахряд расходится. Число
такой, что в точкахряд сходится абсолютно, а в точкахряд расходится. Число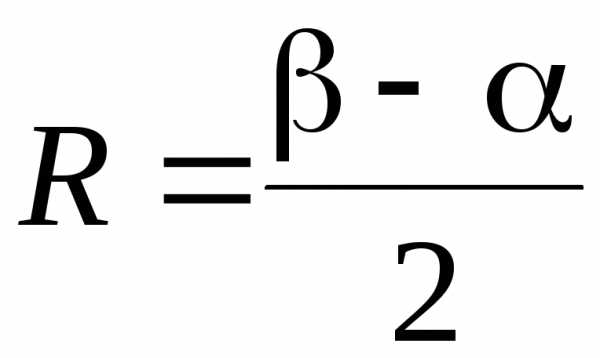 называется при этомрадиусом
сходимости степенного ряда.
называется при этомрадиусом
сходимости степенного ряда.
2. Если областью сходимости является вся числовая ось , то полагают.
3. Если область сходимости состоит только
из нулевой точки, то полагают 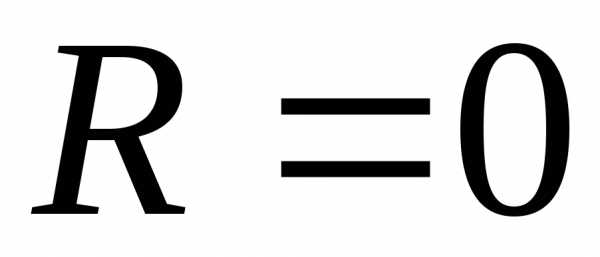 .
.
В граничных точках
интервала сходимости
и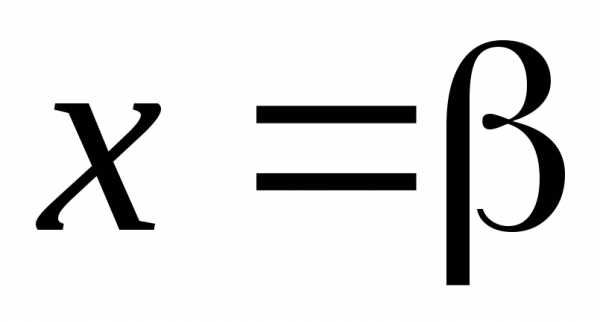 ряд может как сходиться, так и расходиться.
ряд может как сходиться, так и расходиться.
Из теоремы Абеля
следует, что для степенного ряда (21) в
окрестности нулевой точки интервал
сходимости имеет вид 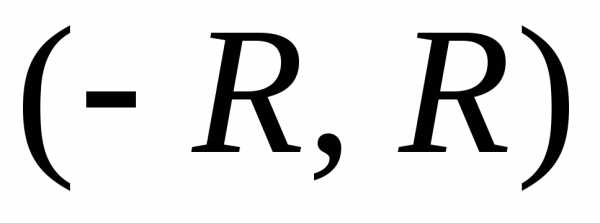 ,
где
,
где — радиус сходимости.
— радиус сходимости.
Пример. Степенной ряд, образованный геометрической
прогрессией со знаменателем 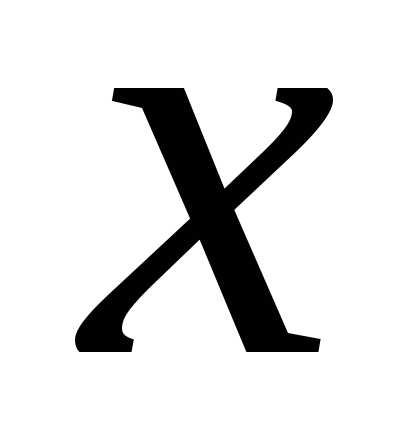
,
сходится при 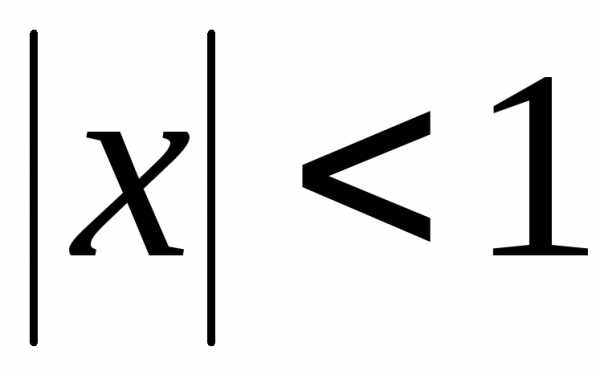 и расходится при
и расходится при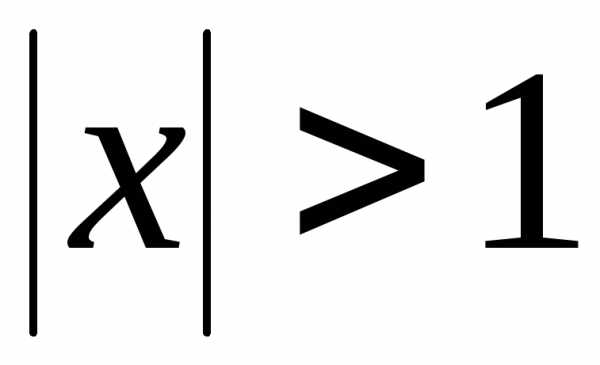 ;
поэтому радиус сходимости этого ряда
;
поэтому радиус сходимости этого ряда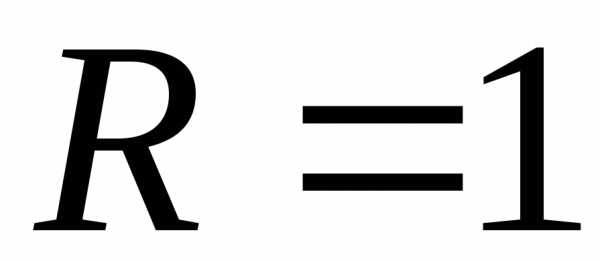 .
.
studfiles.net
Степенные ряды. Область сходимости. Теорема н. Абеля.
Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции.
Определение 1. Степенным рядом называется ряд вида:
где aи коэффициенты а0,… ,аn – постоянный.
При а=0 степенной ряд примет вид:
Определение 2.Совокупность значений x, при которых степенной ряд сходится, называется областью сходимостью степенного ряда.
Пример. Найти область сходимости.
1+x+ x2 + … + xn +…
Это геометрический рядq = x. Он сходится при то есть приилиследовательно, область сходимости (−1; 1).
Структура области сходимости степенного ряда устанавливается с помощью теоремы Н. Абеля:
1. Если степенной ряд (2) сходится приx = x0≠ 0, то он абсолютно сходится и при всех значениях x, удовлетворяет неравенству .
2. Если степенной ряд (2) расходится приx = x1≠ 0, то он расходится и при всех значениях x, удовлетворяет неравенству .
Из теоремы Н. Абеля следует, что существует такое число R ≥ 0, что при всех ряд (2) сходится, а прирасходится.
Число Rназывается радиусом сходимости степенного ряда, а интервал (−R; R) называется интервалом сходимости.
На концах интервала сходимости ряд (2) может, как сходится, так и расходится.
Для ряда (1) получим:
, то есть .Следовательно, интервал сходимости ряда (1) имеет вид:.
Радиус сходимости степенного ряда находится по формуле:
Пример 1.
Решение:
Тогда
Следовательно, (−2; 2) – интервал сходимости.
При ряд расходится, так как
То есть
Следовательно,при ряд расходится.
Пример 2.
Решение:
Тогда (−1;1) – интервал сходимости.
При x=1ряд расходится, как обобщенный гармонический.
При x=−1 получим знакочередующийся ряд.
На основании признака Лейбница он сходится, т.к.
Следовательно, область сходимости −1≤x˂1
Свойства степенных рядов
Пусть степенной ряд
имеет интервал сходимости.
Тогдаряд, полученный из данного ряда почленным дифференцированием или интегрированием, имеет тот же интервал сходимости.
Следовательно, на интервале сходимости степенные ряды можно почленно дифференцировать и интегрировать.
Ряд Маклорена. Ряд Тейлора.
Если функцияразлагается в степенной ряд по степеням, то ряд имеет следующий вид:
Этот ряд называется рядом Тейлора.
В частном случае при a=0 ряд примет вид:
Этот ряд называется рядом Маклорена.
Разложение в степенные ряды элементарных функций
studfiles.net
Степенные ряды
ВЫСШАЯ МАТЕМАТИКА
Степенные ряды
Содержание
1. Определение степенного ряда. Теорема Абеля
2. Свойства степенных рядов
3. Ряды Тейлора, Маклорена для функций
4. Разложение некоторых элементарных функций в ряд Маклорена
5. Приложения степенных рядов
1. Определение степенного ряда. Теорема Абеля
Степенные ряды являются частным случаем функциональных рядов.
Определение 1.1 . Степенным рядом называется функциональный ряд вида
.(1.1)Здесь
– постоянные вещественные числа, называемые коэффициентами степенного ряда; а – некоторое постоянное число, х – переменная, принимающая значения из множества действительных чисел.При
степенной ряд (1.1) принимает вид . (1.2)Степенной ряд (1.1) называют рядом по степеням разности
, ряд (1.2) – рядом по степеням х .Если переменной х придать какое-либо значение, то степенной ряд (1.1) (или (1.2)) превращается в числовой ряд, который может сходиться или расходиться.
Определение 1.2 . Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится.
Ряд (1.1) с помощью подстановки
приводится к более простому виду (1.2), поэтому вначале будем рассматривать степенные ряды вида (1.2).Для нахождения области сходимости степенного ряда важную роль играет следующая теорема.
Теорема 1.1 (Теорема Абеля) :
если степенной ряд (1.2) сходится при , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству ; если же ряд (1.2) расходится при , то он расходится при всех значениях х, удовлетворяющих неравенству .
Теорема Абеля дает ясное представление о структуре области сходимости степенного ряда.
Теорема 1.2:
область сходимости степенного ряда (1.2) совпадает с одним из следующих интервалов:
1)
; 2) ; 3) ; 4) ,где R – некоторое неотрицательное действительное число или .
Число R называется радиусом сходимости , интервал
– интервалом сходимости степенного ряда (1.2).Если
, то интервал сходимости представляет собой всю числовую ось .Если
, то интервал сходимости вырождается в точку .Замечание: если
– интервал сходимости для степенного ряда (1.2), то – интервал сходимости для степенного ряда (1.1).Из теоремы 1.2 следует, что для практического нахождения области сходимости степенного ряда (1.2) достаточно найти его радиус сходимости R и выяснить вопрос о сходимости этого ряда на концах интервала сходимости
, т. е. при и .Радиус сходимости R степенного ряда можно найти по одной из следующих формул:
формула Даламбера:
;(1.3)формула Коши:
.(1.4)Если в формуле Коши
, то полагают , если , то полагают .Пример 1.1. Найти радиус сходимости, интервал сходимости и область сходимости степенного ряда
.Решение
Найдем радиус сходимости данного ряда по формуле
В нашем случае
, .Тогда
.Следовательно, интервал сходимости данного ряда имеет вид
.Исследуем сходимость ряда на концах интервала сходимости.
При
степенной ряд превращается в числовой ряд .который расходится как гармонический ряд.
При
степенной ряд превращается в числовой ряд .Это – знакочередующийся ряд, члены которого убывают по абсолютной величине и
. Следовательно, по признаку Лейбница этот числовой ряд сходится.Таким образом, промежуток
– область сходимости данного степенного ряда.2. Свойства степенных рядов
Степенной ряд (1.2) представляет собой функцию
, определенную в интервале сходимости , т. е. .Приведем несколько свойств функции
.Свойство 1. Функция является непрерывной на любом отрезке , принадлежащем интервалу сходимости .
Свойство 2. Функция дифференцируема на интервале , и ее производная может быть найдена почленным дифференцированием ряда (1.2), т. е.
,для всех
.Свойство 3. Неопределенный интеграл от функции для всех
может быть получен почленным интегрированием ряда (1.2), т. е.для всех
.Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала может измениться.
Приведенные свойства справедливы также и для степенных рядов (1.1).
Пример 2.1. Рассмотрим степенной ряд
.Область сходимости этого ряда, как показано в примере 1.1, есть промежуток
.Почленно продифференцируем этот ряд:
mirznanii.com

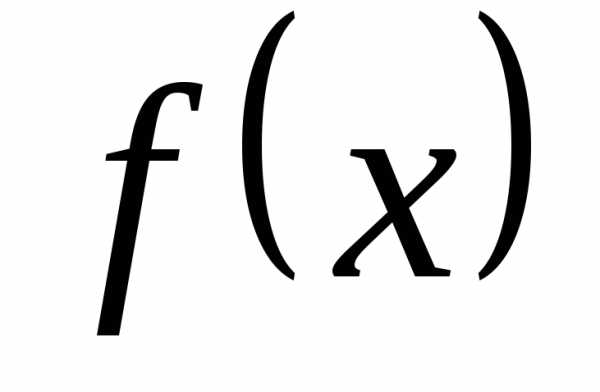 на интервале
на интервале 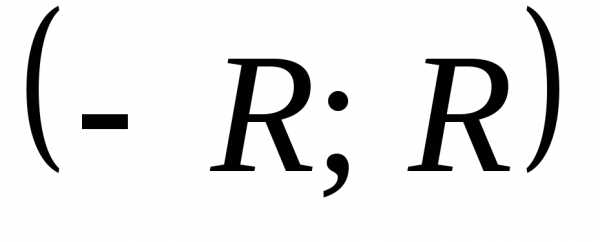 разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная
разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная 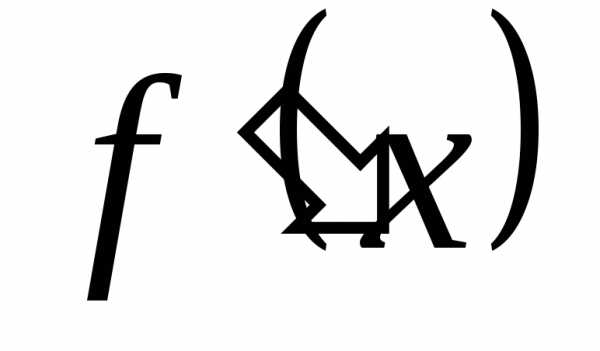 может быть найдена почленным
дифференцированием ряда, т.е.:
может быть найдена почленным
дифференцированием ряда, т.е.: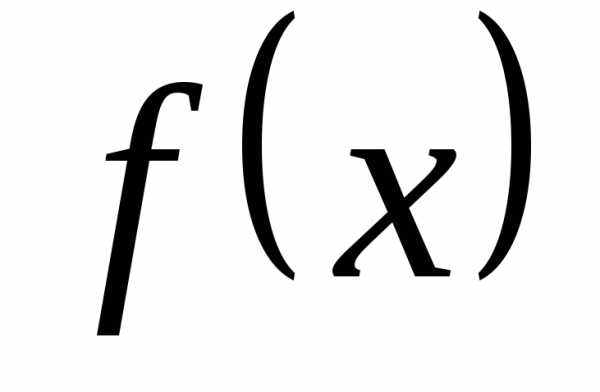
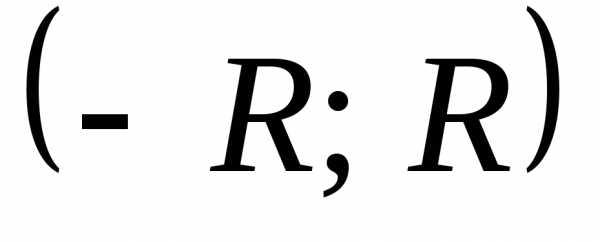 разлагается
в степенной ряд, то она
интегрируема в интервале
разлагается
в степенной ряд, то она
интегрируема в интервале 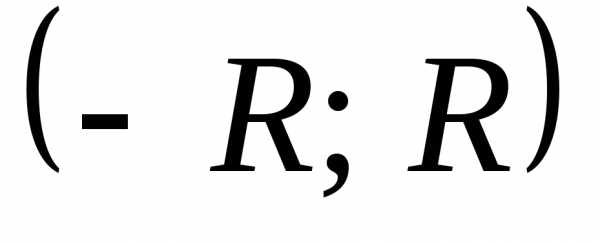 и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если ,
то:
и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если ,
то: