F-тест — Википедия
F-тест или критерий Фишера (F-критерий, φ*-критерий) — статистический критерий, тестовая статистика которого при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение).
Статистика теста так или иначе сводится к отношению выборочных дисперсий (сумм квадратов, деленных на «степени свободы»). Чтобы статистика имела распределение Фишера, необходимо, чтобы числитель и знаменатель были независимыми случайными величинами и соответствующие суммы квадратов имели распределение Хи-квадрат. Для этого требуется, чтобы данные имели нормальное распределение. Кроме того, предполагается, что дисперсия случайных величин, квадраты которых суммируются, одинакова.
Тест проводится путём сравнения значения статистики с критическим значением соответствующего распределения Фишера при заданном уровне значимости. Известно, что если F∼F(m,n){\displaystyle F\sim F(m,n)}, то 1/F∼F(n,m){\displaystyle 1/F\sim F(n,m)}. Кроме того, квантили распределения Фишера обладают свойством F1−α=1/Fα{\displaystyle F_{1-\alpha }=1/F_{\alpha }}. Поэтому обычно на практике в числителе участвует потенциально большая величина, в знаменателе — меньшая и сравнение осуществляется с «правой» квантилью распределения. Тем не менее тест может быть и двусторонним, и односторонним. В первом случае при уровне значимости α{\displaystyle \alpha } используется квантиль Fα/2{\displaystyle F_{\alpha /2}}, а при одностороннем тесте — Fα{\displaystyle F_{\alpha }}
Более удобный способ проверки гипотез — с помощью p-значения p(F){\displaystyle p(F)} — вероятностью того, что случайная величина с данным распределением Фишера превысит данное значение статистики. Если p(F){\displaystyle p(F)} (для двустороннего теста — 2p(F{\displaystyle 2p(F})) меньше уровня значимости α{\displaystyle \alpha }, то нулевая гипотеза отвергается, в противном случае принимается.
F-тест на равенство дисперсий[править | править код]
Две выборки[править | править код]
Пусть имеются две выборки объёмом m и n соответственно случайных величин X и Y, имеющих нормальное распределение. Необходимо проверить равенство их дисперсий. Статистика теста
F=σ^X2σ^Y2 ∼ F(m−1,n−1){\displaystyle F={\frac {{\hat {\sigma }}_{X}^{2}}{{\hat {\sigma }}_{Y}^{2}}}~\sim ~F(m-1,n-1)}
где σ^2{\displaystyle {{\hat {\sigma }}^{2}}} — выборочная дисперсия.
Если статистика больше критического значения, соответствующего выбранному уровню значимости, то дисперсии случайных величин признаются не одинаковыми.
Несколько выборок[править | править код]
Пусть выборка объёмом N случайной величины X разделена на k групп с количеством наблюдений ni{\displaystyle n_{i}} в i-ой группе.
Межгрупповая («объяснённая») дисперсия: σ^BG2=∑i=1kni(xi¯−x¯)2/(k−1){\displaystyle {\hat {\sigma }}_{BG}^{2}=\sum _{i=1}^{k}n_{i}({\overline {x_{i}}}-{\overline {x}})^{2}/(k-1)}
Внутригрупповая («необъяснённая») дисперсия: σ^WG2=∑i=1k∑j=1ni(xij−x¯i)2/(N−k){\displaystyle {\hat {\sigma }}_{WG}^{2}=\sum _{i=1}^{k}\sum _{j=1}^{n_{i}}(x_{ij}-{\overline {x}}_{i})^{2}/(N-k)}
F=σ^BG2σ^WG2 ∼ F(k−1,N−k){\displaystyle F={\frac {{\hat {\sigma }}_{BG}^{2}}{{\hat {\sigma }}_{WG}^{2}}}~\sim ~F(k-1,N-k)}
Данный тест можно свести к тестированию значимости регрессии переменной X на фиктивные переменные-индикаторы групп. Если статистика превышает критическое значение, то гипотеза о равенстве средних в выборках отвергается, в противном случае средние можно считать одинаковыми.
Проверка ограничений на параметры регрессии[править | править код]
Статистика теста для проверки линейных ограничений на параметры классической нормальной линейной регрессии определяется по формуле:
F=(ESSS−ESSL)/qESSL/(n−kL)=(RL2−RS2)/q(1−RL2)/(n−kL) ∼ F(q,n−kL){\displaystyle F={\frac {(ESS_{S}-ESS_{L})/q}{ESS_{L}/(n-k_{L})}}={\frac {(R_{L}^{2}-R_{S}^{2})/q}{(1-R_{L}^{2})/(n-k_{L})}}~\sim ~F(q,n-k_{L})}
где q=kL−kS{\displaystyle q=k_{L}-k_{S}} -количество ограничений, n-объём выборки, k-количество параметров модели, ESS-сумма квадратов остатков модели, R2{\displaystyle R^{2}}-коэффициент детерминации, индексы S и L относятся соответственно к короткой и длинной модели (модели с ограничениями и модели без ограничений).
Замечание[править | править код]
Описанный выше F-тест является точным в случае нормального распределения случайных ошибок модели. Однако F-тест можно применить и в более общем случае. В этом случае он является асимптотическим. Соответствующую F-статистику можно рассчитать на основе статистик других асимптотических тестов — теста Вальда (W), теста множителей Лагранжа(LM) и теста отношения правдоподобия (LR) — следующим образом:
F=n−kqW/n , F=n−kqLMn−LM , F=n−kq(eLR/n−1){\displaystyle F={\frac {n-k}{q}}W/n~,~F={\frac {n-k}{q}}{\frac {LM}{n-LM}}~,~F={\frac {n-k}{q}}(e^{LR/n}-1)} Все эти статистики асимптотически имеют распределение F(q, n-k), несмотря на то, что их значения на малых выборках могут различаться.
Проверка значимости линейной регрессии[править | править код]
Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. В данном случае нулевая гипотеза — об одновременном равенстве нулю всех коэффициентов при факторах регрессионной модели (то есть всего ограничений k-1). В данном случае короткая модель — это просто константа в качестве фактора, то есть коэффициент детерминации короткой модели равен нулю. Статистика теста равна:
F=R2/(k−1)(1−R2)/(n−k) ∼ F(k−1,n−k){\displaystyle F={\frac {R^{2}/(k-1)}{(1-R^{2})/(n-k)}}~\sim ~F(k-1,n-k)}
Соответственно, если значение этой статистики больше критического значения при данном уровне значимости, то нулевая гипотеза отвергается, что означает статистическую значимость регрессии. В противном случае модель признается незначимой.
Пример[править | править код]
Пусть оценивается линейная регрессия доли расходов на питание в общей сумме расходов на константу, логарифм совокупных расходов, количество взрослых членов семьи и количество детей до 11 лет. То есть всего в модели 4 оцениваемых параметра (k=4). Пусть по результатам оценки регрессии получен коэффициент детерминации R2=41.2366%{\displaystyle R^{2}=41.2366\%}. По вышеприведенной формуле рассчитаем значение F-статистики в случае, если регрессия оценена по данным 34 наблюдений и по данным 64 наблюдений: F1=0.412366/(4−1)(1−0.412366)/(34−4)=0,70174∗10=7,02{\displaystyle F_{1}={\frac {0.412366/(4-1)}{(1-0.412366)/(34-4)}}=0,70174*10=7,02}
F2=0.412366/(4−1)(1−0.412366)/(64−4)=0,70174∗20=14.04{\displaystyle F_{2}={\frac {0.412366/(4-1)}{(1-0.412366)/(64-4)}}=0,70174*20=14.04}
Критическое значение статистики при 1 % уровне значимости (в Excel функция FРАСПОБР) в первом случае равно F1%(3,30)=4,51{\displaystyle F_{1\%}(3,30)=4,51}, а во втором случае F1%(3,60)=4,13{\displaystyle F_{1\%}(3,60)=4,13}. В обоих случаях регрессия признается значимой при заданном уровне значимости. В первом случае P-значение равно 0,1 %, а во втором — 0,00005 %. Таким образом, во втором случае уверенность в значимости регрессии существенно выше (существенно меньше вероятность ошибки в случае признания модели значимой).
Проверка гетероскедастичности[править | править код]
См. Тест Голдфелда-Куандта
Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
общая сумма квадратов отклонений (TSS)
сумма квадратов отклонений, обусловленная регрессией (RSS)
остаточная сумма квадратов отклонений (ESS)
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R
Любые задачи по эконометрике решаются здесь
Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
общая сумма квадратов отклонений (TSS)
сумма квадратов отклонений, обусловленная регрессией (RSS)
остаточная сумма квадратов отклонений (
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Критерий Фишера — это… Что такое Критерий Фишера?
- Критерий Фишера
Критерий Фишера (F-критерий, φ*-критерий, критерий наименьшей значимой разности) — апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в установке дисперсионного анализа.
Критерий Фишера широко применяется в задачах статистического оценивания, в частности в аналитической химии.
Пример таблицы критических значений F-критерия для уровня значимости 0.05[1]
f2\f1 1 2 3 4 5 6 7 8 9 10 12 1 161.45 199.50 215.71 224.58 230.16 233.99 236.77 238.88 240.54 241.88 245.95 2 18.51 19.00 19.16 19.25 19.30 19.33 19.35 19.37 19.38 19.40 19.43 3 10.13 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 8.70 4 7.71 6.94 6.59 6.39 6.26 6.16 6.09 6.04 6.00 5.96 5.86 5 6.61 5.79 5.41 5.19 5.05 4.95 4.88 4.82 4.77 4.74 4.62 6 5.99 5.14 4.76 4.53 4.39 4.28 4.21 4.15 4.10 4.06 3.94 7 5.59 4.74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 3.51 8 5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 3.22 9 5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 3.01 10 4.96 4.10 3.71 3.48 3.33 3.22 3.14 3.07 3.02 2.98 2.85 11 4.84 3.98 3.59 3.36 3.20 3.09 3.01 2.95 2.90 2.85 2.72 12 4.75 3.89 3.49 3.26 3.11 3.00 2.91 2.85 2.80 2.75 2.62 13 4.67 3.81 3.41 3.18 3.03 2.92 2.83 2.77 2.71 2.67 2.53 14 4.60 3.74 3.34 3.11 2.96 2.85 2.76 2.70 2.65 2.60 2.46 15 4.54 3.68 3.29 3.06 2.90 2.79 2.71 2.64 2.59 2.54 2.40 16 4.49 3.63 3.24 3.01 2.85 2.74 2.66 2.59 2.54 2.49 2.35 17 4.45 3.59 3.20 2.96 2.81 2.70 2.61 2.55 2.49 2.45 2.31 18 4.41 3.55 3.16 2.93 2.77 2.66 2.58 2.51 2.46 2.41 2.27 19 4.38 3.52 3.13 2.90 2.74 2.63 2.54 2.48 2.42 2.38 2.23 20 4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 2.20
См. также
Примечания
Внешние ссылки
Статистические показатели Описательная
статистикаСтатистический
вывод и
проверка
гипотезКорреляция Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания Линейные модели Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Анализ ковариаций Регрессия Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами - Статистические критерии
Wikimedia Foundation. 2010.
- Киев (энциклопедический справочник)
- Кузьмицкий, Алексей Алексеевич
Смотреть что такое «Критерий Фишера» в других словарях:
критерий Фишера — Fišerio kriterijus statusas T sritis augalininkystė apibrėžtis Veiksnio arba veiksnių sąveikos įtakos bandymo rezultatams patikimumo rodiklis. atitikmenys: angl. Fisher’s test rus. критерий Фишера … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas
КРИТЕРИЙ ФИШЕРА — Показатель достоверности влияния изучаемых факторов на полученный результат. Определяется отношением факториальной вариансы к вариансе ошибок: где F показатель достоверности; || факториальная варианса; варианса ошибок. Уровень вероятности влияния … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных
Критерий Фишера F-критерий — Критерий Фишера, F критерий * крытэрый Фішара, F крытэрый * Fisher’s criterion or F test критерий существенности индивидуального или совместного взаимодействия изучаемых факторов на конечный результат эксперимента. К. Ф. определяется отношением… … Генетика. Энциклопедический словарь
точный критерий Фишера — для таблицы сопряженности 22 используется при проверке гипотезы о независимости переменной строки и переменной столбца. В отличие от критерия хи квадрат, в котором уровень значимости рассчитывается на основе асимптотического распределения, в… … Словарь социологической статистики
F-критерий;критерий Фишера — Критерий, статистика которого подчиняется F распределению, если нулевая гипотеза верна. Примечание. Этот критерий применяется, например, для (см. дисперсионный анализ) : 1. проверки равенства дисперсий двух нормальных совокупностей на основе… … Словарь социологической статистики
Критерий φ* Фишера — Критерий Фишера (F критерий, φ* критерий, критерий наименьшей значимой разности) апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми… … Википедия
Критерий Краскела — Уоллиса предназначен для проверки равенства медиан нескольких выборок. Данный критерий является многомерным обобщением критерия Уилкоксона Манна Уитни. Критерий Краскела Уоллиса является ранговым, поэтому он инвариантен по отношению к любому… … Википедия
Критерий согласия Колмогорова — или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.… … Википедия
Критерий Вальда — (максиминный критерий[1]) один из критериев принятия решений в условиях неопределённости. Критерий крайнего пессимизма. История Критерий Вальда был предложен Абрахамом Вальдом в 1955 году для выборок равного объема, а затем распространен на … Википедия
Критерий согласия Пирсона — Критерий Пирсона, или критерий χ² (Хи квадрат) наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая… … Википедия
Уравнение Фишера — Википедия
Материал из Википедии — свободной энциклопедии
Уравнение Фишера (также называемое эффектом Фишера и гипотезой Фишера) — уравнение, описывающее связь между темпом инфляции, номинальной и реальной ставками процента:
- i=r+π{\displaystyle i=r+\pi },
где i{\displaystyle i} — номинальная ставка процента;
- r{\displaystyle r} — реальная ставка процента;
- π{\displaystyle \pi } — темп инфляции.
Названо в честь Ирвинга Фишера.
Уравнение в приближенной форме (см. #Вывод) описывает явление, которое называется эффектом Фишера. Эффект состоит в том, что номинальная ставка процента может измениться по двум причинам:
- из-за изменений реальной ставки процента;
- из-за изменения темпа инфляции.
Уровень цен в экономике со временем меняется. Инвестор также размещает деньги под проценты на определенный срок. Поэтому он заинтересован в том, чтобы получить не только определенный доход, но и компенсировать падение покупательной способности денег в будущем.
Например, если инвестор положил на банковский счёт сумму денег, приносящую 10 % годовых ежегодно, то номинальная ставка составит 10 %. При уровне инфляции 6 % реальная ставка составит только 4 %.
В уравнении может использоваться как фактический темп инфляции π{\displaystyle \pi }, так и его ожидаемое значение πe{\displaystyle \pi ^{e}}. В первом случае, формула позволяет вычислить реальную ставку на основе полученной номинальной доходности и фактического роста цен. Во втором случае инвестор может определить для себя ожидаемую номинальную доходность, исходя из прогнозируемых значений.
Уравнение в приведенной выше форме является приближенным. Оно выполняется тем точнее, чем меньше по модулю значения r{\displaystyle r} и π{\displaystyle \pi }. Поэтому с математической точки зрения правильно писать приближенное равенство:
- i≈r+π{\displaystyle i\approx r+\pi },
Точная запись уравнения выглядит следующим образом:
- 1+i=(1+r)×(1+π){\displaystyle 1+i=(1+r)\times (1+\pi )}
Если раскрыть скобки, то получится следующая запись:
- 1+i=1+r+π+rπ{\displaystyle 1+i=1+r+\pi +r\pi }
или
- i=r+π+rπ{\displaystyle i=r+\pi +r\pi }
С точки зрения математического анализа, если r{\displaystyle r} и π{\displaystyle \pi } стремятся к нулю, то произведение rπ{\displaystyle r\pi } является бесконечно малой более высокого порядка. Поэтому при малых (по модулю) значениях r{\displaystyle r} и π{\displaystyle \pi } произведением rπ{\displaystyle r\pi } можно пренебречь. В результате получится упомянутая выше приближенная запись.
Пусть, например, r=π=1%{\displaystyle r=\pi =1\%}. Тогда сумма этих величин равна 2 %, а произведение — 0,01 %. Если же взять r=π=10%{\displaystyle r=\pi =10\%}, то сумма получится равной 20 %, а произведение 1 %. Таким образом, с ростом значений погрешность в расчетах становится все больше.
Точную запись можно также преобразовать к следующему виду, предложенному Фишером:
- r=1+i1+π−1=i−π1+π{\displaystyle r={\frac {1+i}{1+\pi }}-1={\frac {i-\pi }{1+\pi }}}
В тривиальных случаях при π=0{\displaystyle \pi =0} или π=i{\displaystyle \pi =i} обе формулы (точная и приближенная) дают одинаковое значение реальной процентной ставки.
- Вечканов Г. C., Вечканова Г. Р. Макроэкономика. — СПб.: Питер, 2008. — С. 55. — (Серия «Краткий курс»). — 3 000 экз. — ISBN 978-5-91180-108-3.
- Четыркин Е. М. Финансовая математика. — М.: Дело, 2005. — С. 400.
Точный тест Фишера — Википедия
У этого термина существуют и другие значения, см. Фишер.Точный тест Фишера — тест статистической значимости, используемый в анализе таблиц сопряжённости для выборок маленьких размеров. Относится к точным тестам значимости, поскольку не использует приближения большой выборки (асимптотики при размере выборки стремящемся к бесконечности).
Назван именем изобретателя — Рональда Фишера, на создание автора побудило высказывание Муриэль Бристоль (англ. Муриэль Бристоль), которая утверждала, будто была в состоянии обнаружить, в какой последовательности чай и молоко были налиты в её чашку.
Тест обычно используется, чтобы исследовать значимость взаимосвязи между двумя переменными в факторной таблице размерности 2×2{\displaystyle 2\times 2} (таблице сопряжённости признаков). Величина вероятности p{\displaystyle p} теста вычисляется, как если бы значения на границах таблицы известны. Например, в случае с дегустацией чая госпожа Бристоль знает число чашек с каждым способом приготовления (молоко или чай сначала), поэтому якобы предоставляет правильное число угадываний в каждой категории. Как было указано Фишером, в предположении нуль-гипотезы о независимости испытаний это ведёт к использованию гипергеометрического распределения для данного счёта в таблице.
С большими выборками в этой ситуации может использоваться тест хи-квадрат. Однако этот тест не является подходящим, когда математическое ожидание значений в любой из ячеек таблицы с заданными границами оказывается ниже 10: вычисленное выборочное распределение испытуемой статистической величины только приблизительно равно теоретическому распределению хи-квадрат, и приближение неадекватно в этих условиях (которые возникают, когда размеры выборки малы, или данные очень неравноценно распределены среди ячеек таблицы). Тест Фишера, как следует из его названия, является точным и может поэтому использоваться независимо от особенностей выборки. Тест становится трудновычислимым для больших выборок или хорошо уравновешенных таблиц, но, к счастью, именно для этих условий хорошо применим критерий Пирсона (χ2{\displaystyle \chi ^{2}}).
Для ручных вычислений тест выполним только в случае размерности факторных таблиц 2×2{\displaystyle 2\times 2}. Однако принцип теста может быть расширен на общий случай таблиц m×n{\displaystyle m\times n}, и некоторые статистические пакеты обеспечивают такие вычисления (иногда используя метод Монте-Карло, чтобы получить приближение).
Точные тесты позволяют получать более аккуратный анализ для маленьких выборок или данных, которые редки. Точные тесты непараметрических исследований — подходящий статистический инструмент для работы с неуравновешенными данными. Неуравновешенные данные, проанализированные асимптотическими методами, имеют тенденцию приводить к ненадёжным результатам. Для больших и хорошо уравновешенных наборов данных точные и асимптотические оценки вероятностей p{\displaystyle p} очень похожи. Но для маленьких, редких, или выведенных из равновесия данных, точные и асимптотические оценки могут быть весьма различными и даже привести к противоположным заключениям относительно разрабатываемой гипотезы[1][2][3].
Потребность в тесте Фишера возникает, когда у нас есть данные, разделённые на две категории двумя отдельными способами. Например, выборка подростков может быть разделена на категории с одной стороны по признаку пола (юноши и девушки), а с другой стороны — по признаку нахождения на диете или нет. Можно выдвинуть гипотезу, о том, что доля находящихся на диете людей выше среди девушек, чем среди юношей, и мы хотим удостовериться, является ли какое-нибудь наблюдаемое различие пропорций статистически значимым.
Данные могли бы быть похожими на следующие:
юноши девушки всего на диете 1 9 10 не на диете 11 3 14 всего 12 12 24
Такие данные не подходят для анализа методом хи-квадрат, потому что математические ожидания в таблице все ниже 10, а в факторной таблице размера 2×2{\displaystyle 2\times 2} число степеней свободы всегда равно одному.
Вопрос, который мы задаём об этих данных: зная, что 10 из 24 подростков — люди, сидящие на диете, и что 12 из этих 24 — девушки, какова вероятность, что 10 диетиков так неравноценно распределены между полами? Если бы мы выбрали 10 подростков наугад, какова вероятность, что 9 из них оказались взяты из набора 12 лиц женского пола и только 1 из числа 12 юношей?
Прежде чем продолжить исследование теста Фишера, введём необходимую нотацию. Обозначим числа в ячейках буквами a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} и d{\displaystyle d} соответственно, назовём итоги суммирования по строкам и столбцам маргинальными (граничными) итогами и представим общий итог буквой n{\displaystyle n}.
Теперь таблица выглядит следующим образом:
Фишер показал, что вероятность получения любого такого набора величин даётся гипергеометрическим распределением:
- p=(a+ba)(c+dc)/(na+c)=(a+b)!(c+d)!(a+c)!(b+d)!n!a!b!c!d!{\displaystyle p={{{a+b} \choose {a}}{{c+d} \choose {c}}}\left/{{n} \choose {a+c}}\right.={\frac {(a+b)!\,(c+d)!\,(a+c)!\,(b+d)!}{n!\,a!\,b!\,c!\,d!}}}
где столбцы в скобках — биномиальные коэффициенты, а символ «!{\displaystyle !}» является оператором факториала.
Эта формула даёт точную вероятность наблюдения любого специфического набора данных при условии заданных маргинальных итогов, общего итога и нулевой гипотезе об одинаковой предрасположенности к диете независимо от пола (соотношение между диетиками и людьми, не находящимися на диете, для юношей такое же, как для девушек).
Фишер показал, что мы можем иметь дело только со случаями, где маргинальные (предельные) итоги (англ. marginal totals) те же самые, что и в приведённой таблице. В приведённом примере таких случаев 11. Из них только один столь же «перекошен» (в сторону женской склонности к диете), как и демонстрационный пример:
Юноши Девушки Всего На диете 0 10 10 Не на диете 12 2 14 Всего 12 12 24
Чтобы оценить статистическую значимость наблюдаемых данных, то есть полную вероятность такого же или более выраженного «перекоса» в сторону нахождения девушек на диете, в предположении нулевой гипотезы мы должны вычислить вероятности ценности p{\displaystyle p} для обеих этих таблиц и сложить их. Это даёт так называемый односторонний тест; для двухстороннего теста мы должны также рассмотреть таблицы, которые так же перекошены, но в противоположном направлении (то есть рассмотреть случай преимущественного нахождения на диете юношей).
Однако классификация таблиц согласно тому, являются ли они «чрезвычайно перекошенными», проблематична. Подход, используемый языком программирования R, предлагает вычислить величину критерия p{\displaystyle p}, суммируя вероятности для всех таблиц с вероятностями, меньше чем или равными вероятности наблюдаемой таблицы. Для таблиц с малыми числами в ячейках двусторонняя оценка критерия может существенно отличаться от удвоенной величины односторонней оценки, в отличие от случая со статистическими данными, у которых есть симметрическое распределение выборки.
Большинство современных статистических пакетов вычисляет значение тестов Фишера, в некоторых случаях даже там, где приближение хи-квадрат также было бы приемлемым. Фактические вычисления, выполненные статистическими пакетами программ, будут, как правило, отличаться от описанных. В частности, числовые трудности могут следовать из больших величин факториалов. Простые, но даже более эффективные вычислительные подходы основаны на использовании гамма-функции или логарифмической гамма-функции, однако точное вычисление гипергеометрических и биномиальных вероятностей — область современных исследований.
- ↑ Mehta, C. R. 1995. SPSS 6.1 Exact test for Windows. Englewood Cliffs, NJ: Prentice Hall
- ↑ Mehta, C. R., Patel, N. R., & Tsiatis, A. A. 1984. Exact significance testing to establish treatment equivalence with ordered categorical data. Biometrics, 40(3), 819—825
- ↑ Mehta, C. R., Patel, N. R. 1997. Exact inference in categorical data. Biometrics, 53(1), 112—117
- Fisher, R. A. 1922. «On the interpretation of χ2 from contingency tables, and the calculation of P». Journal of the Royal Statistical Society 85(1):87-94.
- Fisher, R. A. 1954 Statistical Methods for research workers. Oliver and Boyd.
6.1.3 F — критерий Фишера
Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:
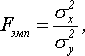 (8)
(8)
где 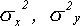 —
дисперсии первой и второй выборки
соответственно.
—
дисперсии первой и второй выборки
соответственно.
Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице.
Число степеней свободы определяется также просто:
k1=nl — 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k2=n2 — 1 для второй выборки.
В Приложении 1 критические значения критерия Фишера находятся по величинам k1 (верхняя строчка таблицы) и k2 (левый столбец таблицы).
Если tэмп>tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся.[3] Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.
Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:
Таблица 3.
№№ учащихся | Первый класс | Второй класс |
1 | 90 | 41 |
2 | 29 | 49 |
3 | 39 | 56 |
4 | 79 | 64 |
5 | 88 | 72 |
6 | 53 | 65 |
7 | 34 | 63 |
8 | 40 | 87 |
9 | 75 | 77 |
10 | 79 | 62 |
Суммы | 606 | 636 |
Среднее | 60,6 | 63,6 |
Рассчитав дисперсии для переменных X и Y, получаем:
sx2=572,83; sy2=174,04
Тогда по формуле (8) для расчета по F критерию Фишера находим:

По таблице из Приложения 1 для F критерия при степенях свободы в обоих случаях равных k=10 — 1 = 9 находим Fкрит=3,18 (<3.29), следовательно, в терминах статистических гипотез можно утверждать, что Н0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н1. Иcследователь может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.
6.2 Непараметрические критерии
Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.
