Четырехугольник является параллелограммом, если
Теорема: Четырехугольник является параллелограммом, если:
- противоположные его углы равны;
- противоположные его стороны попарно равны;
- его диагонали точкой пересечения делятся пополам;
- две его противоположные стороны параллельны и равны.
Доказательство:
A. Пусть в четырехугольнике KLMN углы К и М равны друг другу и равны а, пусть также равны друг другу и равны р углы L и N (рисунок). Учитывая, что сумма углов четырехугольника равна 360°, получаем, что 2α + 2β = 360°, или α + β = 180°. Учитывая, что углы К и L, равные соответственно аир, являются внутренними односторонними углами при прямых KN и LM, пересеченных прямой KL, заключаем, что стороны KN и LM параллельны. Также по углам К и N заключаем, что стороны KL и NM параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник KLMN — параллелограмм.
B. Пусть в четырехугольнике CDEF стороны CD и FE, а также CF и DE попарно равны (рисунок). Проведем одну из диагоналей четырехугольника, например СЕ. Треугольники CDE и EFC равны по трем сторонам. Поэтому углы DEC и FCE равны. Поскольку эти углы являются внутренними накрест лежащими при прямых DE и CF, пересеченных прямой СЕ, то стороны DE и CF параллельны. Также из равенства углов DCE и FEC получаем, что стороны CD и FE параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник CDEF — параллелограмм.
C. Пусть точка В пересечения диагоналей IL и КМ четырехугольника IKLM делит эти диагонали пополам: IB = BL и KB = ВМ (рисунок). Тогда треугольники KBL и MBI равны по двум сторонам и углу между ними. Это позволяет утверждать, что углы 1MB и LKB равны, а значит, стороны IM и KL параллельны. Аналогично из равенства треугольников KBI и MBL делаем вывод о параллельности сторон IK и LM. Теперь по определению параллелограмма можем утверждать, что четырехугольник IKLM — параллелограмм. Очень часто это надо знать при решении олимпиадных задачах на школьных олимпиадах.
D. Пусть в четырехугольнике OPQR противоположные стороны ОР и RQ параллельны и равны (рисунок). Проведем диагональ OQ. Полученные углы POQ и RQO равны, так как они являются внутренними накрест лежащими при параллельных прямых ОР и RQ, пересеченных прямой OQ. Поэтому треугольники OPQ и RQO равны по двум сторонам и углу между ними. Значит, их соответствующие углы PQO и ROQ равны.
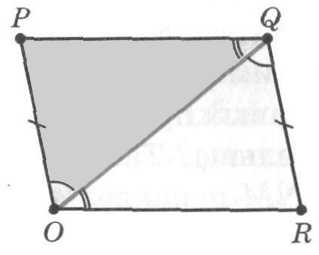
А поскольку они являются внутренними накрест лежащими углами при прямых PQ и OR, пересеченных прямой OQ, то стороны PQ и OR параллельны. Учитывая параллельность сторон ОР и RQ, по определению параллелограмма утверждаем, что четырехугольник OPQR — параллелограмм.
Признаки параллелограмма: доказательства и рисунки
Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков. Рассмотрим три основных признака параллелограмма.
1 признак параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти треугольники равны между собой по двум сторонам и углу между ними (BD — общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.
А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
2 признак параллелограмма
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти два треугольника буду равны между собой по трем сторонам (BD — общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.
3 признак параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы.) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Нужна помощь в учебе?
Предыдущая тема: Параллелограмм: понятие и свойства, примеры изображений
Следующая тема:   Основное тригонометрическое тождество: формулы приведения
Все неприличные комментарии будут удаляться.
www.nado5.ru
Как доказать, что четырехугольник — параллелограмм
Как доказать, что четырехугольник — параллелограмм? Для этого можно использовать определение либо один из признаков параллелограмма.
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.
ABCD — параллелограмм, если
AB ∥ CD, AD ∥ BC.
Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.
Например, это могут быть пары треугольников
1) ABC и CDA,
2) BCD и DAB,
3) AOD и COB,
4) AOB и COD.
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).
Для этого можно доказать равенство одной из тех же пар треугольников.
4) Четырехугольник — параллелограмм, если у него противоположные стороны попарно равны.
Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.
Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.
Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.
www.treugolniki.ru
Определение параллелограмма
Четырёхугольник называется параллелограммом, если его противоположные стороны попарно параллельны.
\(ABCD\) – параллелограмм \(\, \Leftrightarrow \, AB||CD\) и \(BC||AD\)
Свойства параллелограмма
1. Противоположные стороны параллелограмма равны.
2. Противоположные углы параллелограмма равны.
3. Сумма смежных углов параллелограмма равна \(180^{\circ}\).
4. Диагонали параллелограмма делятся точкой пересечения пополам.
\(ABCD\) – параллелограмм \(\Rightarrow\) \( AB=CD, \, BC=AD; \)
\(ABCD\) – параллелограмм \(\Rightarrow\) \(\angle{A}=\angle{C}, \, \angle{B}=\angle{D}; \)
\(ABCD\) – параллелограмм \(\Rightarrow\) \(\angle{A}+\angle{B}=180^{\circ}, \, \angle{A}+\angle{D}=180^{\circ}, \,
\angle{C}+\angle{B}=180^{\circ}, \, \angle{C}+\angle{D}=180^{\circ};\)
\(ABCD\) – параллелограмм, \(AC \cap BD =O\) \(\Rightarrow\) \(AO=CO, \, BO=DO \)
Признаки параллелограмма
1. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
2. Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник – параллелограмм.
3. Если в четырёхугольнике две противоположные стороны параллельны и равны, то этот четырёхугольник – параллелограмм.
4. Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
\( AB=CD, \, BC=AD \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\(\angle{A}=\angle{C}, \, \angle{B}=\angle{D} \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\( AB=CD, \, AB||CD \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\( AO=CO, \, BO=DO \) \(\Rightarrow\) \(ABCD\) – параллелограмм
Виды параллелограммов
Ромб, прямоугольник и квадрат являются параллелограммами. Остальные параллелограммы называют параллелограммами общего вида
Площадь параллелограмма
1. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
\( S=ah \) |
2. Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними.
\( S=ab\sin{\gamma} \) |
3. Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
\( S=\frac{1}{2}d_1d_2\sin{\varphi} \) |
tmath.ru
Какие стороны четырёхугольника называются соседними, а какие противолежащими?
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются. Четырехугольники Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными. Четырехугольники бывают выпуклые (как ABCD) и невыпуклые (A1B1C1D1). Виды четырёхугольников Параллелограмм Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства параллелограммаСвойства параллелограмма * противолежащие стороны равны; * противоположные углы равны; * диагонали точкой пересечения делятся пополам; * сумма углов, прилежащих к одной стороне, равна 180°; * сумма квадратов диагоналей равна сумме квадратов всех сторон: d12+d22=2(a2+b2). Признаки параллелограмма Четырехугольник является параллелограммом, если: 1. Две его противоположные стороны равны и параллельны. 2. Противоположные стороны попарно равны. 3. Противоположные углы попарно равны. 4. Диагонали точкой пересечения делятся пополам. Трапеция Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Трапеция Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой) , если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции * ее средняя линия параллельна основаниям и равна их полусумме; * если трапеция равнобокая, то ее диагонали равны и углы при основании равны; * если трапеция равнобокая, то около нее можно описать окружность; * если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность. Признаки трапеции Четырехугольник является трапецией, если его параллельные стороны не равны Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольникаСвойства прямоугольника * все свойства параллелограмма; * диагонали равны. Признаки прямоугольника Параллелограмм является прямоугольником, если: 1. Один из его углов прямой. 2. Его диагонали равны. Ромб Ромбом называется параллелограмм, у которого все стороны равны. Свойства ромбаСвойства ромба * все свойства параллелограмма; * диагонали перпендикулярны; * диагонали являются биссектрисами его углов. Признаки ромба 1. Параллелограмм является ромбом, если: 2. Две его смежные стороны равны. 3. Его диагонали перпендикулярны. 4. Одна из диагоналей является биссектрисой его угла. Квадрат Квадратом называется прямоугольник, у которого все стороны равны. Свойства квадратаСвойства квадрата * все углы квадрата прямые; * диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Признаки квадрата Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
противолежащие — которые не соединены лруг с другом, напротив лежат эти стороны, не имеют общего угла соседние — которые имеют общий угол, соединяются друг с другом, одна из них вертикальная, а другая горизонтальныя сторона
touch.otvet.mail.ru
Ответы@Mail.Ru: всё о четырёх угольниках
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются. Четырехугольники Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными. Четырехугольники бывают выпуклые (как ABCD) и невыпуклые (A1B1C1D1). Виды четырёхугольников Параллелограмм Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства параллелограммаСвойства параллелограмма * противолежащие стороны равны; * противоположные углы равны; * диагонали точкой пересечения делятся пополам; * сумма углов, прилежащих к одной стороне, равна 180°; * сумма квадратов диагоналей равна сумме квадратов всех сторон: d12+d22=2(a2+b2). Признаки параллелограмма Четырехугольник является параллелограммом, если: 1. Две его противоположные стороны равны и параллельны. 2. Противоположные стороны попарно равны. 3. Противоположные углы попарно равны. 4. Диагонали точкой пересечения делятся пополам. Трапеция Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Трапеция Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой) , если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции * ее средняя линия параллельна основаниям и равна их полусумме; * если трапеция равнобокая, то ее диагонали равны и углы при основании равны; * если трапеция равнобокая, то около нее можно описать окружность; * если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность. Признаки трапеции Четырехугольник является трапецией, если его параллельные стороны не равны Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольникаСвойства прямоугольника * все свойства параллелограмма; * диагонали равны. Признаки прямоугольника Параллелограмм является прямоугольником, если: 1. Один из его углов прямой. 2. Его диагонали равны. Ромб Ромбом называется параллелограмм, у которого все стороны равны. Свойства ромбаСвойства ромба * все свойства параллелограмма; * диагонали перпендикулярны; * диагонали являются биссектрисами его углов. Признаки ромба 1. Параллелограмм является ромбом, если: 2. Две его смежные стороны равны. 3. Его диагонали перпендикулярны. 4. Одна из диагоналей является биссектрисой его угла. Квадрат Квадратом называется прямоугольник, у которого все стороны равны. Свойства квадратаСвойства квадрата * все углы квадрата прямые; * диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Признаки квадрата Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются. Четырехугольники Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными. Четырехугольники бывают выпуклые и невыпуклые Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства параллелограмма * противолежащие стороны равны; * противоположные углы равны; * диагонали точкой пересечения делятся пополам; * сумма углов, прилежащих к одной стороне, равна 180°; * сумма квадратов диагоналей равна сумме квадратов всех сторон: Четырехугольник является параллелограммом, если: 1. Две его противоположные стороны равны и параллельны. 2. Противоположные стороны попарно равны. 3. Противоположные углы попарно равны. 4. Диагонали точкой пересечения делятся пополам. Трапеция Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Трапеция Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой) , если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции * ее средняя линия параллельна основаниям и равна их полусумме; * если трапеция равнобокая, то ее диагонали равны и углы при основании равны; * если трапеция равнобокая, то около нее можно описать окружность; * если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность. Признаки трапеции Четырехугольник является трапецией, если его параллельные стороны не равны Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольника * все свойства параллелограмма; * диагонали равны. Признаки прямоугольника Параллелограмм является прямоугольником, если: 1. Один из его углов прямой. 2. Его диагонали равны. Ромб Ромбом называется параллелограмм, у которого все стороны равны. Свойства ромба * все свойства параллелограмма; * диагонали перпендикулярны; * диагонали являются биссектрисами его углов. Признаки ромба 1. Параллелограмм является ромбом, если: 2. Две его смежные стороны равны. 3. Его диагонали перпендикулярны. 4. Одна из диагоналей является биссектрисой его угла. Квадрат Квадратом называется прямоугольник, у которого все стороны равны. Свойства квадрата * все углы квадрата прямые; * диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Признаки квадрата Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон. Сумма углов выпуклого четырёхугольника равна 360°: ∠A+∠B+∠C+∠D=360°. Не существует четырёхугольников, у которых все углы острые или все углы тупые. Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов: ∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D, ∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D. Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон: a < b+c+d, b < a+c+d, c < a+b+d, d < a+b+c. Площадь произвольного выпуклого четырёхугольника равна: Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины. Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет. Площадь произвольного выпуклого четырёхугольника: Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона. Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны; SABCD = 2SMNPQ . Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника. В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки. Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам: MG=GP, NG=GQ, RG=GS . Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей: MP2+ NQ2+ RS 2 = ¼(AB2+BC2+CD2+AD2+AC2+BD2). Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь: SABCD = MP·NQ·sinβ. Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости. Описанные четырёхугольники Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной. Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны: a+c = b+d. Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно: a+c ≥ 4r, b+d ≥ 4r. Площадь описанного четырёхугольника: S = pr, где r – радиус вписанной окружности, p – полупериметр четырёхугольника. Площадь описанного четырёхугольника: Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника. Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника: AK=AN, BK=BL, CL=CM, DM=DN. Если O – центр окружности, вписанной в четырёхугольник ABCD, то ∠AOB+∠COD=∠BOC+∠AOD=180°. Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения: Вписанные четырёхугольники Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника. Выпуклый четырёхугольник является описанным тогда и только тогда
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются. Четырехугольники Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными. Четырехугольники бывают выпуклые и невыпуклые Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства параллелограмма * противолежащие стороны равны; * противоположные углы равны; * диагонали точкой пересечения делятся пополам; * сумма углов, прилежащих к одной стороне, равна 180°; * сумма квадратов диагоналей равна сумме квадратов всех сторон: Четырехугольник является параллелограммом, если: 1. Две его противоположные стороны равны и параллельны. 2. Противоположные стороны попарно равны. 3. Противоположные углы попарно равны. 4. Диагонали точкой пересечения делятся пополам. Трапеция Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Трапеция Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой) , если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции * ее средняя линия параллельна основаниям и равна их полусумме; * если трапеция равнобокая, то ее диагонали равны и углы при основании равны; * если трапеция равнобокая, то около нее можно описать окружность; * если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность. Признаки трапеции Четырехугольник является трапецией, если его параллельные стороны не равны Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольника * все свойства параллелограмма; * диагонали равны. Признаки прямоугольника Параллелограмм является прямоугольником, если: 1. Один из его углов прямой. 2. Его диагонали равны. Ромб Ромбом называется параллелограмм, у которого все стороны равны. Свойства ромба * все свойства параллелограмма; * диагонали перпендикулярны; * диагонали являются биссектрисами его углов. Признаки ромба 1. Параллелограмм является ромбом, если: 2. Две его смежные стороны равны. 3. Его диагонали перпендикулярны. 4. Одна из диагоналей является биссектрисой его угла. Квадрат Квадратом называется прямоугольник, у которого все стороны равны. Свойства квадрата * все углы квадрата прямые; * диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Признаки квадрата Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются. Четырехугольники Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными. Четырехугольники бывают выпуклые и невыпуклые Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства параллелограмма * противолежащие стороны равны; * противоположные углы равны; * диагонали точкой пересечения делятся пополам; * сумма углов, прилежащих к одной стороне, равна 180°; * сумма квадратов диагоналей равна сумме квадратов всех сторон: Четырехугольник является параллелограммом, если: 1. Две его противоположные стороны равны и параллельны. 2. Противоположные стороны попарно равны. 3. Противоположные углы попарно равны. 4. Диагонали точкой пересечения делятся пополам. Трапеция Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Трапеция Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой) , если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции * ее средняя линия параллельна основаниям и равна их полусумме; * если трапеция равнобокая, то ее диагонали равны и углы при основании равны; * если трапеция равнобокая, то около нее можно описать окружность; * если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность. Признаки трапеции Четырехугольник является трапецией, если его параллельные стороны не равны Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольника * все свойства параллелограмма; * диагонали равны. Признаки прямоугольника Параллелограмм является прямоугольником, если: 1. Один из его углов прямой. 2. Его диагонали равны. Ромб Ромбом называется параллелограмм, у которого все стороны равны. Свойства ромба * все свойства параллелограмма; * диагонали перпендикулярны; * диагонали являются биссектрисами его углов. Признаки ромба 1. Параллелограмм является ромбом, если: 2. Две его смежные стороны равны. 3. Его диагонали перпендикулярны. 4. Одна из диагоналей является биссектрисой его угла. Квадрат Квадратом называется прямоугольник, у которого все стороны равны. Свойства квадрата * все углы квадрата прямые; * диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Признаки квадрата Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
а вот касательно противолежащих углов среди признаков параллелограмма вы не правы
touch.otvet.mail.ru
Две стороны равны и параллельны — Науколандия
Одним из признаков параллелограмма является то, что если в четырехугольнике две стороны равны и параллельны, то такой четырехугольник является параллелограммом. То есть, если у четырехугольника две стороны равны и параллельны, то две другие стороны также оказываются равными между собой и параллельными друг другу, т. к. этот факт является определением и свойством параллелограмма.
Таким образом, параллелограмм можно определить лишь по двум сторонам, которые равны и параллельны друг другу.
Данный признак параллелограмма можно сформулировать как теорему и доказать. В таком случае нам дан четырехугольник, у которого две стороны равны и параллельны друг другу. Требуется доказать, что такой четырехугольник является параллелограммом (т. е. две его другие стороны равны и параллельны друг другу).
Пусть данный четырехугольник ABCD, и в нем стороны AB || CD и AB = CD.
По условию нам дан четырехугольник. Ничего не сказано о том, выпуклый он или нет (хотя параллелограммами могут быть только выпуклые четырехугольники). Однако даже в невыпуклом четырехугольнике всегда есть одна диагональ, которая делит его на два треугольника. Если это будет диагональ AC, то получим два треугольника ABC и ADC. Если это диагональ BD, то будут ∆ABD и ∆BCD.
Допустим, мы получили треугольники ABC и ADC. У них одна сторона общая (диагональ AC), сторона AB одного треугольника равна стороне CD другого (по условию), угол BAC равен углу ACD (как накрест лежащие между секущей и параллельными прямыми). Значит ∆ABC = ∆ADC по двум сторонам и углу между ними.
Из равенства треугольников следует, что их остальные стороны и углы соответственно равны. Но стороне BC треугольника ABC соответствует сторона AD треугольника ADC, значит, BC = AD. Углу B соответствует угол D, значит, ∠B = ∠D. Эти углы могут быть равны друг другу, если BC || AD (так как AB || CD, то эти прямые можно совместить параллельным переносом, тогда ∠B станут накрест лежащими ∠D, а их равенство может быть только при BC || AD).
По определению параллелограмма им является четырехугольник, у которого противоположные стороны равны и параллельны друг другу.
Таким образом было доказано, что если у четырехугольника ABCD стороны AB и CD равны и параллельны и диагональ AC делит его на два треугольника, то у него другая пара сторон оказывается равна друг другу и параллельна.
Если же четырехугольник ABCD был разделен на два треугольника другой диагональю (BD), то рассматривались бы треугольники ABD и BCD. Их равенство доказывалось бы аналогично предыдущему. Оказалось бы, что BC = AD и ∠A = ∠C, откуда следовало, что BC || AD.
scienceland.info
