Ірраціональні числа — Вікіпедія
Математична константа пі (π) є ірраціональним числом.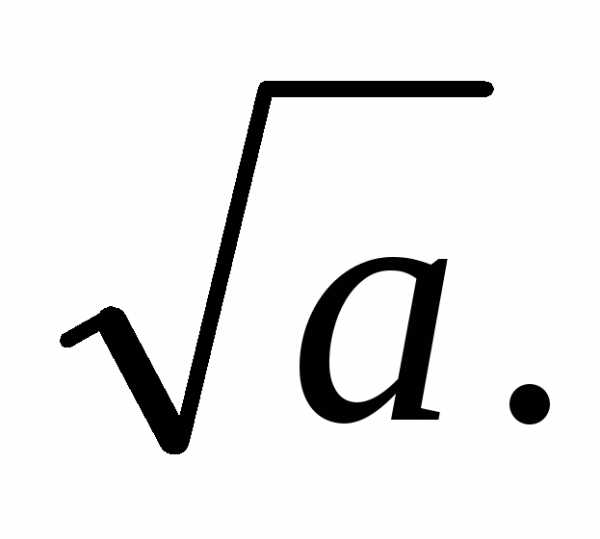 Число 2{\displaystyle \scriptstyle {\sqrt {2}}} є ірраціональним числом.
Число 2{\displaystyle \scriptstyle {\sqrt {2}}} є ірраціональним числом.Ірраціональні числа (позначення для множини — I{\displaystyle \mathbb {I} }) — це всі дійсні числа, що не є раціональними: I=R∖Q{\displaystyle \mathbb {I} =\mathbb {R} \setminus \mathbb {Q} }, — тобто не можуть бути записані як відношення цілих чисел zn{\displaystyle {\frac {z}{n}}} (z∈Z{\displaystyle z\in \mathbb {Z} }, n∈
uk.wikipedia.org
Ірраціональні числа
Які числа є ірраціональними? Ірраціональне число — це не раціональне дійсне число, тобто воно не може бути представлено як дріб (як відношення двох цілих чисел), де m — ціле число, n — натуральне число. Ірраціональне число можна представити як нескінченну неперіодичну десяткову дріб.
Ірраціональне число не може мати точного значення. Тільки у форматі 3,333333…. Наприклад, квадратний корінь з двох – є ірраціональним числом.
Яке число ірраціональне? Ірраціональним числом (на відміну від раціональних) називається нескінченна десяткова неперіодична дріб.
Безліч ірраціональних чисел найчастіше позначають великою латинською літерою в напівжирному накресленні без заливки. Т. о.:
Тобто множина ірраціональних чисел це різниця множин речових і раціональних чисел.
Властивості ірраціональних чисел.
Сума 2-х невід’ємних ірраціональних чисел може бути раціональним числом.
Ірраціональні числа визначають дедекиндовы перерізу в множині раціональних чисел, в нижньому класі у яких немає самого великого числа, а у верхньому немає меншого.
Усяке дійсне трансцендентне число – це ірраціональне число.
Всі ірраціональні числа є або алгебраїчними, або трансцендентними.
Безліч ірраціональних чисел скрізь щільно на числовій прямій: між кожною парою чисел є ірраціональне число.
Порядок на множині ірраціональних чисел изоморфен порядку на множині дійсних трансцендентних чисел.
Безліч ірраціональних чисел нескінченно, є безліччю 2-ї категорії.
Результатом кожної арифметичної операції з раціональними числами (крім, ділення на 0) є раціональні числа. Результатом арифметичних операцій над ірраціональними числами може стати як раціональне, так і ірраціональне число.
Сума раціонального та ірраціонального чисел завжди буде ірраціональним числом.
Сума ірраціональних чисел може бути раціональним числом. Наприклад, нехай x ірраціональне, тоді y=x*(-1) теж ірраціональне; x+y=0, а число 0 раціональне (якщо, наприклад, скласти корінь будь-якого ступеня з 7 і мінус корінь такою ж мірою з семи, то отримаємо раціональне число 0).
Ірраціональні числа, приклади.
γ — ζ(3) — ρ— √2 — √3 — √5 — φ — δs — α — e — π — δ
Числа. Ірраціональні числа. для будь-якого натурального n, що не є точним квадратом;
ex для будь-якого раціонального x ≠ 0;
ln x для будь-якого позитивного раціонального x ≠ 1;
Числа. Ірраціональні числа. (число пі), а також Числа. Ірраціональні числа.n для будь-якого цілого n ≠ 0.
« Ділення раціональних чисел Модуль числа »moyaosvita.com.ua
Ірраціональні числа — Howling Pixel
Ірраціональні числа (позначення для множини — I{\displaystyle \mathbb {I} }) — це всі дійсні числа, що не є раціональними: I=R∖Q{\displaystyle \mathbb {I} =\mathbb {R} \setminus \mathbb {Q} }, — тобто не можуть бути записані як відношення цілих чисел zn{\displaystyle {\frac {z}{n}}} (z∈Z{\displaystyle z\in \mathbb {Z} }, n∈N{\displaystyle n\in \mathbb {N} }), а лише нескінченними неперіодичними десятковими дробами.
Уперше І. ч. постали в геометрії під час вивчення довжин відрізків піфагорцями, які, як стверджує легенда[джерело?], виявили неспівмірність з одиничною деяких геометричних величин. Оскільки це суперечило їхній філософії (цілком побудованій на натуральних числах), відкриття якнайсуворіше були приховували, навіть покаравши на смерть одного зі своїх братів — Гіппаса Метапонтського, який (за різними джерелами) чи-то першим знайшов, чи-то розголосив цей факт.
Відмінності записування дійсних чисел
Десятковий дріб будь-якого раціонального числа має періодично повторювану частину (зокрема це можуть бути нулі, як у скінченних дробів і цілих чисел), н-д:
- 13=.3¯{\displaystyle {\frac {1}{3}}={}.{\overline {3}}},
- 227=3.142857¯{\displaystyle {\frac {22}{7}}=3.{\overline {142857}}}, що означає «три цілих і сто сорок дві тисячі вісімсот п’ятдесят сім у періоді» (довжина періоду — шість), тобто 142857{\displaystyle 142857} повторюється нескінчену кількість разів;
- 265132=2.0075¯{\displaystyle {\frac {265}{132}}=2.00{\overline {75}}}, що означає «дві цілих, нуль сотих і сімдесят п’ять у періоді» (довжина періоду — два), тобто 75{\displaystyle 75} повторюється нескінчену кількість разів;
- 52=2.5≡2.50¯{\displaystyle {\frac {5}{2}}=2.5\equiv 2.5{\overline {0}}}, скінченний дріб «дві цілих, п’ять десятих»,[2] тобто 0{\displaystyle 0} повторюється нескінчену кількість разів;
- 31=3.≡2.9¯{\displaystyle {\frac {3}{1}}=3.{}\equiv 2.{\overline {9}}}, ціле число «три еквівалентне двом цілим і дев’ять у періоді», [3] тобто 9{\displaystyle 9} повторюється нескінчену кількість разів.
Періодичність дробу можна вважати критерієм приналежності числа до множини раціональних чисел.
Розкладання І. ч. у десятковий дріб не позначається такою періодичністю. Наприклад, відомо, що число пі — ірраціональне та навіть трансцендентне, тому, хоча в його десятковому записі окремі цифри та їх комбінації повторюються, не існує групи цифр, яка б нескінченно повторювалася, утворюючи період.
Інший спосіб записування додатних дійсних чисел: за допомогою ланцюгових дробів. Відмінність полягає в тому, що ланцюгові дроби раціональних чисел скінченні, а І. ч. — нескінченні, хоча для квадратичних ірраціональностей ланцюговий дріб періодичний.
Приклади
Квадратні корені
Квадратний корінь з двох — це перше число, ірраціональність якого було доведено. Іншим відомим ірраціональним числом є золотий перетин. Квадратні корені усіх натуральних чисел, які не є квадратними числами, є ірраціональними.
Приклади
- 355113=3+17+116,{\displaystyle {\frac {355}{113}}=3+{\cfrac {1}{7+{\cfrac {1}{16}}}},} — скінченний;
- 2=1+12+12+12+…=[1;2,2,2…]=[1;(2)]{\displaystyle {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ldots }}}}}}=[1;2,2,2\ldots ]=[1;(2)]} — з періодом довжини один;
- 3=1+11+12+11+12+…=[1;1,2,1,2…]=[1;(1,2)]{\displaystyle {\sqrt {3}}=1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+\ldots }}}}}}}}=[1;1,2,1,2\ldots ]=[1;(1,2)]} — з періодом довжини два;
- π=3+17+115+11+1292+…=[3;7,15,1,292,1,1,1,2,…]{\displaystyle \pi =3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+{\cfrac {1}{292+\ldots }}}}}}}}=[3;7,15,1,292,1,1,1,2,\ldots ]} (A001203 в енциклопедії цілих послідовностей) — неперіодичний.
Філософське значення
Про існування неспівмірних відрізків знали вже древні математики: їм була відома, наприклад, неспівмірність діагоналі та сторони квадрата, що рівносильно ірраціональності числа 2{\displaystyle {\sqrt {2}}} (перше знайдене І. ч.).
Піфагорове твердження, що всі речі є числа, відображало метафізичні уявлення стародавніх греків про Всесвіт як місце гармонії, яку власне можна описати відношеннями натуральних чисел. Так поєднання двох звуків, відношення частот яких є раціональним числом, дає приємне для вуха звучання.
З’ясування того, що 2≈1,4142135{\displaystyle {\sqrt {2}}\approx 1{,}4142135} не є раціональним числом, призвело до глибокої кризи давньогрецької математики, яка полягала в усвідомлені факту існування математичних величин, які не можливо відобразити числами, а лише через геометричні побудови. Як наслідок — давньогрецька математика відмовилася від алгебраїчного підходу, на користь геометричного.
Властивості
- Будь-яке дійсне число можна записати нескінченним десятковим дробом, проте тільки І. ч. записують неперіодичними десятковими дробами.
- Сума двох додатніх І. ч. може бути раціональним числом.
- Кожне І. ч. визначає такий переріз Дедекінда у множині раціональних чисел Q{\displaystyle \mathbb {Q} }, для якого в нижньому класі немає найбільшого, а у верхньому — найменшого числа.
- Кожне І. ч. є або алгебраїчним, або трансцендентним. Кожне дійсне трансцендентне — ірраціональним.
- Множина І. ч. скрізь щільна на числовій прямій, тобто між будь-якими двома дійсними числами є І. ч. (і навіть нескінченно багато).
- Порядок на множині І. ч. — ізоморфний порядку на множині дійсних трансцендентних чисел.
- Множина І. ч. є незліченною, другої категорії.
Топологічні властивості R∖Q{\displaystyle \mathbb {R} \setminus \mathbb {Q} }
Примітки
- ↑ Тут використано англійську систему записування дробів без нулів. У пострадянських країнах для розділення цілої частини від дробної використовують кому замість крапки, а для позначення повторюваної частини — дужки замість верхньої риски.
- ↑ Десяткові дроби є нескінченними за побудовою, тому зрозуміло, що після певного десяткового знака можуть стояти самі нулі (a0,a1…an000…{\displaystyle a_{0},a_{1}…a_{n}000…}), відкиданням яких отримують скінченні дроби.
- ↑ Можемо записати як нескінченний періодичний дріб, оскільки з означення маємо, що 2+910+9100+…=3{\displaystyle 2+{\frac {9}{10}}+{\frac {9}{100}}+…=3}.
Література
1.Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology (вид. Dover reprint of 1978). Berlin, New York: Springer-Verlag. ISBN 978-0-486-68735-3. MR 507446.
Історія математикиІсто́рія матема́тики — галузь знань, що займається дослідженням походження та розвитку математичних відкриттів та методів, а також математичних праць минулого.
Слово «математика» походить від грец. μάθημα (мàтема), що означає «пізнання» чи «вивчення»; математик, грец. μαθηματικός (математикóс), — «людина, охоплена жадобою пізнання». Математика первісно виникла як один із напрямків пошуку істини (у грецькій філософії) у сфері просторових відношень (землеміряння — геометрії) та обчислень (арифметики), для практичних потреб людини рахувати, обчислювати, вимірювати, досліджувати форми та рух фізичних тіл. Нині цей термін позначає цілком визначену область знань, пов’язану із дослідженням задач про кількість, просторові форми, процеси розвитку та формальні структури, в основі якого лежать точні означення та строгі дедуктивні методи.
Алгебра (від араб. الجبر аль-джебр — відновлення) — розділ математики, що вивчає математичні операції і відношення, та утворення, що базуються на них: многочлени, алгебраїчні рівняння, алгебраїчні структури. Вивчення властивостей композицій різного виду в XIX столітті привело до думки, що основне завдання алгебри — вивчення властивостей операцій незалежно від об’єктів, до яких вони застосовуються. З того часу алгебру стали розглядати як загальну науку про властивості та закони композиції операцій. В наші дні алгебра — одна з найважливіших частин математики, що має застосування як у суто теоретичних, так і в практичних галузях науки.
Бет (літера)Бет, івр. בֵּי»ת — друга літера гебрайської абетки. Пишеться ב. Має числове значення (гематрію) 2.
Дійсне числоДійсні числа — елементи числової системи, яка містить у собі раціональні числа і, в свою чергу, є підмножиною комплексних чисел. Математична абстракція, яка виникла з потреб вимірювання геометричних і фізичних величин навколишнього світу, а також виконання таких математичних операцій як добування кореня, обчислення логарифмів, розв’язування алгебраїчних рівнянь.
Наочно поняття дійсного числа можна уявити за допомогою числової прямої. Якщо на прямій обрати напрям, початкову точку та одиницю довжини для вимірювання відрізків, то кожному дійсному числу можна поставити у відповідність єдину точку на цій прямій, і навпаки, кожна точка представлятиме єдине дійсне число. Через цю відповідність, термін числова пряма зазвичай використовується як синонім множини дійсних чисел.
Множину дійсних чисел стандартно позначають R{\displaystyle \mathbb {R} } чи R (від англ. real, нім. reel).
З погляду сучасної математики, множина дійсних чисел утворює неперервне впорядковане поле. Це означає, що дійсні числа можна додавати, віднімати, множити та ділити (окрім ділення на нуль), і для них справджуються всі звичні властивості арифметичних дій (комутативність і асоціативність додавання та множення, дистрибутивність додавання та віднімання відносно множення тощо), їх можна порівнювати між собою (відомо котре з двох дійсних чисел більше, а котре менше чи вони рівні між собою), а також, що на числовій прямій немає «дірок» — між будь-якими дійсними числами знайдеться дійсне число.
Евклідова геометріяЕвклі́дова геоме́трія — геометрична теорія, заснована на системі аксіом, вперше викладеній у підручнику «Начала» Евкліда (давньогрецькою: Στοιχεῖα Stoicheia, III століття до н. е.). Метод Евкліда полягає в прийнятті невеликого набору інтуїтивно зрозумілих аксіом і виведення з них багатьох інших теорем. Хоча багато визначень Евкліда були висловлені іншими математиками, Евклід був першим, хто показав, як ці пропозиції могли б використовуватися у всеосяжну дедуктивну та логічну систему. «Начала» починаються з планіметрії, яка і до сьогодні вивчається у середній школі як аксіоматика і базується на доведеннях. Більша частина «Начал» вказує на доведення того, що зараз називають алгеброю та теорією чисел.
Більше двох тисяч років прикметник «евклідова» був непотрібним, оскільки жодна інша форма геометрії ще не існувала. Аксіоми Евкліда здавались настільки очевидними (за винятком аксіоми паралельності), що будь-яка теорема, що випливала з них, вважалася вірною в абсолютному, часто метафізичному сенсі. Сьогодні відомо багато інших несуперечливих неевклідових геометрій, перші з яких з’явилися на початку 19 ст. Зокрема, із загальної теорії відносності Альберта Ейнштейна слідує що фізичний простір неевклідовий, а евклідовий простір для нього існує лише там, де слабке гравітаційне поле.
Евклідова геометрія є прикладом аналітичної геометрії, оскільки вона логічно йде від аксіом до тверджень без використання координат(на відміну від аналітичної геометрії, яка їх використовує).
Закон виключеного третьогоЗакон виключеного третього (поширена лат. назва tertium non datur — «третього не дано») — закон класичної логіки, який полягає в тому, що з двох висловлювань — «А» чи «не А» — одне обов’язково є істинним, тобто два судження, одне з яких є запереченням іншого, не можуть бути одночасно хибними.
Закон виключеного третього є одним з основоположних принципів «класичної математики».
З інтуїцистської (і, зокрема, конструктивістської) точки зору, встановлення істинності висловлювання виду «А чи не А» означає або (а) встановлення істинностіA{\displaystyle A}, або (б) встановлення істинності його заперечення ¬A{\displaystyle \neg A}. Оскільки, взагалі кажучи, не існує загального методу, що дозволяє для будь-якого висловлювання за кінцеве число кроків встановити його істинність або істинність його заперечення, закон виключення третього не повинен застосовуватися в рамках інтуїционістського і конструктивного напрямків в математиці як аксіома.
Золотий перетинУ математиці та мистецтві дві величини утворюють золотий перетин, якщо співвідношення їх суми і більшої величини дорівнює співвідношенню більшої і меншої. Це відношення прийнято позначати грецькою буквою φ{\displaystyle \varphi \,}.
Золотий перетин вважається співвідношенням найвідповіднішим естетичному сприйняттю зображення. Застосовується в мистецтві й архітектурі, найчастіше як золотий прямокутник. Золотий прямокутник утворюється при поділі відрізку АВ в такій точці О, що площа прямокутника, одною стороною якого є весь відрізок, а іншою — менший з відрізків, дорівнює площі квадрата з більшим відрізком як стороною (|АВ| * |OB| = |AO|2).
- φ=AO+OBAO=AOOB{\displaystyle \varphi ={\frac {AO+OB}{AO}}={\frac {AO}{OB}}}
Це рівняння має єдиний додатний розв’язок
- φ=1+52≈1.61803398874989484…{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.61803398874989484\dots }
Відношення двох відрізків приблизно дорівнює 13:8.
Число φ{\displaystyle \varphi \,} деколи називають золотим числом.
Квадратний корінь з двохКвадратний корінь з числа 2 — дійсне число більше нуля, яке при множенні саме на себе дає число 2. Позначення: 2.{\displaystyle {\sqrt {2}}.} Приведемо значення кореня з 2 з 65 знаками після коми:
- 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…
Геометричний корінь з 2 можливо представити як довжину діагоналі квадрата зі стороною 1 (це слідує з теореми Піфагора). Можливо, це було перше відоме в історії математики ірраціональне число (тобто число, яке неможливо точно представити у вигляді дробу).
Гарним і часто використовуваним наближенням до 2{\displaystyle {\sqrt {2}}} є дріб 9970{\displaystyle {\tfrac {99}{70}}}. Незважаючи на те, що чисельник і знаменник дробу лише двозначні цілі, воно відрізняється від реального значення менше, ніж на 1/10000.
КозліченністьПідмножиною Y множини X називається козліченною, якщо її доповнення до X є не більш ніж зліченною множиною. Таким чином, Y містить всі елементи X крім не більше ніж зліченної кількості. Наприклад, раціональні числа є зліченною підмножиною дійсних чисел, тому ірраціональні числа є козліченною підмножиною дійсних. Якщо доповнення є скінченним, тоді Y називають коскінченною підмножиною.
Константи ФейгенбаумаКонстанти Фейгенбаума — дві математичні константи, названі на честь їх відкривача Мітчела Фейгенбаума. Вони виражають відношення в біфуркаційних діаграмах.
- δ={\displaystyle \delta =} 4.66920160910299067185320382… це відношення попереднього біфуркаційного інтервалу до наступного, або відношення діаметрів успішних кіл на осі дійсних чисел множини Мандельброта. Фейгенбаум спочатку відносив це число до періоду подвоєння біфуркацій в логістичному відображенні, але пізніше він показав, що ця константа також зберігається для одновимірних відображень з одиничним квадратичним максимумом. Як результат цього узагальнення, кожна хаотична система, яка має таку поведінку, буде біфуркувати з тією самою швидкістю (константою Фейгенбаума). Константа Фейгенбаума може бути використана для передбачання часу виникнення хаосу в системах. Ця константа була відкрита в 1975 році.
Друга константа Фейгенбаума ,
- α={\displaystyle \alpha =} 2.502907875095892822283902873218…,
це відношення між шириною гілки і шириною однієї з її підгілок (окрім тих, які найближчі до згину). Це число використовується для опису багатьох динамічних систем. Припускається, що обидві константи є трансцентними, хоча це ще не доведено.
Корінь дванадцятої степені з двійкиКорінь дванадцятої степені з двійки або 12√2 — алгебраїчне ірраціональне число. Воно є найбільш важливим для теорії музики, де воно задає співвідношення частоти півтонів в рівномірно-темперованого строю з дванадцяти тонів. Уперше це число було запропоноване для задання музичного строю в 1580 (вперше описано, переписано в 1610) Сімоном Стевіном.
Крістоф Рудольфф|Посада= Крістоф Рудольфф (нім. Christoph Rudolff, 1499—1545) — німецький математик, автор першого підручника з алгебри у якому запропонував знак радикала, який залишився в науці. Належав до школи «косистів» (німецьких алгебраїстів XVI століття).
Лінійно впорядкована множинаЛінійно впорядкована множина (ланцюг) — частково впорядкована множина (множина на якій задане ⩽{\displaystyle \leqslant } відношення нестрогого порядку), в якій для будь-яких двох елементів a{\displaystyle a} і b{\displaystyle b} виконується a⩽b{\displaystyle a\leqslant b} чи b⩽a.{\displaystyle b\leqslant a.}
Тобто, для ⩽{\displaystyle \leqslant } вимога рефлексивності посилена до вимоги повноти.
Частковий випадок лінійно впорядкованої множини — цілком впорядкована множина. Іншими словами: лінійний порядок = частковий порядок з умовою повноти.
Лінійний порядок використовується в
Наївна теорія множинНаївна теорія множин — одна з декількох теорій множин, в якій описуються фундаментальні складові математики.. Термін було популяризовано завдяки книзі Пола Халмоша «Наївна теорія множин» (1960). Неофіційний зміст цієї теорії підтримує обидва аспекти математичної теорії множин: як ті, що відомі з дискретної математики (наприклад, діаграми Венна та їх символічний розгляд у Булевій алгебрі), так і більш «повсякденні» поняття теорії множин, що використовуються більше у сучасній математиці.
Множини відіграють велику роль в математиці. По суті, у багатьох сучасних формальних операціях більшість математичних об’єктів (числа, відношення, функції і т. д.) визначені в термінах множин. Наївна теорія множин може розглядатися як трамплін для розуміння більш формальних процедур і також для багатьох інших цілей.
Неперервна функціяНепере́рвна фу́нкція — одне з основних понять математичного аналізу. Неперервні функції трапляються набагато частіше, ніж диференційовні, множина всіх неперервних функцій замкнена відносно арифметичних операцій (за винятком ділення) і композиції та утворює чи не найважливіший клас функцій в аналізі. Проте строге математичне означення неперервної функції, яке належить Коші, — порівняно нещодавнє, і потребує просунутого рівня математичної абстракції. Інтуїтивне ж означення таке: функція f(x){\displaystyle f(x)} дійсної змінної неперервна, якщо малим змінам Δx{\displaystyle \Delta x} аргумента x{\displaystyle x} відповідають малі зміни Δf{\displaystyle \Delta f} значення функції, що можна записати так: Δf→0{\displaystyle \Delta f\to 0} коли Δx→0.{\displaystyle \Delta x\to 0.} Це означає, що графік неперервної функції не має стрибків, тобто може бути накреслений «не відриваючи олівець від паперу». Всі елементарні функції — неперервні на своїй області визначення.
Тригонометричне числоВ математиці тригонометричне число (англ. trigonometric number) — ірраціональне число, отримане як синус або косинус раціонального числа обертів або, що те ж саме, синус або косинус кута, величина якого в радіанах є раціональним кратним числа пі , або синус або косинус раціонального числа градусів.
Функція ДіріхлеФункція Діріхле — функція визначена на множині дійсних чисел, що набуває значення 1 якщо аргумент є раціональним числом і значення 0 якщо аргумент є числом ірраціональним. Формально визначення можна записати так:
D(x)={1,x∈Q0,x∈R∖Q{\displaystyle D(x)={\begin{cases}1,&x\in \mathbb {Q} \\0,&x\in \mathbb {R} \setminus \mathbb {Q} \end{cases}}}
де Q множина раціональних чисел, а R — множина дійсних чисел.
Цілі числаЦі́лі чи́сла — в математиці елементи множини Z={…−3,−2,−1,0,1,2,3…}{\displaystyle \mathbb {Z} =\lbrace \ldots -3,\,-2,\,-1,\,0,\,1,\,2,\,3\,\ldots \rbrace }, яка утворюється замиканням натуральних чисел відносно віднімання. Таким чином, цілі числа замкнуті відносно додавання, віднімання та множення.
Необхідність розгляду цілих чисел викликана неможливістю в загальному випадку відняти від одного натурального числа інше — можна віднімати тільки менше число від більшого. Введення нуля і від’ємних чисел робить віднімання такою ж повноцінною операцією, як додавання.
Множина цілих чисел складається з
Для позначення множини цілих чисел використовується символ ℤ, який може в різних авторів використовуватися для позначення групи множин: ℤ+, ℤ+ або ℤ> для позначення додатних цілих чисел, ℤ≥ для не від’ємних цілих чисел, ℤ≠ для всіх цілих чисел крім нуля. Деякі автори використовують позначення ℤ* для всіх цілих чисел крім нуля, інші для позначення не від’ємних цілих чисел, або для {–1, 1}.
Дійсне число є цілим, якщо його десяткове подання не містить дробової частини (але може містити знак). Приклади дійсних чисел:
- Числа 142857; 0; -273 є цілими.
- Числа 5½; 9,75 не є цілими.
Число́ є одним з найголовніших об’єктів математики, який використовується для підрахунку, вимірювання та для маркування. Символи, які використовуються для позначення чисел називаються цифрами. Окрім того, що цифри використовуються при лічбі та вимірюванні, вони використовуються також для маркування (наприклад, як номер телефону), упорядкування (серійний номер і для кодування (ISBN). Взагалі, термін число може вказувати на символ, слово або математичну абстракцію.
В математиці, поняття числа розширювалось з плином часу. Було додано такі поняття як нуль, від’ємні числа, раціональні числа ( 1 2 {\displaystyle {\frac {1}{2}}} , −23{\displaystyle -{\frac {2}{3}}}), дійсні числа ( 2 {\displaystyle {\sqrt {2}}} and π {\displaystyle \pi } ), комплексні числа, які розширюють дійсні числа введенням поняття про − 1 {\displaystyle {\sqrt {-1}}} . Над числами виконуються арифметичні операції, такі як додавання, віднімання, множення, ділення та піднесення до степеня. Їх використання називається арифметикою. Деякі властивості натуральних чисел досліджуються у теорії чисел, — великому розділі математики.
Окрім практичного використання, числа мають також культурне значення. Наприклад, у західному суспільстві число 13 вважається нещасливим, а «мільйон» може означати «багато». В наші часи нумерологія вважається псевдонаукою, проте антична та середньовічна думка пронизана вірою в містичне значення чисел. Нумерологія сильно вплинула на давньогрецьку математику, та підштовхнула до дослідження багатьох проблем в теорії чисел, які актуальні й досі.
Протягом XIX століття математики почали розвивати багато різних абстракцій, які мають спільні властивості з числами або які можна розглядати як узагальнення поняття числа. Серед перших були гіперкомплексні числа, які узагальнювали комплексні числа. Тепер системи числення розглядаються як важливі приклади загальних категорій, таких як кільце та поле, і використання терміну «число» є питанням домовленості, без фундаментального значення.
У давнину у слов’янських мовах слово «число» означало «знак», «символ», «поняття», «ідея»[джерело?]. Під словом «числити» розуміли в ті часи «значити», «думати», а також «записувати щось за допомогою знаків», «робити певні дії зі знаками».
This page is based on a Wikipedia article written by authors
(here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
howlingpixel.com
Ірраціональні числа
ірраціональні числа фибоначчи, ірраціональні числа наІрраціональні числа — числа, що не є раціональними, тобто не можуть бути виражені відношенням цілих чисел. Таким чином, ірраціональні числа утворюють множину I = R ∖ Q {\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} } , де R {\displaystyle \mathbb {R} } — множина дійсних чисел, а Q {\displaystyle \mathbb {Q} } — множина раціональних чисел.
Уперше виникли в геометрії при вивченні довжин. Геометрично ірраціональне число виражає собою довжину відрізка, неспільномірного з відрізком одиничної довжини. За легендою, піфагорці відкрили несумірність деяких геометричних величин, але оскільки це суперечило їх філософії, цілком побудованій на натуральних числах, вони утримували це відкриття у найсуворішій таємниці і навіть покарали на смерть одного з членів свого братства — Гіппаса Метапонтського, який (за різними джерелами) чи першим знайшов, чи розголосив цей факт.
Зміст
- 1 Відмінності в записі раціональних та ірраціональних чисел
- 2 Філософське значення
- 3 Властивості
- 3.1 Топологічні властивості
- 4 Література
Відмінності в записі раціональних та ірраціональних чисел
Раціональні числа при записі їх у десятковий дріб мають періодично повторювану частину. Наприклад,
1 3 = 0 , ( 3 ) {\displaystyle {1 \over 3}=0,(3)} , де ( 3 ) {\displaystyle (3)} означає, що трійка повторюється нескінчену кількість раз, довжина періоду — один. 22 7 = 3 , ( 142857 ) {\displaystyle {22 \over 7}=3,(142857)} , довжина періоду — шість.Періодичність дробу можна вважати за критерій приналежності числа до раціональних чисел. При розкладанні ірраціональних чисел у десятковий дріб не спостерігається такої періодичності. Наприклад, відомо, що число пі π = 3 , 1415926 … {\displaystyle \pi =3,1415926\ldots } — ірраціональне, і навіть трансцендентне. Тому, хоча в його десятковому записі окремі цифри та комбінації цифр повторюються, не існує групи цифр, яка б нескінченно повторювалася, утворюючи період.
Існує інший спосіб задання додатних дійсних чисел: за допомогою ланцюгових дробів. У цьому разі, різниця між раціональними та ірраціональними числами полягає в тому, що ланцюгові дроби раціональних чисел скінченні, а ірраціональних нескінченні, хоча для квадратичних ірраціональностей ланцюговий дріб періодичний.
Приклади.
355 113 = 3 + 1 7 + 1 16 , {\displaystyle {\frac {355}{113}}=3+{\cfrac {1}{7+{\cfrac {1}{16}}}},}скінченний;
2 = 1 + 1 2 + 1 2 + 1 2 + … = [ 1 ; 2 , 2 , 2 … ] = [ 1 ; ( 2 ) ] , {\displaystyle {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ldots }}}}}}==,}з періодом довжини один;
3 = 1 + 1 1 + 1 2 + 1 1 + 1 2 + … = [ 1 ; 1 , 2 , 1 , 2 … ] = [ 1 ; ( 1 , 2 ) ] {\displaystyle {\sqrt {3}}=1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+\ldots }}}}}}}}==} ,з періодом довжини два;
π = 3 + 1 7 + 1 15 + 1 1 + 1 292 + … = [ 3 ; 7 , 15 , 1 , 292 , 1 , 1 , 1 , 2 , … ] {\displaystyle \pi =3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+{\cfrac {1}{292+\ldots }}}}}}}}=}(A001203 в енциклопедії цілих послідовностей) — неперіодичний.
Філософське значення
Про існування неспівмірних відрізків знали вже древні математики: їм була відома, наприклад, неспівмірність діагоналі та сторони квадрата, що рівносильно ірраціональності числа 2 {\displaystyle {\sqrt {2}}} (перше знайдене ірраціональне число).
Піфагорове твердження, що всі речі є числа, відображало метафізичні уявлення стародавніх греків. Всесвіт є місцем гармонії, а гармонію, в свою чергу, можна описати відношенням натуральних чисел. Так поєднання двох звуків, відношення частот яких є раціональне число, дає приємне для вуха звучання. Відкриття того, що довжина діагоналі квадрата зі сторонами довжиною 1, тобто 2 ≈ 1 , 4142135 {\displaystyle {\sqrt {2}}\approx 1,4142135} , не є раціональним числом, призвело до глибокої кризи давньогрецької математики.
Криза полягала в усвідомлені факту існування математичних величин, які не можуть бути виражені числами. Але ті самі математичні величини можуть бути виражені через геометричні побудови. Як наслідок — давньогрецька математика відмовилась від алгебраїчного підходу, на користь геометричного.
Властивості
- Всяке дійсне число може бути записане нескінченим десятковим дробом, при цьому ірраціональні числа і тільки вони записуються неперіодичними десятковими дробами.
- Кожне ірраціональне число визначає такий переріз Дедекінда у множині раціональних чисел, для якого в нижньому класі немає найбільшого, а у верхньому класі немає найменшого раціонального числа.
- Кожне ірраціональне число є або алгебраїчним, або трансцендентним, а кожне трансцендентне число є ірраціональним.
- Множина ірраціональних чисел скрізь щільна на числовій прямій, тобто між будь-якими двома дійсними (і навіть раціональними) числами є ірраціональне число (і навіть нескінченно багато ірраціональних чисел).
- Множина ірраціональних чисел — незліченна множина другої категорії.
Топологічні властивості
Підпростір R ∖ Q {\displaystyle \mathbb {R} \setminus \mathbb {Q} } евклідового простору R {\displaystyle \mathbb {R} } має наступні властивості:
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } є Gδ-множиною, але не Fσ-множиною в R {\displaystyle \mathbb {R} } . Фактично, R ∖ Q = ⋂ α ∈ Q ( R ∖ { α } ) {\displaystyle R\setminus \mathbb {Q} =\bigcap _{\alpha \in Q}(R\setminus \{\alpha \})} .
- Евклідова метрика перетворює R ∖ Q {\displaystyle \mathbb {R} \setminus \mathbb {Q} } на метричний простір. Тому R ∖ Q {\displaystyle \mathbb {R} \setminus \mathbb {Q} } є цілком нормальним та паракомпактним.
- Повний метричний простір R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } є простором другої категорії.
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } сепарабельний, бо ірраціональні числа π+q, де q ∈ Q {\displaystyle q\in \mathbb {Q} } утворюють скрізь щільну множину в R ∖ Q {\displaystyle \mathbb {R} \setminus \mathbb {Q} } .
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } задовольняє другу аксіому зліченності.
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } не локально-компактний і не σ-локально компактний.
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } цілком відокремлений.
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } щільний у собі.
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } не розсіяний.
- R {\displaystyle \mathbb {R} } \ Q {\displaystyle \mathbb {Q} } нульвимірний.
Література
1.Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) . Counterexamples in Topology (вид. Dover reprint of 1978). Berlin, New York: Springer-Verlag. ISBN 978-0-486-68735-3. MR 507446.
Статті з математики, пов’язані з числами | |
| Число | Натуральні числа | Цілі числа | Раціональні числа | Ірраціональні числа | Конструктивні числа | Алгебраїчні числа | Трансцендентні числа | Рекурсивні числа | Дійсні числа | Комплексні числа | Подвійні числа | Дуальні числа | Бікомплексні числа | Гіперкомплексні числа | Кватерніони | Октоніони | Седеніони | Супердійсні числа | Гіпердійсні числа | Сюрреальні числа | Номінальні числа | Ординальні числа | Кардинальні числа | P-адичні числа | Послідовності натуральних чисел | Математичні константи | Великі числа | Нескінченність |
ірраціональні числа на, ірраціональні числа сериал, ірраціональні числа фибоначи, ірраціональні числа фибоначчи
Ірраціональні числа Інформацію Про
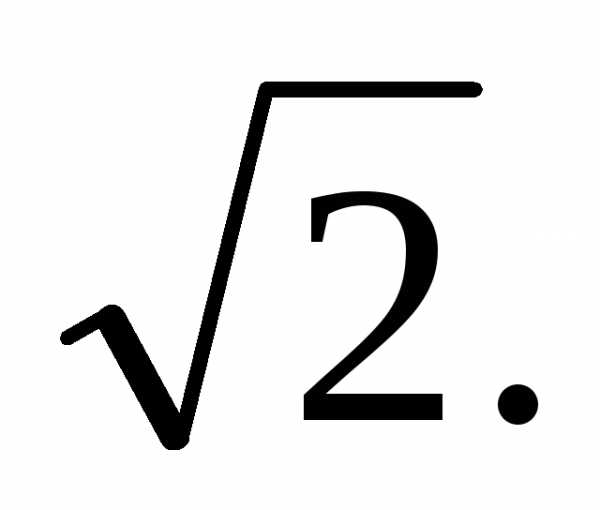
Ірраціональні числа Коментарі
Ірраціональні числа
Ірраціональні числа
Ірраціональні числа Ви переглядаєте суб єкт.
Ірраціональні числа що, Ірраціональні числа хто, Ірраціональні числа опис
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
Раціональні числа
Які числа раціональні? Раціональні числа (на відміну від ірраціональних)– це числа з позитивним чи негативним знаком (цілі і дробові) і нуль. Більш точне поняття раціональних чисел, звучить так:
Раціональне число — число, яке видається звичайної дробу m/n, де чисельник m — цілі числа, а знаменник n — натуральні числа, наприклад 2/3.
Нескінченні неперіодичні дроби НЕ входять в безліч раціональних чисел.
Тому число «Пі» (π = 3,14…), підстава натурального логарифма, e (e = 2,718..) або √2 НЕ є раціональними числами.
Раціональні числа, приклади:
3/4; 9/12; 1/2;
Безліч раціональних чисел.
Крім того, одну дріб можна записати різними способами і видами, але значення її не загубиться. Наприклад, 3/4 і 9/12, будь дріб, яку можна отримати з іншої дробу (і навпаки) множачи їх або ділячи чисельник і знаменник на однакову натуральне число, є одним і тим же раціональним числом). Так як діленням чисельника і знаменника дробу на НОД, можемо отримати єдине подання раціонального числа, яке не можна скоротити, то можемо говорити про їх безлічі як про безліч несократимых дробів з взаємно простими цілим чисельником і натуральним знаменником:
де gcd(m,n) — НСД чисел m і n.
Безліч раціональних чисел – це природне узагальнення безлічі цілих чисел. Якщо раціонального числа a=m/n знаменник n=1, то a=m буде цілим числом.
Кожне раціональне число легко виразити як дріб, в якому чисельник є цілим числом, а знаменник – натуральним числом.
a/b, де a ∈ Z (a належить цілим числам), b∈N (b належить натуральним числам).
Використання раціональних чисел в реальному житті.
У реальному житті безліч раціональних чисел використовується для рахунку частин деяких цілих подільних об’єктів, наприклад, тортів або інших продуктів, які розрізаються на частини перед вживанням, або для грубої оцінки просторових відносин протяжних об’єктів.
Властивості раціональних чисел.
Основні властивості раціональних чисел.
1. Упорядкованість. Для будь-яких раціональних чисел a і b є правило, яке дозволяє однозначно ідентифікувати між ними 1-але й тільки одне з 3-х відносин: «<», «>» або «=». Це правило – правило впорядкування і формулюють його ось так:
2 позитивні числа a=ma/na і b=mb/nb пов’язані тим же відношенням, що і 2 цілих числа ma⋅nb і mb⋅na;
2 від’ємних числа a і b зв’язані відношенням, що і 2 позитивні числа |b| |a|;
коли a позитивно, а b — негативно, то a>b.
∀a,b∈Q (a∨a>b∨a=b)
2. Операція додавання. Для всіх раціональних чисел a і b є правило підсумовування, яке ставить їм у відповідність певне раціональне число c. При цьому саме число c – це сума чисел a і b і її позначають як (a+b), а процес знаходження цього числа називають підсумовування.
Правило підсумовування виглядає так:
ma/na+mb/nb=(ma⋅nb+mb⋅na)/(na⋅nb).
∀a,b∈Q ∃!(a+b)∈Q
3. Операція множення. Для будь-яких раціональних чисел a і b є правило множення, воно ставить їм у відповідність певне раціональне число c. Число c називають добутком чисел a і b і позначають (a⋅b), а процес знаходження цього числа називають множення.
Правило множення виглядає так: mana⋅mbnb=ma⋅mbna⋅nb.
∀a,b∈Q ∃(a⋅b)∈Q
4. Транзитивність відносини порядку. Для будь-яких трьох раціональних чисел a, b і c, якщо a менше b, а b менше c, то a менше c, а якщо a дорівнює b і b дорівнює c, то a одно c.
∀a,b,c∈Q (a∧b⇒a∧(a = b∧b = c ⇒ a = c)
5. Комутативність додавання. Від зміни місць раціональних доданків сума не змінюється.
∀a,b∈Q a+b=b+a
6. Асоціативність додавання. Порядок складання 3-х раціональних чисел не впливає на результат.
∀a,b,c∈Q (a+b)+c=a+(b+c)
7. Наявність нуля. Є раціональне число 0, воно зберігає всяке інше раціональне число при складанні.
∃0∈Q ∀a∈Q a+0=a
8. Наявність протилежних чисел. У будь-якого раціонального числа є протилежне раціональне число, при їх складання виходить 0.
∀a∈Q ∃(−a)∈Q a+(−a)=0
9. Комутативність множення. Від зміни місць раціональних множників добуток не змінюється.
∀a,b∈Q a⋅b=b⋅a
10. Асоціативність множення. Порядок перемноження 3-х раціональних чисел не має впливу на підсумок.
∀a,b,c∈Q (a⋅b)⋅c=a⋅(b⋅c)
11. Наявність одиниці. Є раціональне число 1, воно зберігає всяке інше раціональне число в процесі множення.
∃1∈Q ∀a∈Q a⋅1=a
12. Наявність зворотних чисел. Кожне раціональне число, відмінне від нуля має зворотне раціональне число, помноживши на яке отримаємо 1.
∀a∈Q ∃a−1∈Q a⋅a−1=1
13. Дистрибутивность множення відносно додавання. Операція множення пов’язана зі складанням за допомогою розподільного закону:
∀a,b,c∈Q (a+b)⋅c=a⋅c+b⋅c
14. Зв’язок стосунки порядку з операцією додавання. До лівої і правої частин раціонального нерівності додають одне і те ж раціональне число.
∀a,b,c∈Q a⇒a+c
15. Зв’язок стосунки порядку з операцією множення. Ліву і праву частини раціонального нерівності можна помножити на однакову невід’ємне раціональне число.
∀a,b,c∈Q c>0∧a⇒a⋅c⋅c
16. Аксіома Архімеда. Яким би не було раціональне число a, легко взяти стільки одиниць, що їх сума буде більше a.
« Різниця чисел Системи найменування чисел »moyaosvita.com.ua
1.11. Поняття про ірраціональні числа. Дійсні числа
Арифметичним
квадратним коренем з
невід’ємного числа а називають невід’ємне число, квадрат
якого дорівнює а.
Арифметичний квадратний корінь із числа а позначають 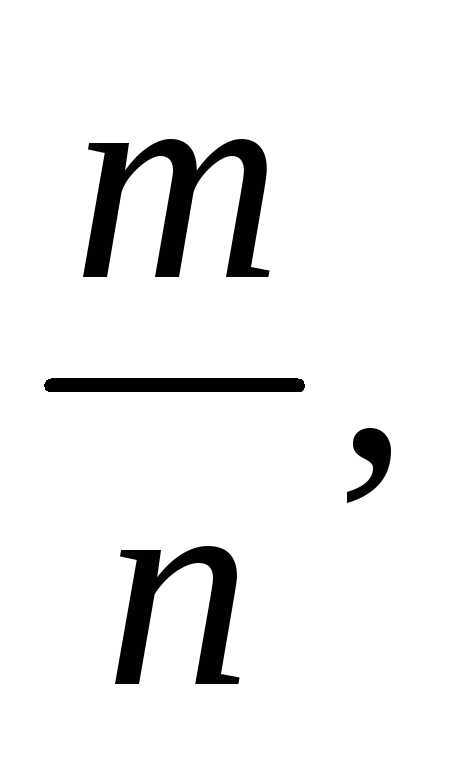
Теорема. Серед
раціональних чисел немає такого, яке
дорівнювало б значенню 
Припустимо
протилежне. Нехай існує таке раціональне
число, квадрат якого дорівнює 2. Це число
можна подати у вигляді нескорочуваного
дробу 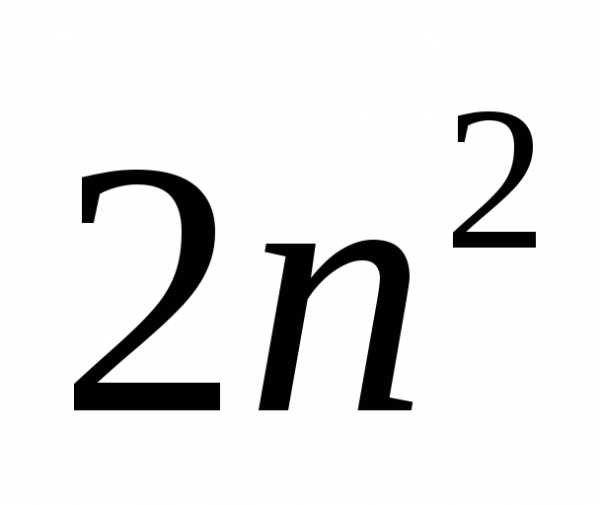 де
де 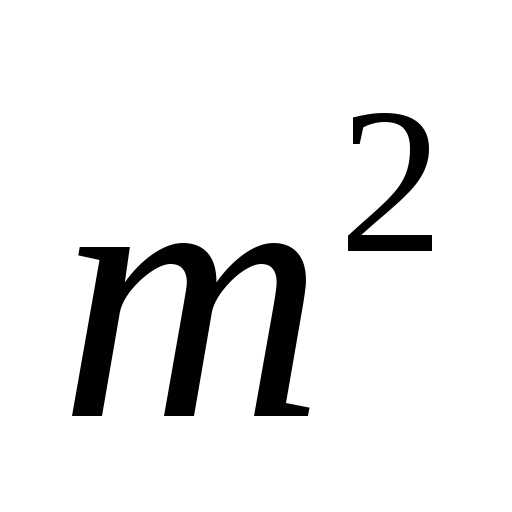 — натуральні числа. Тоді Оскільки число
— натуральні числа. Тоді Оскільки число 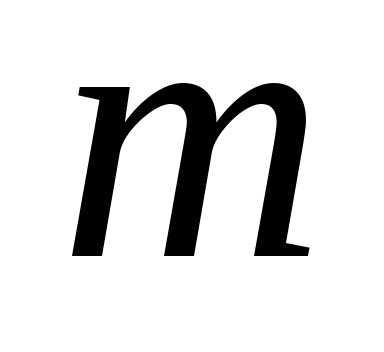 — парне, то й число
— парне, то й число 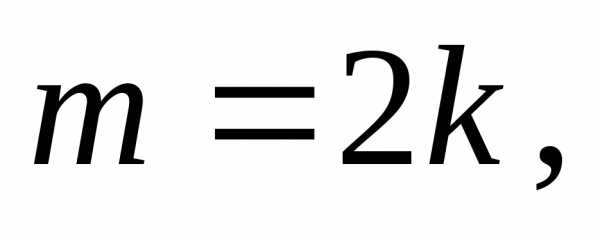 ,
що йому дорівнює також парне, а тому
число
,
що йому дорівнює також парне, а тому
число  — також парне (адже квадрат непарного
числа є непарне число), тобто
— також парне (адже квадрат непарного
числа є непарне число), тобто 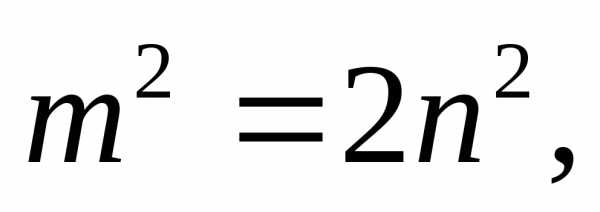 де
де 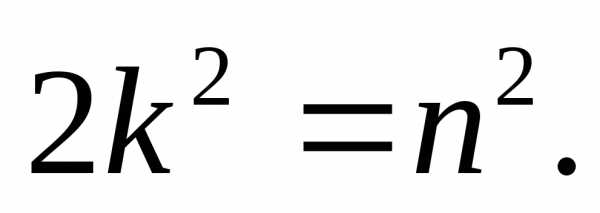 — натуральне число. Підставивши цей
вираз у рівність
— натуральне число. Підставивши цей
вираз у рівність  дістанемо
дістанемо 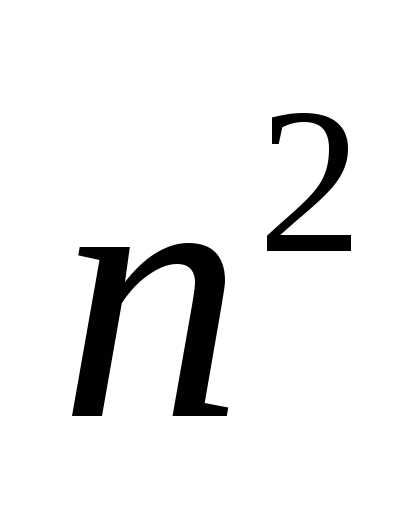 Оскільки
Оскільки 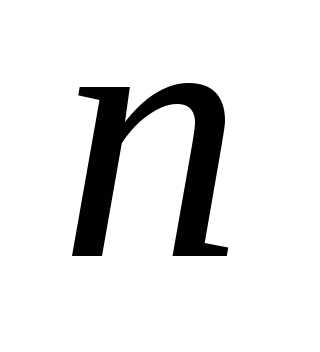 — парне число, то
— парне число, то 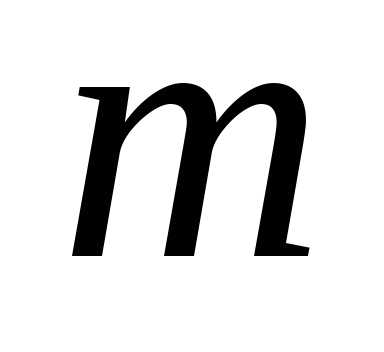 — також парне, тому і
— також парне, тому і 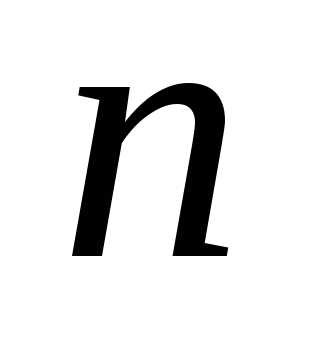 — парне число. Отже,
— парне число. Отже,  і
і  — парні числа, а це суперечить припущенню,
що дріб
— парні числа, а це суперечить припущенню,
що дріб 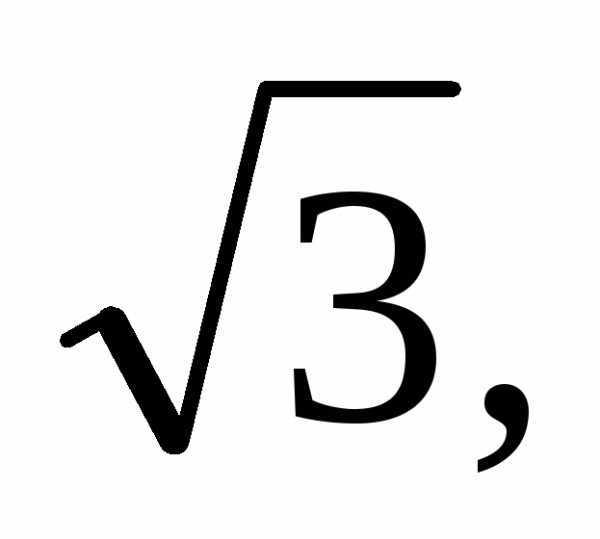 нескоротний. Звідси випливає, що не
існує раціонального числа, квадрат
якого дорівнює 2. Таким чином,
нескоротний. Звідси випливає, що не
існує раціонального числа, квадрат
якого дорівнює 2. Таким чином,  не є раціональним числом.
не є раціональним числом.
Це число
називають ірраціональним. Ірраціональними числами є 
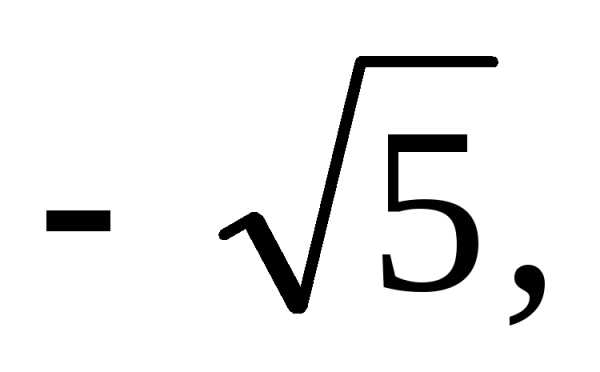


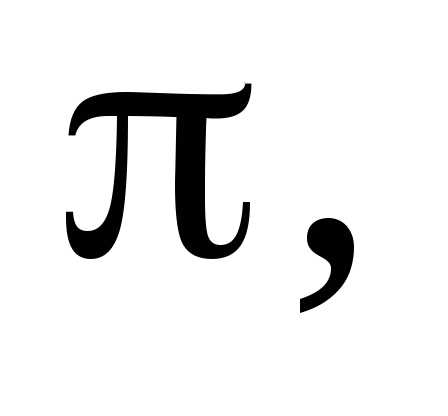
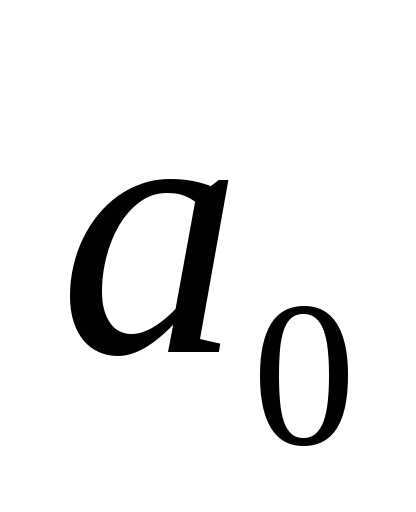 і т. ін.
і т. ін.
Зауважимо,
що до ірраціональних чисел належить
число 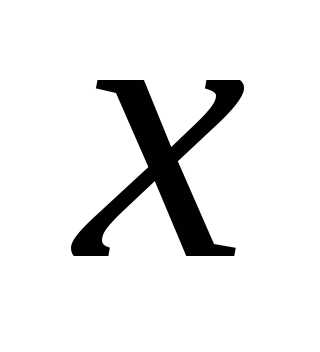 яке виражає відношення довжини кола до
його діаметра.
яке виражає відношення довжини кола до
його діаметра.
У теоремі 1.10 доведено, що кожне раціональне число є нескінченним періодичним десятковим дробом. Було зазначено також, що будь-який періодичний десятковий дріб є поданням деякого раціонального числа.
Крім
періодичних нескінченних десяткових
дробів, існують неперіодичні
дроби: такий, наприклад, дріб в якого після першої двійки одна одиниця,
після другої — дві одиниці і т. д. Кожний
неперіодичний нескінченний десятковий
дріб де  — ціла частина числа х; —
десяткові знаки, є поданням деякого
нового (не раціонального) числа, що
називається ірраціональним. Множину
всіх таких чисел називають множиною
ірраціональних чисел.
— ціла частина числа х; —
десяткові знаки, є поданням деякого
нового (не раціонального) числа, що
називається ірраціональним. Множину
всіх таких чисел називають множиною
ірраціональних чисел.
Множиною дійсних чисел називають множину всіх раціональних і всіх ірраціональних чисел. Таким чином, з’ясовується, що будь-яке дійсне число подається нескінченним десятковим дробом. Множина всіх дійсних чисел позначається R.
Дійсні
числа впорядковано за величиною, тобто
для будь-яких двох дійсних чисел  і
і  справджується лише одне і лише одне із
співвідношень:
справджується лише одне і лише одне із
співвідношень: 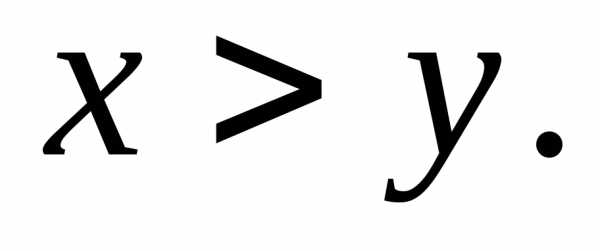
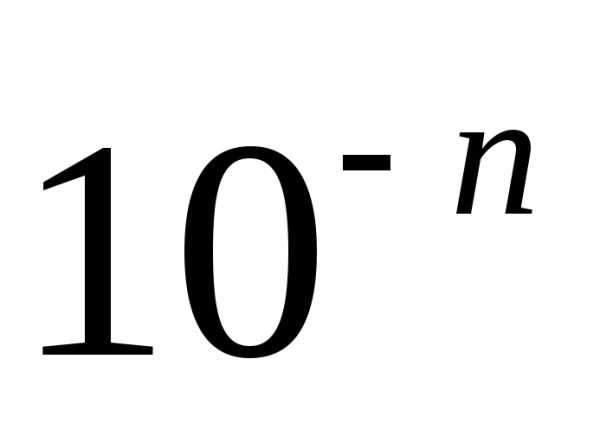 Сенс нерівності між дійсними числами
визначається правилом порівняння
нескінченних десяткових дробів.
Сенс нерівності між дійсними числами
визначається правилом порівняння
нескінченних десяткових дробів.
Для
дійсного числа наближення з точністю до  з недостачею
з недостачею  і з надлишком
і з надлишком 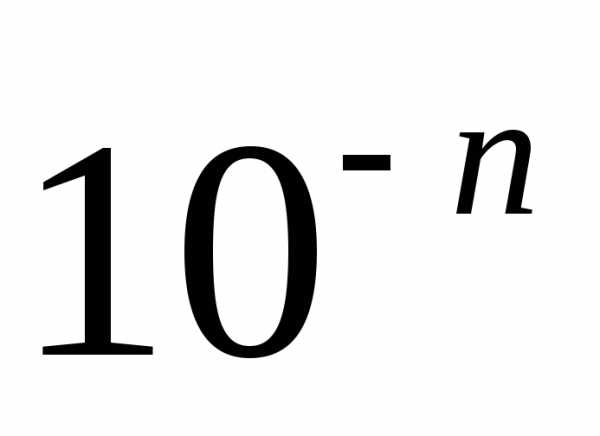 визначаються так:
визначаються так:
Очевидно, що
Додавання
до десяткового дробу числа 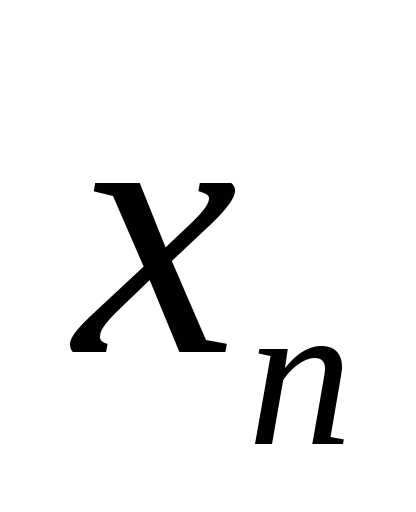 рівносильне збільшенню
останньої цифри дробу на одиницю.
Зауважимо, що кожне з десяткових наближень
рівносильне збільшенню
останньої цифри дробу на одиницю.
Зауважимо, що кожне з десяткових наближень  і
і  дійсного числа
дійсного числа 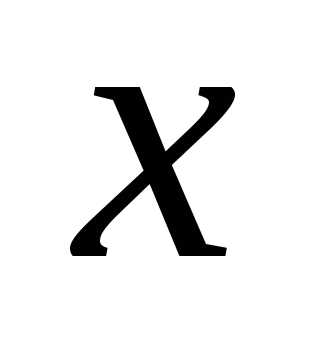 є раціональним числом.
є раціональним числом.
Приклад. Випишемо перші п’ять наближень (з недостачею та надлишком) для числа
Для дійсних чисел можна визначити арифметичні операції додавання і множення. Віднімання визначається як дія, обернена до додавання, а ділення — як дія, обернена до множення. Основні властивості арифметичних дій із цілими числами справеджуються і для дійсних чисел.
Визначимо
суму і добуток двох дійсних чисел  і
і 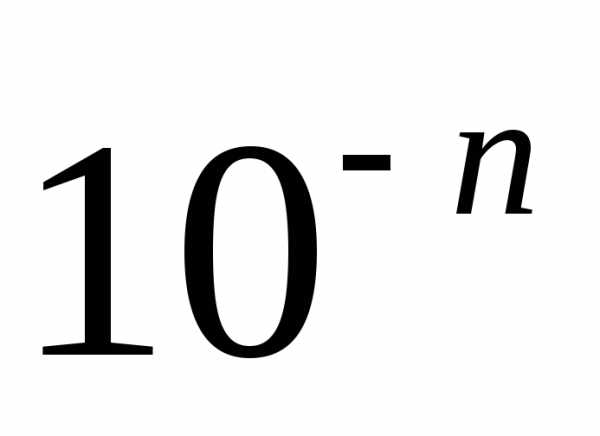 Для їхніх наближень з недостачею та
надлишком із точністю до
Для їхніх наближень з недостачею та
надлишком із точністю до 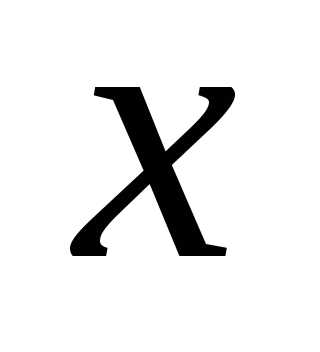 справджуються такі нерівності
справджуються такі нерівності
Сумою
дійсних чисел  і
і  називають таке дійсне число
називають таке дійсне число 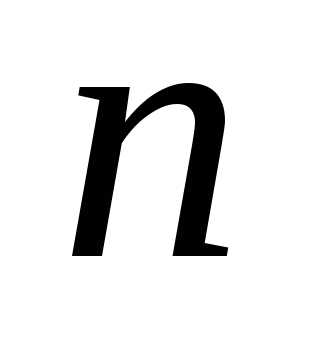 яке при будь-якому цілому невід’ємному
яке при будь-якому цілому невід’ємному 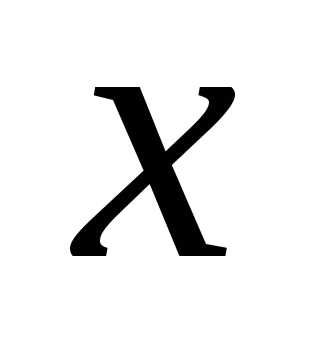 задовольняє нерівності Можна довести, що таке число існує і
єдине.
задовольняє нерівності Можна довести, що таке число існує і
єдине.
Добутком
невід’ємних дійсних чисел  і
і  називають таке дійсне число
називають таке дійсне число 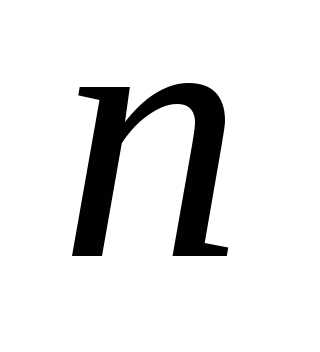 яке при будь-якому цілому невід’ємному
яке при будь-якому цілому невід’ємному  задовольняє нерівності Можна довести, що таке число існує і
єдине.
задовольняє нерівності Можна довести, що таке число існує і
єдине.
Дійсні числа можна зображати точками координатної осі.
Множину всіх дійсних чисел називають числовою віссю; вона зображається всією координатною прямою, її позначають (читається: «проміжок від мінус нескінченності до плюс нескінченності»).
Множина
всіх чисел, що задовольняють подвійну
нерівність називають числовим
проміжком (або проміжком)
і позначають  (читається: «проміжок від
(читається: «проміжок від  до
до 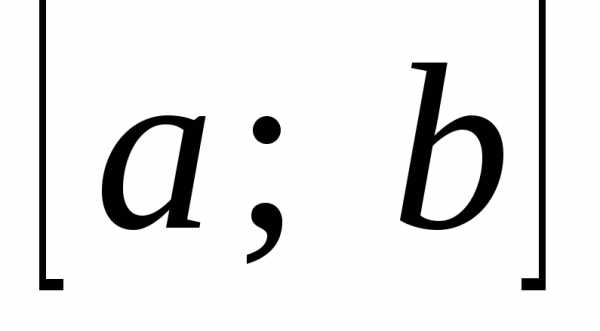 ».
».
Множину
всіх чисел, що задовольняють нерівності і позначають відповідно  (читається: «проміжок від
(читається: «проміжок від 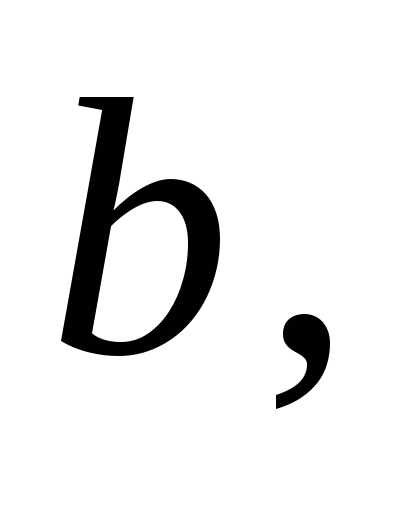 до
до  включаючи
включаючи 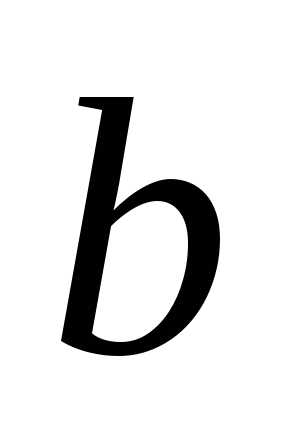 та
та  »),
[a; b)
і (a; b].
»),
[a; b)
і (a; b].
Проміжок  називають інтервалом,
проміжок
називають інтервалом,
проміжок  — відрізком або сегментом,
а проміжки [a; b)
і (a; b]
— напівінтервалами.
— відрізком або сегментом,
а проміжки [a; b)
і (a; b]
— напівінтервалами.
studfiles.net
Ірраціональне число
Ірраціональне число — це дійсне число, яке не є раціональним, тобто яке не може бути представленим у вигляді дробу , Де m — ціле число, n — натуральне число. Про існування ірраціональних чисел, точніше відрізків, непорівнянних із відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумірність діагоналі і сторони квадрата, що рівносильно ірраціональності числа .
Безліч ірраціональних чисел зазвичай позначається заголовною латинською буквою «i» в напівжирному накресленні без заливки — . Таким чином: , Тобто безліч ірраціональних чисел є різниця множин речових і раціональних чисел.
1. Історія
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манаві (бл. 750 р. до н. Е.. — Бл. 690 р. до н. Е..) З’ясував, що квадратні корені деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені.
Перший доказ існування ірраціональних чисел зазвичай приписується Гіппаса з Метапонті (бл. 500 рр.. до н. е..), піфагорійці, який знайшов це доказ, вивчаючи довжини сторін пентаграми. За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число разів входить в будь-який відрізок. Однак Гиппас обгрунтував, що не існує єдиної одиниці довжини, оскільки припущення про її існування призводить до протиріччя. Він показав, що якщо гіпотенуза рівнобедреного прямокутного трикутника містить ціле число одиничних відрізків, то це число повинне бути одночасно і парних, і непарною. Доказ виглядало наступним чином:
- Відношення довжини гіпотенузи до довжини катета рівнобедреного прямокутного трикутника може бути виражене як a: b, де a і b вибрані найменшими з можливих.
- За теоремою Піфагора: a = 2 b.
- Так як a парне, a повинно бути парним (так як квадрат непарного числа був би непарних).
- Оскільки a: b нескоротного, b зобов’язана бути непарним.
- Так як a парне, позначимо a = 2 y.
- Тоді a = 4 y = 2 b.
- b = 2 y, отже b парне, тоді і b парне.
- Однак було доведено, що b непарне. Протиріччя.
Грецькі математики назвали це відношення несумірних величин алогос (невимовним), проте згідно з легендами не віддав Гіппаса належної поваги. Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і його викинуло за борт іншими піфагорійцями «за створення елемента всесвіту, який заперечує доктрину, що всі сутності у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед пифагорейской математикою серйозну проблему, зруйнувавши лежало в основі всієї теорії припущення, що числа та геометричні об’єкти єдині й нероздільні.
Феодор Кіренський довів ірраціональність коренів натуральних чисел до 17 (крім, природно, точні квадрати — 1, 4, 9 і 16), але зупинився на цьому, так як имевшаяся в його інструментарії алгебра не дозволяла довести ірраціональність квадратного кореня з 17. З приводу того, яким могло бути це доказ, істориками математики було висловлено кілька різних припущень. Згідно найбільш правдоподібного припущенням Жана ИТАР (1961), воно було засноване на пифагорейской теорії парних і непарних чисел, у тому числі — на теоремі про те, що непарне квадратне число за вирахуванням одиниці ділиться на вісім трикутних чисел.
Пізніше Евдокс Кнідський (410 або 408 р. до н. е.. — 355 або 347 р. до н. е..) розвинув теорію пропорцій, яка брала до уваги як раціональні, так і ірраціональні відносини. Це послужило підставою для розуміння фундаментальної суті ірраціональних чисел. Величина стала вважатися не числом, але позначенням сутностей, таких як відрізки прямих, кути, площі, обсяги, проміжки часу — сутностей, які можуть змінюватися безперервно (в сучасному розумінні цього слова). Величини були протиставлені числах, які можуть змінюватися лише «стрибками» від одного числа до сусіднього, наприклад, з 4 на 5. Числа складаються з найменшою неподільною величини, в той час як величини можна зменшувати нескінченно.
Оскільки жодне кількісне значення не зіставлялося величині, Евдокс зміг охопити і сумірні, і несумірні величини при визначенні дробу як відносини двох величин, і пропорції як рівності двох дробів. Прибравши з рівнянь кількісні значення (числа), він уникнув пастки, що складається в необхідності назвати ірраціональну величину числом. Теорія Евдокса дозволила грецьким математикам здійснити неймовірний прогрес в геометрії, надавши їм необхідне логічне обгрунтування для роботи з непомірними величинами. «Книга 10 елементів» Евкліда присвячена класифікації ірраціональних величин.
1.1. Середні століття
Середні століття ознаменувалися прийняттям таких понять як нуль, негативні числа, цілі і дробові числа, спершу індійськими, потім китайськими математиками. Пізніше приєдналися арабські математики, які першими стали вважати негативні числа алгебраїчними об’єктами (поряд і на рівних правах з позитивними числами), що дозволило розвинути дисципліну, нині звану алгеброю.
Арабські математики з’єднали давньогрецькі поняття «числа» і «величини» в єдину, більш загальну ідею дійсних чисел. Вони критично ставилися до уявлень Евкліда про відносини, на противагу їй вони розвинули теорію відносин довільних величин і розширили поняття числа до відносин безперервних величин. У своїх коментарях на Книгу 10 елементів Евкліда, перський математик Аль Махане (ок 800 мм. Н. Е..) Досліджував і класифікував квадратичні ірраціональні числа (числа виду) і більш загальні кубічні ірраціональні числа. Він дав визначення раціональним та ірраціональним величинам, які він і називав ірраціональними числами. Він легко оперував цими об’єктами, але міркував як про відокремлені об’єктах, наприклад:
| Раціональної [величиною] є, наприклад, 10, 12, 3%, 6% і так далі, оскільки ці величини вимовлені і виражені кількісно. Що не раціонально, то ірраціонально, і неможливо вимовити або представити відповідну величину кількісно. Наприклад, квадратні корені чисел таких так 10, 15, 20 — не є квадратами. |
На противагу концепції Евкліда, що величини суть в першу чергу відрізки прямих, Аль Махане вважав цілі числа і дроби раціональними величинами, а квадратні і кубічні корені — ірраціональними. Він також ввів арифметичний підхід до безлічі ірраціональних чисел, оскільки саме він показав ірраціональність наступних величин:
| результат додавання ірраціональної величини і раціональної, результат віднімання раціональної величини з ірраціональної, результат віднімання ірраціональної величини з раціональною. |
Єгипетський математик Абу Каміл (бл. 850 р. н. Е.. — Бл. 930 р. н. Е..) Був першим, хто визнав прийнятним визнати ірраціональні числа рішенням квадратних рівнянь або коефіцієнтами в рівняннях — в основному, у вигляді квадратних або кубічних коренів, а також коренів четвертого ступеня. У X столітті іракський математик Аль Хашимі вивів загальні докази (а не наочні геометричні демонстрації) ірраціональності твори, приватного та результатів інших математичних перетворень над ірраціональними та раціональними числами. Ал Хазін (900 р. н. Е.. — 971 р. н. Е..) Подає таке визначення раціональної та ірраціональної величини:
| Нехай одинична величина міститься в даній величині один або кілька разів, тоді ця [дана] величина відповідає цілому числу … Кожна величина, яка становить половину, або третину, або чверть одиничної величини, або, порівняння з одиничною величиною становить три п’ятих від неї, це раціональна величина. І в цілому, будь-яка величина, яка відноситься до одиничної як одне число до іншого, є раціональною. Якщо ж величина не може бути представлена як кілька або частину (l / n), або кілька частин (m / n) одиничної довжини, вона ірраціональна, тобто невимовна інакше як за допомогою коренів. |
Багато з цих ідей були пізніше перейняті європейськими математиками після переведення на латину арабських текстів у XII столітті. Аль Хассар, арабський математик із Магрибу, що спеціалізувався на ісламських законах про спадщину, в XII столітті ввів сучасну символьну математичну нотацію для дробів, розділивши чисельник і знаменник горизонтальній рисою. Та ж нотація з’явилася потім у роботах Фібоначчі в XIII столітті. Протягом XIV-XVI ст. Мадхава з Сангамаграми і представники Керальской школи астрономії та математики досліджували нескінченні ряди, що сходяться до деяких ірраціональним числам, наприклад, до π, а також показали ірраціональність деяких тригонометричних функцій. Джестадева навів ці результати в книзі Йуктібхаза.
1.2. Наш час
У XVII столітті в математиці міцно зміцнилися комплексні числа, вклад у вивчення яких внесли Абрахам де Муавр (1667-1754) і Леонард Ейлер (1707-1783). Коли теорія комплексних чисел в XIX столітті стала замкнутою і чіткою, стало можливим класифікувати ірраціональні числа на алгебраїчні і трансцендентні (довівши при цьому існування трансцендентних чисел), тим самим переосмисливши роботи Евкліда за класифікацією ірраціональних чисел. По цій темі в 1872 були опубліковані роботи Вейерштрасса, Гейне, Кантора і Дедекинда. Хоча ще в 1869 році Мере почав розгляду, схожі з Гейне, саме 1872 прийнято вважати роком народження теорії. Вейерштрасс, Кантор і Гейне обгрунтовували свої теорії за допомогою нескінченних рядів, у той час як Дедекинда працював з (нині так званим) Дедекіндовим перетином безлічі дійсних чисел, розділяючи всі раціональні числа на дві множини з певними характеристичними властивостями.
Ланцюгові дроби, тісно пов’язані з ірраціональними числами (ланцюгова дріб, що представляє дане число, нескінченна тоді і тільки тоді, коли число є ірраціональним), були вперше досліджені Катальді в 1613 році, потім знову привернули до себе увагу в роботах Ейлера, а на початку XIX століття — в роботах Лагранжа. Дирихле також вніс значний вклад у розвиток теорії ланцюгових дробів.
У 1761 році Ламберт показав, що π не може бути раціонально, а також що e n ірраціонально при будь-якому ненулевом раціональному n. Хоча доказ Ламберта можна назвати незавершеним, прийнято вважати його досить суворим, особливо враховуючи час його написання. Лежандр в 1794 році, після введення функції Бесселя-Кліффорда, показав, що π ірраціонально, звідки ірраціональність π слід тривіально (раціональне число у квадраті дало б раціональне). Існування трансцендентних чисел було доведено Ліувіля в 1844-1851 роках. Пізніше Георг Кантор (1873) показав їх існування, використовуючи інший метод, і обгрунтував, що будь-який інтервал речового ряду містить нескінченно багато трансцендентних чисел. Шарль Ерміта довів в 1873 році, що e трансцендентно, а Фердинанд Ліндеман в 1882 році, грунтуючись на цьому результаті, показав трансцендентність π. Доказ Ліндеманна було потім спрощено Вейерштрасом в 1885 році, ще більше спрощено Давидом Гільбертом в 1893 році і, нарешті, доведено до майже елементарного Адольфом Гурвіцем і Паулем Горданом.
2. Властивості
- Усяке дійсне число може бути записано у вигляді нескінченної десяткового дробу, при цьому ірраціональні числа і тільки вони записуються неперіодичними нескінченними десятковими дробами.
- Ірраціональні числа визначають Дедекіндови перетину в множині раціональних чисел, у яких в нижньому класі немає найбільшого, а у верхньому немає найменшого числа.
- Кожне трансцендентне число є ірраціональним.
- Кожне ірраціональне число є або алгебраїчним, або трансцендентним.
- Безліч ірраціональних чисел скрізь щільно на числовій прямій: між будь-якими двома числами є ірраціональне число.
- Безліч ірраціональних чисел незліченно, є безліччю другої категорії. [1]
3. Теореми
3.1. Корінь з 2 — ірраціональне число
Припустимо гидке: раціональний, тобто представляється у вигляді нескоротного дробу , Де m і n — цілі числа. Зведено передбачуване рівність в квадрат:
- .
Звідси випливає, що m 2 парне, отже, четно і m . Нехай m = 2 r , Де r ціле. Тоді
Отже, n 2 парне, отже, четно і n . Ми отримали, що m і n парних, що суперечить нескоротного дробу . Значить, вихідне припущення було невірним, і — Ірраціональне число.
3.2. log 2 Березня — Ірраціональне число
Припустимо гидке: log 2 Березняраціональний, тобто представляється у вигляді дробу , Де m і n — цілі числа. Оскільки log 2 3> 0 , m і n можуть бути обрані позитивними. Тоді
Але 2 m парне, а 3 n непарній. Отримуємо протиріччя.
3.3. e — Ірраціональне число
Див розділ «Доказ ірраціональності» в статті «e».
4. Інші ірраціональні числа
Ірраціональними є:
- для будь-якого натурального n , Яка не є точним квадратом
- e x для будь-якого раціонального
- ln x для будь-якого позитивного раціонального
- π , А також π n для будь-якого натурального n
znaimo.com.ua
