Исследование на совместность матрицы – Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.

1.5. Общий случай линейной алгебраической системы уравнений. Условие совместности Ранг матрицы

Определитель k-го порядка, составленный из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы А, называется минором k-го порядка, порожденным данной матрицей.

Например, для матрицы А

минор второго порядка можно получить, выбрав 1 и 3 строки, а также 1-й и 4-й столбцы: .Очевидно, что минорами, порожденными этой матрицей, являются и другие определители 2-го порядка:

и т.д.

Данная матрица имеет минорами и определители 3-го порядка

Рангом матрицы А (обозначается ) называется наивысший порядок отличных от нуля миноров, порожденных этой матрицей.

В рассматриваемой матрице

А наивысший порядок ее миноров равен трем. Вычислим один из них.

Так как этот минор отличен 0, то .

Вычислять все миноры, порождаемые данной матрицей, затруднительно. Поэтому для определения ранга матрицы можно использовать метод приведения матрицы к ступенчатому виду с помощью элементарных преобразований.

Элементарными преобразованиями матрицы называются:

1) умножение какой-либо строки (столбца) на число ,

2) перестановка двух строк (столбцов),

3) прибавление к элементам одной строки (столбца) соответственных элементов другой строки (столбца), умноженных на одно и то же число .

Элементарные преобразования не меняют ранг матрицы.

Две матрицы называются эквивалентными, если одна из них получена из другой при помощи элементарных преобразований. Эквивалентные матрицы имеют один и тот же ранг.

С помощью эквивалентных преобразований матрицу можно привести к ступенчатому виду.

Матрица называется ступенчатой, если в ее первой строке имеется хотя бы один элемент отличный от 0, а в каждой последующей строке первый отличный от 0 элемент стоит правее первого отличного от 0 элемента предыдущей строки. Например,

.

Ранг ступенчатой матрицы равен числу ее ненулевых строк. Для определения ранга матрицы нужно, применяя элементарные преобразования, привести ее к ступенчатому виду.

Исследование на совместность систем линейных алгебраических уравнений

Рассмотрим систему m линейных алгебраических уравнений с n неизвестными x₁, x₂, …, x_n:

Составим две матрицы:

и ,

где А − основная матрица системы, В − расширенная матрица системы.

Условие совместности любой линейной алгебраической системы определяется теоремой Кронекера-Капелли: для того, чтобы линейная алгебраическая система уравнений была совместна необходимо и достаточно, чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы системы, т. е. .

При этом возможны два случая:

а) , тогда система имеет единственное решение;

б) , тогда система имеет бесконечное множество решений (при этомr неизвестных являются основными, остальные n — r неизвестных – свободными, им можно придавать произвольные значения, в зависимости от которых принимают значения основные переменные).

1.6. Метод Гаусса решения систем линейных алгебраических уравнений

Основная идея метода Гаусса − последовательное исключение неизвестных.

Решение системы линейных алгебраических уравнений методом Гаусса состоит из двух этапов.

На первом этапе (прямой ход

) система приводится к ступенчатому виду.

На втором этапе (обратный ход) идет последовательное определение неизвестных из ступенчатой системы.

На практике удобнее работать не с системой, а с ее расширенной матрицей, выполняя элементарные преобразования над ее строками.

Сущность метода проиллюстрируем на примере решения системы из трех уравнений с тремя неизвестными.

Таким образом, если число уравнений в полученной ступенчатой системе равно числу неизвестных, то система имеет единственное решение. Все неизвестные в этом случае определяются последовательно, начиная с последнего.

Если же число уравнений в ступенчатой системе меньше числа неизвестных (), то система имеетбесконечное множество решений. В этом случае неизвестные x₁, x₂,…, x_n могут быть выражены через остальные неизвестные.

Система не имеет решений, если одно из уравнений имеет отличный от нуля свободный член, а все коэффициенты в левой части равны нулю, т. е. если при преобразованиях получаются уравнения вида

где .

Этому случаю соответствует появление в ступенчатой матрице строки вида

.

23

studfiles.net

Теорема Кронекера-Капелли, формула и примеры

Выпишем основную и расширенную матрицы заданной системы

   

Вычислим ранги этих матриц с помощью элементарных преобразований строк. Рассмотрим расширенную матрицу . Первую строку оставим без изменения, ко второй строке прибавим первую, умноженную на , к третьей строке прибавим первую, умноженную на , получим:

   

Далее первую строку оставим без изменения, третью строку сократим на и переставим вторую и третью строки, получим:

   

Первые две строки оставим без изменения, к третьей прибавим вторую, умноженную на 4:

   

Таким образом, матрицы и имеют по три линейно независимые строки, поэтому их ранги равны . По теореме Кронекера-Капелли, так как ранг основной матрицы равен рангу расширенной матрице и равен количеству неизвестных, то данная система имеет единственное решение. Найдем его. Для этого, используя последнюю матрицу, перейдем к системе уравнений

   

Вычислим последовательно значения неизвестных. Из последнего уравнения получаем, что . Подставляя это значение неизвестной во второе уравнение, будем иметь:

   

Теперь подставим значения найденных неизвестных в первое уравнение:

   

ru.solverbook.com

Условие совместности СЛАУ. Теорема Кронекера-Капелли

Установить, совместна ли система линейных уравнений, с помощью

теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.

Теорема Кронекера-Капелли о совместности системы. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу её расширенной матрицы, то есть чтобы .

Здесь матрица A (матрица системы) — это матрица, составленная из коэффициентов при неизвестных:

В свою очередь матрица В (расширенная матрица) — это матрица, полученная присоединением к матрице системы столбца из свободных членов:

Ранги этих матриц связаны неравенством , при этом ранг матрицы

В может быть лишь на одну единицу больше ранга матрицы A.

Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.

• Если ранг матрицы равен числу неизвестных (), то система имеет единственное решение.
• Если ранг матрицы системы меньше числа неизвестных (), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.

Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть , то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен

m, так как ранг матрицы не может быть больше числа её строчек.

В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:

1) отыскать в матрице системы A ранга отличный от нуля минор порядка, равного рангу матрицы системы, то есть ранга r;

2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор ;

3) члены с коэффициентами, не входящими в , перенести в правую часть, а затем, придавая неизвестным, находящимся в правой части, произвольные значения, определить по формулам Крамера оставшиеся r неизвестных из системы

r уравнений с отличным от нуля определителем .

Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.

Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор

отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному придаём произвольное значение .

Оставшиеся неизвестные определяются из системы

Решая последнюю систему по формулам Крамера или иным способом, находим

,

,

.

Присоединяя сюда , получаем все решения данной системы линейных уравнений.

Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.

Решение. Вычисляем ранг матрицы этой системы:

.

Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:

.

Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:

Решая последнюю систему по формулам Крамера, находим

,

,

.

Всё по теме «Системы уравнений и неравенств»

Начало темы «Линейная алгебра»

Поделиться с друзьями

function-x.ru

СЛАУ примеры решения задач, формулы и онлайн калькуляторы

Задание. Найти общее решение и ФСР однородной системы

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

От четвертой строки отнимем третьей и третью строку умножим на :

Нулевые строки можно далее не рассматривать, тогда получаем, что

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных (в рассматриваемом примере , так как система зависит от пяти переменных) и ранга матрицы (в этом случае получили, что — количество ненулевых строк после приведения матрицы к ступенчатому виду):

Так как ранг матрицы , а количество неизвестных системы , то тогда количество решений в ФСР (для проверки, это число должно равняться количеству свободных переменных).

Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения , получаем, что . Полученные значения записываем в первую строку таблицы. Аналогично, беря , , будем иметь, что , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

Общее решение является линейной комбинацией частных решений:

где коэффициенты не равны нулю одновременно. Или запишем общее решение в таком виде:

  

Придавая константам определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

www.webmath.ru

Критерий совместности системы линейных уравнений.

⇐ ПредыдущаяСтр 6 из 18Следующая ⇒

 

Критерий совместности системы линейных уравнений даёт теорема Кронекера-Капелли.

Леопольд Кронекер (1823 – 1891 гг.) ─ немецкий математик. Теорема, о которой пойдёт речь, содержалась в его лекциях, читавших в Берлинском университете в 1883 – 1891 гг.

Альфред Капели (1858 – 1916) ─ итальянский математик. Он, по-видимому, впервые дал формулировку теоремы с использованием термина «ранг матрицы» в своей работе в 1892г.

 

Теорема Кронекера-Капелли.

Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.

 

Пример. Исследовать систему на совместность

Решение. Приведение матрицы системы и расширенной матрицы системы к ступенчатому виду будем выполнять одновременно.

Ранг матрицы системы равен 2, а ранг расширенной матрицы системы равен 3. По теореме Кронекера-Капелли система несовместна.

 

Метод Гаусса решения системы линейных уравнений.

 

Метод Гаусса применяется для произвольной системы линейных уравнений. Нам понадобится

Определение. Систему линейных уравнений будем называть ступенчатой, если матрица этой системы ступенчатая.

 

При решении системы линейных уравнений применим следующий алгоритм:

 

1. Записываем расширенную матрицу системы (1) и приводим её к ступенчатому виду,

определяем ранги матрицы и расширенной матрицы системы.

2. Если найденные ранги не равны, то система несовместна.

3. Ранг матрицы системы равен рангу расширенной матрицы системы и равен числу r. В

этом случае система совместна и надо найти её решение.

4. Используя ступенчатый вид расширенной матрицы системы, записываем соответствующую ступенчатую систему.

5. Если число r равно числу неизвестных n, то ступенчатая система имеет вид

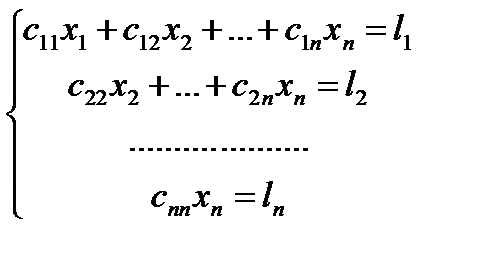(2)

Из системы (2) последовательно находим значения для х₁, х₂,…, х_т, начиная с последнего уравнения. В этом случае система (1) имеет единственное решение.

6. Если число r меньше числа неизвестных, то ступенчатая система имеет вид

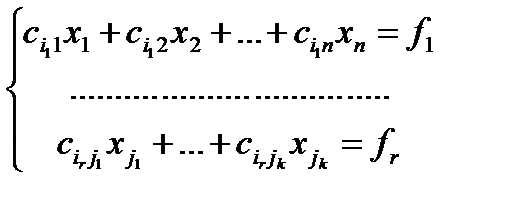(3)

В системе (3) r уравнений и n неизвестных. Неизвестные х₁,…,х_j1, которые первыми встречаются в уравнениях системы (3), назовём главными неизвестными, остальные ─ свободными неизвестными. Из системы (3) последовательно выражаем главные неизвестные через свободные, начиная с последнего уравнения. Свободные неизвестные могут принимать любые значения. В этом случае система имеет бесконечно много решений.

 

Примеры.

1). Ответ: (2;-3;-1).

 

2) Ответ: нет решений.

 

3) Ответ: бесконечно много решений.

 

Правило Крамера решения систем линейных уравнений.

 

Габриэль Крамер (1704 – 1752) ─ швейцарский математик, который в 1750 г. нашёл метод решения систем линейных уравнений, названный впоследствии правилом Крамера.

 

Определение. Система линейных уравнений называется крамеровской,если тело уравнений равно числу неизвестных и определитель матрицы системы отличен от нуля.

 

Теорема 7.1. Крамеровская система имеет единственное решение, которое находится по формулам

где ─ определитель матрицы системы, ─ определитель, полученный из , заменой столбца коэффициентов при на столбец свободных членов.

Доказательство. Пусть дана крамеровская система

(4)

Тогда

│А│= ∆ = ¹ 0.

По теореме 3 лекции 6 матрица системы А имеет обратную матрицу А^-1.

Запишем крамеровскую систему (4) в матричном виде

 

АХ = В (5)

где

А = , Х = , В = .

Умножим обе части матричного уравнения (5) слева на А^-1:

А^-1(АХ) = А^-1В,

Ввиду ассоциативности умножения матриц имеем

А^-1(АХ) = (А^-1А)Х = Е_ТХ = Х.

Таким образом,

Х = А^-1В ─ решение системы.

 

1) Покажем, что такое решение единственно. Предположим, что Х₁ и Х₂ ─ два решения матричного уравнения (5). Тогда АХ₁ = В и АХ₂ = В, откуда АХ₁ = АХ₂. Умножая обе чисти равенства на А^-1 слева, имеем

А^-1(АХ₁) = А^-1(АХ₂),

(А^-1А)Х₁ = (А^-1А)Х₂,

Е_nХ₁ = Е_nХ₂,

Х₁ = Х₂.

Следовательно, система (4) имеет единственное решение.

 

2) Найдём решение системы (4). Из равенства Х = А^-1В имеем:

= ,

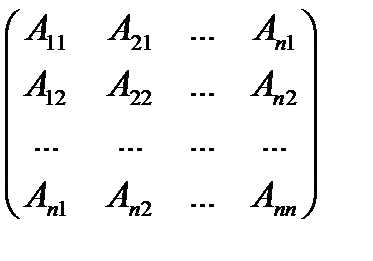откуда

,

,

……………………………………………………..

.

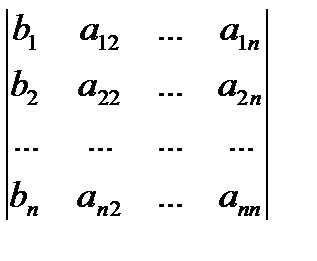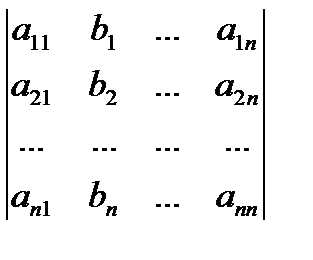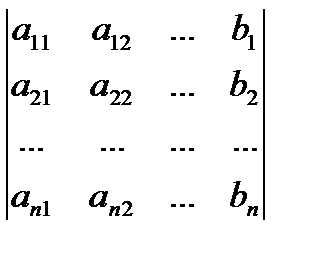Обозначая определители в правой части равенств соответственно, получим формулы .

 

Пример. Решить систему уравнений по правилу Крамера

 

Ответ: (1;1;1).

 

Рекомендуемые страницы:

lektsia.com

Исследование системы на совместимость и решение методом Крамера. Решение системы линейных алгебраических уравнений методом Гаусса

1. Исследовать систему на совместимость и решить методом Крамера.

Решение:

Т-ма Крамера: крамеровская система имеет единственное решение.

Крамеровская система – это система, удовлетворяющая следующим 2-м условиям:

1) число уравнений системы = числу неизвестных

2) определитель, составленный из коэффициентов при неизвестных, отличен от 0

Составим определитель:

 

Система совместима, т.е. имеет хотя бы одно решение.

Ответ: (-4; 1; -2)

2. Решить систему линейных алгебраических уравнений методом Гаусса

                                  .

Решение:Выпишем расширенную матрицу системы

Приведем эту матрицу к ступенчатому  виду. Для этого мы можем делать элементарные преобразования строк.

Т-ма Кронекери-Копелли: СЛУ совместима , когда ранг матрицы = рангу расширенной матрицы системы.

Ранг матрицы – число ненулевых строк в ступенчатом виде матрицы

С – расширенная матрица системы, А – матрица системы

r(C)=2

r(A)=2  r(C)=r(A) и по теореме Кронекери-Копелли система совместима. От ступенчатой матрицы переходим к ступенчатой системе:

Т. к. число уравнений системы < числа неизвестных, то в этом случае система имеет бесконечно много решений. Чтобы найти решение, надо разбить неизвестные на главные и свободные.

главные неизвестные, свободная неизвестная (может быть любым числом),

      

3. Разложить пространство R⁴ на прямую сумму подпространств размерности 2.

Решение:

R⁴ – множество строк длины 4 (4-х мерное арифметическое пространство)

R⁴={(

Если А и В – подпространства пространства V, то через А+В обозначают множество {a+b|aЄA, bЄB}

В случае, если А∩В={Ø} – нулевое подпространство, то такая сумма V=A+B называется прямой и в этом случае пишут V=A. В нашем случае Ø=(0,0,0,0)

Пусть теперь А={( B={(0,0,

Проверим, что пространство задаётся в виде А+В

Пусть 

а=( в==(0,0,, значит R⁴ =A.

Ответ: R⁴ =A, где А={( B={(0,0,

4. Докажите, что в пространстве M(2, R) система векторов  линейно независима.

Решение:

Система векторов а₁,а₂,а₃,а₄ линейно независима, если в любой системе вида

Ø

В нашем случае, пусть

Значит, система векторов Е₁, Е₂, Е₃, Е₄ линейно независима.

5. Найдите  жорданову  нормальную  форму матриц:  .

Решение:

Жорданова нормальная форма матрицы состоит из клеток Жордана вдоль главной диагонали, а все остальные элементы такой матрицы нулевые.

Клетка Жордана – это матрица вида:

Если размер клетки n*n, то она обозначается символом Y_n(a).

Пример: Y₁(a)=а, Y₂(a)=, Y₃(a)=

В искомой матрице записывают характеристический многочлен матрицы А и находят его корни.

Характеристический многочлен имеет единственный корень кратности 3.

Надо выяснить, какой из 3-х случае нам подходит:

Y₁=, Y₂=, Y₃=(1)

Число всех клеток Жордана вычисляют по формуле:

A-E =~

Значит, . Искомая матрица имеет вид: Y=

Ответ: Y=

6. Исследовать, являются ли векторы

векторного  пространства  линейно зависимыми.

Решение:

Пусть

Это приводит к системе:

Т. к. определитель системы ≠ 0, то система имеет единственное нулевое решение. Значит, система векторов f(x), g(x), h(x) являются линейно независимыми.

Ответ: линейно независимы.

7. Найти собственные значения и собственные векторы линейного оператора пространства R², заданного в некотором базисе матрицей

.

Решение:

Характеристический многочлен имеет единственный корень  кратности 2.

Значит,  — собственное значение линейного оператора.

Найдем собственный вектор, отвечающий найденному собственному значению:

Пусть х = (х₁, х₂)  х(А-

θ

Пусть х₂=t →x₁=-t, где t – любое число

Ответ: собственное значение λ = -1, собственный вектор (-t, t), t – любое число.

8. Найти все значения , при которых вектор           линейно выражается через векторы

Решение:

Мы должны найти все λ, для которых уравнение  (1)

имеет решение

что приводит к системе:

Уравнение (1) имеет решение ↔, когда данная система имеет решение. А согласно теореме  Кронекери-Копелли данная система совместима ↔ ранг матрицы системы совпадает с рангом расширенной матрицы.

~~~

vunivere.ru

Исследовать на совместность и решить неоднородные системы линейных уравнений

Примеры выполнения заданий:

1) Дано:

Решение: Запишем расширенную матрицу системы, совмещенную с матрицей А системы:

.

Вычислим ранги обеих матриц методом приведения их к ступенчатому виду с помощью элементарных преобразований строк. С этой целью первую строку вычтем из второй, а вторую – из третьей, получим:

или .

Отсюда видно, что как матрица системы А, так и расширенная матрица имеют одинаковый ранг, равный трем. Делаем вывод, что заданная система совместна, причем все три ее уравнения являются линейно независимыми (число уравнений и ранг матрицы совпадают). Таким образом, заданная система эквивалентна следующей системе:

Вычисляя определители матрицы этой системы:

делаем вывод, что свободной может быть объявлена либо , либо неизвестная. Поэтому в первом уравнении системы в правую часть следует перенести или .

Перенеся , получим:

откуда находим: . Подставляем во второе уравнение системы. Получим

Подставляем найденные значения и в первое уравнение системы, найдем .

.

Записываем общее решение системы:

Найдем какое-нибудь частное решение. Пусть свободная переменная . Тогда частное решение системы будет равно

Ответ:

– общее решение системы

– частное решение системы.

2) Дано:

Решение: Запишем расширенную матрицу системы, совместив ее с матрицей А системы

.

Выполним элементарные преобразования над строками совмещенных матриц, вычислим ранги матриц:

 

Получили матрицу, имеющую две ненулевые строки. Видно, что как матрица системы А, так и расширенная матрица имеют одинаковый ранг, равный двум. Делаем вывод, что заданная система линейных уравнений совместна. Вместе с тем линейно независимы только первые два уравнения (ранг равен двум), а третье – следствие двух первых (при элементарных преобразованиях расширенной матрицы ее последняя строка стала нулевой). Таким образом, заданная система эквивалентна следующей системе:

Для решения полученной системы необходимо определиться со свободными переменными. Так как ранг заданной системы , то базисных переменных будет тоже две. Все остальные – свободные, найдем их.

Вычислим определители второго порядка, составленные из коэффициентов при неизвестных, и отметим отличные от нуля.

Делаем вывод, что переменная обязательно должна быть базисной. Вторую переменную выбираем произвольно из , , . Пусть будет базисной переменной, тогда и будут свободными, переносим их в правую часть уравнений

Решая эту систему находим:

Тогда общее решение системы будет иметь вид:

Найдем какое-нибудь частное решение. Пусть , . Тогда получим:

Ответ: – общее решение системы.

3) Дано:

Решение: Запишем расширенную матрицу системы, совместив ее с матрицей А системы и найдем их ранги:

 

Отсюда видно, что ранг матрицы А заданной системы равен двум (третья строка матрицы А состоит из нулей, а миноры второго порядка отличны от нуля), в то время как ранг расширенной матрицы равен трем. Поэтому, на основании теоремы Кронекера-Капелли, заданная система несовместна, т.е. не имеет решений.

Ответ: система не имеет решений.

4) Дано:

Решение: Запишем расширенную матрицу системы, совместив ее с матрицей А системы, найдем их ранги, делая элементарные преобразования над строками:

 

 

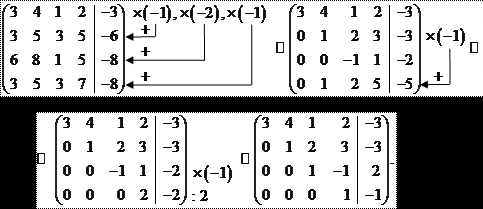Полученный результат свидетельствует, что данная система совместна, так как ранги матриц А и одинаковы и равны четырем. Не трудно заметить, что ранг матрицы системы равен числу уравнений системы, поэтому делаем вывод о том, что все уравнения системы линейно независимы. При этом ранг матрицы системы равен числу неизвестных – это свидетельствует о том, что система имеет единственное решение.

Заданная система эквивалентна следующей:

Решим эту систему:

.

Записываем ответ.

Ответ: – единственное решение заданной системы.

 

Для самостоятельного решения:

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

 

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

No related posts.