Изготовьте математический маятник – Изготовьте математический маятник длиной рассчитанной в…

Математический маятник

 

Математический маят­ник — это материальная точка, подвешенная на невесомой и нерас­тяжимой нити, находящейся в поле тяжести Земли. Математический маятник — это идеализированная модель, правильно описывающая реальный маятник лишь при определенных условиях. Реальный ма­ятник можно считать математическим, если длина нити  много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Колебательную систему в данном случае образуют нить, присо­единенное к ней тело и Земля, без которой эта система не могла бы служить маятником.

,

где а_х – ускорение, g – ускорение свободного падения, х

— смещение, l – длина нити маятника.

Это уравнение называется урав­нением свободных колебаний математического маятника.  Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

1)  будем считать, что силы трения, действующие на тело, пре­небрежимо малы и потому, их можно не учитывать;

2)   рассматриваются лишь малые колебания маятника с небольшим углом размаха.

Свободные колебания любых систем во всех слу­чаях описываются аналогичными уравнениями.

Причинами свободных колебаний математическо­го маятника являются:

1.  Действие на маятник силы натяжения и силы тяжести, пре­пятствующей его смещению из положения равновесия и заставляю­щей его снова опускаться.

2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а проходит через него дальше.

Период свободных колебаний математического ма­ятника

.

Период свободных колебаний математического маятника не за­висит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.

 

 

Превращение энергии при гармонических колебаниях

 

При гармонических колебаниях пружинного маятника проис­ходят превращения потенциальной энергии упруго деформированного телав его кинетическую энергию, гдеk – коэффициент упругости,х — модуль смещения маятника из поло­жения равновесия,m— масса маятника,v— его скорость. В соот­ветствии с уравнением гармонических колебаний:

,.

Полная энергия пружинного маятника:

.

Полная энергия для математического маятника:

В случае математического маятника

Превращения энергии при колебаниях пружинного маятника происходи в соответствии с законом сохранения механической энергии (). При движении маятника вниз или вверх от положения равновесия его потенциальная энергия увеличивается, а кинетическая — уменьшается. Когда маятник проходит положение равно­весия (х = 0), его потенциальная энергия равна нулю и кинетическая энергия маятника имеет наибольшее значение, равное его полной энергии.

Таким образом, в процессе свободных колебаний маятника его потенциальная энергия превращается в кинетическую, кинетическая в потенциальную, потенциальная затем снова в кинетическую и т. д. Но полная механическая энергия при этом остается неизменной.

 

Вынужденные колебания. Резонанс.

 

Колебания, происходящие под действием внеш­ней периодической силы, называются

вынужден­ными колебаниями. Внешняя периодическая си­ла, называемая вынуждающей, сообщает колеба­тельной системе дополнительную энергию, которая идет на восполнение энергетических потерь, проис­ходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или коси­нуса, то вынужденные колебания будут гармониче­скими и незатухающими.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из со­стояния равновесия), в случае вынужден­ных колебаний система поглощает эту энергию от источника внешней периоди­ческой силы непрерывно. Эта энергия восполняет потери, расходуемые на пре­одоление трения, и потому полная энергия колебательной системы no-прежнему ос­тается неизменной.

Частота вынужденных колебаний равна часто­те вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной ча­стотой колебательной системы

υ₀, происходит рез­кое возрастание амплитуды вынужденных колеба­ний — резонанс. Резонанс возникает из-за того, что при υ = υ₀  внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает по­ложительную работу: энергия колеблющегося те­ла увеличивается, и амплитуда его колебаний ста­новится большой. График зависимости амплитуды вынужденных колебаний А_т от частоты вынужда­ющей силы υ  представлен на рисунке, этот график называется резонансной кривой:

 

 

Явление резонанса играет большую роль в ря­де природных, научных и производственных про­цессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены.

 

studfiles.net

Математический маятник, формулы и примеры

Определения и формулы математического маятника

Рис.1. Математический маятник

Математический маятник – это модель системы, совершающей гармонические колебания. Свободные колебания математического маятника при малых углах отклонения описываются уравнением гармонических колебаний.

В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое. При отклонении материальной точки от положения равновесия на малый угол на тело будет действовать возвращающая сила , которая является тангенциальной составляющей силы тяжести:

   

Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки, уменьшаются. В момент прохождения положения равновесия угол отклонения , тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна. Далее материальная точка проходит по инерции положение равновесия и, двигаясь в направлении, противоположном силе , сбавляет скорость. В крайнем положении материальная точка останавливается, и затем начинает двигаться в обратном направлении.

Период колебаний математического маятника

   

Период колебаний математического маятника не зависит от массы груза и амплитуды колебаний.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

№5 Математический маятник

ЛАБОРАТОРНАЯ РАБОТА № 5

Тема: «Изучение зависимости периода колебаний нитяного маятника от длины нити»

Цель:установить математическую зависимость периода нитяного маятника от длины нити маятника.

Оборудование:штатив с держателем, шарик на нити, измерительная лента или линейка, секундомер.

Теоретическая часть

Математическим маятникомназывается материальная точка, подвешенная на невесомой и нерастяжимой нити. Моделью может служить тяжёлый шарик, размеры которого весьма малы по сравнению с длинной нити, на которой он подвешен (не сравнимы с расстоянием от центра тяжести до точки подвеса).

Учёные Галилей, Ньютон, Бессель и др. установили следующие законы колебания математического маятника:

1.Период колебания математического маятника не зависит от массы маятника и от амплитуды, если угол размаха не превышает 10.

2.Период колебания математического маятника прямо пропорционален квадратному корню из длины маятника и обратно пропорционален квадратному корню из ускорения свободного падения. На основании этих законов можно написать формулу для периода колебаний математического маятника:.

Используя модель и законы колебаний математического маятника, можно пронаблюдать свободные колебания, а так же с их помощью определить ускорение свободного падения для своей местности и сравнить со справочным значением g.

Порядок выполнения работы:

1. Укрепить нить маятника в держателе штатива.

2. Измерить длину маятника (длина маятника считается от точки подвеса до центра тяжести шарика).

3. Отклонить шарик на угол не более 10° и отпустить.

4. Определить время, за которое маятник совершил 20 колебаний.

5. Вычислить период колебания маятника, используя формулу Т= t/N.

6. Повторить опыт еще три раза, уменьшая (или увеличивая) длину нити маятника.

7. Данные всех опытов и результаты расчетов внести в таблицу.

№ опыта	Длина нити маятника l, м	Число полных колебаний N	Время колебаний t, с	Период колебаний T, с
1		20
2		20
3		20
4		20

8. Проанализировать результаты опытов и сделать вывод о зависимости периода нитяного маятника от длины его нити.

ОТЧЕТ ПО РАБОТЕ

Контрольные вопросы:

1. Изобразите математический маятник в крайней правой точке и покажите на чертеже силы, действующие на шарик в данной точке траектории. Нарисуйте равнодействующую сил. Как меняется величина и направление равнодействующей сил в течение периода?

2. Каким будет характер движения маятника А) при его перемещении от положения равновесия до амплитудного значения координаты? Б) при его перемещении от амплитудного значения к положению равновесия?

3. Как будет меняться период колебаний ведерка с водой, подвешенного на очень длинном шнуре: А) если из отверстия в его дне постепенно будет вытекать вода?; Б) если увеличить длину шнура? Какой математический закон или формулу вы использовали при ответе на данные вопросы?

ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Изобразите математический маятник в крайней правой точке и покажите на чертеже силы, действующие на шарик в данной точке траектории. Нарисуйте равнодействующую сил. Как меняется величина и направление равнодействующей сил в течение периода?
2.Каким будет характер движения маятника А) при его перемещении от положения равновесия до амплитудного значения координаты? Б) при его перемещении от амплитудного значения к положению равновесия?
3.Как будет меняться период колебаний ведерка с водой, подвешенного на очень длинном шнуре: А) если из отверстия в его дне постепенно будет вытекать вода? Б) если увеличить длину шнура? Какой математический закон или формулу вы использовали при ответе на данные вопросы?

studfiles.net

А. Математический маятник — PhysBook

Математический маятник. Период колебаний математического маятника

Математическим маятником называют материальную точку, подвешенную на невесомой и нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести (или иной силы).

Исследуем колебания математического маятника в инерциальной системе отсчета, относительно которой точка его подвеса находится в покое или движется равномерно прямолинейно. Силой сопротивления воздуха будем пренебрегать (идеальный математический маятник). Первоначально маятник покоится в положении равновесия С. При этом действующие на него сила тяжести \(\vec F\) и сила упругости \(\vec F_{ynp}\) нити взаимно компенсируются.

Выведем маятник из положения равновесия (отклонив его, например, в положение А) и отпустим без начальной скорости (рис. 13.11). В этом случае силы \(\vec F\) и \(\vec F_{ynp}\) не уравновешивают друг друга. Тангенциальная составляющая силы тяжести \(\vec F_\tau\), действуя на маятник, сообщает ему тангенциальное ускорение \(\vec a_\tau\) (составляющая полного ускорения, направленная вдоль касательной к траектории движения математического маятника), и маятник начинает двигаться к положению равновесия с возрастающей по модулю скоростью. Тангенциальная составляющая силы тяжести \(\vec F_\tau\) является, таким образом, возвращающей силой. Нормальная составляющая \(\vec F_n\) силы тяжести направлена вдоль нити против силы упругости \(\vec F_{ynp}\). Равнодействующая сил \(\vec F_n\) и \(\vec F_{ynp}\) сообщает маятнику нормальное ускорение \(~a_n\), которое изменяет при этом направление вектора скорости, и маятник движется по дуге ABCD.

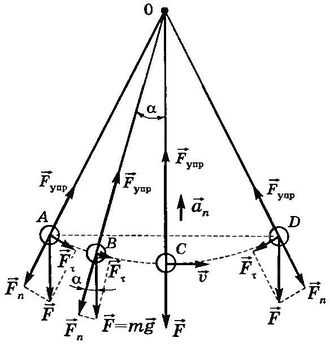
Чем ближе подходит маятник к положению равновесия С, тем меньше становится значение тангенциальной составляющей \(~F_\tau = F \sin \alpha\). В положении равновесия она равна нулю, а скорость достигает максимального значения, и маятник движется по инерции дальше, поднимаясь по дуге вверх. При этом составляющая \(\vec F_\tau\) направлена против скорости. С увеличением угла отклонения а модуль силы \(\vec F_\tau\) увеличивается, а модуль скорости уменьшается, и в точке D скорость маятника становится равной нулю. Маятник на мгновение останавливается, а затем начинает двигаться в обратном направлении к положению равновесия. Вновь пройдя его по инерции, маятник, замедляя движение, дойдет до точки А (трение отсутствует), т.е. совершит полное колебание. После этого движение маятника будет повторяться в уже описанной последовательности.

Получим уравнение, описывающее свободные колебания математического маятника.

Пусть маятник в данный момент времени находится в точке В. Его смещение S от положения равновесия в этот момент равно длине дуги СВ (т.е. S = |СВ|). Обозначим длину нити подвеса l, а массу маятника — m.

Из рисунка 13.11 видно, что \(~F_\tau = F \sin \alpha\), где \(\alpha =\frac{S}{l}.\) При малых углах \(~(\alpha <10^\circ)\) отклонения маятника \(\sin \alpha \approx \alpha,\) поэтому

\(F_\tau = -F\frac{S}{l} = -mg\frac{S}{l}.\)

Знак минус в этой формуле ставят потому, что тангенциальная составляющая силы тяжести направлена к положению равновесия, а смещение отсчитывают от положения равновесия.

Согласно второму закону Ньютона \(m \vec a = m \vec g + F_{ynp}.\) Спроецируем векторные величины этого уравнения на направление касательной к траектории движения математического маятника

\(~F_\tau = ma_\tau .\)

Из этих уравнений получим

\(a_\tau = -\frac{g}{l}S\) — динамическое уравнение движения математического маятника. Тангенциальное ускорение математического маятника пропорционально его смещению и направлено к положению равновесия. Это уравнение можно записать в виде\[a_\tau+\frac{g}{l}S = 0\]. Сравнивая его с уравнением гармонических колебаний \(~a_x + \omega^2x = 0\) (см. § 13.3), можно сделать вывод, что математический маятник совершает гармонические колебания. А так как рассмотренные колебания маятника происходили под действием только внутренних сил, то это были свободные колебания маятника. Следовательно, свободные колебания математического маятника при малых отклонениях являются гармоническими.

Обозначим \(\frac{g}{l} = \omega^2.\) Откуда \(\omega = \sqrt \frac{g}{l}\) — циклическая частота колебаний маятника.

Период колебаний маятника \(T = \frac{2 \pi}{\omega}.\) Следовательно,

\(T = 2 \pi \sqrt{ \frac{l}{g} }\)

Это выражение называют формулой Гюйгенса. Оно определяет период свободных колебаний математического маятника. Из формулы следует, что при малых углах отклонения от положения равновесия период колебаний математического маятника: 1) не зависит от его массы и амплитуды колебаний; 2) пропорционален корню квадратному из длины маятника и обратно пропорционален корню квадратному из ускорения свободного падения. Это согласуется с экспериментальными законами малых колебаний математического маятника, которые были открыты Г. Галилеем.

Подчеркнем, что эту формулу можно использовать для расчета периода при одновременном выполнении двух условий: 1) колебания маятника должны быть малыми; 2) точка подвеса маятника должна покоиться или двигаться равномерно прямолинейно относительно инерциальной системы отсчета, в которой он находится.

Если точка подвеса математического маятника движется с ускорением \(\vec a\) то при этом изменяется сила натяжения нити, что приводит к изменению и возвращающей силы, а следовательно, частоты и периода колебаний. Как показывают расчеты, период колебаний маятника в этом случае можно рассчитать по формуле

\(T = 2 \pi \sqrt{ \frac{l}{g’} }\)

где \(~g’\) — «эффективное» ускорение маятника в неинерциальной системе отсчета. Оно равно геометрической сумме ускорения свободного падения \(\vec g\) и вектора, противоположного вектору \(\vec a\), т.е. его можно рассчитать по формуле

\(\vec g’ = \vec g + (- \vec a).\)

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 374-376.

www.physbook.ru

Математический маятник: задачи среднего уровня

Рассмотрим задачи среднего уровня, связанные с колебаниями тела на нити – то есть с математическим маятником. Навык решения задач – основной навык, который гарантирует высокие баллы на ЕГЭ.

Математический маятник

Задача 1. Один математический маятник имеет период с. ‚ другой – с. Каков период колебаний математического маятника, длина которого равна сумме длин данных маятников

Запишем периоды колебаний обоих маятников:

   

   

Возведем в квадрат оба уравнения:

   

   

Выразим длины нитей обоих маятников:

   

   

Сложим длины нитей:

   

Определим период маятника с такой длиной нити:

   

Ответ:
Задача 2. Математический маятник подвешен вблизи вертикальной стены и колеблется в плоскости, параллельной стене. В стену вбит гвоздь так, что середина нити маятника наталкивается на него каждый раз, когда маятник проходит положение равновесия справа налево (рис.). Найти длину нити, если период колебаний такого маятника (с помехой в виде гвоздя) с.

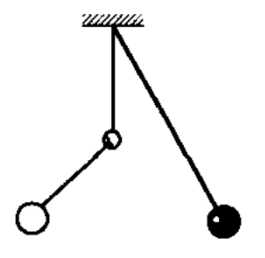
К задаче 2

Период колебаний такого маятника состоит из двух частей: одна часть, соответствующая длине нити , и вторая, соответствующая длине нити .

Тогда

   

   

Период равен

   

Чтобы найти длину нити, возведем в квадрат период:

   

«Вытащим» :

   

Немного «причешем»:

   

Домножим на 2 числитель и знаменатель:

   

   

Ответ:
Задача 3. Шарик подвешен на длинной нити. Первый раз его поднимают по вертикали до точки подвеса, второй раз отклоняют на небольшой угол. В каком из этих случаев шарик быстрее возвратится к начальному положению?

Если шарик висел на нити длиной и его подняли на высоту , то, когда он будет отпущен, он упадет за время согласно формулам кинематики:

   

Если шарик отклонить, то для возвращения ему потребуется полпериода:

   

Понятно, что число больше, чем .

Задача 4. Два математических маятника начинают колебаться одновременно. Когда первый маятник совершил полных колебаний, второй совершил только полных колебаний. Какова длина первого маятника, если длина второго м?

Так как второй маятник успевает выполнить вдвое меньше колебаний, то, следовательно, период этих колебаний вдвое больше, чем у первого маятника: . Вычислим отношение периодов:

   

По условию, отношение периодов равно 2:

   

   

Если , то .

Ответ:  м.
Задача 5. Маятниковые часы за сут отстают  на 1 час. Что нужно сделать с маятником, чтобы они шли верно?

Если часы отстают на 1 час, то, следовательно, то количество качаний, которые эти часы должны выполнять за 24 часа, они выполняют за 23 часа. Пусть это количество качаний . Найдем положенный период и фактический:

   

   

Отношение периодов маятников

   

Тогда, возводя в квадрат, получим:

   

   

То есть фактическая длина меньше, чем надо, следовательно, нить маятника нужно удлинить на .

easy-physic.ru

Математический маятник

«Мир, в котором мы живём,

удивительно склонен к колебаниям….

Колеблются даже атомы,

из которых мы состоим».

Данная тема посвящена решению задач на математический маятник.

Задача 1. Математический маятник совершил 30 колебаний за минуту. Найдите период и частоту колебаний, а также длину маятника.

ДАНО:	СИ	РЕШЕНИЕ Период колебаний можно определить по формуле Частота колебаний рассчитывается по формуле Период колебаний математического маятника рассчитывается также по формуле Преобразуем эту формулу и выразим из неё длину маятника

Ответ: период – 2 с, частота – 0,5 Гц, длина маятника – 99 см.

Задача 2. При уменьшении длины математического маятника на 2 см, период его колебаний уменьшается в 1,5 раза. Найдите первоначальную длину маятника.

ДАНО:	СИ	РЕШЕНИЕ Период колебаний математического маятника определяется по формуле В соответствии с этим, составим выражения для начального и конечного периода колебаний Т.к. период колебаний уменьшился в 1,5 раза, то получаем Преобразуем полученную формулу

Ответ: 3,6 см.

Задача 3. Математический маятник, проходя нижнюю точку имеет скорость 1 м/с, а его длина равна 20 см. Определите вертикальное отклонение маятника от положения равновесия в момент времени t = 5 с, если в начальный момент времени маятник находится на максимальной высоте.

ДАНО:	СИ	РЕШЕНИЕ Поскольку в начальный момент времени отклонение максимально, мы можем заключить, что маятник колеблется по закону косинуса. Запишем уравнение гармонических колебаний в общем виде Исходя из начального условия, сдвиг фаз равен нулю. Очевидно, что максимальное значение y – это и есть амплитуда колебаний. Запишем закон сохранения энергии, который выполняется для математического маятника Тогда Циклическая частота математического маятника рассчитывается по формуле Т.к амплитуда и циклическая частота соответственно равны То уравнение гармонических колебаний представленного математического маятника примет вид А по прошествии 5 с

Ответ: 4,5 см.

Задача 4. Шарик массой 200 г, подвешенный на нити совершает колебания. Шарику сообщили заряд 300 мкКл и поместили всю систему в электростатическое поле, линии напряжённости которого направлены вертикально вниз. После этого циклическая частота колебаний увеличилась вдвое. Найдите напряжённость поля.

ДАНО:	СИ	РЕШЕНИЕ Циклическая частота математического маятника определяется по формуле Сила тяжести Электростатическая сила равна произведению заряда и напряжённости электрического поля В электростатике заряд – это величина, аналогичная массе в механике. Ускорение свободного падения – это силовая характеристика гравитационного поля, а напряжённость – это силовая характеристика электрического поля. Поэтому, необходимо найти, так называемое, эффективное ускорение свободного падения, в соответствии с тем, что на маятник действует ещё и электростатическая сила Запишем теперь выражение для начальной циклической частоты (то есть, до сообщения шарику заряда) Для конечной циклической частоты Т.к. по условию задачи Преобразуем данную формулу и выразим из неё Напряженность поля

Ответ: 1960 Н/Кл.

Задача 5. Материальная точка на нерастяжимой нити длиной 0,3 м совершает колебания, так что максимальный угол отклонения нити от вертикали составляет 30º. Найдите положение материальной точки в момент времени t = 5 с в системе отсчёта, связанной с положением равновесия. В начальный момент времени точка находится в положении равновесия.

ДАНО:	РЕШЕНИЕ Запишем уравнение гармонических колебаний для каждой оси с учетом того, что сдвиг фаз равен нулю Очевидно, что амплитуда равны максимальным отклонениям Циклическая частота математического маятника определяется по формуле Тогда с учётом того, что Уравнения гармонических колебаний для каждой оси принимают вид Тогда координаты точки через 5 с равны

Ответ: (–4,8 см; 1,3 см).

videouroki.net

Математический маятник, теория и онлайн калькуляторы

Физический маятник

Определение

Физическим маятником считают твердое тело, которое может качаться вокруг неподвижной оси, расположенной горизонтально.

Точка пересечения этой оси с вертикальной плоскостью, которая проходит через центр масс маятника называют точкой подвеса маятника. Положение тела в каждый момент времени физического маятника характеризуют углом отклонения его от положения равновесия ($\varphi $). Угол $\varphi $ выполняет роль обобщенной координаты. Кинетическая энергия ($E_k$) качающегося физического маятника может быть определена как:

\[E_k=\frac{J{\dot{\varphi }}^2}{2}\left(1\right),\]

где $J$ — момент инерции маятника по отношению к точке подвеса; $\omega =\frac{d\varphi }{dt}=\dot{\varphi }$ — угловая скорость.

Потенциальная энергия ($E_p$) в случае малых колебаний маятника вычисляется как:

\[E_p=\frac{mga}{2}{\varphi }^2\left(2\right),\]

где $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса мятника; $g$ — ускорение свободного падения.

Малые колебания физического маятника можно считать гармоническими с циклической частотой (${\omega }_0$) равной:

\[{\omega }_0=\sqrt{\frac{mga}{J}}\left(3\right).\]

Полная энергия колебаний маятника равна:

\[E=\frac{mA^2{\omega }^2_0}{2}\left(4\right),\]

где $A$ — амплитуда колебаний.

Математический маятник — частный случай физического маятника

Определение

Математическим маятником называют физический маятник, вся масса которого сосредоточена в одной точке, центре масс маятника.

Чаще всего математический маятник рассматривают как шарик, который подвешен на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая колебания под действием силы тяжести. Хорошим приближением к математическому маятнику считают тяжелый маленький шарик, совершающий колебания на тонкой длинной нити.

Для математического маятника расстояние между центром масс маятника и точкой подвеса ($a$) равно длине нити ($l$), момент инерции шарика равен $J=ml^2$тогда формулу для циклической частоты колебаний математического маятника запишем как:

\[{\omega }_0=\sqrt{\frac{g}{l}}\left(5\right).\]

Период колебаний математического маятника ($T$) при этом:

\[T=\frac{2\pi }{{\omega }_0}=2\pi \sqrt{\frac{l}{g}}\left(6\right).\]

Уравнение движения математического маятника и его решение

Математический маятник является примером гармонического осциллятора, совершающим гармонические колебания описываемые уравнением:

\[\ddot{\varphi }+{\omega }^2_0\varphi =0\ \left(7\right).\]

Решением уравнения (7) является выражение:

\[\varphi ={\varphi }_0{\cos \left({\omega }_0t+\alpha \right)\left(8\right),\ }\]

где $\alpha $ — начальная фаза колебаний; ${\varphi }_0$ — амплитуда колебаний.

Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической или квантовой механики.

Примеры задач с математическим маятником

Пример 1

Задание. Каков период (T) колебаний математического маятника, который подвешен к потолку кабины лифта, движущегося вертикально вниз 1) равномерно; 2) с ускорением $a$? Длина нити маятника равна $l$.

Решение. Сделаем рисунок.

Период колебаний при равномерном движении математического маятника равен:

\[T=2\pi \sqrt{\frac{l}{g}}\left(1.1\right).\]

При движении с ускорением вниз период равен:

\[T=2\pi \sqrt{\frac{l}{g-a}}\left(1.2\right).\]

Ответ. 1) $T=2\pi \sqrt{\frac{l}{g}}.$ 2) $T=2\pi \sqrt{\frac{l}{g-a}}$

Пример 2

Задание.Какова возвращающая сила ($F$), действующая на шарик, массой $m$, математического мятника при $t’$ и его полная энергия (E), если колебания совершаются по закону $x=0,2{\cos ({\omega }_0t)\ }$, где ${\omega }_0=\frac{2\pi }{3}$($\frac{рад}{с}$)?

Решение. 1) Для нахождения силы, действующей на материальную точку в которой сосредоточена масса математического маятника, воспользуемся вторым законом Ньютона:

\[ma=F\ \left(2.1\right).\]

Ускорение шарика найдем как:

\[a=\frac{d^2x}{dt^2}=\frac{d}{dt}\left(\frac{d}{dt}\left(A{cos \left({\omega }_0t\right)\ }\right)\right)=-A{\omega }^2_0{cos \left({\omega }_0t\right)\ }=-\frac{0,8\cdot {\pi }^2}{9}{cos \left({\omega }_0t\right)\ }.\]

Получаем, то сила равна:

\[F=ma=-m\frac{4{\pi }^2}{45}{cos \left({\omega }_0t’\right)\ }.\]

2) Полная энергия маятника:

\[E=\frac{mA^2{\omega }^2_0}{2}=m\frac{0,4}{2}\cdot \frac{4{\pi }^2}{3}=\frac{4}{15}{\pi }^2m.\]

Ответ. $F$=$-m\frac{4{\pi }^2}{45}{cos \left({\omega }_0t’\right)\ \left(Н\right)\ }.E=\frac{4}{15}{\pi }^2m\ Дж$

Читать дальше: механика.

www.webmath.ru