Изменить порядок интегрирования в двойном интеграле
Разберемся как можно изменить порядок интегрирования в двойном интеграле на конкретном примере. Так должно быть гораздо понятнее, чем изучать скучную теорию.
Рассмотрим следующий интеграл:
Решение.
Пределы интегрирования нам известны, поэтому можем найти границы области интегрирования, которую принято обозначать буквой D.
Итак, область интегрирования D:
Построим эти области на координатной плоскости: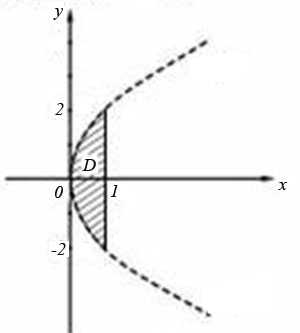
Область D располагается между прямыми х = 0 и х = 1 и ограничена сверху и снизу ветвями параболы . На рисунке эта область заштрихована.
Новые пределы интегрирования должны быть изменены так, чтобы внешний интеграл был от у, а внутренний — от х.
Рассмотрим область интегрирования D на рисунке.
Если ее спроецировать на ось Оу, то ее границами будут точки —2 и 2. Эти точки — пределы внешнего интегрирования.
Справа область D ограничена прямой х = 1.
Запишем двойной интеграл с изменением порядка интегрирования:
Таким образом, самое главное в изменении порядка интегрирования — это правильно найти новые его пределы.
ru.solverbook.com
Изменение порядка интегрирования в двойном интеграле
Если область D является простой , то для вычисления двойного интеграла применимы обе формулы (1.5) и (1.6) .Следовательно :
.
Это равенство показывает , что повторное интегрирование не зависит от порядка интегрирования .
Этим обстоятельством часто пользуются при вычислении двойных интегралов , выбирая ту из двух формул , которая приводит к более простым выкладкам .
Пример 6.8.4.
Изменить порядок интегрирования в следующем интеграле :
.
Решение
Область интегрирования непосредственно не дана . Мы должны выяснить её вид по пределам повторных интегралов .Итак , по пределам повторных интегралов восстановим область D интегрирования .
Так как внутренний интеграл берётся по х , то пределы внутреннего интеграла показывают , какими линиями область D ограничена слева и справа .
Уравнения этих линий : Û (х –1)2 + у2 = 1; х =2 ; х= у
Приступим к изменению порядка интегрирования :
Этот пример показывает , как важно с самого начала продумать порядок интегрирования , т.е. предварительно следует посмотреть , для какой переменной лучше выбрать постоянные пределы интегрирования и выбрать тот способ . при котором двойной интеграл будет представлен меньшим числом повторного интеграла .
Пример 6.8.4. – Изменить порядок интегрирования в интеграле
y =ex ,
y = 2 ,Ûex = 2 Þx = ln 2 .
Пример 6.8.5.Вычислить по области D , ограниченной линиями :
Похожие статьи:
poznayka.org
поменять порядок интегрирования | VseSdam.ru
Разделы
- Журналистика
- Рефераты по журналистике
- История
- Рефераты по истории
- Литература
- Рефераты по литературе
- Математика
- Системы линейных алгебраических уравнений
- Векторная алгебра
- Область определения функции одной переменной
- Непрерывность функции одной переменной
- Аналитическая геометрия в пространстве
- Прямая и плоскость в пространстве
- Поверхности
- Матрицы и определители
- Матрицы и действия с ними
- Обратная матрица
- Вычисление определителей
- Собственные числа и собственные векторы
- Ранг матрицы
- Матричные уравнения
- Аналитическая геометрия на плоскости
- Прямая линия на плоскости
- Кривые второго порядка
- Геометрическое место точек
- Полярная система координат
- Пределы функций одной переменной
- Отношение двух многочленов
- Пределы с иррациональностями
- Первый замечательный предел
- Второй замечательный предел
- Эквивалентные бесконечно малые функции
- Производная функции одной переменной
- Производные функций, заданных в явном виде
- Производные неявно заданных функций
- Производные параметрически заданных функций
- Логарифмическое дифференцирование
- Производные высших порядков
- Применение производной функции одной переменной
- Убывание и возрастание функций
- Выпуклость и вогнутость функций
- Наибольшее и наименьшее значения функции на отрезке
- Задачи на наибольшее и наименьшее значения функций
- Уравнения касательной и нормали
- Приближенные вычисления с помощью дифференциала
- Полное исследование функции и построение графика
- Функции многих переменных
- Область определения функций двух переменных
- Частные производные функции многих переменных
- Полная производная
- Локальный экстремум функции двух переменных
- Условный экстремум функции двух переменных
- Полный дифференциал
- Приближенные вычисления с помощью полного дифференциала
- Наибольшее и наименьшее значения функции двух переменных в замкнутой области
- Касательная плоскость и нормаль к поверхности
- Пределы функций нескольких переменных
- Линии и поверхности уровня
- Неопределенные интегралы
- Интегрирование по таблице
- Интегрирование по частям
- Интегрирование рациональных дробей
- Интегрирование подстановкой
- Определенные интегралы
- Вычисление определенных интегралов
- Нахождение площадей плоских фигур
- Вычисление длины линии
- Вычисление объемов тел вращения
- Несобственные интегралы
- Дифференциальные уравнения
- Дифференциальные уравнения с разделяющимися переменными
- Линейные дифференциальные уравнения первого порядка
- Однородные дифференциальные уравнения первого порядка
- Понижение порядка дифференциальных уравнений
- Линейные дифференциальные уравнения высших порядков
- Метод вариации производных постоянных (метод Лагранжа)
- Системы дифференциальных уравнений
- Числовые ряды
- Нахождение сумм числовых рядов
- Исследование сходимости знакопостоянных числовых рядов с помощью достаточных признаков сходимости (признаки сравнения, Д’Аламбера и Коши)
- Знакочередующиеся и знакопеременные ряды. Абсолютная и условная сходимость.
- Приближенное вычисление суммы ряда.
- Функциональные ряды
- Область сходимости степенных рядов
- Разложение функций в ряд Тейлора (Маклорена)
- Вычисление интегралов с помощью рядов
- Приближенное решение дифференциальных уравнений
- Ряды Фурье
- Область сходимости функциональных рядов
- Криволинейные интегралы
- Криволинейные интегралы второго рода (по координатам)
- Криволинейные интегралы первого рода (по длине дуги)
- Кратные интегралы
- Двойные интегралы в прямоугольной декартовой системе координат
- Двойные интегралы в полярной системе координат
- Тройные интегралы в прямоугольной декартовой системе координат
- Тройные интегралы в цилиндрической системе координат
- Тройные интегралы в сферической системе координат
- Теория поля
- Потенциал
- Поток и циркуляция
- Производная по направлению и градиент
- Отдельные разделы
- Метод наименьших квадратов
- Вспомогательные материалы
- Рефераты по журналистике
- Рефераты по истории
- Рефераты по литературе
vsesdam.ru
12.1. Изменение порядка интегрирования
Г л а ва 12 К Р А Т Н Ы Е ИНТЕГРАЛЫ
При изучении темы КРАТНЫЕ ИНТЕГРАЛЫ вы научитесь за писывать области (на плоскости и в пространстве) с помощью нера венств в декартовых, полярных, цилиндрических и сферических ко ординатах, расставлять пределы интегрирования и сводить кратные интегралы к повторным. Вы научитесь также решать задачи гео метрии и механики с использованием двойных и тройных интегралов (в декартовых, полярных, обобщенных полярных, цилиндрических и сферических координатах).
С помощью пакета РЕШЕБНИК.ВМ вы можете решить неравен ства, вычислить полученные повторные интегралы, выполнить все численные расчеты и проверить правильность полученных вами ре зультатов.
ПОСТАНОВКА ЗАДАЧИ. Изменить порядок интегрирования
b | Х2(у) | d | х^{у) |
|
I = | dy / f{x,y)dx+ | dy | / | f{x,y)dx. |
a | xi{y) | с | хз(у) |
|
ПЛАН РЕШЕНИЯ.
1. Область интегрирования состоит из двух областей Di и JD2. Зададим их неравенствами
п — /г | ^ | ^ ^ 2 / ^ ^ ? | 1 |
286 | Гл. 12. Кратные интегралы |
2. Решаем системы неравенств, определяющих области Di и D25 относительноу и получаем
у\^Чх) < у < у^^\х), | у[^\х) <у< 2/f (:г). |
3. Определяем границы изменения а:, решая неравенства
| y[‘\x)<yi’\x), | y f \ x ) < y f ( x ) . |
| |
Получаем h < х < mi | VL I2 < х < т2. |
| ||
4. Области D\ иD2 можно представить в виде |
| |||
п | \f | \ | h<x<mi, | \ |
^^= [^-^У)—у^^\х)<у<у^^\х)]^
5.Записываем интегралы / с измененным порядком интегриро
вания:
|
| mi |
| У2^Чх) | т г |
| У^^Ч^) |
| ||
| I | = | dx | / | f{x,y)dy+ | dx |
| f{x,y)dy. | ||
|
| ^^ | у[‘Чх) |
| ‘- |
| yfHx) |
| ||
6. | Если | /i = | /2 | = /, | mi | = 7712 = | m | и | У2 (^) | == У1 (^)^^^ |
2/2 (^) ~ 2/1 | (^)? TO J можно представить одним интегралом | |||||||||
I | — 1 | dx | / | f{x,y)dy | или I | = | dx | / | f{x,y)dy. | |
Записываем ответ.
ПРИМЕР. Изменить порядок интегрирования
I =’ dy | /(х, y)dx-^ | dy | / | /(ж, 2/) с^ж. |
12.1. Изменение порядка интегрирования | 287 |
РЕШЕНИЕ.
1.Область интегрирования состоит из двух областей Di и 1)2. Зададим их неравенствами
2.Решаем системы неравенств, определяюш;их области Di и D2, относительноу и получаем
а^^<У<1, 1 < У < \/2 — а:2 .
3. Определяем границы изменения ж, решая неравенства ^2 < 1, 1 < \ / 2 — ж 2 .
Учитывая, что х > О, в обоих случаях получаем О < х < 1.
4.Области Di и £)2 можно представить в виде
5.Записываем интегралы I с измененным порядком интегриро
вания:
1 | 1 |
| 1 | л / 2 ^ ^ ^ |
I = | dx | f{x,y)dy-\- | dx | f{x,y)dy. |
о |
| x2 | 0 | 1 |
6. Пользуясь линейностью и аддитивностью интегралов, получаем
1 | ( | 1 |
| >/2-х2 | «j | 1 \/2-х^ |
| |
1= | dxl | f{x,y)dy+ | / f{x,y)dy | У = | dx | / | f{x,y)dy. | |
|
| 1 | yj JL — X» |
|
|
|
|
|
Ответ. I = dx / /(x,?/)(f{x,y)dy
studfiles.net
Кратные интегралы. Определение кратного интеграла. Двойные интегралы, страница 2
Теорема 14.2. Если :1) функция f(x,y) интегрируема в правильной в направлении Ox области , т.е. существует двойной интеграл , 2) существует повторный интеграл , то
. (2.4)
Из вышеприведенных теорем следует, что при вычислении повторного интеграла можно изменять порядок интегрирования.
Пример 4. Изменить порядок интегрирования в интеграле .
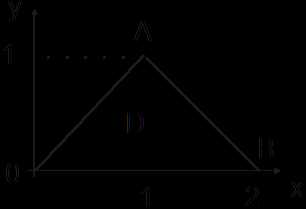Ñ Так как из (2.4) имеем , то правильная в направлении Ox область D ограничена линиями x=y, x=2—y, y=0, y=1
(линия y =1 выродилась в точку) (рис. 14.7).
Эта область является правильной и в направлении Oy. Так как участок OABграницы состоит из отрезков прямых и , то , где (см. (2.1)) ,
. Итак, = = =.#
Пример 5. Вычислить по области D, ограниченной линиями и .
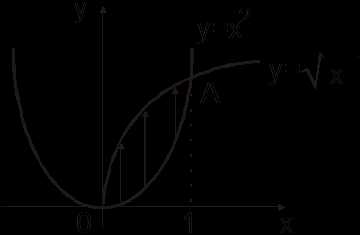Ñ Изобразим область D. Для отыскания точек пересечения
парабол и решаем
уравнение , откуда имеем действительные
корни , . Таким
образом, параболы пересекаются в точках ( рис.
14.8). Рассматривая D как правильную в направлении Oy (рис.14.8а), имеем (см.(2.1)) . По формуле (2.3)
Рис.14.8 а)
=.
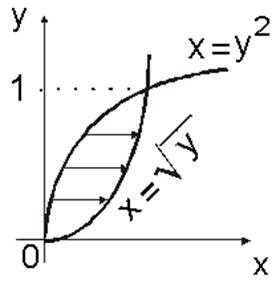Если область D рассматривать как правильную в направлении Ox (рис.14.8б), то (см. (2.2)) . По формуле (2.4)
=
=. #
Задачи для самостоятельного решения
Изменить порядок интегрирования в следующих повторных интегралах:
8. . 9. .
10. . 11..
Перейти от двойного интеграла по конечной области D к повторному интегралу и расставить пределы интегрирования:
12. Область D – параллелограмм со сторонами .
13. . 14. .
15. — треугольник со сторонами .
16. .
17. — треугольник с вершинами .
18. D – сегмент, ограниченный линиями .
Вычислить двойные интегралы:
19. . 20. — круг .
21. — область, ограниченная линиями .
22. — область, ограниченная линиями .
23. — область, ограниченная линиями .
24.- четверть круга , лежащая в первом квадранте.
25. — область, ограниченная параболой и прямой .
26. , если D ограничена осью абсцисс и первой аркой циклоиды , , .
14.2.4. Замена переменных в двойном интеграле.
Пусть функции осуществляют взаимно однозначное непрерывно дифференцируемое отображение области P плоскости на область S плоскости . Тогда существует обратное непрерывно дифференцируемое отображение , области S на область P, если якобиан преобразования
=.
Величины u и v можно рассматривать как прямоугольные координаты для точек области P и в то же время как криволинейные координаты точек области S. Точки плоскости Oxy, для которых одна из координат u и v сохраняет постоянное значение, образуют координатную линию. Всего будет два семейства таких линий.
Теорема 14.3. Пусть есть дифференцируемое преобразование области P из плоскости на область Sиз плоскости . Тогда справедливо равенство
(2.5)
Замечание. Равенство (2.5) сохраняет справедливость, когда условие взаимно однозначного соответствия между областями S и P нарушается в отдельных точках или вдоль отдельных линий.
Переход в двойном интеграле к полярным координатам
Формулы
(2.6)
преобразуют полярные координаты точки в декартовы координаты этой точки и переводят область (или область ) на всю плоскость Oxy.
Обратное преобразование декартовых координат в полярные осуществляется по формулам:
Фиксируя в последних формулах и, получим координатные линии из разных семейств: окружность с центром в точке и луч, исходящий из точки .
Якобиан преобразования
и формула (2.5) принимает вид:
(2.7)
Рекомендация. К полярным координатам целесообразно переходить, когда в подынтегральное выражение или в уравнения границы области интегрирования входит комбинация .
В некоторых случаях при вычислении двойного интеграла удобно перейти от декартовых координат к эллиптическим полярным координатам по формулам
, (2.8)
— постоянные, . Тогда
, (2.9)
Пример 6. Записать в полярной системе координат область S , заданную в декартовой системе координат неравенством (круг радиуса R с центром в точке ).
Ñ Перейдем от декартовых координат x, y к полярным по формулам , . Подставим x и y в исходное неравенство, получим: или . На координату j дополнительных ограничений не накладывается, поэтому (или ).
В полярной системе координат круг записывается неравенствами: . #
vunivere.ru
Изменить порядок интегрирования в двойном интеграле
Изменить порядок интегрирования в двойном интеграле — примеры решения двойных интегралов.На данной странице Вы найдете примеры решения двойных интегралов. Многим, кто изучает курс высшей математики часто попадаются задачи в которых требуется изменить порядок интегрирования в двойном интеграле. Множество примеров решения таких задач приведено ниже.
Если эти решения не помогут Вам в решении Вашего примера, то Вы можете заказать решение контрольной работы по высшей математике у нас.
НЕ трогать!
Используются технологии uCozintegralzz.narod.ru
Изменить порядок интегрирования
Доброй ночи! Да, действительно, это не сложно сделать и Вы правильно подметили, что самое сложное в том, как изменить порядок интегрирования в повторном интеграле — определить какие шаги за какими следует делать.
Давайте сначала разберёмся, что же такое интегрирование. Другими словами интегрирование — это процесс суммирования.
А теперь к Вашему вопросу. Нам нужно определится, какие шаги и в какой последовательности следует делать.
Схема решения такова:
- Следует определить подынтегральную функцию как функцию переменных и
- Надо задать кривые, которые ограничивают область интегрирования в двух видах: выразить как функцию от и, наоборот — , как функцию от
- Построить на одном графике линии, которые ограничивают данную область интегрирования
- Графически следует определить координаты точек пересечения графиков функций, что называется пределами интегрирования.
- Потом находят точное значение координат точек, в которых пересекаются графики и нужно сравнить полученные результаты.
- И напоследок, следует вычислить нужный интеграл, расставив пределы интегрирования
Надеюсь, эта схема (алгоритм) действий в дальнейшем поможет Вам решать задания и Вы более не зададитесь вопросом, когда встретите задание о том, как изменить порядок интегрирования. Спасибо за то, что обращайтесь к нам. Нам приятно помогать людям разобраться, если они сами того хотят.
Удачи Вам!
ru.solverbook.com