Построить график функции без применения производной
Построим схему графика функции вблизи точки разрыва:

Задание 2. Построить график функции без применения производной
Решение:
1. Область определения функции ,
— не существует, значит — точка разрыва.
2. Найдём односторонние пределы функции:
Вычислим левосторонний предел в точке:
Вычислим правосторонний предел в точке:
Значит, точка — точка разрыва II рода.
3. Найдём пределы функции на бесконечности:
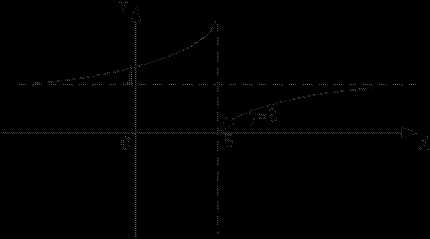
Строим график функции по результатам исследования:
Методические указания и пример типового расчёта
задания №32 «Математического тренинга» по теме
«Исследование функции на экстремум по второй производной»
Если в критической точке (в которой производная или не существует) вторая производная функции положительна, то в этой критической точке будет точка минимума (Рис.1), а если в критической точке вторая производная отрицательна, то в этой точке будет точка максимума (Рис.2).
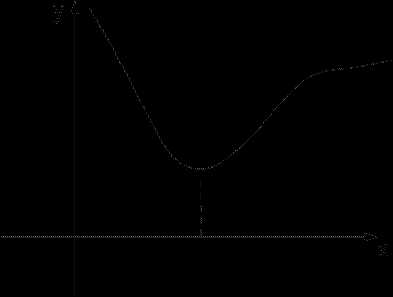
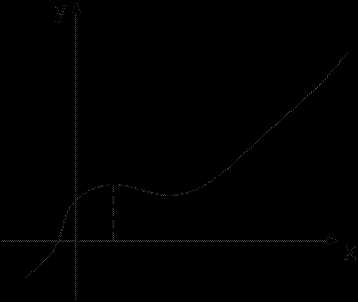
Рис.1 Рис.2
Правило исследования функции на экстремум по второй производной:
1. Найти производную .
2. Найти критические точки функции, решив уравнение
3. Найти производную .
4. Вычислить в найденных критических точках значение производной.
5. По знаку производной сделать вывод о том, является ли критическая точка точкой максимума или точкой минимума.
6. Вычислить в найденной точке экстремума сам экстремум функции.
Примечание:
Если в критической точке вторая производная оказалась равна нулю, то это неопределённый случай, и тогда исследовать на экстремум придётся по первой производной.
Пример 1. Исследовать функцию на экстремум по второй производной.
Решение:
1. Найдём первую производную: ;
2. Найдём критические точки функции: , тогда получим уравнение
,
,
,
, — критические точки функции;
3. Найдём вторую производную: ;
4. Определим знак второй производной в найденных критических точках:
, значит, точка — точка max,
, значит, точка — точка min;
5. Вычислим значение экстремума функции в точках экстремума:
;
Ответ: при ,
при .
Методические указания и примеры типового расчёта
задания №34 «Математического тренинга» по теме
«Исследование функции по первой и второй производной
и построение графика функции»
Пример 1. Исследовать функцию по первой и второй производной и построить её график:
Решение:
1. Область определения функции ;
Построить графики функций с помощью производной первого порядка
Работа добавлена на сайт samzan.ru: 2015-07-05 Заказать написание уникльной работыЗагрузка…

Задача 1. Построить графики функций с помощью производной первого порядка.
1) .
2) Функция ни четная, ни нечетная.
3) .
При ,
(0;0)- точка минимума,
(2;0)- точка минимума,
(1;1)- точка максимума.
Задача 2. Построить графики функций с помощью производной первого порядка.
1) .
2) Функция ни четная, ни нечетная.
3)
При , ; не существует в точках и .(-1;2)- точка максимума.
Задача 3. Найти наибольшее и наименьшее значения функций на заданных отрезках.
ОДЗ .
При , ;
не существует при .
Задача 4. При подготовке к экзамену студент за дней изучает часть курса, а забывает часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?
k=1/2,
не удовлетворяет условию задачи.
Точка является точкой минимума.
Ответ: 4 дня.
Задача 5. Исследовать поведение функций в окрестностях заданных точек с помощью производных высших порядков.
Т.к. то в точке функция имеет максимум.
Задача 6. Найти асимптоты и построить графики функций.
1) .
2) Функция ни четная, ни нечетная.
3)
а) ,
-вертикальная асимптота.
б)
.
Следовательно, — наклонная асимптота.
4)
не существует при
5) Найдем точки пересечения с осями:
При .
При .
Задача 7. Провести полное исследование функций и построить их график.
1) .
2) Функция ни четная, ни нечетная.
3)
а) ,
-вертикальная асимптота.
б)
.
Следовательно, — наклонная асимптота.
4)
при
не существует при-точка максимума функции.
-точка минимума функции.
5)
не существует при
6) Найдем точки пересечения с осями:
При .
При квадратное уравнение не имеет корней, следовательно график не пересекается с осью
Задача 8. Провести полное исследование функций и построить их графики.
1) .
2) Функция ни четная, ни нечетная.
3)
а) ,
-вертикальная асимптота.
б)
.
Следовательно, — горизонтальная асимптота.
4)
при ,
не существует при
-точка минимума функции.
5)
не существует при
При .
При квадратное уравнение не имеет корней, следовательно график не пересекается с осью
Задача 9. Провести полное исследование функций и построить их графики.
1)
2) Функция ни четная, ни нечетная.
3)
а) вертикальных асимптот нет.
б)
.
Следовательно, — наклонная асимптота.
4)
при ,
не существует при
-точка минимума функции,
— точка максимума функции.
5)
при ,
не существует при
6) Найдем точки пересечения с осями:
При .
При
Задача 10. Провести полное исследование функций и построить их графики.
1)
2) Функция ни четная, ни нечетная.
3)
а) вертикальных асимптот нет.
б) наклонных асимптот нет.
4) функция является периодической
5)
,тогда
.
6)
при ,
Прифункция вогнута, т.к. .
Прифункция выпукла, т.к. .
Точки перегиба:
.
samzan.ru
Подскажите пожалуйста как по графику функции построить эскизы графиков первой и второй производной? (9 задание)
Графическое построение первой производной — довольно простое по своей сути (у меня нет возможности вставить рисунок, поэтому объясняю словесно) 1) проведите прямую х = 1 (она проходит через координату х=1 параллельно оси ОУ) 2) берете произвольную точку А (m ; n) на имеющемся графике 3) к выбранной точке А (m ; n) — проводите касательную y = f(A) 4) через начало координат О(0;0) проводите прямую t, параллельную данной касательной y = f(A) 5) отмечаете на вертикальной прямой х = 1 точку С(1; к) пересечения прямой t c вертикальной прямой x = 1 6) из полученной точки С(1; к) проводите горизонтальную линию связи, параллельную оси ОХ 7) из точки А (m ; n) проводите вертикальную линию связи, параллельную оси ОУ 8) на пересечении полученных вертикальной и горизонтальных связей — отмечаете точку В(m ;к) 9) подобную операцию повторите для наиблее характерных участков имеющегося графика! в результате — получите график первой производной от данной кривой.. 10) чтобы построить график второй производной, необходимо проделать аналогичные опрерации на основе поcтроенного графика первой производной! ————————————————————————————— ПРИМЕЧАНИЕ: а) данный графический метод основан на том факте, что производная от прямой вида у = кх + b — равняется величине «к» б) в свою очередь, величина «к» — есть тангенс угла наклона данной прямой у = кх + b к оси абсцисс ОХ в) натуральная величина «к» (которая есть тангенс угла наклона к оси ОХ) находится по теореме: катет прямоугольного треугольника равен другому катету, умноженному на тангенс противоположного угла, что и реализуется в пунктах 3) — 6), поскольку горизонтальный катет полученного прямоугольного треугольника [построенного на основе прямой х=1, прямой y = 0, точки С(1; к) и точки О(0;0) начала координат] всегда равен 1, т.к. была проведена изначально вертикальная прямая х = 1
