Касательная к окружности и свойства отрезков касательных
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.
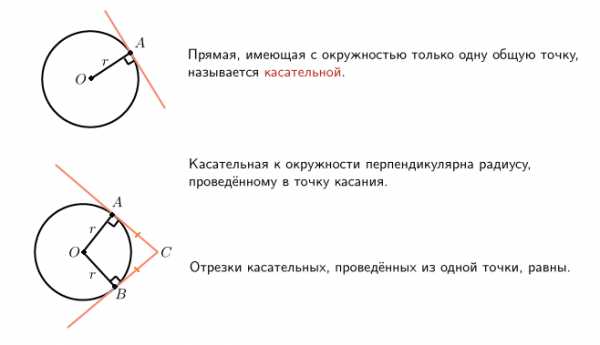
. Угол равен , где — центр окружности. Его сторона касается окружности. Найдите величину меньшей дуги окружности, заключенной внутри этого угла. Ответ дайте в градусах.
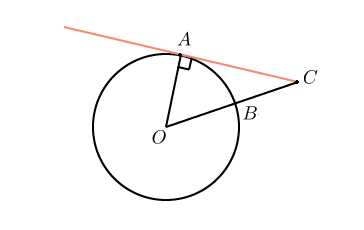
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол — прямой. Из треугольника получим, что угол равен градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги — тоже градуса.
Ответ: .
. Найдите угол , если его сторона касается окружности, — центр окружности, а большая дуга окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
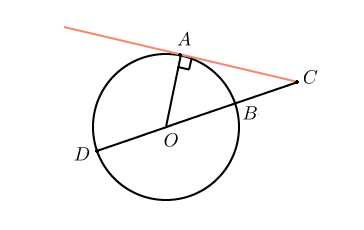
Это чуть более сложная задача. Центральный угол опирается на дугу , следовательно, он равен градусов. Тогда угол равен . Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол — прямой. Тогда угол равен .
Ответ: .
. Хорда стягивает дугу окружности в . Найдите угол между этой хордой и касательной к окружности, проведенной через точку . Ответ дайте в градусах.
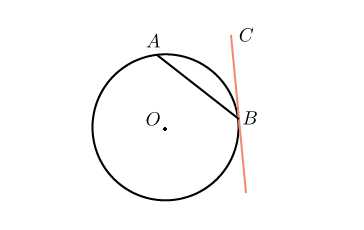
Проведем радиус в точку касания, а также радиус . Угол равен . Треугольник — равнобедренный. Нетрудно найти, что угол равен градуса, и тогда угол равен градусов, то есть половине угловой величины дуги .
Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними
.. К окружности, вписанной в треугольник , проведены три касательные. Периметры отсеченных треугольников равны , , . Найдите периметр данного треугольника.
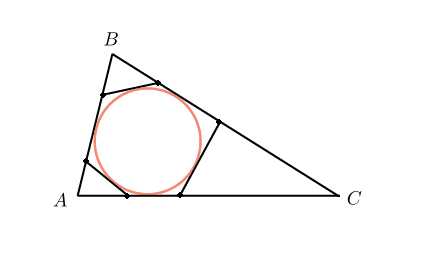
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника складывается из периметров отсеченных треугольников.
Ответ: .
Ты нашел то, что искал? Поделись с друзьями!
Вот более сложная задача из вариантов ЕГЭ:
. Около окружности описан многоугольник, площадь которого равна . Его периметр равен . Найдите радиус этой окружности.
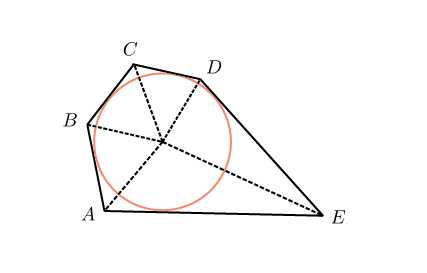
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку с вершинами . Получились треугольники и .
Очевидно, что площадь многоугольника .
Как вы думаете, чему равны высоты всех этих треугольников и как, пользуясь этим, найти радиус окружности?
Ответ: .
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Уравнение касательной — 14 Октября 2015 — Примеры решений задач
Здесь необходимо отсеять неверные определения касательной.
Толковый словарь Ушакова; Касательная — прямая линия, имеющая одну общую точку с кривой.
Определение верно для окружности рис.1, в общем случае неверно рис.2.
Академический словарь, за ним повторяет толковый словарь Кузнецова, Ефремовой и т.д.: Касательная — Прямая, имеющая общую точку с кривой, но не пересекающая её.
Определение в общем случае неверно рис.3.
Определение: Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Формула уравнения касательной
Если существует конечная производная
Особый случай когда f'(x0) бесконечна, разберем отдельно.
Пример 1. Найти уравнение касательной к графику функции y=x2 в точке 2.
Алгоритм решения следующий:
1. Находим производную функции:
2. Находим значение производной в точке x0=2:
3. Находим значение функции в точке x0=2:
4. Найденные значения подставляем в формулу уравнения касательной:
5. Получаем уравнение касательной в точке x0=2:
Получить уравнение касательной онлайн, а также графическое решение, можно с помощью данного калькулятора.
www.reshim.su
Уравнение касательной
Однако не следует думать, что непрерывная функция не дифференцируема только в точках излома, то есть там, где отсутствует касательная. Может случиться, что касательную к графику функции провести можно, но, тем не менее, производная функции в этой точке не существует. Соответствующий пример показан на рис. 9.Y
y = f(x)
C
Рис. 9. Касательная есть, а производной нет
Вточке C касательная имеется, но она перпендикулярна оси X. Угол наклона касательной
‘= 90 , поэтому tg ‘ не существует. Следовательно, не существует и f0(x0).
Вэтом случае перестаёт быть справедливым и уравнение касательной (22), поскольку касательная на рис.9 не имеет углового коэффициента. Уравнение данной касательной выглядит
так: x = x0.
p
Упражнение. Напишите уравнение касательной к графику функции y = 3 x в точке (0; 0).
1.11Исследование функций
Все функции, которые рассматриваются нами далее, считаются дифференцируемыми в нужных точках. Поэтому существование касательных подразумевается по умолчанию.
На рис. 10 изображён график функции y = f(x) и проведены касательные в двух точках с абсциссами x1 и x2.
|
| ‘2 |
‘1 |
|
|
x1 | x2 | X |
|
| y = f(x) |
Рис. 10. Возрастание и убывание функции: f0(x1) > 0, f0(x2) < 0
Вблизи точки x1 функция возрастает. Это приводит к тому, что касательная в точке x1 наклонена под острым углом ‘1 к оси X. Тангенс острого угла положителен; значит, положи-
тельна и производная в точке x1:
f0(x1) = tg ‘1 > 0:
Вблизи точки x2 функция убывает. Вследствие этого касательная в точке x2 образует тупой угол ‘2 с осью X. Тангенс тупого угла отрицателен, а вместе с ним отрицательна и производная
в точке x2:
f0(x2) = tg ‘2 < 0:
studfiles.net
как составить и решить задачу с его помощью
Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Как составлять уравнение касательной в заданной точке
При написании уравнения будем использовать следующие обозначения:
- x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
- f(x) — исходная функция;
- f'(x) — производная от функции;
- k — угловой коэффициент.
Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.
Алгоритм написания уравнения
После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:
- Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
- Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
- Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
- Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.
В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.
Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.
Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.
Задачи на написание уравнения касательной
Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.
Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.
Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.
- Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
- Возьмем от функции производную: f'(x) = 4x.
- Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
- Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
- Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.
В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.
Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).
- Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
- Запишем производную: g'(x) = 6x².
- Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
- Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
- Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
- В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.
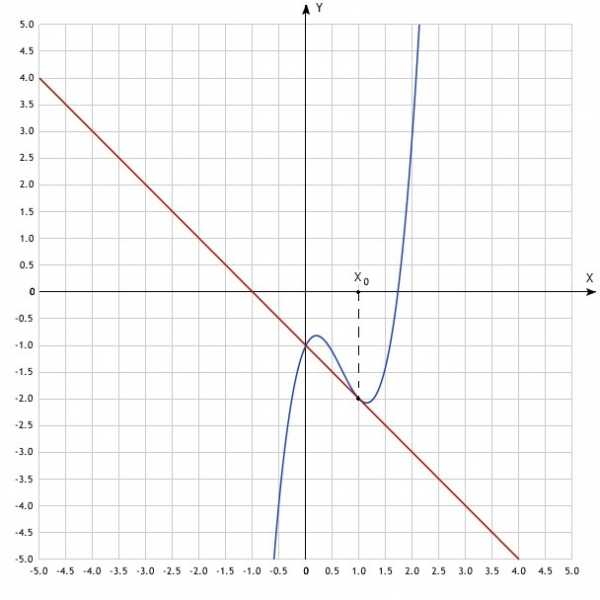
Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.
Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.
Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.
Видео
Закрепить это тему вам поможет видео.
liveposts.ru
Касательная. Задачи на касательную | Статья в журнале «Молодой ученый»
Чтобы правильно и рационально решать задачи, связанные с уравнением касательной, нужно четко понимать, что такое касательная, владеть техникой составления уравнения касательной к графику функции и представлять себе, для решения каких задач (в том числе и задач с параметрами) можно использовать метод касательной.
Опр.
1. Касательной к графику функции у
= f(x)
называется
предельное положение секущей MN
при
 (рис. 1).
(рис. 1).
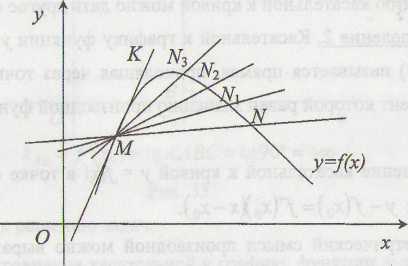
Рис. 1
Касательная к кривой может иметь с ней несколько общих точек или пересекать ее. Можно дать и другое определение касательной к кривой.
Опр. 2. Касательной к графику функции у = f(x) в точке A0(x0; f(x0)) называется прямая, проходящая через точку A0, угловой коэффициент которой равен значению производной функции у =f(x) в точке с абсциссой x0.
Уравнение касательной к кривой у = f(x) в точке с абсциссой х0имеет вид: .
Между
понятием касательной и понятие производной имеется тесная
связь. Геометрический
смысл производной можно выразить так: если функция
у = f(x)
в точке
х0
имеет
производную, то в точке с этой абсциссой определена касательная к
графику функции
 ,
причем ее
угловой коэффициент
равен
,
причем ее
угловой коэффициент
равен
 .
Вывод: если в точке х0
есть производная
функции
.
Вывод: если в точке х0
есть производная
функции
 ,
то в точке с
этой абсциссой есть касательная к графику
функции
,
то в точке с
этой абсциссой есть касательная к графику
функции
 и наоборот; если
в точке х0
нет производной
функции
и наоборот; если
в точке х0
нет производной
функции
 ,
то в точке с
этой абсциссой нет касательной к графику функции
,
то в точке с
этой абсциссой нет касательной к графику функции
 и наоборот.
и наоборот.
Укажем
случаи, когда
функция не имеет в точке касательной, и, следовательно, не
имеет и производной. Таких случаев три: угловая точка, точка
возврата, узловая точка
(рис. 2 а, б, в). Особо
отметим случай, когда в точке функция имеет бесконечную
производную (рис. 2 г).

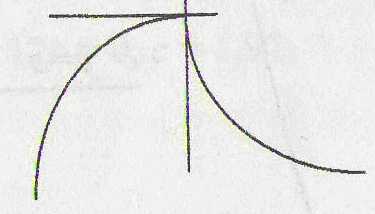

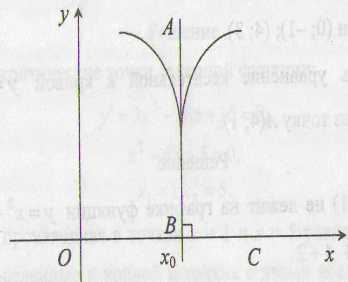
угловая точка точка возврата узловая точка
а) б) в) г)
Рис. 2
Рассмотрим решение некоторых задач.
Задачи, связанные с определением того, является ли прямая у = kx + b касательной к графику функции у = f(x). Можно указать два способа решения таких задач.
Находим общие точки графиков, т. е. решаем уравнение f(x) = kx + b, а затем для каждого из его решений вычисляем
 .
В тех случаях, когда
.
В тех случаях, когда
 = k,
имеет место касание, в других —
пересечение.
= k,
имеет место касание, в других —
пересечение.Находим корни уравнения
 = k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
= k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
Обобщая
оба способа, заметим, что для того чтобы прямая у
= kx
+ b
была касательной к графику функции
у = f(x),
необходимо и достаточно существование хотя
бы одного числа х0,
для которого выполняется система
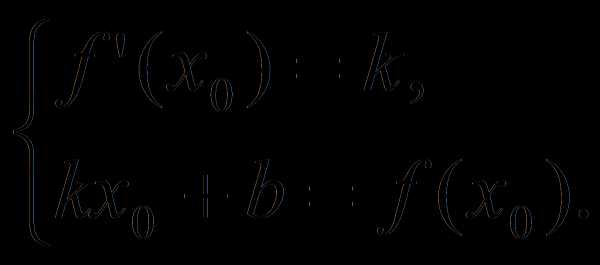
При каких значениях b прямая у = 3х +b является касательной к графику функции у =
 ?
?
Решение.
Записав условие касания
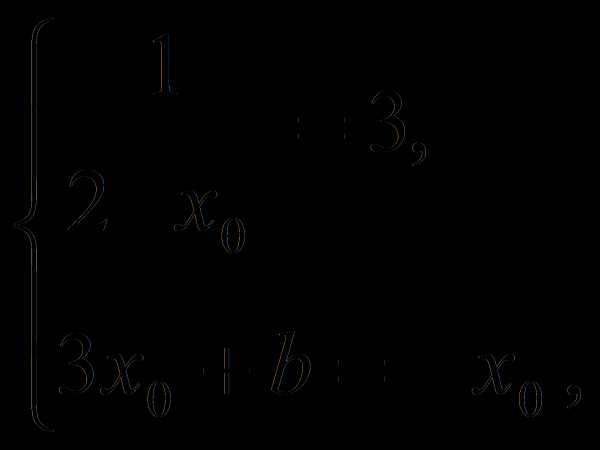 получим
получим

Ответ:
 .
.
При каких значениях а прямая у=ах+2 является касательной к графику функции

Указание.
Ответ: а = e-3
При каких значениях а прямая является касательной к графику функции
Указание.
Ответ: а = 7 или а = -1.
Является ли прямая касательной к графику функции ? Если является, то найти координаты точки касания.
Решение.
Пусть
.
Из условия следует, что должны выполняться равенство
,
где
 -
возможная абсцисса точки касания. Имеем:
-
возможная абсцисса точки касания. Имеем:
Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке
 как раз и получится
.
Значит, точка касания имеет координаты (1;-1).
как раз и получится
.
Значит, точка касания имеет координаты (1;-1).
К графику функции проведена касательная, параллельная прямой . Найти ординату точки касания.
Решение.
.
Абсцисса интересующей нас точки касания удовлетворяет уравнению
 .
Имеем:
.
Имеем:
Таким образом, . Значит, - абсцисса точки касания. Чтобы найти ординату точки касания преобразуем выражение, задающее функцию:
Ответ: 1.
Написать уравнение всех касательных к графику функции , параллельных прямой
 .
.
Решение.
Так как касательная должна быть параллельна прямой
 ,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
 .
Отсюда
.
Отсюда
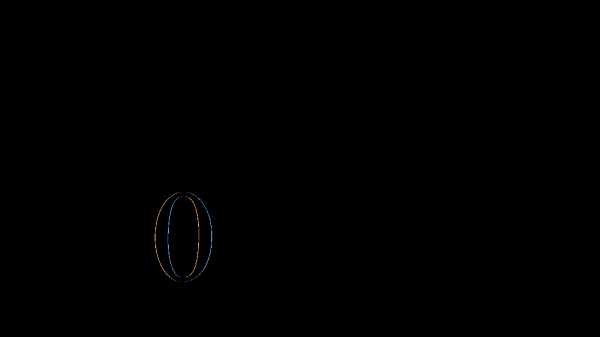 или
или

 .
Далее составляем уравнение касательной для каждой точки.
.
Далее составляем уравнение касательной для каждой точки.
Ответ:

 ,
, .
.
Найти все значения
 ,
при каждом из которых касательная к графикам функций
и
в
точках с абсциссой
,
при каждом из которых касательная к графикам функций
и
в
точках с абсциссой
 параллельны.
параллельны.
Решение.
Известно, что тангенс угла наклона касательной к графику функций
 в точке с абсциссой
в точке с абсциссой
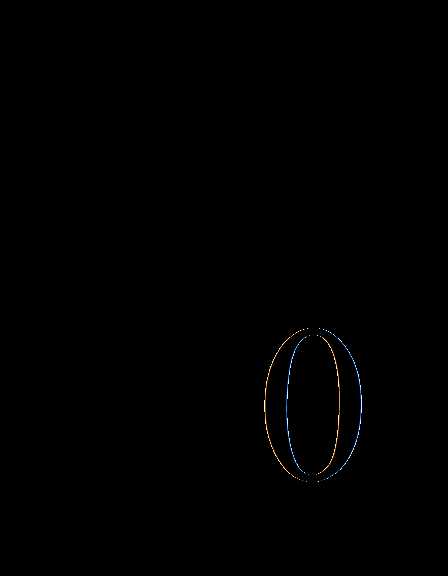 равен
равен
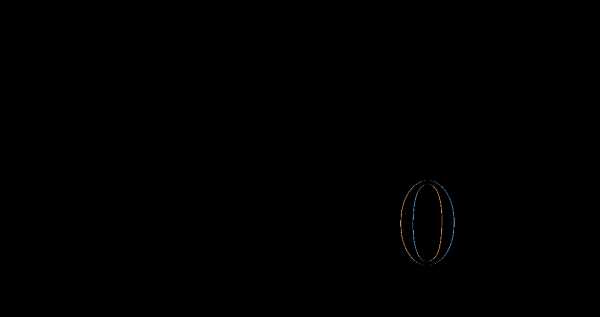 .
Следовательно, все искомые значения
.
Следовательно, все искомые значения
 будут корнями уравнения
,
откуда
.
Используя формулу разности синусов углов, будем иметь
.
Решая полученное уравнение, получаем
будут корнями уравнения
,
откуда
.
Используя формулу разности синусов углов, будем иметь
.
Решая полученное уравнение, получаем
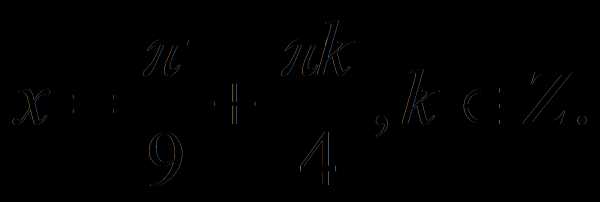
Найти расстояние между касательными к графику функции , расположенными параллельно оси
 .
.
Решение. Найдем критические точки заданной функции:
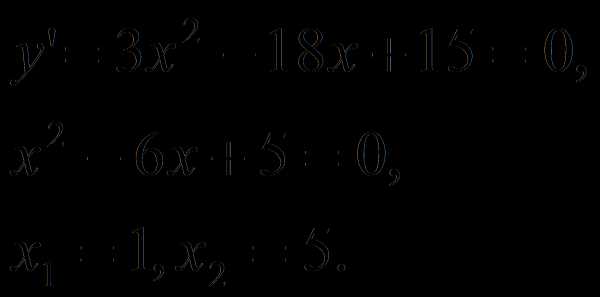
Так как,
производная в точках
 и
и
 равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
 .
Найдем значения функций в этих точках.
.
Найдем значения функций в этих точках.
Итак,
расстояние d
между касательными, параллельными оси
 ,
равно
,
равно
С составлением уравнения касательной, параллельной данной прямой, связана задача о нахождении кратчайшего расстояния между графиком некоторой функции f(x) и прямой .
Во многих
случаях удается найти касательную к графику
 ,
параллельную данной прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
,
параллельную данной прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
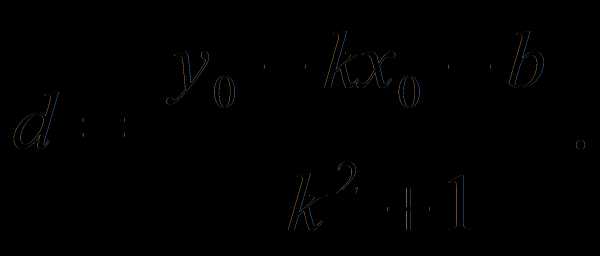
Найти кратчайшее расстояние между параболой
 и прямой
и прямой

Решение.
Убедившись, что графики не имеют общих
точек (уравнение
 не имеет решений), запишем
уравнение такой касательной к графику функции
не имеет решений), запишем
уравнение такой касательной к графику функции
 ,
которая параллельна прямой
,
которая параллельна прямой
 Уравнение касательной имеет
вид
Уравнение касательной имеет
вид
 касание происходит в точке
касание происходит в точке
 Прямая у =
Прямая у =
 х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
 .
.
Ответ:

Довольно сложной является задача составления уравнения всех касательных к графику функции у = f(x), проходящих через заданную точку М(х0; у0), вообще говоря, не лежащую на графике. Приведем алгоритм решения этой задачи.
1. Составляем
уравнение касательной к графику функции
у = f(x)
в произвольной
точке графика с абсциссой
t:

2. Решаем
относительно t
уравнение
и для каждого его
решения t
записываем
соответствующую
касательную в виде
 .
.
Написать уравнение всех касательных к графику функции , проходящих через точку М(2; -2).
Указание.
Уравнение касательной в точке с абсциссой t
имеет вид
.
Так как эта
касательная проходит через точку
(2; -2), то
,
откуда
.
Ответ: .
Найти площадь треугольника, образованного касательными, проведенными к графику функции
 через точку
через точку
 и секущей,
проходящей через точки касания.
и секущей,
проходящей через точки касания.
Указание. Уравнение дает два решения: t1 = 1, t2 = 4. Таким образом, точки K1 (1;1) и K2(4;2) являются точками касания.
Ответ: 0,25.
Говорят, что
прямая
является общей касательной графиков функции
 и
и
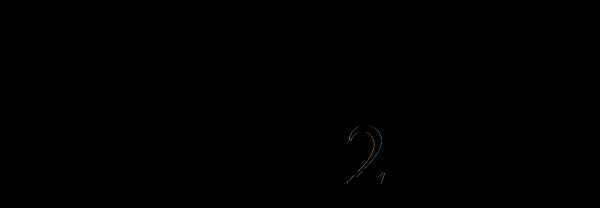 ,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
является общей касательной графиков функций
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
является общей касательной графиков функций
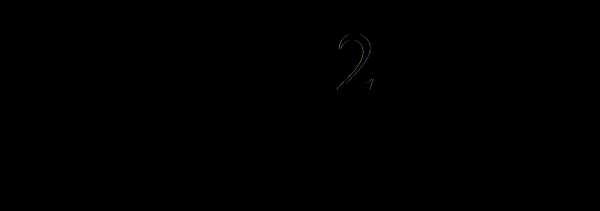 (в точке М(2; 5) и
(в точке K(0,5;
-1)). Заметим, что графики функций
(в точке М(2; 5) и
(в точке K(0,5;
-1)). Заметим, что графики функций
 и
и
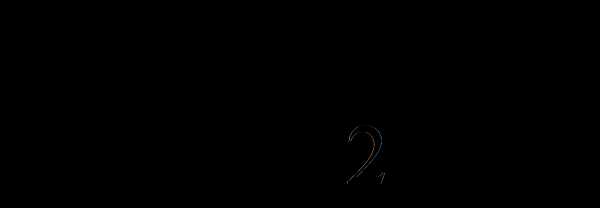 имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.
имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.
Доказать, что параболы и имеют в их общей точке общую касательную. Найти уравнение этой общей касательной. Решение. Уравнение имеет единственный корень х=2, т. е. параболы имеют единственную общую точку М(2;0). Убедимся, что значения производных для обеих функций в точке х = 2 равны; действительно,
 и
и
 .
Далее составляем уравнение касательной.
.
Далее составляем уравнение касательной.
Ответ:.
В завершении рассмотрим решение еще нескольких задач на касательную с параметром.
При каких значениях параметра
 касательная
к графику функции
в точке
касательная
к графику функции
в точке
 проходит через точку (2;3)?
проходит через точку (2;3)?
Решение.
Составим уравнение касательной к графику заданной функции в точке
 :
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
,
откуда находим:
:
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
,
откуда находим:
 .
.
Может ли касательная к кривой
 в какой-либо ее точке составлять острый угол с положительным
направлением оси
в какой-либо ее точке составлять острый угол с положительным
направлением оси
 ?
?
Решение.
Найдем производную функции
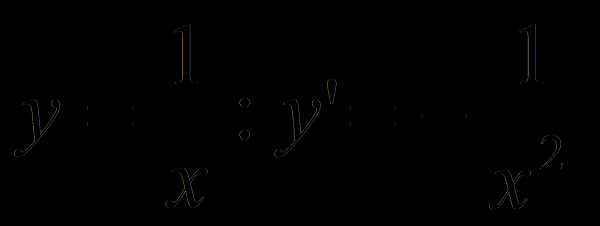 .
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Ответ: Не может.
Найти значение параметра
 ,
при котором касательная к графику функции
в точке
,
при котором касательная к графику функции
в точке
 проходит через точку М(1;7).
проходит через точку М(1;7).
Решение. Пусть тогда . Составим уравнение касательной:
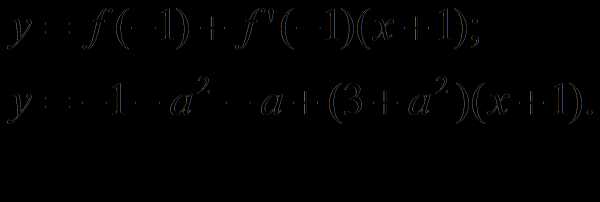
По условию эта касательная проходит через точку М(1;7), значит, , откуда получаем:
При каких значениях параметра
 прямая
является касательной к графику функции
?
прямая
является касательной к графику функции
?
Решение.
Из условия следует, что должно выполнятся равенство
где
 абсцисса
точки касания. Значит,
абсцисса
точки касания. Значит,
 и
и
 связаны между собой равенством
связаны между собой равенством
 (1). Составим уравнение касательной к графику заданной функции в
точке
(1). Составим уравнение касательной к графику заданной функции в
точке

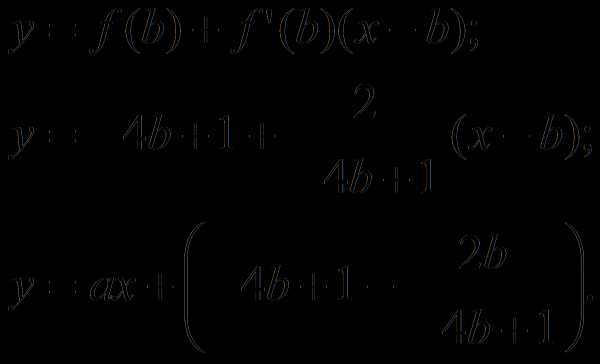
Из условия
следует, что должно выполняться равенство
.
Решив это уравнение, получим
 .
Тогда из (1) получаем, что
.
Тогда из (1) получаем, что
 .
.
При каком значении
 прямая
является касательной у графику
?
прямая
является касательной у графику
?
Решение.
Так как прямая
является касательной к графику функции
,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
,
откуда
 ,
следовательно,
,
следовательно,
 -
абсцисса точки касания. Найдем теперь
-
абсцисса точки касания. Найдем теперь
 из
условия равенства значений функций
и
при
из
условия равенства значений функций
и
при
 .
Имеем
,
откуда
.
Имеем
,
откуда
 .
.
При каких значениях параметра а касательные к графику функции , проведенные в точках его пересечения с осью оx, образуют между собой угол 60о?
Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
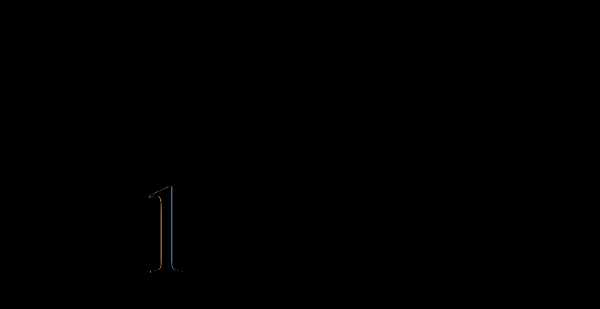 и
и
 учитываем,
что х2>0
(рис. 3)
учитываем,
что х2>0
(рис. 3)
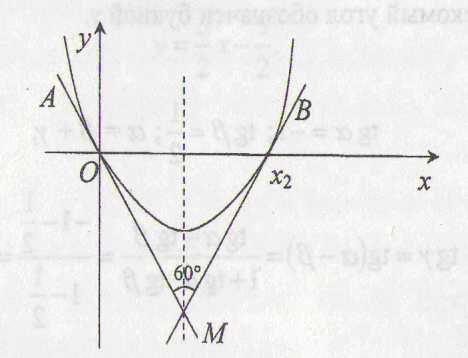
Рис. 3
Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
 Далее имеем:
.
Таким образом, получаем, что
,
то
Далее имеем:
.
Таким образом, получаем, что
,
то
 .
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
.
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
 .
Таким образом, получаем, что
.
Таким образом, получаем, что
 ,
то есть
,
то есть

Ответ:
 .
.
Литература:
Далингер, В.А. Начала математического анализа в задачах [Текст]: учебное пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. – 312 с.
Звавич, Л.И. Алгебра и начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В. Чинкина.– М.: Дрофа, 1999. – 352 с.
moluch.ru
Уравнение касательной и уравнение нормали к графику функции
Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.
Уравнение касательной выводится из уравнения прямой.
Выведем уравнение касательной, а затем — уравнение нормали к графику функции.
Значение производной f ‘(x0) функции y = f(x) в точке x0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M0(x0, y0), где y0 = f(x0). В этом состоит геометрический смысл производной.
Таким образом, можем заменить k на f ‘(x0) и получить следующее уравнение касательной к графику функции:
y — y0 = f ‘(x0)(x — x0).
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:
(x — x0) + f ‘(x0)(y — y0) = 0
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.
Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).
Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Внимание! Данная функция — сложная, так как аргумент тангенса (2x) сам является функцией. Поэтому найдём производную функции как производную сложной функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Как и в предыдущем примере, данная функция — сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Поделиться с друзьями
Весь блок «Производная»
function-x.ru
уравнение касательной — 24 Августа 2013 — Примеры решений задач
Тема: Как найти уравнение касательной к графику функции
Уравнение касательной к графику функции y=f(x) в точке x0 имеет вид
в точке x0=2.
Алгоритм решения следующий:
1) Находим производную функции
2) Вычисляем значение производной в точке x0=2
3) Вычисляем значение функции в точке x0=2
4) Найденные значения подставляем в формулу уравнения касательной
Получаем уравнение касательной
Для наглядности рекомендуем построить график самой функции и касательной на координатной плоскости с помощью калькулятора. Для этого вводим в калькулятор функцию в виде 3x^2-5x+1 и касательную в виде 7x-11, задаем интервал построения графиков от x1=-2 до x2=4 (для данного примера функции вводить не требуется, они уже введены автором), нажимаем Ok, получаем ответ.
Разберем более сложный случай, когда касательная должна проходить через точку не принадлежащую кривой.
Пример 2. Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 6).
Решение. Точка M(– 3; 6) не является точкой касания, так как f(– 3)=-9+12+2=5
1. a – абсцисса точки касания.
2. f(a) = – a2 – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.
Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.
6 = – a2 – 4a + 2 – 2(a + 2)(– 3 – a),
a2 + 6a + 8 = 0 ^ a1 = – 4, a2 = – 2.
Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.
Если a = – 2, то уравнение касательной имеет вид y = 6.
www.reshim.su

 .
В тех случаях, когда
.
В тех случаях, когда
 = k,
имеет место касание, в других —
пересечение.
= k,
имеет место касание, в других —
пересечение. = k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
= k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания. ?
?
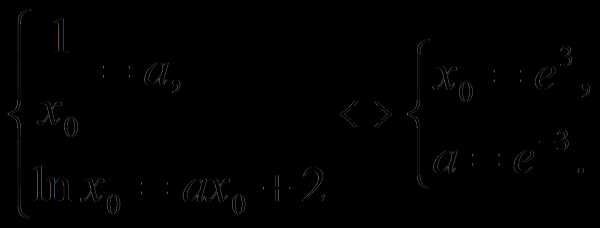
 .
. ,
при каждом из которых касательная к графикам функций
и
в
точках с абсциссой
,
при каждом из которых касательная к графикам функций
и
в
точках с абсциссой
 параллельны.
параллельны. .
. и прямой
и прямой

 через точку
через точку
 и секущей,
проходящей через точки касания.
и секущей,
проходящей через точки касания. и
и
 .
Далее составляем уравнение касательной.
.
Далее составляем уравнение касательной. касательная
к графику функции
в точке
касательная
к графику функции
в точке
 проходит через точку (2;3)?
проходит через точку (2;3)? в какой-либо ее точке составлять острый угол с положительным
направлением оси
в какой-либо ее точке составлять острый угол с положительным
направлением оси
 ?
? ,
при котором касательная к графику функции
в точке
,
при котором касательная к графику функции
в точке
 проходит через точку М(1;7).
проходит через точку М(1;7). прямая
является касательной к графику функции
?
прямая
является касательной к графику функции
? прямая
является касательной у графику
?
прямая
является касательной у графику
?