Как найти площадь фигуры – Как найти площадь фигуры?

Как найти площадь сложной фигуры

Каждый человек представляет, что такое площадь комнаты, площадь участка земли, площадь поверхности, которую надо покрасить. Он также понимает, что если земельные участки одинаковы, то площади их равны; что площадь квартиры складывается из площади комнат и площади других ее помещений.

Это обыденное представление о площади используется при ее определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому, когда говорят о площади, выделяют определенный класс фигур.

Как вычислить и обозначить площадь

Например, рассматривают площадь многоугольника, площадь произвольной плоской фигуры, площадь поверхности многогранника и др. В нашем курсе речь будет идти только о площади многоугольника и произвольной плоской фигуры.

Так же, как и при рассмотрении длины отрезка и величины угла, будем использовать понятие «состоять из», определяя его следующим образом: фигура F состоит (составлена) из фигур F₁ и F₂, если она является их объединением и у них нет общих внутренних точек.

 

В этой же ситуации можно говорить, что фигура F разбита на фигуры F₁ и F₂. Например, о фигуре F, изображенной на рисунке 2, а, можно сказать, что она состоит из фигур F₁ и F₂, поскольку они не имеют общих внутренних точек. Фигуры F₁ и F₂ на рисунке 2, b имеют общие внутренние точки, поэтому нельзя утверждать, что фигура F состоит из фигур F₁ и F₂. Если фигура F состоит из фигур F₁ и F₂, то пишут: F=F₁ Å F₂.

Определение.Площадью фигуры называется положительная величина, определенная для каждой фигуры так, что: 1) равные фигуры имеют равные площади; 2) если фигура состоит из двух частей, то ее площадь равна сумме площадей этих частей.

Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, такой единицей является площадь квадрата со стороной, равной единичному отрезку. Условимся площадь единичного квадрата обозначать буквой Е, а число, которое получается в результате изме­рения площади фигуры – S(F). Это число называют численным значе­нием площади фигуры F при выбранной единице площади Е. Оно должно удовлетворять условиям:

1. Число S(F) — положительное.

2. Если фигуры равны, то равны численные значения их площадей.

3. Если фигура F состоит из фигур F₁ и F₂, то численное значение площади фигуры равно сумме численных значений площадей фигур F₁ и F₂.

4. При замене единицы площади численное значение площади данной фигуры F увеличивается (уменьшается) во столько же раз, во сколько новая единица меньше (больше) старой.

5. Численное значение площади единичного квадрата принимается равным 1, т.е. S(F) = 1.

6. Если фигура F₁ является частью фигуры F₂, то численное значе­ние площади фигуры F₁

не больше численного значения площади фи­гуры F₂, т.е. F₁ Ì F₂ Þ S (F₁) ≤ S (F₂) .

В геометрии доказано, что для многоугольников и произвольных плоских фигур такое число всегда существует и единственно для каждой фигуры.

Фигуры, у которых площади равны, называются равновеликими.

Дата добавления: 2014-12-29; Просмотров: 3671; Нарушение авторских прав?;

steptosleep.ru

Вычисление площадей плоских фигур с помощью интеграла

На этом уроке будем учиться вычислять площади плоских фигур, которые ограничены осью абсцисс (Ox), отрезками прямых x = a, x = b и графиком непрерывной и неотрицательной функции y = f(x) для значений «икса», принадлежащих отрезку [

a, b]. Такая фигура называется криволинейной трапецией. Боковые отрезки могут вырождаться в точки.

Примеры таких фигур — на рисунке ниже.

Площадь s этой криволинейной трапеции может быть вычислена по формуле

 (1).

Итак, определённый интеграл от неотрицательной непрерывной функции f(x) по [a, b] (график функции расположен выше оси Ox) численно равен площади криволинейной трапеции с основанием [a, b], ограниченной сверху графиком функции y = f(x). В этом заключается геометрический смысл определённого интеграла. Рисунки таких фигур — в примерах.

Если же f(x) ≤ 0 (график функции расположен ниже оси Ox), то

площадь криволинейной трапеции может быть вычислена по формуле

. (2)

Есть ещё случаи, когда и верхняя, и нижняя границы фигуры — функции, соответственно y = f(x) и y = φ(x), то площадь такой фигуры вычисляется по формуле

. (3)

Таким образом, вычисление площадей плоских фигур — одна из важнейших прикладных задач, в которой определённый интеграл находит наиболее плодотворное применение. Все мы изучали сведения из элементарной геометрии, которые позволяют вычислять площади прямолинейных фигур — прямоугольников, треугольников и многоугольников. Что же касается криволинейных фигур, то здесь для нахождения площади средств из элементарной геометрии уже недостаточно. Итак, к делу. Учимся применять то, что изложено в самом верху этой статьи.

Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).

Пример 1. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox) и прямыми x = 1, x = 3.

Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):

.

Пример 3. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox) и прямой x = 4.

Решение. Фигура, соответствующая условию задачи — криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку , по формуле (1) находим площадь криволинейной трапеции:

.

Пример 4. Найти площадь фигуры, ограниченной линиями , , и находящейся в 1-й четверти.

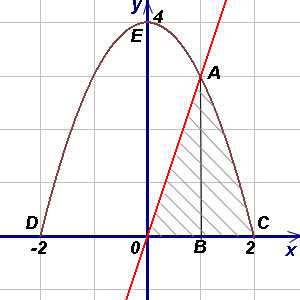
Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции ABC. При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC — абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C — точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим (абсциссу точки A) и (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим , (абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:

Пример 5. Найти площадь криволинейной трапеции ACDB, если уравнение кривой CD и абсциссы A и B соответственно 1 и 2.

Решение. Выразим данное уравнение кривой через игрек: Площадь криволинейной трапеции находим по формуле (1):

.

Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).

Пример 7. Найти площадь, заключённую между осью абсцисс (Ox) и двумя соседними волнами синусоиды.

Решение. Площадь данной фигуры можем найти по формуле (2):

.

Найдём отдельно каждое слагаемое:

.

.

Окончательно находим площадь:

.

Пример 8. Найти площадь фигуры, заключённой между параболой и кривой .

Решение. Выразим уравнения линий через игрек:

Площадь по формуле (2) получим как

,

где a и b — абсциссы точек A и B. Найдём их, решая совместно уравнения:

Отсюда

Окончательно находим площадь:

И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3). Первый из этих примеров предлагается решить самостоятельно, а затем можно посмотреть правильное решение.

Начало темы «Интеграл»

function-x.ru

Как найти площадь фигуры | Сделай все сам

Уметь обнаружить площадь фигуры может быть благотворно и позже окончания школы. К примеру, это познание сгодится, если вы делаете ремонт, и хотите знать, сколько понадобится краски для поверхности произвольной формы. Либо внезапно вам захотелось сотворить цветник, а дабы рассчитать число необходимых материалов, следует определить его площадь.

Инструкция

1. Комфортно делать, если ваша фигура – многоугольник. Вы неизменно сумеете разбить его на финальное число треугольников, и вам довольно помнить одну только формулу – расчета площади треугольника. Выходит, площадь треугольника – это половина от произведения длины его стороны на длину высоты, проведенной к этой самой стороне. Суммировав площади отдельных треугольников, в которые вашей свободой преобразована больше трудная форма, вы узнаете желанный итог.

2. Труднее решить задачку с определением площади произвольной фигуры. У такой фигуры могут быть не только прямые, но и криволинейные границы. Есть методы для примерного вычисления. Примитивные.

3. Во-первых, вы можете применять палетку. Это инструмент из прозрачного материала с нанесенной на его поверхность сеткой квадратов либо треугольников с знаменитой площадью. Наложив палетку поверх фигуры, для которой ищете площадь, вы пересчитываете число ваших единиц измерения, которые перекрывают изображение. Сочетайте неполностью закрытые единицы измерения друг с ином, дополняя их в уме до полных. Дальше, умножив площадь одной фигуры палетки на число, которое подсчитали, вы узнаете примерную площадь вашей произвольной фигуры. Ясно, что чем больше частая сетка нанесена на вашей палетке, тем вернее ваш итог.

4. Во-вторых, вы можете внутри границ произвольной фигуры, для которой определяете площадь, очертить наивысшее число треугольников. Определить площадь всякого и сложить их площади. Это будет дюже примерный итог. Если вы хотите, то можете также раздельно определить площадь секций, ограниченных дугами. Для этого представьте себе, что секция – часть от круга. Постройте данный круг, а позже от его центра проведите радиусы к краям дуги. Отрезки образуют между собой угол ?. Площадь каждого сектора определяется по формуле ?*R^2*?/360. Для всей больше мелкой части вашей фигуры вы определяете площадь и получаете всеобщий итог, сложив полученные значения.

5. 3-й метод труднее, но вернее и для кого-то, проще. Площадь всякий фигуры дозволено определить с подмогой интегрального исчисления. Определенный интеграл функции показывает площадь от графика функции до абсциссы. Площадь заключенную между двумя графиками, дозволено определить вычитанием определенного интеграла, с меньшим значением, из интеграла в тех же границах, но с огромным значением. Для применения этого способа комфортно перенести вашу произвольную фигуру в систему координат и дальше определить их функции и делать способами высшей математики, в которую тут и теперь углубляться не станем.

С всем годом задачи по геометрии становятся труднее. Теснее неудовлетворительно знать, как считать по готовым формулам. Нужно уметь из теснее готовой вывести новую формулу, дабы узнать ту либо другую величину.

Инструкция

1. Вычисление сторон квадрата. Формула площади квадрата а?, где а – сторона данной фигуры. Для вычисления площади квадрата необходимо знать лишь одну сторону, потому что все его стороны равны. Отсель вычислить сторону дюже примитивно: ?а. Пример: Площадь равна 49. Выделите квадратный корень из 49. Результат: 7.

2. Вычисление сторон прямоугольника. Обнаружить стороны этой фигуры, зная лишь значение площади, немыслимо. Необходимо знать еще одну величину – его периметр. Вот пример, площадь равна 12, а периметр 14.Обозначьте стороны прямоугольника «х» и «у». Из формулы вычисления периметра P=2(a+b) подставьте значения нашей задачи 2(х+у)=14.Из формулы вычисления площади S=ab подставьте значения нашей задачи ху=12, т. е. х=12/у. Подставьте значение «х» в уравнение 2(х+у)=14. Получится 2(12/у+у)=14. Перенесите сходственные 12/y+y=14/2. 12/у+у=7. Умножьте обе части уравнения на «у». Получится 12+у^2=7у. у^2-7у+12=0 – квадратное уравнение, считайте через дискриминант. У уравнения 2 корня у=4; у=3.Результат: стороны прямоугольника равны 3 и 4 см соответственно.

3. Вычисление сторон ромба. Для того дабы узнать стороны ромба (EWYP), помимо площади надобно иметь еще какое-либо значение. Скажем, высота – WH, она же длина перпендикуляра, опущенного из вершины (W) на сторону (EP). Следует помнить, что стороны ромба равны между собой. В этом случае дюже легко определить сторону ромба (EW). Как знаменито, ромб дозволено представить как два треугольника EWP и PWY, площадь всего из которых равняется половине произведения высоты на основание. Дозволено сделать итог, что площадь ромба будет равна произведению высоты на длину стороны. Отсель получается простая формула для вычисления длины стороны ромбы: необходимо его площадь поделить на длину высоты – |EW|=S/|WH|. Пример: Пускай площадь ромба EWYP равна 20. А высота WH=5. Подставьте значения в приведенную формулу: |EW|=20/|5 . Результат: сторона равна 4.

4. Вычисление сторон равностороннего треугольника. Для того дабы узнать его сторону (а все его стороны равны), помимо площади нужно знать высоту. Если знамениты две эти величины, то расчет дозволено совершить по этой формуле: b=2S/h, где b – сторона треугольника, S – площадь, h – высота. Пример: Пускай площадь равностороннего треугольника ABC равна 25. Высота BH = 5.Подставьте значения в формулу: b=2*25/5. Результат: сторона равна 10.

Обратите внимание!
Расчет сторон остальных фигур, имеющих стороны разные по длине друг к другу, требует умения большего числа величин.

Обратите внимание!
Нкжно разбить неровную фигуру на типовые фигуры (треугольники, квадраты, прямоугольники и т.д.), вычислить площадь всей такой фигура, а потом сложить. Всеобщая сумма площадей – есть площадь неровной фигуры.  Обнаружить площадь фигуры, ограниченной линиями

Полезный совет
Площадь плоской фигуры — аддитивная числовая колляция фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру дозволено разбить на финальное уйма единичных квадратов, площадь равна числу квадратов.  Формальное вступление представления площадь и объём дозволено обнаружить в статье мера Жордана, тут мы приводим лишь намётки определения с комментариями. Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости и удовлетворяющая…

jprosto.ru

Как вычислить площадь фигуры с помощью определенного интеграла — Мегаобучалка

Переходим к рассмотрению приложений интегрального исчисления. На этом уроке мы разберем типовую и наиболее распространенную задачу вычисления площади плоской фигуры с помощью определенного интеграла. Наконец-то все ищущие смысл в высшей математике – да найдут его. Мало ли. Придется вот в жизни приближать дачный участок элементарными функциями и находить его площадь с помощью определенного интеграла.

Для успешного освоения материала, необходимо:

1) Разбираться в неопределенном интеграле хотя бы на среднем уровне. Таким образом, чайникам для начала следует ознакомиться с уроком Неопределенный интеграл. Примеры решений.

2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл. Наладить теплые дружеские отношения с определенными интегралами можно на странице Определенный интеграл. Примеры решений. Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа, поэтому актуальным вопросом будут также ваши знания и навыки построения чертежей. Как минимум, надо уметь строить прямую, параболу и гиперболу.

Начнем с криволинейной трапеции. Криволинейной трапеция — это плоская фигура, ограниченная графиком некоторой функции y = f(x), осью OX и линиями x = a; x = b.

 

 

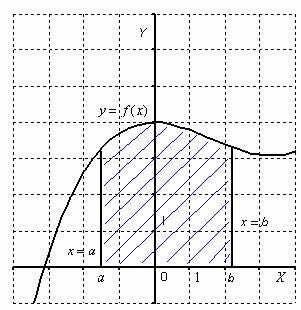
Площадь криволинейной трапеции численно равна определенному интегралу

.

У любого определенного интеграла (который существует) есть очень хороший геометрический смысл. На уроке Определенный интеграл. Примеры решениймы говорили, что определенный интеграл – это число. А сейчас пришла пора констатировать еще один полезный факт. С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ. То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Рассмотрим определенный интеграл

.

Подынтегральная функция

задает на плоскости кривую (её при желании можно начертить), а сам определенный интеграл численно равен площади соответствующей криволинейной трапеции.

 

Пример 1

Вычислить площадь фигуры, ограниченной линиями , , , .

Это типовая формулировка задания. Важнейший момент решения – построение чертежа. Причем, чертеж необходимо построить ПРАВИЛЬНО.

При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. С техникой поточечного построения можно ознакомиться в справочном материале Графики и свойства элементарных функций. Там же можно найти очень полезный применительно к нашему уроку материал – как быстро построить параболу.

В данной задаче решение может выглядеть так.

Выполним чертеж (обратите внимание, что уравнение y = 0 задает ось OX):

Штриховать криволинейную трапецию не будем, здесь очевидно, о какой площади идет речь. Решение продолжается так:

На отрезке [-2; 1] график функции y = x² + 2 расположен над осьюOX, поэтому:

.

Ответ: .

У кого возникли трудности с вычислением определенного интеграла и применением формулы Ньютона-Лейбница

,

обратитесь к лекции Определенный интеграл. Примеры решений. После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ. В данном случае «на глазок» подсчитываем количество клеточек в чертеже – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получился, скажем, ответ: 20 квадратных единиц, то, очевидно, что где-то допущена ошибка – в рассматриваемую фигуру 20 клеточек явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 2

Вычислить площадь фигуры, ограниченной линиями xy = 4, x = 2, x = 4 и осью OX.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

 

Что делать, если криволинейная трапеция расположена под осьюOX?

Пример 3

Вычислить площадь фигуры, ограниченной линиями y = e^—x, x = 1 и координатными осями.

Решение: Выполним чертеж:

 

 

Если криволинейная трапеция полностью расположена под осью OX, то её площадь можно найти по формуле:

.

В данном случае:

.

Ответ: .

 

Внимание! Не следует путать два типа задач:

1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.

2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.

 

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому, от простейших школьных задачек переходим к более содержательным примерам.

 

Пример 4

Найти площадь плоской фигуры, ограниченной линиями y = 2x – x², y = —x.

Решение: Сначала нужно выполнить чертеж. При построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы y = 2x – x² и прямой y = —x. Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:

.

Значит, нижний предел интегрирования a = 0, верхний предел интегрирования b = 3. Часто выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Тем не менее, аналитический способ нахождения пределов все-таки приходится иногда применять, если, например, график достаточно большой, или поточенное построение не выявило пределов интегрирования (они могут быть дробными или иррациональными). Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж:

 

Повторимся, что при поточечном построении пределы интегрирования чаще всего выясняются «автоматоматически».

 

А теперь рабочая формула:

Если на отрезке [a; b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь соответствующей фигуры можно найти по формуле:

Здесь уже не надо думать, где расположена фигура – над осью или под осью, а важно, какой график ВЫШЕ(относительно другого графика), а какой – НИЖЕ.

В рассматриваемом примере очевидно, что на отрезке [0; 3] парабола располагается выше прямой, а поэтому из 2x – x² необходимо вычесть –x.

Завершение решения может выглядеть так:

 

Искомая фигура ограничена параболой y = 2x – x² сверху и прямой y = —x снизу.

На отрезке [0; 3] 2x – x² ≥ —x. По соответствующей формуле:

.

Ответ: .

На самом деле, школьная формула для площади криволинейной трапеции в нижней полуплоскости (см. пример №3) – частный случай формулы

.

Поскольку ось OX задается уравнением y = 0, а график функции g(x) расположен ниже оси OX, то

.

А сейчас пара примеров для самостоятельного решения

 

Пример 5

Найти площадь фигуры, ограниченной линиями

, .

 

Пример 6

Найти площадь фигуры, ограниченной линиями

, .

 

В ходе решения задач на вычисление площади с помощью определенного интеграла иногда случается забавный казус. Чертеж выполнен правильно, расчеты – правильно, но, по невнимательности,… найдена площадь не той фигуры.

Далее, реальный случай:

 

Пример 7

Вычислить площадь фигуры, ограниченной линиями , , , .

Сначала выполним чертеж:

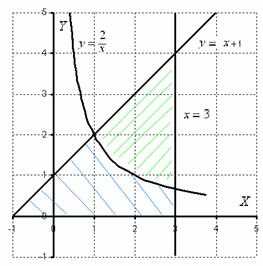
Фигура, площадь которой нам нужно найти, заштрихована синим цветом(внимательно смотрите на условие – чем ограничена фигура!). Но на практике, по невнимательности, нередко решают, что нужно найти площадь фигуры, которая заштрихована зеленым цветом!

Этот пример еще и полезен тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:

1) На отрезке [-1; 1] над осью OX расположен график прямой y = x+1;

2) На отрезке [1; 3] над осью OX расположен график гиперболы y = (2/x).

Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:

Ответ:

 

Пример 8

Вычислить площадь фигуры, ограниченной линиями

, .

Представим уравнения в «школьном» виде

, .

и выполним поточечный чертеж:

 

 

Из чертежа видно, что верхний предел у нас «хороший»: b = 1.

Но чему равен нижний предел?! Понятно, что это не целое число, но какое?

Может быть, a=(-1/3)? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что a=(-1/4). А если мы вообще неправильно построили график?

В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.

Найдем точки пересечения графиков

и .

Для этого решаем уравнение:

.

, .

Следовательно, a=(-1/3).

Дальнейшее решение тривиально. Главное, не запутаться в подстановках и знаках. Вычисления здесь не самые простые. На отрезке

, ,

по соответствующей формуле:

Ответ:

В заключение урока, рассмотрим два задания сложнее.

 

Пример 9

Вычислить площадь фигуры, ограниченной линиями

, , .

Решение: Изобразим данную фигуру на чертеже.

Для поточечного построения чертежа необходимо знать внешний вид синусоиды. Вообще, полезно знать графики всех элементарных функций, а также некоторые значения синуса. Их можно найти в таблице значений тригонометрических функций. В ряде случаев (например, в этом) допускается построение схематического чертежа, на котором принципиально правильно должны быть отображены графики и пределы интегрирования.

С пределами интегрирования здесь проблем нет, они следуют прямо из условия:

– «икс» изменяется от нуля до «пи». Оформляем дальнейшее решение:

На отрезке [0; π] график функции y = sin³x расположен над осью OX, поэтому:

(1) Как интегрируются синусы и косинусы в нечетных степенях, можно посмотреть на уроке Интегралы от тригонометрических функций. Отщипываем один синус.

(2) Используем основное тригонометрическое тождество в виде

(3) Проведем замену переменной t = cos x, тогда:

Новые переделы интегрирования:

У кого совсем плохи дела с заменами, прошу пройти на урок Метод замены в неопределенном интеграле. Кому не очень понятен алгоритм замены в определенном интеграле, посетите страницу Определенный интеграл. Примеры решений.

.

(4) Здесь мы использовали свойство определенного интеграла

,

расположив пределы интегрирования в «привычном» порядке

Ответ: .

 

Пример 10

Вычислить площадь фигуры, ограниченной линиями

, , .

Это пример для самостоятельного решения. Полное решение и ответ ниже.

 

Рассмотрим интересный пример с арккотангенсом:

 

Пример 11

Вычислить площадь фигуры, ограниченной линиями

;

и координатными осями. Полного решения не будет. Правильный ответ:

.

 

 

Решения и ответы:

Пример 2: Решение: Выполним чертеж:

 

 

На отрезке [2; 4] график функции y = 4/x расположен над осью OX, поэтому:

.

Ответ:

Примечание: В задачах на нахождение площадей преподаватели часто требуют записывать ответ не только точно, но и, в том числе, приближенно.

 

Пример 5: Решение: Выполним чертеж:

На отрезке [-1; 3] , , по соответствующей формуле:

.

Ответ:

Пример 6: Решение: Выполним чертеж.

На отрезке [1; 3], (4-x)≥(3/x), по соответствующей формуле:

.

Ответ:

 

Пример 10: Решение: Изобразим данную фигуру на чертеже:

На отрезке график функции расположен над осью , поэтому:

.

Ответ:

.

Примечание: обратите внимание, как берется интеграл от тангенса в кубе, здесь использовано следствие основного тригонометрического тождества

.

Далее в интегралах использован метод подведения функций под знак дифференциала (можно использовать замену в определенном интеграле, но решение будет длиннее).

 

megaobuchalka.ru

Как найти геометрические площади фигур

Существует бесконечное количество плоских фигур самой разной формы, как правильных, так и неправильных. Общее свойство всех фигур – любая из них обладает площадью. Площади фигур – это размеры части плоскости, занимаемой этими фигурами, выраженные в определенных единицах. Величина эта всегда бывает выражена положительным числом. Единицей измерения служит площадь квадрата, чья сторона равняется единице длины (например, одному метру или одному сантиметру). Приблизительное значение площади любой фигуры можно вычислить, умножив количество единичных квадратов, на которые она разбита, на площадь одного квадрата.

Другие определения данного понятия выглядят следующим образом:

1. Площади простых фигур – скалярные положительные величины, удовлетворяющие условиям:

– у равных фигур – равные величины площадей;

– если фигура делится на части (простые фигуры), то ее площадь – сумма площадей данных фигур;

– квадрат, имеющий стороной единицу измерения, служит единицей площади.

2. Площади фигур сложной формы (многоугольников) – положительные величины, имеющие свойства:

– у равных многоугольников – одинаковые величины площадей;

– в случае, если многоугольник составляют несколько других многоугольников, его площадь равняется сумме площадей последних. Это правило справедливо для неперекрывающихся многоугольников.

В качестве аксиомы принято утверждение, что площади фигур (многоугольников) – положительные величины.

Определение площади круга дается отдельно как величины, к которой стремится площадь правильного многоугольника, вписанного в окружность данного круга – при том, что число его сторон стремится к бесконечности.

Площади фигур неправильной формы (произвольных фигур) не имеют определения, определяются лишь способы их вычисления.

Вычисление площадей уже в древности было важной практической задачей при определении размеров земельных участков. Правила вычисления площадей за несколько сотен лет до нашей эры были сформулированы греческими учеными и изложены в «Началах» Евклида как теоремы. Интересно, что правила определения площадей простых фигур в них – те же, что и в настоящее время. Площади геометрических фигур, имеющих криволинейный контур, рассчитывались с применением предельного перехода.

Вычисление площадей простых фигур (треугольника, прямоугольника, квадрата), знакомых всем со школьной скамьи, достаточно просто. Необязательно даже запоминать содержащие буквенные обозначения формулы площадей фигур. Достаточно помнить несколько простых правил:

1. Чтобы рассчитать площадь квадрата, нужно длину его стороны умножить саму на себя (или возвести во вторую степень).

2. Площадь прямоугольника вычисляется умножением его длины на ширину. При этом необходимо, чтобы длина и ширина были выражены в одних и тех же единицах измерения.

3. Площадь сложной фигуры вычисляем, разделив ее на несколько простых и сложив полученные площади.

4. Диагональ прямоугольника делит его на два треугольника, чьи площади равны и равняются половине его площади.

5. Площадь треугольника вычисляется как половина произведения его высоты и основания.

6. Площадь круга равняется произведению квадрата радиуса на всем известное число «π».

7. Площадь параллелограмма вычисляем как произведение смежных сторон и синуса лежащего между ними угла.

8. Площадь ромба – ½  результата умножения диагоналей на синус внутреннего угла.

9. Площадь трапеции находим умножением ее высоты на длину средней линии, которая равняется среднему арифметическому оснований. Другой вариант определения площади трапеции – перемножить ее диагонали и синус лежащего между ними угла.

Детям в начальной школе для наглядности часто даются задания: найти площадь нарисованной на бумаге фигуры с помощью палетки или листа прозрачной бумаги, разграфленной на клеточки. Такой лист бумаги накладывается на измеряемую фигуру, считается число полных клеточек (единиц площади), поместившихся в ее контуре, затем число неполных, которое делится пополам.

fb.ru

Как найти площадь фигуры с разными сторонами 3 класс

Формула Герона. S = vp(p — a)(p — b)(p — c). Формула площади треугольника по двум сторонам и углу между ними. Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

Как найти площадь фигуры с разными сторонами 3 класс

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S EFKL = 10 • 3 = 30 м 2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.

S = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Вначале найдём площадь прямоугольника по формуле.

Как найти площадь фигуры с разными сторонами 3 класс

Как найти площадь фигуры

Существует множество различных геометрических фигур и множество причин для того, чтобы найти их площадь. Прочитайте эту статью, если вы делаете домашнее задание по геометрии или просто хотите выяснить количество краски для ремонта комнаты. Примечание: результаты расчетов, приведенных в данной статье, даются округленными.

Шаги Править

Метод 1 из 7:

Квадрат, прямоугольник, параллелограмм Править

Как найти площадь фигуры с разными сторонами 3 класс

Формулы площади геометрических фигур.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

Формула Герона

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Где S — площадь треугольника,

A, b, c — длины сторон треугольника,

H — высота треугольника,

Γ — угол между сторонами a и b,

R — радиус вписанной окружности,

R — радиус описанной окружности,

Формулы площади квадрата

Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.

Площадь квадрата равна половине квадрата длины его диагонали.

Где S — Площадь квадрата,

A — длина стороны квадрата,

D — длина диагонали квадрата.

Формула площади прямоугольника

Где S — Площадь прямоугольника,

A, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

Где S — Площадь параллелограмма,

A, b — длины сторон параллелограмма,

H — длина высоты параллелограмма,

D 1, d 2 — длины диагоналей параллелограмма,

Α — угол между сторонами параллелограмма,

γ — угол между диагоналями параллелограмма.

Формулы площади ромба

Формула площади ромба по длине стороны и высоте

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

Площадь ромба равна половине произведению длин его диагоналей.

Где S — Площадь ромба,

A — длина стороны ромба,

H — длина высоты ромба,

Α — угол между сторонами ромба,

Формулы площади трапеции

Формула Герона для трапеции

Площадь трапеции равна произведению полусуммы ее оснований на высоту

A, b — длины основ трапеции,

C, d — длины боковых сторон трапеции,

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними

Площадь выпуклого четырехугольника равна полов

poiskvstavropole.ru

Как найти площадь фигуры ограниченной кривыми линиями

В одном из предыдущих постов, посвященных применению интегрального исчисления, уже обсуждался вопрос Как найти площадь плоской фигуры в Wolfram|Alpha.

И было сказано, что запрос area between, который  в Wolfram|Alpha служит для вычисления площадей плоских фигур при помощи интегралов, срабатывает корректно лишь в некоторых относительно простых случаях. А для решения более сложных задач можно обратится к «ручному» способу — пошаговой процедуре вычисления площади плоской фигуры при помощи интеграла. То есть, на первом шаге определяем пределы интегрирования, а затем, используя найденные пределы, вычисляем определенный интеграл — площадь фигуры. Как это сделать практически, описано в упомянутом выше посте.

Однако, для решения большинства прикладных задач, особенно для не математиков, этот «ручной» способ не очень-то удобен. Поэтому Wolfram|Alpha предлагает и другие способы как найти площадь фигуры ограниченной двумя кривыми.

Во-первых, в самых простых случаях, как уже говорилось, площадь между кривыми можно вычислить с помощью запроса area between:

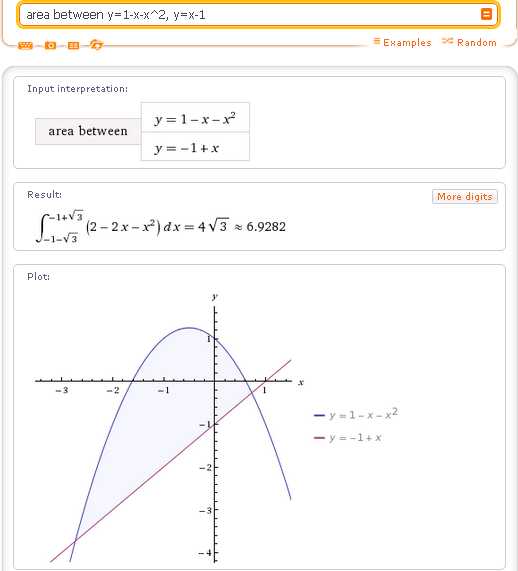
Во-вторых, если известны пределы интегрирования, то для вычисления площади фигуры, ограниченной двумя линиями, в запросе area between можно указать дополнительно область определения (domain) — отрезок по оси Ox, над которым вычисляется площадь:

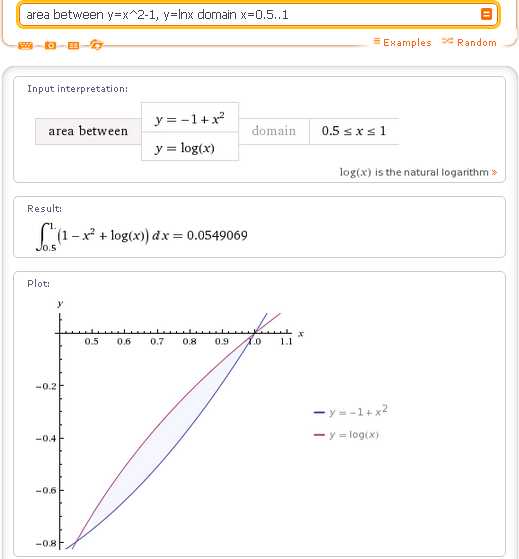
Если вы сравните этот результат с тем, который уже был получен ранее по запросу integrate lnx-(x^2-1) dx, x=0.450764..1, то увидите, что способ area between … domain … более удобный, и выводит более наглядный результат.

Наконец, если нужно вычислить площадь, ограниченную замкнутой кривой, например, площадь внутри эллипса, используйте для этого запрос area inside:

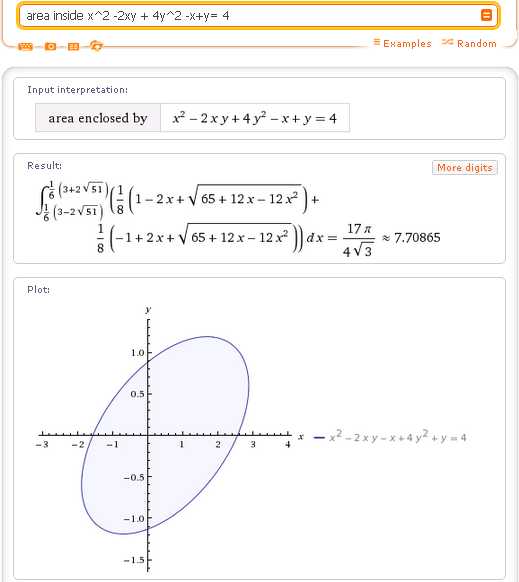
Таким образом, для вычисления площадей плоских фигур, ограниченных кривыми линиями, Wolfram|Alpha использует такие запросы: area between, area between … domain … и area inside.

www.wolframalpha-ru.com