Как найти длину окружности, зная ее радиус 🚩 как найти периметр круга 🚩 Математика
Автор КакПросто!
Окружность представляет собой замкнутую кривую на плоскости, у которой все точки в равной степени удалены от единого центра окружности. Под радиусом окружности понимается отрезок, который объединяет между собой центр окружности с любой точкой данной замкнутой кривой. Зная лишь один радиус окружности, можно с легкостью найти ее длину.
Статьи по теме:
Вам понадобится
- Величина радиуса окружности, диаметра, значение константы π.
Инструкция
Сначала надо проанализировать исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова длина радиуса окружности. Вместо этого в задаче может быть дана длина диаметра окружности. Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности, проходя через ее центр. Проанализировав определения окружности и диаметра, можно сказать, что длина диаметра равна удвоенной длине радиуса. Теперь можно принять радиус окружности равным R. Тогда для нахождения длины окружности необходимо воспользоваться формулой:L = 2πR = πD, где L — длина окружности, D — диаметр окружности, который всегда в 2 раза больше радиуса.
Можно рассмотреть пример применения данной формулы: дана окружность с диаметром 8 см. Требуется найти длину окружности.
Решение: L = 2*3,14*4 = 3,14*8 = 25,12 см
Ответ: длина окружности с диаметром 8 см равна 25,12 см
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — это фигура, которая состоит из всех точек плоскости, одинаково удаленных от данной точки (центра), лежащей в той же плоскости. Отрезок, соединяющий точку окружности с центром называется радиусом. Если вы знаете радиус окружности, то сможете вычислить и ее длину.
Вам понадобится
- Бумага, ручка, калькулятор
Инструкция
Сначала найдем диаметр D (диаметр — это прямая, которая соединяет две наиболее удаленные друг от друга точки окружности и всегда проходит через центр). Для этого удвоим радиус окружности r: D=2r. Теперь у вас есть все данные для того, чтобы найти длину окружности L. Воспользуйтесь формулой L=?D. Число ? — это отношение длины окружности к её диаметру, оно одинаково для всех окружностей и приблизительно равно 3.14. Таким образом, чтобы вычислить длину окружности, умножьте 3.14 на диаметр.Зная радиус, вы можете также вычислить площадь круга, умножив число ? (3.14) на радиус, возведенный в квадрат: S = ?R2.
Полезный совет
Число π (читается число «пи») — это бесконечная непериодическая десятичная дробь: 3,141592653589793238462643… Для удобства вычислений ее обычно сокращают до 3.14.
Выбрав любую точку на плоскости и назвав ее центром, можно задать геометрическую фигуру, все точки которой будут находиться на одинаковом расстоянии от этого центра. Такая геометрическая фигура будет называться кругом, а расстояние от центра до любой точки на ее границе — радиусом. Границу круга чаще называют окружностью, а ее длина связана с радиусом постоянным соотношением.

Инструкция
Используйте для определения длины окружности по заданному радиусу круга самую известную константу — число Пи. Именно она выражает соотношение между длиной окружности и диаметром круга. А поскольку диаметр — это прямая, проходящая через центр и соединяющая две точки окружности, то радиус составляет половину диаметра и тоже связан постоянным соотношением с длиной окружности.Умножайте известный радиус круга (R) на удвоенное число Пи (π), чтобы рассчитать длину окружности (L): L=2∗π∗R. В практических вычислениях число Пи надо округлять до нужной вам степени точности, так как это число представляет собой бесконечную дробь (иррациональное число). Если потребуются уж очень точные вычисления, то первую тысячу цифр после запятой в этой константе можно найти по этой ссылке — http://math.com/tables/constants/pi.htm.
Воспользуйтесь для расчетов каким-либо калькулятором, так как эта константа не является круглым числом и производить расчеты с ее участием в уме не очень удобно. Калькулятор не обязательно должен быть самостоятельным гаджетом, это может быть и программа — например, та, что входит в состав любой версии ОС Windows. Запускается она, как и большинство программ, через главное меню — соответствующая ссылка находится в секции «Служебные» подраздела «Стандартные» раздела «Все программы».
Задействуйте альтернативный способ вычислений, если щелкать по кнопкам калькуляторов вам не очень нравится. Например, перейдите на сайт поисковой системы Google или Nigma и введите в них запрос с нужным математическим действием. Например, если надо вычислить длину окружности, радиус которой составляет 15 сантиметров, то введите такой запрос: «2*Пи*15». Эти поисковики имеют встроенные калькуляторы, поэтому переходить куда-то по ссылкам не потребуется — нажав кнопку, вы сразу получите ответ (94.2477796).
www.kakprosto.ru
Как определить радиус окружности, зная ее длину 🚩 длина окружности и радиус 🚩 Школы
По учебной программе шестого класса учащиеся общеобразовательных школ в курсе геометрии изучают круг и окружность как геометрическую фигуру, и все, что с этой фигурой связано. Ребята знакомятся с такими понятиями, как радиус и диаметр, длина окружности или периметр круга, площадь круга. Именно на этой теме они узнают про загадочное число Пи – это лудольфово число, как оно называлось раньше. Число Пи иррационально, так как его представление в виде десятичной дроби бесконечно. На практике используется его усеченный вариант из трех цифр: 3.14. Эта константа выражает отношение длины любой окружности к ее диаметру.
Шестиклассники решают задачи, выводя по одной данности и числа «Пи» остальные характеристики окружности и круга. В тетрадях и на классной доске они в масштабе вычерчивают абстрактные сферы и производят мало что говорящие вычисления.
На практике такая задача может возникнуть в ситуации, когда, например, возникает необходимость проложить трассу определенной протяженности для проведения каких-либо состязаний со стартом и финишем в одном месте. Высчитав радиус, вы сможете на плане выбрать прохождение этой трассы, с циркулем в руке рассматривая варианты с учетом географических особенностей региона. Перемещая ножку циркуля – равноудаленного центра от будущей трассы, можно уже на этом этапе предусмотреть, где на участках будут подъемы, где спуски, учитывая естественные перепады рельефа. Также сразу можно определиться и с участками, где лучше разместить трибуны для болельщиков.
Итак, предположим, что вам для проведения соревнований по автокроссу необходима круговая трасса длиной 10 000 м. Вот нужная формула для определения радиуса (R) окружности при известной её длине (C):
R=C/2п (п – число, равное 3.14).
Подставив имеющиеся значения, вы легко получаете результат:
R = 10 000:3.14 = 3 184. 71 (м) или 3 км 184 м и 71 см.
Зная радиус окружности, легко можно определить площадь, которая будет изъята из ландшафта. Формула площади круга (S): S=пR2
При R = 3 184. 71 м она составит: S = 3.14 х 3 184. 71 х 3 184. 71 = 31 847 063 (кв. м) или почти 32 квадратных километров.
Подобные вычисления могут быть полезными при огораживании. Например, у вас имеется материал на ограду на столько-то погонных метров. Взяв эту величину за периметр круга, вы легко определите его диаметр (радиус) и площадь, а, следовательно, зримо представите величину будущего огороженного участка.
www.kakprosto.ru
Как найти длину окружности, зная ее радиус
Окружность представляет собой замкнутую кривую на плоскости, у которой все точки в равной степени удалены от цельного центра окружности . Под радиусом окружности воспринимается отрезок, тот, что объединяет между собой центр окружности с всякий точкой данной замкнутой косой. Зная лишь один радиус окружности , дозволено с легкостью обнаружить ее длину.
Вам понадобится
- Величина радиуса окружности, диаметра, значение константы ?.
Инструкция
1. Вначале нужно проанализировать начальные данные к задаче. Дело в том, что ее условии не может быть очевидно сказано, какова длина радиуса окружности . Взамен этого в задаче может быть дана длина диаметра окружности . Диаметр окружности – отрезок, тот, что объединяет между собой две противоположные точки окружности
2. Сейчас дозволено принять радиус окружности равным R. Тогда для нахождения длины окружности нужно воспользоваться формулой:L = 2?R = ?D, где L – длина окружности , D – диаметр окружности , тот, что неизменно в 2 раза огромнее радиуса.
3. Дозволено разглядеть пример использования данной формулы: дана окружность с диаметром 8 см. Требуется обнаружить длину окружности .Решение: L = 2*3,14*4 = 3,14*8 = 25,12 смОтвет: длина окружности с диаметром 8 см равна 25,12 см
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка – центр окружности, а отрезок между точкой на косой и ее центром именуется радиусом окружности.

Инструкция
1. Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью именуется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиусокружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
2. Начертите несколько окружностей различным раствором циркуля. Визуальное сопоставление разрешает сделать итог, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следственно, между диаметром окружности и ее длиной существует прямо пропорциональная связанность.
3. По физическому смыслу параметр «длина окружности» соответствует периметру многоугольника, ограниченного ломаной линией. Если вписать в окружность верный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (?/n), где R — радиус окружности, в которую вписали n-угольник.
4. При увеличении числа сторон периметр вписанного многоугольника будет все огромнее приближаться к длине окружности L. Р= b*n=2n*R*Sin (?/n)=n*D*Sin (?/n). Связанность между длиной окружности L и ее диаметром D непрерывна. Отношение L/D=n*Sin (?/n) при тяготении числа сторон вписанного многоугольника к бесконечности тяготится к числу ?, непрерывной величине, называемой «число пи» и выраженной безграничной десятичной дробью. Для расчетов без использования вычислительной техники принимается значение ?=3,14. Длина окружности и ее диаметр связаны формулой: L= ?D. Для вычисления диаметра окружности поделите ее длину на число ?=3,14.
Обратите внимание!
Окружность дозволено вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет разделять их напополам. Дабы узнать радиус вписанной окружности, надобно поделить площадь многоугольника на половину его периметра:R = S/p.Если окружность описана вокруг треугольника, то ее радиус находится по дальнейшей формуле:R = a*b*c/4S, где a, b, c – это стороны данного треугольника, S – площадь треугольника, вокруг которого описана окружность.Если требуется описать окружность вокруг четырехугольника, то это дозволено будет сделать при соблюдении 2-х условий:Четырехугольник должен быть выпуклым.В сумме противоположные углы четырехугольника обязаны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности дозволено использовать и трафареты. В современных трафаретах включены окружность различных диаметров. Данные трафареты дозволено купить в любом магазине канцтоваров.
Как рассчитать окружность 🚩 как высщитать площадь круга имея окружность 🚩 Математика
Автор КакПросто!
Окружность — это такая геометрическая фигура, которая состоит из множества точек, которые удалены от центра О на равное от него расстояние, образуя замкнутую фигуру. Для подсчета длины окружности можно воспользоваться двумя методами:
Статьи по теме:
Вам понадобится
- Знание радиуса окружности, диаметра.
Инструкция
Метод 1. Расчет длины окружности, исходя из знания ее радиуса. Радиусом окружности называется отрезок, соединяющий центр О с любой из точек окружности, например, R:D = πR*2, где
R = OR — радиус этой окружности,
π — постоянное значение, равное, приблизительно, 3.14.
Метод 2. Вытекает из первого метода. Известно, что радиус окружности равен половине ее диаметра. Тогда рассчитать по формуле:
D = πS, где
S — диаметр этой окружности. Диаметр окружности — это отрезок, проходящий через центр окружности О и соединяющие любые 2 противоположные между собой точки.
Периметром геометрической фигуры называется длина ограничивающей ее линии. Если эта фигура – круг, то для нахождения его периметра достаточно определить длину соответствующей окружности. Это можно сделать непосредственно, измерив длину этой окружности, или рассчитав ее по математическим формулам.
Вам понадобится
- — калькулятор;
- — линейка;
- — циркуль;
- — бечевка.
Инструкция
Если круг материальный (т.е. не нарисован на бумаге, а представляет собой физический объект), возьмите кусок бечевки (веревки, шнура, нитки) и расположите ее по границе круга. Отметьте на бечевке точки, соответствующие началу и концу измерений (для надежности можно завязать узелки). Затем измерьте длину этого участка бечевки с помощью линейки или строительной рулетки. Полученное число и будет периметром круга. Если круг (колесо, лежащую бочку) можно катать, то просто прокатите его на один оборот. Затем измерьте линейкой или рулеткой длину оставленного кругом следа. Если след при качении не остается, отметьте точки начала и конца движения круглого предмета. Бечевка в этом случае не понадобится. Если колесико очень маленькое (например, роликовый стеклорез), то для большей точности измерения прокатите его на несколько оборотов, а затем разделите длину пройденного пути на количество оборотов.Если измерить периметр круга или прокатить его затруднительно, то измерьте его диаметр. Это лучше сделать с помощью бечевки. Закрепите один конец бечевки в любой точке окружности и найдите на противоположной стороне самую удаленную точку. Если круг очень большой, то закрепив один конец бечевки, просто перейдите на противоположную сторону. Затем измерьте длину бечевки и умножьте это число на 3,14 (пи).
Если на круге каким-либо образом отмечен его центр, то измерьте его радиус. Для этого просто измерьте расстояние между центром и любой точкой на границе круга. Затем умножьте это значение на 6,28 (2πи). Аналогичным образом вычисляется и периметр начерченного круга.
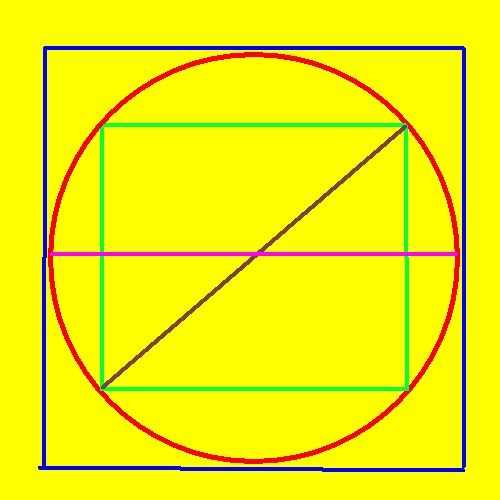
Если круг вписан в квадрат (на практике это может быть какая-нибудь упаковка, например, коробка от лампочки), то измерьте длину стороны этого квадрата. Это и будет диаметром вписанной в квадрат окружности. Если же, наоборот, квадрат вписан в окружность, то измерьте длину диагонали квадрата. Это число также будет диаметром (но уже описанной) окружности.
Видео по теме
Длину тела, отрезка или траектории движения можно найти, измерив ее, вычислив при помощи математических формул или по параметрам движения тел, преодолевающих расстояние, длина которого измеряется. Во всех случаях длина узнается по своей методике.

Вам понадобится
- — линейка;
- — рулетка;
- — лазерный дальномер;
- — роликовый дальномер.
Инструкция
Для измерения длины отрезка используйте линейку. Приложите ее к измеряемому отрезку и совместив один из его концов нулем. По шкале линейки определите расстояние, на котором находится другой конец отрезка. Это и будет его длина. Отрезки большего размера измеряйте при помощи рулетки таким же образом. Измерьте длину лазерным дальномером, направив луч из начальной точки в конечную, и на экране сразу высветится длина измеряемого отрезка. Чтобы измерить длину предмета или линии, которая не является прямой, используйте рулетку. Она должна полностью повторять все изгибы линии, длина которой измеряется. Если есть такая возможность, для измерения длины непрямой траектории используйте роликовый дальномер (курвиметр). Поставьте его колесо в начальной точке траектории, и проведите ним до конечной точки. На специальной шкале или табло появится расстояние, пройденное колесом. Длина всех сторон геометрической фигуры называется периметром. Чтобы найти его измерьте каждую из сторон фигуры, и найдите их сумму. Для некоторых фигур периметр можно найти по формулам:• чтобы найти периметр равностороннего треугольника, измерьте его сторону и умножьте на 3;
• для квадрата и ромба длину стороны умножьте на 4;
• для параллелограмма, в том числе прямоугольника сумму неравных сторон умножьте на 2;
• для прямоугольного треугольника к сумме катетов, прибавьте гипотенузу, которая равна корню квадратному из суммы квадратов катетов.
Чтобы найти длину окружности, ее радиус умножьте на число 6,28, или диаметр на число 3,14.
Чтобы узнать длину пути, которую прошло тело S, его среднюю скорость v на этом пути умножьте на время, которое понадобилось на его преодоление t (S=v∙t). Таким же образом рассчитывайте путь тела при равномерном движении. Если тело движется равноускоренно, с начальной скоростью v0 и ускорением a в течение времени t, то длину пути узнайте, найдя сумму произведения начальной скорости на время и половины ускорения на время в квадрате S= V0•t+a•t²/2. При расчетах учитывайте, что если тело замедляется, то ускорение имеет знак «минус».
Видео по теме
Длину линии, ограничивающей внутреннее пространство плоской геометрической фигуры, обычно называют периметром. Однако применительно к кругу этот параметр фигуры не менее часто обозначают понятием «длина окружности». Свойства круга, связанные с длиной окружности, известны очень давно, а способы вычисления этого параметра достаточно просты.

Инструкция
Если известен диаметр круга (D), то для вычисления длины окружности (L) умножьте это значение на число Пи: L=π*D. Эта константа (число Пи) и была введена математиками именно как числовое выражение постоянного соотношения между длиной окружности и ее диаметром.
Если известен радиус круга (R), то можно и им заменить единственную переменную величину в формуле из предыдущего шага. Поскольку радиус по определению равен половине диаметра, то формулу приведите к такому виду: L=2*π*R. Если известна площадь плоскости (S), заключенной внутри периметра круга, то этот параметр однозначно определяет длину окружности (L). Извлеките квадратный корень из произведения площади на число Пи, а результат удвойте: L=2*√(π*S). Если о самом круге ничего не известно, но есть данные о прямоугольнике, в который вписана эта фигура, то этого может быть достаточно для вычисления длины окружности. Поскольку единственным прямоугольником, в который возможно вписать окружность, является квадрат, то диаметр круга и длина стороны многоугольника (a) будут совпадать. Используйте формулу из первого шага, заменив в ней диаметр длиной стороны квадрата: L=π*a.Если длина стороны описанного около окружности прямоугольника неизвестна, но в условиях задачи дана длина его диагонали (c), то для нахождения длины окружности (L) воспользуйтесь теоремой Пифагора. Из нее вытекает, что сторона квадрата равна соотношению между длиной диагонали и квадратным корнем из двойки. Подставьте это значение в формулу из предыдущего шага и станет ясно, что для нахождения длины окружности вам нужно произведение длины диагонали на число Пи поделить на корень из двух: L=π*с/√2.
Если данная окружность описана около правильного многоугольника с любым количеством вершин (n), то для нахождения периметра круга (L) будет достаточным знать длину стороны вписанной фигуры (b). Разделите длину стороны на удвоенный синус числа Пи, поделенного на количество вершин многоугольника: L=b/(2*sin(π/n)).
Обратите внимание
Окружность — это замкнутая плоская кривая, все точки которой одинаково удалены от определенной точки (центра окружности), лежащей в той же плоскости, что и сама кривая.Круг — это часть плоскости, ограниченная окружностью. Радиус окружности — это отрезок, соединяющий центр окружности с какой-либо её точкой.
Полезный совет
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Круг — часть плоскости, ограниченная окружностью. Диаметр всегда проходит через центр окружности. Обычно обозначается D или Ø. Диаметр равен удвоенному радиусу окружности: D = 2R, R = D/2. Отношение длины окружности к её диаметру одинаково для всех окружностей.
Источники:
- как узнать длину окружности
В геометрии периметром называют суммарную длину всех сторон, образующих замкнутую плоскую фигуру. У круга такая сторона всего одна и называют ее окружностью. Поэтому говорить о периметре окружности не совсем правильно — это два названия одного и того же параметра. Правильнее будет назвать эту процедуру вычислением периметра круга или длины окружности.

Инструкция
Чаще всего в задачах требуется вычислить длину окружности (L) по известному радиусу круга (R). Эти два параметра связаны между собой через самую, пожалуй, известную среди населения нашей планеты математическую константу — число Пи. Она и появилась в математике как выражение постоянного соотношения между длиной окружности и диаметром, то есть удвоенным радиусом. Поэтому для решения задачи умножайте радиус на два числа Пи: L = R*2*π.Так как площадь круга (S) может быть выражена через его радиус, формулу из предыдущего шага можно трансформировать для вычисления периметра круга (L) по известной площади. Радиус равен квадратному корню из соотношения между площадью и числом Пи — подставьте это выражение в формулу из предыдущего шага. У вас должна получиться такая формула: L = √(S/π)*2*π. Ее можно немного упростить: L = 2*√(S*π).
Длину окружности в целом можно рассчитать и зная длину какой-нибудь ее части (l) вместе с величиной сопоставленного этой дуге центрального угла (α). Соотношение двух исходных величин равно радиусу круга, если угол выражен в радианах. Подставьте это выражение радиуса в формулу из первого шага, и вы получите такое равенство: L = l/α*2*π.
Если в исходных условиях приведена длина стороны квадрата (А), вписанного в окружность, одного этого значения будет достаточно для нахождения периметра круга. Радиус в этом случае будет равен произведению длины стороны четырехугольника на квадратный корень из двойки. Подставьте это выражение во все ту же формулу из первого шага, чтобы получить такое равенство: L = А*√2*2*π.
Зная ту же величину — длину стороны (А) — квадрата, описанного около окружности, можно получить еще более простую формулу расчета периметра круга (L). Так как в этом случае длина стороны будет совпадать с диаметром, используйте для вычисления такую формулу: L = А*π.
Периметром плоской геометрической фигуры называется суммарная длина всех составляющих ее сторон. У круга такая сторона всего одна, и ее протяженность обычно называют длиной окружности, а не периметром. В зависимости от известных параметров круга вычислять эту величину можно разными способами.

Инструкция
Для измерения периметра круга на местности используйте специальное устройство — курвиметр. Чтобы узнать с его помощью длину окружности, агрегат нужно просто прокатить по ней колесом. Такие же приборы, но гораздо меньших размеров, используются и для определения длины любых кривых линий, включая окружности, на чертежах и картах.Если нужно вычислить длину окружности (L) по известному диаметру (d), умножьте его на число Пи (3,1415926535897932384626433832795…), округлив количество знаков до нужной степени точности: L=d*π. Так как диаметр равен удвоенному радиусу (r), если известна эта величина, добавьте в формулу соответствующий множитель: L=2*r*π.
Зная площадь круга (S), тоже можно вычислить длину окружности (L). Соотношение и этих двух величин выражается через число Пи, поэтому удвойте квадратный корень из произведения площади на эту математическую константу: L = 2*√(S*π).
Если известна площадь (s) не всего круга, а лишь сектора с заданным центральным углом (θ), то при вычислении длины окружности (L) исходите из формулы предыдущего шага. Если угол выражен в градусах, площадь сектора будет составлять θ/360 от общей площади круга, которую можно выразить формулой s*360/θ. Подставьте ее в приведенное выше равенство: L = 2*√((s*360/θ)*π) = 2*√(s*360*π/θ). Однако чаще для измерения центрального угла используют не градусы, а радианы. В этом случае площадь сектора будет составлять θ/(2*π) от общей площади круга, а формула вычисления длины окружности приобретет такой вид: L = 2*√((s*2*π/θ)*π) = 2*√(s*2*π²/θ) = 2*π*√(2*s/θ).Аналогичные пропорции применяйте и при вычислении длины окружности (L) по известным длине дуги (l) и соответствующему ей центральному углу (θ) — в этом случае формулы будут проще. При центральном угле, выраженном в градусах, используйте такое тождество: L = l*360/θ, а если он дан в радианах, формула должна быть такой: L = l*2*π/θ.
Видео по теме
www.kakprosto.ru
Как найти диаметр окружности, если известна длина окружности
Автор КакПросто!
Отрезок, соединяющий две точки окружности и проходящий через ее центр, имеет постоянное соотношение с замкнутой линией, не имеющей самопересечения, все точки которой находятся на одинаковом расстоянии от центра. Это же можно сформулировать проще: диаметр любой окружности примерно в 3 раза меньше ее длины.

Статьи по теме:
Вам понадобится
- Ручка, бумага, таблицы для вычисления длины окружности по диаметру.
Инструкция
Запишите длину окружности, диаметр которой вы намерены определить. Еще много веков назад люди брали для изготовления круглой корзины нужного размера, или диаметра, прутья в три раза более длинные. Позже ученые доказали, что при делении длины каждой окружности на ее диаметр получается одно и то же не натуральное число. Его величина всё время уточнялась, хотя точность расчетов всегда была высока. Например, в Древнем Египте его выражали неправильной дробью 256/8, имеющей отклонение не более одного процента. Вспомните, что впервые математически вычислил это соотношение Архимед. Он построил правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря английскому математику Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр и окружность (периферия). Сегодня компьютер легко вычисляет миллионы знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7 : 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности по диаметру. Эти таблицы включают в разные справочники. Например, они есть в книге «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
www.kakprosto.ru
