Как по точкам найти функцию
Во многих случаях данные статистики или измерений какого-либо процесса бывают представлены в виде набора дискретных значений. Но для того, чтобы на их основе построить непрерывный график, нужно по этим точкам найти функцию. Сделать это можно путем интерполяции. Для этого хорошо подходит полином Лагранжа.Вам понадобится
- — бумага;
- — карандаш.
Инструкция
- Определите степень полинома, который будет использован для интерполирования. Он имеет вид: Кn*Х^n + К(n-1)*Х^(n-1) +… + К0*Х^0. Число n здесь на 1 меньше количества известных точек с различными Х, через которые должна проходить результирующая функция. Поэтому просто пересчитайте точки и отнимите от полученного значения единицу.
- Определите общей вид искомой функции. Поскольку Х^0 = 1, то она примет вид: f(Хn) = Кn*Х^n + К(n-1)*Х^ (n-1) +… + К1*Х + К0, где n — найденное на первом шаге значение степени полинома.
- Начните составление системы линейных алгебраических уравнений с целью нахождения коэффициентов интерполирующего полинома. Исходный набор точек задает ряд соответствий значений координат Хn искомой функции по оси абсцисс и оси ординат f(Хn). Поэтому поочередная подстановка величин Хn в полином, значение которого будет равно f(Хn), позволяет получить нужные уравнения:
Кn*Хn^n + К(n-1)*Хn^ (n-1) +… + К1*Хn + К0 = f(Хn)
Кn*Х(n-1)^n + К(n-1)*Х(n-1)^ (n-1) +… + К1*Х(n-1) + К0 = f(Х(n-1))
…
Кn*Х1n + К(n-1)*Х1^ (n-1) + … + К1*Х1 + К0 = f(Х1). - Представьте систему линейных алгебраических уравнений в удобном для решения виде. Вычислите значения Хn^n… Х1^2 и Х1…Хn, а затем подставьте их в уравнения. При этом значения (также известные) перенесите в левую часть уравнений. Получится система вида:
Сnn*Кn + Сn(n-1)*К(n-1) +… + Сn1*К1 + К0 — Сn = 0
С(n-1)n*Кn + С(n-q)(n-1)*К(n-1) +… + С(n-1)1*К1 + К0 — С(n-1) = 0
…
С1n*Кn + С1(n-1)*К(n-1) +… + С11*К1 + К0 — С1 = 0
Здесь Сnn = Хn^n, а Сn = f(Хn). - Решите систему линейных алгебраических уравнений. Используйте любой известный способ. Например, метод Гаусса или Крамера. В результате решения будут получены значения коэффициентов полинома Кn…К0.
- Найдите функцию по точкам. Подставьте коэффициенты Кn…К0, найденные в предыдущем шаге, в полином Кn*Х^n + К(n-1)*Х^ (n-1) +… + К0*Х^0. Данное выражение и будет являться уравнением функции. Т.е. искомая f(Х) = Кn*Х^n + К(n-1)*Х^ (n-1) +… + К0*Х^0.
completerepair.ru
Онлайн калькулятор: Вычисление значений функции
Данный онлайн калькулятор вычисляет значения функции одной переменной для заданных значений переменной . Функция задается при помощи формулы, в которой могут участвовать математические операции, константы и математические функции. Синтаксис описания формулы см. ниже.
Значения переменной x через запятую, для указания десятичной точки используйте точку.
Точность вычисленияЗнаков после запятой: 1
Сохранить share extension
В формуле допускается использование одной переменной (обозначается как x), числа пи ( pi), следующих математических операторов:
+ — сложение
— — вычитание
* — умножение
/ — деление
^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) — кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
planetcalc.ru
По графику функции найти y по x
В прошлый раз мы находили значение функции по значению аргумента с помощью формулы.
Рассмотрим, как по данному графику функции найти y по x.
Рисунок 1
1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение функции,если значение аргумента равно 1; 3; -3, -1; 0.
Решение:
Аргумент — это x, функция — y.
Найти значение функции по значению аргумента — значит, по данному значению x найти, чему равен y.
Начнём с x=1. На оси абсцисс Ox находим x=1. Чтобы найти соответствующее значение y, надо из точки на Ox идти либо вверх, либо вниз, чтобы попасть на график.
От x=1 идём вверх. От полученной точки на графике надо двигаться либо влево, либо вправо, чтобы попасть на ось Oy. В данном случае идем влево и попадаем с ординатой y=2 (стрелочки помогают увидеть направление движения).
Следовательно, при x=1 y=2.
Аналогично, если x=3, идем вверх до пересечения с графиком, затем влево до пересечения с осью ординат Oy.
Получаем, что при x=3 y=4.
Если x=-3, чтобы попасть на график функции, нужно идти вниз, затем — вправо, до пересечения с осью Oy.
При x=-3 н=-2.
При x=-1 ни вверх, ни вниз двигаться не надо — эта точка уже на графике функции. Следовательно, y=0.
Записываем: при x=-1 y=0.
При x=0 идем до графика вверх и попадаем в точку с ординатой y=2.
2) На рисунке 2 изображен график функции y=f(x).
Пользуясь графиком, найдите значение функции, если значение аргумента равно 1; 3; 5; 7; -1; -5.
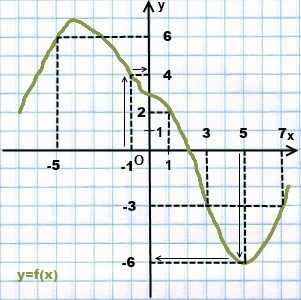
Рисунок 2
Решение:
Чтобы по графику функции найти y по x, сначала надо от точки с данной абсциссой попасть на график, двигаясь вверх либо вниз, а затем от точки на графике идти к оси Oy, двигаясь влево или вправо.
При x=1 идем до графика функции вверх, затем влево — на ось Oy. Попадаем в точку с ординатой y=2.
Пишем: при x=1 y=2.
При x равном -1 и -5 идем сначала вверх, затем — вправо.
При x= -1 y=4.
При x= -5 y=6.
При иксах равных 3; 5 и 7 идём вниз и влево.
При x=3 y= -3.
При x=5 y= -6.
При x=7 y= -3.
Обратите внимание: различным значениям икса может соответствовать одно значение y:
(при x=3 и x=7 y= -3).
www.algebraclass.ru
Как найти график функции?
С задачей построения графика функции школьники сталкиваются в самом начале изучения алгебры и продолжают строить их из года в год. Начиная с графика линейной функции, для построения которой нужно знать всего две точки, к параболе, для которой нужно уже 6 точек, гиперболе и синусоиде. С каждым годом функции становятся все сложнее и построения их графиков уже невозможно выполнить по шаблону, необходимо проводить более сложные исследования, пользуясь производными и пределами.
Давайте разберемся, как найти график функции? Для этого начнем с самых простых функций, графики которых строятся по точкам, а потом рассмотрим план для построения более сложных функций.
Построение графика линейной функции
Для построения простейших графиков используют таблицу значений функции. Графиком линейной функции является прямая. Давайте попробуем найти точки графика функции y=4x+5.
- Для это возьмем два произвольных значения переменной x, подставим их поочередно в функцию, найдем значение переменной y и занесем все в таблицу.
- Возьмем значение x=0 и подставим в функцию вместо x — 0. Получим: y=4*0+5, то есть y=5 запишем это значение в таблицу под 0. Аналогично возьмем x=0 получим y=4*1+5, y=9.
- Теперь, чтобы построить график функции нужно нанести на координатную плоскость эти точки. Затем необходимо провести прямую.
Построение графика квадратичной функции
Квадратичная функция — это функция вида y=ax2+bx +c, где x-переменная, a,b,c — числа (a не равно 0). Например: y=x2, y=x2+5, y=(x-3)2, y=2x2+3x+5.
Для построения простейшей квадратичной функции y=x2 обычно берут 5-7 точек. Возьмем значения для переменной x: -2, -1, 0, 1, 2 и найдем значения y также как и при построении первого графика.
График квадратичной функции называют параболой. После построения графиков функции у учеников появляются новые задачи, связанные с графиком.
Пример 1: найдите абсциссу точки графика функции y=x2, если ордината равна 9. Для решения задачи необходимо в функцию вместо y
elhow.ru
Полное исследование функции и построение графика, примеры решений
Задание. Исследовать функцию $y(x)=\frac{x^{2}-x-1}{x^{2}-2 x}$ и построить ее график.
Решение. 1) Область определения функции.
$D(y) : x^{2}-2 x \neq 0 \Rightarrow x_{1} \neq 0, x_{2} \neq 2 \Rightarrow$
$\Rightarrow x \in(-\infty ; 0) \cup(0 ; 2) \cup(2 ;+\infty)$
2) Четность, нечетность.
$y(-x)=\frac{(-x)^{2}-(-x)-1}{(-x)^{2}-2 \cdot(-x)}=\frac{x^{2}+x+1}{x^{2}+2 x} \neq \left\{\begin{array}{l}{y(x)} \\ {-y(x)}\end{array}\right.$
Функция общего вида.
3) Точки пересечения с осями.
а) с осью $O x : y=0$ :
$\frac{x^{2}-x-1}{x^{2}-2 x}=0 \Rightarrow x^{2}-x-1=0 \Rightarrow$
$\Rightarrow x_{1}=\frac{1+\sqrt{5}}{2}, x_{2}=\frac{1-\sqrt{5}}{2}$
то есть точки $A_{1}\left(\frac{1+\sqrt{5}}{2} ; 0\right), A_{2}\left(\frac{1-\sqrt{5}}{2} ; 0\right)$
б) с осью $O y : x=0$ : в данной точке функция неопределенна.
4) Асимптоты.
а) вертикальные: прямые $x=0$ и $x=2$ — вертикальные асимптоты.
б) горизонтальные асимптоты:
$\lim _{x \rightarrow \infty} \frac{x^{2}-x-1}{x^{2}-2 x}=1$
то есть прямая $y=1$ — горизонтальная асимптота.
в) наклонные асимптоты $y=k x+b$ :
$k=\lim _{x \rightarrow \infty} \frac{x^{2}-x-1}{x\left(x^{2}-2 x\right)}=0$
Таким образом, наклонных асимптот нет.
5) Критические точки функции, интервалы возрастания, убывания.
$y^{\prime}=\left(\frac{x^{2}-x-1}{x^{2}-2 x}\right)^{\prime}=\frac{(2 x-1)\left(x^{2}-2 x\right)-\left(x^{2}-x-1\right)(2 x-2)}{\left(x^{2}-2 x\right)^{2}}=$
$=\frac{2 x^{3}-4 x^{2}-x^{2}+2 x-\left(2 x^{3}-2 x^{2}-2 x^{2}+2 x-2 x+2\right)}{\left(x^{2}-2 x\right)^{2}}=$
$=\frac{2 x^{3}-5 x^{2}+2 x-2 x^{3}+4 x^{2}-2}{\left(x^{2}-2 x\right)^{2}}=\frac{-x^{2}+2 x-2}{\left(x^{2}-2 x\right)^{2}}$
Найдем точки, в которых первая производная равна нулю или не существует: $y^{\prime} \neq 0$ для любого $x$ из области определения функции; $y^{\prime}$ не существует при $x_{1}=0$ и $x_{2}=2$ .
Таким образом, функция убывает на всей области существования. Точек экстремума нет.
6) Точки перегиба, интервалы выпуклости, вогнутости.
$y^{\prime \prime}=\left(y^{\prime}\right)^{\prime}=\left(\frac{-x^{2}+2 x-2}{\left(x^{2}-2 x\right)^{2}}\right)^{\prime}=$
$=\frac{(-2 x+2)\left(x^{2}-2 x\right)^{2}-\left(-x^{2}+2 x-2\right) \cdot 2\left(x^{2}-2 x\right)(2 x-2)}{\left(x^{2}-2 x\right)^{4}}=$
$=\frac{(-2 x+2)\left(x^{2}-2 x\right)-\left(-x^{2}+2 x-2\right) \cdot 2(2 x-2)}{\left(x^{2}-2 x\right)^{3}}=$
$=\frac{-2 x^{3}+6 x^{2}-4 x+4 x^{3}-12 x^{2}+16 x-8}{\left(x^{2}-2 x\right)^{3}}=$
$=\frac{2 x^{3}-6 x^{2}+12 x-8}{\left(x^{2}-2 x\right)^{3}}$
Найдем точки, в которых вторая производная равна нулю или не существует: $y^{\prime \prime}=0 : x=1$ ; при $x=0$ и $x=2$ вторая производная не существует.
Таким образом, на промежутках $(0 ; 1)$ и $(2 ;+\infty)$ функция вогнута, а на промежутках $(-\infty ; 0)$ и $(1 ; 2)$ — выпукла. Так как при переходе через точку $x=1$ вторая производная поменяла знак, то эта точка является точкой перегиба.
7) Эскиз графика.
www.webmath.ru
