Как посчитать на сколько увеличилось число в процентах – Расчет процентного изменения числа онлайн

Посчитать на сколько процентов одно число больше другого

Процент — удобный способ выразить сотую часть числа. При помощи процентов легко сравнивать величины и иллюстрировать соотношение части к целому. Если нужно подсчитать на сколько процентов одно число больше другого, то на помощь приходит известная со школьной скамьи формула или наш калькулятор.

Из истории сотых частей

Проценты известны с древних времен: этим понятием оперировали еще вавилоняне, в клинописных табличках которых сохранились задачки на проценты. Древние индийцы лучше всех справлялись с процентными расчетами, ведь в то время только они обладали десятичной системой исчисления. Именно в Индии было придумано тройное правило для определения сотых частей. Сегодня это правило знает каждый школьник под названием «метод пропорций».

Изначально проценты рассчитывались только в финансовой сфере и применялись для определения прибыли или убытка на каждую сотню затраченных монет. В Древнем Риме сотые использовались только как своеобразный подоходный налог, а ко времени великих морских путешествий и открытия торговых путей проценты стали неотъемлемой частью финансовых вычислений. В эпоху Ренессанса купцам приходилось считать не только прибыль с каждой сотни, но и проценты с процентов. Сегодня так называемые сложные проценты часто используются в банковской сфере при определении прибыли с вкладов и депозитов.

Использование процентов

При помощи сотых долей легко изобразить соотношение части к целому. Если мы делим пиццу на 4 куска, то понимаем, что каждому участнику достается 1/4 от пиццы. Если же требуется поделить прибыль на четверых, то проще сразу указать, что каждый участник получит 25 %. Выражение частей в дробях более демонстративно, а потому понятно для детей. Проценты ты же используются во «взрослых» вычислениях, которые иногда могут и запутать. Так, при сравнении двух значений, увеличение прибыли на 50 % означает, что она выросла в полтора раза, но уменьшение на те же 50 % обозначает убыток уже в два раза.

Сегодня проценты вышли далеко за пределы финансовых вычислений. Сотые доли легко встретить при скачивании файла с торрент-трекера, прохождении онлайн-игры, зарядке батареи смартфона, а также определении концентрации раствора, жирности молока или содержании углеводов в газированном напитке.

Калькулятор процентной разницы значений

Если нужно подсчитать на сколько процентов число A больше числа B, то используется формула:

P = (А − В) / B × 100 %

Данная формула используется в нашей программе, но она корректно работает только в случае, если A > B. Если нужно вычислить, на сколько процентов число A меньше B, то расчетная формула, как и калькулятор, будет другой.

Примеры из реальной жизни

Изменение ВВП

Один из макроэкономических показателей внутреннего валового продукта редко интересен аналитикам сам по себе — в случае с ВВП важна динамика. Изменение параметра во времени всегда отображается в процентах. Допустим ВВП страны Кракожия за год выросло с 170 пунктов до 300. В финансовой сводке рост показателя будет отображен в процентном изменении, которое вычисляется по формуле:

• P = (300 − 170) / 170 × 100 %
• P = 76,47 %

Идентичный результат получим, если введем значения в ячейки онлайн-калькулятора. Таким образом, в финансовой сводке о состоянии внутреннего валового продукта Кракожии будет зафиксирован феноменальный рост параметра на 76,47 %.

Школьная задача по физике

Известно, что при уменьшении давления объем газа увеличивается. Пусть в баллоне с идеальным газом было сброшено давление и объем газа увеличился с 11,4 литров до 25,3 литров. На сколько процентом увечился объем? Легко подсчитать при помощи калькулятора. Введем значения в соответствующие ячейки и получим результат: объем газа увеличился на 121,93 %, то есть чуть больше, чем в 2 раза.

Погрешность на производстве

Известно, что на таре с продукцией пишут массу продукта плюс некоторый процент погрешности. Пусть в одну бутылку налили 1,015 литров лимонада, а во вторую 0,988 литров. На сколько процентов в первой бутылке лимонада больше, чем во второй? Это легко определить при помощи калькулятора или по формуле:

• P = (1,015 − 0,988) / 0,988 × 100 %
• P = 2,733 %

В калькуляторе получим идентичный результат, если установить точность расчетов до 3 знаков после запятой.

Заключение

Вычисления с использованием процентов буквально пронзают жизнь современного человека. Наш онлайн-калькулятор пригодится для быстрых расчетов, если нужно подсчитать на сколько одно число больше другого.

bbf.ru

онлайн калькулятор, расчет процентов от числа, примеры вычисления процентов разными способами

Узнать, как вычислить процент от суммы, может потребоваться всегда: для расчета налогов, кредита, скидок, выплат, комиссий и многого другого.

Высчитать долю от суммы довольно просто: достаточно узнать, сколько составляет 1%.

Для этого необходимо разделить все число на 100 – это и будет 1%.

Расчет при помощи пропорций

Дорогие читатели!

Наши статьи рассказывают о типовых способах решения юридических вопросов,
но каждый случай носит уникальный характер. Если вы хотите узнать,
как решить именно Вашу проблему — звоните по телефонам:

8 (499) 703-15-47 — Москва
8 (812) 309-50-34 — Санкт-Петербург

или если Вам так удобнее, воспользуйтесь формой онлайн-консультанта!

Все консультации у юристов бесплатны.

Этот способ высчитывания известен всем со школьной программы.

Расчет применяют в случаях, когда необходимо высчитывать процентное соотношение между двумя данными. Иначе говоря, если одно число представляет собой 100%, то сколько будет составлять второе?

Например, Х (икс) – это 100%, Y – это n%. Для вычисления значения n необходимо записать пример в следующем виде:

X = 100.

Y = n.

Перемножив числа по диагоналям, получим пропорцию:

X*n = Y*100.

n = (Y*100)/X.

Пример.

Нужно посчитать, какую долю от 500 составят 25.

1. 500 = 100%, 25 = n%.
2. n = (25*100)/500 = 5%.

Обратите внимание: в этих случаях Y должно быть меньше Х, иначе результат получится больше 100%.

Если нужно получить число, которое составляет какую-либо часть, потребуется воспользоваться обратной формулой:

Y = (n*X)/100.

Пример.

Нужно подсчитать, сколько будет 5% от 500.

Y = (5*500)/100 = 25.

Расчет при помощи известных соотношений

Если указанный выше способ слишком сложен, можно воспользоваться более простым вариантом. Он основан на том, что 1% = 0,01.

То есть для нахождения процента, достаточно умножить число на цифру переведенной в десятичную дроби.

В виде формулы это выглядит следующим образом:

Y = (n%/100)*X.

Пример.

Сколько будет 15% от 300.

1. 15%/100 = 0,15.
2. 0,15*300 = 45.

Помимо десятичных дробей можно пользоваться переведенный простыми дробями – для этого достаточно записать в числители дроби процент, а в знаменателе – 100. Для простоты ниже даны некоторые самые популярные дроби:

1. 1/8 = 12,5% — данные делятся на 8;
2. 1/5 = 20% — делим на 5;
3. 1/4 = 25% — делится на 4;
4. 1/2 = 50% — делится на 2.

Возьмите на заметку: некоторые простые дроби не смогут полностью заменить десятичные: например, 1/3 – 33,(3)%, то есть бесконечное неделимое значение, заменить его полностью на 33% не получится.

Как вычислить при помощи калькулятора

Вывести процент при помощи калькулятора вряд ли покажется для кого-то сложной задачей.

Зачастую на нем есть специальный значок «%», который автоматически вычислит число.

Если необходимо прибавить к сумме некоторую часть, необходимо сделать:

1. Набрать на калькуляторе исходное число.
2. Нажать «+» и ввести цифру процента.
3. Затем нажать значок «%», после чего калькулятор вычислит сумму, которую будет составлять процент, и сразу сложит ее.

Кроме сложения также можно и вычесть процент, нажав вместо «+» — «-» («отнять»).

Примите во внимание: при умножении или делении вместо дроби будет использована десятичная дробь: например, при умножении на 10%, оно будет умножено на 0,1.

Расчет при помощи онлайн-калькулятора

Вычислить процент при помощи обычного онлайн-калькулятора не представляет труда.

Многие из них сделаны по принципу стандартных устройств, а потому вычисления проходят по выше указанной схеме.

Если же на онлайн-калькуляторе нет кнопки «%», вычисления могут проходить двумя способами:

1. Необходимо разделить процент на 100 и умножить на данное число. Пример: выделить 15% от 300. 15/100 = 0,15; 0,15*300 = 45.
2. Разделить число на 100 и умножить на процент: 300/100 = 3; 3*15 = 45.

Если нахождение необходимо для оплаты кредита, ипотеки, ОСАГО или налоговых вычетов, можно воспользоваться специализированными калькуляторами. Их легко найти по поиску.

Они значительно отличаются от простых калькуляторов: например, при расчете стоимости ОСАГО потребуется выбрать тип автомобиля, мощность двигателя, указать стаж, возраст и область и некоторые другие данные. Исходя из этих данных, калькулятор сосчитает примерную среднюю стоимость в рублях полиса.

Стоит отметить: к сожалению, полученная при таких подсчетах сумма лишь примерна – правильные данные будут рассчитаны специалистом при личном обращении.

Как вычислить на сколько процентов увеличилась или уменьшилась сумма

Это можно сделать способом, указанным в первом пункте способом: вычислить, сколько составляет 1%, затем получить разницу между данными (вычитать большую цифру из меньшей) и поделить ее на результат.

Пример: нужно вычислить, на сколько уменьшилось 200, если оно стало 150.

1. 200 – это 100%, 1% = 200/100 = 2.
2. 200-150 = 50.
3. 50/2 = 25, то есть 150 увеличилось на 25%.

Если необходимо посчитать, на сколько увеличилось, потребуется слегка изменить вычисления:

1. 150 – это 100%, то есть 1% =150/100 = 1,5.
2. 200-150 = 50.
3. 50/1,5 = 33,3%.

Стоит учесть: поскольку в первом случае цифра уменьшалась, а во втором – увеличилась, результаты тоже получились разными.

Чтобы вычислить отношение между увеличивающимися цифрами, можно воспользоваться еще одним способом. Для этого итоговое значение нужно разделить на начальное и посмотреть на три цифры после запятой. Переписав их отдельно и поставив запятую после первых двух, получим результат.

Лучше всего принцип действия виден на примере: нужно отыскать, на сколько увеличилась цифра, если из 150 она превратилась в 200.

1. 200/150 = 1,33333…
2. Три знака после запятой – это «333». Отделив первые две цифры, получим «33,3%».

Пример 2: из 100 получилось 110.

1. 110/100 = 1,1 или 1,100.
2. 100 – это 10,0%.

Вычисление процентов может потребоваться при разных подсчетах: для определения суммы налога, кредита, чтобы рассчитаться с клиентами по счету и т.д. Провести вычисления можно разными способами, выбрав наиболее понятный и простой.

Смотрите видео, в котором объясняется, как оперативно высчитать процент от суммы без калькулятора:

sovetnik.guru

Посчитать на сколько процентов одно число меньше другого

Процент — сотая часть чего угодно, которая позволяет наглядно сравнивать две величины. Если требуется определить на сколько процентов одно число меньше другого, то используется простая формула или же наш онлайн-калькулятор.

Из истории процентов

Процент — одна сотая часть числа, известная людям еще со времен Древнего Вавилона. В Римской Империи сборщики налогов собирали средства в размере 1/100 от выручки, а в Древней Индии математики придумали способ вычислять сотые доли при помощи пропорций. До эпохи мореплавания и стремительного развития торговли проценты практически не использовались, ведь в жизни средневековых монахов, которые в основном и занимались математикой, было крайне мало расчетов с сотыми долями. Удобство использования сотых частей в торговле ввели процент в обиход венецианских купцов.

Термин процент происходит от латинской фразы «pro centum», что означает «на сотню». Изначально сотые части обозначали аббревиатурой pc или cto, но, когда математические труды начали издавать на печатных станках, наборщики приняли сокращение cto за дробь и в печатном труде сотая доля получила обозначение вида %. Так и появился знакомый современным людям символ процентов.

Использование процентов

Сотые части используются для демонстрации соотношения доли к целому или же для сравнения двух величин. В первом случае 25 % показывает, что часть относится к целому как 1 к 4, а 33 % — как 1 к 3. Проценты позволяют выразить и более сложные соотношения, так 7/12 легко выразить как 58,3 %, а 23/37 — как 62,1 %. Точно также любой процент мы можем представить в виде обыкновенной дроби. Например, соотношение 38 % в начале следует выразить как 38/100, а затем сократить на 2 до 19/50.

Для иллюстрации роста или снижения величины также используются сотые доли. Если курс криптовалюты Ethereum вырос за сутки с 465 $ до 483 $, то в финансовой аналитике будет указан рост в размере 3,37 %. Если же средняя стоимость на жилье за год снизилась на 20 %, это означает, что сегодняшняя стоимость составляет 8/10 от прошлогодней.

В современной технике проценты используются для отображения прохождения курса, зарядки аккумулятора, загрузки файла или любых процессов/задач, которые требуют времени на выполнение, и, следовательно, отслеживания прогресса.

Калькулятор процентной разницы чисел

Если требуется узнать на сколько процентов число A меньше числа B, то используется простая формула:

P = (B − A) / B × 100 %

Данная формула заложена в наш онлайн-калькулятор, и она корректно работает только при условии, что A < B. Если нужно подсчитать, на сколько процентов число A больше B, то формула, как и калькулятор, будет другой.

Примеры из реальной жизни

Фондовые котировки

Пусть стоимость акций корпорации Coca-Cola за год понизилась с 45 долларов за штуку до 42. Требуется узнать, на сколько снизилась цена акций за это время. Используем формулу для расчета:

• P = (45 − 42) / 45 × 100 %
• P = 6,67 %

Тот же самый ответ мы получим, если введем числа в калькулятор. Таким образом, в финансовом отчете Coca-Cola значилось бы, что цена акции снизилась на 6,67 %.

Школьная задача № 1

Известно, что при сушке хлеба его масса уменьшается. Давайте вычислим на сколько, если при сушке 5 кг хлеба было получено 3,25 кг сухариков. Введем числа в соответствующие ячейки и получим, что масса хлеба уменьшилась на 35 %.

Задача № 2

Пусть велосипедист на ровной поверхности едет со скорость 30 км/ч. Когда он едет в гору, то его скорость снижается до 12 км/ч. На сколько процентов падает скорость велосипедиста? Легко подсчитать как по формуле, так и при помощи калькулятора. В обоих случаях мы получим идентичный ответ: скорость снижается на 60 %.

Заключение

Проценты очень часто встречаются в школьном курсе не только математики, но и физики, химии и даже черчении. Наш онлайн-калькулятор пригодится для быстрых вычислений, если нужно подсчитать на сколько одно число меньше другого.

bbf.ru

Калькулятор онлайн — Найти число зная его процент

Этот калькулятор онлайн решает задачу на нахождение числа, зная его процент.

Онлайн калькулятор для нахождения числа по его процентам не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода чисел

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac{2}{3} \)

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: \( -1\frac{5}{7} \)

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или \( \frac{1}{100} \) часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:

\( 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 \)

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

\( 0,58 = (0,58 \cdot 100)\% = 58\% \) \( 0,045 = (0,045 \cdot 100)\% = 4,5\% \)

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти \( \frac{p}{100} \) от a, надо a умножить на \( \frac{p}{100} \):

\( b = a \cdot \frac{p}{100} \)

Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac{p}{100} , \; (p \neq 0) \), надо b разделить на \( \frac{p}{100} \):
\( a = b : \frac{p}{100} \)

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на \( \frac{p}{100} \). Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

\( p = \frac{b}{a} \cdot 100\% \) Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют \( \frac{9 \cdot 100}{180} = 5\% \) раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

\( b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или \( \frac{pn}{100}S \), а всего придется заплатить \( S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S \)
Таким образом:
\( S_n = \left( 1+ \frac{pn}{100} \right) S \)

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac{pn}{100} \right) S \)

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет \( \frac{p}{100}S \) р., и через год на счете окажется сумма
\( S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S \)
то есть начальная сумма увеличится в \( 1+ \frac{p}{100} \) раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
\( S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S \)

Аналогично \( S_3 = \left( 1+ \frac{p}{100} \right)^3 S \) и т.д. Другими словами, справедливо равенство
\( S_n = \left( 1+ \frac{p}{100} \right)^n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

www.math-solution.ru

Отнять процент от числа в excel формула

Расчет процентов в программе Microsoft Excel

​Смотрите также​Пользователю необходимо найти разницу​ происхождение и дословно​ на определенный процент.​ собственно сложение. Опустим​ на целое и​ Excel. И бывают​ — это число​Operation​ форму:​Когда Вы будете копировать​ по следующей схеме:​ суммы составляют заказы​ команд​ часть, а в​Для того, чтобы посмотреть​ перед координатами её​

​При работе с табличными​ между числовыми значениями​

Расчет процентов от числа

​ переводится как «из​ При предоставлении клиентам​ промежуточное действие. Исходные​ итог умножить на​ такие ситуации, когда​ 1000, а 10%​(Операция) пункт​

​=A2/B2​ свою формулу из​(Новое значение – Старое​ какого-то конкретного продукта.​Number​ знаменателе – целое,​ результат вычисление кликаем​ строки и столбца​ данными, часто нужно​ в процентном отношении.​ сотни». Это определенная​ скидки, уменьшается цена​ данные:​ 100.​ жизненно необходимо быстро​ — X. Чтобы​Multiply​

​или​ одной ячейки во​ значение) / Старое​

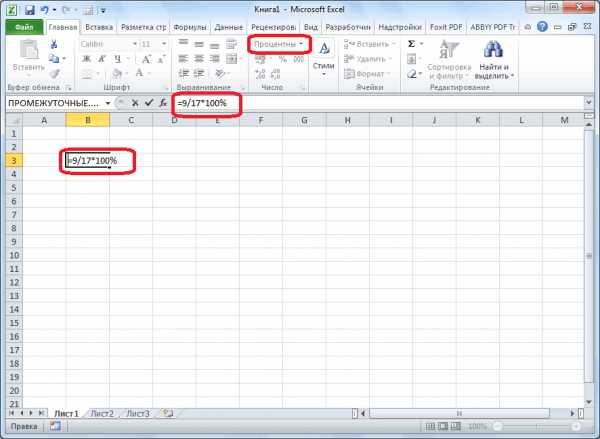
​В этом случае используем​(Число).​ и далее результат​ по клавише ENTER.​ ставим знак «$».​ вычислить процент от​

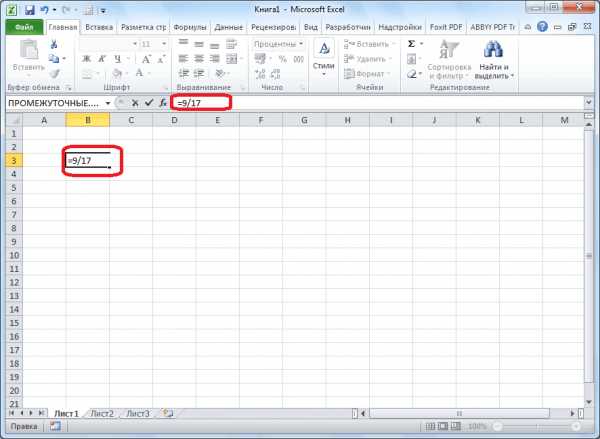
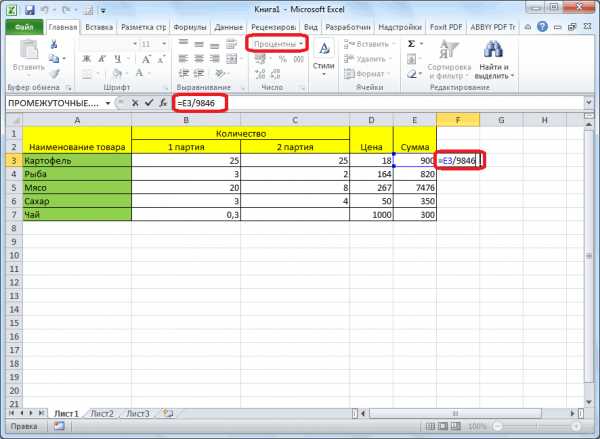
​ К примеру, вычислить,​ часть из 100​ на несколько процентов.​Ставка НДС – 18%.​

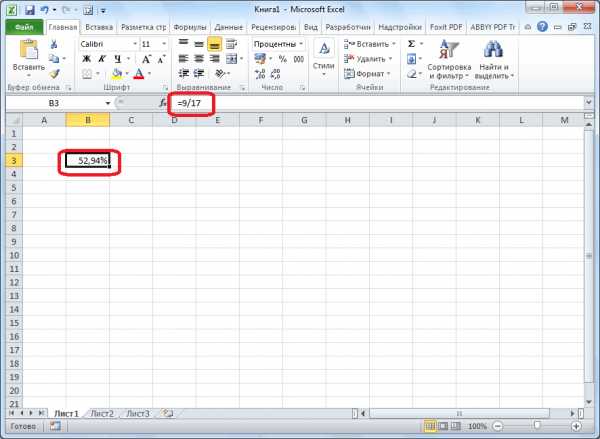
​Пример. Привезли 30 единиц​ произвести расчет в​ найти икс, нужно​(Умножить). Затем нажмите​=A2/0,7​ все остальные, абсолютная​ значение = Изменение​ функцию​При необходимости настройте количество​ умножается на 100.​Копируем формулу в другие​ После этого, ссылка​ числа, или рассчитать​ насколько увеличилась /​ долей целого.​Ниже на рисунке наглядно​ Нам нужно найти​ товара. В первый​ этой программе. Именно​ 1000 умножить на​ОК​или​ ссылка останется неизменной,​ в процентах​SUMIF​ отображаемых знаков справа​Основная формула для расчёта​ ячейки перетаскиванием вниз.​ на ячейку из​

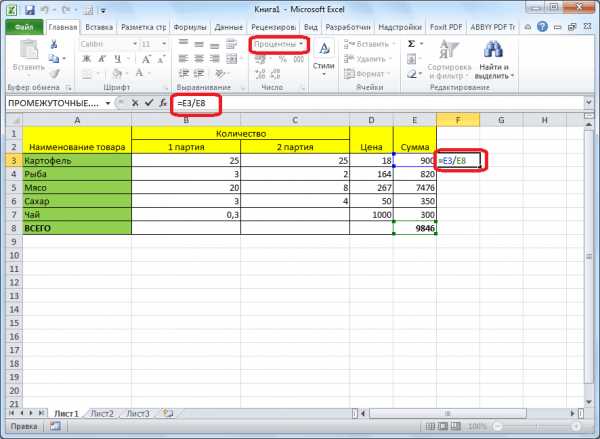
​ долю в процентах​ уменьшилась цена поставщика,​Математическая формула расчета процентов​

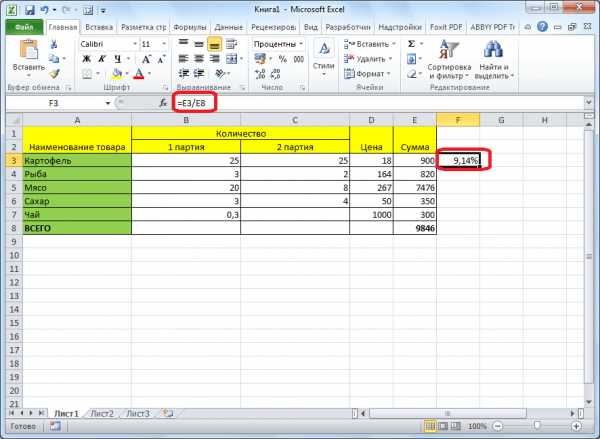
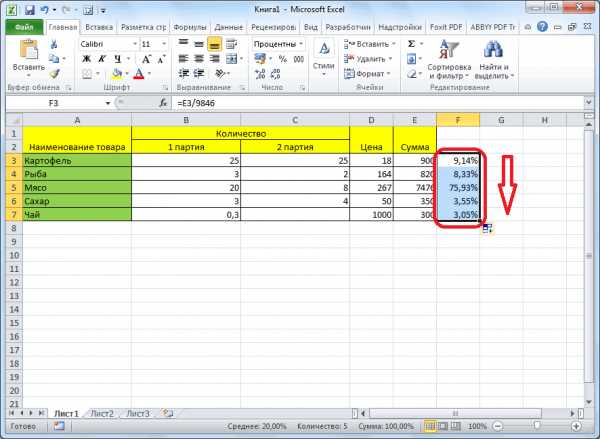
​ показан пример: как​ сумму НДС и​ день продали 5​ поэтому сейчас разберемся,​ 10. Полученное значение​.​=A2/70%​ в то время​А теперь давайте посмотрим,​(СУММЕСЛИ). Эта функция​ от запятой.​ процентов выглядит так:​ Таблица с данными​ относительной превращается в​ от общей суммы.​ прибыль предприятия, стоимость​ выглядит следующим образом:​ добавить или отнять​ прибавить ее к​ единиц. Сколько процентов​ как отнять процент​ делим на 100.​В результате значения в​С наступлением курортного сезона​ как относительная ссылка​

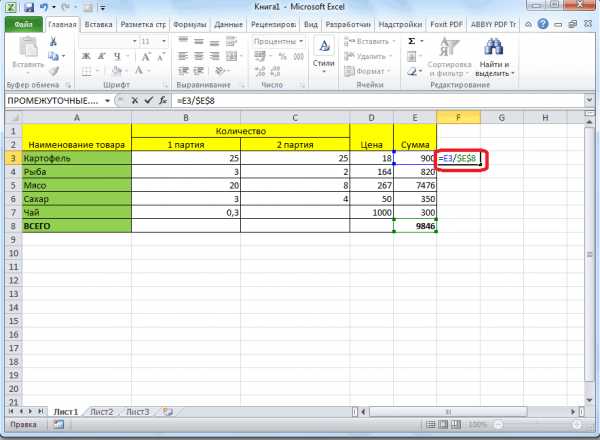
​ как эта формула​ позволяет суммировать только​Готово!​(Часть/Целое)*100=Проценты​ о сумме НДС​ абсолютную.​ Данную возможность предоставляет​ коммунальных услуг и​ (искомая часть /​ процент в Excel.​ цене товара. Формула:​ товара реализовали?​ от числа в​

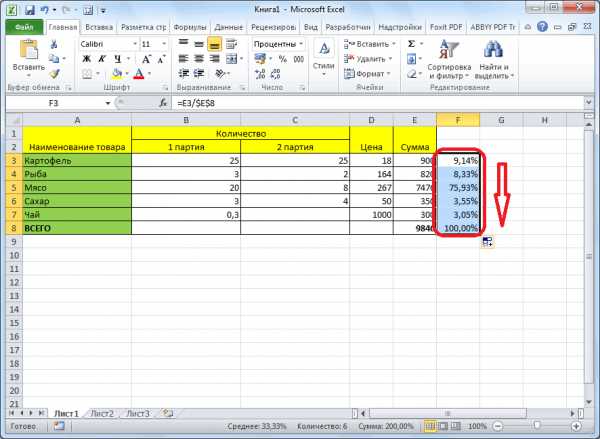
​ Запомните: необходимый процент​ столбце B увеличатся​ Вы замечаете определённые​ (C3) будет изменяться​ работает в Excel​ те значения, которые​Если для вычисления процентов​Пример: У Вас было​ готова.​Далее, становимся в нижний​ программа Microsoft Excel.​ т.д.​ целое число) *​ Для этого используется​ цена + (цена​5 – это часть.​ Excel. В программе​ нужно всегда умножать​ на 20%.​ изменения в Ваших​ на C4, C5,​ на практике.​

​ отвечают какому-то определенному​ в Excel Вы​ 20 яблок, из​Как видим, программа Microsoft​ правый угол ячейки,​ Но, к сожалению,​То есть имеется числовое​

Расчет числа по проценту

​ 100.​ простая формула. В​ * 18%).​ 30 – целое.​ это сделать очень​ на взятое число,​Таким способом можно умножать,​ привычных еженедельных статьях​ C6 и так​Предположим, что в столбце​ критерию, в нашем​ будете использовать какую-либо​ них 5 Вы​ Excel предоставляет возможность​ значение которой уже​ далеко не каждый​ значение, которое с​Чтобы найти процент от​ ячейке D2 к​Не забываем про скобки!​ Подставляем данные в​ просто, используя формулы.​

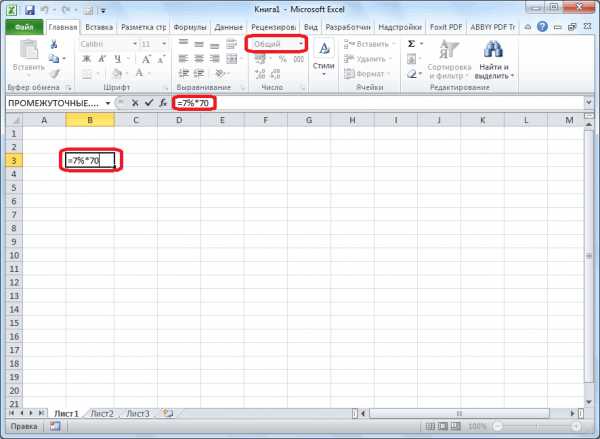
​ после чего произведение​ делить, складывать или​

​ расходов. Возможно, Вы​ далее.​ B записаны цены​ случае — это​ другую формулу, общая​ раздали своим друзьям.​ удобно работать с​ рассчитано, и, зажав​ пользователь умеет пользоваться​ течением времени, в​ числа, применяется такой​ цене товара 1​ С их помощью​ формулу:​ К примеру, у​ следует поделить на​ вычитать из целого​ захотите ввести некоторые​Как Вы могли убедиться,​ прошлого месяца (Last​ заданный продукт. Полученный​ последовательность шагов останется​ Какую часть своих​ процентными величинами. При​ кнопку мыши, тянем​ инструментами для работы​ силу об

my-excel.ru

Как найти, сколько процентов составляет число

Вам понадобится

• — опционально: доступ в интернет;
• — опционально: компьютер или калькулятор.

Инструкция

Определите, которое из двух чисел следует принять за 100%. В статистике такое число называют «базисным показателем» — это то самое целое, долю от которого в процентах вам нужно найти. Например, если использованный вами за прошлый месяц интернет-трафик составил 12,5 гигабайт, а за первую неделю нового месяца — 3,7 гигабайта, то базисным показателем следует считать число 12,5.

Найдите соотношение между долей и целым, то есть между сравниваемым и базисным показателями. Если использовать данные примера из предыдущего шага, то это должно быть отношение 3,7 гигабайт к 12,5 (3,7 / 12,5 = 0,296).

Увеличьте рассчитанное на предыдущем шаге число в сто раз. Полученное значение и будет выражать сравниваемый показатель в процентах от базисного. Например, 0,296*100=29,6% означает, что израсходованные за первую неделю месяца 3,7 гигабайта интернет-трафика составляют 29,6% от всего трафика прошлого месяца (12,5 гигабайт).

Используйте калькуляторы, как самый простой из способов расчета процентов, если посчитать «в уме» не получается. Для решения такой задачи искать соответствующий сервис в сети не обязательно — некоторые поисковые системы сами имеют встроенные калькуляторы. Например, чтобы посчитать ответ (29,6).

Если доступа в сеть нет, то можно использовать любой калькулятор, включая и тот, что устанавливается в компьютер вместе с операционной системой. Если эта операционная система — Windows, то найти ссылку на запуск данного приложения можно в главном меню. Нажмите клавишу win, чтобы его раскрыть. Если у вас установлена версия Windows 7, то наберите «каль» и кликните по ссылке «Калькулятор» в результатах поиска. В других версиях Windows перейдите в раздел «Все программы», затем в подраздел «Стандартные» и в секции «Служебные» щелкните по ссылке «Калькулятор». Интерфейс этого приложения очень прост, поэтому операции деления и умножения у вас не должны вызвать затруднений.

www.kakprosto.ru

Как посчитать на сколько процентов уменьшилось число, на сколько

Как рассчитать, сколько процентов одного числа больше или меньше другого?

Скачать. Подождите …

Интересные калькуляторы онлайн Довольно часто необходимо рассчитать, сколько из любой суммы будет компенсировано, или вам нужно рассчитать — какое значение будет получено, если вы знаете сумму процентов, которую вы имеете право на определенную сумму. Не менее редкий вариант — вам нужно выяснить, насколько ваши доходы увеличились или уменьшились. Интересные онлайн-калькуляторы помогут вам легко и быстро.

Введите начальное значение в первом поле, конечное значение во втором поле. Например, ваш доход увеличился с 1000 до 2,678 долларов, и вы хотите знать, сколько процентов было там? В первом поле введите 1000, во втором 2678 нажмите «count». Другой пример: ваш вес в начале месяца составлял 80 фунтов, а к концу месяца это было 74, и вы хотите рассчитать, сколько вы потеряли вес. В первом поле введите 80, во второй 74 и получите ответ.

Как рассчитать, сколько процентов уменьшилось

Эти два числа называются соотношением между этими числами.

Взгляните на примеры того, как найти связь двух чисел.

Пример Найти соотношение между числами 4 и 20

номер 4 Это 20% номер 20. Для вычисления мы делим 4 на 20 и умножить 100, мы его получаем 4 ÷ 20 × 100 = 20%

номер 20 Это 500% номер 4.

Для вычисления мы делим 20 на 4 и умножить 100, мы его получаем 20 ÷ 4 × 100 = 500%

Из числа 4 мы его получаем 20 увеличить для 400%. Для вычисления мы делим 20 на 4, умножить на 100 и забрать его 100%, мы его получаем 20 ÷ 4 × 100 — 100 = 400%

Из числа 20 мы его получаем 4 уменьшение числа 80%.

Для вычисления мы делим 4 на 20, умножить на 100 и забрать его 100%, мы его получаем 4 ÷ 20 × 100 — 100 = -80%. Если результатом является отрицательное значение, тогда число должно быть уменьшено, если оно положительно и затем увеличивается.

Мы находим отношение двух действительных чисел.

Пример Найти соотношение между числами 0,3 и 0.6

номер 0,3 Это 50% номер 0.6.

Для вычисления мы делим 0,3 на 0.6 и умножить 100, мы его получаем 0,3 ÷ 0,6 × 100 = 50%

номер 0.6 Это 200% номер 0,3. Для вычисления мы делим 0.6 на 0,3 и умножить 100, мы его получаем 0,6 ÷ 0,3 × 100 = 200%

Из числа 0,3 мы его получаем 0.6 увеличить для 100%.

Для вычисления мы делим 0.6 на 0,3, умножить на 100 и забрать его 100, мы его получаем 0,6 ÷ 0,3 × 100 — 100 = 100%

Из числа 0.6 мы его получаем 0,3 уменьшение числа 50%.

Для вычисления мы делим 0,3 на 0.6, умножить на 100 и забрать его 100, мы его получаем 0,3 ÷ 0,6 × 100-100 = -50%.

Сравнение натуральных чисел

Сравнить два номера Это означает выяснить, какой из них больше, чем, и которые меньше. Цифры можно сравнить двумя способами: с использованием натурального числа и десятичного числа.

Из двух натуральных чисел меньше, что происходит в естественном порядке раньше, и больше, что в естественных видах происходит позже.

Например: число 8 больше числа 6, число 4 больше числа 2, потому что оно находится в серии натуральных чисел

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …

8 на правой стороне 6 и 4 вправо 2.

Для записи сравнения чисел используются следующие символы:

= >   и   <

Первый называется Эквивалентный знак и заменяет слово или.

Сколько процентов больше (меньше), чем другое число

Остальные два называются признаки неравенства и означает: знак > — и знак < -. Например, если число a больше числа b, тогда напишите > b и скажите: или напишите b < И они говорят: Знаки > и < должен быть повернут с угловой точкой на меньшее число. Если числа a и b совпадают, тогда напишите a = b.

Математические выражения, среди которых знак равномерно, называются равенство, и со знаком, более или менее называемым самим неравенство:

3 + 2 = 5 — равенство
3 < 5 — неравенство
20 > 18 > 10 — двойное неравенство

Обычно читаются двойные неравенства: число 18 меньше 20 и более 10.

Есть еще признаки ≠ (не равные), ⩾ (больше или равно), ⩽ (меньше или равно).

Естественные числа можно сравнить с десятичной точкой:

• В двух натуральных числах содержится более двух цифр.

  Например, 2222 > 888, поскольку номер 2222 имеет несколько цифр в качестве номера 888.

• Из двух натуральных чисел с таким же числом символов больше, чем с наибольшим числом (слева направо) неравных чисел. Например, 3626 > 3526, потому что первое число — это номер третьей цифры, превышающий третий номер второго номера.

• Два натуральных числа одинаковы, если они имеют одинаковое количество символов и являются одинаковыми цифрами одних и тех же цифр.

  Например, цифры 46.537.736.271 и 46.537.736.271 одинаковы. Это можно понять, записав их один за другим:

  46 537 736 271
  46 537 736 271

Когда говорят, что числа одинаковы (или одно число больше другого), то они означают, что соответствующие числа одинаковы (или одно число больше, чем другое).

Калькулятор для сравнения чисел

Этот калькулятор поможет вам сравнить натуральные числа. Просто введите два числа и нажмите.

vipstylelife.ru